(苏科版2024)七年级上册 2.1.2 正数与负数:有理数的概念与分类 同步课件 (共37张PPT)
文档属性
| 名称 | (苏科版2024)七年级上册 2.1.2 正数与负数:有理数的概念与分类 同步课件 (共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 46.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 14:10:22 | ||
图片预览









文档简介
(共37张PPT)
第2章 有理数
2.1.2正数与负数:有理数的概念与分类
教学目标
能对整数与分数按正负性进行分类,理解小数与分数之间的关系
理解有理数的概念,掌握有理数的两种分类
01
02
掌握“六非”问题的解决策略
03
整数与分数的分类
既然有了正负数之分,那么整数与分数就可以进一步分类
整数
01
课堂引入
正整数
0
负整数
分数
正分数
负分数
02
知识精讲
正整数
负整数
6,210
-7,-43
1.如图,把-,6,-6.5,0,-,3,-7,210,0.0,-43,-5%,π填入相应的圈内
整数
0
思考——正整数与自然数有何关联?
【总结】自然数包括0和正整数
正整数:1,2,3,4,……
自然数:0,1,2,3,4,……
02
知识精讲
整数
正整数
0
负整数
自然数
【思维拓展】自然数与正整数一样多吗?(不作要求)
02
知识精讲
2.如图,把-,6,-6.5,0,-,3,-7,210,0.0,-43,-5%,π填入相应的圈内
分数
负分数
正分数
-,-6.5,
-,-5%
3,
0.0,π是否放入正分数?
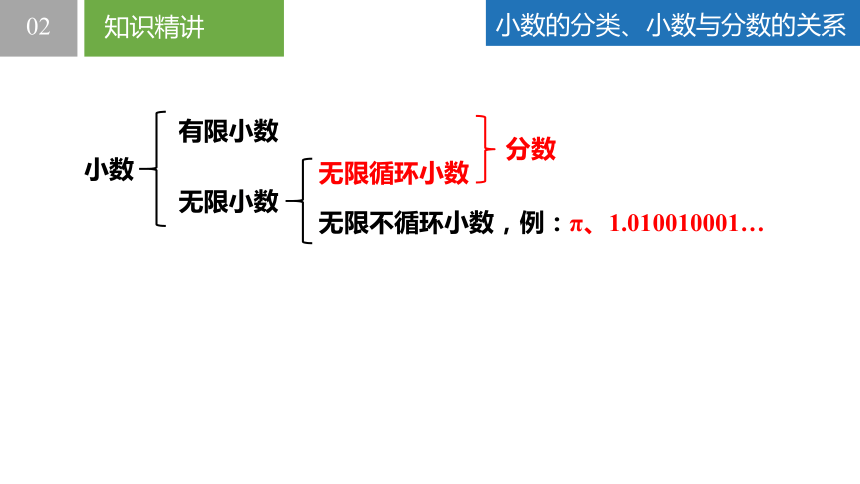
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
为了解决以上问题,我们必须回顾小学学过的小数的分类及小数与分数的关系
02
知识精讲
小数的分类、小数与分数的关系
请同学们将下列各分数表示成小数,并说说你发现了什么?
分数 小数 小数的类型
-
【总结】分数可以化为有限小数与无限循环小数
小数 小数的类型
0.8 有限小数
小数 小数的类型
0.8 有限小数
0.555555555555555… 无限循环小数
小数 小数的类型
0.8 有限小数
0.555555555555555… 无限循环小数
-0.177777777777… 无限循环小数
小数 小数的类型
0.8 有限小数
0.555555555555555… 无限循环小数
-0.177777777777… 无限循环小数
0.18181818181818… 无限循环小数
02
知识精讲
小数的分类、小数与分数的关系
四、小数的分类
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
分数
小数的分类、小数与分数的关系
02
知识精讲
02
知识精讲
0.0,π是否放入正分数?
2.如图,把-,6,-6.5,0,-,3,-7,210,0.0,-43,-5%,π填入相应的圈内
分数
负分数
3,
正分数
-,-6.5,
-,-5%
【问题解决】
0.0是正的无限循环小数,可以表示为正分数;
π是正的无限不循环小数,不可以表示为正分数。
0.0
02
知识精讲
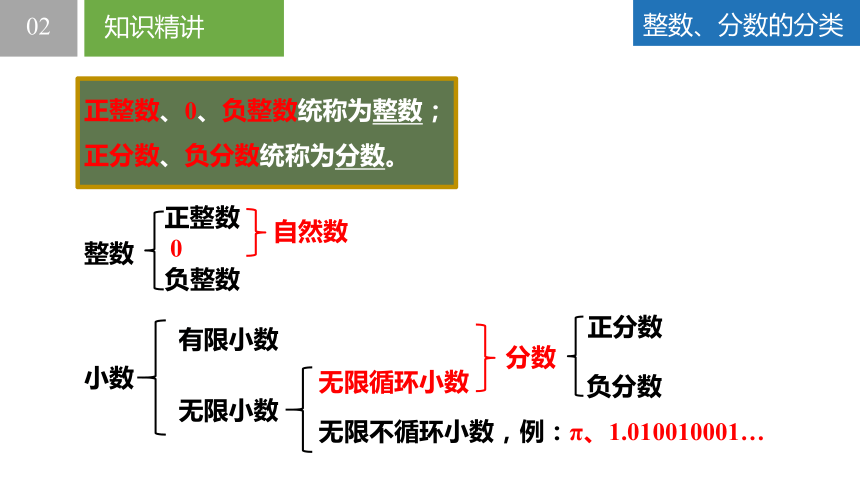
整数、分数的分类
正整数、0、负整数统称为整数;
正分数、负分数统称为分数。
整数
正整数
0
负整数
自然数
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
分数
正分数
负分数
例1、将下列小数转化成分数。
0.7=________ 0.42=________
9.85=________ 0.2=________
3.36=________ 0.35=________
5.75=________ 0.625=________
03
典例精析
例2、把下列各数填入相应的集合中:-3.14,2π,-,0.618,,0,-1,6%,+3,3.010010001…(每相邻两个1之间依次多一个0)
正整数集合{ };
负整数集合{ };
整数集合{ };
正分数集合{ };
负分数集合{ };
分数集合{ }。
03
典例精析
+3
0,-1,+3
-1
0.618,,6%
-3.14,-
-3.14,-,0.618,,6%
有理数的概念
与分类
01
课堂引入
讨论——1.请列举几个分数,并总结分数的形式?
【总结】分数的形式:(m、n是整数,n≠0)
、 、- 、 ……
2.分数形式的数一定是分数吗?整数可以写成分数的形式吗?
不一定,整数也可以写成分数的形式,
eg:,,。
02
知识精讲
有理数的概念
整数和分数统称为有理数,
即能够写成分数形式(m、n是整数,n≠0)的数叫做有理数。
02
知识精讲
有理数的概念
同样地,按正负性,有理数也可以分为正有理数、0和负有理数。
有理数
正有理数
负有理数
0
02
知识精讲
思考——小数是有理数吗?
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
分数
有限小数和无限循环小数可以化成分数,故是有理数;
无限不循环小数不可以化成分数,也不是整数,故不是有理数。
有理数的分类
先定义 后正负
请按照要求对有理数进行分类
有理数
分数
整数
正整数
负整数
0
正分数
负分数
有理数
正有理数
负有理数
0
正整数
正分数
负整数
负分数
先正负 后定义
02
知识精讲
有理数的分类
例1、在下列提供的数有-,-16,75%,,0.1010010001…(相邻两个1之间依次增加一个0),3.14,0,-0.23333…中,属于分数的有( )个
A.2 B.3 C.4 D.5
-看起来像分数,但其实不是,
π是无限不循环小数,-也是无限不循环小数;
=2,分数形式的数不一定是分数,整数也可以写成分数的形式。
03
典例精析
例1、在下列提供的数有-,-16,75%,,0.1010010001…(相邻两个1之间依次增加一个0),3.14,0,-0.23333…中,属于分数的有( )个
A.2 B.3 C.4 D.5
03
典例精析
小数 小数的类型 是否为分数 是否为有理数
0.1010010001
0.10101…
0.1010010001…
小数的类型 是否为分数 是否为有理数
有限小数 √ √
无限循环小数 √ √
无限不循环小数 × ×
B
例2、在数0,3.141592653,-,,0.,5.2%,2.020020002……(相邻两个2之间依次增加一个0)中有理数有( )个
A.5 B.4 C.3 D.2
A
03
典例精析
例1、把下列各数分别填入相应的框线内:
-10,6,-7,0,+3,-2.25,0.01,+67,-,10%,,2000,-18。
正整数:_________________________________________
负整数:_________________________________________
正分数:_________________________________________
负分数:_________________________________________
正有理数:_______________________________________
负有理数:_______________________________________
6,+67,2000
-10,-18
+3,0.01,10%,
-7,-2.25,-
6,+3,0.01,+67,10%,,2000
-10,-7,-2.25,-,-18
03
典例精析
例2、下列说法中,不正确的是( )
A.若一个数是整数,则它一定是有理数
B.若一个数不是有理数,则它一定不是整数
C.0既不是正有理数,也不是负有理数
D.正有理数和负有理数组成有理数
D
有理数
正有理数
负有理数
0
03
典例精析
例3、判断正误
(1)一个整数不是正数就是负数( )
(2)0是最小的有理数( )
(3)有最小的正整数,有最大的负整数 ( )
(4)有最小的正数,有最大的负数( )
-0.1<-0.000…1(中间有无数个0)<0<0.000…1(中间有无数个0)<0.1
负有理数<0
√
×
最小的正整数是1,最大的负整数是-1
×
整数
正整数
负整数
0
×
03
典例精析
【挑战题】现有 8 个有理数,已知其中有 4 个正数、3 个负数、5 个整数、1 个负分数,则正整数有( )个
A.0 B.1 C.2 D.3
C
有理数
分数
整数
正整数
负整数
0
正分数
负分数
8
5
1
2
2
1
03
典例精析
“六非”问题
“六非问题”
0和正数
非正数——0和负数
讨论——1.如果一个数不是正数,那么这个数是什么数?
2.非负数包含哪些数?
非负有理数
0和正整数
自然数
3.非负整数包含哪些数?其“曾用名”是?
4.0和正有理数可以统称为?
注意断句
01
课堂引入
口诀:见非写0,非后取反
非正有理数:
非负有理数:
非正整数:
非负整数:
非正数:
非负数:
0+负整数
0+正整数
0+负有理数
0+正有理数
0+负数
0+正数
02
知识精讲
“六非”问题
例1、请在下列表格中打
整数 分数 正数 负整数 正分数 非负数 非负整数
0
-2.5
-3
0.3
π
-
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
03
典例精析
例2、下列说法正确的是( )
A.非负整数就是正整数,非正整数就是负整数
B.非正整数就是除了正整数以外的所有数
C.0既是非负整数又是非正整数
D.没有最大的正整数,也没有最大的非正整数
C
0和
03
典例精析
0和
不是正的整数:
0和负整数
最大的非正整数是0
例3、填空:
最小的非负整数是__________,
是负数而不是分数的有理数是__________,
是整数而不是正数的有理数是__________。
0
负整数
非正整数
03
典例精析
课后总结
课后总结
整数和分数统称为有理数,
即能够写成分数形式(m、n是整数,n≠0)的数叫做有理数。
口诀:见非写0,非后取反
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第2章 有理数
2.1.2正数与负数:有理数的概念与分类
教学目标
能对整数与分数按正负性进行分类,理解小数与分数之间的关系
理解有理数的概念,掌握有理数的两种分类
01
02
掌握“六非”问题的解决策略
03
整数与分数的分类
既然有了正负数之分,那么整数与分数就可以进一步分类
整数
01
课堂引入
正整数
0
负整数
分数
正分数
负分数
02
知识精讲
正整数
负整数
6,210
-7,-43
1.如图,把-,6,-6.5,0,-,3,-7,210,0.0,-43,-5%,π填入相应的圈内
整数
0
思考——正整数与自然数有何关联?
【总结】自然数包括0和正整数
正整数:1,2,3,4,……
自然数:0,1,2,3,4,……
02
知识精讲
整数
正整数
0
负整数
自然数
【思维拓展】自然数与正整数一样多吗?(不作要求)
02
知识精讲
2.如图,把-,6,-6.5,0,-,3,-7,210,0.0,-43,-5%,π填入相应的圈内
分数
负分数
正分数
-,-6.5,
-,-5%
3,
0.0,π是否放入正分数?
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
为了解决以上问题,我们必须回顾小学学过的小数的分类及小数与分数的关系
02
知识精讲
小数的分类、小数与分数的关系
请同学们将下列各分数表示成小数,并说说你发现了什么?
分数 小数 小数的类型
-
【总结】分数可以化为有限小数与无限循环小数
小数 小数的类型
0.8 有限小数
小数 小数的类型
0.8 有限小数
0.555555555555555… 无限循环小数
小数 小数的类型
0.8 有限小数
0.555555555555555… 无限循环小数
-0.177777777777… 无限循环小数
小数 小数的类型
0.8 有限小数
0.555555555555555… 无限循环小数
-0.177777777777… 无限循环小数
0.18181818181818… 无限循环小数
02
知识精讲
小数的分类、小数与分数的关系
四、小数的分类
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
分数
小数的分类、小数与分数的关系
02
知识精讲
02
知识精讲
0.0,π是否放入正分数?
2.如图,把-,6,-6.5,0,-,3,-7,210,0.0,-43,-5%,π填入相应的圈内
分数
负分数
3,
正分数
-,-6.5,
-,-5%
【问题解决】
0.0是正的无限循环小数,可以表示为正分数;
π是正的无限不循环小数,不可以表示为正分数。
0.0
02
知识精讲
整数、分数的分类
正整数、0、负整数统称为整数;
正分数、负分数统称为分数。
整数
正整数
0
负整数
自然数
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
分数
正分数
负分数
例1、将下列小数转化成分数。
0.7=________ 0.42=________
9.85=________ 0.2=________
3.36=________ 0.35=________
5.75=________ 0.625=________
03
典例精析
例2、把下列各数填入相应的集合中:-3.14,2π,-,0.618,,0,-1,6%,+3,3.010010001…(每相邻两个1之间依次多一个0)
正整数集合{ };
负整数集合{ };
整数集合{ };
正分数集合{ };
负分数集合{ };
分数集合{ }。
03
典例精析
+3
0,-1,+3
-1
0.618,,6%
-3.14,-
-3.14,-,0.618,,6%
有理数的概念
与分类
01
课堂引入
讨论——1.请列举几个分数,并总结分数的形式?
【总结】分数的形式:(m、n是整数,n≠0)
、 、- 、 ……
2.分数形式的数一定是分数吗?整数可以写成分数的形式吗?
不一定,整数也可以写成分数的形式,
eg:,,。
02
知识精讲
有理数的概念
整数和分数统称为有理数,
即能够写成分数形式(m、n是整数,n≠0)的数叫做有理数。
02
知识精讲
有理数的概念
同样地,按正负性,有理数也可以分为正有理数、0和负有理数。
有理数
正有理数
负有理数
0
02
知识精讲
思考——小数是有理数吗?
小数
有限小数
无限小数
无限循环小数
无限不循环小数,例:π、1.010010001…
分数
有限小数和无限循环小数可以化成分数,故是有理数;
无限不循环小数不可以化成分数,也不是整数,故不是有理数。
有理数的分类
先定义 后正负
请按照要求对有理数进行分类
有理数
分数
整数
正整数
负整数
0
正分数
负分数
有理数
正有理数
负有理数
0
正整数
正分数
负整数
负分数
先正负 后定义
02
知识精讲
有理数的分类
例1、在下列提供的数有-,-16,75%,,0.1010010001…(相邻两个1之间依次增加一个0),3.14,0,-0.23333…中,属于分数的有( )个
A.2 B.3 C.4 D.5
-看起来像分数,但其实不是,
π是无限不循环小数,-也是无限不循环小数;
=2,分数形式的数不一定是分数,整数也可以写成分数的形式。
03
典例精析
例1、在下列提供的数有-,-16,75%,,0.1010010001…(相邻两个1之间依次增加一个0),3.14,0,-0.23333…中,属于分数的有( )个
A.2 B.3 C.4 D.5
03
典例精析
小数 小数的类型 是否为分数 是否为有理数
0.1010010001
0.10101…
0.1010010001…
小数的类型 是否为分数 是否为有理数
有限小数 √ √
无限循环小数 √ √
无限不循环小数 × ×
B
例2、在数0,3.141592653,-,,0.,5.2%,2.020020002……(相邻两个2之间依次增加一个0)中有理数有( )个
A.5 B.4 C.3 D.2
A
03
典例精析
例1、把下列各数分别填入相应的框线内:
-10,6,-7,0,+3,-2.25,0.01,+67,-,10%,,2000,-18。
正整数:_________________________________________
负整数:_________________________________________
正分数:_________________________________________
负分数:_________________________________________
正有理数:_______________________________________
负有理数:_______________________________________
6,+67,2000
-10,-18
+3,0.01,10%,
-7,-2.25,-
6,+3,0.01,+67,10%,,2000
-10,-7,-2.25,-,-18
03
典例精析
例2、下列说法中,不正确的是( )
A.若一个数是整数,则它一定是有理数
B.若一个数不是有理数,则它一定不是整数
C.0既不是正有理数,也不是负有理数
D.正有理数和负有理数组成有理数
D
有理数
正有理数
负有理数
0
03
典例精析
例3、判断正误
(1)一个整数不是正数就是负数( )
(2)0是最小的有理数( )
(3)有最小的正整数,有最大的负整数 ( )
(4)有最小的正数,有最大的负数( )
-0.1<-0.000…1(中间有无数个0)<0<0.000…1(中间有无数个0)<0.1
负有理数<0
√
×
最小的正整数是1,最大的负整数是-1
×
整数
正整数
负整数
0
×
03
典例精析
【挑战题】现有 8 个有理数,已知其中有 4 个正数、3 个负数、5 个整数、1 个负分数,则正整数有( )个
A.0 B.1 C.2 D.3
C
有理数
分数
整数
正整数
负整数
0
正分数
负分数
8
5
1
2
2
1
03
典例精析
“六非”问题
“六非问题”
0和正数
非正数——0和负数
讨论——1.如果一个数不是正数,那么这个数是什么数?
2.非负数包含哪些数?
非负有理数
0和正整数
自然数
3.非负整数包含哪些数?其“曾用名”是?
4.0和正有理数可以统称为?
注意断句
01
课堂引入
口诀:见非写0,非后取反
非正有理数:
非负有理数:
非正整数:
非负整数:
非正数:
非负数:
0+负整数
0+正整数
0+负有理数
0+正有理数
0+负数
0+正数
02
知识精讲
“六非”问题
例1、请在下列表格中打
整数 分数 正数 负整数 正分数 非负数 非负整数
0
-2.5
-3
0.3
π
-
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
03
典例精析
例2、下列说法正确的是( )
A.非负整数就是正整数,非正整数就是负整数
B.非正整数就是除了正整数以外的所有数
C.0既是非负整数又是非正整数
D.没有最大的正整数,也没有最大的非正整数
C
0和
03
典例精析
0和
不是正的整数:
0和负整数
最大的非正整数是0
例3、填空:
最小的非负整数是__________,
是负数而不是分数的有理数是__________,
是整数而不是正数的有理数是__________。
0
负整数
非正整数
03
典例精析
课后总结
课后总结
整数和分数统称为有理数,
即能够写成分数形式(m、n是整数,n≠0)的数叫做有理数。
口诀:见非写0,非后取反
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
