《函数及其图象》18.3水平测试(三)
文档属性
| 名称 | 《函数及其图象》18.3水平测试(三) |  | |
| 格式 | rar | ||
| 文件大小 | 162.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-17 19:01:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第18章《函数及其图象》18.3水平测试
山东 石少玉
跟踪反馈 挑战自我
一、慧眼识金选一选!(每小题3分,共24分)
1. 下列函数中,一次函数是( ).
(A) (B) (C) (D)
2. 如果点M在直线上,则M点的坐标可以是( )
(A)(-1,0) (B)(0,1) (C)(1,0) (D)(1,-1)
3. 一次函数不经过的象限是( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
4. 如果一次函数的图象经过第一象限,且与轴负半轴相交,那么( )
(A),(B), (C), (D),
5. 若把直线向下平移4个单位,得到的直线的解析式是( ).
(A) (B) (C) (D)
6. 下列四个点中,有三个点在同一条直线上,不在这条直线上的点是( )
(A) (B) (C) (D)
7. 直线与轴、轴所围成的三角形的面积是( ).
(A)3 (B)6 (C) (D)
8. 已知正比例函数()的函数值随的增大而增大,则一次函数的图象大致是( )
二、画龙点睛填一填!(每小题3分,共24分)
9.若函数是关于的一次函数,则满足的条件是______;若该函数是正比例函数,则的值是______,此时函数的解析式为______.
10.函数与轴交点的坐标为__________;与轴交点的坐标为__________;图象经过_________象限;随的增大而__________.
11.某型号汽油的数量与相应金额的关系如下图所示,那么这种汽油的单价是每升______元.
12.点(,),点(,)是一次函数图象上的两个点,且,则与的大小关系是____________.
13.写出一个一次函数,使随的增大而增大,且经过点(2,0),这个一次函数可以是(只需写一个即可):___________.
14.随着海拔高度的升高,大气压强下降,空气中的含氧量也随之下降,即含氧量 与大气压强成正比例函数关系.当时,,请写出与的函数关系式 .
15.一次函数的自变量的取值范围是-3≤≤6,相应的函数值的取值范围是-5 ≤≤-2,则这个函数的解析式为________________.
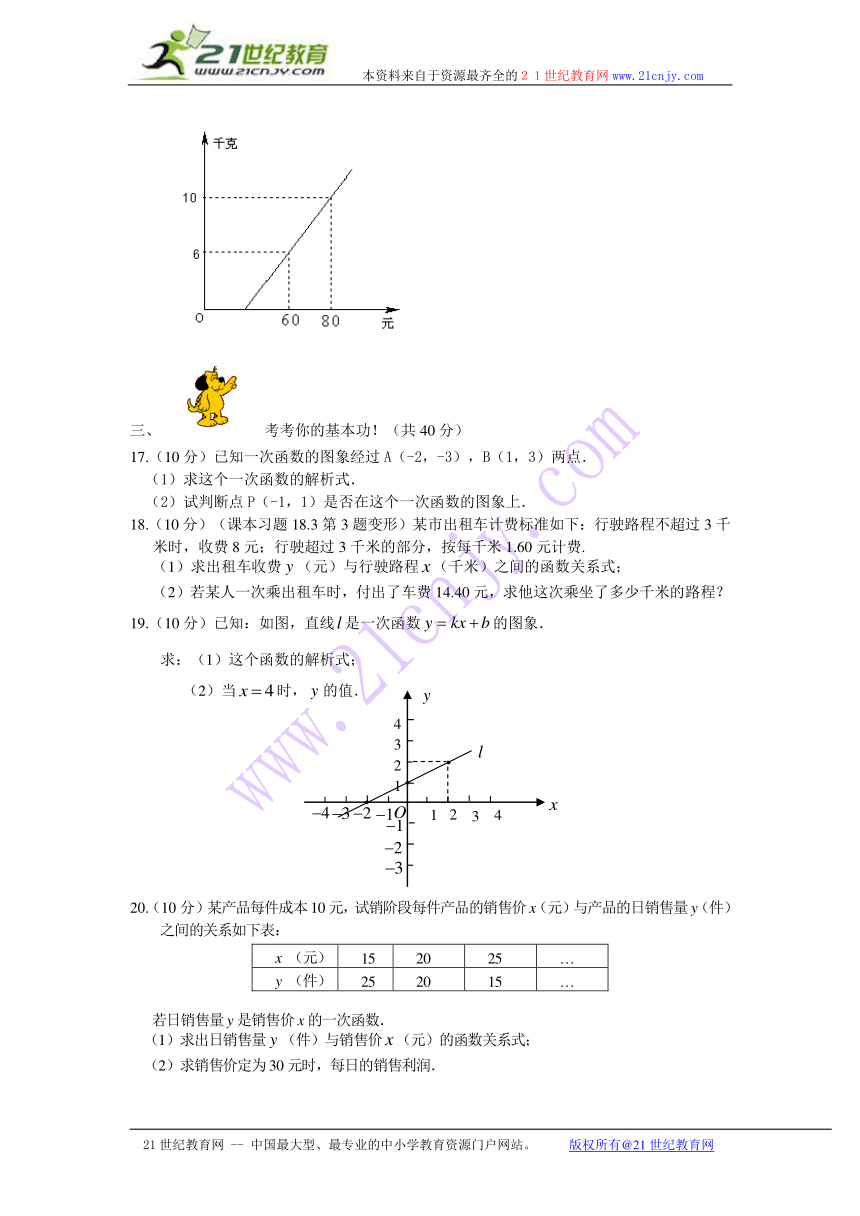
16. (课本习题变形)某地长途客运公司规定:旅客可以免费携带一定重量的行李,如果超过规定,则需要购买行李票.行李费用(元)是行李重量(千克)的一次函数,其图象如图所示,则与的函数关系是_____________.
( http: / / www. / )
三、考考你的基本功!(共40分)
17.(10分)已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式.
(2)试判断点P(-1,1)是否在这个一次函数的图象上.
18.(10分)(课本习题18.3第3题变形)某市出租车计费标准如下:行驶路程不超过3千米时,收费8元;行驶超过3千米的部分,按每千米1.60元计费.
(1)求出租车收费(元)与行驶路程(千米)之间的函数关系式;
(2)若某人一次乘出租车时,付出了车费14.40元,求他这次乘坐了多少千米的路程?
19.(10分)已知:如图,直线是一次函数的图象.
求:(1)这个函数的解析式;
(2)当时,的值.
20.(10分)某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x (元) 15 20 25 …
y (件) 25 20 15 …
若日销售量y是销售价x的一次函数.
(1)求出日销售量(件)与销售价(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
四、同步大闯关!(12分)
21.(12分)点(,)在第一象限,且,点的坐标为(6,0),设 的面积为.
(1)用含的解析式表示,写出的取值范围,画出函数的图象.
(2)当点的横坐标为5时,的面积为多少?
(3)的面积能大于24吗?为什么?
参考答案:
1.B;
2.C;
3.A;
4.B;
5.A;
6.D;
7.A;
8.A;
9.,5,;
10.,,一、三、四,增大;
11.5.09;
12.;
13.答案不唯一,如;
14. ;
15. 或;提示:分情况讨论:
(1)当时,,当 时,,所以解得
所以所求的函数解析式为.
(2)当时,,当时,时:解得
所以所求的一次函数解析式为.故应填或.
16.;
17. (1);
(2)点(-1,1)不在这个一次函数的图象上.
18. 解:(1)因为当时,,
又因为当时,行驶里程超过3千米的部分是千米,
所以,即.
综上:出租车收费与行驶路程的函数关系式是
(2)因为14.40元8元.
由(1)得:,解得.
答:当付车费14.40元时,乘路程为7千米.
19. 解:(1)依题意,得
解得.
所以.
(2)当时,.
20. 解:(1)设此一次函数解析式为
则
解得k=1,b=40.
即一次函数解析式为.
(2)每日的销售量为y=-30+40=10件,
所获销售利润为(3010)×10=200元.
21.(1)(),图象略.
(2)9;
(3)不能,当时,的最大值为24.
提升能力 超越自我
1. 小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后分钟时,他所在的位置与家的距离为千米,且与之间的函数关系的图像如图中的折线段所示.
(1)试求折线段所对应的函数关系式;
(2)请解释图中线段的实际意义;
(3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离(千米)与小明出发后的时间(分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)
2. 如图,已知直线的图象与轴交于A、B两点.直线经过原点,与线段AB交于点C,把△AOB的面积分为2︰1的两部分.求直线的解析式.
( http: / / www. / )
答案:
1. 解:(1)线段对应的函数关系式为:()
线段对应的函数关系式为:.
(2)图中线段的实际意义是:小明出发12分钟后,沿着以他家为圆心,1千米为半径的圆弧形道路上匀速步行了8分钟.
(3)如图中折线段.
2. 由题意,可求得A(-3,0)、B(0,3).
(1)当时
如图1,当直线把△ABO的面积分为时,作CF⊥OA于F,CE⊥OB于E,,则.
∴,即.
∴CF = 2,同理,解得CF = 1.
∴C(-1,2).
∴直线的解析式为.
(2)当时(如图2),同样可求得直线的解析式为.
图1 图2
(A)
(B)
(C)
(D)
金额(单位:元)
数量(单位:升)
100
0
509
11题
1
2
3
4
1
2
3
4
1
A
B
20
12
t(分钟)
s(千米)
O
1
A
B
20
12
t(分钟)
s(千米)
O
10
16
D
C
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第18章《函数及其图象》18.3水平测试
山东 石少玉
跟踪反馈 挑战自我
一、慧眼识金选一选!(每小题3分,共24分)
1. 下列函数中,一次函数是( ).
(A) (B) (C) (D)
2. 如果点M在直线上,则M点的坐标可以是( )
(A)(-1,0) (B)(0,1) (C)(1,0) (D)(1,-1)
3. 一次函数不经过的象限是( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
4. 如果一次函数的图象经过第一象限,且与轴负半轴相交,那么( )
(A),(B), (C), (D),
5. 若把直线向下平移4个单位,得到的直线的解析式是( ).
(A) (B) (C) (D)
6. 下列四个点中,有三个点在同一条直线上,不在这条直线上的点是( )
(A) (B) (C) (D)
7. 直线与轴、轴所围成的三角形的面积是( ).
(A)3 (B)6 (C) (D)
8. 已知正比例函数()的函数值随的增大而增大,则一次函数的图象大致是( )
二、画龙点睛填一填!(每小题3分,共24分)
9.若函数是关于的一次函数,则满足的条件是______;若该函数是正比例函数,则的值是______,此时函数的解析式为______.
10.函数与轴交点的坐标为__________;与轴交点的坐标为__________;图象经过_________象限;随的增大而__________.
11.某型号汽油的数量与相应金额的关系如下图所示,那么这种汽油的单价是每升______元.
12.点(,),点(,)是一次函数图象上的两个点,且,则与的大小关系是____________.
13.写出一个一次函数,使随的增大而增大,且经过点(2,0),这个一次函数可以是(只需写一个即可):___________.
14.随着海拔高度的升高,大气压强下降,空气中的含氧量也随之下降,即含氧量 与大气压强成正比例函数关系.当时,,请写出与的函数关系式 .
15.一次函数的自变量的取值范围是-3≤≤6,相应的函数值的取值范围是-5 ≤≤-2,则这个函数的解析式为________________.
16. (课本习题变形)某地长途客运公司规定:旅客可以免费携带一定重量的行李,如果超过规定,则需要购买行李票.行李费用(元)是行李重量(千克)的一次函数,其图象如图所示,则与的函数关系是_____________.
( http: / / www. / )
三、考考你的基本功!(共40分)
17.(10分)已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式.
(2)试判断点P(-1,1)是否在这个一次函数的图象上.
18.(10分)(课本习题18.3第3题变形)某市出租车计费标准如下:行驶路程不超过3千米时,收费8元;行驶超过3千米的部分,按每千米1.60元计费.
(1)求出租车收费(元)与行驶路程(千米)之间的函数关系式;
(2)若某人一次乘出租车时,付出了车费14.40元,求他这次乘坐了多少千米的路程?
19.(10分)已知:如图,直线是一次函数的图象.
求:(1)这个函数的解析式;
(2)当时,的值.
20.(10分)某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x (元) 15 20 25 …
y (件) 25 20 15 …
若日销售量y是销售价x的一次函数.
(1)求出日销售量(件)与销售价(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
四、同步大闯关!(12分)
21.(12分)点(,)在第一象限,且,点的坐标为(6,0),设 的面积为.
(1)用含的解析式表示,写出的取值范围,画出函数的图象.
(2)当点的横坐标为5时,的面积为多少?
(3)的面积能大于24吗?为什么?
参考答案:
1.B;
2.C;
3.A;
4.B;
5.A;
6.D;
7.A;
8.A;
9.,5,;
10.,,一、三、四,增大;
11.5.09;
12.;
13.答案不唯一,如;
14. ;
15. 或;提示:分情况讨论:
(1)当时,,当 时,,所以解得
所以所求的函数解析式为.
(2)当时,,当时,时:解得
所以所求的一次函数解析式为.故应填或.
16.;
17. (1);
(2)点(-1,1)不在这个一次函数的图象上.
18. 解:(1)因为当时,,
又因为当时,行驶里程超过3千米的部分是千米,
所以,即.
综上:出租车收费与行驶路程的函数关系式是
(2)因为14.40元8元.
由(1)得:,解得.
答:当付车费14.40元时,乘路程为7千米.
19. 解:(1)依题意,得
解得.
所以.
(2)当时,.
20. 解:(1)设此一次函数解析式为
则
解得k=1,b=40.
即一次函数解析式为.
(2)每日的销售量为y=-30+40=10件,
所获销售利润为(3010)×10=200元.
21.(1)(),图象略.
(2)9;
(3)不能,当时,的最大值为24.
提升能力 超越自我
1. 小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后分钟时,他所在的位置与家的距离为千米,且与之间的函数关系的图像如图中的折线段所示.
(1)试求折线段所对应的函数关系式;
(2)请解释图中线段的实际意义;
(3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离(千米)与小明出发后的时间(分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)
2. 如图,已知直线的图象与轴交于A、B两点.直线经过原点,与线段AB交于点C,把△AOB的面积分为2︰1的两部分.求直线的解析式.
( http: / / www. / )
答案:
1. 解:(1)线段对应的函数关系式为:()
线段对应的函数关系式为:.
(2)图中线段的实际意义是:小明出发12分钟后,沿着以他家为圆心,1千米为半径的圆弧形道路上匀速步行了8分钟.
(3)如图中折线段.
2. 由题意,可求得A(-3,0)、B(0,3).
(1)当时
如图1,当直线把△ABO的面积分为时,作CF⊥OA于F,CE⊥OB于E,,则.
∴,即.
∴CF = 2,同理,解得CF = 1.
∴C(-1,2).
∴直线的解析式为.
(2)当时(如图2),同样可求得直线的解析式为.
图1 图2
(A)
(B)
(C)
(D)
金额(单位:元)
数量(单位:升)
100
0
509
11题
1
2
3
4
1
2
3
4
1
A
B
20
12
t(分钟)
s(千米)
O
1
A
B
20
12
t(分钟)
s(千米)
O
10
16
D
C
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
