11.1.1 三角形的边 学案 (含答案)人教版数学八年级上册数学
文档属性
| 名称 | 11.1.1 三角形的边 学案 (含答案)人教版数学八年级上册数学 |  | |
| 格式 | docx | ||
| 文件大小 | 390.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-18 17:08:54 | ||
图片预览


文档简介
11.1.1 三角形的边
学习目标
1.了解三角形的有关概念.
2.理解三角形两边的和大于第三边,会根据三条线段的长度判断它们能否构成三角形 .
3.掌握三角形的两种分类方法.
要点梳理
1.三角形的有关概念
三角形的定义:由不在同一条直线的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边,相邻两边的公共端点叫做三角形的顶点,相邻两边组成的角叫做三角形的角.
2.三角形及其边角的表示方法:
如图,顶点是A,B,C的三角形记作:“△ABC”,读作三角形ABC,∠A,∠B,∠C三角形的角,线段AB,BC,CD是三角形的边△ABC的三边有时也用a,b,c表示,顶点A所对的边用a表示,顶点B所对的边用b表示,顶点C所对的边用c表示.
3.三角形的分类:
三角形按边分类:
三角形按角的大小分类:
三角形
4.三角形的三边关系:
三角形任意两边之和大于第三边;任意两边之差小于第三边
例题讲解
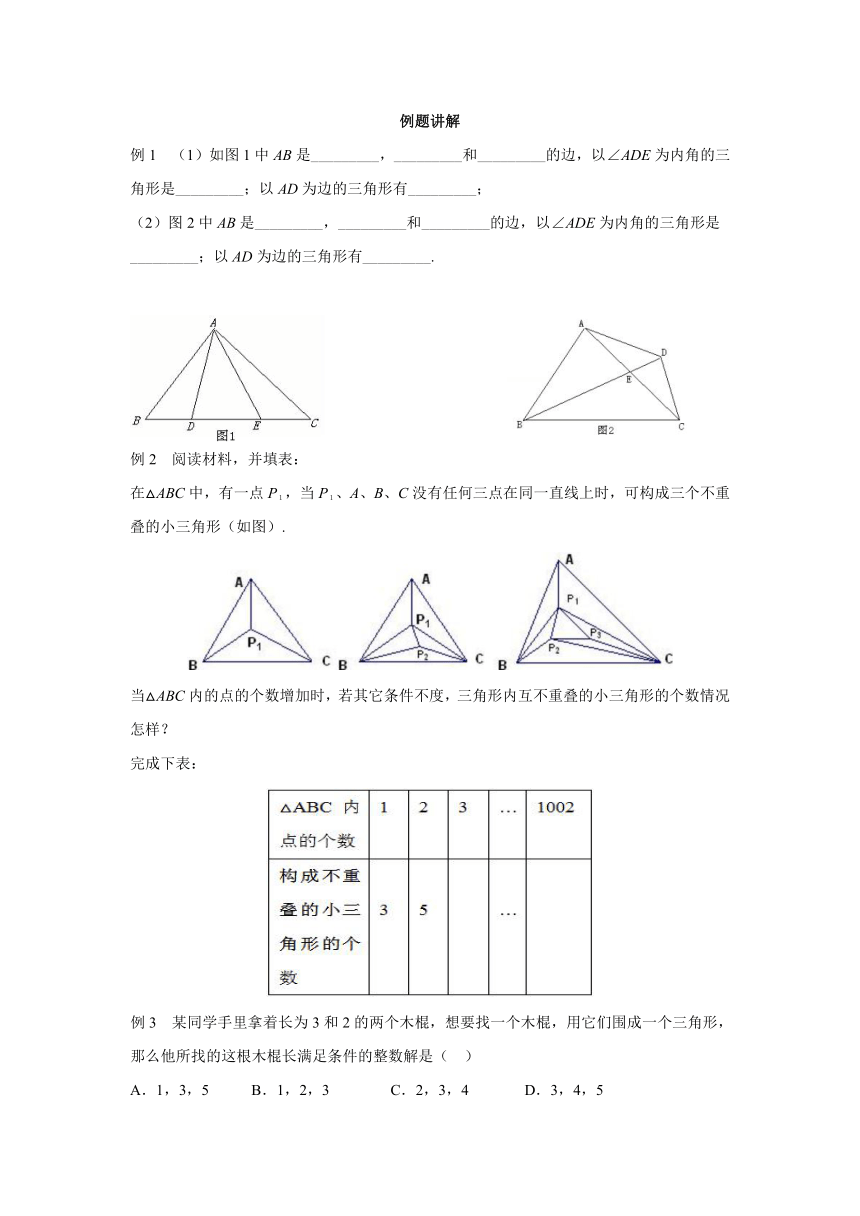
例1 (1)如图1中AB是_________,_________和_________的边,以∠ADE为内角的三角形是_________;以AD为边的三角形有_________;
(2)图2中AB是_________,_________和_________的边,以∠ADE为内角的三角形是
_________;以AD为边的三角形有_________.
例2 阅读材料,并填表:
在△ABC中,有一点P1,当P1、A、B、C没有任何三点在同一直线上时,可构成三个不重叠的小三角形(如图).
当△ABC内的点的个数增加时,若其它条件不度,三角形内互不重叠的小三角形的个数情况怎样?
完成下表:
例3 某同学手里拿着长为3和2的两个木棍,想要找一个木棍,用它们围成一个三角形,
那么他所找的这根木棍长满足条件的整数解是( )
A.1,3,5 B.1,2,3 C.2,3,4 D.3,4,5
例4 (1)已知一个等腰三角形的一边长是5,一边长是12,求这个三角形的周长.
(2)已知△ABC是等腰三角形,如果它的周长为18㎝,一条边长4㎝,那么腰长是多少?
例5 (1)已知△ABC的AB=7,BC=8,求第三边AC的取值范围.
(2)已知三角形的分别2,,3,求的取值范围.
课堂练习
1.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3㎝ 4㎝ 8㎝ B.8㎝ 7㎝ 15㎝
C.13㎝ 12㎝ 20㎝ D.5㎝ 5㎝ 11㎝
2.现有两根木棒,它们长分别是40㎝和50㎝,若要钉成一个三角形木架,则下列四根木棒应选取( )
A.10㎝ 的木棒 B.40㎝的木棒
C.90㎝的木棒 D.100㎝的木棒
3.下列长度的三条线段能组成三角形的是( )
A.1,2,3 B.3,4,5
C.3,1,1 D.3,4,7
4.以长为2㎝,3㎝,5㎝,7㎝的四条线段中的的三条线段为边,可以画出的三角形的个
数为( )
A. 1个 B. 2个 C. 3个 D.0个
5.下列长度的三条线段能组成三角形的是 ( )
A. 3,4,8 B.5,6,11 C. 1,2,3 D. 5,6,10
6.已知三角形三边长分别为2,x,13,若x为正整数 则这样的三角形个数为( )
A.2 B.3 C.5 D.13
7.关于三角形的边的叙述正确的是( )
A.三边互不相等
B.至少有两边相等
C.任意两边之和一定大于第三边
D.最多有两边相等
8.已知三角形的两边长为4,8,则第三边的长度可以是____(写出一个即可).
9.一个三角形有两条边相等,周长为20 cm,三角形的一边长为5 cm,那么其它两边长分别为 .
10.在△ABC中,ac=12 cm,ab=8 cm,那么bc的最大长度应小于 ,最小长度应大于 .
11.现有四条钢线,长度分别为(单位:cm)7,6,3,2,从中取出三根连成一个三角形,这三根的长度可以为____.(写出一种即可).
12.一个等腰三角形的两条边长分别为8 cm和3 cm,那么它的周长为 .
13.如图,图中有___个三角形,把它们用符号分别表示为________.
14.为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB
=12m,那么AB间的距离不可能是( )
A.5m B.15m
C.20m D.28m
15.长为11,8,6,4的四根木条,选其中三根组成三角形有 种选法,它们分别是 .
16.填表:用长度相等的火柴棒拼成如图所示的图形.
17.若等腰三角形的一边长为12,且腰长是底边长的,求这个三角形的周长.
参考答案
例题讲解
例1 【答案】(1)△ABD △ABE △ABC
△ADE、△ADC
△ADB、△ADE、△ADC;
(2)△ABD △ABE △ABC
△ADE、△ADB
△ADE、△ADB、△ADC
例2 【答案】当△ABC内的点的个数为3个时,三角形内互不重叠的小三角形的个数为7个;
当△ABC内的点的个数为1002个时,三角形内互不重叠的小三角形的个数为2005个.
例3 【答案】C
例4 解:(1)29;(2)7㎝.
例5 解:(1)1<AC<15;(2)2<x<6.
课堂操练
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】C
8. 【答案】在4<x<12之间的数都可
9.【答案】7.5 cm,7.5 cm
10.【答案】20 cm,4 cm
11.【答案】7 cm,6 cm,3 cm(或7 cm、6 cm、2 cm).
12.【答案】19 cm
13.【答案】8,△ABE,△ADE,△CDE,△BCE,△ABD,△BCD,△ABC,△ACD.
14.【答案】D
15.【答案】3 ①4,6,8;③4,8,11;④6,8,11
16.【答案】11 2n+1
17.解:∵等腰三角形一边长为12cm,且腰长是底边长的,
①如果腰长为12cm,则底边为16cm,
等腰三角形的三边为12、12、16,能构成三角形,∴C△=12+12+16=40cm;
②如果底长为12cm,则腰长为9cm,
等腰三角形的三边为12、9、9,能构成三角形,∴C△=9+9+12=30cm.
学习目标
1.了解三角形的有关概念.
2.理解三角形两边的和大于第三边,会根据三条线段的长度判断它们能否构成三角形 .
3.掌握三角形的两种分类方法.
要点梳理
1.三角形的有关概念
三角形的定义:由不在同一条直线的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边,相邻两边的公共端点叫做三角形的顶点,相邻两边组成的角叫做三角形的角.
2.三角形及其边角的表示方法:
如图,顶点是A,B,C的三角形记作:“△ABC”,读作三角形ABC,∠A,∠B,∠C三角形的角,线段AB,BC,CD是三角形的边△ABC的三边有时也用a,b,c表示,顶点A所对的边用a表示,顶点B所对的边用b表示,顶点C所对的边用c表示.
3.三角形的分类:
三角形按边分类:
三角形按角的大小分类:
三角形
4.三角形的三边关系:
三角形任意两边之和大于第三边;任意两边之差小于第三边
例题讲解
例1 (1)如图1中AB是_________,_________和_________的边,以∠ADE为内角的三角形是_________;以AD为边的三角形有_________;
(2)图2中AB是_________,_________和_________的边,以∠ADE为内角的三角形是
_________;以AD为边的三角形有_________.
例2 阅读材料,并填表:
在△ABC中,有一点P1,当P1、A、B、C没有任何三点在同一直线上时,可构成三个不重叠的小三角形(如图).
当△ABC内的点的个数增加时,若其它条件不度,三角形内互不重叠的小三角形的个数情况怎样?
完成下表:
例3 某同学手里拿着长为3和2的两个木棍,想要找一个木棍,用它们围成一个三角形,
那么他所找的这根木棍长满足条件的整数解是( )
A.1,3,5 B.1,2,3 C.2,3,4 D.3,4,5
例4 (1)已知一个等腰三角形的一边长是5,一边长是12,求这个三角形的周长.
(2)已知△ABC是等腰三角形,如果它的周长为18㎝,一条边长4㎝,那么腰长是多少?
例5 (1)已知△ABC的AB=7,BC=8,求第三边AC的取值范围.
(2)已知三角形的分别2,,3,求的取值范围.
课堂练习
1.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3㎝ 4㎝ 8㎝ B.8㎝ 7㎝ 15㎝
C.13㎝ 12㎝ 20㎝ D.5㎝ 5㎝ 11㎝
2.现有两根木棒,它们长分别是40㎝和50㎝,若要钉成一个三角形木架,则下列四根木棒应选取( )
A.10㎝ 的木棒 B.40㎝的木棒
C.90㎝的木棒 D.100㎝的木棒
3.下列长度的三条线段能组成三角形的是( )
A.1,2,3 B.3,4,5
C.3,1,1 D.3,4,7
4.以长为2㎝,3㎝,5㎝,7㎝的四条线段中的的三条线段为边,可以画出的三角形的个
数为( )
A. 1个 B. 2个 C. 3个 D.0个
5.下列长度的三条线段能组成三角形的是 ( )
A. 3,4,8 B.5,6,11 C. 1,2,3 D. 5,6,10
6.已知三角形三边长分别为2,x,13,若x为正整数 则这样的三角形个数为( )
A.2 B.3 C.5 D.13
7.关于三角形的边的叙述正确的是( )
A.三边互不相等
B.至少有两边相等
C.任意两边之和一定大于第三边
D.最多有两边相等
8.已知三角形的两边长为4,8,则第三边的长度可以是____(写出一个即可).
9.一个三角形有两条边相等,周长为20 cm,三角形的一边长为5 cm,那么其它两边长分别为 .
10.在△ABC中,ac=12 cm,ab=8 cm,那么bc的最大长度应小于 ,最小长度应大于 .
11.现有四条钢线,长度分别为(单位:cm)7,6,3,2,从中取出三根连成一个三角形,这三根的长度可以为____.(写出一种即可).
12.一个等腰三角形的两条边长分别为8 cm和3 cm,那么它的周长为 .
13.如图,图中有___个三角形,把它们用符号分别表示为________.
14.为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB
=12m,那么AB间的距离不可能是( )
A.5m B.15m
C.20m D.28m
15.长为11,8,6,4的四根木条,选其中三根组成三角形有 种选法,它们分别是 .
16.填表:用长度相等的火柴棒拼成如图所示的图形.
17.若等腰三角形的一边长为12,且腰长是底边长的,求这个三角形的周长.
参考答案
例题讲解
例1 【答案】(1)△ABD △ABE △ABC
△ADE、△ADC
△ADB、△ADE、△ADC;
(2)△ABD △ABE △ABC
△ADE、△ADB
△ADE、△ADB、△ADC
例2 【答案】当△ABC内的点的个数为3个时,三角形内互不重叠的小三角形的个数为7个;
当△ABC内的点的个数为1002个时,三角形内互不重叠的小三角形的个数为2005个.
例3 【答案】C
例4 解:(1)29;(2)7㎝.
例5 解:(1)1<AC<15;(2)2<x<6.
课堂操练
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】C
8. 【答案】在4<x<12之间的数都可
9.【答案】7.5 cm,7.5 cm
10.【答案】20 cm,4 cm
11.【答案】7 cm,6 cm,3 cm(或7 cm、6 cm、2 cm).
12.【答案】19 cm
13.【答案】8,△ABE,△ADE,△CDE,△BCE,△ABD,△BCD,△ABC,△ACD.
14.【答案】D
15.【答案】3 ①4,6,8;③4,8,11;④6,8,11
16.【答案】11 2n+1
17.解:∵等腰三角形一边长为12cm,且腰长是底边长的,
①如果腰长为12cm,则底边为16cm,
等腰三角形的三边为12、12、16,能构成三角形,∴C△=12+12+16=40cm;
②如果底长为12cm,则腰长为9cm,
等腰三角形的三边为12、9、9,能构成三角形,∴C△=9+9+12=30cm.
