21.2.4一元二次方程的根与系数的关系教学设计
文档属性
| 名称 | 21.2.4一元二次方程的根与系数的关系教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 32.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-30 00:00:00 | ||
图片预览

文档简介
一元二次方程根与系数的关系教学设计
一、教学任务分析
教学目标 知识技能 1、使学生掌握一元二次方程的根与系数的关系,并能初步应用。2、提高学生的观察、分析以及推理论证的能力。
数学思考 学生经历观察→发现→猜想→证明的思维过程,培养学生的分析能力和解决问题的能力。
解决问题 能运用根与系数的关系求:已知方程的一个根,求方程的另一个根及待定系数;根据方程求代数式的值。
情感态度 使学生理解事物都是相互联系、相互制约的辩证唯物主义观点以及“特殊——一般——特殊”的基本思想方法。
重点 一元二次方程的根与系数的关系及应用。
难点 一元二次方程的根与系数的关系的发现和准确掌握。
二、教学流程安排
活动流程图 活动内容和目的
创设情景二、探索新知根与系数关系的发现。三、应用新知四、信息反馈五、课堂小结与作业布置 引入课题让学生在特殊情况中发现一般规律激发学生的探究欲望,提高学习的积极性知识考查知识巩固
三、教学过程设计
问题与情境 师生行为 设计意图
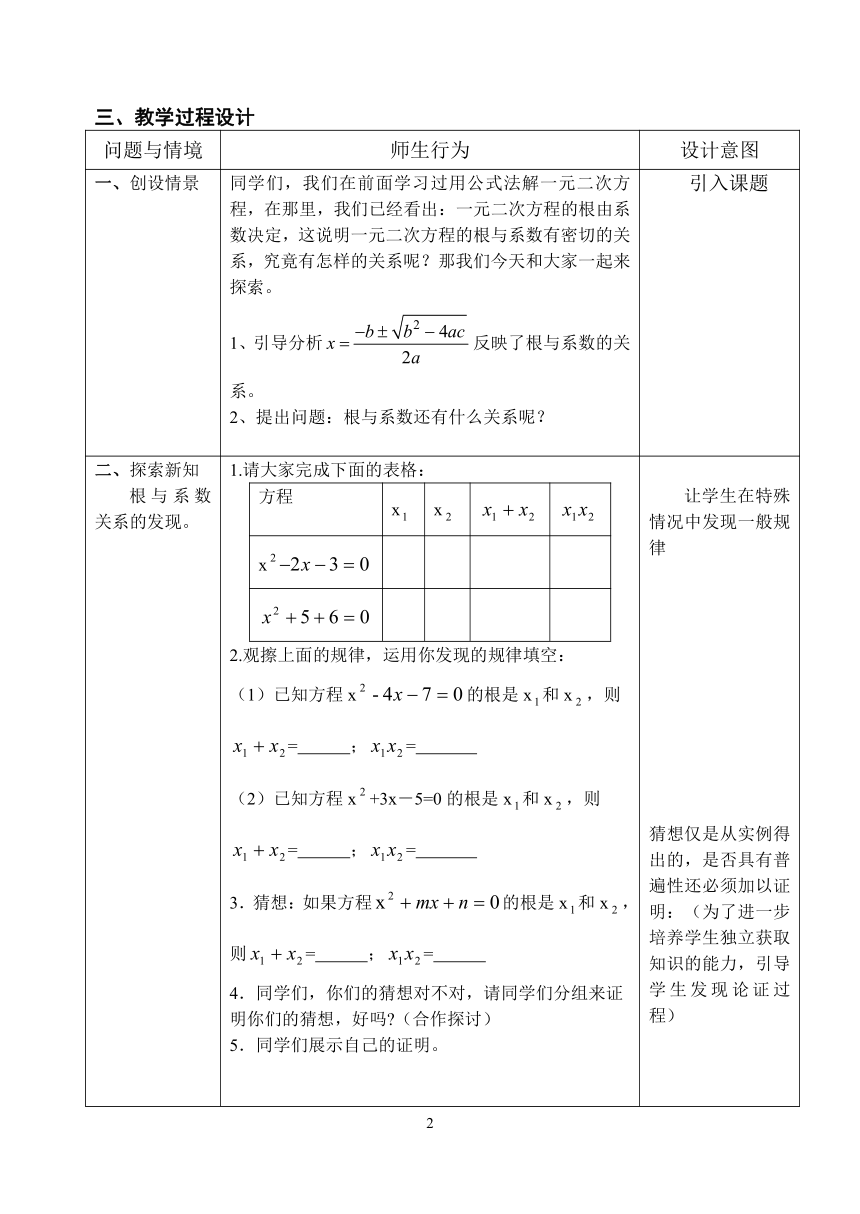
一、创设情景 同学们,我们在前面学习过用公式法解一元二次方程,在那里,我们已经看出:一元二次方程的根由系数决定,这说明一元二次方程的根与系数有密切的关系,究竟有怎样的关系呢?那我们今天和大家一起来探索。1、引导分析反映了根与系数的关系。2、提出问题:根与系数还有什么关系呢? 引入课题
二、探索新知根与系数关系的发现。 1.请大家完成下面的表格:方程xxx2.观擦上面的规律,运用你发现的规律填空:(1)已知方程x的根是x和x,则= ;= (2)已知方程x+3x-5=0的根是x和x,则= ;= 3.猜想:如果方程的根是x和x,则= ;= 4.同学们,你们的猜想对不对,请同学们分组来证明你们的猜想,好吗 (合作探讨)5.同学们展示自己的证明。6.(教师演示) 如果方程的根是x和x,那么=-m,=n 证明:方程的△=m 当△=m≥0时,方程的根是x=,x= =+=m==n7.(分组合作)如果方程的根是x和x,那么 = ;= 这个问题如果学生能正确作出猜想,又可以追问学生是怎么猜出来的,让其回顾思维过程,加深理解,如果猜不出可以启发:二次项系数不是1时,怎样把它化为1?此时你的猜想是什么?学生定能根据问题1的规律,顺利地作出猜想,而且还可以发现两个猜想之间的关系(由特殊到一般),还可以使学生今后运用这一知识时减少忘记除以二次项系数的错误。 让学生在特殊情况中发现一般规律猜想仅是从实例得出的,是否具有普遍性还必须加以证明:(为了进一步培养学生独立获取知识的能力,引导学生发现论证过程)这两个问题的设计,既使学生复习了一元二次方程的两种重要解法,又为学生发现根与系数的关系的规律起到了牵线搭桥的作用,通过已有的知识引出了根与系数的关系的“发现过程”,有利于难点的突破,培养了学生观察、分析、归纳的能力。让学生了解数学知识的严密性,当学生证出了自己探索出来的结论时,会表现出一种成就感。
三、应用新知 例1已知方程的一个根是3,求方程的另一个根及c的值。解.设方程的另一个根是,则 3+=2 解之得=-1。 ∵3=c ∴3×(-1)=c ∴c=-3 故:方程的另一个根是-1,c=-3。例2已知方程的根是x和x,求下列式子的值: (1) + (2)解.由一元二次方程根与系数的关系知:=5,=-6 (1)原式=+2- = =5-(-6) =31(2)原式= = = = 激发学生的探究欲望,提高学习的积极性
四、信息反馈 填空:如果方程2的两个根分别是x和x,则= ; = 已知方程的一个根是2,求方程的另一个根及的值。 考查学生掌握情况
五、课堂小结与作业布置 小结:1、一元二次方程根与系数关系;2、(1)要把方程化为一般形式;(2)不要忘记除以二次项的系数“a”;(3)不要漏掉“”中的“-”号.作业:课本43页 第7题 知识巩固
PAGE
1
一、教学任务分析
教学目标 知识技能 1、使学生掌握一元二次方程的根与系数的关系,并能初步应用。2、提高学生的观察、分析以及推理论证的能力。
数学思考 学生经历观察→发现→猜想→证明的思维过程,培养学生的分析能力和解决问题的能力。
解决问题 能运用根与系数的关系求:已知方程的一个根,求方程的另一个根及待定系数;根据方程求代数式的值。
情感态度 使学生理解事物都是相互联系、相互制约的辩证唯物主义观点以及“特殊——一般——特殊”的基本思想方法。
重点 一元二次方程的根与系数的关系及应用。
难点 一元二次方程的根与系数的关系的发现和准确掌握。
二、教学流程安排
活动流程图 活动内容和目的
创设情景二、探索新知根与系数关系的发现。三、应用新知四、信息反馈五、课堂小结与作业布置 引入课题让学生在特殊情况中发现一般规律激发学生的探究欲望,提高学习的积极性知识考查知识巩固
三、教学过程设计
问题与情境 师生行为 设计意图
一、创设情景 同学们,我们在前面学习过用公式法解一元二次方程,在那里,我们已经看出:一元二次方程的根由系数决定,这说明一元二次方程的根与系数有密切的关系,究竟有怎样的关系呢?那我们今天和大家一起来探索。1、引导分析反映了根与系数的关系。2、提出问题:根与系数还有什么关系呢? 引入课题
二、探索新知根与系数关系的发现。 1.请大家完成下面的表格:方程xxx2.观擦上面的规律,运用你发现的规律填空:(1)已知方程x的根是x和x,则= ;= (2)已知方程x+3x-5=0的根是x和x,则= ;= 3.猜想:如果方程的根是x和x,则= ;= 4.同学们,你们的猜想对不对,请同学们分组来证明你们的猜想,好吗 (合作探讨)5.同学们展示自己的证明。6.(教师演示) 如果方程的根是x和x,那么=-m,=n 证明:方程的△=m 当△=m≥0时,方程的根是x=,x= =+=m==n7.(分组合作)如果方程的根是x和x,那么 = ;= 这个问题如果学生能正确作出猜想,又可以追问学生是怎么猜出来的,让其回顾思维过程,加深理解,如果猜不出可以启发:二次项系数不是1时,怎样把它化为1?此时你的猜想是什么?学生定能根据问题1的规律,顺利地作出猜想,而且还可以发现两个猜想之间的关系(由特殊到一般),还可以使学生今后运用这一知识时减少忘记除以二次项系数的错误。 让学生在特殊情况中发现一般规律猜想仅是从实例得出的,是否具有普遍性还必须加以证明:(为了进一步培养学生独立获取知识的能力,引导学生发现论证过程)这两个问题的设计,既使学生复习了一元二次方程的两种重要解法,又为学生发现根与系数的关系的规律起到了牵线搭桥的作用,通过已有的知识引出了根与系数的关系的“发现过程”,有利于难点的突破,培养了学生观察、分析、归纳的能力。让学生了解数学知识的严密性,当学生证出了自己探索出来的结论时,会表现出一种成就感。
三、应用新知 例1已知方程的一个根是3,求方程的另一个根及c的值。解.设方程的另一个根是,则 3+=2 解之得=-1。 ∵3=c ∴3×(-1)=c ∴c=-3 故:方程的另一个根是-1,c=-3。例2已知方程的根是x和x,求下列式子的值: (1) + (2)解.由一元二次方程根与系数的关系知:=5,=-6 (1)原式=+2- = =5-(-6) =31(2)原式= = = = 激发学生的探究欲望,提高学习的积极性
四、信息反馈 填空:如果方程2的两个根分别是x和x,则= ; = 已知方程的一个根是2,求方程的另一个根及的值。 考查学生掌握情况
五、课堂小结与作业布置 小结:1、一元二次方程根与系数关系;2、(1)要把方程化为一般形式;(2)不要忘记除以二次项的系数“a”;(3)不要漏掉“”中的“-”号.作业:课本43页 第7题 知识巩固
PAGE
1
同课章节目录
