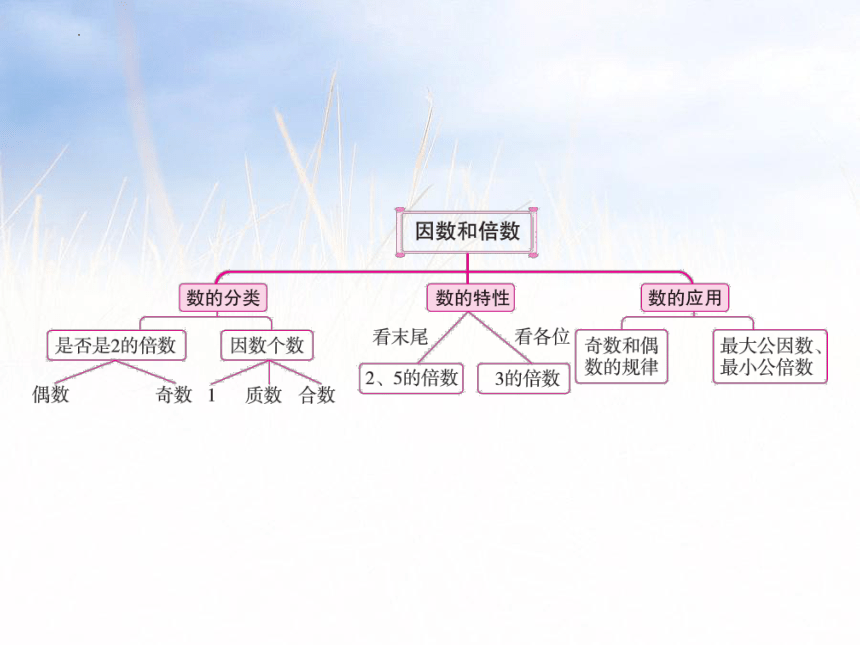
六年级下册数学通用版总复习 第2课时 因数和倍数课件(共29张PPT)
文档属性
| 名称 | 六年级下册数学通用版总复习 第2课时 因数和倍数课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 27.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-18 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
小学数学系统总复习
通用版
数与代数
专题一 数的认识
第2课时 因数和倍数
考点一
因数和倍数的意义
1.因数和倍数是相互依存的关系,不能说“ A 是因数”或“ C 是倍数”。
2.方法:
(1)找因数:把一个数写成两个自然数相乘的形式,所有算式
中的因数即为这个数的全部因数。如 12=1×12=2×6=3×4 ,
所以12的因数有1、2、3、4、6、12。一个数的因数的个数是
有限的,其中最小的是1,最大的是它本身。
(2)找倍数:一个数和任意非零自然数的乘积都是这个数的倍
数。一个数的倍数的个数是无限的,其中最小的是它本身。
例1 雪雪在写24的所有因数时写了8个:1、24、2、3、8、4、
6,按照她的思考方法,她漏掉了排在( ) 后面的( ) 。
2
12
根据上面总结的方法,我们可以将24写成两数相乘的形式,即24=1×24=2×12=3×8=4×6,将算式的每个因数与雪雪写的顺序进行对比,即可得到答案。
【解答】答案请填在题中。
【跟踪练习】
1.下面说法正确的是( ) 。
D
A. 16÷2=8 ,16是倍数,2是因数
B.10是2.5的4倍,所以10是2.5的倍数, 2.5 是10的因数
C.一个数的倍数一定大于它的因数
D.如果自然数 a 是自然数 b 的倍数,那么 a≥b
2.任何一个自然数的因数中都有1和它本身,我们把小于它本身的
因数叫作这个自然数的真因数。如6的所有真因数是1、2、3,而
且 6=1+2+3 ,像这样的数叫完全数。下列各数中( ) 是完全数。
C
A.8 B.16 C.28 D.30
考点二
2、3、5的倍数特征
2的倍数特征:个位上的数字是0、2、4、6或8。
3的倍数特征:各个数位上的数字之和是3的倍数。
5的倍数特征:个位上的数字是0或5。
例2 一个三位数,既含有因数2,又是3和5的倍数,这个数最
大是( ) ,最小是( ) 。
990
120
分析题意可知,我们要找的三位数必须同时具备2、3、5的倍数特征。2和5的倍数的共同特征是个位上的数字是0,再结合3的倍数特征,要让这个数最大,百位和十位上都要是9。而要让这个数最小,则百位上为1,十位上为2。
【解答】答案请填在题中。
【跟踪练习】
3.下面是四个用字母表示的五位数,其中 a 、 b 各代表一个数字,
且 a=0 , b≠0 。下面各数一定既是3的倍数又是5的倍数的是
( ) 。
C
A. B. C. D.
4.一个三位数46 ,当 里填( ) 时,它同时是2和5的倍
数;当 里填( ) 时,它同时是3和5的倍数;当 里填
( ) 时,它同时是2和3的倍数。
0
5
2或8
5.从3、4、5、6、0这五个数字中任选三个,组成的三位数是2、
3和5的公倍数,这个三位数最大是( ) 。
630
考点三
奇数和偶数
类别 加减法规律 乘法规律
两个奇数 奇 + 奇 = 偶 奇-奇 = 偶 奇×奇 = 奇
两个偶数 偶 ± 偶 = 偶 偶×偶 = 偶
一奇一偶 奇 ± 偶 = 奇 偶-奇 = 奇 奇×偶 = 偶
例3 在 7a+3 、 2a 1 、 3a+2 、 a 、 a+5 表示数的式子( a 为整
数)中,至少有( ) 个偶数。
2
根据奇数与偶数的加减法和乘法规律分情况讨论:当a为偶数
时, 3a+2 、 a 为偶数;当 a 为奇数时, 7a+3 、 a+5 为偶数,
因此至少有2个偶数。本题也可用假设法,首先假设 a 为某个具
体的奇数或偶数,然后计算出每个算式的得数,最后判断奇偶。
【解答】答案请填在题中。
【跟踪练习】
6. m 是一个偶数, n 是一个奇数,下面的算式中,结果是奇数
的是( ) 。
B
A. 2(m+n) B. m+n2 C. 5m+4n D. 3mn+2
7.已知五个连续的奇数之和是135,这五个连续的奇数中最小的
奇数是( ) 。
23
考点四
质数和合数
1.0和1既不是质数,也不是合数。除0和2以外所有的偶数都是
合数,除2以外所有的质数都是奇数。
2.分解质因数的方法:(以80为例)
分解法: 短除法:
例4 小安的电脑开机密码是一个四位数 ABCD ,其中 A 是10以
内最大的质数, B 是最小的奇数, C 是最小的合数, D 既是奇数
又是合数,这个密码是( ) 。
7149
根据条件,将每个字母代表的数字找出来。10以内最大的质数是7,最小的奇数是1,最小的合数是4,既是奇数又是合数的一位数为9,按照字母顺序写出答案即可。
【解答】答案请填在题中。
【跟踪练习】
8.用 和 这两张数字卡片组成的所有两位数,一定都是
( ) 。
D
A.奇数 B.偶数 C.质数 D.合数
9.一个九位数亿位上是最小的合数,百万位上是最小的质数,
千位上是最大的一位数,其余各位上都是0,这个数写作
( ) ,读作( ) 。
402009000
四亿零二百万九千
10.已知 M×N 1=A ,其中 M 和 N 均为质数且小于100, A 是奇
数,那么 A 最大是( ) 。
193
考点五
公因数与公倍数
1.求最大公因数的方法:
(1)枚举法、短除法。
(2)当两数成倍数关系时,较小数就是这两个数的最大公因数;
当两数互质时,它们的最大公因数是1。
2.求最小公倍数的方法:
(1)枚举法、短除法。
(2)当两数成倍数关系时,较大数就是这两个数的最小公倍数;
当两数互质时,最小公倍数是它们的乘积。
例5 已知 P=2×3×n , Q=3×3×n ,如果 P 、 Q 的最大公因数是1
5,那么 n=(5) , P 、 Q 的最小公倍数是( ) 。
90
P 和 Q 公有的质因数是3和 n ,最大公因数是
3×n=15 ,即可求出 n 的值。将 P 和 Q 公有的质因数与独有的质
因数相乘即可得到 P 和 Q 的最小公倍数。
【解答】答案请填在题中。
【跟踪练习】
11.把自然数 a 、 b 分解质因数,若分别得到 a=2×5×7×m ,
b=3×5×m ,则 a 与 b 的最大公因数是( ) ,最小公倍数是
( ) 。
5m
210m
12.明明帮妈妈裁纸,要将一张长 30 cm 、宽 20 cm 的长方形彩
纸裁成一些大小相同的小正方形,且没有材料剩余,这个小正
方形的边长最大是( ) cm 。如果要用几张同样的这种长方
形彩纸拼成一个大正方形,那么这个大正方形的边长最小是
( ) cm 。
10
60
13.实验小学六年级同学参加植树活动,无论每行植4棵、6棵还是7棵,最后一行都会多1棵,已知树苗的总棵数不超过100棵,这批树苗一共有多少棵?
4、6和7的最小公倍数为 84 84+1=85 (棵)
85<100 ,树苗一共有85棵
谢谢!同学们再见!
小学数学系统总复习
通用版
数与代数
专题一 数的认识
第2课时 因数和倍数
考点一
因数和倍数的意义
1.因数和倍数是相互依存的关系,不能说“ A 是因数”或“ C 是倍数”。
2.方法:
(1)找因数:把一个数写成两个自然数相乘的形式,所有算式
中的因数即为这个数的全部因数。如 12=1×12=2×6=3×4 ,
所以12的因数有1、2、3、4、6、12。一个数的因数的个数是
有限的,其中最小的是1,最大的是它本身。
(2)找倍数:一个数和任意非零自然数的乘积都是这个数的倍
数。一个数的倍数的个数是无限的,其中最小的是它本身。
例1 雪雪在写24的所有因数时写了8个:1、24、2、3、8、4、
6,按照她的思考方法,她漏掉了排在( ) 后面的( ) 。
2
12
根据上面总结的方法,我们可以将24写成两数相乘的形式,即24=1×24=2×12=3×8=4×6,将算式的每个因数与雪雪写的顺序进行对比,即可得到答案。
【解答】答案请填在题中。
【跟踪练习】
1.下面说法正确的是( ) 。
D
A. 16÷2=8 ,16是倍数,2是因数
B.10是2.5的4倍,所以10是2.5的倍数, 2.5 是10的因数
C.一个数的倍数一定大于它的因数
D.如果自然数 a 是自然数 b 的倍数,那么 a≥b
2.任何一个自然数的因数中都有1和它本身,我们把小于它本身的
因数叫作这个自然数的真因数。如6的所有真因数是1、2、3,而
且 6=1+2+3 ,像这样的数叫完全数。下列各数中( ) 是完全数。
C
A.8 B.16 C.28 D.30
考点二
2、3、5的倍数特征
2的倍数特征:个位上的数字是0、2、4、6或8。
3的倍数特征:各个数位上的数字之和是3的倍数。
5的倍数特征:个位上的数字是0或5。
例2 一个三位数,既含有因数2,又是3和5的倍数,这个数最
大是( ) ,最小是( ) 。
990
120
分析题意可知,我们要找的三位数必须同时具备2、3、5的倍数特征。2和5的倍数的共同特征是个位上的数字是0,再结合3的倍数特征,要让这个数最大,百位和十位上都要是9。而要让这个数最小,则百位上为1,十位上为2。
【解答】答案请填在题中。
【跟踪练习】
3.下面是四个用字母表示的五位数,其中 a 、 b 各代表一个数字,
且 a=0 , b≠0 。下面各数一定既是3的倍数又是5的倍数的是
( ) 。
C
A. B. C. D.
4.一个三位数46 ,当 里填( ) 时,它同时是2和5的倍
数;当 里填( ) 时,它同时是3和5的倍数;当 里填
( ) 时,它同时是2和3的倍数。
0
5
2或8
5.从3、4、5、6、0这五个数字中任选三个,组成的三位数是2、
3和5的公倍数,这个三位数最大是( ) 。
630
考点三
奇数和偶数
类别 加减法规律 乘法规律
两个奇数 奇 + 奇 = 偶 奇-奇 = 偶 奇×奇 = 奇
两个偶数 偶 ± 偶 = 偶 偶×偶 = 偶
一奇一偶 奇 ± 偶 = 奇 偶-奇 = 奇 奇×偶 = 偶
例3 在 7a+3 、 2a 1 、 3a+2 、 a 、 a+5 表示数的式子( a 为整
数)中,至少有( ) 个偶数。
2
根据奇数与偶数的加减法和乘法规律分情况讨论:当a为偶数
时, 3a+2 、 a 为偶数;当 a 为奇数时, 7a+3 、 a+5 为偶数,
因此至少有2个偶数。本题也可用假设法,首先假设 a 为某个具
体的奇数或偶数,然后计算出每个算式的得数,最后判断奇偶。
【解答】答案请填在题中。
【跟踪练习】
6. m 是一个偶数, n 是一个奇数,下面的算式中,结果是奇数
的是( ) 。
B
A. 2(m+n) B. m+n2 C. 5m+4n D. 3mn+2
7.已知五个连续的奇数之和是135,这五个连续的奇数中最小的
奇数是( ) 。
23
考点四
质数和合数
1.0和1既不是质数,也不是合数。除0和2以外所有的偶数都是
合数,除2以外所有的质数都是奇数。
2.分解质因数的方法:(以80为例)
分解法: 短除法:
例4 小安的电脑开机密码是一个四位数 ABCD ,其中 A 是10以
内最大的质数, B 是最小的奇数, C 是最小的合数, D 既是奇数
又是合数,这个密码是( ) 。
7149
根据条件,将每个字母代表的数字找出来。10以内最大的质数是7,最小的奇数是1,最小的合数是4,既是奇数又是合数的一位数为9,按照字母顺序写出答案即可。
【解答】答案请填在题中。
【跟踪练习】
8.用 和 这两张数字卡片组成的所有两位数,一定都是
( ) 。
D
A.奇数 B.偶数 C.质数 D.合数
9.一个九位数亿位上是最小的合数,百万位上是最小的质数,
千位上是最大的一位数,其余各位上都是0,这个数写作
( ) ,读作( ) 。
402009000
四亿零二百万九千
10.已知 M×N 1=A ,其中 M 和 N 均为质数且小于100, A 是奇
数,那么 A 最大是( ) 。
193
考点五
公因数与公倍数
1.求最大公因数的方法:
(1)枚举法、短除法。
(2)当两数成倍数关系时,较小数就是这两个数的最大公因数;
当两数互质时,它们的最大公因数是1。
2.求最小公倍数的方法:
(1)枚举法、短除法。
(2)当两数成倍数关系时,较大数就是这两个数的最小公倍数;
当两数互质时,最小公倍数是它们的乘积。
例5 已知 P=2×3×n , Q=3×3×n ,如果 P 、 Q 的最大公因数是1
5,那么 n=(5) , P 、 Q 的最小公倍数是( ) 。
90
P 和 Q 公有的质因数是3和 n ,最大公因数是
3×n=15 ,即可求出 n 的值。将 P 和 Q 公有的质因数与独有的质
因数相乘即可得到 P 和 Q 的最小公倍数。
【解答】答案请填在题中。
【跟踪练习】
11.把自然数 a 、 b 分解质因数,若分别得到 a=2×5×7×m ,
b=3×5×m ,则 a 与 b 的最大公因数是( ) ,最小公倍数是
( ) 。
5m
210m
12.明明帮妈妈裁纸,要将一张长 30 cm 、宽 20 cm 的长方形彩
纸裁成一些大小相同的小正方形,且没有材料剩余,这个小正
方形的边长最大是( ) cm 。如果要用几张同样的这种长方
形彩纸拼成一个大正方形,那么这个大正方形的边长最小是
( ) cm 。
10
60
13.实验小学六年级同学参加植树活动,无论每行植4棵、6棵还是7棵,最后一行都会多1棵,已知树苗的总棵数不超过100棵,这批树苗一共有多少棵?
4、6和7的最小公倍数为 84 84+1=85 (棵)
85<100 ,树苗一共有85棵
谢谢!同学们再见!
