27.3位似 教学设计
图片预览

文档简介
位似作图教学设计
一、教学任务分析
教学目标 知识技能 1.掌握图形的位似概念,会判断简单的位似图形和位似中心。2.理解位似图形的性质,掌握以坐标原点为位似中心的位似变换的性质。
数学思考 1.理解位似图形的概念,选择适当的方式进行图形放大与缩小.2.从具体操作活动中,培养学生动手操作能力。
解决问题 能够熟练准确地利用坐标变化将一个图形放大与缩小,并能解决一些简单的实际问题。
情感态度 在观察、操作、推理、归纳等探索过程中,获得成功的体验,感受数学的无处不在,锻炼克服困难的意志,建立学好数学的自信心.
重点 能根据位似图形的特征, 及坐标变化规律.将一个图形放大与缩小.
难点 选择适当的方式进行图形放大与缩小.
二、教学流程安排
活动流程图 活动内容和目的
活动一.创设情景,复习概念和性质活动二.复习画位似图形的步骤活动三.在平面直角坐标系中进行位似变换活动四.应用练习,拓展提高活动五.回顾小结,梳理知识活动六.自我评价,检测知识 复习位似概念、性质,通过练习辨别位似图形,巩固位似图形的概念,并从生活中实例来认识理解位似图形与相似图形的区别与联系,从而加深对位似图形概念的理解. 及性质的掌握:相似,对应顶点的连线相交于一点, 对应边平行或在一条直线上。掌握位似图形的画法步骤,通过作图理解符合要求的图形不惟一,这和所作的图形与所确定的位似中心的位置有关。因此,位似中心的确定是作出图形的关键.以坐标原点为位似中心的位似变换的性质:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k。的掌握,认识到在平面直角坐标系中,用图形的坐标的变化来表示图形的位似变换的关键是要确定位似图形各个顶点的坐标,而不同方法得到的图形坐标是不同的.通过练习进一步巩固概念、性质、规律、作图方法,使学生能真正的把握知识。谈谈本节课的收获:知识点,数学思想和方法。能回顾整理知识和数学思想方法,能力得以升华。通过作图,填空,选择,等形式的训练内容,引导学生攀登知识高峰。
三、教学过程设计
问题与情境 师生行为 设计意图
活动一.创设情景,复习概念和性质1.复习位似概念、性质2.练习:判断下面的正方形是不是位似图形? 3.生活中,哪些应用到位似 学生回答,举生活中实例说明. 概念强调:相似,对应顶点的连线相交于一点, 对应边平行或在一条直线上。显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形 性质:位似图形上的任意一对对应点到位似中心的距离之比等于位似比 学生举例,交流 通过练习辨别位似图形,巩固位似图形的概念,从生活中实例来认识理解位似图形与相似图形的区别与联系,从而加深对位似图形概念的理解.
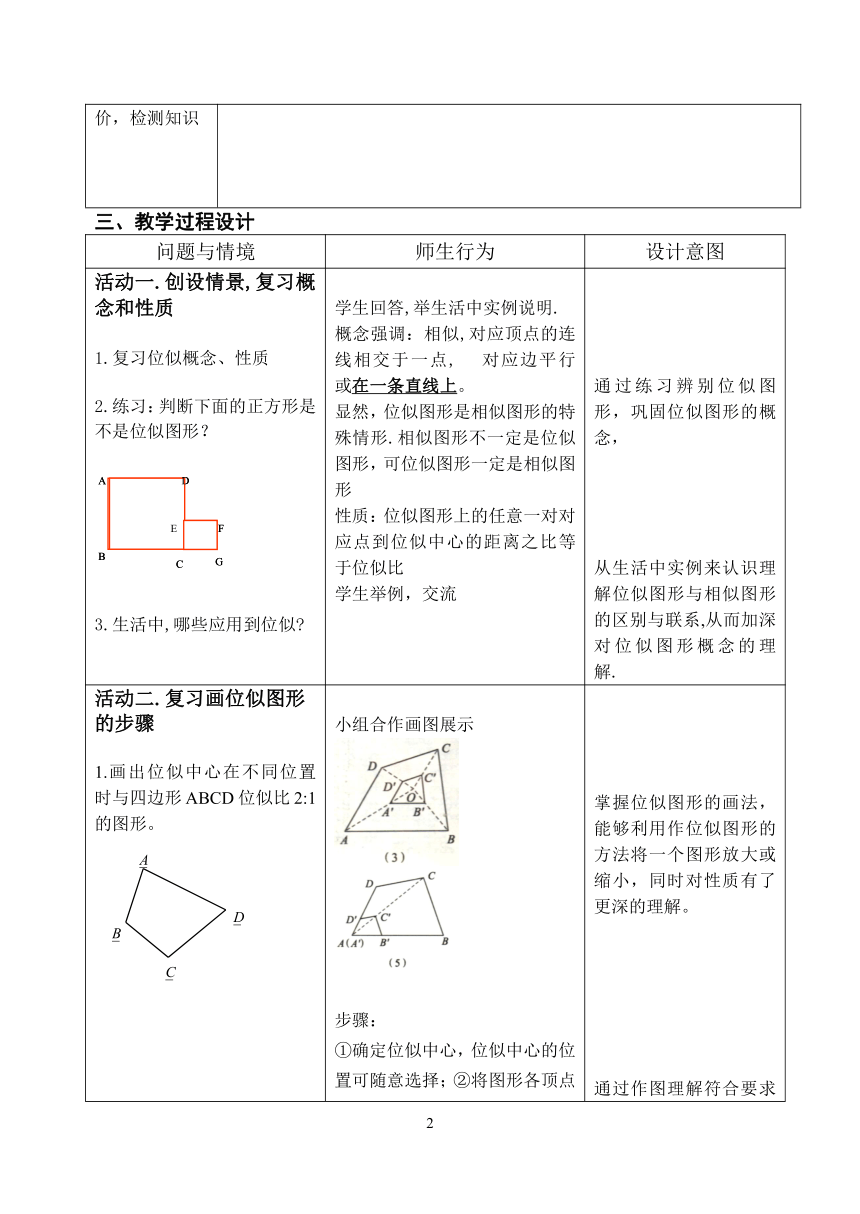
活动二.复习画位似图形的步骤1.画出位似中心在不同位置时与四边形ABCD位似比2:1的图形。 小组合作画图展示步骤:①确定位似中心,位似中心的位置可随意选择;②将图形各顶点与位似中心连接(或延长);③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;④顺次连接各点,所得的图形就是所求的图形.巡视指导,帮助学困生。 掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小,同时对性质有了更深的理解。通过作图理解符合要求的图形不惟一,这和所作的图形与所确定的位似中心的位置有关。因此,位似中心的确定是作出图形的关键.
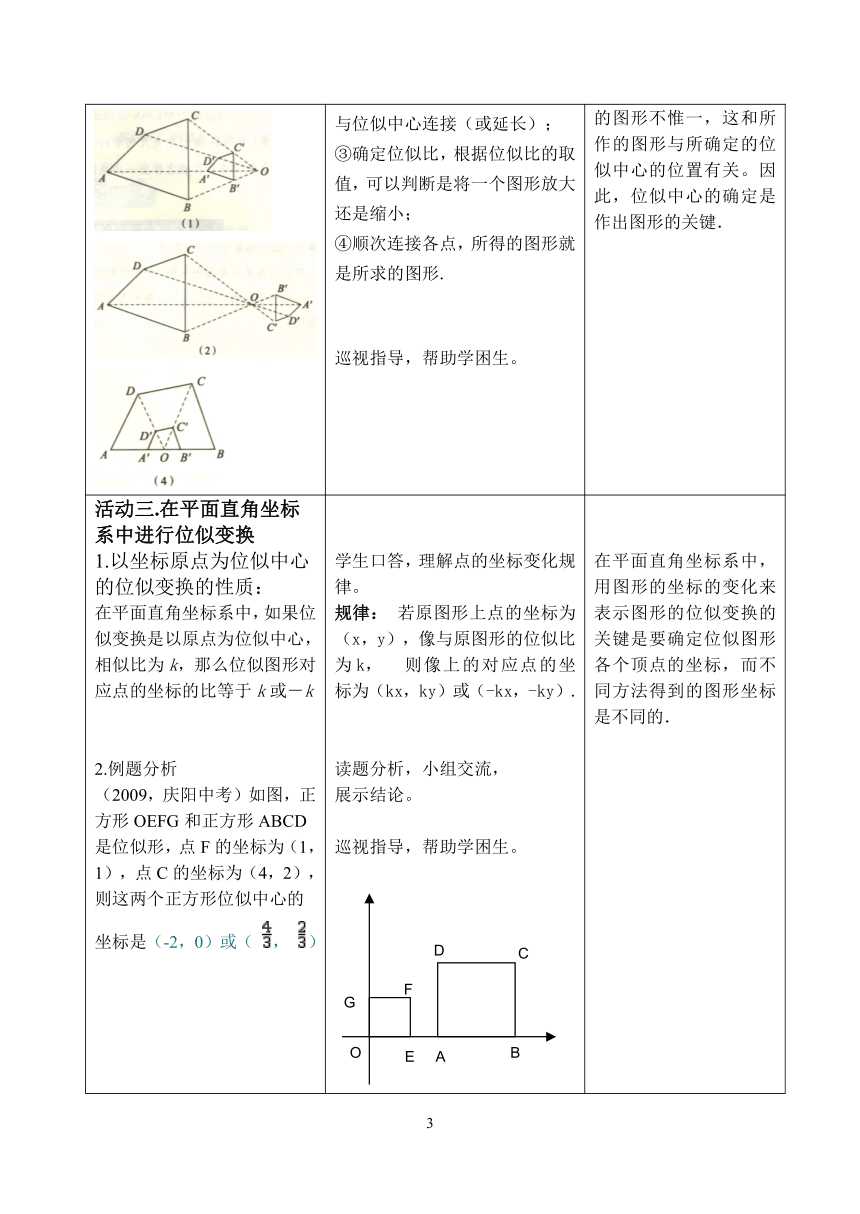
活动三.在平面直角坐标系中进行位似变换1.以坐标原点为位似中心的位似变换的性质:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k2.例题分析(2009,庆阳中考)如图,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是(-2,0)或( , )(-2,0)或( )活动四.应用练习,拓展提高1.如图,菱形ABCD中,对角线AC、BD相交于点O,M、N分别是边AB、AD的中点,连接OM、ON、MN,则下列叙述正确的是(C)A.△AOM和△AON都是等边三角形B.四边形MBON和四边形MODN都是菱形C.四边形AMON和四边形ABCD是位似图形D.四边形MBCO和四边形NDCO都是等腰梯形2、(2010,湖州)如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标是_( 9,0)_.3、如图所示ΔABC在方格纸中,(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;(2)以原点O为位似中心,相似比为2,在第一象限内将ΔABC放大,画出放大后的图形ΔA1B1C1(3)计算ΔA1B1C1的面积S 学生口答,理解点的坐标变化规律。规律: 若原图形上点的坐标为(x,y),像与原图形的位似比为k, 则像上的对应点的坐标为(kx,ky)或(-kx,-ky).读题分析,小组交流,展示结论。巡视指导,帮助学困生。独立完成练习,并进行相互纠错。在学生独立完成的基础上,引导学生进行自我纠错。【解析】因为菱形ABCD的内角度数不确定,所以△AOM与△AON不一定是等边三角形;四边形MBON和四边形MODN是平行四边形,但不一定是菱形;同样,因为AB不一定等于AC,所以BM不一定等于OC,所以四边形MBCO和四边形NDCO不一定是等腰梯形,故只有C正确.点评:利用位似将图形放大或缩小的作图步骤:第一步:在原图上选取关键点若干个,并在原图外任取一点P;第二步:以点P为端点向关键点作射线;第三步:分别在射线上取关键点的对应点,满足放缩比例;第四步:顺次连接截取点,即可得到符合要求的新图形。 在平面直角坐标系中,用图形的坐标的变化来表示图形的位似变换的关键是要确定位似图形各个顶点的坐标,而不同方法得到的图形坐标是不同的.通过本题巩固位似概念,加深理解:判断两个图形位似时,一要注意两个图形是相似图形;二要两个图形每组对应顶点所在的直线都相交于一点;三要对应边互相平行或重合.考察学生对位似中心的掌握通过本体熟练把握作图的基本步骤
活动五.回顾小结,梳理知识今天你学会了什么? 谈谈本节课的收获:知识点,数学思想和方法。生生互动、师生互动 回顾整理知识和数学思想方法,能力升华。
活动六.自我评价,检测知识1.任给一个△ABC,你能利用位似图形的特点,在三角形内作出有一边在BC上的最大的正方形吗?试一试,若能,则画出示意图并写出作法和理由。2.(2008青海)如图, HYPERLINK "http://www./" 是由经过位似变换得到的,点是位似中心,分别是的中点,则与的面积比是( ) A. B. C. D.3.(2008威海市)如图,已知△EFH和△MNK是位似图形,那么其位似中心是点( )4.如图,△ABC三个顶点的坐标分别为A (2,7),B (6,8),C (8,2),请你分别完成下面的作图并标出所有顶点的坐标.(不要求写出作法)⑴以O为位似中心,在第三象限内作出△A1B1C1,使△A1B1C1与△ABC的位似比为1:2;
⑵以O为旋转中心,将△ABC沿顺时针方向旋转900得到△A2B2C2.(3)向左平移8个单位;5.(江苏淮安)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1). (1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形; (2)分别写出B、C两点的对应点B′、C′的坐标; (3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标. 合作学习、生生互动 给出课外合作学习内容,引导学生攀登知识高峰。反思:★若以点O为位似中心在y轴的左侧将△OBC放大到n倍,则对应点坐标为原坐标的倍★若以点O为位似中心在y轴的右侧将△OBC放大到n倍,则对应点坐标为原坐标的倍
A
C
D
B
F
E
G
A
C
D
B
F
E
G
_
D
_
C
_
B
_
A
第15题
x
10
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
11
A1
B1
C1
A
B
C
y
第13题图
A
x
y
B
C
1
1
-1
O
A
B
C
D
O
E
F
G
C
A
BA
DA
OA
EA
FA
第2题图
H
E
F
M
N
K
A
B
C
D
y
B
C
A
O
x
PAGE
6
一、教学任务分析
教学目标 知识技能 1.掌握图形的位似概念,会判断简单的位似图形和位似中心。2.理解位似图形的性质,掌握以坐标原点为位似中心的位似变换的性质。
数学思考 1.理解位似图形的概念,选择适当的方式进行图形放大与缩小.2.从具体操作活动中,培养学生动手操作能力。
解决问题 能够熟练准确地利用坐标变化将一个图形放大与缩小,并能解决一些简单的实际问题。
情感态度 在观察、操作、推理、归纳等探索过程中,获得成功的体验,感受数学的无处不在,锻炼克服困难的意志,建立学好数学的自信心.
重点 能根据位似图形的特征, 及坐标变化规律.将一个图形放大与缩小.
难点 选择适当的方式进行图形放大与缩小.
二、教学流程安排
活动流程图 活动内容和目的
活动一.创设情景,复习概念和性质活动二.复习画位似图形的步骤活动三.在平面直角坐标系中进行位似变换活动四.应用练习,拓展提高活动五.回顾小结,梳理知识活动六.自我评价,检测知识 复习位似概念、性质,通过练习辨别位似图形,巩固位似图形的概念,并从生活中实例来认识理解位似图形与相似图形的区别与联系,从而加深对位似图形概念的理解. 及性质的掌握:相似,对应顶点的连线相交于一点, 对应边平行或在一条直线上。掌握位似图形的画法步骤,通过作图理解符合要求的图形不惟一,这和所作的图形与所确定的位似中心的位置有关。因此,位似中心的确定是作出图形的关键.以坐标原点为位似中心的位似变换的性质:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k。的掌握,认识到在平面直角坐标系中,用图形的坐标的变化来表示图形的位似变换的关键是要确定位似图形各个顶点的坐标,而不同方法得到的图形坐标是不同的.通过练习进一步巩固概念、性质、规律、作图方法,使学生能真正的把握知识。谈谈本节课的收获:知识点,数学思想和方法。能回顾整理知识和数学思想方法,能力得以升华。通过作图,填空,选择,等形式的训练内容,引导学生攀登知识高峰。
三、教学过程设计
问题与情境 师生行为 设计意图
活动一.创设情景,复习概念和性质1.复习位似概念、性质2.练习:判断下面的正方形是不是位似图形? 3.生活中,哪些应用到位似 学生回答,举生活中实例说明. 概念强调:相似,对应顶点的连线相交于一点, 对应边平行或在一条直线上。显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形 性质:位似图形上的任意一对对应点到位似中心的距离之比等于位似比 学生举例,交流 通过练习辨别位似图形,巩固位似图形的概念,从生活中实例来认识理解位似图形与相似图形的区别与联系,从而加深对位似图形概念的理解.
活动二.复习画位似图形的步骤1.画出位似中心在不同位置时与四边形ABCD位似比2:1的图形。 小组合作画图展示步骤:①确定位似中心,位似中心的位置可随意选择;②将图形各顶点与位似中心连接(或延长);③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;④顺次连接各点,所得的图形就是所求的图形.巡视指导,帮助学困生。 掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小,同时对性质有了更深的理解。通过作图理解符合要求的图形不惟一,这和所作的图形与所确定的位似中心的位置有关。因此,位似中心的确定是作出图形的关键.
活动三.在平面直角坐标系中进行位似变换1.以坐标原点为位似中心的位似变换的性质:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k2.例题分析(2009,庆阳中考)如图,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是(-2,0)或( , )(-2,0)或( )活动四.应用练习,拓展提高1.如图,菱形ABCD中,对角线AC、BD相交于点O,M、N分别是边AB、AD的中点,连接OM、ON、MN,则下列叙述正确的是(C)A.△AOM和△AON都是等边三角形B.四边形MBON和四边形MODN都是菱形C.四边形AMON和四边形ABCD是位似图形D.四边形MBCO和四边形NDCO都是等腰梯形2、(2010,湖州)如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标是_( 9,0)_.3、如图所示ΔABC在方格纸中,(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;(2)以原点O为位似中心,相似比为2,在第一象限内将ΔABC放大,画出放大后的图形ΔA1B1C1(3)计算ΔA1B1C1的面积S 学生口答,理解点的坐标变化规律。规律: 若原图形上点的坐标为(x,y),像与原图形的位似比为k, 则像上的对应点的坐标为(kx,ky)或(-kx,-ky).读题分析,小组交流,展示结论。巡视指导,帮助学困生。独立完成练习,并进行相互纠错。在学生独立完成的基础上,引导学生进行自我纠错。【解析】因为菱形ABCD的内角度数不确定,所以△AOM与△AON不一定是等边三角形;四边形MBON和四边形MODN是平行四边形,但不一定是菱形;同样,因为AB不一定等于AC,所以BM不一定等于OC,所以四边形MBCO和四边形NDCO不一定是等腰梯形,故只有C正确.点评:利用位似将图形放大或缩小的作图步骤:第一步:在原图上选取关键点若干个,并在原图外任取一点P;第二步:以点P为端点向关键点作射线;第三步:分别在射线上取关键点的对应点,满足放缩比例;第四步:顺次连接截取点,即可得到符合要求的新图形。 在平面直角坐标系中,用图形的坐标的变化来表示图形的位似变换的关键是要确定位似图形各个顶点的坐标,而不同方法得到的图形坐标是不同的.通过本题巩固位似概念,加深理解:判断两个图形位似时,一要注意两个图形是相似图形;二要两个图形每组对应顶点所在的直线都相交于一点;三要对应边互相平行或重合.考察学生对位似中心的掌握通过本体熟练把握作图的基本步骤
活动五.回顾小结,梳理知识今天你学会了什么? 谈谈本节课的收获:知识点,数学思想和方法。生生互动、师生互动 回顾整理知识和数学思想方法,能力升华。
活动六.自我评价,检测知识1.任给一个△ABC,你能利用位似图形的特点,在三角形内作出有一边在BC上的最大的正方形吗?试一试,若能,则画出示意图并写出作法和理由。2.(2008青海)如图, HYPERLINK "http://www./" 是由经过位似变换得到的,点是位似中心,分别是的中点,则与的面积比是( ) A. B. C. D.3.(2008威海市)如图,已知△EFH和△MNK是位似图形,那么其位似中心是点( )4.如图,△ABC三个顶点的坐标分别为A (2,7),B (6,8),C (8,2),请你分别完成下面的作图并标出所有顶点的坐标.(不要求写出作法)⑴以O为位似中心,在第三象限内作出△A1B1C1,使△A1B1C1与△ABC的位似比为1:2;
⑵以O为旋转中心,将△ABC沿顺时针方向旋转900得到△A2B2C2.(3)向左平移8个单位;5.(江苏淮安)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1). (1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形; (2)分别写出B、C两点的对应点B′、C′的坐标; (3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标. 合作学习、生生互动 给出课外合作学习内容,引导学生攀登知识高峰。反思:★若以点O为位似中心在y轴的左侧将△OBC放大到n倍,则对应点坐标为原坐标的倍★若以点O为位似中心在y轴的右侧将△OBC放大到n倍,则对应点坐标为原坐标的倍
A
C
D
B
F
E
G
A
C
D
B
F
E
G
_
D
_
C
_
B
_
A
第15题
x
10
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
11
A1
B1
C1
A
B
C
y
第13题图
A
x
y
B
C
1
1
-1
O
A
B
C
D
O
E
F
G
C
A
BA
DA
OA
EA
FA
第2题图
H
E
F
M
N
K
A
B
C
D
y
B
C
A
O
x
PAGE
6
