第一章 反比例函数 章末复习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第一章 反比例函数
章末复习
类型一 反比例函数的图象和性质
1.反比例函数 的图象在第二、四象限,则m的值是 ( )
B.1 或1 或
2.已知反比例函数 在每一个象限内,y随x的增大而增大,则下列点可能在这个函数图象上的为( )
A.(2,3) C.(0,3)
3.已知反比例函数 当 时,y 的取值范围是 ( )
4.已知反比例函数 当 -1时,y的最大值是4,则当x≥2时,y有( )
A.最小值-4 B.最小值-2 C.最大值-4 D.最大值-2
5.若y与 成正比例关系,z与x 成正比例关系,则y与z成__________关系.
6.如图,在平面直角坐标系xOy 中有一矩形,顶点坐标分别为(1,1),(4,1),(4,3),(1,3),有一反比例函数 它的图象与此矩形没有交点,该表达式可以为_______________.
类型二 反比例函数与图形面积的综合
7.如图,在平面直角坐标系中,反比例函数 的图象经过平行四边形OABC的顶点A,将该反比例函数图象沿 y轴对称,所得图象恰好经过BC中点M,则平行四边形OABC 的面积为____________.
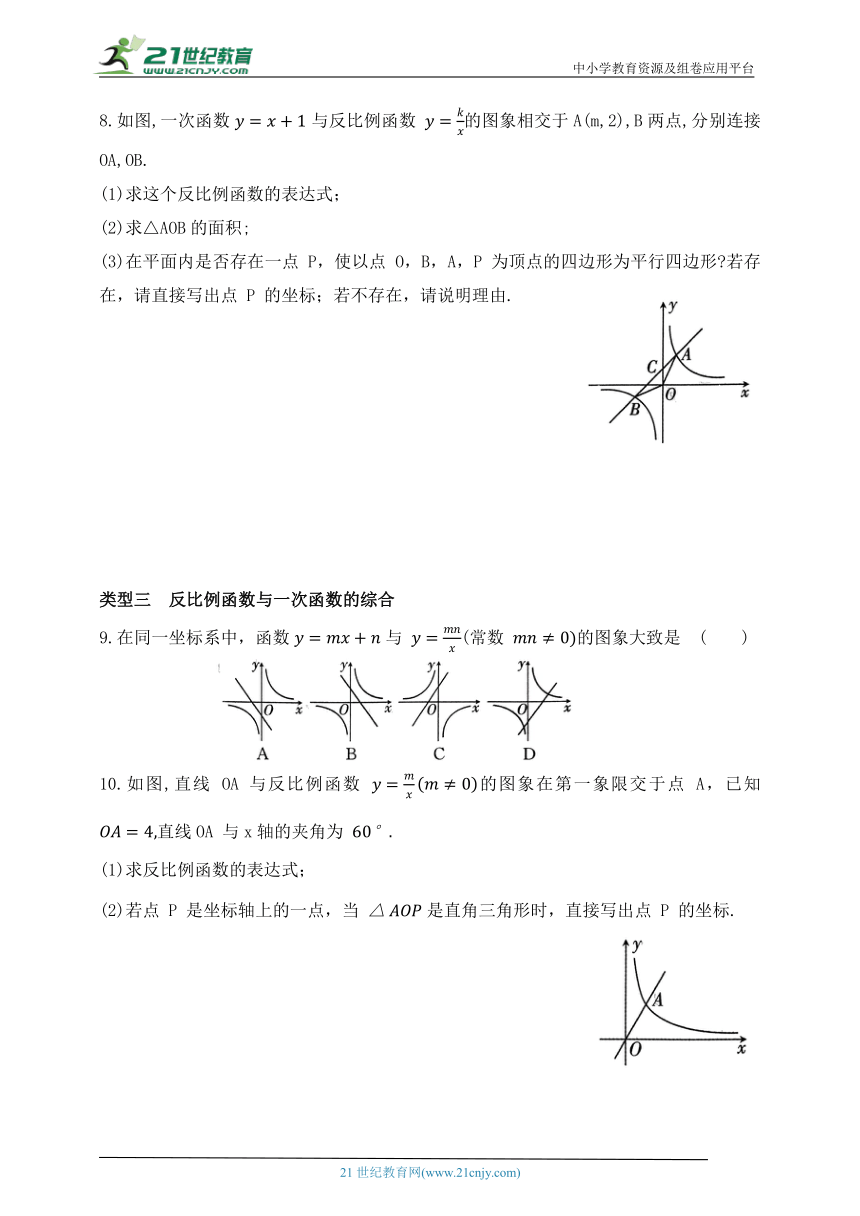
8.如图,一次函数与反比例函数 的图象相交于A(m,2),B两点,分别连接OA,OB.
(1)求这个反比例函数的表达式;
(2)求△AOB的面积;
(3)在平面内是否存在一点 P,使以点 O,B,A,P 为顶点的四边形为平行四边形 若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
类型三 反比例函数与一次函数的综合
9.在同一坐标系中,函数与 (常数 的图象大致是 ( )
10.如图,直线 OA 与反比例函数 的图象在第一象限交于点 A,已知 直线OA 与x轴的夹角为
(1)求反比例函数的表达式;
(2)若点 P 是坐标轴上的一点,当 是直角三角形时,直接写出点 P 的坐标.
类型四 反比例函数的实际应用
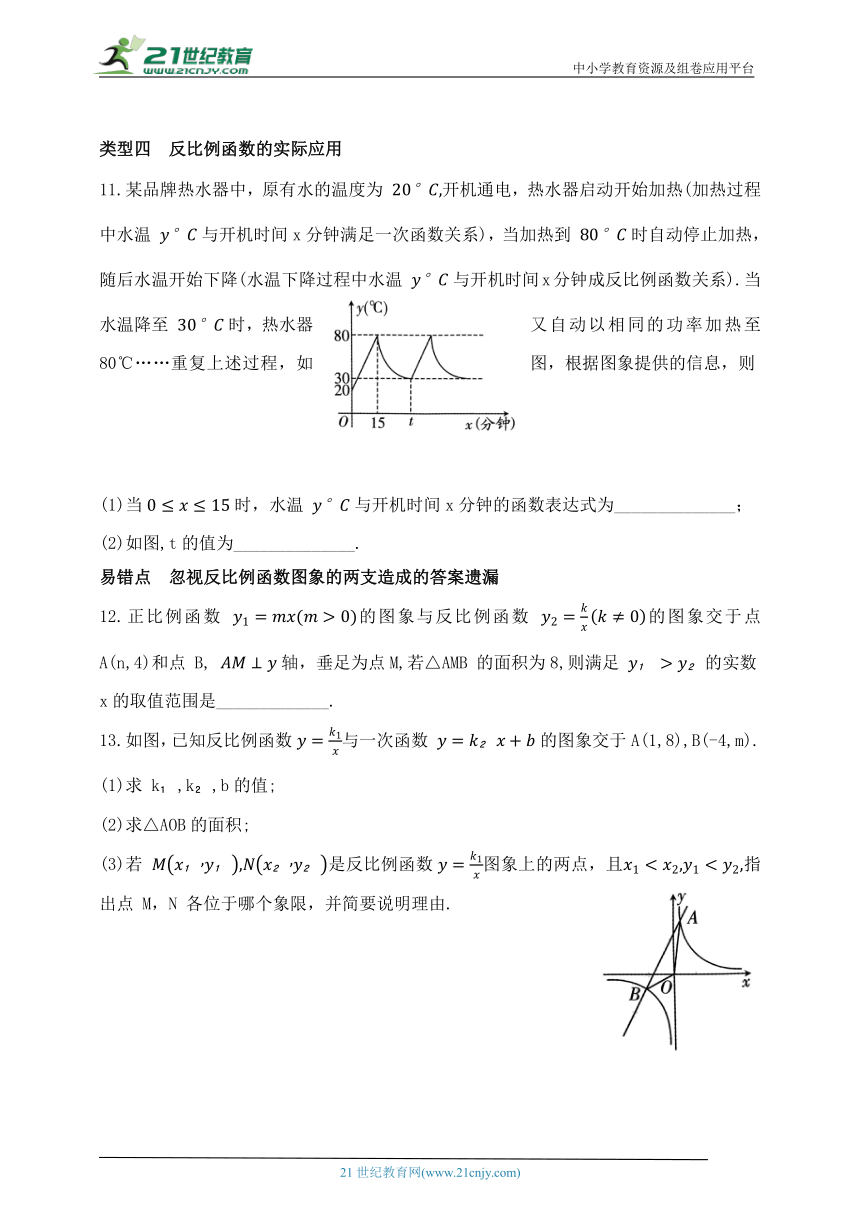
11.某品牌热水器中,原有水的温度为 开机通电,热水器启动开始加热(加热过程中水温 与开机时间x分钟满足一次函数关系),当加热到 时自动停止加热,随后水温开始下降(水温下降过程中水温 与开机时间x分钟成反比例函数关系).当水温降至 时,热水器又自动以相同的功率加热至 80℃……重复上述过程,如图,根据图象提供的信息,则
(1)当时,水温 与开机时间x分钟的函数表达式为______________;
(2)如图,t的值为______________.
易错点 忽视反比例函数图象的两支造成的答案遗漏
12.正比例函数 的图象与反比例函数 的图象交于点 A(n,4)和点 B, 轴,垂足为点M,若△AMB 的面积为8,则满足 的实数x的取值范围是_____________.
13.如图,已知反比例函数与一次函数 的图象交于A(1,8),B(-4,m).
(1)求 k ,k ,b的值;
(2)求△AOB的面积;
(3)若 是反比例函数图象上的两点,且指出点 M,N 各位于哪个象限,并简要说明理由.
参考答案
1. A 2. B 3. C 4. B 5.反比例
(答案不唯一, 或 即可)
7.10 解析: 的图象经过平行四边形 OABC的顶点A,∴设
∵∥轴,∴点 B 的纵坐标为
∵图象沿y轴对称所得图象为 这个图象恰好经过 BC中点 M,
∵点O,A 的水平距离为a,∥∴点 B,C的水平距离也为a,
∴点 M,B的水平距离为
8.解:(1)∵一次函数 经过点A(m,2),
解得 ∴A(1,2).
∵反比例函数 经过点A(1,2),∴k=1×2=2,
∴反比例函数的表达式为
(2)联立 解得 或 ∴B(-2,-1).
∵C(0,1),
(3)有三种情形,如图所示,满足条件的点 P 的坐标为( 或 或(3,3).
9. A
10.解:(1)如图1,过点 A 作 轴于点E,
由勾股定理,得
∴点 A的坐标为(
∵反比例函数 的图象过点A,
∴反比例函数表达式为
(2)如图2,
①当点. 在 y 轴上,且时,
又
∴点
②当点 在x轴上,且 时,由(1),得点
③当点 在 y轴上,且 时,
又
∴点
④当点 在 x轴上,且. 时,
∴点
综上所述,点 P 的坐标为( 或(2,0)或或(8,0).
11.(1) (2)40
或
13.解:(1)把 A(1,8), 分别代入 得
∴
∵点A,B在 图象上, 解得
(2)设直线 与x轴交于点C,当. 0时,x=-3,∴OC=3,
(3)点 M 在第三象限,点 N 在第一象限.
①若 点 M,N 在第三象限,则 不合题意;
②若 点 M,N 在第一象限,则 不合题意;
③若 点 M 在第三象限,点 N 在第一象限,则 符合题意.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章 反比例函数
章末复习
类型一 反比例函数的图象和性质
1.反比例函数 的图象在第二、四象限,则m的值是 ( )
B.1 或1 或
2.已知反比例函数 在每一个象限内,y随x的增大而增大,则下列点可能在这个函数图象上的为( )
A.(2,3) C.(0,3)
3.已知反比例函数 当 时,y 的取值范围是 ( )
4.已知反比例函数 当 -1时,y的最大值是4,则当x≥2时,y有( )
A.最小值-4 B.最小值-2 C.最大值-4 D.最大值-2
5.若y与 成正比例关系,z与x 成正比例关系,则y与z成__________关系.
6.如图,在平面直角坐标系xOy 中有一矩形,顶点坐标分别为(1,1),(4,1),(4,3),(1,3),有一反比例函数 它的图象与此矩形没有交点,该表达式可以为_______________.
类型二 反比例函数与图形面积的综合
7.如图,在平面直角坐标系中,反比例函数 的图象经过平行四边形OABC的顶点A,将该反比例函数图象沿 y轴对称,所得图象恰好经过BC中点M,则平行四边形OABC 的面积为____________.
8.如图,一次函数与反比例函数 的图象相交于A(m,2),B两点,分别连接OA,OB.
(1)求这个反比例函数的表达式;
(2)求△AOB的面积;
(3)在平面内是否存在一点 P,使以点 O,B,A,P 为顶点的四边形为平行四边形 若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
类型三 反比例函数与一次函数的综合
9.在同一坐标系中,函数与 (常数 的图象大致是 ( )
10.如图,直线 OA 与反比例函数 的图象在第一象限交于点 A,已知 直线OA 与x轴的夹角为
(1)求反比例函数的表达式;
(2)若点 P 是坐标轴上的一点,当 是直角三角形时,直接写出点 P 的坐标.
类型四 反比例函数的实际应用
11.某品牌热水器中,原有水的温度为 开机通电,热水器启动开始加热(加热过程中水温 与开机时间x分钟满足一次函数关系),当加热到 时自动停止加热,随后水温开始下降(水温下降过程中水温 与开机时间x分钟成反比例函数关系).当水温降至 时,热水器又自动以相同的功率加热至 80℃……重复上述过程,如图,根据图象提供的信息,则
(1)当时,水温 与开机时间x分钟的函数表达式为______________;
(2)如图,t的值为______________.
易错点 忽视反比例函数图象的两支造成的答案遗漏
12.正比例函数 的图象与反比例函数 的图象交于点 A(n,4)和点 B, 轴,垂足为点M,若△AMB 的面积为8,则满足 的实数x的取值范围是_____________.
13.如图,已知反比例函数与一次函数 的图象交于A(1,8),B(-4,m).
(1)求 k ,k ,b的值;
(2)求△AOB的面积;
(3)若 是反比例函数图象上的两点,且指出点 M,N 各位于哪个象限,并简要说明理由.
参考答案
1. A 2. B 3. C 4. B 5.反比例
(答案不唯一, 或 即可)
7.10 解析: 的图象经过平行四边形 OABC的顶点A,∴设
∵∥轴,∴点 B 的纵坐标为
∵图象沿y轴对称所得图象为 这个图象恰好经过 BC中点 M,
∵点O,A 的水平距离为a,∥∴点 B,C的水平距离也为a,
∴点 M,B的水平距离为
8.解:(1)∵一次函数 经过点A(m,2),
解得 ∴A(1,2).
∵反比例函数 经过点A(1,2),∴k=1×2=2,
∴反比例函数的表达式为
(2)联立 解得 或 ∴B(-2,-1).
∵C(0,1),
(3)有三种情形,如图所示,满足条件的点 P 的坐标为( 或 或(3,3).
9. A
10.解:(1)如图1,过点 A 作 轴于点E,
由勾股定理,得
∴点 A的坐标为(
∵反比例函数 的图象过点A,
∴反比例函数表达式为
(2)如图2,
①当点. 在 y 轴上,且时,
又
∴点
②当点 在x轴上,且 时,由(1),得点
③当点 在 y轴上,且 时,
又
∴点
④当点 在 x轴上,且. 时,
∴点
综上所述,点 P 的坐标为( 或(2,0)或或(8,0).
11.(1) (2)40
或
13.解:(1)把 A(1,8), 分别代入 得
∴
∵点A,B在 图象上, 解得
(2)设直线 与x轴交于点C,当. 0时,x=-3,∴OC=3,
(3)点 M 在第三象限,点 N 在第一象限.
①若 点 M,N 在第三象限,则 不合题意;
②若 点 M,N 在第一象限,则 不合题意;
③若 点 M 在第三象限,点 N 在第一象限,则 符合题意.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
