1.1.1 空间向量及其运算 同步练习(含解析)——高二数学人教B版(2019)选择性必修第一册课时优化训练
文档属性
| 名称 | 1.1.1 空间向量及其运算 同步练习(含解析)——高二数学人教B版(2019)选择性必修第一册课时优化训练 |

|
|
| 格式 | docx | ||
| 文件大小 | 448.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-18 00:00:00 | ||
图片预览


文档简介
1.1.1 空间向量及其运算
——高二数学人教B版(2019)选择性必修第一册课时优化训练
1.如图,在平行六面体中,( )
A. B. C. D.
2.已知空间中非零向量a,b,且,,,则的值为( )
A. B.97 C. D.61
3.在四面体OABC中,E为OA中点,,若,,,则( )
A. B.
C. D.
4.如图,在正方体中,点E是的中点,点F在线段AE上,且,则( )
A. B.
C. D.
5.在平行六面体中,,,若,则( )
A. B. C. D.
6.已知空间四边形ABCD中,G为CD的中点,则等于( )
A. B. C. D.
7.已知不共面的三个向量a,b,c都是单位向量,且两两夹角都是,则向量和b的夹角为( )
A. B. C. D.
8.已知正四面体的棱长为1,且,则( )
A. B. C. D.
9.(多选)已知四面体ABCD中,AB,AC,AD两两互相垂直,则下列结论中一定成立的是( )
A.
B.
C.
D.
10.(多选)如图,在三棱柱中,M,N分别是,上的点,且,.设,,,若,,,则( )
A. B.
C. D.
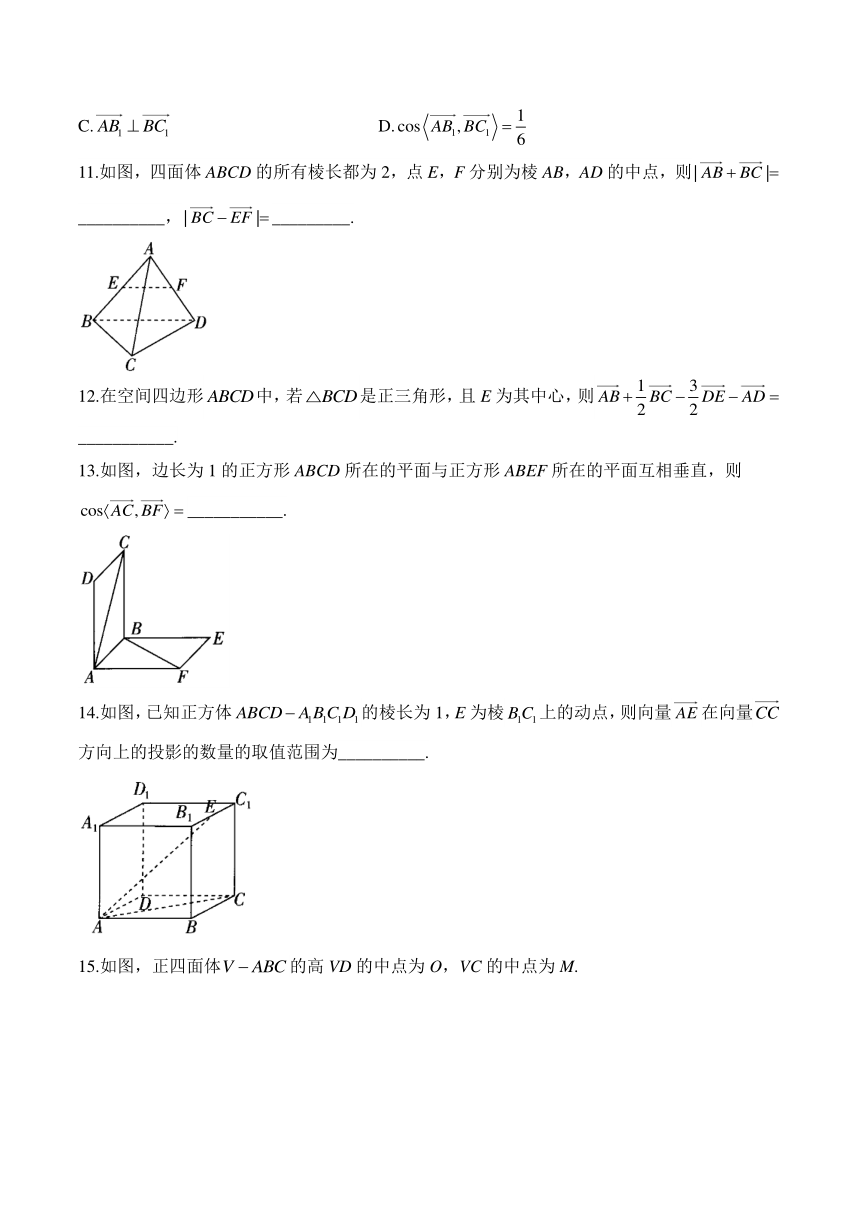
11.如图,四面体ABCD的所有棱长都为2,点E,F分别为棱AB,AD的中点,则__________,_________.
12.在空间四边形中,若是正三角形,且E为其中心,则___________.
13.如图,边长为1的正方形ABCD所在的平面与正方形ABEF所在的平面互相垂直,则___________.
14.如图,已知正方体的棱长为1,E为棱上的动点,则向量在向量方向上的投影的数量的取值范围为__________.
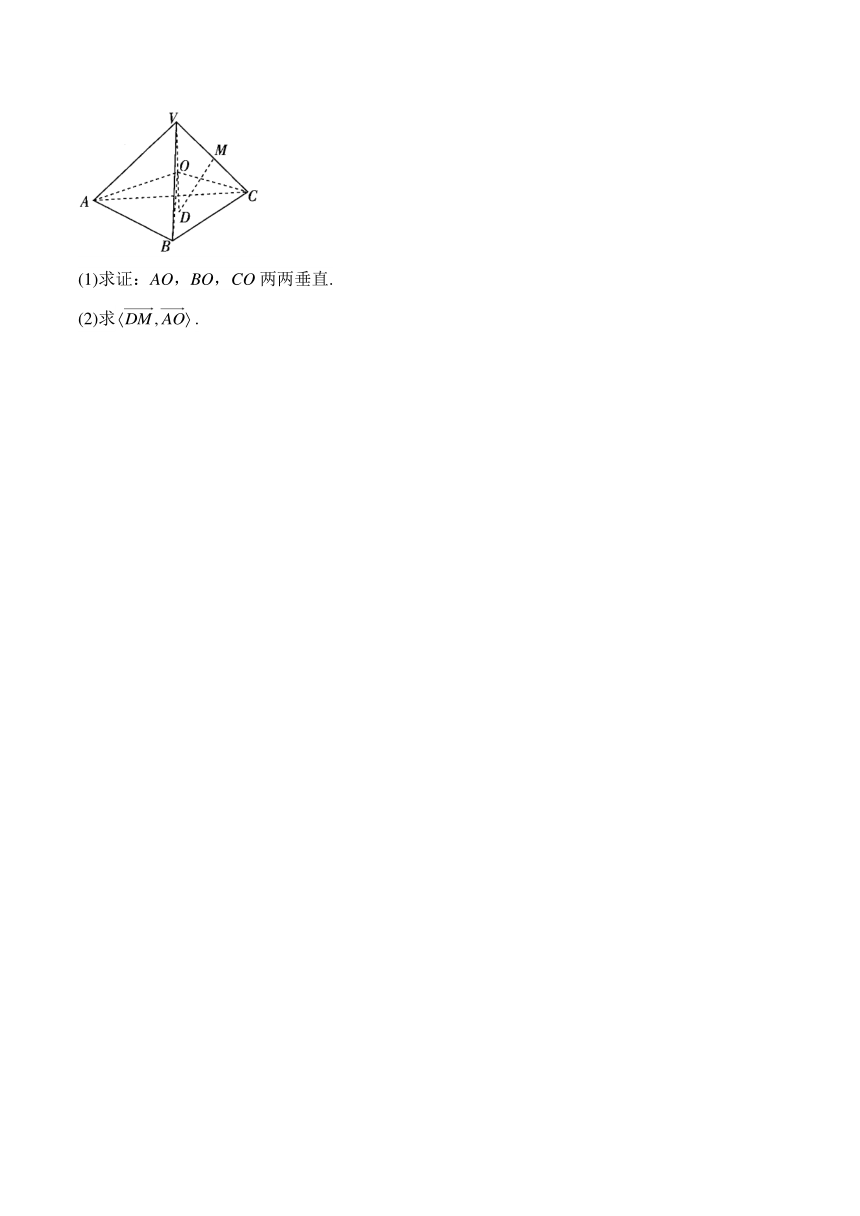
15.如图,正四面体的高VD的中点为O,VC的中点为M.
(1)求证:AO,BO,CO两两垂直.
(2)求.
答案以及解析
1.答案:C
解析:.故选C.
2.答案:C
解析:
,.
3.答案:D
解析:
.故选D.
4.答案:D
解析:由题意知,,,,,,所以.
5.答案:A
解析:如图,,所以,解得.
6.答案:A
解析:如图,因为G为CD的中点,所以,
所以.
7.答案:C
解析:,,,.设向量和b的夹角为,则,又,.
8.答案:C
解析:因为,所以.
根据向量的减法法则,得,
所以.
.
9.答案:ABD
解析:方法一:,,,A,B正确.,结果不一定为0,C错误.,同理,D正确.
方法二:如图,将四面体ABCD补成长方体,AE为此长方体的体对角线,易知正确.,在长方体中,不一定有,故C错误.
由图可知,,,,故D正确.
10.答案:BD
解析:,A错误;
,,,
,,B正确;
由题意知,,
则,C错误,D正确.故选BD.
11.答案:2;
解析:因为,所以.取BD的中点M,则,所以.
12.答案:0
解析:如图,连接,,取的中点F,连接.
是正三角形,且E为其中心,
,
.
13.答案:
解析:方法一:因为,,,所以.
方法二:连接CF,则,所以,又,,所以.
方法三:可将题图补形为如图所示的正方体,连接CG,则,所以,所以.
14.答案:
解析:设.,,向量在向量方向上的投影的数量为,又,,向量在向量方向上的投影的数量的取值范围为.
15.答案:(1)证明见解析
(2)
解析:设,,,正四面体的棱长为1.
(1),
,
,
,
所以,
所以,即.
同理,,,所以AO,BO,CO两两垂直.
(2),
所以,
,
,
所以.
又,所以.
——高二数学人教B版(2019)选择性必修第一册课时优化训练
1.如图,在平行六面体中,( )
A. B. C. D.
2.已知空间中非零向量a,b,且,,,则的值为( )
A. B.97 C. D.61
3.在四面体OABC中,E为OA中点,,若,,,则( )
A. B.
C. D.
4.如图,在正方体中,点E是的中点,点F在线段AE上,且,则( )
A. B.
C. D.
5.在平行六面体中,,,若,则( )
A. B. C. D.
6.已知空间四边形ABCD中,G为CD的中点,则等于( )
A. B. C. D.
7.已知不共面的三个向量a,b,c都是单位向量,且两两夹角都是,则向量和b的夹角为( )
A. B. C. D.
8.已知正四面体的棱长为1,且,则( )
A. B. C. D.
9.(多选)已知四面体ABCD中,AB,AC,AD两两互相垂直,则下列结论中一定成立的是( )
A.
B.
C.
D.
10.(多选)如图,在三棱柱中,M,N分别是,上的点,且,.设,,,若,,,则( )
A. B.
C. D.
11.如图,四面体ABCD的所有棱长都为2,点E,F分别为棱AB,AD的中点,则__________,_________.
12.在空间四边形中,若是正三角形,且E为其中心,则___________.
13.如图,边长为1的正方形ABCD所在的平面与正方形ABEF所在的平面互相垂直,则___________.
14.如图,已知正方体的棱长为1,E为棱上的动点,则向量在向量方向上的投影的数量的取值范围为__________.
15.如图,正四面体的高VD的中点为O,VC的中点为M.
(1)求证:AO,BO,CO两两垂直.
(2)求.
答案以及解析
1.答案:C
解析:.故选C.
2.答案:C
解析:
,.
3.答案:D
解析:
.故选D.
4.答案:D
解析:由题意知,,,,,,所以.
5.答案:A
解析:如图,,所以,解得.
6.答案:A
解析:如图,因为G为CD的中点,所以,
所以.
7.答案:C
解析:,,,.设向量和b的夹角为,则,又,.
8.答案:C
解析:因为,所以.
根据向量的减法法则,得,
所以.
.
9.答案:ABD
解析:方法一:,,,A,B正确.,结果不一定为0,C错误.,同理,D正确.
方法二:如图,将四面体ABCD补成长方体,AE为此长方体的体对角线,易知正确.,在长方体中,不一定有,故C错误.
由图可知,,,,故D正确.
10.答案:BD
解析:,A错误;
,,,
,,B正确;
由题意知,,
则,C错误,D正确.故选BD.
11.答案:2;
解析:因为,所以.取BD的中点M,则,所以.
12.答案:0
解析:如图,连接,,取的中点F,连接.
是正三角形,且E为其中心,
,
.
13.答案:
解析:方法一:因为,,,所以.
方法二:连接CF,则,所以,又,,所以.
方法三:可将题图补形为如图所示的正方体,连接CG,则,所以,所以.
14.答案:
解析:设.,,向量在向量方向上的投影的数量为,又,,向量在向量方向上的投影的数量的取值范围为.
15.答案:(1)证明见解析
(2)
解析:设,,,正四面体的棱长为1.
(1),
,
,
,
所以,
所以,即.
同理,,,所以AO,BO,CO两两垂直.
(2),
所以,
,
,
所以.
又,所以.
