湖北省仙桃市2023-2024学年八年级下学期期末数学试卷(含详细解答)
文档属性
| 名称 | 湖北省仙桃市2023-2024学年八年级下学期期末数学试卷(含详细解答) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-18 00:00:00 | ||
图片预览




文档简介
湖北省仙桃市2023-2024学年八年级下学期期末数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.如图,四边形的对角线交于点O,下列能判断四边形是平行四边形的是( )
A., B.,
C., D.,
4.在直角坐标系中,点到原点的距离是( )
A. B. C. D.3
5.已知正比例函数,若y随x的增大而增大,则k的取值范围是( )
A. B. C. D.
6.如图,正方形的面积为169,G是上的一点,于点E,,且交于点F.若,则的长是( ).
A.5 B.7 C.8 D.13
7.为了调查某校同学的体质健康状况,随机抽查了若干名同学的每天锻炼时间如表:
每天锻炼时间(分钟) 20 40 60 90
学生数 2 3 4 1
则关于这些同学的每天锻炼时间,下列说法错误的是( )
A.众数是60 B.平均数是21
C.抽查了10个同学 D.中位数是50
8.如图①,点P为矩形ABCD边上一个动点,运动路线是,设点P运动的路径长为x,,图②是y随x变化的函数图象,则矩形对角线AC的长是( )
A. B.6 C.12 D.24
9.如图,把放在直角坐标系内,其中,,点A、B的坐标分别为、,将沿x轴向右平移,当点C落在直线上时,线段BC扫过的面积为( ).
A.80 B.88 C.96 D.100
10.如图,点E是正方形的边延长线一点,连接交于F,作,交的延长线于G,连接,当时,作于H,连接,则:①点F是的中点;②;③;④.其中正确的结论有( )
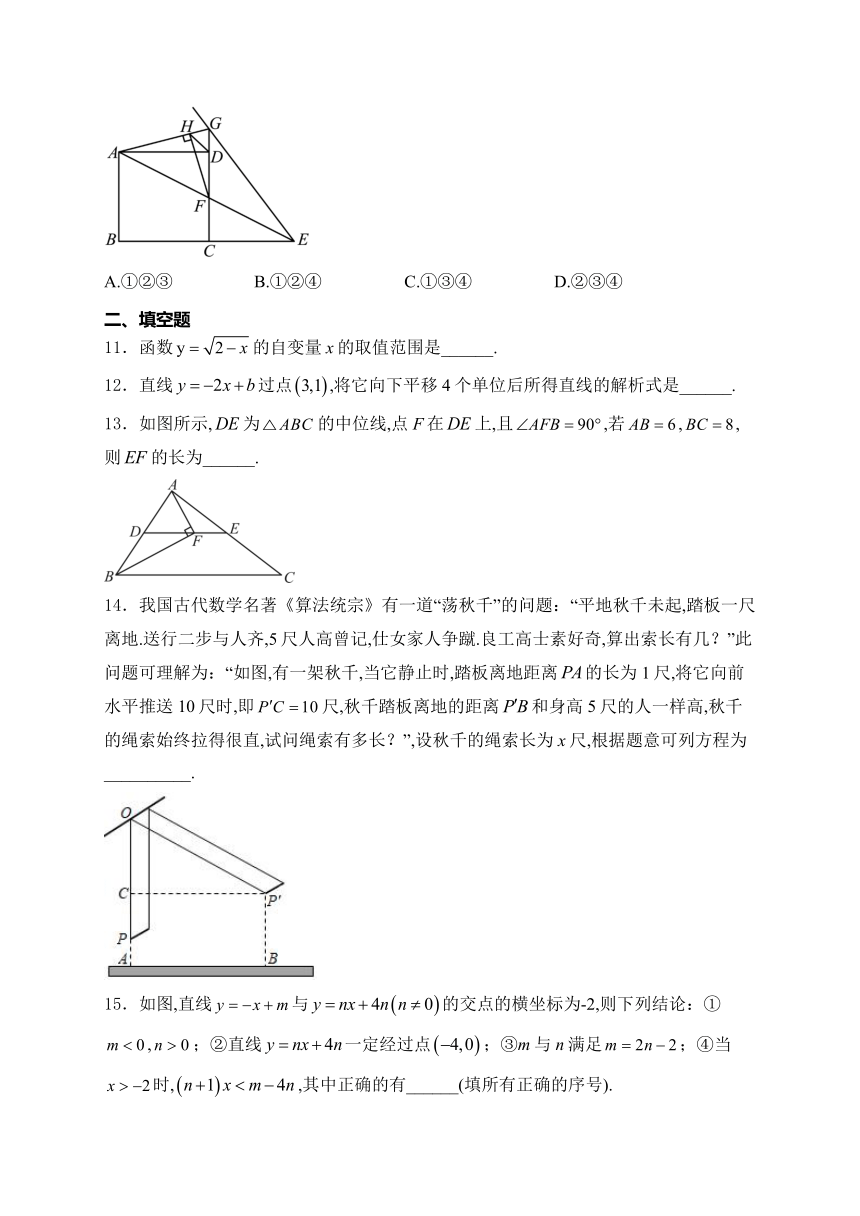
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
11.函数的自变量x的取值范围是______.
12.直线过点,将它向下平移4个单位后所得直线的解析式是______.
13.如图所示,为的中位线,点F在上,且,若,,则的长为______.
14.我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离的长为1尺,将它向前水平推送10尺时,即尺,秋千踏板离地的距离和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,设秋千的绳索长为x尺,根据题意可列方程为__________.
15.如图,直线与的交点的横坐标为-2,则下列结论:①,;②直线一定经过点;③m与n满足;④当时,,其中正确的有______(填所有正确的序号).
三、解答题
16.计算:
(1);
(2).
17.求值:
(1)已知,,求的值;
(2)先化简,再求值:,其中.
18.2023年3月5日,中华人民共和国第十四届全国人民代表大会第一次会议在北京召开,某校为使学生更好地了解“两会”,争做新时代好少年,开展了“两会”知识竞赛活动,分别从八(1)班和八(2)班各随机抽取10名学生的竞赛成绩(单位:分,满分100分),并对数据进行了如下分析与整理:
收集数据
八(1)班学生知识竞赛成绩:84,75,82,70,91,83,80,74,79,82
八(2)班学生知识竞赛成绩:80,65,75,68,95,82,84,80,92,79
分析数据
平均数/分 中位数/分 众数/分 方差
八(1)班 80 b 82 31.6
八(2)班 a 80 c 78.4
根据以上信息,解答下列问题:
(1)填空:______,______,______.
(2)请你对八(1)班和八(2)班抽取的这10名学生的知识竞赛成绩作出评价.
(3)该校除开展两会知识竞赛活动外,还组织了制作关于“两会”手抄报的评比活动,并对手抄报进行评分(单位:分,满分100分).在八(2)班抽取的这10名学生中,甲同学和乙同学的知识竞赛成绩分别为95分和92分,手抄报成绩分别为70分和80分.现对甲同学和乙同学进行综合评分,若知识竞赛成绩占70%,手抄报成绩占30%,则哪位同学的综合成绩较好?
19.如图,在矩形中,E,F两点在对角线上,.
(1)求证:四边形是平行四边形;
(2)若,,,直接写出四边形的面积.
20.阅读与思考
在函数的学习过程中,我们利用描点法画出函数的图象,并借助图象研究该函数的性质,最后运用函数解决问题.现我们对函数(x的取值范围为任意实数)进行探究.
(1)请将下面的表格补充完整.
x … 0 1 2 3 …
… 4 ___ 2 1 0 ___ 2 …
(2)请根据上表中的数据,在如图所示的平面直角坐标系中画出这个函数的图象,并填写:当时,y的值随x值的增大而_________.
(3)请在如图所示的平面直角坐标系中画出正比例函数的图象,并直接写出不等式的解集.
21.如图,在四边形中,,于点B,,,点P从点A出发,以的速度向点D运动,同时点Q从点C出发,以的速度向点B运动,其中一个动点到达端点时另一个动点也随之停止运动,设运动时间为.
(1)填空:当________s时,四边形为矩形;
(2)若,求t的值;
(3)填空:当________时,在点P、Q运动过程中,四边形能构成菱形.
22.在一条笔直的公路上有A,B两地,甲,乙二人同时出发,甲从A地步行匀速前往B地,到达B地后,立刻以原速度沿原路返回A地.乙从B地步行匀速前往A地(甲,乙二人到达A地后均停止运动),甲,乙二人之间的距离y(米)与出发时间x(分钟)之间的函数关系如图所示,请结合图象解答下列问题:
(1)A,B两地之间的距离是_________米,乙的步行速度是_________米/分;
(2)求线段的函数解析式;
(3)在乙运动的过程中,请直接写出何时两人相距80米.
23.A城有肥料200吨,B城有肥料300吨.现要把这些肥料全部运往C,D两乡,C乡需要肥料240吨,D乡需要肥料260吨,其运往C,D两乡的运费如下表:
两乡两城 C/(元/吨) D/(元/吨)
A 20 24
B 15 17
设从A城运往C乡的肥料为x吨,从A城运往两乡的总运费为元,从B城运往两乡的总运费为元.
(1)分别直接写出,与x之间的函数关系式(不要求写自变量的取值范围);
(2)当城运往两乡的总运费不低于4200元时,怎样调运,才能使A,B两城运往两乡的总费用的和最小?并求出最小值;
(3)因路况原因,从B城到C,D两乡的运费分别增加了m元/吨和元/吨,A城运往两乡的总运费不低于4400元且不高于4600元,当A,B两城运往两乡的总费用的和的最小值为10960元时,请直接写出m的值.
24.如图1,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为.D是AB边上一点(不与点A、B重合),将沿直线CD翻折,使点B落在点E处.
(1)求直线AC所表示的函数的表达式;
(2)如图2,当点E恰好落在矩形的对角线AC上时,求点D的坐标;
(3)如图3,当以O、E、C三点为顶点的三角形是等腰三角形时,求的面积.
参考答案
1.答案:A
解析:A:不能化简,是最简二次根式;
B:,不是最简二次根式;
C:,不是最简二次根式;
D:,不是最简二次根式.
故选:A.
2.答案:D
解析:、和不是同类项不可以合并,计算错误,不符合题意;
、,计算错误,不符合题意;
、,计算错误,不符合题意;
、,正确,符合题意.
故选:D.
3.答案:C
解析:A、由,,不能判定四边形是平行四边形,故本选项不符合题意;
B、由,,不能判定四边形是平行四边形,故本选项不符合题意;
C、,
,,
,
,
四边形是平行四边形,故本选项符合题意;
D、由,,不能判定四边形是平行四边形,故本选项不符合题意;
故选:C
4.答案:B
解析:如图所示,
作轴于点A,则,,
在中,
,
故选:B.
5.答案:D
解析:根据y随x的增大而增大,知:,
即.
故答案选:D.
6.答案:B
解析:∴正方形的边长,
∴
∵,
∴,,
∴,
∵,
∴,即,
∴,
∴,
∴.
故选B.
7.答案:B
解析:A、60出现了4次,出现的次数最多,则众数是60,故A选项说法正确;
B、这组数据的平均数是:,故B选项说法错误;
C、调查的户数是,故C选项说法正确;
D、把这组数据从小到大排列,最中间的两个数的平均数是,则中位数是50,故D选项说法正确;
故选B.
8.答案:A
解析:由图像及题意可得:,
当点P运动到C点时三角形ABP的面积为4,即,
,,在中,;
故选A.
9.答案:B
解析:∵点A、B的坐标分别为、,
∴,
∵,,
∴,
∴C点纵坐标为:8,
∵将沿x轴向右平移,当点C落在直线上时,
∴时,,解得:,即A点向右平移个单位,
∴线段BC扫过的面积为:.
故选B.
10.答案:A
解析:∵四边形是正方形,,
∴,,
∴,,
∴,
∴,,即点F是的中点;①正确;
过点A作于点J,如图所示:
四边形是正方形,
,
,
,
,
在与中,
,
,
,
在与中,
,
,
,
延长交于点M,作,,
,,
,,
在中,,
.
∵,
,
,
,即是等腰直角三角形,
∵,
∴,,
∴,
∴,
∴,②正确;
在与中,
,
∵,
∴,
∴,
∵,,
∴是的平分线,
∴;③正确;
在等腰与等腰中,
,
,
,
四边形是正方形,,,
,,
,
,④错误,
综上,①②③正确,
故选:A.
11.答案:
解析:在实数范围内有意义,
则;解得
故答案为.
12.答案:
解析:将代入,
得:,
解得:,
∴,
将直线向下平移4个单位后所得直线的解析式是,即y=-2x+3.
故答案为:.
13.答案:1
解析:在中,D为的中点,,
,
为的中位线,,
,
,
故答案为:1.
14.答案:
解析:由题意知:
,,,
在中,由勾股定理得:
.
故答案为:.
15.答案:①②③
解析:①∵直线与y轴交于负半轴,
∴;
∵的图象从左往右逐渐上升,
∴,
故结论①正确;
②将代入,得,
∴直线一定经过点.
故结论②正确;
③∵直线与的交点的横坐标为-2,
∴当时,,
∴.
故结论③正确;
④∵当时,直线在直线的上方,
∴当时,,
∴
故结论④错误.
故答案为:①②③.
16.答案:(1)
(2)
解析:(1)
;
(2)
.
17.答案:(1)6
(2)
解析:(1),,
,,
;
(2)
,
将代入,得:
原式.
18.答案:(1)80,81,80
(2)见解析
(3)乙的综合成绩较好
解析:(1)八(2)班学生知识竞赛的平均成绩,
八(1)班的成绩从小到大排列,排在中间的两个数分别是80,82,则中位数,
八(2)班的成绩中,80出现的次数最多,故众数;
故答案为:80,81,80;
(2)两个班平均成绩相同,但八(1)班的中位数及众数均高于八(2)班,并且方差小于八(2)班,所以八(1)班成绩更稳定且优于八(2)班;
(3)甲的综合成绩为:分,
乙的综合成绩为:分,
故乙的综合成绩较好.
19.答案:(1)证明见解析
(2)84
解析:(1)证明:连,交于O点,如图所示:
四边形为矩形,
,,
,
,
,
,
四边形是平行四边形;
(2)如图所示:
;,
由图可知,
,,,
,
由等面积法得到,则在中,,
,
.
20.答案:(1)表格见解析
(2)图见解析,增大
(3)图见解析,解集为
解析:(1)由题意,填表得,
x … 0 1 2 3 …
… 4 3 2 1 0 1 2 …
(2)根据题意,画图象,如图;
由图象可知,当时,y的值随x值的增大而增大.
故答案为:增大;
(3)如图,画出直线的图象,
由图象可知,
当时,,
当时,,
不等式的解集为.
21.答案:(1)
(2)t的值为或
(3)
解析:(1)根据题意得:,
∵,,
∴,,
∵,,
∴当时,四边形是矩形,
∴,
解得:,
即当时,四边形是矩形;
故答案为:6.5;
(2)若,分两种情况:
①时,则四边形是平行四边形,,即,
解得:,
②与不平行时,四边形为等腰梯形,
则即
解得:,
∴的值为6或7;
(3)若四边形为菱形,则
解得:
作于M如图所示:
则,
,
在中,
,
,
∴当时,在点P,Q运动过程中,四边形能构成菱形,
故答案为:.
22.答案:(1)1200,60
(2)()
(3)经过8分钟和分钟时两人相距80米
解析:(1)由函数图象可知,最开始时甲乙两人之间的距离为1200米,
因为甲从A地出发,乙从B地出发,两人最开始时的距离就是A、B两地之间的距离,
所以A、B两地之间距离为1200米;
由图象可知乙经过20分时到达A地,
∴乙的步行速度为(米/分);
故答案为:1200,60;
(2)由函数图象可知,经过分钟时两人相遇,点M表示此时甲到达B地,乙未到达A地,经过20分钟时乙到达A地,此时两人相距b米,
设甲的步行速度为x米/分,则,
解得:(米/分)
(分)
∴(米),(米).
则M、N的坐标分别为,,
设线段的解析式为,
则有,
解得:,
∴线段的函数解析式是();
(3)设经过x分钟两人相距80米,两人相遇前和相遇后都可相距80米,
相遇前:,解得:;
相遇后:,解得:,
所以经过8分钟和分钟时两人相距80米.
23.答案:(1)①
②
(2)A城运150吨肥料到C城,运50吨肥料到D城,B城运90吨肥料到C城,运210吨肥料到D城总费用和最小,最小费用为9120元
(3)4
解析:(1)由题意得,,
;
(2)依题意:,
解得:
设两城总费用和为w元,则,
∵,
∴w随着x的增大而减小,
当时,,
此时调运方案为:A城运150吨肥料到C城,运50吨肥料到D城;B城运90吨肥料到C城,运210吨肥料到D城.
(3)依题意,,解得:.
设调整之后的总费用为元,则,
①若,则,随着x的增大而减小,
当时,,解得:(舍去);
②若时,则(舍去);
③若时,随着x的增大而增大,
当时,,解得:.
综上所得:m的值是4.
24.答案:(1)
(2)
(3)12或
解析:(1)∵点B的坐标为且四边形OABC是矩形,
∴点A、C的坐标分别为、,
设AC的表达式为,
把A、C两点的坐标分别代入上式得,解得,
∴直线AC所表示的函数的表达式;
(2)∵点A的坐标为,点C的坐标为,
∴,.
∴中,,
∵四边形OABC是矩形,
∴,,,
∵沿CD折叠,
∴,,,,
∴,
设,则,
∵中,由勾股定理得:,
∴,解得,
∴点D的坐标为;
(3)过点E分别作x、y轴的垂线,垂足分别为M、N,
∵,,,
∴,
∴四边形OMEN是矩形,
∴.
①当时,
∵,,
∴,
的面积;
②当时,
∵,
∴,
设,则,
在中,,
在中,,
即,
解得:,
则,
的面积;
故的面积为12或.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.如图,四边形的对角线交于点O,下列能判断四边形是平行四边形的是( )
A., B.,
C., D.,
4.在直角坐标系中,点到原点的距离是( )
A. B. C. D.3
5.已知正比例函数,若y随x的增大而增大,则k的取值范围是( )
A. B. C. D.
6.如图,正方形的面积为169,G是上的一点,于点E,,且交于点F.若,则的长是( ).
A.5 B.7 C.8 D.13
7.为了调查某校同学的体质健康状况,随机抽查了若干名同学的每天锻炼时间如表:
每天锻炼时间(分钟) 20 40 60 90
学生数 2 3 4 1
则关于这些同学的每天锻炼时间,下列说法错误的是( )
A.众数是60 B.平均数是21
C.抽查了10个同学 D.中位数是50
8.如图①,点P为矩形ABCD边上一个动点,运动路线是,设点P运动的路径长为x,,图②是y随x变化的函数图象,则矩形对角线AC的长是( )
A. B.6 C.12 D.24
9.如图,把放在直角坐标系内,其中,,点A、B的坐标分别为、,将沿x轴向右平移,当点C落在直线上时,线段BC扫过的面积为( ).
A.80 B.88 C.96 D.100
10.如图,点E是正方形的边延长线一点,连接交于F,作,交的延长线于G,连接,当时,作于H,连接,则:①点F是的中点;②;③;④.其中正确的结论有( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
11.函数的自变量x的取值范围是______.
12.直线过点,将它向下平移4个单位后所得直线的解析式是______.
13.如图所示,为的中位线,点F在上,且,若,,则的长为______.
14.我国古代数学名著《算法统宗》有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:“如图,有一架秋千,当它静止时,踏板离地距离的长为1尺,将它向前水平推送10尺时,即尺,秋千踏板离地的距离和身高5尺的人一样高,秋千的绳索始终拉得很直,试问绳索有多长?”,设秋千的绳索长为x尺,根据题意可列方程为__________.
15.如图,直线与的交点的横坐标为-2,则下列结论:①,;②直线一定经过点;③m与n满足;④当时,,其中正确的有______(填所有正确的序号).
三、解答题
16.计算:
(1);
(2).
17.求值:
(1)已知,,求的值;
(2)先化简,再求值:,其中.
18.2023年3月5日,中华人民共和国第十四届全国人民代表大会第一次会议在北京召开,某校为使学生更好地了解“两会”,争做新时代好少年,开展了“两会”知识竞赛活动,分别从八(1)班和八(2)班各随机抽取10名学生的竞赛成绩(单位:分,满分100分),并对数据进行了如下分析与整理:
收集数据
八(1)班学生知识竞赛成绩:84,75,82,70,91,83,80,74,79,82
八(2)班学生知识竞赛成绩:80,65,75,68,95,82,84,80,92,79
分析数据
平均数/分 中位数/分 众数/分 方差
八(1)班 80 b 82 31.6
八(2)班 a 80 c 78.4
根据以上信息,解答下列问题:
(1)填空:______,______,______.
(2)请你对八(1)班和八(2)班抽取的这10名学生的知识竞赛成绩作出评价.
(3)该校除开展两会知识竞赛活动外,还组织了制作关于“两会”手抄报的评比活动,并对手抄报进行评分(单位:分,满分100分).在八(2)班抽取的这10名学生中,甲同学和乙同学的知识竞赛成绩分别为95分和92分,手抄报成绩分别为70分和80分.现对甲同学和乙同学进行综合评分,若知识竞赛成绩占70%,手抄报成绩占30%,则哪位同学的综合成绩较好?
19.如图,在矩形中,E,F两点在对角线上,.
(1)求证:四边形是平行四边形;
(2)若,,,直接写出四边形的面积.
20.阅读与思考
在函数的学习过程中,我们利用描点法画出函数的图象,并借助图象研究该函数的性质,最后运用函数解决问题.现我们对函数(x的取值范围为任意实数)进行探究.
(1)请将下面的表格补充完整.
x … 0 1 2 3 …
… 4 ___ 2 1 0 ___ 2 …
(2)请根据上表中的数据,在如图所示的平面直角坐标系中画出这个函数的图象,并填写:当时,y的值随x值的增大而_________.
(3)请在如图所示的平面直角坐标系中画出正比例函数的图象,并直接写出不等式的解集.
21.如图,在四边形中,,于点B,,,点P从点A出发,以的速度向点D运动,同时点Q从点C出发,以的速度向点B运动,其中一个动点到达端点时另一个动点也随之停止运动,设运动时间为.
(1)填空:当________s时,四边形为矩形;
(2)若,求t的值;
(3)填空:当________时,在点P、Q运动过程中,四边形能构成菱形.
22.在一条笔直的公路上有A,B两地,甲,乙二人同时出发,甲从A地步行匀速前往B地,到达B地后,立刻以原速度沿原路返回A地.乙从B地步行匀速前往A地(甲,乙二人到达A地后均停止运动),甲,乙二人之间的距离y(米)与出发时间x(分钟)之间的函数关系如图所示,请结合图象解答下列问题:
(1)A,B两地之间的距离是_________米,乙的步行速度是_________米/分;
(2)求线段的函数解析式;
(3)在乙运动的过程中,请直接写出何时两人相距80米.
23.A城有肥料200吨,B城有肥料300吨.现要把这些肥料全部运往C,D两乡,C乡需要肥料240吨,D乡需要肥料260吨,其运往C,D两乡的运费如下表:
两乡两城 C/(元/吨) D/(元/吨)
A 20 24
B 15 17
设从A城运往C乡的肥料为x吨,从A城运往两乡的总运费为元,从B城运往两乡的总运费为元.
(1)分别直接写出,与x之间的函数关系式(不要求写自变量的取值范围);
(2)当城运往两乡的总运费不低于4200元时,怎样调运,才能使A,B两城运往两乡的总费用的和最小?并求出最小值;
(3)因路况原因,从B城到C,D两乡的运费分别增加了m元/吨和元/吨,A城运往两乡的总运费不低于4400元且不高于4600元,当A,B两城运往两乡的总费用的和的最小值为10960元时,请直接写出m的值.
24.如图1,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为.D是AB边上一点(不与点A、B重合),将沿直线CD翻折,使点B落在点E处.
(1)求直线AC所表示的函数的表达式;
(2)如图2,当点E恰好落在矩形的对角线AC上时,求点D的坐标;
(3)如图3,当以O、E、C三点为顶点的三角形是等腰三角形时,求的面积.
参考答案
1.答案:A
解析:A:不能化简,是最简二次根式;
B:,不是最简二次根式;
C:,不是最简二次根式;
D:,不是最简二次根式.
故选:A.
2.答案:D
解析:、和不是同类项不可以合并,计算错误,不符合题意;
、,计算错误,不符合题意;
、,计算错误,不符合题意;
、,正确,符合题意.
故选:D.
3.答案:C
解析:A、由,,不能判定四边形是平行四边形,故本选项不符合题意;
B、由,,不能判定四边形是平行四边形,故本选项不符合题意;
C、,
,,
,
,
四边形是平行四边形,故本选项符合题意;
D、由,,不能判定四边形是平行四边形,故本选项不符合题意;
故选:C
4.答案:B
解析:如图所示,
作轴于点A,则,,
在中,
,
故选:B.
5.答案:D
解析:根据y随x的增大而增大,知:,
即.
故答案选:D.
6.答案:B
解析:∴正方形的边长,
∴
∵,
∴,,
∴,
∵,
∴,即,
∴,
∴,
∴.
故选B.
7.答案:B
解析:A、60出现了4次,出现的次数最多,则众数是60,故A选项说法正确;
B、这组数据的平均数是:,故B选项说法错误;
C、调查的户数是,故C选项说法正确;
D、把这组数据从小到大排列,最中间的两个数的平均数是,则中位数是50,故D选项说法正确;
故选B.
8.答案:A
解析:由图像及题意可得:,
当点P运动到C点时三角形ABP的面积为4,即,
,,在中,;
故选A.
9.答案:B
解析:∵点A、B的坐标分别为、,
∴,
∵,,
∴,
∴C点纵坐标为:8,
∵将沿x轴向右平移,当点C落在直线上时,
∴时,,解得:,即A点向右平移个单位,
∴线段BC扫过的面积为:.
故选B.
10.答案:A
解析:∵四边形是正方形,,
∴,,
∴,,
∴,
∴,,即点F是的中点;①正确;
过点A作于点J,如图所示:
四边形是正方形,
,
,
,
,
在与中,
,
,
,
在与中,
,
,
,
延长交于点M,作,,
,,
,,
在中,,
.
∵,
,
,
,即是等腰直角三角形,
∵,
∴,,
∴,
∴,
∴,②正确;
在与中,
,
∵,
∴,
∴,
∵,,
∴是的平分线,
∴;③正确;
在等腰与等腰中,
,
,
,
四边形是正方形,,,
,,
,
,④错误,
综上,①②③正确,
故选:A.
11.答案:
解析:在实数范围内有意义,
则;解得
故答案为.
12.答案:
解析:将代入,
得:,
解得:,
∴,
将直线向下平移4个单位后所得直线的解析式是,即y=-2x+3.
故答案为:.
13.答案:1
解析:在中,D为的中点,,
,
为的中位线,,
,
,
故答案为:1.
14.答案:
解析:由题意知:
,,,
在中,由勾股定理得:
.
故答案为:.
15.答案:①②③
解析:①∵直线与y轴交于负半轴,
∴;
∵的图象从左往右逐渐上升,
∴,
故结论①正确;
②将代入,得,
∴直线一定经过点.
故结论②正确;
③∵直线与的交点的横坐标为-2,
∴当时,,
∴.
故结论③正确;
④∵当时,直线在直线的上方,
∴当时,,
∴
故结论④错误.
故答案为:①②③.
16.答案:(1)
(2)
解析:(1)
;
(2)
.
17.答案:(1)6
(2)
解析:(1),,
,,
;
(2)
,
将代入,得:
原式.
18.答案:(1)80,81,80
(2)见解析
(3)乙的综合成绩较好
解析:(1)八(2)班学生知识竞赛的平均成绩,
八(1)班的成绩从小到大排列,排在中间的两个数分别是80,82,则中位数,
八(2)班的成绩中,80出现的次数最多,故众数;
故答案为:80,81,80;
(2)两个班平均成绩相同,但八(1)班的中位数及众数均高于八(2)班,并且方差小于八(2)班,所以八(1)班成绩更稳定且优于八(2)班;
(3)甲的综合成绩为:分,
乙的综合成绩为:分,
故乙的综合成绩较好.
19.答案:(1)证明见解析
(2)84
解析:(1)证明:连,交于O点,如图所示:
四边形为矩形,
,,
,
,
,
,
四边形是平行四边形;
(2)如图所示:
;,
由图可知,
,,,
,
由等面积法得到,则在中,,
,
.
20.答案:(1)表格见解析
(2)图见解析,增大
(3)图见解析,解集为
解析:(1)由题意,填表得,
x … 0 1 2 3 …
… 4 3 2 1 0 1 2 …
(2)根据题意,画图象,如图;
由图象可知,当时,y的值随x值的增大而增大.
故答案为:增大;
(3)如图,画出直线的图象,
由图象可知,
当时,,
当时,,
不等式的解集为.
21.答案:(1)
(2)t的值为或
(3)
解析:(1)根据题意得:,
∵,,
∴,,
∵,,
∴当时,四边形是矩形,
∴,
解得:,
即当时,四边形是矩形;
故答案为:6.5;
(2)若,分两种情况:
①时,则四边形是平行四边形,,即,
解得:,
②与不平行时,四边形为等腰梯形,
则即
解得:,
∴的值为6或7;
(3)若四边形为菱形,则
解得:
作于M如图所示:
则,
,
在中,
,
,
∴当时,在点P,Q运动过程中,四边形能构成菱形,
故答案为:.
22.答案:(1)1200,60
(2)()
(3)经过8分钟和分钟时两人相距80米
解析:(1)由函数图象可知,最开始时甲乙两人之间的距离为1200米,
因为甲从A地出发,乙从B地出发,两人最开始时的距离就是A、B两地之间的距离,
所以A、B两地之间距离为1200米;
由图象可知乙经过20分时到达A地,
∴乙的步行速度为(米/分);
故答案为:1200,60;
(2)由函数图象可知,经过分钟时两人相遇,点M表示此时甲到达B地,乙未到达A地,经过20分钟时乙到达A地,此时两人相距b米,
设甲的步行速度为x米/分,则,
解得:(米/分)
(分)
∴(米),(米).
则M、N的坐标分别为,,
设线段的解析式为,
则有,
解得:,
∴线段的函数解析式是();
(3)设经过x分钟两人相距80米,两人相遇前和相遇后都可相距80米,
相遇前:,解得:;
相遇后:,解得:,
所以经过8分钟和分钟时两人相距80米.
23.答案:(1)①
②
(2)A城运150吨肥料到C城,运50吨肥料到D城,B城运90吨肥料到C城,运210吨肥料到D城总费用和最小,最小费用为9120元
(3)4
解析:(1)由题意得,,
;
(2)依题意:,
解得:
设两城总费用和为w元,则,
∵,
∴w随着x的增大而减小,
当时,,
此时调运方案为:A城运150吨肥料到C城,运50吨肥料到D城;B城运90吨肥料到C城,运210吨肥料到D城.
(3)依题意,,解得:.
设调整之后的总费用为元,则,
①若,则,随着x的增大而减小,
当时,,解得:(舍去);
②若时,则(舍去);
③若时,随着x的增大而增大,
当时,,解得:.
综上所得:m的值是4.
24.答案:(1)
(2)
(3)12或
解析:(1)∵点B的坐标为且四边形OABC是矩形,
∴点A、C的坐标分别为、,
设AC的表达式为,
把A、C两点的坐标分别代入上式得,解得,
∴直线AC所表示的函数的表达式;
(2)∵点A的坐标为,点C的坐标为,
∴,.
∴中,,
∵四边形OABC是矩形,
∴,,,
∵沿CD折叠,
∴,,,,
∴,
设,则,
∵中,由勾股定理得:,
∴,解得,
∴点D的坐标为;
(3)过点E分别作x、y轴的垂线,垂足分别为M、N,
∵,,,
∴,
∴四边形OMEN是矩形,
∴.
①当时,
∵,,
∴,
的面积;
②当时,
∵,
∴,
设,则,
在中,,
在中,,
即,
解得:,
则,
的面积;
故的面积为12或.
同课章节目录
