2023-2024学年陕西省部分学校高一下学期期末考试数学试题(含答案)
文档属性
| 名称 | 2023-2024学年陕西省部分学校高一下学期期末考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 407.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-19 13:51:23 | ||
图片预览


文档简介
2023-2024学年陕西省部分学校高一下学期期末考试
数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.( )
A. B. C. D.
2.中国古代科举制度始于隋而成于唐,兴盛于明、清两朝.明代会试分南卷、北卷、中卷,按的比例录取,若某年会试录取人数为,则北卷录取人数为( )
A. B. C. D.
3.已知向量,满足,,,则( )
A. B. C. D.
4.一件产品要经过道独立的加工程序,第一道工序的次品率为,第二道工序的次品率为,则产品的正品率为( )
A. B.
C. D.
5.已知水平放置的的直观图如图所示,,,则边上的中线的实际长度为( )
A.
B.
C.
D.
6.如图,在等腰梯形中,,,点为线段的中点,点是线段上的一点,且,则( )
A.
B.
C.
D.
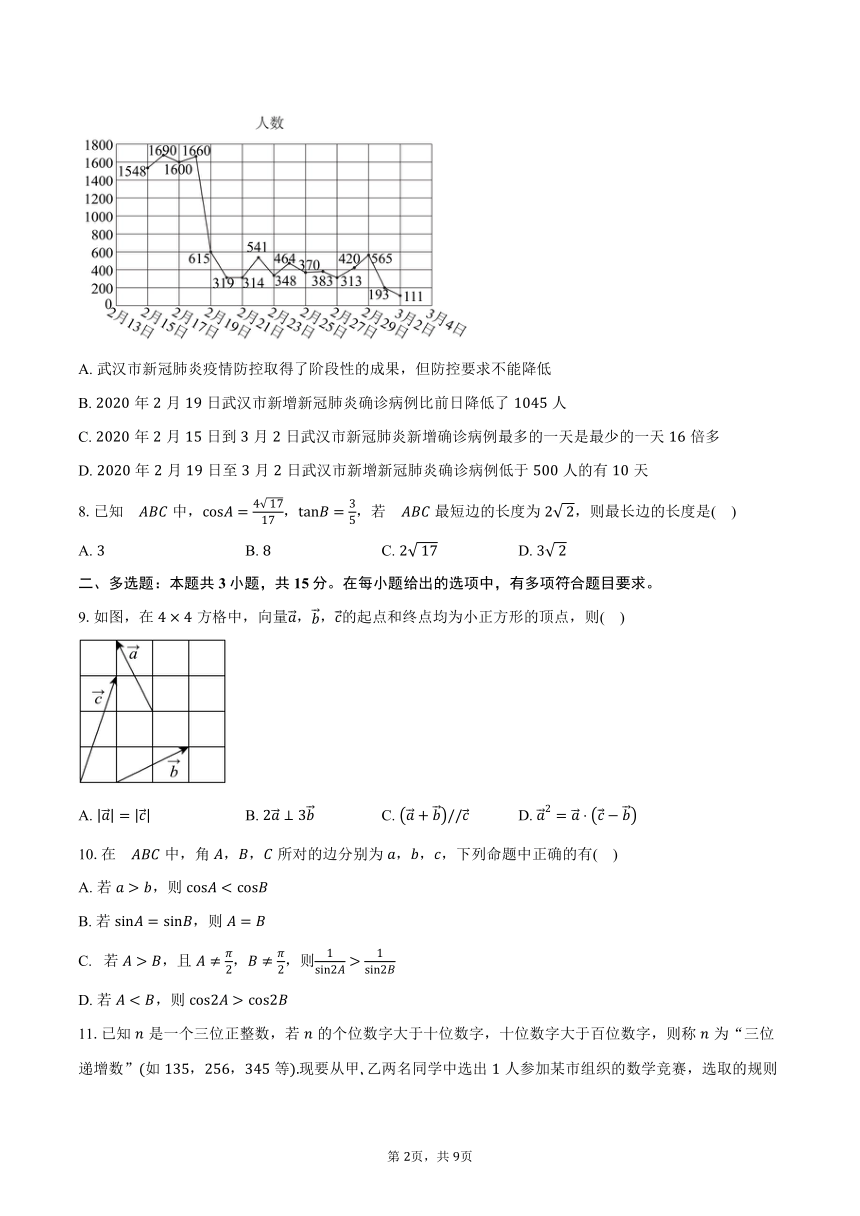
7.如图是年月日至月日武汉市新冠肺炎新增确诊病例的折线统计图.则下列说法不正确的是( )
A. 武汉市新冠肺炎疫情防控取得了阶段性的成果,但防控要求不能降低
B. 年月日武汉市新增新冠肺炎确诊病例比前日降低了人
C. 年月日到月日武汉市新冠肺炎新增确诊病例最多的一天是最少的一天倍多
D. 年月日至月日武汉市新增新冠肺炎确诊病例低于人的有天
8.已知中,,,若最短边的长度为,则最长边的长度是( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.如图,在方格中,向量,,的起点和终点均为小正方形的顶点,则( )
A. B. C. D.
10.在中,角,,所对的边分别为,,,下列命题中正确的有( )
A. 若,则
B. 若,则
C. 若,且,,则
D. 若,则
11.已知是一个三位正整数,若的个位数字大于十位数字,十位数字大于百位数字,则称为“三位递增数”如,,等现要从甲乙两名同学中选出人参加某市组织的数学竞赛,选取的规则如下:从由,,,,组成的所有“三位递增数”中随机抽取个数,若抽取的“三位递增数”是偶数,则甲参加数学竞赛;否则,乙参加数学竞赛则下列说法正确的是( )
A. 甲参赛的概率大 B. 乙参赛的概率大
C. 这种选取规则公平 D. 这种选取规则不公平
三、填空题:本题共3小题,每小题5分,共15分。
12.光明中学举办以“喜迎二十大、争做新青年、永远跟党走、奋进新征程”为主题的演讲比赛.其中人比赛的成绩为:,,,,,,,单位:分,则这人成绩的第百分位数和第百分位数的和为 .
13.如图所示,圆锥的底面半径为,高为,则该圆锥的表面积为 .
14.如图,已知,在平面内,是平面的斜线,且,,则直线与平面所成的角的大小为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知复数是虚数单位.
求复数的共轭复数和模;
若求,的值.
16.本小题分
如图所示,四边形为空间四边形的一个截面,且截面为平行四边形.
求证:平面.
若,且,,求四边形的面积.
17.本小题分
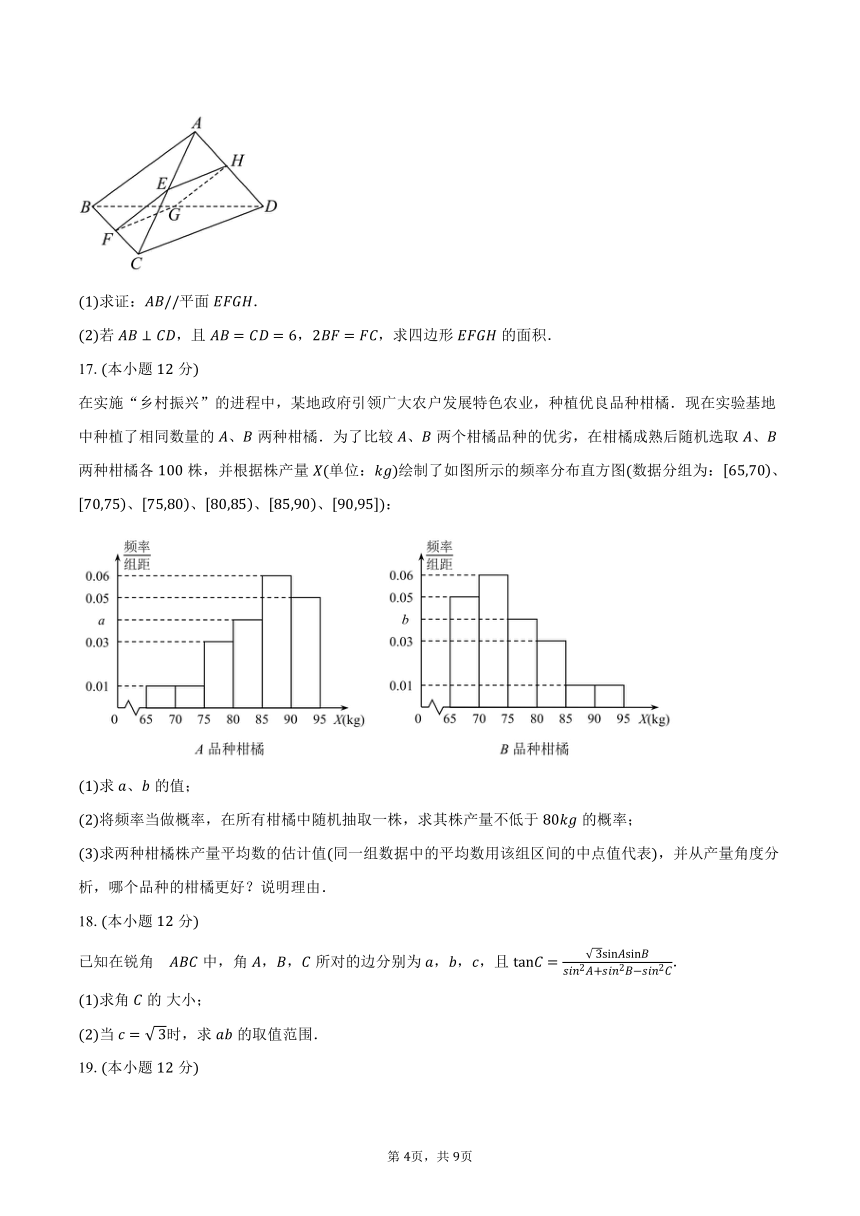
在实施“乡村振兴”的进程中,某地政府引领广大农户发展特色农业,种植优良品种柑橘.现在实验基地中种植了相同数量的、两种柑橘.为了比较、两个柑橘品种的优劣,在柑橘成熟后随机选取、两种柑橘各株,并根据株产量单位:绘制了如图所示的频率分布直方图数据分组为:、、、、、:
求、的值;
将频率当做概率,在所有柑橘中随机抽取一株,求其株产量不低于的概率;
求两种柑橘株产量平均数的估计值同一组数据中的平均数用该组区间的中点值代表,并从产量角度分析,哪个品种的柑橘更好?说明理由.
18.本小题分
已知在锐角中,角,,所对的边分别为,,,且.
求角的 大小;
当时,求的取值范围.
19.本小题分
如图,在三棱锥中,已知是正三角形,平面,,为的中点,在棱上,且.
求证:平面平面;
求三棱锥的体积;
若为的中点,是否存在在棱上,,且平面若存在,求的值并说明理由;若不存在,给出证明.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:,
所以的共轭复数,
;
因为,
即,
也即,
所以.
16.解:证明:四边形为平行四边形,
,平面,平面,
平面.
平面,平面平面,
,又平面,平面,
平面.
四边形为平行四边形,
,又平面,平面,
平面
又平面,平面平面,
,又,,
,
平行四边形为矩形,
由知,
与相似,
又,即,
,又,
,解得,
,,
同理,
与相似,
,又,可得,
四边形的面积为.
17.解:由频率分布直方图可得,解得,,解得.
品种柑橘株产量不低于的频率为,
品种柑橘株产量不低于的频率为,
故株柑橘中产量不低于的频率为,
所以在所有柑橘中随机抽取一株,其株产量不低于的概率为.
品种柑橘株产量平均数的估计值为,
,
设品种柑橘株产量平均数的估计值为,
,
品种的柑橘更好.理由如下:
方法一:的平均产量大于的平均产量.
方法二:由频率分布直方图可知,品种柑橘株产量在及以上的占比为,
品种柑橘株产量在及以上的占比为,故品种的柑橘更好.
18.解:因为,
由正弦定理可得,
由余弦定理,即,
所以,又为锐角,.
由正弦定理得,
,,
则
,
由,可得,,
,.
即的取值范围为.
19.解:证明:取的中点,连接,
因为,可得,
又因为,可得为的中点,因为为的中点,所以,
则,又因为是正三角形,所以,
因为平面,平面,所以,
又因为,平面,所以平面,
又平面,所以,
因为且平面,所以平面,
平面,所以平面平面;
平面,是正三角形,为的中点,
平面平面,,平面,
又,
;
存在这样的点,当时,平面,
当时,即,连接,设,连接,
由条件知为的重心,所以,所以当时,,
因为平面,平面,所以平面,
即时,平面.
第1页,共1页
数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.( )
A. B. C. D.
2.中国古代科举制度始于隋而成于唐,兴盛于明、清两朝.明代会试分南卷、北卷、中卷,按的比例录取,若某年会试录取人数为,则北卷录取人数为( )
A. B. C. D.
3.已知向量,满足,,,则( )
A. B. C. D.
4.一件产品要经过道独立的加工程序,第一道工序的次品率为,第二道工序的次品率为,则产品的正品率为( )
A. B.
C. D.
5.已知水平放置的的直观图如图所示,,,则边上的中线的实际长度为( )
A.
B.
C.
D.
6.如图,在等腰梯形中,,,点为线段的中点,点是线段上的一点,且,则( )
A.
B.
C.
D.
7.如图是年月日至月日武汉市新冠肺炎新增确诊病例的折线统计图.则下列说法不正确的是( )
A. 武汉市新冠肺炎疫情防控取得了阶段性的成果,但防控要求不能降低
B. 年月日武汉市新增新冠肺炎确诊病例比前日降低了人
C. 年月日到月日武汉市新冠肺炎新增确诊病例最多的一天是最少的一天倍多
D. 年月日至月日武汉市新增新冠肺炎确诊病例低于人的有天
8.已知中,,,若最短边的长度为,则最长边的长度是( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.如图,在方格中,向量,,的起点和终点均为小正方形的顶点,则( )
A. B. C. D.
10.在中,角,,所对的边分别为,,,下列命题中正确的有( )
A. 若,则
B. 若,则
C. 若,且,,则
D. 若,则
11.已知是一个三位正整数,若的个位数字大于十位数字,十位数字大于百位数字,则称为“三位递增数”如,,等现要从甲乙两名同学中选出人参加某市组织的数学竞赛,选取的规则如下:从由,,,,组成的所有“三位递增数”中随机抽取个数,若抽取的“三位递增数”是偶数,则甲参加数学竞赛;否则,乙参加数学竞赛则下列说法正确的是( )
A. 甲参赛的概率大 B. 乙参赛的概率大
C. 这种选取规则公平 D. 这种选取规则不公平
三、填空题:本题共3小题,每小题5分,共15分。
12.光明中学举办以“喜迎二十大、争做新青年、永远跟党走、奋进新征程”为主题的演讲比赛.其中人比赛的成绩为:,,,,,,,单位:分,则这人成绩的第百分位数和第百分位数的和为 .
13.如图所示,圆锥的底面半径为,高为,则该圆锥的表面积为 .
14.如图,已知,在平面内,是平面的斜线,且,,则直线与平面所成的角的大小为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知复数是虚数单位.
求复数的共轭复数和模;
若求,的值.
16.本小题分
如图所示,四边形为空间四边形的一个截面,且截面为平行四边形.
求证:平面.
若,且,,求四边形的面积.
17.本小题分
在实施“乡村振兴”的进程中,某地政府引领广大农户发展特色农业,种植优良品种柑橘.现在实验基地中种植了相同数量的、两种柑橘.为了比较、两个柑橘品种的优劣,在柑橘成熟后随机选取、两种柑橘各株,并根据株产量单位:绘制了如图所示的频率分布直方图数据分组为:、、、、、:
求、的值;
将频率当做概率,在所有柑橘中随机抽取一株,求其株产量不低于的概率;
求两种柑橘株产量平均数的估计值同一组数据中的平均数用该组区间的中点值代表,并从产量角度分析,哪个品种的柑橘更好?说明理由.
18.本小题分
已知在锐角中,角,,所对的边分别为,,,且.
求角的 大小;
当时,求的取值范围.
19.本小题分
如图,在三棱锥中,已知是正三角形,平面,,为的中点,在棱上,且.
求证:平面平面;
求三棱锥的体积;
若为的中点,是否存在在棱上,,且平面若存在,求的值并说明理由;若不存在,给出证明.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:,
所以的共轭复数,
;
因为,
即,
也即,
所以.
16.解:证明:四边形为平行四边形,
,平面,平面,
平面.
平面,平面平面,
,又平面,平面,
平面.
四边形为平行四边形,
,又平面,平面,
平面
又平面,平面平面,
,又,,
,
平行四边形为矩形,
由知,
与相似,
又,即,
,又,
,解得,
,,
同理,
与相似,
,又,可得,
四边形的面积为.
17.解:由频率分布直方图可得,解得,,解得.
品种柑橘株产量不低于的频率为,
品种柑橘株产量不低于的频率为,
故株柑橘中产量不低于的频率为,
所以在所有柑橘中随机抽取一株,其株产量不低于的概率为.
品种柑橘株产量平均数的估计值为,
,
设品种柑橘株产量平均数的估计值为,
,
品种的柑橘更好.理由如下:
方法一:的平均产量大于的平均产量.
方法二:由频率分布直方图可知,品种柑橘株产量在及以上的占比为,
品种柑橘株产量在及以上的占比为,故品种的柑橘更好.
18.解:因为,
由正弦定理可得,
由余弦定理,即,
所以,又为锐角,.
由正弦定理得,
,,
则
,
由,可得,,
,.
即的取值范围为.
19.解:证明:取的中点,连接,
因为,可得,
又因为,可得为的中点,因为为的中点,所以,
则,又因为是正三角形,所以,
因为平面,平面,所以,
又因为,平面,所以平面,
又平面,所以,
因为且平面,所以平面,
平面,所以平面平面;
平面,是正三角形,为的中点,
平面平面,,平面,
又,
;
存在这样的点,当时,平面,
当时,即,连接,设,连接,
由条件知为的重心,所以,所以当时,,
因为平面,平面,所以平面,
即时,平面.
第1页,共1页
同课章节目录
