2024年中考数学解答题分类汇编——统计与概率(含解析)
文档属性
| 名称 | 2024年中考数学解答题分类汇编——统计与概率(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 10:26:11 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024年中考数学解答题分类汇编——统计与概率
一.解答题(共30小题)
1.(2024 黑龙江)为贯彻落实教育部办公厅关于“保障学生每天校内、校外各一小时体育活动时间”的要求,某学校要求学生每天坚持体育锻炼.学校从全体男生中随机抽取了部分学生,调查他们的立定跳远成绩,整理如下不完整的频数分布表和统计图,结合图解答下列问题:
(1)频数分布表中m= ,扇形统计图中n= ;
(2)本次调查立定跳远成绩的中位数落在 组别;
(3)该校有600名男生,若立定跳远成绩大于200cm为合格,请估计该校立定跳远成绩合格的男生有多少人?
组别 分组(cm) 频数
A 50<x≤100 3
B 100<x≤150 m
C 150<x≤200 20
D 200<x≤250 14
E 250<x≤300 5
2.(2024 包头)《国家学生体质健康标准(2014年修订)》将九年级男生的立定跳远测试成绩分为四个等级:优秀(x≥240),良好(225≤x<240),及格(185≤x<225),不及格(x<185),其中x表示测试成绩(单位:cm).某校为了解本校九年级全体男生立定跳远测试的达标情况,精准找出差距,进行科学合理的工作规划,整理了本校及所在区县九年级全体男生近期一次测试成绩的相关数据,信息如下:
a.本校测试成绩频数(人数)分布表:
等级 优秀 良好 及格 不及格
频数(人数) 40 70 60 30
b.本校测试成绩统计表:
平均数 中位数 优秀率 及格率
222.5 228 p 85%
c.本校所在区县测试成绩统计表:
平均数 中位数 优秀率 及格率
218.7 223 23% 91%
请根据所给信息,解答下列问题:
(1)求出p的值;
(2)本校甲、乙两名同学本次测试成绩在本校排名(从高到低)分别是第100名、第101名,甲同学的测试成绩是230cm,请你计算出乙同学的测试成绩是多少?
(3)请你结合该校所在区县测试成绩,从平均数、中位数、优秀率和及格率四个方面中任选两个,对该校九年级全体男生立定跳远测试的达标情况做出评价,并为该校提出一条合理化建议.
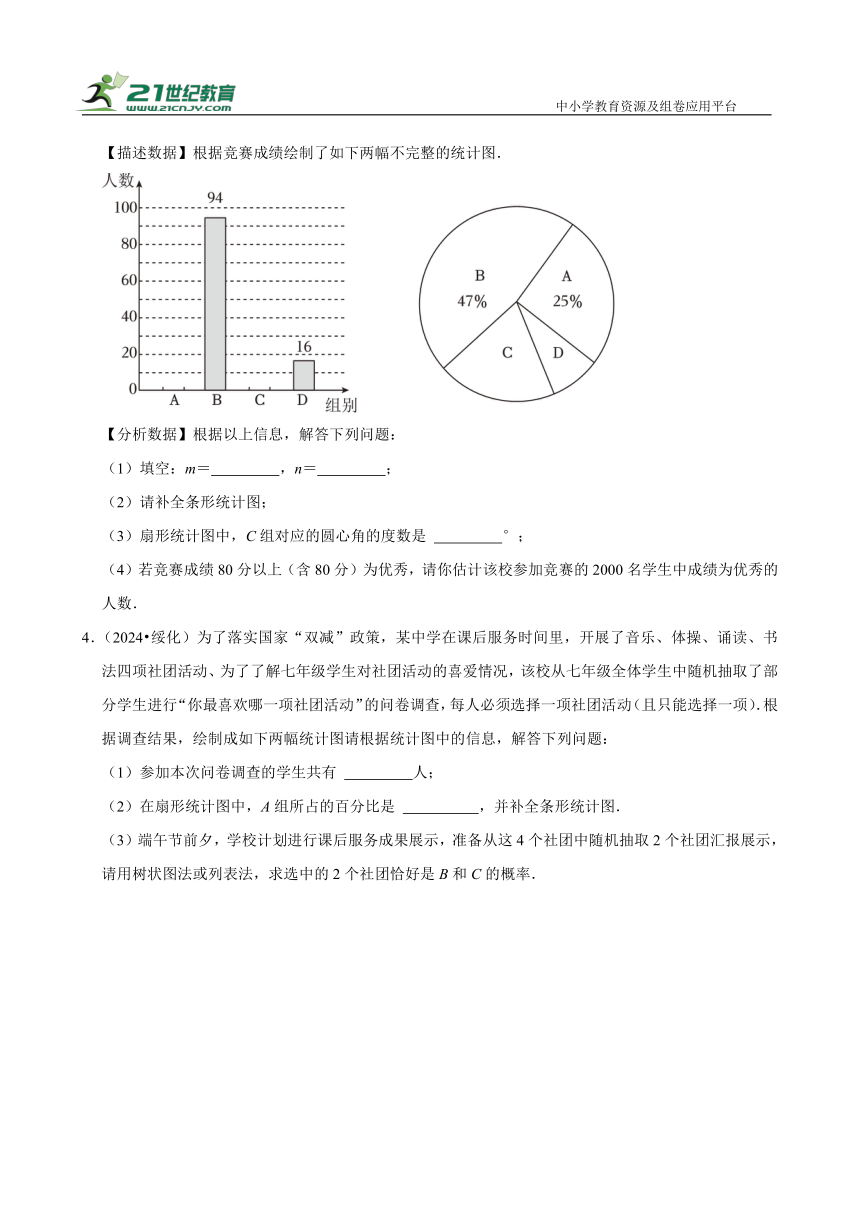
3.(2024 齐齐哈尔)为提高学生的环保意识,某校举行了“爱护环境,人人有责”环保知识竞赛,对收集到的数据进行了整理、描述和分析.
【收集数据】随机抽取部分学生的竞赛成绩组成一个样本.
【整理数据】将学生竞赛成绩的样本数据分成A,B,C,D四组进行整理.(满分100分,所有竞赛成绩均不低于60分)如表:
组别 A B C D
成绩(x/分) 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
人数(人) m 94 n 16
【描述数据】根据竞赛成绩绘制了如下两幅不完整的统计图.
【分析数据】根据以上信息,解答下列问题:
(1)填空:m= ,n= ;
(2)请补全条形统计图;
(3)扇形统计图中,C组对应的圆心角的度数是 °;
(4)若竞赛成绩80分以上(含80分)为优秀,请你估计该校参加竞赛的2000名学生中成绩为优秀的人数.
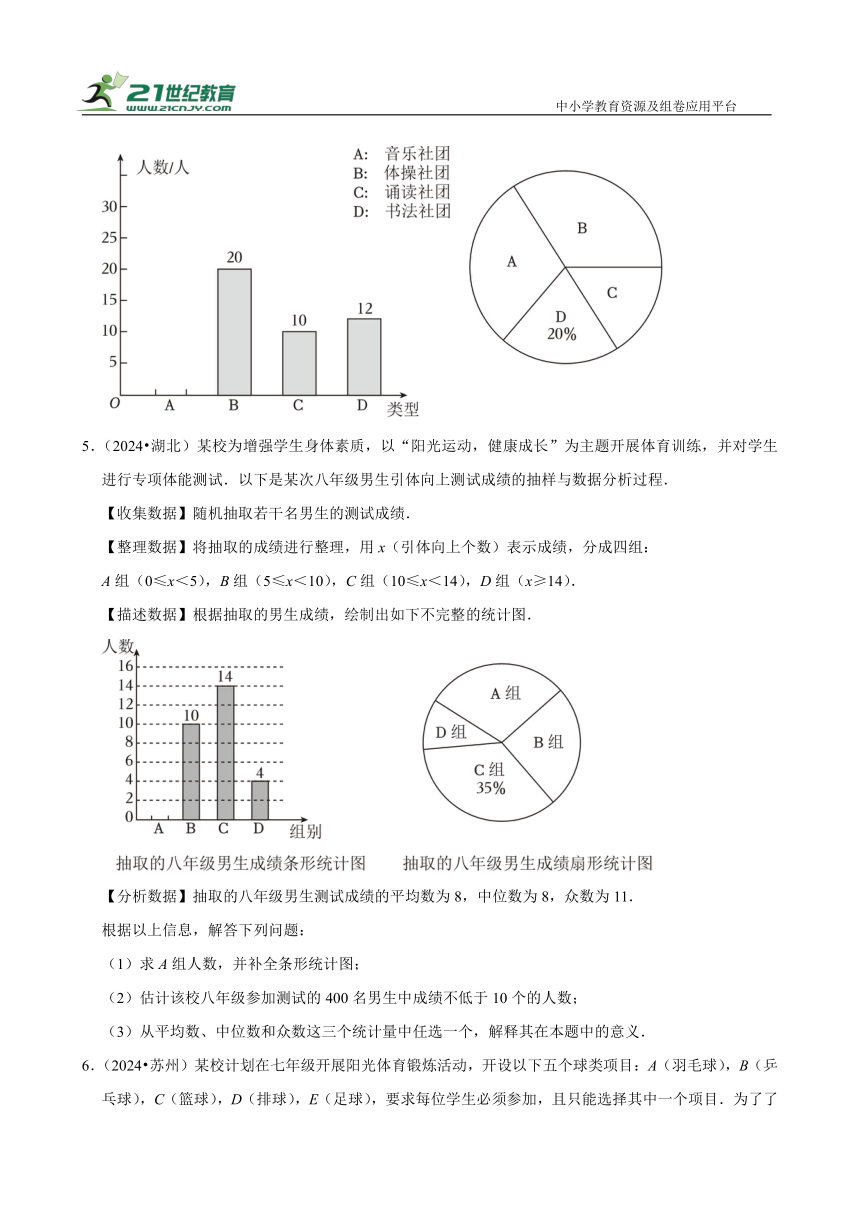
4.(2024 绥化)为了落实国家“双减”政策,某中学在课后服务时间里,开展了音乐、体操、诵读、书法四项社团活动、为了了解七年级学生对社团活动的喜爱情况,该校从七年级全体学生中随机抽取了部分学生进行“你最喜欢哪一项社团活动”的问卷调查,每人必须选择一项社团活动(且只能选择一项).根据调查结果,绘制成如下两幅统计图请根据统计图中的信息,解答下列问题:
(1)参加本次问卷调查的学生共有 人;
(2)在扇形统计图中,A组所占的百分比是 ,并补全条形统计图.
(3)端午节前夕,学校计划进行课后服务成果展示,准备从这4个社团中随机抽取2个社团汇报展示,请用树状图法或列表法,求选中的2个社团恰好是B和C的概率.
5.(2024 湖北)某校为增强学生身体素质,以“阳光运动,健康成长”为主题开展体育训练,并对学生进行专项体能测试.以下是某次八年级男生引体向上测试成绩的抽样与数据分析过程.
【收集数据】随机抽取若干名男生的测试成绩.
【整理数据】将抽取的成绩进行整理,用x(引体向上个数)表示成绩,分成四组:
A组(0≤x<5),B组(5≤x<10),C组(10≤x<14),D组(x≥14).
【描述数据】根据抽取的男生成绩,绘制出如下不完整的统计图.
【分析数据】抽取的八年级男生测试成绩的平均数为8,中位数为8,众数为11.
根据以上信息,解答下列问题:
(1)求A组人数,并补全条形统计图;
(2)估计该校八年级参加测试的400名男生中成绩不低于10个的人数;
(3)从平均数、中位数和众数这三个统计量中任选一个,解释其在本题中的意义.
6.(2024 苏州)某校计划在七年级开展阳光体育锻炼活动,开设以下五个球类项目:A(羽毛球),B(乒乓球),C(篮球),D(排球),E(足球),要求每位学生必须参加,且只能选择其中一个项目.为了了解学生对这五个项目的选择情况,学校从七年身全体学生中随机抽取部分学生进行问卷调查,对调查所得到的数据进行整理、描述和分析,部分信息如下:
根据上信息,解决下列问题:
(1)将图①中的条形统计图补充完整(画图并标注相应数据);
(2)图②中项目E对应的圆心角的度数为 °;
(3)根据抽样调查结果,请估计本校七年级800名学生中选择项目B(乒乓球)的人数.
7.(2024 贵州)根据《国家体质健康标准》规定,七年级男生、女生50米短跑时间分别不超过7.7秒、8.3秒为优秀等次.某校在七年级学生中挑选男生、女生各5人进行集训,经多次测试得到10名学生的平均成绩(单位:秒)记录如下:男生成绩:7.61,7.38,7.65,7.38,7.38
女生成绩:8.23,8.27,8.16,8.26,8.32
根据以上信息,解答下列问题:
(1)男生成绩的众数为 ,女生成绩的中位数为 ;
(2)判断下列两位同学的说法是否正确.
(3)教练从成绩最好的3名男生(设为甲,乙,丙)中,随机抽取2名学生代表学校参加比赛,请用画树状图或列表的方法求甲被抽中的概率.
8.(2024 新疆)为丰富学生的校园生活,提升学生的综合素质,某校计划开设丰富多彩的社团活动.为了解全校学生对各类社团活动的喜爱情况,该校随机抽取部分学生进行问卷调查(每名学生必选且只选一类),并根据调查结果制成如下统计图(不完整):
结合调查信息,回答下列问题:
(1)本次共调查了 名学生,喜爱“艺术类”社团活动的学生人数是 ;
(2)若该校有1000名学生,请估计其中大约有多少名学生喜爱“阅读类”社团活动?
(3)某班有2名男生和1名女生参加“体育类”社团中“追风篮球社”的选拔,2名学生被选中.请用列表法或画树状图法求选中的2名学生恰好为1名男生和1名女生的概率.
9.(2024 乐山)乐山作为闻名世界的文化旅游胜地,吸引了大量游客.为更好地提升服务质量,某旅行社随机调查了部分游客对四种美食的喜好情况(每人限选一种),并将调查结果绘制成统计图,如图所示.根据以上信息,回答下列问题:
(1)本次抽取的游客总人数为 人,扇形统计图中m的值为 ;
(2)请补全条形统计图;
(3)旅行社推出每人可免费品尝两种美食的活动,某游客从上述4种美食中随机选择两种,请用画树状图或列表的方法求选到“钵钵鸡和跷脚牛肉”的概率.
10.(2024 河北)某公司为提高员工的专业能力,定期对员工进行技能测试.考虑多种因素影响,需将测试的原始成绩x(分)换算为报告成绩y(分).已知原始成绩满分150分,报告成绩满分100分、换算规则如下:
当0≤x<p时,y=;
当p≤x≤150时,y=+80.
(其中p是小于150的常数,是原始成绩的合格分数线,80是报告成绩的合格分数线)公司规定报告成绩为80分及80分以上(即原始成绩为p及p以上)为合格.
(1)甲、乙的原始成绩分别为95分和130分,若p=100,求甲、乙的报告成绩;
(2)丙、丁的报告成绩分别为92分和64分,若丙的原始成绩比丁的原始成绩高40分,请推算p的值;
(3)下表是该公司100名员工某次测试的原始成绩统计表:
原始成绩(分) 95 100 105 110 115 120 125 130 135 140 145 150
人数 1 2 2 5 8 10 7 16 20 15 9 5
①直接写出这100名员工原始成绩的中位数;
②若①中的中位数换算成报告成绩为90分,直接写出该公司此次测试的合格率.
11.(2024 威海)为增强学生体质,某校在八年级男生中试行“每日锻炼,每月测试”的引体向上训练活动,设定6个及以上为合格.体育组为了解一学期的训练效果,随机抽查了20名男生2至6月份的测试成绩.其中,2月份测试成绩如表1,6月份测试成绩如图1(尚不完整).整理本学期测试数据得到表2和图2(尚不完整).
表1:2月份测试成绩统计表
个数 0 1 3 6 8 10
人数 4 8 4 1 2 1
表2:本学期测试成绩统计表
平均数/个 众数/个 中位数/个 合格率
2月 2.6 a 1 20%
3月 3.1 3 4 25%
4月 4 4 5 35%
5月 4.55 5 5 40%
6月 b 8 6 c
请根据图表中的信息,解答下列问题:
(1)将图1和图2中的统计图补充完整,并直接写出a,b,c的值;
(2)从多角度分析本次引体向上训练活动的效果;
(3)若将此活动在邻校八年级推广,该校八年级男生按400人计算,以随机抽查的20名男生训练成绩为样本,估算经过一学期的引体向上训练,可达到合格水平的男生人数.
12.(2024 安徽)综合与实践
【项目背景】
无核柑橘是我省西南山区特产,该地区某村有甲、乙两块成龄无核柑橘园.在柑橘收获季节,班级同学前往该村开展综合实践活动,其中一个项目是:在日照、土质、空气湿度等外部环境基本一致的条件下,对两块柑橘园的优质柑橘情况进行调查统计,为柑橘园的发展规划提供一些参考.
【数据收集与整理】
从两块柑橘园采摘的柑橘中各随机选取200个.在技术人员指导下,测量每个柑橘的直径,作为样本数据.柑橘直径用x(单位:cm)表示.
将所收集的样本数据进行如下分组:
组别 A B C D E
x 3.5≤x<4.5 4.5≤x<5.5 5.5≤x<6.5 6.5≤x<7.5 7.5≤x≤8.5
整理样本数据,并绘制甲、乙两园样本数据的频数分布直方图,部分信息如下:
任务1 求图1中a的值.
【数据分析与运用】
任务2 A,B,C,D,E五组数据的平均数分别取为4,5,6,7,8,计算乙园样本数据的平均数.
任务3 下列结论一定正确的是 (填正确结论的序号).
①两园样本数据的中位数均在C组;
②两园样本数据的众数均在C组;
③两园样本数据的最大数与最小数的差相等.
任务4 结合市场情况,将C,D两组的柑橘认定为一级,B组的柑橘认定为二级,其它组的柑橘认定为三级,其中一级柑橘的品质最优,二级次之,三级最次.试估计哪个园的柑橘品质更优,并说明理由.
根据所给信息,请完成以上所有任务.
13.(2024 苏州)一个不透明的盒子里装有4张书签,分别描绘“春”,“夏”,“秋”,“冬”四个季节,书签除图案外都相同,并将4张书签充分搅匀.
(1)若从盒子中任意抽取1张书签,恰好抽到“夏”的概率为 ;
(2)若从盒子中任意抽取2张书签(先抽取1张书签,且这张书签不放回,再抽取1张书签),求抽取的书签恰好1张为“春”,1张为“秋”的概率.(请用画树状图或列表等方法说明理由)
14.(2024 滨州)某校劳动实践基地共开设五门劳动实践课程,分别是A:床铺整理,B:衣物清洗,C:手工制作,D:简单烹饪,E:绿植栽培.课程开设一段时间后,李老师采用抽样调查的方式在全校学生中开展了“我最喜欢的劳动实践课程”为主题的问卷调查.根据调查所收集的数据进行整理,绘制了如下两幅不完整的统计图.
根据图中信息,请回答下列问题:
(1)请将条形统计图补充完整,并直接写出“手工制作”对应的扇形圆心角度数;
(2)若该校共有1800名学生,请你估计全校最喜欢“绿植栽培”的学生人数;
(3)小兰同学从B,C,D三门课程中随机选择一门参加劳动实践,小亮同学从C,D,E三门课程中随机选择一门参加劳动实践,求两位同学选择相同课程的概率.
15.(2024 内江)某校为了解学生对“生命、生态与安全”课程的学习掌握情况,从八年级学生中随机抽取了部分学生进行综合测试.测试结果分为A级、B级、C级、D级四个等级,并将测试结果绘制成了如下两幅不完整的统计图.根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
(2)扇形统计图中表示D级的扇形圆心角的度数是 ,并把条形统计图补充完整;
(3)该校八年级共有学生600人,如果全部参加这次测试,测试成绩为A级的学生大约有多少人?
16.(2024 山东)某学校开展了“校园科技节”活动,活动包含模型设计、科技小论文两个项目.为了解学生的模型设计水平,从全校学生的模型设计成绩中随机抽取部分学生的模型设计成绩(成绩为百分制,用x表示),并将其分成如下四组:60≤x<70,70≤x<80,80≤x<90,90≤x≤100.
下面给出了部分信息:
80≤x<90的成绩为:81,81,82,82,83,83,84,84,84,85,86,86,86,87,88,88,88,89,89,89.
根据以上信息解决下列问题:
(1)请补全频数分布直方图;
(2)所抽取学生的模型设计成绩的中位数是 分;
(3)请估计全校1000名学生的模型设计成绩不低于80分的人数;
(4)根据活动要求,学校将模型设计成绩、科技小论文成绩按3:2的比例确定这次活动各人的综合成绩.
某班甲、乙两位学生的模型设计成绩与科技小论文成绩(单位:分)如下:
模型设计 科技小论文
甲的成绩 94 90
乙的成绩 90 95
通过计算,甲、乙哪位学生的综合成绩更高?
17.(2024 广安)睡眠管理作为“五项管理”中的重要内容之一,也是学校教育重点关注的内容.某校为了解学生平均每天睡眠时间,随机抽取该校部分学生进行问卷调查,并将结果进行了统计和整理,绘制成如下统计表和不完整的统计图.
学生类别 学生平均每大睡眠时间x(单位:小时)
A 7≤x<7.5
B 7.5≤x<8
C 8≤x<8.5
D 8.5≤x<9
E x≥9
(1)本次抽取调查的学生共有 人,扇形统计图中表示C类学生平均每天睡眠时间的扇形的圆心角度数为 ;
(2)请补全条形统计图;
(3)被抽取调查的E类4名学生中有2名女生,2名男生.从这4人中随机抽取2人进行电话回访,请用画树状图或列表的方法,求恰好抽到2名男生的概率.
18.(2024 成都)2024年成都世界园艺博览会以“公园城市美好人居”为主题,秉持“绿色低碳、节约持续、共享包容”的理念,以园艺为媒介,向世界人民传递绿色发展理念和诗意栖居的美好生活场景.在主会场有多条游园线路,某单位准备组织全体员工前往参观,每位员工从其中四条线路(国风古韵观赏线、世界公园打卡线、亲子互动慢游线、园艺小清新线)中选择一条.现随机选取部分员工进行了“线路选择意愿”的摸底调查,并根据调查结果绘制成如下统计图表.
游园线路 人数
国风古韵观赏线 44
世界公园打卡线 x
亲子互动慢游线 48
园艺小清新线 y
根据图表信息,解答下列问题:
(1)本次调查的员工共有 人,表中x的值为 ;
(2)在扇形统计图中,求“国风古韵观赏线”对应的圆心角度数;
(3)若该单位共有2200人,请你根据调查结果,估计选择“园艺小清新线”的员工人数.
19.(2024 德阳)2024年中国龙舟公开赛(四川 德阳站),在德阳旌湖沱江桥水域举行,预计来自全国各地1000余名选手将参赛.旌湖两岸高颜值的绿色生态景观绿化带“德阳之窗”将迎接德阳市民以及来自全国各地的朋友近距离的观看比赛.比赛设置男子组、女子组、本地组三个组别,其中男子组将进行A:100米直道竞速赛,B:200米直道竞速赛,C:500米直道竞速赛,D:3000米绕标赛.为了了解德阳市民对于这四个比赛项目的关注程度,随机对部分市民进行了问卷调查(参与问卷调查的每位市民只能选择其中一个项目),将调查得到的数据绘制成数据统计表和扇形统计图(表、图都未完全制作完成):
市民最关注的比赛项目人数统计表
比赛项目 A B C D
关注人数 42 30 a b
(1)直接写出a、b的值和D所在扇形圆心角的度数;
(2)若当天观看比赛的市民有10000人,试估计当天观看比赛的市民中关注哪个比赛项目的人数最多?大约有多少人?
(3)为了缓解比赛当天城市交通压力,维护交通秩序,德阳交警旌阳支队派出4名交警(2男2女)对该路段进行值守,若在4名交警中任意抽取2名交警安排在同一路口执勤,请用列举法(画树状图或列表)求出恰好抽到的两名交警性别相同的概率.
20.(2024 泸州)某地两块试验田中分别栽种了甲、乙两种小麦,为了考查这两种小麦的长势,分别从中随机抽取16株麦苗,测得苗高(单位:cm)如表.
甲 7 8 10 11 11 12 13 13 14 14 14 14 15 16 16 18
乙 7 10 13 11 18 12 13 13 10 13 13 14 15 16 11 17
将数据整理分析,并绘制成以下不完整的统计表格和频数分布直方图.
苗高分组 甲种小麦的频数
7≤x<10 a
10≤x<13 b
13≤x<16 7
16≤x<19 3
小麦种类 统计量 甲 乙
平均数 12.875 12.875
众数 14 d
中位数 c 13
方差 8.65 7.85
根据所给出的信息,解决下列问题:
(1)a= ,b= ,并补全乙种小麦的频数分布直方图;
(2)c= ,d= ;
(3)甲、乙两种小麦的苗高长势比较整齐的是 (填甲或乙);若从栽种乙种小麦的试验田中随机抽取1200株,试估计苗高在10≤x<13(单位:cm)的株数.
21.(2024 重庆)为了解学生的安全知识掌握情况,某校举办了安全知识竞赛.现从七、八年级的学生中各随机抽取20名学生的竞赛成绩(百分制)进行收集、整理、描述、分析.所有学生的成绩均高于60分(成绩得分用x表示,共分成四组:A.60<x≤70;B.70<x≤80;C.80<x≤90;D.90<x≤100),下面给出了部分信息:七年级20名学生的竞赛成绩为:
66,67,68,68,75,83,84,86,86,86,
86,87,87,89,95,95,96,98,98,100.
八年级20名学生的竞赛成绩在C组的数据是:81,82,84,87,88,89.七、八年级所抽学生的竞赛成绩统计表
年级 七年级 八年级
平均数 85 85
中位数 86 b
众数 a 79
根据以上信息,解答下列问题:
(1)上述图表中a= ,b= ,m= ;
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好?请说明理由(写出一条理由即可);
(3)该校七年级有400名学生、八年级有500名学生参加了此次安全知识竞赛,估计该校七、八年级参加此次安全知识竞赛成绩优秀(x>90)的学生人数是多少?
22.(2024 遂宁)遂宁市作为全国旅游城市,有众多著名景点,为了解“五一”假期同学们的出游情况,某实践探究小组对部分同学假期旅游地做了调查,以下是调查报告的部分呢,请完善报告:
××小组关于××学校学生“五一”出游情况调查报告
数据收集
调查方式 抽样调查 调查对象 ××学校学生
数据的整理与描述
景点 A:中国死海 B:龙风古镇 C:灵泉风景区 D:金华山 E:未出游 F:其他
数据分析及运用
(1)本次被抽样调查的学生总人数为 ,扇形统计图中,m= ,“B:龙风古镇”对应圆心角的度数是 ; (2)请补全条形统计图; (3)该学校总人数为1800人,请你估计该学校学生“五一”假期未出游的人数; (4)未出游中的甲、乙两位同学计划下次假期从A、B、C、D四个景点中任选一个景点旅游,请用树状图或列表的方法求出他们选择同一景点的概率.
23.(2024 自贡)某校为了解学生身体健康状况,从全校600名学生的体质健康测试结果登记表中,随机选取了部分学生的测试数据进行初步整理(如表),并绘制出不完整的条形统计图(如图).
学生体质健康统计表
成绩 频数 百分比
不及格 3 a
及格 b 20%
良好 45 c
优秀 32 32%
(1)如表中a= ,b= ,c= ;
(2)请补全如图的条形统计图,并估计该校学生体质健康测试结果为“良好”和“优秀”的总人数;
(3)为听取测试建议,学校选出了3名“良好”1名“优秀”学生,再从这4名学生中随机抽取2人参加学校体质健康测试交流会,请用列表或画树状图的方法,计算所抽取的两人均为“良好”的概率.
24.(2024 宜宾)某校为了落实“五育并举”,提升学生的综合素养.在课外活动中开设了四个兴趣小组:A.插花组;B.跳绳组;C.话剧组;D.书法组.为了解学生对每个兴趣小组的参与情况,随机抽取了部分学生进行调查,并将调查结果绘制成不完整的统计图.
请结合图中信息解答下列问题:
(1)本次共调查了 名学生,并将条形统计图补充完整;
(2)话剧组所对应扇形的圆心角为 度;
(3)书法组成绩最好的4名学生由3名男生和1名女生构成.从中随机抽取2名参加比赛,请用列表或画树状图的方法,求刚好抽到1名男生与1名女生的概率.
25.(2024 临夏州)环球网消息称:近年来的电动自行车火灾事故80%都是充电时发生的,超过一半的电动自行车火灾发生在夜间充电的过程中.为了规避风险,某校政教处对学生进行规范充电培训活动,并对培训效果按10分制进行检测评分.为了解这次培训的效果,现从各年级随机抽取男、女生各10名的检测成绩作为样本进行整理,并绘制成如下不完整的统计图表:
抽取的10名女生检测成绩统计表
成绩/分 6 7 8 9 10
人数 1 2 m 3 n
注:10名女生检测成绩的中位数为8.5分.
请根据以上信息,完成下列问题:
(1)样本中男生检测成绩为10分的学生数是 ,众数为 分;
(2)女生检测成绩表中的m= ,n= ;
(3)已知该校有男生545人,女生360人,若认定检测成绩不低于9分为“优秀”,估计全校检测成绩达到“优秀”的人数.
26.(2024 广州)善于提问是应用人工智能解决问题的重要因素之一.为了解同学们的提问水平,对A,B两组同学进行问卷调查,并根据结果对每名同学的提问水平进行评分,得分情况如下(单位:分):
A组 75 78 82 82 84 86 87 88 93 95
B组 75 77 80 83 85 86 88 88 92 96
(1)求A组同学得分的中位数和众数;
(2)现从A,B两组得分超过90分的4名同学中随机抽取2名同学参与访谈,求这2名同学恰好来自同一组的概率.
27.(2024 吉林)吉林省以“绿水青山就是金山银山,冰天雪地也是金山银山”为指引,不断加大冰雪旅游的宣传力度,推出各种优惠活动,“小土豆”“小砂糖橘”等成为一道舰丽的风景线.某滑雪场为吸引游客,每天抽取一定数量的幸运游客,每名幸运游客可以从“滑雪”“滑雪圈”“雪地摩托”三个项目中随机抽取一个免费游玩.若三个项目被抽中的可能性相等,用画树状图或列表的方法,求幸运游客小明与小亮恰好抽中同一个项目的概率.
28.(2024 广东)端午假期,王先生计划与家人一同前往景区游玩.为了选择一个最合适的景区,王先生对A、B、C三个景区进行了调查与评估.他依据特色美食、自然风光、乡村民宿及科普基地四个方面,为每个景区评分(10分制).三个景区的得分如表所示:
景区 特色美食 自然风光 乡村民宿 科普基地
A 6 8 7 9
B 7 7 8 7
C 8 8 6 6
(1)若四项所占百分比如图所示,通过计算回答:王先生会选择哪个景区去游玩?
(2)如果王先生认为四项同等重要,通过计算回答:王先生将会选择哪个景区去游玩?
(3)如果你是王先生,请按你认为的各项“重要程度”设计四项得分的百分比,选择最合适的景区,并说明理由.
29.(2024 武汉)为加强体育锻炼,增强学生体质,某校在“阳光体育一小时”活动中组织九年级学生定点投篮技能测试,每人投篮4次,投中一次计1分.随机抽取m名学生的成绩作为样本,将收集的数据整理并绘制成如下的统计图表.
测试成绩频数分布表
成绩/分 频数
4 12
3 a
2 15
1 b
0 6
根据以上信息,解答下列问题:
(1)直接写出m,n的值和样本的众数;
(2)若该校九年级有900名学生参加测试,估计得分超过2分的学生人数.
30.(2024 河北)甲、乙、丙三张卡片正面分别写有a+b,2a+b,a﹣b,除正面的代数式不同外,其余均相同.
(1)将三张卡片背面向上并洗匀,从中随机抽取一张,当a=1,b=﹣2时,求取出的卡片上代数式的值为负数的概率;
(2)将三张卡片背面向上并洗匀,从中随机抽取一张,放回后重新洗匀,再随机抽取一张.请在表格中补全两次取出的卡片上代数式之和的所有可能结果(化为最简),并求出和为单项式的概率.
第一次 和 第二次 a+b 2a+b a﹣b
a+b 2a+2b 2a
2a+b
a﹣b 2a
统计与概率
参考答案与试题解析
一.解答题(共30小题)
1.(2024 黑龙江)为贯彻落实教育部办公厅关于“保障学生每天校内、校外各一小时体育活动时间”的要求,某学校要求学生每天坚持体育锻炼.学校从全体男生中随机抽取了部分学生,调查他们的立定跳远成绩,整理如下不完整的频数分布表和统计图,结合图解答下列问题:
(1)频数分布表中m= 50 ,扇形统计图中n= 40 ;
(2)本次调查立定跳远成绩的中位数落在 C 组别;
(3)该校有600名男生,若立定跳远成绩大于200cm为合格,请估计该校立定跳远成绩合格的男生有多少人?
组别 分组(cm) 频数
A 50<x≤100 3
B 100<x≤150 m
C 150<x≤200 20
D 200<x≤250 14
E 250<x≤300 5
【分析】(1)根据A组的频数和百分比求出抽取总数,用总数减其他的频数可得求出m的值,求出C组所占百分比,即可求解;
(2)根据中位数的定义即可求解;
(3)用样本估计总体即可.
【解答】解:(1)由题意可得,3÷6%=50,
m=50﹣3﹣20﹣14﹣5=8,
扇形统计图中C组所在的百分比==40%,
∴n=40,
故答案为:50,40;
(2)被抽取的50名学生立定跳远成绩按从小到大的顺序排列第25个和第26 个的平均数,3+8<25,3+8+20=31>25
被抽取的50名学生这一天的体育活动时间数据的中位数在C组;
(3)600×=228(名),
答:估计该校立定跳远成绩合格的男生有228人.
【点评】本题考查频数分布表、扇形统计图、用样本估计总体,解答本题的关键是求出样本容量,利用数形结合的思想解答.
2.(2024 包头)《国家学生体质健康标准(2014年修订)》将九年级男生的立定跳远测试成绩分为四个等级:优秀(x≥240),良好(225≤x<240),及格(185≤x<225),不及格(x<185),其中x表示测试成绩(单位:cm).某校为了解本校九年级全体男生立定跳远测试的达标情况,精准找出差距,进行科学合理的工作规划,整理了本校及所在区县九年级全体男生近期一次测试成绩的相关数据,信息如下:
a.本校测试成绩频数(人数)分布表:
等级 优秀 良好 及格 不及格
频数(人数) 40 70 60 30
b.本校测试成绩统计表:
平均数 中位数 优秀率 及格率
222.5 228 p 85%
c.本校所在区县测试成绩统计表:
平均数 中位数 优秀率 及格率
218.7 223 23% 91%
请根据所给信息,解答下列问题:
(1)求出p的值;
(2)本校甲、乙两名同学本次测试成绩在本校排名(从高到低)分别是第100名、第101名,甲同学的测试成绩是230cm,请你计算出乙同学的测试成绩是多少?
(3)请你结合该校所在区县测试成绩,从平均数、中位数、优秀率和及格率四个方面中任选两个,对该校九年级全体男生立定跳远测试的达标情况做出评价,并为该校提出一条合理化建议.
【分析】(1)利用优秀的人数除以总人数即可求出p的值;
(2)根据中位数的定义即可求出答案;
(3)从平均数和优秀率分析即可,答案不唯一,合理即可
【解答】解:(1)p=×100%=20%;
(2)设乙同学的成绩为x cm,
∵中位数为228,
∴=228,
解得x=226,
答:乙同学的测试成绩是226cm;
(3)从平均数来看,该校九年级全体男生立定跳远测试高于全县平均数,从优秀率来看,该校九年级全体男生立定跳远测试低于全县的优秀率,所以要加强训练强度,努力提高优秀率.
【点评】本题考查了频数(率)分布表,中位数,平均数,弄清题意是解本题的关键.
3.(2024 齐齐哈尔)为提高学生的环保意识,某校举行了“爱护环境,人人有责”环保知识竞赛,对收集到的数据进行了整理、描述和分析.
【收集数据】随机抽取部分学生的竞赛成绩组成一个样本.
【整理数据】将学生竞赛成绩的样本数据分成A,B,C,D四组进行整理.(满分100分,所有竞赛成绩均不低于60分)如表:
组别 A B C D
成绩(x/分) 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
人数(人) m 94 n 16
【描述数据】根据竞赛成绩绘制了如下两幅不完整的统计图.
【分析数据】根据以上信息,解答下列问题:
(1)填空:m= 50 ,n= 40 ;
(2)请补全条形统计图;
(3)扇形统计图中,C组对应的圆心角的度数是 72 °;
(4)若竞赛成绩80分以上(含80分)为优秀,请你估计该校参加竞赛的2000名学生中成绩为优秀的人数.
【分析】(1)先有B人数及其所占百分比求出被调查总人数,再用总人数乘以A的百分比求出m的值,再根据各组人数之和等于总人数求出n的值;
(2)根据m和n的值即可补全条形统计图;
(3)用360°乘以C组人数所占比例可求得其对应圆心角度数;
(4)用总人数乘以样本中80分以上(含80分)的人数所占比例即可得.
【解答】解:(1)本次随机抽取的学生人数为94÷47%=200(人),
∴m=200×25%=50,
∴n=200﹣50﹣94﹣16=40;
故答案为:50,40;
(2)补全条形统计图如图所示:
(3)扇形统计图中,C组对应的圆心角的度数是360°×=72°;
故答案为:72;
(4)2000×=560(名),
答:估计该校参加竞赛的2000名学生中成绩为优秀的人数有560名.
【点评】本题考查条形统计图,频数(率)分布表,用样本估计总体及扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.
4.(2024 绥化)为了落实国家“双减”政策,某中学在课后服务时间里,开展了音乐、体操、诵读、书法四项社团活动、为了了解七年级学生对社团活动的喜爱情况,该校从七年级全体学生中随机抽取了部分学生进行“你最喜欢哪一项社团活动”的问卷调查,每人必须选择一项社团活动(且只能选择一项).根据调查结果,绘制成如下两幅统计图请根据统计图中的信息,解答下列问题:
(1)参加本次问卷调查的学生共有 60 人;
(2)在扇形统计图中,A组所占的百分比是 30% ,并补全条形统计图.
(3)端午节前夕,学校计划进行课后服务成果展示,准备从这4个社团中随机抽取2个社团汇报展示,请用树状图法或列表法,求选中的2个社团恰好是B和C的概率.
【分析】(1)用条形统计图中D的人数除以扇形统计图中D的百分比可得参加本次问卷调查的学生人数.
(2)求出A组的学生人数,用A组的学生人数除以参加本次问卷调查的学生人数再乘以100%可得A组所占的百分比,最后补全条形统计图即可.
(3)列表可得出所有等可能的结果数以及选中的2个社团恰好是B和C的结果数,再利用概率公式可得出答案.
【解答】解:(1)参加本次问卷调查的学生共有12÷20%=60(人).
故答案为:60.
(2)A组的人数为60﹣20﹣10﹣12=18(人),
∴在扇形统计图中,A组所占的百分比是18÷60×100%=30%.
故答案为:30%.
补全条形统计图如图所示.
(3)列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
共有12种等可能的结果,其中选中的2个社团恰好是B和C的结果有:(B,C),(C,B),共2种,
∴选中的2个社团恰好是B和C的概率为=.
【点评】本题考查列表法与树状图法、条形统计图、扇形统计图,能够读懂统计图,掌握列表法与树状图法是解答本题的关键.
5.(2024 湖北)某校为增强学生身体素质,以“阳光运动,健康成长”为主题开展体育训练,并对学生进行专项体能测试.以下是某次八年级男生引体向上测试成绩的抽样与数据分析过程.
【收集数据】随机抽取若干名男生的测试成绩.
【整理数据】将抽取的成绩进行整理,用x(引体向上个数)表示成绩,分成四组:
A组(0≤x<5),B组(5≤x<10),C组(10≤x<14),D组(x≥14).
【描述数据】根据抽取的男生成绩,绘制出如下不完整的统计图.
【分析数据】抽取的八年级男生测试成绩的平均数为8,中位数为8,众数为11.
根据以上信息,解答下列问题:
(1)求A组人数,并补全条形统计图;
(2)估计该校八年级参加测试的400名男生中成绩不低于10个的人数;
(3)从平均数、中位数和众数这三个统计量中任选一个,解释其在本题中的意义.
【分析】(1)用C组的频数除以C组的频率,可得样本容量,再用样本容量分别减去其它三组的频数,即可得出A组的频数,进而补全条形统计图;
(2)用400乘样本中成绩不低于10个的人数所占比例即可;
(3)根据平均数、中位数和众数解答即可.
【解答】解:(1)样本容量为:14÷35%=40,
故A组人数为:40﹣10﹣14﹣4=12(人),
补全条形统计图如下:
(2)400×=180(人),
答:估计该校八年级参加测试的400名男生中成绩不低于10个的人数大约有180人;
(3)平均数表示抽取的40名学生的平均成绩;
众数表示抽取的40名学生中得分在某个分数的人数最多;
中位数表示取的40名学生中,将成绩从小到大排列后,位于中间位置的成绩(答案不唯一,任选其中一个说明即可).
【点评】本题考查频数分布直方图,中位数、众数、方差和加权平均数,理解中位数、众数、方差的意义以及和加权平均数的计算方法是解决问题的关键.
6.(2024 苏州)某校计划在七年级开展阳光体育锻炼活动,开设以下五个球类项目:A(羽毛球),B(乒乓球),C(篮球),D(排球),E(足球),要求每位学生必须参加,且只能选择其中一个项目.为了了解学生对这五个项目的选择情况,学校从七年身全体学生中随机抽取部分学生进行问卷调查,对调查所得到的数据进行整理、描述和分析,部分信息如下:
根据上信息,解决下列问题:
(1)将图①中的条形统计图补充完整(画图并标注相应数据);
(2)图②中项目E对应的圆心角的度数为 72 °;
(3)根据抽样调查结果,请估计本校七年级800名学生中选择项目B(乒乓球)的人数.
【分析】(1)用C的人数除以所占的百分比求出总人数,再求出D的人数即可补全条形统计图;
(2)用360°乘以E的人数所占比例即可;
(3)用总人数乘以样本中B的人数所占比例即可得.
【解答】解:(1)此次调查的总人数为9÷15%=60(人),
D项目的人数有60﹣6﹣18﹣9﹣12=15(人),
补全条形统计图如下:
(2)图②中项目E对应的圆心角的度数为360°×=72°;
故答案为:72;
(3)800×=240(名),
答:估计本校七年级800名学生中选择项目B(乒乓球)的人数为240名.
【点评】本题考查了条形统计图,扇形统计图和用样本估计总体,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
7.(2024 贵州)根据《国家体质健康标准》规定,七年级男生、女生50米短跑时间分别不超过7.7秒、8.3秒为优秀等次.某校在七年级学生中挑选男生、女生各5人进行集训,经多次测试得到10名学生的平均成绩(单位:秒)记录如下:男生成绩:7.61,7.38,7.65,7.38,7.38
女生成绩:8.23,8.27,8.16,8.26,8.32
根据以上信息,解答下列问题:
(1)男生成绩的众数为 7.38 ,女生成绩的中位数为 8.26 ;
(2)判断下列两位同学的说法是否正确.
(3)教练从成绩最好的3名男生(设为甲,乙,丙)中,随机抽取2名学生代表学校参加比赛,请用画树状图或列表的方法求甲被抽中的概率.
【分析】(1)根据众数、中位数的定义可得答案.
(2)由题意可知,5名男生中成绩最好的是7.38秒,5名女生的成绩不都是优秀等次,即可得出答案.
(3)列表可得出所有等可能的结果数以及甲被抽中的结果数,再利用概率公式可得出答案.
【解答】解:(1)由题意得,男生成绩的众数为7.38.
将5名女生的成绩按照从小到大的顺序排列,排在第3名的成绩为8.26,
∴女生成绩的中位数为8.26.
故答案为:7.38;8.26.
(2)5名男生中成绩最好的是7.38秒,
故小星同学的说法正确.
5名女生的成绩中超过8.3秒的有8.32秒,
∴5名女生的成绩不都是优秀等次,
故小红同学的说法不正确.
(3)列表如下:
甲 乙 丙
甲 (甲,乙) (甲,丙)
乙 (乙,甲) (乙,丙)
丙 (丙,甲) (丙,乙)
共有6种等可能的结果,其中甲被抽中的结果有:(甲,乙),(甲,丙),(乙,甲),(丙,甲),共4种,
∴甲被抽中的概率为=.
【点评】本题考查概率公式,列表法与树状图法、众数、中位数,熟练掌握列表法与树状图法、众数、中位数的定义是解答本题的关键.
8.(2024 新疆)为丰富学生的校园生活,提升学生的综合素质,某校计划开设丰富多彩的社团活动.为了解全校学生对各类社团活动的喜爱情况,该校随机抽取部分学生进行问卷调查(每名学生必选且只选一类),并根据调查结果制成如下统计图(不完整):
结合调查信息,回答下列问题:
(1)本次共调查了 100 名学生,喜爱“艺术类”社团活动的学生人数是 25人 ;
(2)若该校有1000名学生,请估计其中大约有多少名学生喜爱“阅读类”社团活动?
(3)某班有2名男生和1名女生参加“体育类”社团中“追风篮球社”的选拔,2名学生被选中.请用列表法或画树状图法求选中的2名学生恰好为1名男生和1名女生的概率.
【分析】(1)用条形统计图中“体育类”的人数除以扇形统计图中“体育类”的百分比可得本次共调查的学生人数;用本次共调查的学生人数乘以扇形统计图中“艺术类”的百分比可得喜爱“艺术类”社团活动的学生人数.
(2)根据用样本估计总体,用1000乘以样本中“阅读类”的学生人数所占的百分比,即可得出答案.
(3)列表可得出所有等可能的结果数以及选中的2名学生恰好为1名男生和1名女生的结果数,再利用概率公式可得出答案.
【解答】解:(1)本次共调查了30÷30%=100(名)学生.
喜爱“艺术类”社团活动的学生人数是100×25%=25(人).
故答案为:100;25人.
(2)1000×=150(名).
∴估计其中大约有150名学生喜爱“阅读类”社团活动.
(3)列表如下:
男 男 女
男 (男,男) (男,女)
男 (男,男) (男,女)
女 (女,男) (女,男)
共有6种等可能的结果,其中选中的2名学生恰好为1名男生和1名女生的结果有4种,
∴选中的2名学生恰好为1名男生和1名女生的概率为=.
【点评】本题考查列表法与树状图法、条形统计图、扇形统计图、用样本估计总体,能够读懂统计图,掌握列表法与树状图法以及用样本估计总体是解答本题的关键.
9.(2024 乐山)乐山作为闻名世界的文化旅游胜地,吸引了大量游客.为更好地提升服务质量,某旅行社随机调查了部分游客对四种美食的喜好情况(每人限选一种),并将调查结果绘制成统计图,如图所示.根据以上信息,回答下列问题:
(1)本次抽取的游客总人数为 240 人,扇形统计图中m的值为 35 ;
(2)请补全条形统计图;
(3)旅行社推出每人可免费品尝两种美食的活动,某游客从上述4种美食中随机选择两种,请用画树状图或列表的方法求选到“钵钵鸡和跷脚牛肉”的概率.
【分析】(1)由喜好跷脚牛肉的人数除以所占百分比得出本次抽取的游客总人数,即可解决问题;
(2)求出喜好甜皮鸡的人数,补全条形统计图即可;
(3)画树状图,共有12种可能出现的结果,其中选到“钵钵鸡和跷脚牛肉”的结果有2种,再由概率公式求解即可.
【解答】解:(1)本次抽取的游客总人数为72÷30%=240(人),
∴m%=84÷240×100%=35%,
故答案为:240,35;
(2)喜好甜皮鸡的人数为:240﹣48﹣72﹣84=36(人),
补全条形统计图如下:
(3)把四种美食分别记为A:麻辣烫,B:跷脚牛肉,C:钵钵鸡,D:甜皮鸭,
画树状图如下:
共有12种可能出现的结果,其中选到“钵钵鸡和跷脚牛肉”的结果有2种,
∴选到“钵钵鸡和跷脚牛肉”的概率为=.
【点评】此题考查的是用列表法或树状图法求概率以及条形统计图和扇形统计图等知识.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
10.(2024 河北)某公司为提高员工的专业能力,定期对员工进行技能测试.考虑多种因素影响,需将测试的原始成绩x(分)换算为报告成绩y(分).已知原始成绩满分150分,报告成绩满分100分、换算规则如下:
当0≤x<p时,y=;
当p≤x≤150时,y=+80.
(其中p是小于150的常数,是原始成绩的合格分数线,80是报告成绩的合格分数线)公司规定报告成绩为80分及80分以上(即原始成绩为p及p以上)为合格.
(1)甲、乙的原始成绩分别为95分和130分,若p=100,求甲、乙的报告成绩;
(2)丙、丁的报告成绩分别为92分和64分,若丙的原始成绩比丁的原始成绩高40分,请推算p的值;
(3)下表是该公司100名员工某次测试的原始成绩统计表:
原始成绩(分) 95 100 105 110 115 120 125 130 135 140 145 150
人数 1 2 2 5 8 10 7 16 20 15 9 5
①直接写出这100名员工原始成绩的中位数;
②若①中的中位数换算成报告成绩为90分,直接写出该公司此次测试的合格率.
【分析】(1)利用换算规则的公式解答即可;
(2)设丙的原始成绩为x1分,则丁的原始成绩为(x1﹣40)分,利用分类讨论的方法依据换算规则的公式解答即可;
(3)①利用中位数的定义解答即可;
②当p>130时,利用换算规则的公式解答即可;当p≤130时,则,由表格得到原始成绩为110及110以上的人数为100﹣5=95,利用合格率的公式解答即可.
【解答】解:(1)当p=100时,甲的报告成绩为: (分),
乙的探告成绩为: (分);
(2)设丙的原始成绩为x1分,则丁的原始成绩为(x1﹣40)分,
①0≤x<p时,y丙=92=…①,
,
由①﹣②得:,
∴,
∴,故不成立,舍;
②p≤x1﹣40≤150 时,y丙=92=+80…③, ……④,
由③﹣④得:,
∴p=.
∴92=+80,
∴,
∴,故不成立,舍;
③0≤x1﹣40<p,p≤x1≤150 时,
y丙=92=+80…⑤,
……⑥,
联立⑤⑥解得:p=125,x1=140,且符合题意,
综上所述p=125;
(3)①共计100名员工,且成绩已经排列好,
∴中位数是第50,51名员工成绩的平均数,
由表格得第50,51名员工成绩都是130分,
∴中位数为130;
②当p>130时,则,
解得 ,
故不成立,舍;
当p≤130时,
则,
解得p=110,符合题意,
∴.由表格得到原始成绩为110及110以上的人数为100﹣(1+2+2)=95,
∴合格率为:.
【点评】本题考查了函数关系式,自变量与函数值,中位数的定义,合格率,解分式方程,熟练知识点正确理解题意是解决本题的关键.
11.(2024 威海)为增强学生体质,某校在八年级男生中试行“每日锻炼,每月测试”的引体向上训练活动,设定6个及以上为合格.体育组为了解一学期的训练效果,随机抽查了20名男生2至6月份的测试成绩.其中,2月份测试成绩如表1,6月份测试成绩如图1(尚不完整).整理本学期测试数据得到表2和图2(尚不完整).
表1:2月份测试成绩统计表
个数 0 1 3 6 8 10
人数 4 8 4 1 2 1
表2:本学期测试成绩统计表
平均数/个 众数/个 中位数/个 合格率
2月 2.6 a 1 20%
3月 3.1 3 4 25%
4月 4 4 5 35%
5月 4.55 5 5 40%
6月 b 8 6 c
请根据图表中的信息,解答下列问题:
(1)将图1和图2中的统计图补充完整,并直接写出a,b,c的值;
(2)从多角度分析本次引体向上训练活动的效果;
(3)若将此活动在邻校八年级推广,该校八年级男生按400人计算,以随机抽查的20名男生训练成绩为样本,估算经过一学期的引体向上训练,可达到合格水平的男生人数.
【分析】(1)根据总人数减去引体向上为其他个数的人数,进而补充条形统计图,根据题意求得合格率c,补充折线统计图,根据平均数,众数的定义,即可得出a和b的值;
(2)根据平均数,众数,中位数,合格率,分析;
(3)根据样本估计总体即可求解.
【解答】解:(1)6月测试成绩中,引体向上3个的人数为20﹣4﹣1﹣6﹣4=5(人),
补充统计图如下:
c=×100%=55%,
根据表2可得a=1,
b=(4×1+5×3+1×6+6×8+4×10)=5.65,
(2)本次引体向上训练活动的效果明显,理由如下:
从平均数和合格率看,平均数和合格率逐月增加,
从中位数看,引体向上个数逐月增加,
从众数看,引体向上的个数越来越大(答案不唯一,合理即可);
(3)400×55%=220(人),
答:估算经过一学期的引体向上训练,可达到合格水平的男生人数约220人.
【点评】本题考查了条形统计图,折线统计图,统计表,样本估计总体,以及求平均数,众数,中位数的意义;掌握相关的统计量的意义是解题的关键.
12.(2024 安徽)综合与实践
【项目背景】
无核柑橘是我省西南山区特产,该地区某村有甲、乙两块成龄无核柑橘园.在柑橘收获季节,班级同学前往该村开展综合实践活动,其中一个项目是:在日照、土质、空气湿度等外部环境基本一致的条件下,对两块柑橘园的优质柑橘情况进行调查统计,为柑橘园的发展规划提供一些参考.
【数据收集与整理】
从两块柑橘园采摘的柑橘中各随机选取200个.在技术人员指导下,测量每个柑橘的直径,作为样本数据.柑橘直径用x(单位:cm)表示.
将所收集的样本数据进行如下分组:
组别 A B C D E
x 3.5≤x<4.5 4.5≤x<5.5 5.5≤x<6.5 6.5≤x<7.5 7.5≤x≤8.5
整理样本数据,并绘制甲、乙两园样本数据的频数分布直方图,部分信息如下:
任务1 求图1中a的值.
【数据分析与运用】
任务2 A,B,C,D,E五组数据的平均数分别取为4,5,6,7,8,计算乙园样本数据的平均数.
任务3 下列结论一定正确的是 ① (填正确结论的序号).
①两园样本数据的中位数均在C组;
②两园样本数据的众数均在C组;
③两园样本数据的最大数与最小数的差相等.
任务4 结合市场情况,将C,D两组的柑橘认定为一级,B组的柑橘认定为二级,其它组的柑橘认定为三级,其中一级柑橘的品质最优,二级次之,三级最次.试估计哪个园的柑橘品质更优,并说明理由.
根据所给信息,请完成以上所有任务.
【分析】(1)用200分别减去其它各组的频数可得a 的值;
(2)根据加权平均数公式计算即可;
(3)分别根据中位数、众数和极差的定义解答即可;
(4)根据统计图数据判断即可.
【解答】解:(1)由题意得,a=200﹣(15+70+50+25)=40;
(2)(15×4+50×5+70×6+50×7+15×8)=6,
故乙园样本数据的平均数为6;
(3)由统计图可知,两园样本数据的中位数均在C组,故①正确;
甲园的众数在B组,乙园的众数在C组,故②结论错误;
两园样本数据的最大数与最小数的差不一定相等,故③结论错误;
故答案为:①;
(4)乙园的柑橘品质更优,理由如下:
由样本数据频数分布直方图可得,乙园一级柑橘所占比例大于甲园,因此可以认为乙园的柑橘品质更优.
【点评】本题考查频数分布直方图,样本估计总体,频数分布表,加权平均数、中位数、众数以及极差,解题的关键是读懂图象信息,属于中考常考题型.
13.(2024 苏州)一个不透明的盒子里装有4张书签,分别描绘“春”,“夏”,“秋”,“冬”四个季节,书签除图案外都相同,并将4张书签充分搅匀.
(1)若从盒子中任意抽取1张书签,恰好抽到“夏”的概率为 ;
(2)若从盒子中任意抽取2张书签(先抽取1张书签,且这张书签不放回,再抽取1张书签),求抽取的书签恰好1张为“春”,1张为“秋”的概率.(请用画树状图或列表等方法说明理由)
【分析】(1)直接由概率公式求解即可;
(2)画树状图,共有12种等可能的结果,其中抽取的书签恰好1张为“春”,1张为“秋”的结果有2种,再由概率公式求解即可.
【解答】解:(1)∵一个不透明的盒子里装有4张书签,分别描绘“春”,“夏”,“秋”,“冬”四个季节,
∴从盒子中任意抽取1张书签,恰好抽到“夏”的概率为,
故答案为:;
(2)画树状图如下:
共有12种等可能的结果,其中抽取的书签恰好1张为“春”,1张为“秋”的结果有2种,
∴抽取的书签恰好1张为“春”,1张为“秋”的概率为=.
【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.
14.(2024 滨州)某校劳动实践基地共开设五门劳动实践课程,分别是A:床铺整理,B:衣物清洗,C:手工制作,D:简单烹饪,E:绿植栽培.课程开设一段时间后,李老师采用抽样调查的方式在全校学生中开展了“我最喜欢的劳动实践课程”为主题的问卷调查.根据调查所收集的数据进行整理,绘制了如下两幅不完整的统计图.
根据图中信息,请回答下列问题:
(1)请将条形统计图补充完整,并直接写出“手工制作”对应的扇形圆心角度数;
(2)若该校共有1800名学生,请你估计全校最喜欢“绿植栽培”的学生人数;
(3)小兰同学从B,C,D三门课程中随机选择一门参加劳动实践,小亮同学从C,D,E三门课程中随机选择一门参加劳动实践,求两位同学选择相同课程的概率.
【分析】(1)由E的学生人数除以所占百分比得出调查的学生人数,即可解决问题;
(2)由全校学生人数乘以最喜欢“绿植栽培”的学生人数所占的百分比即可;
(3)画树状图,共有9种等可能的结果,其中两位同学选择相同课程的结果有2种,再由概率公式求解即可.
【解答】解:(1)调查的学生人数为:30÷30%=100(人),
∴D的学生人数为:100×25%=25(人),
∴A的人数为:100﹣10﹣20﹣25﹣30=15(人),
将条形统计图补充完整如下:
“手工制作”对应的扇形圆心角度数为360°×=72°;
(2)1800×30%=540(人),
答:估计全校最喜欢“绿植栽培”的学生人数为540人;
(3)画树状图如下:
共有9种等可能的结果,其中两位同学选择相同课程的结果有2种,即CC、DD,
∴两位同学选择相同课程的概率为.
【点评】本题考查的是用列表法或画树状图法求概率以及条形统计图和扇形统计图等知识.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
15.(2024 内江)某校为了解学生对“生命、生态与安全”课程的学习掌握情况,从八年级学生中随机抽取了部分学生进行综合测试.测试结果分为A级、B级、C级、D级四个等级,并将测试结果绘制成了如下两幅不完整的统计图.根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 40 ;
(2)扇形统计图中表示D级的扇形圆心角的度数是 72° ,并把条形统计图补充完整;
(3)该校八年级共有学生600人,如果全部参加这次测试,测试成绩为A级的学生大约有多少人?
【分析】(1)根据B级的人数和所占的百分比,可以求得本次抽样测试的学生人数;
(2)用360°乘以D级人数所占的百分比即可求出D级的扇形圆心角的度数,用总人数乘以C级的人数所占的百分比求出C级的人数,即可把条形统计图补充完整;
(3)求出A级的学生人数所占的百分比乘以该校八年级学生总数600即可.
【解答】解:(1)本次抽样测试的学生人数是:12÷30%=40(人),
故答案为:40;
(2)扇形统计图中表示D级的扇形圆心角的度数是:360°×=72°,
C级的人数为:40×35%=14(人),
补充完整的条形统计图如图所示;
故答案为:72°;
(3)600×=90(人),
答:测试成绩为A级的学生大约有90人.
【点评】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
16.(2024 山东)某学校开展了“校园科技节”活动,活动包含模型设计、科技小论文两个项目.为了解学生的模型设计水平,从全校学生的模型设计成绩中随机抽取部分学生的模型设计成绩(成绩为百分制,用x表示),并将其分成如下四组:60≤x<70,70≤x<80,80≤x<90,90≤x≤100.
下面给出了部分信息:
80≤x<90的成绩为:81,81,82,82,83,83,84,84,84,85,86,86,86,87,88,88,88,89,89,89.
根据以上信息解决下列问题:
(1)请补全频数分布直方图;
(2)所抽取学生的模型设计成绩的中位数是 83 分;
(3)请估计全校1000名学生的模型设计成绩不低于80分的人数;
(4)根据活动要求,学校将模型设计成绩、科技小论文成绩按3:2的比例确定这次活动各人的综合成绩.
某班甲、乙两位学生的模型设计成绩与科技小论文成绩(单位:分)如下:
模型设计 科技小论文
甲的成绩 94 90
乙的成绩 90 95
通过计算,甲、乙哪位学生的综合成绩更高?
【分析】(1)先求解总人数,再求解70≤x<80的人数,再补全图形即可;
(2)根据中位数的含义确定第25个,第26个数据的平均数即可得到中位数;
(3)由总人数乘以80分(含80以上)的人数百分比即可得到答案;
(4)根据加权平均数公式分别计算甲,乙二人成绩,再比较即可
【解答】解:(1)∵5÷10%=50,而80≤x<90有20人,
∴70≤x<80有50﹣20﹣5﹣10=15,
补全图形如下:
(2)∵5+15=20,
而80≤x<90的成绩为:81,81,82,82,83,83,84,84,84,85,86,86,86,87,88,88,88,89,89,89.
∴50个成绩按照从小到大排列后,排在第25个,第26个数据分别是:83,83;
中位数为:,
故答案为:83;
(3)全校1000名学生的模型设计成绩不低于80分的人数为:
(人);
(4)甲的成绩为:(分);
乙的成绩为:(分);
∴甲的综合成绩比乙高.
【点评】本题考查的是频数分布直方图,中位数的含义,利用样本估计总体,加权平均数的含义,掌握基础的统计知识是解本题的感觉.
17.(2024 广安)睡眠管理作为“五项管理”中的重要内容之一,也是学校教育重点关注的内容.某校为了解学生平均每天睡眠时间,随机抽取该校部分学生进行问卷调查,并将结果进行了统计和整理,绘制成如下统计表和不完整的统计图.
学生类别 学生平均每大睡眠时间x(单位:小时)
A 7≤x<7.5
B 7.5≤x<8
C 8≤x<8.5
D 8.5≤x<9
E x≥9
(1)本次抽取调查的学生共有 50 人,扇形统计图中表示C类学生平均每天睡眠时间的扇形的圆心角度数为 144° ;
(2)请补全条形统计图;
(3)被抽取调查的E类4名学生中有2名女生,2名男生.从这4人中随机抽取2人进行电话回访,请用画树状图或列表的方法,求恰好抽到2名男生的概率.
【分析】(1)由B的人数除以所占百分比得出本次抽取调查的学生人数,即可解决问题;
(2)求出D的人数,补全条形统计图即可;
(3)画树状图,共有12种等可能的结果,其中恰好抽到2名男生的结果有2种,再由概率公式求解即可.
【解答】解:(1)本次抽取调查的学生共有14÷28%=50(人),
扇形统计图中表示C类学生平均每天睡眠时间的扇形的圆心角度数为360°×=144°,
故答案为:50,144°;
(2)D的人数为:50﹣6﹣14﹣20﹣4=6(人),
补全条形统计图如下:
(3)画树状图如下:
共有12种等可能的结果,其中恰好抽到2名男生的结果有2种,
∴恰好抽到2名男生的概率==.
【点评】本题考查的是用列表法或画树状图法求概率以及条形统计图和扇形统计图等知识.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
18.(2024 成都)2024年成都世界园艺博览会以“公园城市美好人居”为主题,秉持“绿色低碳、节约持续、共享包容”的理念,以园艺为媒介,向世界人民传递绿色发展理念和诗意栖居的美好生活场景.在主会场有多条游园线路,某单位准备组织全体员工前往参观,每位员工从其中四条线路(国风古韵观赏线、世界公园打卡线、亲子互动慢游线、园艺小清新线)中选择一条.现随机选取部分员工进行了“线路选择意愿”的摸底调查,并根据调查结果绘制成如下统计图表.
游园线路 人数
国风古韵观赏线 44
世界公园打卡线 x
亲子互动慢游线 48
园艺小清新线 y
根据图表信息,解答下列问题:
(1)本次调查的员工共有 160 人,表中x的值为 40 ;
(2)在扇形统计图中,求“国风古韵观赏线”对应的圆心角度数;
(3)若该单位共有2200人,请你根据调查结果,估计选择“园艺小清新线”的员工人数.
【分析】(1)根据选择亲子互动慢游线的人数和所占的百分比即可求出调查的总人数,用总人数乘以选择世界公园打卡线的百分比即可求出x的值;
(2)用360°乘以选择“国风古韵观赏线”所占的百分比即可求出对应的圆心角度数;
(3)用2200乘以选择“园艺小清新线”的员工人数所占百分比即可.
【解答】解:(1)本次调查的员工共有48÷30%=160(人),
表中x的值为160×=40;
故答案为:160,40;
(2)360°×=99°,
答:在扇形统计图中,“国风古韵观赏线”对应的圆心角度数为99°;
(3)2200×=385(人),
答:估计选择“园艺小清新线”的员工人数为385人.
【点评】本题考查扇形统计图,条形统计图和用样本估计总体,能从统计图中获取有用信息是解题的关键.
19.(2024 德阳)2024年中国龙舟公开赛(四川 德阳站),在德阳旌湖沱江桥水域举行,预计来自全国各地1000余名选手将参赛.旌湖两岸高颜值的绿色生态景观绿化带“德阳之窗”将迎接德阳市民以及来自全国各地的朋友近距离的观看比赛.比赛设置男子组、女子组、本地组三个组别,其中男子组将进行A:100米直道竞速赛,B:200米直道竞速赛,C:500米直道竞速赛,D:3000米绕标赛.为了了解德阳市民对于这四个比赛项目的关注程度,随机对部分市民进行了问卷调查(参与问卷调查的每位市民只能选择其中一个项目),将调查得到的数据绘制成数据统计表和扇形统计图(表、图都未完全制作完成):
市民最关注的比赛项目人数统计表
比赛项目 A B C D
关注人数 42 30 a b
(1)直接写出a、b的值和D所在扇形圆心角的度数;
(2)若当天观看比赛的市民有10000人,试估计当天观看比赛的市民中关注哪个比赛项目的人数最多?大约有多少人?
(3)为了缓解比赛当天城市交通压力,维护交通秩序,德阳交警旌阳支队派出4名交警(2男2女)对该路段进行值守,若在4名交警中任意抽取2名交警安排在同一路口执勤,请用列举法(画树状图或列表)求出恰好抽到的两名交警性别相同的概率.
【分析】(1)首先求出部分市民的人数为42÷28%=150,根据C:500米直道竞速赛人数所占的百分比求得a,根据题意即可得到结论;
(2)根据扇形统计图即可得到结论;
(3)设2名男性交警用A,B表示,2名女性交警用C,D表示,根据题意即可画树状图,进而求出恰好抽到的两名交警性别相同的概率.
【解答】解:(1)部分市民的人数为42÷28%=150(人),
∴a=150×12%=18,b=150﹣42﹣18﹣30=60(人),
D所在扇形圆心角的度数为360×=144°;
(2)当天观看比赛的市民中关注D:3000米绕标赛比赛项目的人数最多,
10000×=4000(人),
答:当天观看比赛的市民中关注D:3000米绕标赛比赛项目的人数最多大约有4000人;
(3)设2名男性交警用A,B表示,2名女性交警用C,D表示,
根据题意,画树状图如下:
由图可知:共有12种等可能的结果,符合条件的结果有4种,
所以恰好抽到的两名交警性别相同的概率为:=.
【点评】本题考查了列表法与树状图法、频率分布表、扇形统计图,解决本题的关键是掌握概率公式.
20.(2024 泸州)某地两块试验田中分别栽种了甲、乙两种小麦,为了考查这两种小麦的长势,分别从中随机抽取16株麦苗,测得苗高(单位:cm)如表.
甲 7 8 10 11 11 12 13 13 14 14 14 14 15 16 16 18
乙 7 10 13 11 18 12 13 13 10 13 13 14 15 16 11 17
将数据整理分析,并绘制成以下不完整的统计表格和频数分布直方图.
苗高分组 甲种小麦的频数
7≤x<10 a
10≤x<13 b
13≤x<16 7
16≤x<19 3
小麦种类 统计量 甲 乙
平均数 12.875 12.875
众数 14 d
中位数 c 13
方差 8.65 7.85
根据所给出的信息,解决下列问题:
(1)a= 2 ,b= 4 ,并补全乙种小麦的频数分布直方图;
(2)c= 13.5 ,d= 13 ;
(3)甲、乙两种小麦的苗高长势比较整齐的是 乙 (填甲或乙);若从栽种乙种小麦的试验田中随机抽取1200株,试估计苗高在10≤x<13(单位:cm)的株数.
【分析】(1)由表格可直接得出a,b的值;求出乙种小麦苗高在13≤x<16的频数,补全乙种小麦的频数分布直方图即可.
(2)根据中位数、众数的定义可得答案.
(3)根据方差的意义可知,甲、乙两种小麦的苗高长势比较整齐的是乙;根据用样本估计总体,用1200乘以样本中乙种小麦苗高在10≤x<13(单位:cm)的株数所占的百分比,即可得出答案.
【解答】解:(1)由表格可知,a=2,b=4.
故答案为:2;4.
由题意知,乙种小麦苗高在13≤x<16的频数为7,
补全乙种小麦的频数分布直方图如图所示.
(2)将甲种16株小麦的苗高按照从小到大的顺序排列,排在第8和第9的苗高为13,14,
∴c=(13+14)÷2=13.5.
由表格可知,d=13.
故答案为:13.5;13.
(3)∵甲种小麦的方差大于乙种小麦的方差,
∴甲、乙两种小麦的苗高长势比较整齐的是乙.
故答案为:乙.
1200×=375(株).
∴估计苗高在10≤x<13(单位:cm)的株数约375株.
【点评】本题考频数(率)分布直方图、频数(率)分布表、用样本估计总体、中位数、众数、方差,能够读懂统计图表,掌握用样本估计总体、中位数、众数、方差的定义是解答本题的关键.
21.(2024 重庆)为了解学生的安全知识掌握情况,某校举办了安全知识竞赛.现从七、八年级的学生中各随机抽取20名学生的竞赛成绩(百分制)进行收集、整理、描述、分析.所有学生的成绩均高于60分(成绩得分用x表示,共分成四组:A.60<x≤70;B.70<x≤80;C.80<x≤90;D.90<x≤100),下面给出了部分信息:七年级20名学生的竞赛成绩为:
66,67,68,68,75,83,84,86,86,86,
86,87,87,89,95,95,96,98,98,100.
八年级20名学生的竞赛成绩在C组的数据是:81,82,84,87,88,89.七、八年级所抽学生的竞赛成绩统计表
年级 七年级 八年级
平均数 85 85
中位数 86 b
众数 a 79
根据以上信息,解答下列问题:
(1)上述图表中a= 86 ,b= 87.5 ,m= 40 ;
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好?请说明理由(写出一条理由即可);
(3)该校七年级有400名学生、八年级有500名学生参加了此次安全知识竞赛,估计该校七、八年级参加此次安全知识竞赛成绩优秀(x>90)的学生人数是多少?
【分析】(1)分别根据众数和中位数的定义可得a、b的值;用“1”分别减去其它部分占比可得m的值;
(2)根据平均数和中位数的意义解答即可;
(3)利用样本估计总体思想求解可得.
【解答】解:(1)在七年级20名学生的竞赛成绩中86出现的次数最多,故众数a=86;
把八年级20名学生的竞赛成绩从小到大排列,排在中间的两个数分别是87,88,故中位数b==87.5,
m%=1﹣10%﹣20%﹣=40%,即m=40.
故答案为:86,87.5,40;
(2)八年级学生安全知识竞赛成绩较好,理由如下:
因为两个年级成绩的平均数相同,但八年级的中位数高于七年级,所以得到八年级学生安全知识竞赛成绩较好(答案不唯一);
(3)400×+500×40%
=120+200
=320(人),
答:估计该校七、八年级参加此次安全知识竞赛成绩优秀(x>90)的学生人数大约是320人.
【点评】本题考查了扇形统计图、频数分布表、中位数、众数以及用样本估计总体,掌握相关统计量的意义以及计算方法是解答本题的关键.
22.(2024 遂宁)遂宁市作为全国旅游城市,有众多著名景点,为了解“五一”假期同学们的出游情况,某实践探究小组对部分同学假期旅游地做了调查,以下是调查报告的部分呢,请完善报告:
××小组关于××学校学生“五一”出游情况调查报告
数据收集
调查方式 抽样调查 调查对象 ××学校学生
数据的整理与描述
景点 A:中国死海 B:龙风古镇 C:灵泉风景区 D:金华山 E:未出游 F:其他
数据分析及运用
(1)本次被抽样调查的学生总人数为 100 ,扇形统计图中,m= 10 ,“B:龙风古镇”对应圆心角的度数是 72° ; (2)请补全条形统计图; (3)该学校总人数为1800人,请你估计该学校学生“五一”假期未出游的人数; (4)未出游中的甲、乙两位同学计划下次假期从A、B、C、D四个景点中任选一个景点旅游,请用树状图或列表的方法求出他们选择同一景点的概率.
【分析】(1)将出游景点F的人数除以其所占百分比,即可得到本次被抽样调查的学生总人数;求出出游景点C的人数,再除以总人数,乘以100,即可求出m的值;将出游景点B的人数除以总人数,再乘以360°,即可得到“B:龙风古镇”对应圆心角的度数;
(2)求出出游景点C的人数,再补全条形统计图即可;
(3)将未出游的人数出游总人数,再乘以1800,即可估计该学校学生“五一”假期未出游的人数;
(4)用树状图或列表的方法即可求出他们选择同一景点的概率.
【解答】解:(1)∵30÷30%=100(人),
∴本次被抽样调查的学生总人数为100人;
∵出游C景点的人数为:100﹣(12+20+20+8+30)=10(人),
∴m=×100=10;
∵×360°=72°,
∴“B:龙风古镇”对应圆心角的度数是72°,
故答案为:100,10,72°;
(2)由(1)知:出游景点C的人数为10人,
补全条形统计图如下:
(3)×1800=144(人),
答:估计该学校学生“五一”假期未出游的有144人;
(4)画树状图如下:
一共有16种等可能的结果,其中两人选择同一景点有4种可能的结果,
∴P(选择同一景点)==.
【点评】本题考查条形统计图,扇形统计图,用样本估计总体,用列表法和树状图法求等可能事件的概率,能从统计图种获取数据,掌握用列表法和树状图法求等可能事件的概率的方法是解题的关键.
23.(2024 自贡)某校为了解学生身体健康状况,从全校600名学生的体质健康测试结果登记表中,随机选取了部分学生的测试数据进行初步整理(如表),并绘制出不完整的条形统计图(如图).
学生体质健康统计表
成绩 频数 百分比
不及格 3 a
及格 b 20%
良好 45 c
优秀 32 32%
(1)如表中a= 3% ,b= 20 ,c= 45% ;
(2)请补全如图的条形统计图,并估计该校学生体质健康测试结果为“良好”和“优秀”的总人数;
(3)为听取测试建议,学校选出了3名“良好”1名“优秀”学生,再从这4名学生中随机抽取2人参加学校体质健康测试交流会,请用列表或画树状图的方法,计算所抽取的两人均为“良好”的概率.
【分析】(1)先根据选取的优秀人数和百分比求出选取的人数,再根据总数、频数、百分比的关系即可求得答案;
(2)根据及格的人数,补全条形统计图即可;
(3)画树状图列出所有等可能的结果,再找出恰好选中两人均为“良好”的结果,利用概率公式可得出答案.
【解答】解:(1)这次调查的人数为:32÷32%=100(人),
a=×100%=3%,b=100×20%=20,c=×100%=45%,
故答案为:3%,20,45%;
(2)补全条形统计图如下:
600×(45%+32%)=462(人),
估计该校学生体质健康测试结果为“良好”和“优秀”的总人数为462人;
(3)设3名“良好”分别为甲、乙、丙,1名“优秀”学生为丁,
画树状图如图:
∵共有12种等可能的结果,其中恰好选中两人均为“良好”的结果有6种,
∴所抽取的两人均为“良好”的概率为=.
【点评】本题考查条形统计图、扇形统计图、用样本估计总体、列表法与树状图法,熟练掌握条形统计图与扇形统计图以及列表法与树状图法求概率是解答本题的关键.
24.(2024 宜宾)某校为了落实“五育并举”,提升学生的综合素养.在课外活动中开设了四个兴趣小组:A.插花组;B.跳绳组;C.话剧组;D.书法组.为了解学生对每个兴趣小组的参与情况,随机抽取了部分学生进行调查,并将调查结果绘制成不完整的统计图.
请结合图中信息解答下列问题:
(1)本次共调查了 40 名学生,并将条形统计图补充完整;
(2)话剧组所对应扇形的圆心角为 72 度;
(3)书法组成绩最好的4名学生由3名男生和1名女生构成.从中随机抽取2名参加比赛,请用列表或画树状图的方法,求刚好抽到1名男生与1名女生的概率.
【分析】(1)用条形统计图中A的人数除以扇形统计图中A的百分比可得本次调查的学生人数;求出C组的人数,补全条形统计图即可.
(2)用360°乘以本次调查中C组的人数所占的百分比,即可得出答案.
(3)画树状图得出所有等可能的结果数以及刚好抽到1名男生与1名女生的结果数,再利用概率公式可得出答案.
【解答】(1)此次调查的学生人数为:4÷10%=40(人),“C”类兴趣课的人数为:40﹣4﹣16﹣12=8(人),
补全条形统计图如下:
故答案为:40;
(2)“C”类兴趣课所对应扇形的圆心角的度数为:360°×=72°;
故答案为:72;
(3)将1名女生记为A,3名男生分别记为B,C,D,
画树状图如下:
共有12种等可能的结果,其中刚好抽到1名男生与1名女生的结果有:AB,AC,AD,BA,CA,DA,共6种,
∴刚好抽到1名男生与1名女生的概率为.
【点评】此题考查的是用树状图法求概率以及扇形统计图和条形统计图等知识.树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步或两步以上完成的事件;解题时要注意此题是放回试验还是不放回试验.
25.(2024 临夏州)环球网消息称:近年来的电动自行车火灾事故80%都是充电时发生的,超过一半的电动自行车火灾发生在夜间充电的过程中.为了规避风险,某校政教处对学生进行规范充电培训活动,并对培训效果按10分制进行检测评分.为了解这次培训的效果,现从各年级随机抽取男、女生各10名的检测成绩作为样本进行整理,并绘制成如下不完整的统计图表:
抽取的10名女生检测成绩统计表
成绩/分 6 7 8 9 10
人数 1 2 m 3 n
注:10名女生检测成绩的中位数为8.5分.
请根据以上信息,完成下列问题:
(1)样本中男生检测成绩为10分的学生数是 2 ,众数为 8 分;
(2)女生检测成绩表中的m= 2 ,n= 2 ;
(3)已知该校有男生545人,女生360人,若认定检测成绩不低于9分为“优秀”,估计全校检测成绩达到“优秀”的人数.
【分析】(1)用总人数乘以10分的学生数所占的百分比即可,然后根据众数定义即可求得众数;
(2)根据中位数的定义将八年级的活动成绩从小到大排列,那么其中位数应是第5个和第6个数据的平均数,结合已知条件易得第5个和第6个数据分别为8,9,再根据表格中数据即可求得答案;
(3)分别用男生和女生的总人数乘以样本中成绩不低于9分的人数所占的百分比即可,
【解答】解:(1)样本中男生检测成绩为10分的学生数是10×(1﹣10%﹣50%﹣20%)=2(人),
∵出现次数最多的为8分,
∴七年级活动成绩的众数为8分;
故答案为:2,8;
(2)将女生检测成绩绩从小到大排列后,它的中位数应是第5个和第6个数据的平均数,
∵女生检测成绩的中位数为8.5分,
∴第5个和第6个数据的和为8.5×2=17=8+9,
∴第5个和第6个数据分别为8分,9分,
∵成绩为6分和7分的人数为1+2=3(人),
∴成绩为8分的人数为5﹣3=2(人),
成绩为10分的人数为5﹣3=2(人),
即m=2,n=2;
故答案为:2,2;
(3)545×(20%+20%)+360×=218+180=398(人),
答:估计全校检测成绩达到“优秀”的人数为398人.
【点评】本题主要考查扇形统计图相关知识,众数,中位数及用样本估计总体,熟练掌握各知识点是解答本题的关键.
26.(2024 广州)善于提问是应用人工智能解决问题的重要因素之一.为了解同学们的提问水平,对A,B两组同学进行问卷调查,并根据结果对每名同学的提问水平进行评分,得分情况如下(单位:分):
A组 75 78 82 82 84 86 87 88 93 95
B组 75 77 80 83 85 86 88 88 92 96
(1)求A组同学得分的中位数和众数;
(2)现从A,B两组得分超过90分的4名同学中随机抽取2名同学参与访谈,求这2名同学恰好来自同一组的概率.
【分析】(1)根据中位数和众数的定义可得答案.
(2)列表可得出所有等可能的结果数以及这2名同学恰好来自同一组的结果数,再利用概率公式可得出答案.
【解答】解:(1)将10名A组同学的得分按照从小到大的顺序排列,排在第5和第6名的成绩为84,86,
∴A组同学得分的中位数为(84+86)÷2=85(分).
由表格可知,A组同学得分的众数为82分.
(2)将A组的两名同学分别记为甲、乙,将B组的两名同学分别记为丙,丁,
画树状图如下:
共有12种等可能的结果,其中这2名同学恰好来自同一组的结果有:甲乙,乙甲,丙丁,丁丙,共4种,
∴这2名同学恰好来自同一组的概率为.
【点评】本题考查列表法与树状图法、中位数、众数,熟练掌握列表法与树状图法、中位数、众数的定义是解答本题的关键.
27.(2024 吉林)吉林省以“绿水青山就是金山银山,冰天雪地也是金山银山”为指引,不断加大冰雪旅游的宣传力度,推出各种优惠活动,“小土豆”“小砂糖橘”等成为一道舰丽的风景线.某滑雪场为吸引游客,每天抽取一定数量的幸运游客,每名幸运游客可以从“滑雪”“滑雪圈”“雪地摩托”三个项目中随机抽取一个免费游玩.若三个项目被抽中的可能性相等,用画树状图或列表的方法,求幸运游客小明与小亮恰好抽中同一个项目的概率.
【分析】画树状图,共有9种等可能的结果,其中幸运游客小明与小亮恰好抽中同一个项目的结果有3种,再由概率公式求解即可.
【解答】解:把“滑雪”“滑雪圈”“雪地摩托”三个项目分别记为A、B、C,
画树状图如下:
共有9种等可能的结果,其中幸运游客小明与小亮恰好抽中同一个项目的结果有3种,
∴幸运游客小明与小亮恰好抽中同一个项目的概率为=.
【点评】此题考查的是用列表法或树状图法求概率以及概率公式.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.
28.(2024 广东)端午假期,王先生计划与家人一同前往景区游玩.为了选择一个最合适的景区,王先生对A、B、C三个景区进行了调查与评估.他依据特色美食、自然风光、乡村民宿及科普基地四个方面,为每个景区评分(10分制).三个景区的得分如表所示:
景区 特色美食 自然风光 乡村民宿 科普基地
A 6 8 7 9
B 7 7 8 7
C 8 8 6 6
(1)若四项所占百分比如图所示,通过计算回答:王先生会选择哪个景区去游玩?
(2)如果王先生认为四项同等重要,通过计算回答:王先生将会选择哪个景区去游玩?
(3)如果你是王先生,请按你认为的各项“重要程度”设计四项得分的百分比,选择最合适的景区,并说明理由.
【分析】(1)分别计算加权平均数即可判断出答案;
(2)分别计算算术平均数即可判断出答案;
(2)将特色美食、自然风光、乡村民宿和科普基地四项得分的百分比定为20%,30%,30%,20%,通过计算再判断即可(答案不唯一).
【解答】解:(1)景区A得分为:=7.15,
景区B得分为:=7.4,
景区C得分为:=6.9,
∵7.4>7.15>6.9,
∴王先生会选择B景区去游玩;
(2)景区A得分为:=7.5,
景区B得分为:=7.25,
景区C得分为:=7,
∵7.5>7.25>7,
∴王先生会选择A景区去游玩;
(3)将特色美食、自然风光、乡村民宿和科普基地四项得分的百分比定为20%,30%,30%,20%,
景区A得分为:=7.5,
景区B得分为:=7.3,
景区C得分为:=7,
∵7.5>7.3>7,
∴选择A景区去游玩.
【点评】本题考查了扇形统计图和平均数,加权平均数是将各数值乘以相应的权数,然后加总求和得到总体值,再除以总的单位数,平均数的大小不仅取决于总体中各单位的标志值(变量值)的大小,而且取决于各标志值出现的次数(频数),由于各标志值出现的次数对其在平均数中的影响起着权衡轻重的作用,因此叫做权数.
29.(2024 武汉)为加强体育锻炼,增强学生体质,某校在“阳光体育一小时”活动中组织九年级学生定点投篮技能测试,每人投篮4次,投中一次计1分.随机抽取m名学生的成绩作为样本,将收集的数据整理并绘制成如下的统计图表.
测试成绩频数分布表
成绩/分 频数
4 12
3 a
2 15
1 b
0 6
根据以上信息,解答下列问题:
(1)直接写出m,n的值和样本的众数;
(2)若该校九年级有900名学生参加测试,估计得分超过2分的学生人数.
【分析】(1)用频数分布表中2分的频数除以扇形统计图中2分的百分比可得m的值,用总人数乘以3分百分比求出a的值,即可求出b的值,用b的值除以总人数即可求出n的值,根据众数的定义即可求出众数;
(2)根据用样本估计总体,用900乘以样本中超过2分的学生人数所占的百分比,即可得出答案.
【解答】解:(1)由题意得,m=15÷25%=60,
∴a=60×30%=18,
∴b=60﹣12﹣18﹣15﹣6=9,
∴n%=×100%=15%,
∴n=15,
样本的众数为3;
(2)900×=450(名),
答:估计得分超过2分的学生人数有450名.
【点评】本题考查扇形统计图、频数(率)分布表、众数、用样本估计总体,能够读懂统计图表,掌握用样本估计总体、众数的定义是解答本题的关键.
30.(2024 河北)甲、乙、丙三张卡片正面分别写有a+b,2a+b,a﹣b,除正面的代数式不同外,其余均相同.
(1)将三张卡片背面向上并洗匀,从中随机抽取一张,当a=1,b=﹣2时,求取出的卡片上代数式的值为负数的概率;
(2)将三张卡片背面向上并洗匀,从中随机抽取一张,放回后重新洗匀,再随机抽取一张.请在表格中补全两次取出的卡片上代数式之和的所有可能结果(化为最简),并求出和为单项式的概率.
第一次 和 第二次 a+b 2a+b a﹣b
a+b 2a+2b 2a
2a+b
a﹣b 2a
【分析】(1)当a=1,b=﹣2时,a+b=﹣1,2a+b=0,a﹣b=3.从三张卡片中随机抽取一张,共有3种等可能的结果,其中取出的卡片上代数式的值为负数的结果有1种,利用概率公式可得答案.
(2)根据题意把表格补充完整,由表格可得出所有等可能的结果数以及和为单项式的结果数,再利用概率公式可得出答案.
【解答】解:(1)当a=1,b=﹣2时,a+b=﹣1,2a+b=0,a﹣b=3.
从三张卡片中随机抽取一张,共有3种等可能的结果,其中取出的卡片上代数式的值为负数的结果有1种,
∴取出的卡片上代数式的值为负数的概率为.
(2)补全表格如下:
第一次 和 第二次 a+b 2a+b a﹣b
a+b 2a+2b 3a+2b 2a
2a+b 3a+2b 4a+2b 3a
a﹣b 2a 3a 2a﹣2b
共有9种等可能的结果,其中和为单项式的结果有:2a,3a,2a,3a,共4种,
∴和为单项式的概率为.
【点评】本题考查列表法与树状图法、概率公式、整式的加减、多项式与单项式,熟练掌握列表法与树状图法、概率公式、整式的加减、多项式与单项式的概念是解答本题的关键.
2024年中考数学解答题分类汇编——统计与概率
一.解答题(共30小题)
1.(2024 黑龙江)为贯彻落实教育部办公厅关于“保障学生每天校内、校外各一小时体育活动时间”的要求,某学校要求学生每天坚持体育锻炼.学校从全体男生中随机抽取了部分学生,调查他们的立定跳远成绩,整理如下不完整的频数分布表和统计图,结合图解答下列问题:
(1)频数分布表中m= ,扇形统计图中n= ;
(2)本次调查立定跳远成绩的中位数落在 组别;
(3)该校有600名男生,若立定跳远成绩大于200cm为合格,请估计该校立定跳远成绩合格的男生有多少人?
组别 分组(cm) 频数
A 50<x≤100 3
B 100<x≤150 m
C 150<x≤200 20
D 200<x≤250 14
E 250<x≤300 5
2.(2024 包头)《国家学生体质健康标准(2014年修订)》将九年级男生的立定跳远测试成绩分为四个等级:优秀(x≥240),良好(225≤x<240),及格(185≤x<225),不及格(x<185),其中x表示测试成绩(单位:cm).某校为了解本校九年级全体男生立定跳远测试的达标情况,精准找出差距,进行科学合理的工作规划,整理了本校及所在区县九年级全体男生近期一次测试成绩的相关数据,信息如下:
a.本校测试成绩频数(人数)分布表:
等级 优秀 良好 及格 不及格
频数(人数) 40 70 60 30
b.本校测试成绩统计表:
平均数 中位数 优秀率 及格率
222.5 228 p 85%
c.本校所在区县测试成绩统计表:
平均数 中位数 优秀率 及格率
218.7 223 23% 91%
请根据所给信息,解答下列问题:
(1)求出p的值;
(2)本校甲、乙两名同学本次测试成绩在本校排名(从高到低)分别是第100名、第101名,甲同学的测试成绩是230cm,请你计算出乙同学的测试成绩是多少?
(3)请你结合该校所在区县测试成绩,从平均数、中位数、优秀率和及格率四个方面中任选两个,对该校九年级全体男生立定跳远测试的达标情况做出评价,并为该校提出一条合理化建议.
3.(2024 齐齐哈尔)为提高学生的环保意识,某校举行了“爱护环境,人人有责”环保知识竞赛,对收集到的数据进行了整理、描述和分析.
【收集数据】随机抽取部分学生的竞赛成绩组成一个样本.
【整理数据】将学生竞赛成绩的样本数据分成A,B,C,D四组进行整理.(满分100分,所有竞赛成绩均不低于60分)如表:
组别 A B C D
成绩(x/分) 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
人数(人) m 94 n 16
【描述数据】根据竞赛成绩绘制了如下两幅不完整的统计图.
【分析数据】根据以上信息,解答下列问题:
(1)填空:m= ,n= ;
(2)请补全条形统计图;
(3)扇形统计图中,C组对应的圆心角的度数是 °;
(4)若竞赛成绩80分以上(含80分)为优秀,请你估计该校参加竞赛的2000名学生中成绩为优秀的人数.
4.(2024 绥化)为了落实国家“双减”政策,某中学在课后服务时间里,开展了音乐、体操、诵读、书法四项社团活动、为了了解七年级学生对社团活动的喜爱情况,该校从七年级全体学生中随机抽取了部分学生进行“你最喜欢哪一项社团活动”的问卷调查,每人必须选择一项社团活动(且只能选择一项).根据调查结果,绘制成如下两幅统计图请根据统计图中的信息,解答下列问题:
(1)参加本次问卷调查的学生共有 人;
(2)在扇形统计图中,A组所占的百分比是 ,并补全条形统计图.
(3)端午节前夕,学校计划进行课后服务成果展示,准备从这4个社团中随机抽取2个社团汇报展示,请用树状图法或列表法,求选中的2个社团恰好是B和C的概率.
5.(2024 湖北)某校为增强学生身体素质,以“阳光运动,健康成长”为主题开展体育训练,并对学生进行专项体能测试.以下是某次八年级男生引体向上测试成绩的抽样与数据分析过程.
【收集数据】随机抽取若干名男生的测试成绩.
【整理数据】将抽取的成绩进行整理,用x(引体向上个数)表示成绩,分成四组:
A组(0≤x<5),B组(5≤x<10),C组(10≤x<14),D组(x≥14).
【描述数据】根据抽取的男生成绩,绘制出如下不完整的统计图.
【分析数据】抽取的八年级男生测试成绩的平均数为8,中位数为8,众数为11.
根据以上信息,解答下列问题:
(1)求A组人数,并补全条形统计图;
(2)估计该校八年级参加测试的400名男生中成绩不低于10个的人数;
(3)从平均数、中位数和众数这三个统计量中任选一个,解释其在本题中的意义.
6.(2024 苏州)某校计划在七年级开展阳光体育锻炼活动,开设以下五个球类项目:A(羽毛球),B(乒乓球),C(篮球),D(排球),E(足球),要求每位学生必须参加,且只能选择其中一个项目.为了了解学生对这五个项目的选择情况,学校从七年身全体学生中随机抽取部分学生进行问卷调查,对调查所得到的数据进行整理、描述和分析,部分信息如下:
根据上信息,解决下列问题:
(1)将图①中的条形统计图补充完整(画图并标注相应数据);
(2)图②中项目E对应的圆心角的度数为 °;
(3)根据抽样调查结果,请估计本校七年级800名学生中选择项目B(乒乓球)的人数.
7.(2024 贵州)根据《国家体质健康标准》规定,七年级男生、女生50米短跑时间分别不超过7.7秒、8.3秒为优秀等次.某校在七年级学生中挑选男生、女生各5人进行集训,经多次测试得到10名学生的平均成绩(单位:秒)记录如下:男生成绩:7.61,7.38,7.65,7.38,7.38
女生成绩:8.23,8.27,8.16,8.26,8.32
根据以上信息,解答下列问题:
(1)男生成绩的众数为 ,女生成绩的中位数为 ;
(2)判断下列两位同学的说法是否正确.
(3)教练从成绩最好的3名男生(设为甲,乙,丙)中,随机抽取2名学生代表学校参加比赛,请用画树状图或列表的方法求甲被抽中的概率.
8.(2024 新疆)为丰富学生的校园生活,提升学生的综合素质,某校计划开设丰富多彩的社团活动.为了解全校学生对各类社团活动的喜爱情况,该校随机抽取部分学生进行问卷调查(每名学生必选且只选一类),并根据调查结果制成如下统计图(不完整):
结合调查信息,回答下列问题:
(1)本次共调查了 名学生,喜爱“艺术类”社团活动的学生人数是 ;
(2)若该校有1000名学生,请估计其中大约有多少名学生喜爱“阅读类”社团活动?
(3)某班有2名男生和1名女生参加“体育类”社团中“追风篮球社”的选拔,2名学生被选中.请用列表法或画树状图法求选中的2名学生恰好为1名男生和1名女生的概率.
9.(2024 乐山)乐山作为闻名世界的文化旅游胜地,吸引了大量游客.为更好地提升服务质量,某旅行社随机调查了部分游客对四种美食的喜好情况(每人限选一种),并将调查结果绘制成统计图,如图所示.根据以上信息,回答下列问题:
(1)本次抽取的游客总人数为 人,扇形统计图中m的值为 ;
(2)请补全条形统计图;
(3)旅行社推出每人可免费品尝两种美食的活动,某游客从上述4种美食中随机选择两种,请用画树状图或列表的方法求选到“钵钵鸡和跷脚牛肉”的概率.
10.(2024 河北)某公司为提高员工的专业能力,定期对员工进行技能测试.考虑多种因素影响,需将测试的原始成绩x(分)换算为报告成绩y(分).已知原始成绩满分150分,报告成绩满分100分、换算规则如下:
当0≤x<p时,y=;
当p≤x≤150时,y=+80.
(其中p是小于150的常数,是原始成绩的合格分数线,80是报告成绩的合格分数线)公司规定报告成绩为80分及80分以上(即原始成绩为p及p以上)为合格.
(1)甲、乙的原始成绩分别为95分和130分,若p=100,求甲、乙的报告成绩;
(2)丙、丁的报告成绩分别为92分和64分,若丙的原始成绩比丁的原始成绩高40分,请推算p的值;
(3)下表是该公司100名员工某次测试的原始成绩统计表:
原始成绩(分) 95 100 105 110 115 120 125 130 135 140 145 150
人数 1 2 2 5 8 10 7 16 20 15 9 5
①直接写出这100名员工原始成绩的中位数;
②若①中的中位数换算成报告成绩为90分,直接写出该公司此次测试的合格率.
11.(2024 威海)为增强学生体质,某校在八年级男生中试行“每日锻炼,每月测试”的引体向上训练活动,设定6个及以上为合格.体育组为了解一学期的训练效果,随机抽查了20名男生2至6月份的测试成绩.其中,2月份测试成绩如表1,6月份测试成绩如图1(尚不完整).整理本学期测试数据得到表2和图2(尚不完整).
表1:2月份测试成绩统计表
个数 0 1 3 6 8 10
人数 4 8 4 1 2 1
表2:本学期测试成绩统计表
平均数/个 众数/个 中位数/个 合格率
2月 2.6 a 1 20%
3月 3.1 3 4 25%
4月 4 4 5 35%
5月 4.55 5 5 40%
6月 b 8 6 c
请根据图表中的信息,解答下列问题:
(1)将图1和图2中的统计图补充完整,并直接写出a,b,c的值;
(2)从多角度分析本次引体向上训练活动的效果;
(3)若将此活动在邻校八年级推广,该校八年级男生按400人计算,以随机抽查的20名男生训练成绩为样本,估算经过一学期的引体向上训练,可达到合格水平的男生人数.
12.(2024 安徽)综合与实践
【项目背景】
无核柑橘是我省西南山区特产,该地区某村有甲、乙两块成龄无核柑橘园.在柑橘收获季节,班级同学前往该村开展综合实践活动,其中一个项目是:在日照、土质、空气湿度等外部环境基本一致的条件下,对两块柑橘园的优质柑橘情况进行调查统计,为柑橘园的发展规划提供一些参考.
【数据收集与整理】
从两块柑橘园采摘的柑橘中各随机选取200个.在技术人员指导下,测量每个柑橘的直径,作为样本数据.柑橘直径用x(单位:cm)表示.
将所收集的样本数据进行如下分组:
组别 A B C D E
x 3.5≤x<4.5 4.5≤x<5.5 5.5≤x<6.5 6.5≤x<7.5 7.5≤x≤8.5
整理样本数据,并绘制甲、乙两园样本数据的频数分布直方图,部分信息如下:
任务1 求图1中a的值.
【数据分析与运用】
任务2 A,B,C,D,E五组数据的平均数分别取为4,5,6,7,8,计算乙园样本数据的平均数.
任务3 下列结论一定正确的是 (填正确结论的序号).
①两园样本数据的中位数均在C组;
②两园样本数据的众数均在C组;
③两园样本数据的最大数与最小数的差相等.
任务4 结合市场情况,将C,D两组的柑橘认定为一级,B组的柑橘认定为二级,其它组的柑橘认定为三级,其中一级柑橘的品质最优,二级次之,三级最次.试估计哪个园的柑橘品质更优,并说明理由.
根据所给信息,请完成以上所有任务.
13.(2024 苏州)一个不透明的盒子里装有4张书签,分别描绘“春”,“夏”,“秋”,“冬”四个季节,书签除图案外都相同,并将4张书签充分搅匀.
(1)若从盒子中任意抽取1张书签,恰好抽到“夏”的概率为 ;
(2)若从盒子中任意抽取2张书签(先抽取1张书签,且这张书签不放回,再抽取1张书签),求抽取的书签恰好1张为“春”,1张为“秋”的概率.(请用画树状图或列表等方法说明理由)
14.(2024 滨州)某校劳动实践基地共开设五门劳动实践课程,分别是A:床铺整理,B:衣物清洗,C:手工制作,D:简单烹饪,E:绿植栽培.课程开设一段时间后,李老师采用抽样调查的方式在全校学生中开展了“我最喜欢的劳动实践课程”为主题的问卷调查.根据调查所收集的数据进行整理,绘制了如下两幅不完整的统计图.
根据图中信息,请回答下列问题:
(1)请将条形统计图补充完整,并直接写出“手工制作”对应的扇形圆心角度数;
(2)若该校共有1800名学生,请你估计全校最喜欢“绿植栽培”的学生人数;
(3)小兰同学从B,C,D三门课程中随机选择一门参加劳动实践,小亮同学从C,D,E三门课程中随机选择一门参加劳动实践,求两位同学选择相同课程的概率.
15.(2024 内江)某校为了解学生对“生命、生态与安全”课程的学习掌握情况,从八年级学生中随机抽取了部分学生进行综合测试.测试结果分为A级、B级、C级、D级四个等级,并将测试结果绘制成了如下两幅不完整的统计图.根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
(2)扇形统计图中表示D级的扇形圆心角的度数是 ,并把条形统计图补充完整;
(3)该校八年级共有学生600人,如果全部参加这次测试,测试成绩为A级的学生大约有多少人?
16.(2024 山东)某学校开展了“校园科技节”活动,活动包含模型设计、科技小论文两个项目.为了解学生的模型设计水平,从全校学生的模型设计成绩中随机抽取部分学生的模型设计成绩(成绩为百分制,用x表示),并将其分成如下四组:60≤x<70,70≤x<80,80≤x<90,90≤x≤100.
下面给出了部分信息:
80≤x<90的成绩为:81,81,82,82,83,83,84,84,84,85,86,86,86,87,88,88,88,89,89,89.
根据以上信息解决下列问题:
(1)请补全频数分布直方图;
(2)所抽取学生的模型设计成绩的中位数是 分;
(3)请估计全校1000名学生的模型设计成绩不低于80分的人数;
(4)根据活动要求,学校将模型设计成绩、科技小论文成绩按3:2的比例确定这次活动各人的综合成绩.
某班甲、乙两位学生的模型设计成绩与科技小论文成绩(单位:分)如下:
模型设计 科技小论文
甲的成绩 94 90
乙的成绩 90 95
通过计算,甲、乙哪位学生的综合成绩更高?
17.(2024 广安)睡眠管理作为“五项管理”中的重要内容之一,也是学校教育重点关注的内容.某校为了解学生平均每天睡眠时间,随机抽取该校部分学生进行问卷调查,并将结果进行了统计和整理,绘制成如下统计表和不完整的统计图.
学生类别 学生平均每大睡眠时间x(单位:小时)
A 7≤x<7.5
B 7.5≤x<8
C 8≤x<8.5
D 8.5≤x<9
E x≥9
(1)本次抽取调查的学生共有 人,扇形统计图中表示C类学生平均每天睡眠时间的扇形的圆心角度数为 ;
(2)请补全条形统计图;
(3)被抽取调查的E类4名学生中有2名女生,2名男生.从这4人中随机抽取2人进行电话回访,请用画树状图或列表的方法,求恰好抽到2名男生的概率.
18.(2024 成都)2024年成都世界园艺博览会以“公园城市美好人居”为主题,秉持“绿色低碳、节约持续、共享包容”的理念,以园艺为媒介,向世界人民传递绿色发展理念和诗意栖居的美好生活场景.在主会场有多条游园线路,某单位准备组织全体员工前往参观,每位员工从其中四条线路(国风古韵观赏线、世界公园打卡线、亲子互动慢游线、园艺小清新线)中选择一条.现随机选取部分员工进行了“线路选择意愿”的摸底调查,并根据调查结果绘制成如下统计图表.
游园线路 人数
国风古韵观赏线 44
世界公园打卡线 x
亲子互动慢游线 48
园艺小清新线 y
根据图表信息,解答下列问题:
(1)本次调查的员工共有 人,表中x的值为 ;
(2)在扇形统计图中,求“国风古韵观赏线”对应的圆心角度数;
(3)若该单位共有2200人,请你根据调查结果,估计选择“园艺小清新线”的员工人数.
19.(2024 德阳)2024年中国龙舟公开赛(四川 德阳站),在德阳旌湖沱江桥水域举行,预计来自全国各地1000余名选手将参赛.旌湖两岸高颜值的绿色生态景观绿化带“德阳之窗”将迎接德阳市民以及来自全国各地的朋友近距离的观看比赛.比赛设置男子组、女子组、本地组三个组别,其中男子组将进行A:100米直道竞速赛,B:200米直道竞速赛,C:500米直道竞速赛,D:3000米绕标赛.为了了解德阳市民对于这四个比赛项目的关注程度,随机对部分市民进行了问卷调查(参与问卷调查的每位市民只能选择其中一个项目),将调查得到的数据绘制成数据统计表和扇形统计图(表、图都未完全制作完成):
市民最关注的比赛项目人数统计表
比赛项目 A B C D
关注人数 42 30 a b
(1)直接写出a、b的值和D所在扇形圆心角的度数;
(2)若当天观看比赛的市民有10000人,试估计当天观看比赛的市民中关注哪个比赛项目的人数最多?大约有多少人?
(3)为了缓解比赛当天城市交通压力,维护交通秩序,德阳交警旌阳支队派出4名交警(2男2女)对该路段进行值守,若在4名交警中任意抽取2名交警安排在同一路口执勤,请用列举法(画树状图或列表)求出恰好抽到的两名交警性别相同的概率.
20.(2024 泸州)某地两块试验田中分别栽种了甲、乙两种小麦,为了考查这两种小麦的长势,分别从中随机抽取16株麦苗,测得苗高(单位:cm)如表.
甲 7 8 10 11 11 12 13 13 14 14 14 14 15 16 16 18
乙 7 10 13 11 18 12 13 13 10 13 13 14 15 16 11 17
将数据整理分析,并绘制成以下不完整的统计表格和频数分布直方图.
苗高分组 甲种小麦的频数
7≤x<10 a
10≤x<13 b
13≤x<16 7
16≤x<19 3
小麦种类 统计量 甲 乙
平均数 12.875 12.875
众数 14 d
中位数 c 13
方差 8.65 7.85
根据所给出的信息,解决下列问题:
(1)a= ,b= ,并补全乙种小麦的频数分布直方图;
(2)c= ,d= ;
(3)甲、乙两种小麦的苗高长势比较整齐的是 (填甲或乙);若从栽种乙种小麦的试验田中随机抽取1200株,试估计苗高在10≤x<13(单位:cm)的株数.
21.(2024 重庆)为了解学生的安全知识掌握情况,某校举办了安全知识竞赛.现从七、八年级的学生中各随机抽取20名学生的竞赛成绩(百分制)进行收集、整理、描述、分析.所有学生的成绩均高于60分(成绩得分用x表示,共分成四组:A.60<x≤70;B.70<x≤80;C.80<x≤90;D.90<x≤100),下面给出了部分信息:七年级20名学生的竞赛成绩为:
66,67,68,68,75,83,84,86,86,86,
86,87,87,89,95,95,96,98,98,100.
八年级20名学生的竞赛成绩在C组的数据是:81,82,84,87,88,89.七、八年级所抽学生的竞赛成绩统计表
年级 七年级 八年级
平均数 85 85
中位数 86 b
众数 a 79
根据以上信息,解答下列问题:
(1)上述图表中a= ,b= ,m= ;
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好?请说明理由(写出一条理由即可);
(3)该校七年级有400名学生、八年级有500名学生参加了此次安全知识竞赛,估计该校七、八年级参加此次安全知识竞赛成绩优秀(x>90)的学生人数是多少?
22.(2024 遂宁)遂宁市作为全国旅游城市,有众多著名景点,为了解“五一”假期同学们的出游情况,某实践探究小组对部分同学假期旅游地做了调查,以下是调查报告的部分呢,请完善报告:
××小组关于××学校学生“五一”出游情况调查报告
数据收集
调查方式 抽样调查 调查对象 ××学校学生
数据的整理与描述
景点 A:中国死海 B:龙风古镇 C:灵泉风景区 D:金华山 E:未出游 F:其他
数据分析及运用
(1)本次被抽样调查的学生总人数为 ,扇形统计图中,m= ,“B:龙风古镇”对应圆心角的度数是 ; (2)请补全条形统计图; (3)该学校总人数为1800人,请你估计该学校学生“五一”假期未出游的人数; (4)未出游中的甲、乙两位同学计划下次假期从A、B、C、D四个景点中任选一个景点旅游,请用树状图或列表的方法求出他们选择同一景点的概率.
23.(2024 自贡)某校为了解学生身体健康状况,从全校600名学生的体质健康测试结果登记表中,随机选取了部分学生的测试数据进行初步整理(如表),并绘制出不完整的条形统计图(如图).
学生体质健康统计表
成绩 频数 百分比
不及格 3 a
及格 b 20%
良好 45 c
优秀 32 32%
(1)如表中a= ,b= ,c= ;
(2)请补全如图的条形统计图,并估计该校学生体质健康测试结果为“良好”和“优秀”的总人数;
(3)为听取测试建议,学校选出了3名“良好”1名“优秀”学生,再从这4名学生中随机抽取2人参加学校体质健康测试交流会,请用列表或画树状图的方法,计算所抽取的两人均为“良好”的概率.
24.(2024 宜宾)某校为了落实“五育并举”,提升学生的综合素养.在课外活动中开设了四个兴趣小组:A.插花组;B.跳绳组;C.话剧组;D.书法组.为了解学生对每个兴趣小组的参与情况,随机抽取了部分学生进行调查,并将调查结果绘制成不完整的统计图.
请结合图中信息解答下列问题:
(1)本次共调查了 名学生,并将条形统计图补充完整;
(2)话剧组所对应扇形的圆心角为 度;
(3)书法组成绩最好的4名学生由3名男生和1名女生构成.从中随机抽取2名参加比赛,请用列表或画树状图的方法,求刚好抽到1名男生与1名女生的概率.
25.(2024 临夏州)环球网消息称:近年来的电动自行车火灾事故80%都是充电时发生的,超过一半的电动自行车火灾发生在夜间充电的过程中.为了规避风险,某校政教处对学生进行规范充电培训活动,并对培训效果按10分制进行检测评分.为了解这次培训的效果,现从各年级随机抽取男、女生各10名的检测成绩作为样本进行整理,并绘制成如下不完整的统计图表:
抽取的10名女生检测成绩统计表
成绩/分 6 7 8 9 10
人数 1 2 m 3 n
注:10名女生检测成绩的中位数为8.5分.
请根据以上信息,完成下列问题:
(1)样本中男生检测成绩为10分的学生数是 ,众数为 分;
(2)女生检测成绩表中的m= ,n= ;
(3)已知该校有男生545人,女生360人,若认定检测成绩不低于9分为“优秀”,估计全校检测成绩达到“优秀”的人数.
26.(2024 广州)善于提问是应用人工智能解决问题的重要因素之一.为了解同学们的提问水平,对A,B两组同学进行问卷调查,并根据结果对每名同学的提问水平进行评分,得分情况如下(单位:分):
A组 75 78 82 82 84 86 87 88 93 95
B组 75 77 80 83 85 86 88 88 92 96
(1)求A组同学得分的中位数和众数;
(2)现从A,B两组得分超过90分的4名同学中随机抽取2名同学参与访谈,求这2名同学恰好来自同一组的概率.
27.(2024 吉林)吉林省以“绿水青山就是金山银山,冰天雪地也是金山银山”为指引,不断加大冰雪旅游的宣传力度,推出各种优惠活动,“小土豆”“小砂糖橘”等成为一道舰丽的风景线.某滑雪场为吸引游客,每天抽取一定数量的幸运游客,每名幸运游客可以从“滑雪”“滑雪圈”“雪地摩托”三个项目中随机抽取一个免费游玩.若三个项目被抽中的可能性相等,用画树状图或列表的方法,求幸运游客小明与小亮恰好抽中同一个项目的概率.
28.(2024 广东)端午假期,王先生计划与家人一同前往景区游玩.为了选择一个最合适的景区,王先生对A、B、C三个景区进行了调查与评估.他依据特色美食、自然风光、乡村民宿及科普基地四个方面,为每个景区评分(10分制).三个景区的得分如表所示:
景区 特色美食 自然风光 乡村民宿 科普基地
A 6 8 7 9
B 7 7 8 7
C 8 8 6 6
(1)若四项所占百分比如图所示,通过计算回答:王先生会选择哪个景区去游玩?
(2)如果王先生认为四项同等重要,通过计算回答:王先生将会选择哪个景区去游玩?
(3)如果你是王先生,请按你认为的各项“重要程度”设计四项得分的百分比,选择最合适的景区,并说明理由.
29.(2024 武汉)为加强体育锻炼,增强学生体质,某校在“阳光体育一小时”活动中组织九年级学生定点投篮技能测试,每人投篮4次,投中一次计1分.随机抽取m名学生的成绩作为样本,将收集的数据整理并绘制成如下的统计图表.
测试成绩频数分布表
成绩/分 频数
4 12
3 a
2 15
1 b
0 6
根据以上信息,解答下列问题:
(1)直接写出m,n的值和样本的众数;
(2)若该校九年级有900名学生参加测试,估计得分超过2分的学生人数.
30.(2024 河北)甲、乙、丙三张卡片正面分别写有a+b,2a+b,a﹣b,除正面的代数式不同外,其余均相同.
(1)将三张卡片背面向上并洗匀,从中随机抽取一张,当a=1,b=﹣2时,求取出的卡片上代数式的值为负数的概率;
(2)将三张卡片背面向上并洗匀,从中随机抽取一张,放回后重新洗匀,再随机抽取一张.请在表格中补全两次取出的卡片上代数式之和的所有可能结果(化为最简),并求出和为单项式的概率.
第一次 和 第二次 a+b 2a+b a﹣b
a+b 2a+2b 2a
2a+b
a﹣b 2a
统计与概率
参考答案与试题解析
一.解答题(共30小题)
1.(2024 黑龙江)为贯彻落实教育部办公厅关于“保障学生每天校内、校外各一小时体育活动时间”的要求,某学校要求学生每天坚持体育锻炼.学校从全体男生中随机抽取了部分学生,调查他们的立定跳远成绩,整理如下不完整的频数分布表和统计图,结合图解答下列问题:
(1)频数分布表中m= 50 ,扇形统计图中n= 40 ;
(2)本次调查立定跳远成绩的中位数落在 C 组别;
(3)该校有600名男生,若立定跳远成绩大于200cm为合格,请估计该校立定跳远成绩合格的男生有多少人?
组别 分组(cm) 频数
A 50<x≤100 3
B 100<x≤150 m
C 150<x≤200 20
D 200<x≤250 14
E 250<x≤300 5
【分析】(1)根据A组的频数和百分比求出抽取总数,用总数减其他的频数可得求出m的值,求出C组所占百分比,即可求解;
(2)根据中位数的定义即可求解;
(3)用样本估计总体即可.
【解答】解:(1)由题意可得,3÷6%=50,
m=50﹣3﹣20﹣14﹣5=8,
扇形统计图中C组所在的百分比==40%,
∴n=40,
故答案为:50,40;
(2)被抽取的50名学生立定跳远成绩按从小到大的顺序排列第25个和第26 个的平均数,3+8<25,3+8+20=31>25
被抽取的50名学生这一天的体育活动时间数据的中位数在C组;
(3)600×=228(名),
答:估计该校立定跳远成绩合格的男生有228人.
【点评】本题考查频数分布表、扇形统计图、用样本估计总体,解答本题的关键是求出样本容量,利用数形结合的思想解答.
2.(2024 包头)《国家学生体质健康标准(2014年修订)》将九年级男生的立定跳远测试成绩分为四个等级:优秀(x≥240),良好(225≤x<240),及格(185≤x<225),不及格(x<185),其中x表示测试成绩(单位:cm).某校为了解本校九年级全体男生立定跳远测试的达标情况,精准找出差距,进行科学合理的工作规划,整理了本校及所在区县九年级全体男生近期一次测试成绩的相关数据,信息如下:
a.本校测试成绩频数(人数)分布表:
等级 优秀 良好 及格 不及格
频数(人数) 40 70 60 30
b.本校测试成绩统计表:
平均数 中位数 优秀率 及格率
222.5 228 p 85%
c.本校所在区县测试成绩统计表:
平均数 中位数 优秀率 及格率
218.7 223 23% 91%
请根据所给信息,解答下列问题:
(1)求出p的值;
(2)本校甲、乙两名同学本次测试成绩在本校排名(从高到低)分别是第100名、第101名,甲同学的测试成绩是230cm,请你计算出乙同学的测试成绩是多少?
(3)请你结合该校所在区县测试成绩,从平均数、中位数、优秀率和及格率四个方面中任选两个,对该校九年级全体男生立定跳远测试的达标情况做出评价,并为该校提出一条合理化建议.
【分析】(1)利用优秀的人数除以总人数即可求出p的值;
(2)根据中位数的定义即可求出答案;
(3)从平均数和优秀率分析即可,答案不唯一,合理即可
【解答】解:(1)p=×100%=20%;
(2)设乙同学的成绩为x cm,
∵中位数为228,
∴=228,
解得x=226,
答:乙同学的测试成绩是226cm;
(3)从平均数来看,该校九年级全体男生立定跳远测试高于全县平均数,从优秀率来看,该校九年级全体男生立定跳远测试低于全县的优秀率,所以要加强训练强度,努力提高优秀率.
【点评】本题考查了频数(率)分布表,中位数,平均数,弄清题意是解本题的关键.
3.(2024 齐齐哈尔)为提高学生的环保意识,某校举行了“爱护环境,人人有责”环保知识竞赛,对收集到的数据进行了整理、描述和分析.
【收集数据】随机抽取部分学生的竞赛成绩组成一个样本.
【整理数据】将学生竞赛成绩的样本数据分成A,B,C,D四组进行整理.(满分100分,所有竞赛成绩均不低于60分)如表:
组别 A B C D
成绩(x/分) 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
人数(人) m 94 n 16
【描述数据】根据竞赛成绩绘制了如下两幅不完整的统计图.
【分析数据】根据以上信息,解答下列问题:
(1)填空:m= 50 ,n= 40 ;
(2)请补全条形统计图;
(3)扇形统计图中,C组对应的圆心角的度数是 72 °;
(4)若竞赛成绩80分以上(含80分)为优秀,请你估计该校参加竞赛的2000名学生中成绩为优秀的人数.
【分析】(1)先有B人数及其所占百分比求出被调查总人数,再用总人数乘以A的百分比求出m的值,再根据各组人数之和等于总人数求出n的值;
(2)根据m和n的值即可补全条形统计图;
(3)用360°乘以C组人数所占比例可求得其对应圆心角度数;
(4)用总人数乘以样本中80分以上(含80分)的人数所占比例即可得.
【解答】解:(1)本次随机抽取的学生人数为94÷47%=200(人),
∴m=200×25%=50,
∴n=200﹣50﹣94﹣16=40;
故答案为:50,40;
(2)补全条形统计图如图所示:
(3)扇形统计图中,C组对应的圆心角的度数是360°×=72°;
故答案为:72;
(4)2000×=560(名),
答:估计该校参加竞赛的2000名学生中成绩为优秀的人数有560名.
【点评】本题考查条形统计图,频数(率)分布表,用样本估计总体及扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.
4.(2024 绥化)为了落实国家“双减”政策,某中学在课后服务时间里,开展了音乐、体操、诵读、书法四项社团活动、为了了解七年级学生对社团活动的喜爱情况,该校从七年级全体学生中随机抽取了部分学生进行“你最喜欢哪一项社团活动”的问卷调查,每人必须选择一项社团活动(且只能选择一项).根据调查结果,绘制成如下两幅统计图请根据统计图中的信息,解答下列问题:
(1)参加本次问卷调查的学生共有 60 人;
(2)在扇形统计图中,A组所占的百分比是 30% ,并补全条形统计图.
(3)端午节前夕,学校计划进行课后服务成果展示,准备从这4个社团中随机抽取2个社团汇报展示,请用树状图法或列表法,求选中的2个社团恰好是B和C的概率.
【分析】(1)用条形统计图中D的人数除以扇形统计图中D的百分比可得参加本次问卷调查的学生人数.
(2)求出A组的学生人数,用A组的学生人数除以参加本次问卷调查的学生人数再乘以100%可得A组所占的百分比,最后补全条形统计图即可.
(3)列表可得出所有等可能的结果数以及选中的2个社团恰好是B和C的结果数,再利用概率公式可得出答案.
【解答】解:(1)参加本次问卷调查的学生共有12÷20%=60(人).
故答案为:60.
(2)A组的人数为60﹣20﹣10﹣12=18(人),
∴在扇形统计图中,A组所占的百分比是18÷60×100%=30%.
故答案为:30%.
补全条形统计图如图所示.
(3)列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
共有12种等可能的结果,其中选中的2个社团恰好是B和C的结果有:(B,C),(C,B),共2种,
∴选中的2个社团恰好是B和C的概率为=.
【点评】本题考查列表法与树状图法、条形统计图、扇形统计图,能够读懂统计图,掌握列表法与树状图法是解答本题的关键.
5.(2024 湖北)某校为增强学生身体素质,以“阳光运动,健康成长”为主题开展体育训练,并对学生进行专项体能测试.以下是某次八年级男生引体向上测试成绩的抽样与数据分析过程.
【收集数据】随机抽取若干名男生的测试成绩.
【整理数据】将抽取的成绩进行整理,用x(引体向上个数)表示成绩,分成四组:
A组(0≤x<5),B组(5≤x<10),C组(10≤x<14),D组(x≥14).
【描述数据】根据抽取的男生成绩,绘制出如下不完整的统计图.
【分析数据】抽取的八年级男生测试成绩的平均数为8,中位数为8,众数为11.
根据以上信息,解答下列问题:
(1)求A组人数,并补全条形统计图;
(2)估计该校八年级参加测试的400名男生中成绩不低于10个的人数;
(3)从平均数、中位数和众数这三个统计量中任选一个,解释其在本题中的意义.
【分析】(1)用C组的频数除以C组的频率,可得样本容量,再用样本容量分别减去其它三组的频数,即可得出A组的频数,进而补全条形统计图;
(2)用400乘样本中成绩不低于10个的人数所占比例即可;
(3)根据平均数、中位数和众数解答即可.
【解答】解:(1)样本容量为:14÷35%=40,
故A组人数为:40﹣10﹣14﹣4=12(人),
补全条形统计图如下:
(2)400×=180(人),
答:估计该校八年级参加测试的400名男生中成绩不低于10个的人数大约有180人;
(3)平均数表示抽取的40名学生的平均成绩;
众数表示抽取的40名学生中得分在某个分数的人数最多;
中位数表示取的40名学生中,将成绩从小到大排列后,位于中间位置的成绩(答案不唯一,任选其中一个说明即可).
【点评】本题考查频数分布直方图,中位数、众数、方差和加权平均数,理解中位数、众数、方差的意义以及和加权平均数的计算方法是解决问题的关键.
6.(2024 苏州)某校计划在七年级开展阳光体育锻炼活动,开设以下五个球类项目:A(羽毛球),B(乒乓球),C(篮球),D(排球),E(足球),要求每位学生必须参加,且只能选择其中一个项目.为了了解学生对这五个项目的选择情况,学校从七年身全体学生中随机抽取部分学生进行问卷调查,对调查所得到的数据进行整理、描述和分析,部分信息如下:
根据上信息,解决下列问题:
(1)将图①中的条形统计图补充完整(画图并标注相应数据);
(2)图②中项目E对应的圆心角的度数为 72 °;
(3)根据抽样调查结果,请估计本校七年级800名学生中选择项目B(乒乓球)的人数.
【分析】(1)用C的人数除以所占的百分比求出总人数,再求出D的人数即可补全条形统计图;
(2)用360°乘以E的人数所占比例即可;
(3)用总人数乘以样本中B的人数所占比例即可得.
【解答】解:(1)此次调查的总人数为9÷15%=60(人),
D项目的人数有60﹣6﹣18﹣9﹣12=15(人),
补全条形统计图如下:
(2)图②中项目E对应的圆心角的度数为360°×=72°;
故答案为:72;
(3)800×=240(名),
答:估计本校七年级800名学生中选择项目B(乒乓球)的人数为240名.
【点评】本题考查了条形统计图,扇形统计图和用样本估计总体,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
7.(2024 贵州)根据《国家体质健康标准》规定,七年级男生、女生50米短跑时间分别不超过7.7秒、8.3秒为优秀等次.某校在七年级学生中挑选男生、女生各5人进行集训,经多次测试得到10名学生的平均成绩(单位:秒)记录如下:男生成绩:7.61,7.38,7.65,7.38,7.38
女生成绩:8.23,8.27,8.16,8.26,8.32
根据以上信息,解答下列问题:
(1)男生成绩的众数为 7.38 ,女生成绩的中位数为 8.26 ;
(2)判断下列两位同学的说法是否正确.
(3)教练从成绩最好的3名男生(设为甲,乙,丙)中,随机抽取2名学生代表学校参加比赛,请用画树状图或列表的方法求甲被抽中的概率.
【分析】(1)根据众数、中位数的定义可得答案.
(2)由题意可知,5名男生中成绩最好的是7.38秒,5名女生的成绩不都是优秀等次,即可得出答案.
(3)列表可得出所有等可能的结果数以及甲被抽中的结果数,再利用概率公式可得出答案.
【解答】解:(1)由题意得,男生成绩的众数为7.38.
将5名女生的成绩按照从小到大的顺序排列,排在第3名的成绩为8.26,
∴女生成绩的中位数为8.26.
故答案为:7.38;8.26.
(2)5名男生中成绩最好的是7.38秒,
故小星同学的说法正确.
5名女生的成绩中超过8.3秒的有8.32秒,
∴5名女生的成绩不都是优秀等次,
故小红同学的说法不正确.
(3)列表如下:
甲 乙 丙
甲 (甲,乙) (甲,丙)
乙 (乙,甲) (乙,丙)
丙 (丙,甲) (丙,乙)
共有6种等可能的结果,其中甲被抽中的结果有:(甲,乙),(甲,丙),(乙,甲),(丙,甲),共4种,
∴甲被抽中的概率为=.
【点评】本题考查概率公式,列表法与树状图法、众数、中位数,熟练掌握列表法与树状图法、众数、中位数的定义是解答本题的关键.
8.(2024 新疆)为丰富学生的校园生活,提升学生的综合素质,某校计划开设丰富多彩的社团活动.为了解全校学生对各类社团活动的喜爱情况,该校随机抽取部分学生进行问卷调查(每名学生必选且只选一类),并根据调查结果制成如下统计图(不完整):
结合调查信息,回答下列问题:
(1)本次共调查了 100 名学生,喜爱“艺术类”社团活动的学生人数是 25人 ;
(2)若该校有1000名学生,请估计其中大约有多少名学生喜爱“阅读类”社团活动?
(3)某班有2名男生和1名女生参加“体育类”社团中“追风篮球社”的选拔,2名学生被选中.请用列表法或画树状图法求选中的2名学生恰好为1名男生和1名女生的概率.
【分析】(1)用条形统计图中“体育类”的人数除以扇形统计图中“体育类”的百分比可得本次共调查的学生人数;用本次共调查的学生人数乘以扇形统计图中“艺术类”的百分比可得喜爱“艺术类”社团活动的学生人数.
(2)根据用样本估计总体,用1000乘以样本中“阅读类”的学生人数所占的百分比,即可得出答案.
(3)列表可得出所有等可能的结果数以及选中的2名学生恰好为1名男生和1名女生的结果数,再利用概率公式可得出答案.
【解答】解:(1)本次共调查了30÷30%=100(名)学生.
喜爱“艺术类”社团活动的学生人数是100×25%=25(人).
故答案为:100;25人.
(2)1000×=150(名).
∴估计其中大约有150名学生喜爱“阅读类”社团活动.
(3)列表如下:
男 男 女
男 (男,男) (男,女)
男 (男,男) (男,女)
女 (女,男) (女,男)
共有6种等可能的结果,其中选中的2名学生恰好为1名男生和1名女生的结果有4种,
∴选中的2名学生恰好为1名男生和1名女生的概率为=.
【点评】本题考查列表法与树状图法、条形统计图、扇形统计图、用样本估计总体,能够读懂统计图,掌握列表法与树状图法以及用样本估计总体是解答本题的关键.
9.(2024 乐山)乐山作为闻名世界的文化旅游胜地,吸引了大量游客.为更好地提升服务质量,某旅行社随机调查了部分游客对四种美食的喜好情况(每人限选一种),并将调查结果绘制成统计图,如图所示.根据以上信息,回答下列问题:
(1)本次抽取的游客总人数为 240 人,扇形统计图中m的值为 35 ;
(2)请补全条形统计图;
(3)旅行社推出每人可免费品尝两种美食的活动,某游客从上述4种美食中随机选择两种,请用画树状图或列表的方法求选到“钵钵鸡和跷脚牛肉”的概率.
【分析】(1)由喜好跷脚牛肉的人数除以所占百分比得出本次抽取的游客总人数,即可解决问题;
(2)求出喜好甜皮鸡的人数,补全条形统计图即可;
(3)画树状图,共有12种可能出现的结果,其中选到“钵钵鸡和跷脚牛肉”的结果有2种,再由概率公式求解即可.
【解答】解:(1)本次抽取的游客总人数为72÷30%=240(人),
∴m%=84÷240×100%=35%,
故答案为:240,35;
(2)喜好甜皮鸡的人数为:240﹣48﹣72﹣84=36(人),
补全条形统计图如下:
(3)把四种美食分别记为A:麻辣烫,B:跷脚牛肉,C:钵钵鸡,D:甜皮鸭,
画树状图如下:
共有12种可能出现的结果,其中选到“钵钵鸡和跷脚牛肉”的结果有2种,
∴选到“钵钵鸡和跷脚牛肉”的概率为=.
【点评】此题考查的是用列表法或树状图法求概率以及条形统计图和扇形统计图等知识.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
10.(2024 河北)某公司为提高员工的专业能力,定期对员工进行技能测试.考虑多种因素影响,需将测试的原始成绩x(分)换算为报告成绩y(分).已知原始成绩满分150分,报告成绩满分100分、换算规则如下:
当0≤x<p时,y=;
当p≤x≤150时,y=+80.
(其中p是小于150的常数,是原始成绩的合格分数线,80是报告成绩的合格分数线)公司规定报告成绩为80分及80分以上(即原始成绩为p及p以上)为合格.
(1)甲、乙的原始成绩分别为95分和130分,若p=100,求甲、乙的报告成绩;
(2)丙、丁的报告成绩分别为92分和64分,若丙的原始成绩比丁的原始成绩高40分,请推算p的值;
(3)下表是该公司100名员工某次测试的原始成绩统计表:
原始成绩(分) 95 100 105 110 115 120 125 130 135 140 145 150
人数 1 2 2 5 8 10 7 16 20 15 9 5
①直接写出这100名员工原始成绩的中位数;
②若①中的中位数换算成报告成绩为90分,直接写出该公司此次测试的合格率.
【分析】(1)利用换算规则的公式解答即可;
(2)设丙的原始成绩为x1分,则丁的原始成绩为(x1﹣40)分,利用分类讨论的方法依据换算规则的公式解答即可;
(3)①利用中位数的定义解答即可;
②当p>130时,利用换算规则的公式解答即可;当p≤130时,则,由表格得到原始成绩为110及110以上的人数为100﹣5=95,利用合格率的公式解答即可.
【解答】解:(1)当p=100时,甲的报告成绩为: (分),
乙的探告成绩为: (分);
(2)设丙的原始成绩为x1分,则丁的原始成绩为(x1﹣40)分,
①0≤x<p时,y丙=92=…①,
,
由①﹣②得:,
∴,
∴,故不成立,舍;
②p≤x1﹣40≤150 时,y丙=92=+80…③, ……④,
由③﹣④得:,
∴p=.
∴92=+80,
∴,
∴,故不成立,舍;
③0≤x1﹣40<p,p≤x1≤150 时,
y丙=92=+80…⑤,
……⑥,
联立⑤⑥解得:p=125,x1=140,且符合题意,
综上所述p=125;
(3)①共计100名员工,且成绩已经排列好,
∴中位数是第50,51名员工成绩的平均数,
由表格得第50,51名员工成绩都是130分,
∴中位数为130;
②当p>130时,则,
解得 ,
故不成立,舍;
当p≤130时,
则,
解得p=110,符合题意,
∴.由表格得到原始成绩为110及110以上的人数为100﹣(1+2+2)=95,
∴合格率为:.
【点评】本题考查了函数关系式,自变量与函数值,中位数的定义,合格率,解分式方程,熟练知识点正确理解题意是解决本题的关键.
11.(2024 威海)为增强学生体质,某校在八年级男生中试行“每日锻炼,每月测试”的引体向上训练活动,设定6个及以上为合格.体育组为了解一学期的训练效果,随机抽查了20名男生2至6月份的测试成绩.其中,2月份测试成绩如表1,6月份测试成绩如图1(尚不完整).整理本学期测试数据得到表2和图2(尚不完整).
表1:2月份测试成绩统计表
个数 0 1 3 6 8 10
人数 4 8 4 1 2 1
表2:本学期测试成绩统计表
平均数/个 众数/个 中位数/个 合格率
2月 2.6 a 1 20%
3月 3.1 3 4 25%
4月 4 4 5 35%
5月 4.55 5 5 40%
6月 b 8 6 c
请根据图表中的信息,解答下列问题:
(1)将图1和图2中的统计图补充完整,并直接写出a,b,c的值;
(2)从多角度分析本次引体向上训练活动的效果;
(3)若将此活动在邻校八年级推广,该校八年级男生按400人计算,以随机抽查的20名男生训练成绩为样本,估算经过一学期的引体向上训练,可达到合格水平的男生人数.
【分析】(1)根据总人数减去引体向上为其他个数的人数,进而补充条形统计图,根据题意求得合格率c,补充折线统计图,根据平均数,众数的定义,即可得出a和b的值;
(2)根据平均数,众数,中位数,合格率,分析;
(3)根据样本估计总体即可求解.
【解答】解:(1)6月测试成绩中,引体向上3个的人数为20﹣4﹣1﹣6﹣4=5(人),
补充统计图如下:
c=×100%=55%,
根据表2可得a=1,
b=(4×1+5×3+1×6+6×8+4×10)=5.65,
(2)本次引体向上训练活动的效果明显,理由如下:
从平均数和合格率看,平均数和合格率逐月增加,
从中位数看,引体向上个数逐月增加,
从众数看,引体向上的个数越来越大(答案不唯一,合理即可);
(3)400×55%=220(人),
答:估算经过一学期的引体向上训练,可达到合格水平的男生人数约220人.
【点评】本题考查了条形统计图,折线统计图,统计表,样本估计总体,以及求平均数,众数,中位数的意义;掌握相关的统计量的意义是解题的关键.
12.(2024 安徽)综合与实践
【项目背景】
无核柑橘是我省西南山区特产,该地区某村有甲、乙两块成龄无核柑橘园.在柑橘收获季节,班级同学前往该村开展综合实践活动,其中一个项目是:在日照、土质、空气湿度等外部环境基本一致的条件下,对两块柑橘园的优质柑橘情况进行调查统计,为柑橘园的发展规划提供一些参考.
【数据收集与整理】
从两块柑橘园采摘的柑橘中各随机选取200个.在技术人员指导下,测量每个柑橘的直径,作为样本数据.柑橘直径用x(单位:cm)表示.
将所收集的样本数据进行如下分组:
组别 A B C D E
x 3.5≤x<4.5 4.5≤x<5.5 5.5≤x<6.5 6.5≤x<7.5 7.5≤x≤8.5
整理样本数据,并绘制甲、乙两园样本数据的频数分布直方图,部分信息如下:
任务1 求图1中a的值.
【数据分析与运用】
任务2 A,B,C,D,E五组数据的平均数分别取为4,5,6,7,8,计算乙园样本数据的平均数.
任务3 下列结论一定正确的是 ① (填正确结论的序号).
①两园样本数据的中位数均在C组;
②两园样本数据的众数均在C组;
③两园样本数据的最大数与最小数的差相等.
任务4 结合市场情况,将C,D两组的柑橘认定为一级,B组的柑橘认定为二级,其它组的柑橘认定为三级,其中一级柑橘的品质最优,二级次之,三级最次.试估计哪个园的柑橘品质更优,并说明理由.
根据所给信息,请完成以上所有任务.
【分析】(1)用200分别减去其它各组的频数可得a 的值;
(2)根据加权平均数公式计算即可;
(3)分别根据中位数、众数和极差的定义解答即可;
(4)根据统计图数据判断即可.
【解答】解:(1)由题意得,a=200﹣(15+70+50+25)=40;
(2)(15×4+50×5+70×6+50×7+15×8)=6,
故乙园样本数据的平均数为6;
(3)由统计图可知,两园样本数据的中位数均在C组,故①正确;
甲园的众数在B组,乙园的众数在C组,故②结论错误;
两园样本数据的最大数与最小数的差不一定相等,故③结论错误;
故答案为:①;
(4)乙园的柑橘品质更优,理由如下:
由样本数据频数分布直方图可得,乙园一级柑橘所占比例大于甲园,因此可以认为乙园的柑橘品质更优.
【点评】本题考查频数分布直方图,样本估计总体,频数分布表,加权平均数、中位数、众数以及极差,解题的关键是读懂图象信息,属于中考常考题型.
13.(2024 苏州)一个不透明的盒子里装有4张书签,分别描绘“春”,“夏”,“秋”,“冬”四个季节,书签除图案外都相同,并将4张书签充分搅匀.
(1)若从盒子中任意抽取1张书签,恰好抽到“夏”的概率为 ;
(2)若从盒子中任意抽取2张书签(先抽取1张书签,且这张书签不放回,再抽取1张书签),求抽取的书签恰好1张为“春”,1张为“秋”的概率.(请用画树状图或列表等方法说明理由)
【分析】(1)直接由概率公式求解即可;
(2)画树状图,共有12种等可能的结果,其中抽取的书签恰好1张为“春”,1张为“秋”的结果有2种,再由概率公式求解即可.
【解答】解:(1)∵一个不透明的盒子里装有4张书签,分别描绘“春”,“夏”,“秋”,“冬”四个季节,
∴从盒子中任意抽取1张书签,恰好抽到“夏”的概率为,
故答案为:;
(2)画树状图如下:
共有12种等可能的结果,其中抽取的书签恰好1张为“春”,1张为“秋”的结果有2种,
∴抽取的书签恰好1张为“春”,1张为“秋”的概率为=.
【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.
14.(2024 滨州)某校劳动实践基地共开设五门劳动实践课程,分别是A:床铺整理,B:衣物清洗,C:手工制作,D:简单烹饪,E:绿植栽培.课程开设一段时间后,李老师采用抽样调查的方式在全校学生中开展了“我最喜欢的劳动实践课程”为主题的问卷调查.根据调查所收集的数据进行整理,绘制了如下两幅不完整的统计图.
根据图中信息,请回答下列问题:
(1)请将条形统计图补充完整,并直接写出“手工制作”对应的扇形圆心角度数;
(2)若该校共有1800名学生,请你估计全校最喜欢“绿植栽培”的学生人数;
(3)小兰同学从B,C,D三门课程中随机选择一门参加劳动实践,小亮同学从C,D,E三门课程中随机选择一门参加劳动实践,求两位同学选择相同课程的概率.
【分析】(1)由E的学生人数除以所占百分比得出调查的学生人数,即可解决问题;
(2)由全校学生人数乘以最喜欢“绿植栽培”的学生人数所占的百分比即可;
(3)画树状图,共有9种等可能的结果,其中两位同学选择相同课程的结果有2种,再由概率公式求解即可.
【解答】解:(1)调查的学生人数为:30÷30%=100(人),
∴D的学生人数为:100×25%=25(人),
∴A的人数为:100﹣10﹣20﹣25﹣30=15(人),
将条形统计图补充完整如下:
“手工制作”对应的扇形圆心角度数为360°×=72°;
(2)1800×30%=540(人),
答:估计全校最喜欢“绿植栽培”的学生人数为540人;
(3)画树状图如下:
共有9种等可能的结果,其中两位同学选择相同课程的结果有2种,即CC、DD,
∴两位同学选择相同课程的概率为.
【点评】本题考查的是用列表法或画树状图法求概率以及条形统计图和扇形统计图等知识.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
15.(2024 内江)某校为了解学生对“生命、生态与安全”课程的学习掌握情况,从八年级学生中随机抽取了部分学生进行综合测试.测试结果分为A级、B级、C级、D级四个等级,并将测试结果绘制成了如下两幅不完整的统计图.根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 40 ;
(2)扇形统计图中表示D级的扇形圆心角的度数是 72° ,并把条形统计图补充完整;
(3)该校八年级共有学生600人,如果全部参加这次测试,测试成绩为A级的学生大约有多少人?
【分析】(1)根据B级的人数和所占的百分比,可以求得本次抽样测试的学生人数;
(2)用360°乘以D级人数所占的百分比即可求出D级的扇形圆心角的度数,用总人数乘以C级的人数所占的百分比求出C级的人数,即可把条形统计图补充完整;
(3)求出A级的学生人数所占的百分比乘以该校八年级学生总数600即可.
【解答】解:(1)本次抽样测试的学生人数是:12÷30%=40(人),
故答案为:40;
(2)扇形统计图中表示D级的扇形圆心角的度数是:360°×=72°,
C级的人数为:40×35%=14(人),
补充完整的条形统计图如图所示;
故答案为:72°;
(3)600×=90(人),
答:测试成绩为A级的学生大约有90人.
【点评】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
16.(2024 山东)某学校开展了“校园科技节”活动,活动包含模型设计、科技小论文两个项目.为了解学生的模型设计水平,从全校学生的模型设计成绩中随机抽取部分学生的模型设计成绩(成绩为百分制,用x表示),并将其分成如下四组:60≤x<70,70≤x<80,80≤x<90,90≤x≤100.
下面给出了部分信息:
80≤x<90的成绩为:81,81,82,82,83,83,84,84,84,85,86,86,86,87,88,88,88,89,89,89.
根据以上信息解决下列问题:
(1)请补全频数分布直方图;
(2)所抽取学生的模型设计成绩的中位数是 83 分;
(3)请估计全校1000名学生的模型设计成绩不低于80分的人数;
(4)根据活动要求,学校将模型设计成绩、科技小论文成绩按3:2的比例确定这次活动各人的综合成绩.
某班甲、乙两位学生的模型设计成绩与科技小论文成绩(单位:分)如下:
模型设计 科技小论文
甲的成绩 94 90
乙的成绩 90 95
通过计算,甲、乙哪位学生的综合成绩更高?
【分析】(1)先求解总人数,再求解70≤x<80的人数,再补全图形即可;
(2)根据中位数的含义确定第25个,第26个数据的平均数即可得到中位数;
(3)由总人数乘以80分(含80以上)的人数百分比即可得到答案;
(4)根据加权平均数公式分别计算甲,乙二人成绩,再比较即可
【解答】解:(1)∵5÷10%=50,而80≤x<90有20人,
∴70≤x<80有50﹣20﹣5﹣10=15,
补全图形如下:
(2)∵5+15=20,
而80≤x<90的成绩为:81,81,82,82,83,83,84,84,84,85,86,86,86,87,88,88,88,89,89,89.
∴50个成绩按照从小到大排列后,排在第25个,第26个数据分别是:83,83;
中位数为:,
故答案为:83;
(3)全校1000名学生的模型设计成绩不低于80分的人数为:
(人);
(4)甲的成绩为:(分);
乙的成绩为:(分);
∴甲的综合成绩比乙高.
【点评】本题考查的是频数分布直方图,中位数的含义,利用样本估计总体,加权平均数的含义,掌握基础的统计知识是解本题的感觉.
17.(2024 广安)睡眠管理作为“五项管理”中的重要内容之一,也是学校教育重点关注的内容.某校为了解学生平均每天睡眠时间,随机抽取该校部分学生进行问卷调查,并将结果进行了统计和整理,绘制成如下统计表和不完整的统计图.
学生类别 学生平均每大睡眠时间x(单位:小时)
A 7≤x<7.5
B 7.5≤x<8
C 8≤x<8.5
D 8.5≤x<9
E x≥9
(1)本次抽取调查的学生共有 50 人,扇形统计图中表示C类学生平均每天睡眠时间的扇形的圆心角度数为 144° ;
(2)请补全条形统计图;
(3)被抽取调查的E类4名学生中有2名女生,2名男生.从这4人中随机抽取2人进行电话回访,请用画树状图或列表的方法,求恰好抽到2名男生的概率.
【分析】(1)由B的人数除以所占百分比得出本次抽取调查的学生人数,即可解决问题;
(2)求出D的人数,补全条形统计图即可;
(3)画树状图,共有12种等可能的结果,其中恰好抽到2名男生的结果有2种,再由概率公式求解即可.
【解答】解:(1)本次抽取调查的学生共有14÷28%=50(人),
扇形统计图中表示C类学生平均每天睡眠时间的扇形的圆心角度数为360°×=144°,
故答案为:50,144°;
(2)D的人数为:50﹣6﹣14﹣20﹣4=6(人),
补全条形统计图如下:
(3)画树状图如下:
共有12种等可能的结果,其中恰好抽到2名男生的结果有2种,
∴恰好抽到2名男生的概率==.
【点评】本题考查的是用列表法或画树状图法求概率以及条形统计图和扇形统计图等知识.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
18.(2024 成都)2024年成都世界园艺博览会以“公园城市美好人居”为主题,秉持“绿色低碳、节约持续、共享包容”的理念,以园艺为媒介,向世界人民传递绿色发展理念和诗意栖居的美好生活场景.在主会场有多条游园线路,某单位准备组织全体员工前往参观,每位员工从其中四条线路(国风古韵观赏线、世界公园打卡线、亲子互动慢游线、园艺小清新线)中选择一条.现随机选取部分员工进行了“线路选择意愿”的摸底调查,并根据调查结果绘制成如下统计图表.
游园线路 人数
国风古韵观赏线 44
世界公园打卡线 x
亲子互动慢游线 48
园艺小清新线 y
根据图表信息,解答下列问题:
(1)本次调查的员工共有 160 人,表中x的值为 40 ;
(2)在扇形统计图中,求“国风古韵观赏线”对应的圆心角度数;
(3)若该单位共有2200人,请你根据调查结果,估计选择“园艺小清新线”的员工人数.
【分析】(1)根据选择亲子互动慢游线的人数和所占的百分比即可求出调查的总人数,用总人数乘以选择世界公园打卡线的百分比即可求出x的值;
(2)用360°乘以选择“国风古韵观赏线”所占的百分比即可求出对应的圆心角度数;
(3)用2200乘以选择“园艺小清新线”的员工人数所占百分比即可.
【解答】解:(1)本次调查的员工共有48÷30%=160(人),
表中x的值为160×=40;
故答案为:160,40;
(2)360°×=99°,
答:在扇形统计图中,“国风古韵观赏线”对应的圆心角度数为99°;
(3)2200×=385(人),
答:估计选择“园艺小清新线”的员工人数为385人.
【点评】本题考查扇形统计图,条形统计图和用样本估计总体,能从统计图中获取有用信息是解题的关键.
19.(2024 德阳)2024年中国龙舟公开赛(四川 德阳站),在德阳旌湖沱江桥水域举行,预计来自全国各地1000余名选手将参赛.旌湖两岸高颜值的绿色生态景观绿化带“德阳之窗”将迎接德阳市民以及来自全国各地的朋友近距离的观看比赛.比赛设置男子组、女子组、本地组三个组别,其中男子组将进行A:100米直道竞速赛,B:200米直道竞速赛,C:500米直道竞速赛,D:3000米绕标赛.为了了解德阳市民对于这四个比赛项目的关注程度,随机对部分市民进行了问卷调查(参与问卷调查的每位市民只能选择其中一个项目),将调查得到的数据绘制成数据统计表和扇形统计图(表、图都未完全制作完成):
市民最关注的比赛项目人数统计表
比赛项目 A B C D
关注人数 42 30 a b
(1)直接写出a、b的值和D所在扇形圆心角的度数;
(2)若当天观看比赛的市民有10000人,试估计当天观看比赛的市民中关注哪个比赛项目的人数最多?大约有多少人?
(3)为了缓解比赛当天城市交通压力,维护交通秩序,德阳交警旌阳支队派出4名交警(2男2女)对该路段进行值守,若在4名交警中任意抽取2名交警安排在同一路口执勤,请用列举法(画树状图或列表)求出恰好抽到的两名交警性别相同的概率.
【分析】(1)首先求出部分市民的人数为42÷28%=150,根据C:500米直道竞速赛人数所占的百分比求得a,根据题意即可得到结论;
(2)根据扇形统计图即可得到结论;
(3)设2名男性交警用A,B表示,2名女性交警用C,D表示,根据题意即可画树状图,进而求出恰好抽到的两名交警性别相同的概率.
【解答】解:(1)部分市民的人数为42÷28%=150(人),
∴a=150×12%=18,b=150﹣42﹣18﹣30=60(人),
D所在扇形圆心角的度数为360×=144°;
(2)当天观看比赛的市民中关注D:3000米绕标赛比赛项目的人数最多,
10000×=4000(人),
答:当天观看比赛的市民中关注D:3000米绕标赛比赛项目的人数最多大约有4000人;
(3)设2名男性交警用A,B表示,2名女性交警用C,D表示,
根据题意,画树状图如下:
由图可知:共有12种等可能的结果,符合条件的结果有4种,
所以恰好抽到的两名交警性别相同的概率为:=.
【点评】本题考查了列表法与树状图法、频率分布表、扇形统计图,解决本题的关键是掌握概率公式.
20.(2024 泸州)某地两块试验田中分别栽种了甲、乙两种小麦,为了考查这两种小麦的长势,分别从中随机抽取16株麦苗,测得苗高(单位:cm)如表.
甲 7 8 10 11 11 12 13 13 14 14 14 14 15 16 16 18
乙 7 10 13 11 18 12 13 13 10 13 13 14 15 16 11 17
将数据整理分析,并绘制成以下不完整的统计表格和频数分布直方图.
苗高分组 甲种小麦的频数
7≤x<10 a
10≤x<13 b
13≤x<16 7
16≤x<19 3
小麦种类 统计量 甲 乙
平均数 12.875 12.875
众数 14 d
中位数 c 13
方差 8.65 7.85
根据所给出的信息,解决下列问题:
(1)a= 2 ,b= 4 ,并补全乙种小麦的频数分布直方图;
(2)c= 13.5 ,d= 13 ;
(3)甲、乙两种小麦的苗高长势比较整齐的是 乙 (填甲或乙);若从栽种乙种小麦的试验田中随机抽取1200株,试估计苗高在10≤x<13(单位:cm)的株数.
【分析】(1)由表格可直接得出a,b的值;求出乙种小麦苗高在13≤x<16的频数,补全乙种小麦的频数分布直方图即可.
(2)根据中位数、众数的定义可得答案.
(3)根据方差的意义可知,甲、乙两种小麦的苗高长势比较整齐的是乙;根据用样本估计总体,用1200乘以样本中乙种小麦苗高在10≤x<13(单位:cm)的株数所占的百分比,即可得出答案.
【解答】解:(1)由表格可知,a=2,b=4.
故答案为:2;4.
由题意知,乙种小麦苗高在13≤x<16的频数为7,
补全乙种小麦的频数分布直方图如图所示.
(2)将甲种16株小麦的苗高按照从小到大的顺序排列,排在第8和第9的苗高为13,14,
∴c=(13+14)÷2=13.5.
由表格可知,d=13.
故答案为:13.5;13.
(3)∵甲种小麦的方差大于乙种小麦的方差,
∴甲、乙两种小麦的苗高长势比较整齐的是乙.
故答案为:乙.
1200×=375(株).
∴估计苗高在10≤x<13(单位:cm)的株数约375株.
【点评】本题考频数(率)分布直方图、频数(率)分布表、用样本估计总体、中位数、众数、方差,能够读懂统计图表,掌握用样本估计总体、中位数、众数、方差的定义是解答本题的关键.
21.(2024 重庆)为了解学生的安全知识掌握情况,某校举办了安全知识竞赛.现从七、八年级的学生中各随机抽取20名学生的竞赛成绩(百分制)进行收集、整理、描述、分析.所有学生的成绩均高于60分(成绩得分用x表示,共分成四组:A.60<x≤70;B.70<x≤80;C.80<x≤90;D.90<x≤100),下面给出了部分信息:七年级20名学生的竞赛成绩为:
66,67,68,68,75,83,84,86,86,86,
86,87,87,89,95,95,96,98,98,100.
八年级20名学生的竞赛成绩在C组的数据是:81,82,84,87,88,89.七、八年级所抽学生的竞赛成绩统计表
年级 七年级 八年级
平均数 85 85
中位数 86 b
众数 a 79
根据以上信息,解答下列问题:
(1)上述图表中a= 86 ,b= 87.5 ,m= 40 ;
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好?请说明理由(写出一条理由即可);
(3)该校七年级有400名学生、八年级有500名学生参加了此次安全知识竞赛,估计该校七、八年级参加此次安全知识竞赛成绩优秀(x>90)的学生人数是多少?
【分析】(1)分别根据众数和中位数的定义可得a、b的值;用“1”分别减去其它部分占比可得m的值;
(2)根据平均数和中位数的意义解答即可;
(3)利用样本估计总体思想求解可得.
【解答】解:(1)在七年级20名学生的竞赛成绩中86出现的次数最多,故众数a=86;
把八年级20名学生的竞赛成绩从小到大排列,排在中间的两个数分别是87,88,故中位数b==87.5,
m%=1﹣10%﹣20%﹣=40%,即m=40.
故答案为:86,87.5,40;
(2)八年级学生安全知识竞赛成绩较好,理由如下:
因为两个年级成绩的平均数相同,但八年级的中位数高于七年级,所以得到八年级学生安全知识竞赛成绩较好(答案不唯一);
(3)400×+500×40%
=120+200
=320(人),
答:估计该校七、八年级参加此次安全知识竞赛成绩优秀(x>90)的学生人数大约是320人.
【点评】本题考查了扇形统计图、频数分布表、中位数、众数以及用样本估计总体,掌握相关统计量的意义以及计算方法是解答本题的关键.
22.(2024 遂宁)遂宁市作为全国旅游城市,有众多著名景点,为了解“五一”假期同学们的出游情况,某实践探究小组对部分同学假期旅游地做了调查,以下是调查报告的部分呢,请完善报告:
××小组关于××学校学生“五一”出游情况调查报告
数据收集
调查方式 抽样调查 调查对象 ××学校学生
数据的整理与描述
景点 A:中国死海 B:龙风古镇 C:灵泉风景区 D:金华山 E:未出游 F:其他
数据分析及运用
(1)本次被抽样调查的学生总人数为 100 ,扇形统计图中,m= 10 ,“B:龙风古镇”对应圆心角的度数是 72° ; (2)请补全条形统计图; (3)该学校总人数为1800人,请你估计该学校学生“五一”假期未出游的人数; (4)未出游中的甲、乙两位同学计划下次假期从A、B、C、D四个景点中任选一个景点旅游,请用树状图或列表的方法求出他们选择同一景点的概率.
【分析】(1)将出游景点F的人数除以其所占百分比,即可得到本次被抽样调查的学生总人数;求出出游景点C的人数,再除以总人数,乘以100,即可求出m的值;将出游景点B的人数除以总人数,再乘以360°,即可得到“B:龙风古镇”对应圆心角的度数;
(2)求出出游景点C的人数,再补全条形统计图即可;
(3)将未出游的人数出游总人数,再乘以1800,即可估计该学校学生“五一”假期未出游的人数;
(4)用树状图或列表的方法即可求出他们选择同一景点的概率.
【解答】解:(1)∵30÷30%=100(人),
∴本次被抽样调查的学生总人数为100人;
∵出游C景点的人数为:100﹣(12+20+20+8+30)=10(人),
∴m=×100=10;
∵×360°=72°,
∴“B:龙风古镇”对应圆心角的度数是72°,
故答案为:100,10,72°;
(2)由(1)知:出游景点C的人数为10人,
补全条形统计图如下:
(3)×1800=144(人),
答:估计该学校学生“五一”假期未出游的有144人;
(4)画树状图如下:
一共有16种等可能的结果,其中两人选择同一景点有4种可能的结果,
∴P(选择同一景点)==.
【点评】本题考查条形统计图,扇形统计图,用样本估计总体,用列表法和树状图法求等可能事件的概率,能从统计图种获取数据,掌握用列表法和树状图法求等可能事件的概率的方法是解题的关键.
23.(2024 自贡)某校为了解学生身体健康状况,从全校600名学生的体质健康测试结果登记表中,随机选取了部分学生的测试数据进行初步整理(如表),并绘制出不完整的条形统计图(如图).
学生体质健康统计表
成绩 频数 百分比
不及格 3 a
及格 b 20%
良好 45 c
优秀 32 32%
(1)如表中a= 3% ,b= 20 ,c= 45% ;
(2)请补全如图的条形统计图,并估计该校学生体质健康测试结果为“良好”和“优秀”的总人数;
(3)为听取测试建议,学校选出了3名“良好”1名“优秀”学生,再从这4名学生中随机抽取2人参加学校体质健康测试交流会,请用列表或画树状图的方法,计算所抽取的两人均为“良好”的概率.
【分析】(1)先根据选取的优秀人数和百分比求出选取的人数,再根据总数、频数、百分比的关系即可求得答案;
(2)根据及格的人数,补全条形统计图即可;
(3)画树状图列出所有等可能的结果,再找出恰好选中两人均为“良好”的结果,利用概率公式可得出答案.
【解答】解:(1)这次调查的人数为:32÷32%=100(人),
a=×100%=3%,b=100×20%=20,c=×100%=45%,
故答案为:3%,20,45%;
(2)补全条形统计图如下:
600×(45%+32%)=462(人),
估计该校学生体质健康测试结果为“良好”和“优秀”的总人数为462人;
(3)设3名“良好”分别为甲、乙、丙,1名“优秀”学生为丁,
画树状图如图:
∵共有12种等可能的结果,其中恰好选中两人均为“良好”的结果有6种,
∴所抽取的两人均为“良好”的概率为=.
【点评】本题考查条形统计图、扇形统计图、用样本估计总体、列表法与树状图法,熟练掌握条形统计图与扇形统计图以及列表法与树状图法求概率是解答本题的关键.
24.(2024 宜宾)某校为了落实“五育并举”,提升学生的综合素养.在课外活动中开设了四个兴趣小组:A.插花组;B.跳绳组;C.话剧组;D.书法组.为了解学生对每个兴趣小组的参与情况,随机抽取了部分学生进行调查,并将调查结果绘制成不完整的统计图.
请结合图中信息解答下列问题:
(1)本次共调查了 40 名学生,并将条形统计图补充完整;
(2)话剧组所对应扇形的圆心角为 72 度;
(3)书法组成绩最好的4名学生由3名男生和1名女生构成.从中随机抽取2名参加比赛,请用列表或画树状图的方法,求刚好抽到1名男生与1名女生的概率.
【分析】(1)用条形统计图中A的人数除以扇形统计图中A的百分比可得本次调查的学生人数;求出C组的人数,补全条形统计图即可.
(2)用360°乘以本次调查中C组的人数所占的百分比,即可得出答案.
(3)画树状图得出所有等可能的结果数以及刚好抽到1名男生与1名女生的结果数,再利用概率公式可得出答案.
【解答】(1)此次调查的学生人数为:4÷10%=40(人),“C”类兴趣课的人数为:40﹣4﹣16﹣12=8(人),
补全条形统计图如下:
故答案为:40;
(2)“C”类兴趣课所对应扇形的圆心角的度数为:360°×=72°;
故答案为:72;
(3)将1名女生记为A,3名男生分别记为B,C,D,
画树状图如下:
共有12种等可能的结果,其中刚好抽到1名男生与1名女生的结果有:AB,AC,AD,BA,CA,DA,共6种,
∴刚好抽到1名男生与1名女生的概率为.
【点评】此题考查的是用树状图法求概率以及扇形统计图和条形统计图等知识.树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步或两步以上完成的事件;解题时要注意此题是放回试验还是不放回试验.
25.(2024 临夏州)环球网消息称:近年来的电动自行车火灾事故80%都是充电时发生的,超过一半的电动自行车火灾发生在夜间充电的过程中.为了规避风险,某校政教处对学生进行规范充电培训活动,并对培训效果按10分制进行检测评分.为了解这次培训的效果,现从各年级随机抽取男、女生各10名的检测成绩作为样本进行整理,并绘制成如下不完整的统计图表:
抽取的10名女生检测成绩统计表
成绩/分 6 7 8 9 10
人数 1 2 m 3 n
注:10名女生检测成绩的中位数为8.5分.
请根据以上信息,完成下列问题:
(1)样本中男生检测成绩为10分的学生数是 2 ,众数为 8 分;
(2)女生检测成绩表中的m= 2 ,n= 2 ;
(3)已知该校有男生545人,女生360人,若认定检测成绩不低于9分为“优秀”,估计全校检测成绩达到“优秀”的人数.
【分析】(1)用总人数乘以10分的学生数所占的百分比即可,然后根据众数定义即可求得众数;
(2)根据中位数的定义将八年级的活动成绩从小到大排列,那么其中位数应是第5个和第6个数据的平均数,结合已知条件易得第5个和第6个数据分别为8,9,再根据表格中数据即可求得答案;
(3)分别用男生和女生的总人数乘以样本中成绩不低于9分的人数所占的百分比即可,
【解答】解:(1)样本中男生检测成绩为10分的学生数是10×(1﹣10%﹣50%﹣20%)=2(人),
∵出现次数最多的为8分,
∴七年级活动成绩的众数为8分;
故答案为:2,8;
(2)将女生检测成绩绩从小到大排列后,它的中位数应是第5个和第6个数据的平均数,
∵女生检测成绩的中位数为8.5分,
∴第5个和第6个数据的和为8.5×2=17=8+9,
∴第5个和第6个数据分别为8分,9分,
∵成绩为6分和7分的人数为1+2=3(人),
∴成绩为8分的人数为5﹣3=2(人),
成绩为10分的人数为5﹣3=2(人),
即m=2,n=2;
故答案为:2,2;
(3)545×(20%+20%)+360×=218+180=398(人),
答:估计全校检测成绩达到“优秀”的人数为398人.
【点评】本题主要考查扇形统计图相关知识,众数,中位数及用样本估计总体,熟练掌握各知识点是解答本题的关键.
26.(2024 广州)善于提问是应用人工智能解决问题的重要因素之一.为了解同学们的提问水平,对A,B两组同学进行问卷调查,并根据结果对每名同学的提问水平进行评分,得分情况如下(单位:分):
A组 75 78 82 82 84 86 87 88 93 95
B组 75 77 80 83 85 86 88 88 92 96
(1)求A组同学得分的中位数和众数;
(2)现从A,B两组得分超过90分的4名同学中随机抽取2名同学参与访谈,求这2名同学恰好来自同一组的概率.
【分析】(1)根据中位数和众数的定义可得答案.
(2)列表可得出所有等可能的结果数以及这2名同学恰好来自同一组的结果数,再利用概率公式可得出答案.
【解答】解:(1)将10名A组同学的得分按照从小到大的顺序排列,排在第5和第6名的成绩为84,86,
∴A组同学得分的中位数为(84+86)÷2=85(分).
由表格可知,A组同学得分的众数为82分.
(2)将A组的两名同学分别记为甲、乙,将B组的两名同学分别记为丙,丁,
画树状图如下:
共有12种等可能的结果,其中这2名同学恰好来自同一组的结果有:甲乙,乙甲,丙丁,丁丙,共4种,
∴这2名同学恰好来自同一组的概率为.
【点评】本题考查列表法与树状图法、中位数、众数,熟练掌握列表法与树状图法、中位数、众数的定义是解答本题的关键.
27.(2024 吉林)吉林省以“绿水青山就是金山银山,冰天雪地也是金山银山”为指引,不断加大冰雪旅游的宣传力度,推出各种优惠活动,“小土豆”“小砂糖橘”等成为一道舰丽的风景线.某滑雪场为吸引游客,每天抽取一定数量的幸运游客,每名幸运游客可以从“滑雪”“滑雪圈”“雪地摩托”三个项目中随机抽取一个免费游玩.若三个项目被抽中的可能性相等,用画树状图或列表的方法,求幸运游客小明与小亮恰好抽中同一个项目的概率.
【分析】画树状图,共有9种等可能的结果,其中幸运游客小明与小亮恰好抽中同一个项目的结果有3种,再由概率公式求解即可.
【解答】解:把“滑雪”“滑雪圈”“雪地摩托”三个项目分别记为A、B、C,
画树状图如下:
共有9种等可能的结果,其中幸运游客小明与小亮恰好抽中同一个项目的结果有3种,
∴幸运游客小明与小亮恰好抽中同一个项目的概率为=.
【点评】此题考查的是用列表法或树状图法求概率以及概率公式.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.
28.(2024 广东)端午假期,王先生计划与家人一同前往景区游玩.为了选择一个最合适的景区,王先生对A、B、C三个景区进行了调查与评估.他依据特色美食、自然风光、乡村民宿及科普基地四个方面,为每个景区评分(10分制).三个景区的得分如表所示:
景区 特色美食 自然风光 乡村民宿 科普基地
A 6 8 7 9
B 7 7 8 7
C 8 8 6 6
(1)若四项所占百分比如图所示,通过计算回答:王先生会选择哪个景区去游玩?
(2)如果王先生认为四项同等重要,通过计算回答:王先生将会选择哪个景区去游玩?
(3)如果你是王先生,请按你认为的各项“重要程度”设计四项得分的百分比,选择最合适的景区,并说明理由.
【分析】(1)分别计算加权平均数即可判断出答案;
(2)分别计算算术平均数即可判断出答案;
(2)将特色美食、自然风光、乡村民宿和科普基地四项得分的百分比定为20%,30%,30%,20%,通过计算再判断即可(答案不唯一).
【解答】解:(1)景区A得分为:=7.15,
景区B得分为:=7.4,
景区C得分为:=6.9,
∵7.4>7.15>6.9,
∴王先生会选择B景区去游玩;
(2)景区A得分为:=7.5,
景区B得分为:=7.25,
景区C得分为:=7,
∵7.5>7.25>7,
∴王先生会选择A景区去游玩;
(3)将特色美食、自然风光、乡村民宿和科普基地四项得分的百分比定为20%,30%,30%,20%,
景区A得分为:=7.5,
景区B得分为:=7.3,
景区C得分为:=7,
∵7.5>7.3>7,
∴选择A景区去游玩.
【点评】本题考查了扇形统计图和平均数,加权平均数是将各数值乘以相应的权数,然后加总求和得到总体值,再除以总的单位数,平均数的大小不仅取决于总体中各单位的标志值(变量值)的大小,而且取决于各标志值出现的次数(频数),由于各标志值出现的次数对其在平均数中的影响起着权衡轻重的作用,因此叫做权数.
29.(2024 武汉)为加强体育锻炼,增强学生体质,某校在“阳光体育一小时”活动中组织九年级学生定点投篮技能测试,每人投篮4次,投中一次计1分.随机抽取m名学生的成绩作为样本,将收集的数据整理并绘制成如下的统计图表.
测试成绩频数分布表
成绩/分 频数
4 12
3 a
2 15
1 b
0 6
根据以上信息,解答下列问题:
(1)直接写出m,n的值和样本的众数;
(2)若该校九年级有900名学生参加测试,估计得分超过2分的学生人数.
【分析】(1)用频数分布表中2分的频数除以扇形统计图中2分的百分比可得m的值,用总人数乘以3分百分比求出a的值,即可求出b的值,用b的值除以总人数即可求出n的值,根据众数的定义即可求出众数;
(2)根据用样本估计总体,用900乘以样本中超过2分的学生人数所占的百分比,即可得出答案.
【解答】解:(1)由题意得,m=15÷25%=60,
∴a=60×30%=18,
∴b=60﹣12﹣18﹣15﹣6=9,
∴n%=×100%=15%,
∴n=15,
样本的众数为3;
(2)900×=450(名),
答:估计得分超过2分的学生人数有450名.
【点评】本题考查扇形统计图、频数(率)分布表、众数、用样本估计总体,能够读懂统计图表,掌握用样本估计总体、众数的定义是解答本题的关键.
30.(2024 河北)甲、乙、丙三张卡片正面分别写有a+b,2a+b,a﹣b,除正面的代数式不同外,其余均相同.
(1)将三张卡片背面向上并洗匀,从中随机抽取一张,当a=1,b=﹣2时,求取出的卡片上代数式的值为负数的概率;
(2)将三张卡片背面向上并洗匀,从中随机抽取一张,放回后重新洗匀,再随机抽取一张.请在表格中补全两次取出的卡片上代数式之和的所有可能结果(化为最简),并求出和为单项式的概率.
第一次 和 第二次 a+b 2a+b a﹣b
a+b 2a+2b 2a
2a+b
a﹣b 2a
【分析】(1)当a=1,b=﹣2时,a+b=﹣1,2a+b=0,a﹣b=3.从三张卡片中随机抽取一张,共有3种等可能的结果,其中取出的卡片上代数式的值为负数的结果有1种,利用概率公式可得答案.
(2)根据题意把表格补充完整,由表格可得出所有等可能的结果数以及和为单项式的结果数,再利用概率公式可得出答案.
【解答】解:(1)当a=1,b=﹣2时,a+b=﹣1,2a+b=0,a﹣b=3.
从三张卡片中随机抽取一张,共有3种等可能的结果,其中取出的卡片上代数式的值为负数的结果有1种,
∴取出的卡片上代数式的值为负数的概率为.
(2)补全表格如下:
第一次 和 第二次 a+b 2a+b a﹣b
a+b 2a+2b 3a+2b 2a
2a+b 3a+2b 4a+2b 3a
a﹣b 2a 3a 2a﹣2b
共有9种等可能的结果,其中和为单项式的结果有:2a,3a,2a,3a,共4种,
∴和为单项式的概率为.
【点评】本题考查列表法与树状图法、概率公式、整式的加减、多项式与单项式,熟练掌握列表法与树状图法、概率公式、整式的加减、多项式与单项式的概念是解答本题的关键.
同课章节目录
