2024年中考数学解答题分类汇编——图形的变化(含解析)
文档属性
| 名称 | 2024年中考数学解答题分类汇编——图形的变化(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 10:29:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024年中考数学解答题分类汇编——图形的变化
一.解答题(共30小题)
1.(2024 凉山州)为建设全城旅游西昌,加快旅游产业发展.2022年9月29日位于西昌主城区东部的历史风貌核心区唐园正式开园,坐落于唐园内的怀远塔乃唐园至高点,为七层密檐式八角砖混结构阁楼式塔楼,建筑面积为1845.4平方米,塔顶金碧辉煌,为“火珠垂莲”窣(sū)堵坡造型.某校为了让学生进一步了解怀远塔,组织九年级(2)班学生利用综合实践课测量怀远塔的高度.小江同学站在如图所示的怀远塔前的平地上A点处,测得塔顶C的仰角为30°,眼睛B距离地面1.8m,向塔前行67m,到达点D处,测得塔顶C的仰角为60°,求塔高CF. (参考数据:≈1.414,≈1.732,结果精确到0.01m)
2.(2024 烟台)根据收集的素材,探索完成任务.
探究太阳能热水器的安装
素材一 太阳能热水器是利用绿色能源造福人类的一项发明.某品牌热水器主要部件太阳能板需要安装在每天都可以有太阳光照射到的地方,才能保证使用效果,否则不予安装.
素材二 某市位于北半球,太阳光线与水平线的夹角为α,冬至日时,14°≤α≤29°;夏至日时,43°≤α≤76°. sin14°≈0.24,cos14°≈0.97,tan14°≈0.25 sin29°≈0.48,cos29°≈0.87,tan29°≈0.55 sin43°≈0.68,cos43°≈0.73,tan43°=0.94 sin76°≈0.97,cos76°≈0.24,tan76°≈4.01
素材三 如图,该市甲楼位于乙楼正南方向,两楼东西两侧都无法获得太阳光照射.现准备在乙楼南面墙上安装该品牌太阳能板.已知两楼间距为54米,甲楼AB共11层,乙楼CD共15层,一层从地面起,每层楼高皆为3.3米.AE为某时刻的太阳光线.
问题解决
任务一 确定使用数据 要判断乙楼哪些楼层不能安装该品牌太阳能板,应选择 日(填冬至或夏至)时,α为 (填14°,29°,43°,76°中的一个)进行计算.
任务二 探究安装范围 利用任务一中选择的数据进行计算,确定乙楼中哪些楼层不能安装该品牌太阳能热水器.
3.(2024 连云港)图1是古代数学家杨辉在《详解九章算法》中对“邑的计算”的相关研究.数学兴趣小组也类比进行了如下探究:如图2,正八边形游乐城A1A2A3A4A5A6A7A8的边长为km,南门O设立在A6A7边的正中央,游乐城南侧有一条东西走向的道路BM,A6A7在BM上(门宽及门与道路间距离忽略不计),东侧有一条南北走向的道路BC,C处有一座雕塑.在A1处测得雕塑在北偏东45°方向上,在A2处测得雕塑在北偏东59°方向上.
(1)∠CA1A2= °,∠CA2A1= °;
(2)求点A1到道路BC的距离;
(3)若该小组成员小李出南门O后沿道路MB向东行走,求她离B处不超过多少千米,才能确保观察雕塑不会受到游乐城的影响?
(结果精确到0.1km,参考数据,sin76°≈0.97,tan76°≈4.00,sin59°≈0.86,tan59°≈1.66)
4.(2024 重庆)在Rt△ABC中,∠ACB=90°,AC=BC,过点B作BD∥AC.
(1)如图1,若点D在点B的左侧,连接CD,过点A作AE⊥CD交BC于点E.若点E是BC的中点,求证:AC=2BD;
(2)如图2,若点D在点B的右侧,连接AD,点F是AD的中点,连接BF并延长交AC于点G,连接CF.过点F作FM⊥BG交AB于点M,CN平分∠ACB交BG于点N,求证:AM=CN+BD;
(3)若点D在点B的右侧,连接AD,点F是AD的中点,且AF=AC.点P是直线AC上一动点,连接FP,将FP绕点F逆时针旋转60°得到FQ,连接BQ,点R是直线AD上一动点,连接BR,QR.在点P的运动过程中,当BQ取得最小值时,在平面内将△BQR沿直线QR翻折得到△TQR,连接FT.在点R的运动过程中,直接写出的最大值.
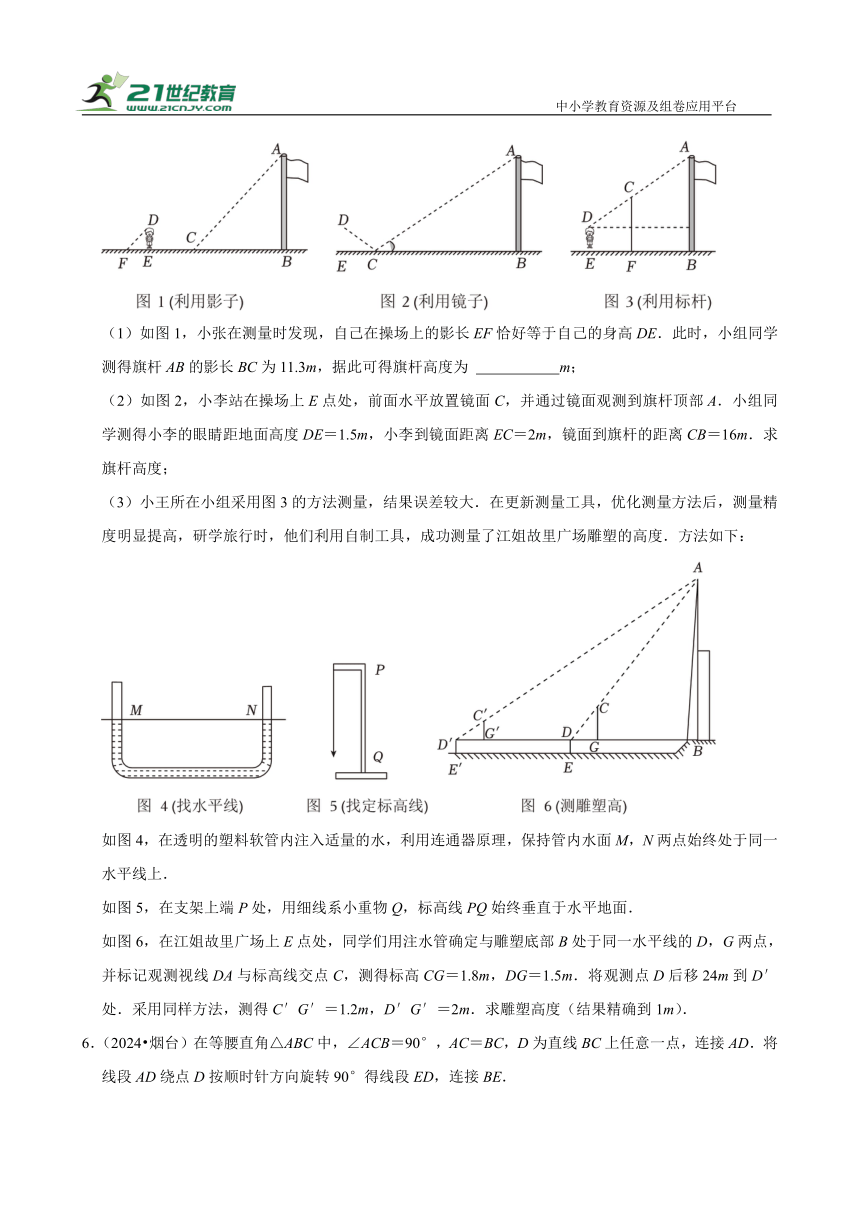
5.(2024 自贡)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3m,据此可得旗杆高度为 m;
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5m,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16m.求旗杆高度;
(3)小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图6,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8m,DG=1.5m.将观测点D后移24m到D′处.采用同样方法,测得C′G′=1.2m,D′G′=2m.求雕塑高度(结果精确到1m).
6.(2024 烟台)在等腰直角△ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD.将线段AD绕点D按顺时针方向旋转90°得线段ED,连接BE.
【尝试发现】
(1)如图1,当点D在线段BC上时,线段BE与CD的数量关系为 ;
【类比探究】
(2)当点D在线段BC的延长线上时,先在图2中补全图形,再探究线段BE与CD的数量关系并证明;
【联系拓广】
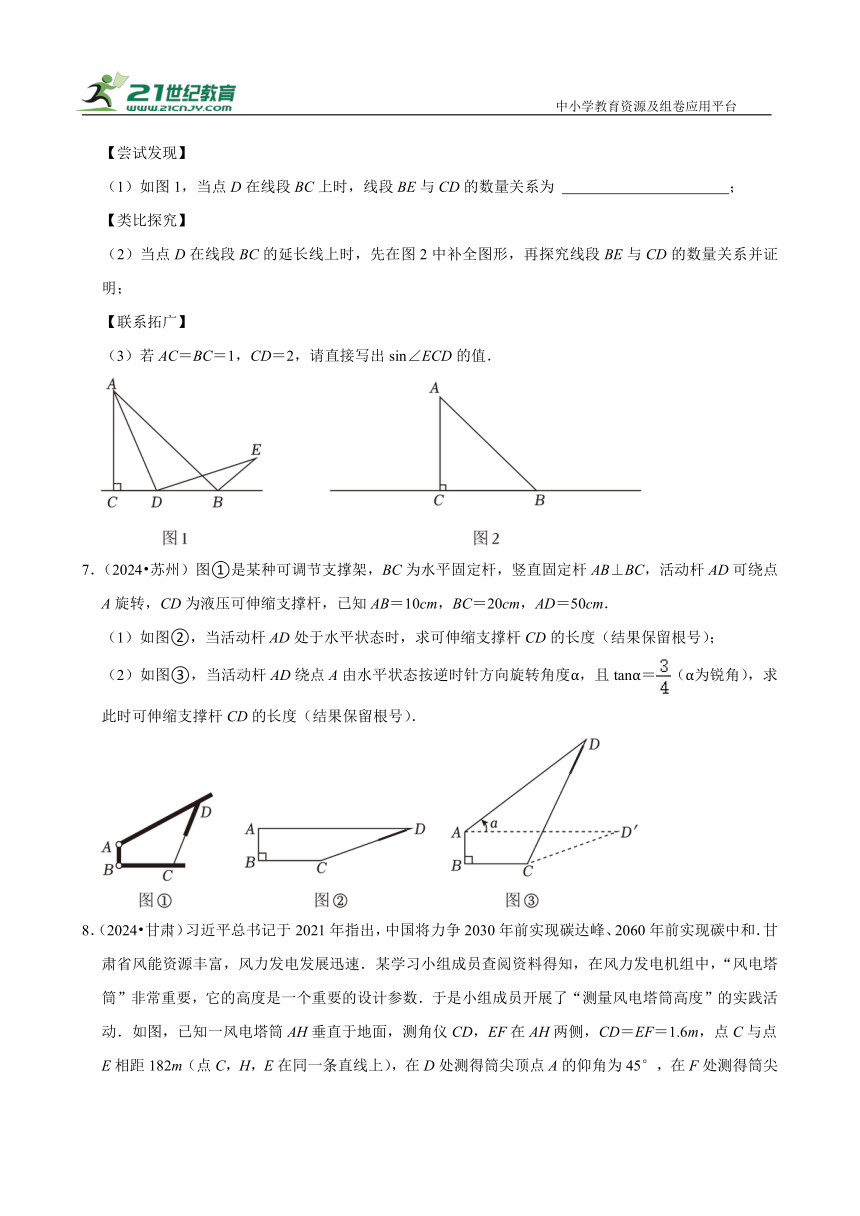
(3)若AC=BC=1,CD=2,请直接写出sin∠ECD的值.
7.(2024 苏州)图①是某种可调节支撑架,BC为水平固定杆,竖直固定杆AB⊥BC,活动杆AD可绕点A旋转,CD为液压可伸缩支撑杆,已知AB=10cm,BC=20cm,AD=50cm.
(1)如图②,当活动杆AD处于水平状态时,求可伸缩支撑杆CD的长度(结果保留根号);
(2)如图③,当活动杆AD绕点A由水平状态按逆时针方向旋转角度α,且tanα=(α为锐角),求此时可伸缩支撑杆CD的长度(结果保留根号).
8.(2024 甘肃)习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富,风力发电发展迅速.某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒AH垂直于地面,测角仪CD,EF在AH两侧,CD=EF=1.6m,点C与点E相距182m(点C,H,E在同一条直线上),在D处测得筒尖顶点A的仰角为45°,在F处测得筒尖顶点A的仰角为53°.求风电塔简AH的高度.(参考数据:sin53°≈,cos53°≈,tan53°≈.)
9.(2024 江西)图1是世界第一“大碗”——景德镇昌南里文化艺术中心主体建筑,其造型灵感来自于宋代湖田窑影青斗笠碗,寓意“万瓷之母”.如图2,“大碗”的主视图由“大碗”主体ABCD和矩形碗底BEFC组成,已知AD∥EF,AM,DN是太阳光线,AM⊥MN,DN⊥MN,点M,E,F,N在同一条直线上.经测量ME=FN=20.0m,EF=40.0m,BE=2.4m,∠ABE=152°.(结果精确到0.1m)
(1)求“大碗”的口径AD的长;
(2)求“大碗”的高度AM的长.
(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
10.(2024 广安)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机,如图(1),某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图(2)为测量示意图(点A,B,C,D均在同一平面内,AB⊥BC).已知斜坡CD长为20米,斜坡CD的坡角为60°,在斜坡顶部D处测得风力发电机塔杆顶端A点的仰角为20°,坡底与塔杆底的距离BC=30米,求该风力发电机塔杆AB的高度.(结果精确到个位;参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,≈1.73)
11.(2024 重庆)如图,甲、乙两艘货轮同时从A港出发,分别向B,D两港运送物资,最后到达A港正东方向的C港装运新的物资.甲货轮沿A港的东南方向航行40海里后到达B港,再沿北偏东60°方向航行一定距离到达C港.乙货轮沿A港的北偏东60°方向航行一定距离到达D港,再沿南偏东30°方向航行一定距离到达C港.
(参考数据:≈1.41,≈1.73,≈2.45)
(1)求A,C两港之间的距离(结果保留小数点后一位);
(2)若甲、乙两艘货轮的速度相同(停靠B,D两港的时间相同),哪艘货轮先到达C港?请通过计算说明.
12.(2024 宜宾)宜宾地标广场位于三江汇合口(如图1,左侧是岷江,右侧是金沙江,正面是长江).某同学在数学实践中测量长江口的宽度,他在长江口的两岸选择两个标点C、D,在地标广场上选择两个观测点A、B(点A、B、C、D在同一水平面,且AB∥CD).如图2所示,在点A处测得点C在北偏西18.17°方向上,测得点D在北偏东21.34°方向上;在B处测得点C在北偏西21.34°方向上,测得点D在北偏东18.17°方向上,测得AB=100米.求长江口的宽度CD的值(结果精确到1米).(参考数据:sin18.17°≈0.31,cos18.17°≈0.95,tan18.17°≈0.33,sin21.34°≈0.36,cos21.34°≈0.93,tan21.34°≈0.39)
13.(2024 广东)【知识技能】
(1)如图1,在△ABC中,DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A′DC′.当点E的对应点E′与点A重合时,求证:AB=BC.
【数学理解】
(2)如图2,在△ABC中(AB<BC),DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A′DC′,连接A′B,C′C,作△A′BD的中线DF.求证:2DF CD=BD CC′.
【拓展探索】
(3)如图3,在△ABC中,tanB=,点D在AB上,AD=.过点D作DE⊥BC,垂足为E,BE=3,CE=.在四边形ADEC内是否存在点G,使得∠AGD+∠CGE=180°?若存在,请给出证明;若不存在,请说明理由.
14.(2024 武汉)如图是由小正方形组成的3×4网格,每个小正方形的顶点叫做格点.△ABC三个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.
(1)在图(1)中,画射线AD交BC于点D,使AD平分△ABC的面积;
(2)在(1)的基础上,在射线AD上画点E,使∠ECB=∠ACB;
(3)在图(2)中,先画点F,使点A绕点F顺时针旋转90°到点C,再画射线AF交BC于点G;
(4)在(3)的基础上,将线段AB绕点G旋转180°,画对应线段MN(点A与点M对应,点B与点N对应).
15.(2024 临夏州)如图1,在矩形ABCD中,点E为AD边上不与端点重合的一动点,点F是对角线BD上一点,连接BE,AF交于点O,且∠ABE=∠DAF.
【模型建立】
(1)求证:AF⊥BE;
【模型应用】
(2)若AB=2,AD=3,DF=BF,求DE的长;
【模型迁移】
(3)如图2,若矩形ABCD是正方形,DF=BF,求的值.
16.(2024 滨州)(1)如图1,△ABC中,点D,E,F分别在三边BC,CA,AB上,且满足DF∥AC,DE∥AB.
①求证:四边形AFDE为平行四边形;
②若,求证:四边形AFDE为菱形;
(2)把一块三角形余料MNH(如图2所示)加工成菱形零件,使它的一个顶点与△MNH的顶点M重合,另外三个顶点分别在三边MN,NH,HM上,请在图2上作出这个菱形.(用尺规作图,保留作图痕迹,不写作法)
17.(2024 齐齐哈尔)综合与实践
如图1,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”.如图2,在△ABC中,∠A=90°,将线段BC绕点B顺时针旋转90°得到线段BD,作DE⊥AB交AB的延长线于点E.
(1)【观察感知】如图2,通过观察,线段AB与DE的数量关系是 ;
(2)【问题解决】如图3,连接CD并延长交AB的延长线于点F,若AB=2,AC=6,求△BDF的面积;
(3)【类比迁移】在(2)的条件下,连接CE交BD于点N,则= ;
(4)【拓展延伸】在(2)的条件下,在直线AB上找点P,使tan∠BCP=,请直接写出线段AP的长度.
18.(2024 湖北)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
19.(2024 广西)如图1,△ABC中,∠B=90°,AB=6.AC的垂直平分线分别交AC,AB于点M,O,CO平分∠ACB.
(1)求证:△ABC∽△CBO;
(2)如图2,将△AOC绕点O逆时针旋转得到△A'OC',旋转角为α(0°<α<360°).连接A′M,C′M.
①求△A'MC'面积的最大值及此时旋转角α的度数,并说明理由;
②当△A'MC'是直角三角形时,请直接写出旋转角α的度数.
20.(2024 安徽)如图1, ABCD的对角线AC与BD交于点O,点M,N分别在边AD,BC上,且AM=CN.点E,F分别是BD与AN,CM的交点.
(1)求证:OE=OF;
(2)连接BM交AC于点H,连接HE,HF.
(ⅰ)如图2,若HE∥AB,求证:HF∥AD;
(ⅱ)如图3,若 ABCD为菱形,且MD=2AM,∠EHF=60°,求的值.
21.(2024 江西)综合与实践
如图,在Rt△ABC中,点D是斜边AB上的动点(点D与点A不重合),连接CD,以CD为直角边在CD的右侧构造Rt△CDE,∠DCE=90°,连接BE,=m.
特例感知
(1)如图1,当m=1时,BE与AD之间的位置关系是 ,数量关系是 .
类比迁移
(2)如图2,当m≠1时,猜想BE与AD之间的位置关系和数量关系,并证明猜想.
拓展应用
(3)在(1)的条件下,点F与点C关于DE对称,连接DF,EF,BF,如图3.已知AC=6,设AD=x,四边形CDFE的面积为y.
①求y与x的函数表达式,并求出y的最小值;
②当BF=2时,请直接写出AD的长度.
22.(2024 凉山州)如图,在菱形ABCD中,∠ABC=60°,AB=2,E是BC边上一个动点,连接AE,AE的垂直平分线MN交AE于点M,交BD于点N,连接EN、CN.
(1)求证:EN=CN;
(2)求2EN+BN的最小值.
23.(2024 辽宁)如图,在△ABC中,∠ABC=90°,∠ACB=α(0°<α<45°).将线段CA绕点C顺时针旋转90°得到线段CD,过点D作DE⊥BC,垂足为E.
(1)如图1,求证:△ABC≌△CED.
(2)如图2,∠ACD的平分线与AB的延长线相交于点F,连接DF,DF的延长线与CB的延长线相交于点P,猜想PC与PD的数量关系,并加以证明.
(3)如图3,在(2)的条件下,将△BFP沿AF折叠,在α变化过程中,当点P落在点E的位置时,连接EF.
①求证:点F是PD的中点;
②若CD=20,求△CEF的面积.
24.(2024 牡丹江)数学老师在课堂上给出了一个问题,让同学们探究.在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.
(1)当点D在线段BC上时,如图①,求证:BD+EF=AB;
分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论:
推理证明:写出图①的证明过程:
探究问题:
(2)当点D在线段BC的延长线上时,如图②:当点D在线段CB的延长线上时,如图③,请判断并直接写出线段BD,EF,AB之间的数量关系;
拓展思考:
(3)在(1)(2)的条件下,若AC=6,CD=2BD,则EF= .
25.(2024 赤峰)数学课上,老师给出以下条件,请同学们经过小组讨论,提出探究问题.如图1,在△ABC中,AB=AC,点D是AC上的一个动点,过点D作DE⊥BC于点E,延长ED交BA延长线于点F.
请你解决下面各组提出的问题:
(1)求证:AD=AF;
(2)探究与的关系;
某小组探究发现,当时,;当时,.
请你继续探究:
①当时,直接写出的值;
②当时,猜想的值(用含m,n的式子表示),并证明;
(3)拓展应用:在图1中,过点F作FP⊥AC,垂足为点P,连接CF,得到图2,当点D运动到使∠ACF=∠ACB时,若,直接写出的值(用含m,n的式子表示).
26.(2024 绥化)综合与实践
问题情境
在一次综合与实践课上,老师让同学们以两个全等的等腰直角三角形纸片为操作对象.纸片△ABC和△DEF满足∠ACB=∠EDF=90°,AC=BC=DF=DE=2cm.
下面是创新小组的探究过程.
操作发现
(1)如图1,取AB的中点O,将两张纸片放置在同一平面内,使点O与点F重合.当旋转△DEF纸片交AC边于点H、交BC边于点G时,设AH=x(1<x<2),BG=y,请你探究出y与x的函数关系式,并写出解答过程.
问题解决
(2)如图2,在(1)的条件下连接GH,发现△CGH的周长是一个定值.请你写出这个定值,并说明理由.
拓展延伸
(3)如图3,当点F在AB边上运动(不包括端点A、B),且始终保持∠AFE=60°.请你直接写出△DEF纸片的斜边EF与△ABC纸片的直角边所夹锐角的正切值 (结果保留根号).
27.(2024 贵州)综合与探究:如图,∠AOB=90°,点P在∠AOB的平分线上,PA⊥OA于点A.
(1)【操作判断】
如图①,过点P作PC⊥OB于点C,根据题意在图①中画出PC,图中∠APC的度数为 度;
(2)【问题探究】
如图②,点M在线段AO上,连接PM,过点P作PN⊥PM交射线OB于点N,求证:OM+ON=2PA;
(3)【拓展延伸】
点M在射线AO上,连接PM,过点P作PN⊥PM交射线OB于点N,射线NM与射线PO相交于点F,若ON=3OM,求的值.
28.(2024 重庆)在△ABC中,AB=AC,点D是BC边上一点(点D不与端点重合).点D关于直线AB的对称点为点E,连接AD,DE.在直线AD上取一点F,使∠EFD=∠BAC,直线EF与直线AC交于点G.
(1)如图1,若∠BAC=60°,BD<CD,∠BAD=α,求∠AGE的度数(用含α的代数式表示);
(2)如图1,若∠BAC=60°,BD<CD,用等式表示线段CG与DE之间的数量关系,并证明;
(3)如图2,若∠BAC=90°,点D从点B移动到点C的过程中,连接AE,当△AEG为等腰三角形时,请直接写出此时的值.
29.(2024 成都)数学活动课上,同学们将两个全等的三角形纸片完全重合放置,固定一个顶点,然后将其中一个纸片绕这个顶点旋转,来探究图形旋转的性质.已知三角形纸片ABC和ADE中,AB=AD=3,BC=DE=4,∠ABC=∠ADE=90°.
【初步感知】
(1)如图1,连接BD,CE,在纸片ADE绕点A旋转过程中,试探究的值.
【深入探究】
(2)如图2,在纸片ADE绕点A旋转过程中,当点D恰好落在△ABC的中线BM的延长线上时,延长ED交AC于点F,求CF的长.
【拓展延伸】
(3)在纸片ADE绕点A旋转过程中,试探究C,D,E三点能否构成直角三角形.若能,直接写出所有直角三角形CDE的面积;若不能,请说明理由.
30.(2024 南充)如图,正方形ABCD边长为6cm,点E为对角线AC上一点,CE=2AE,点P在AB边上以1cm/s的速度由点A向点B运动,同时点Q在BC边上以2cm/s的速度由点C向点B运动,设运动时间为t秒(0<t≤3).
(1)求证:△AEP∽△CEQ.
(2)当△EPQ是直角三角形时,求t的值.
(3)连接AQ,当tan∠AQE=时,求△AEQ的面积.
图形的变化
参考答案与试题解析
一.解答题(共30小题)
1.(2024 凉山州)为建设全城旅游西昌,加快旅游产业发展.2022年9月29日位于西昌主城区东部的历史风貌核心区唐园正式开园,坐落于唐园内的怀远塔乃唐园至高点,为七层密檐式八角砖混结构阁楼式塔楼,建筑面积为1845.4平方米,塔顶金碧辉煌,为“火珠垂莲”窣(sū)堵坡造型.某校为了让学生进一步了解怀远塔,组织九年级(2)班学生利用综合实践课测量怀远塔的高度.小江同学站在如图所示的怀远塔前的平地上A点处,测得塔顶C的仰角为30°,眼睛B距离地面1.8m,向塔前行67m,到达点D处,测得塔顶C的仰角为60°,求塔高CF. (参考数据:≈1.414,≈1.732,结果精确到0.01m)
【分析】先用CG表示EG,BG,再根据BG﹣EG=67m,列方程求出CG,进一步可求出CF,从而解决问题.
【解答】解:由题意,知∠CBG=30°,∠CEG=60°,∠CGB=∠CGE=90°,GF=ED=BA=1.8m,BE=67m,
在Rt△CBG中,
BG==CG,
在Rt△CEG中,
EG==CG,
∵BG﹣EG=BE,
∴CG﹣CG=67,
解得CG≈58.02(m),
∴CF=CG+GF=58.02+1.8=59.82(m),
答:塔高CF为59.82m.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,理解题意,熟练运用三角函数关系是解题的关键.
2.(2024 烟台)根据收集的素材,探索完成任务.
探究太阳能热水器的安装
素材一 太阳能热水器是利用绿色能源造福人类的一项发明.某品牌热水器主要部件太阳能板需要安装在每天都可以有太阳光照射到的地方,才能保证使用效果,否则不予安装.
素材二 某市位于北半球,太阳光线与水平线的夹角为α,冬至日时,14°≤α≤29°;夏至日时,43°≤α≤76°. sin14°≈0.24,cos14°≈0.97,tan14°≈0.25 sin29°≈0.48,cos29°≈0.87,tan29°≈0.55 sin43°≈0.68,cos43°≈0.73,tan43°=0.94 sin76°≈0.97,cos76°≈0.24,tan76°≈4.01
素材三 如图,该市甲楼位于乙楼正南方向,两楼东西两侧都无法获得太阳光照射.现准备在乙楼南面墙上安装该品牌太阳能板.已知两楼间距为54米,甲楼AB共11层,乙楼CD共15层,一层从地面起,每层楼高皆为3.3米.AE为某时刻的太阳光线.
问题解决
任务一 确定使用数据 要判断乙楼哪些楼层不能安装该品牌太阳能板,应选择 冬至 日(填冬至或夏至)时,α为 14° (填14°,29°,43°,76°中的一个)进行计算.
任务二 探究安装范围 利用任务一中选择的数据进行计算,确定乙楼中哪些楼层不能安装该品牌太阳能热水器.
【分析】任务一:根据题意直接求解即可;
任务二:过E作EF⊥AB于F,利用正切定义求得.
【解答】解:任务一:根据题意,要判断乙楼哪些楼层不能安装该品牌太阳能板,只需α为冬至日时的最小角度,即α=14°,
故答案为:冬至,14°;
任务二:过E作EF⊥AB于F,则∠AFE=90°,EF=54米,BF=DE,
在Rt△AFE中,,
∴AF=EF tan14°≈54×0.25=13.5(米),
∵AB=11×3.3=36.3(米),
∴DE=BF=AB﹣AF=36.3﹣13.5=22.8(米),
∴22.8÷3.3≈7(层),
答:乙楼中7层(含7层)以下不能安装该品牌太阳能热水器.
想法二:题干中说品牌热水器主要部件太阳能板需要安装在每天都可以有太阳光照射到的地方,才能保证使用效果,否则不予安装,而冬至日时,14°≤α≤29°,指一天当中的变化,所以任务一选择29°,任务二结果为一、二层不能照到.
【点评】本题考查了解直角三角形的应用,理解题意是解答的关键.
3.(2024 连云港)图1是古代数学家杨辉在《详解九章算法》中对“邑的计算”的相关研究.数学兴趣小组也类比进行了如下探究:如图2,正八边形游乐城A1A2A3A4A5A6A7A8的边长为km,南门O设立在A6A7边的正中央,游乐城南侧有一条东西走向的道路BM,A6A7在BM上(门宽及门与道路间距离忽略不计),东侧有一条南北走向的道路BC,C处有一座雕塑.在A1处测得雕塑在北偏东45°方向上,在A2处测得雕塑在北偏东59°方向上.
(1)∠CA1A2= 90 °,∠CA2A1= 76 °;
(2)求点A1到道路BC的距离;
(3)若该小组成员小李出南门O后沿道路MB向东行走,求她离B处不超过多少千米,才能确保观察雕塑不会受到游乐城的影响?
(结果精确到0.1km,参考数据,sin76°≈0.97,tan76°≈4.00,sin59°≈0.86,tan59°≈1.66)
【分析】(1)求出正八边形的一个外角的度数,再根据角的和差关系进行求解即可;
(2)过点A作AD⊥BC于点D,解Rt△CA2A1,求出(km),解Rt△CA1D,求出(km);
(3)连接CA8并延长交BM于点E,延长A1A8交BE于点G,过点A8作AF⊥BC,垂足为F,解Rt△A7A8G,求出A8G,证明△CA8F∽△CEB,列出比例式进行求解即可.
【解答】解:(1)∵正八边形A1A2A3A4A5A6A7A8,
∴外角=,
∴∠CA1A2=45°+45°=90°,∠CA2A1=45°+(90°﹣59°)=76°,
故答案为:90;76;
(2)过点A1作A1D⊥BC于点D,
在Rt△CA2A1中,,∠CA2A1=76°,
∴(km),
在Rt△CA1D中,易知∠CA1D=45°
∴,
答:点A1到道路BC的距离为2.0千米.
(3)连接CA8并延长交BM于点E,延长A1A8交BE于点G,过点A8作A8F⊥BC于点F,
∵正八边形的外角均为45°,
∴在Rt△A7A8G中,,
∴,
又∵A8F=A1D=CD=2,,
∴,
∵∠CFA8=∠B,∠FCA8=∠BCE,
∴△CA8F∽△CEB,
∴,
∴,
∵,
∴EB=2.4(km).
答:小李离点B不超过2.4km,才能确保观察雕塑不会受到游乐城的影响.
【点评】本题考查了正多边形的外角,解直角三角形,相似三角形的判定和性质,掌握综合推理能力是解题的关键.
4.(2024 重庆)在Rt△ABC中,∠ACB=90°,AC=BC,过点B作BD∥AC.
(1)如图1,若点D在点B的左侧,连接CD,过点A作AE⊥CD交BC于点E.若点E是BC的中点,求证:AC=2BD;
(2)如图2,若点D在点B的右侧,连接AD,点F是AD的中点,连接BF并延长交AC于点G,连接CF.过点F作FM⊥BG交AB于点M,CN平分∠ACB交BG于点N,求证:AM=CN+BD;
(3)若点D在点B的右侧,连接AD,点F是AD的中点,且AF=AC.点P是直线AC上一动点,连接FP,将FP绕点F逆时针旋转60°得到FQ,连接BQ,点R是直线AD上一动点,连接BR,QR.在点P的运动过程中,当BQ取得最小值时,在平面内将△BQR沿直线QR翻折得到△TQR,连接FT.在点R的运动过程中,直接写出的最大值.
【分析】(1)证明△ACE≌△CBD(ASA),得到BD=CE;
(2)作出辅助线证明△HFM≌△CFN(AAS),得到HM=CN;
(3)通过手拉手模型证明点Q的运动轨迹是直线,从而根据垂线段最短确定点Q的位置.
【解答】证明:(1)∵∠ACB=90°,BD∥AC,
∴∠CBD=180°﹣∠ACB=90°,
∵AE⊥CD,
∴∠ACD+∠CAE=90°,
∵∠ACD+∠BCD=90°,
∴∠CAE=∠BCD,
又∵AC=CB,∠CBD=∠ACE=90°,
∴△ACE≌△CBD(ASA),
∴BD=CE,
∵点E是BC的中点,
∴BC=2CE=2BD,
∴AC=2BD;
证明:(2)过点G作GH⊥AB于H,连接HF,
∵BD∥AC,
∴∠FBD=∠FGA,∠D=∠FAG,
∵点F是AD的中点,
∴AF=DF,
∴△AGF≌△DBF(AAS),
∴AG=BD,BF=GF,
∵AC=BC,∠ACB=90°,
∴∠CAB=∠ACB=45°,
∵GH⊥AH,
∴△AHG是等腰直角三角形,
∴,
∵∠BHG=∠BCG=90°,BF=GF,
∴,
∴∠FBH=∠FHB,∠FBC=∠FCB,
∴∠GFH=∠FBH+∠FHB=2∠FBH,∠GFC=∠FBC+∠FCB=2∠FBC,
∴∠HFC=∠GFH+∠GFC=2∠FBH+2∠FBC=2∠ABC=90°,
∵FM⊥BG,
∴∠BFM=90°,
∴∠HFM=∠CFN,
设∠CBG=x,则∠ABG=45°﹣x,∠CGB=90°﹣x,
∴∠HMF=∠BFM+∠FBM=135°﹣x,
∵CN平分∠ACB,
∴,
∴∠CNF=∠CGN+∠GCN=135°﹣x,
∴∠HMF=∠CNF,
∴△HFM≌△CFN(AAS),
∴HM=CN,
∵AM=AH+HM,
∴;
(3)解:过点D作DH⊥AC交AC延长线与H,连接FH,
∵BD∥AC,∠ACB=90°,
∴∠BCH=∠CBD=90°,
∵DH⊥AC,
∴四边形BCHD是矩形,
∴BC=DH=AC,
∵点F是AD的中点,且AF=AC,
∴AD=2AF=2DH=2FH=2DF,
∴△FDH是等边三角形,
∴∠DFH=∠FDH=60°,
∴∠BDA=∠DAH=30°,
∴∠FHA=∠FAH=30°,
由旋转的性质可得FQ=FP,∠PFQ=60°=∠DFH,
∴∠DFQ=∠HFP,
∴△DFQ≌△HFP(SAS),
∴∠FDQ=∠FHP=30°,
∴点Q在直线DQ上运动,
设直线DQ交FH于K,则DK⊥FH,,,
∴∠BDQ=60°,
由垂线段最短可知,当BQ⊥DQ时,BQ有最小值,
∴∠DBQ=30°,
设AC=DH=6a,则,
∴,
∴,
∴,
在Rt△DFK中,,
∴,
∴QK=DK﹣DQ=3a,
在Rt△FQK中,由勾股定理得,
∵△DFQ≌△HFP,
∴,
∴,
∴由折叠的性质可得:,
∵FT≤FQ+TQ,
∴,
∴当点Q在线段FT上时,此时有最大值,最大值为,
∴的最大值为.
【点评】本题主要考查了全等三角形的性质与判定,勾股定理,等边三角形的性质与判定,等腰直角三角形的性质与判定,旋转的性质,折叠的性质,垂线段最短,矩形的性质与判定等等,属于综合题,难度较大.
5.(2024 自贡)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3m,据此可得旗杆高度为 11.3 m;
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5m,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16m.求旗杆高度;
(3)小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图6,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8m,DG=1.5m.将观测点D后移24m到D′处.采用同样方法,测得C′G′=1.2m,D′G′=2m.求雕塑高度(结果精确到1m).
【分析】(1)由影长EF恰好等于自己的身高DE,知△DEF是等腰直角三角形,△ABC是等腰直角三角形,故AB=BC=11.3m,
(2)证明△DEC∽△ABC,可得=,故AB=12,即旗杆高度为12米;
(3)由△DCG∽△DAB,得=,设AB=x m,BD=y m,则=,知y=x,同理可得=,即得=,从而=,解出x即可得雕塑高度约为31m.
【解答】解:(1)∵影长EF恰好等于自己的身高DE,
∴△DEF是等腰直角三角形,
由平行投影性质可知,△ABC是等腰直角三角形,
∴AB=BC=11.3m,
故答案为:11.3;
(2)如图:
由反射定律可知,∠DCE=∠ACB,
又∠DEC=90°=∠ABC,
∴△DEC∽△ABC,
∴=,即=,
解得AB=12,
∴旗杆高度为12米;
(3)如图:
∵∠CDG=∠ADB,∠CGD=90°=∠ABD,
∴△DCG∽△DAB,
∴=,
设AB=x m,BD=y m,则=,
∴y=x,
同理可得=,
∴=,
∴=,
解得x=28.8;
经检验,x=28.8是原方程的解,
故AB≈29m,
∴雕塑高度AB约为29m.
【点评】本题考查解直角三角形应用,涉及相似三角形判定与性质,解题的关键是读懂题意,列出方程解决问题.
6.(2024 烟台)在等腰直角△ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD.将线段AD绕点D按顺时针方向旋转90°得线段ED,连接BE.
【尝试发现】
(1)如图1,当点D在线段BC上时,线段BE与CD的数量关系为 ;
【类比探究】
(2)当点D在线段BC的延长线上时,先在图2中补全图形,再探究线段BE与CD的数量关系并证明;
【联系拓广】
(3)若AC=BC=1,CD=2,请直接写出sin∠ECD的值.
【分析】(1)过点E作EM⊥CB延长线于点M,利用一线三垂直全等模型证明△ACD≌△DME,再证明BM=EM即可;
(2)同(1)中方法证明△ACD≌△DME,再证明BM=EM即可;
(3)过点E作EM⊥CB,求出EM,CE即可.
【解答】解:(1)如图,过点E作EM⊥CB延长线于点M,
由旋转得AD=DE,∠ADE=90°,
∴∠ADC+∠EDM=90°,
∵∠ACB=90°,
∴∠ACD=∠DME,∠ADC+∠CAD=90°,
∴∠CAD=∠EDM,
∴△ACD≌△DME(AAS),
∴CD=EM,AC=DM,
∵AC=BC,
∴BM=DM﹣BD=AC﹣BD=BC﹣BD=CD,
∴BM=EM,
∵EM⊥CB,
∴,
故答案为:;
(2)补全图形如图,,理由如下:
过点E作EM⊥BC于点M,
由旋转得AD=DE,∠ADE=90°,
∴∠ADC+∠EDM=90°,
∵∠ACB=90°,
∴∠ACD=∠DME,∠ADC+∠CAD=90°,
∴∠CAD=∠EDM,
∴△ACD≌△DME(AAS),
∴CD=EM,AC=DM,
∵AC=BC,
∴DM=BC,
∴DM﹣CM=BC﹣CM,
∴CD=BM,
∴EM=BM,
∵EM⊥CB,
∴;
(3)如图,当点D在CB延长线上时,过点E作EM⊥CB延长线于点M,
由(2)得DM=AC=1,EM=CD=2,
∴CM=CD+DM=3,
∴,
∴;
当点D在BC延长线上时,过点E作EM⊥CB于点M,
同理可得:△ACD≌△DME,
∴DM=AC=1,ME=CD=2,
∴CM=2﹣1=1,
∴CE=,
∴sin∠ECD=,
综上,sin∠ECD=或.
【点评】本题考查三角形全等的判定与性质,三角函数,掌握一线三垂直全等模型是解题的关键.
7.(2024 苏州)图①是某种可调节支撑架,BC为水平固定杆,竖直固定杆AB⊥BC,活动杆AD可绕点A旋转,CD为液压可伸缩支撑杆,已知AB=10cm,BC=20cm,AD=50cm.
(1)如图②,当活动杆AD处于水平状态时,求可伸缩支撑杆CD的长度(结果保留根号);
(2)如图③,当活动杆AD绕点A由水平状态按逆时针方向旋转角度α,且tanα=(α为锐角),求此时可伸缩支撑杆CD的长度(结果保留根号).
【分析】(1)过点C作CE⊥AD,垂足为E,根据题意可得:AB=CE=10cm,BC=AE=20cm,从而可得ED=30cm,然后在Rt△CED中,利用勾股定理进行计算,即可解答;
(2)过点D作DF⊥BC,交BC的延长线于点F,交AD′于点G,根据题意可得:AB=FG=10cm,AG=BF,∠AGD=90°,然后在Rt△ADG中,利用锐角三角函数的定义可设DG=3x cm,则AG=4x cm,从而利用勾股定理进行计算可求出AG和DG的长,进而可求出DF和CF的长,最后在Rt△CFD中,利用勾股定理进行计算,即可解答.
【解答】解:(1)过点C作CE⊥AD,垂足为E,
由题意得:AB=CE=10cm,BC=AE=20cm,
∵AD=50cm,
∴ED=AD﹣AE=50﹣20=30(cm),
在Rt△CED中,CD===10(cm),
∴可伸缩支撑杆CD的长度为10cm;
(2)过点D作DF⊥BC,交BC的延长线于点F,交AD′于点G,
由题意得:AB=FG=10cm,AG=BF,∠AGD=90°,
在Rt△ADG中,tanα==,
∴设DG=3x cm,则AG=4x cm,
∴AD===5x(cm),
∵AD=50cm,
∴5x=50,
解得:x=10,
∴AG=40cm,DG=30cm,
∴DF=DG+FG=30+10=40(cm),
∴BF=AG=40cm,
∵BC=20cm,
∴CF=BF﹣BC=40﹣20=20(cm),
在Rt△CFD中,CD===20(cm),
∴此时可伸缩支撑杆CD的长度为20cm.
【点评】本题考查了解直角三角形的应用,勾股定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
8.(2024 甘肃)习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富,风力发电发展迅速.某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒AH垂直于地面,测角仪CD,EF在AH两侧,CD=EF=1.6m,点C与点E相距182m(点C,H,E在同一条直线上),在D处测得筒尖顶点A的仰角为45°,在F处测得筒尖顶点A的仰角为53°.求风电塔简AH的高度.(参考数据:sin53°≈,cos53°≈,tan53°≈.)
【分析】连接DF交AH于点G,根据题意可得:CD=EF=GH=1.6m,DF=CE=182m,DF⊥AH,然后设DG=x m,则FG=(182﹣x)m,分别在Rt△ADG和Rt△AFG中,利用锐角三角函数的定义求出AG的长,从而列出关于x的方程,进行计算即可解答.
【解答】解:连接DF交AH于点G,
由题意得:CD=EF=GH=1.6m,DF=CE=182m,DF⊥AH,
设DG=x m,
∴FG=DF﹣DG=(182﹣x)m,
在Rt△ADG中,∠ADG=45°,
∴AG=DG tan45°=x(m),
在Rt△AFG中,∠AFG=53°,
∴AG=FG tan53°≈(182﹣x)m,
∴x=(182﹣x),
解得:x=104,
∴AG=104m,
∴AH=AG+GH=104+1.6=105.6(m),
∴风电塔简AH的高度约为105.6m.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
9.(2024 江西)图1是世界第一“大碗”——景德镇昌南里文化艺术中心主体建筑,其造型灵感来自于宋代湖田窑影青斗笠碗,寓意“万瓷之母”.如图2,“大碗”的主视图由“大碗”主体ABCD和矩形碗底BEFC组成,已知AD∥EF,AM,DN是太阳光线,AM⊥MN,DN⊥MN,点M,E,F,N在同一条直线上.经测量ME=FN=20.0m,EF=40.0m,BE=2.4m,∠ABE=152°.(结果精确到0.1m)
(1)求“大碗”的口径AD的长;
(2)求“大碗”的高度AM的长.
(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
【分析】(1)根据垂直定义可得∠AMN=∠DNM=90°,再利用平行线的性质可得∠DAM=90°,从而可得四边形AMND是矩形,然后利用矩形的性质可得AD=MN,从而利用线段的和差关系进行计算即可解答;
(2)延长CB交AM于点G,根据题意可得:BE=GM=2.4m,BG=ME=20.0m,BG⊥AM,∠EBG=90°,从而可得∠ABG=62°,然后在Rt△ABG中,利用锐角三角函数的定义求出AG的长,从而利用线段的和差关系进行计算,即可解答.
【解答】解:(1)∵AM⊥MN,DN⊥MN,
∴∠AMN=∠DNM=90°,
∵AD∥MN,
∴∠DAM=180°﹣∠AMN=90°,
∴四边形AMND是矩形,
∴AD=MN=ME+EF+FN=20.0+40.0+20.0=80.0(m),
∴“大碗”的口径AD的长为80.0m;
(2)延长CB交AM于点G,
由题意得:BE=GM=2.4m,BG=ME=20.0m,BG⊥AM,∠EBG=90°,
∵∠ABE=152°,
∴∠ABG=∠ABE﹣∠EBG=62°,
在Rt△ABG中,AG=BG tan62°≈20.0×1.88=37.6(m),
∴AM=AG+MG=37.6+2.4=40.0(m),
∴“大碗”的高度AM的长约为40.0m.
【点评】本题考查了解直角三角形的应用,矩形的判定与性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
10.(2024 广安)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机,如图(1),某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图(2)为测量示意图(点A,B,C,D均在同一平面内,AB⊥BC).已知斜坡CD长为20米,斜坡CD的坡角为60°,在斜坡顶部D处测得风力发电机塔杆顶端A点的仰角为20°,坡底与塔杆底的距离BC=30米,求该风力发电机塔杆AB的高度.(结果精确到个位;参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,≈1.73)
【分析】过点D作DF⊥AB于点F,作DH⊥BE于点H,由题意得:DC=20m,∠DCH=60°,根据三角函数的定义得到CH=CD cos60°=10m,D,根据矩形的性质得到BH=FD,BF=DH,求得FD=40m,根据三角函数的定义即可得到结论.
【解答】解:过点D作DF⊥AB于点F,作DH⊥BE于点H,
由题意得:DC=20m,∠DCH=60°,
在Rt△DCH中,
∵,,
∴CH=CD cos60°=10m,
∴D,
∵∠DFB=∠B=∠DHB=90°,
∴四边形DFBH为矩形,
∴BH=FD,BF=DH,
∵BH=BC+CH=(30+10)m=40m,
∴FD=40m,
在Rt△AFD中,,
∴AF=FD tan20°=40×0.36m=14.4m,
∴AB=AF+BF=(17.3+14.4)m=31.7m≈32m,
答:该风力发电机塔杆AB的高度为32m.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,解直角三角形的应用﹣坡度坡角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.
11.(2024 重庆)如图,甲、乙两艘货轮同时从A港出发,分别向B,D两港运送物资,最后到达A港正东方向的C港装运新的物资.甲货轮沿A港的东南方向航行40海里后到达B港,再沿北偏东60°方向航行一定距离到达C港.乙货轮沿A港的北偏东60°方向航行一定距离到达D港,再沿南偏东30°方向航行一定距离到达C港.
(参考数据:≈1.41,≈1.73,≈2.45)
(1)求A,C两港之间的距离(结果保留小数点后一位);
(2)若甲、乙两艘货轮的速度相同(停靠B,D两港的时间相同),哪艘货轮先到达C港?请通过计算说明.
【分析】(1)过点B作BE⊥AC,垂足为E,先在Rt△ABE中,利用锐角三角函数的定义求出AE和BE的长,再在Rt△BCE中,利用锐角三角函数的定义求出CE的长,从而利用线段的和差关系进行计算,即可解答;
(2)根据题意可得:∠CDF=30°,DF∥AG,从而可得∠GAD=∠ADF=60°,然后利用角的和差关系可得∠ADC=90°,从而在Rt△ACD中,利用含30度角的直角三角形的性质求出CD和AD的长,再在Rt△BCE中,利用锐角三角函数的定义求出BC的长,最后进行计算比较即可解答.
【解答】解:(1)过点B作BE⊥AC,垂足为E,
在Rt△ABE中,∠BAE=90°﹣45°=45°,AB=40海里,
∴AE=AB cos45°=40×=20(海里),
BE=AB sin45°=40×=20(海里),
在Rt△BCE中,∠CBE=60°,
∴CE=BE tan60°=20×=20(海里),
∴AC=AE+CE=20+20≈77.2(海里),
∴A,C两港之间的距离约为77.2海里;
(2)甲货轮先到达C港,
理由:如图:
由题意得:∠CDF=30°,DF∥AG,
∴∠GAD=∠ADF=60°,
∴∠ADC=∠ADF+∠CDF=90°,
在Rt△ACD中,∠CAD=90°﹣∠GAD=30°,
∴CD=AC=(10+10)海里,
AD=CD=(10+30)海里,
在Rt△BCE中,∠CBE=60°,BE=20海里,
∴BC===40(海里),
∴甲货轮航行的路程=AB+BC=40+40≈96.4(海里),
乙货轮航行的路程=AD+CD=10+30+10+10=20+40=105.4(海里),
∵96.4海里<105.4海里,
∴甲货轮先到达C港.
【点评】本题考查了解直角三角形的应用﹣方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
12.(2024 宜宾)宜宾地标广场位于三江汇合口(如图1,左侧是岷江,右侧是金沙江,正面是长江).某同学在数学实践中测量长江口的宽度,他在长江口的两岸选择两个标点C、D,在地标广场上选择两个观测点A、B(点A、B、C、D在同一水平面,且AB∥CD).如图2所示,在点A处测得点C在北偏西18.17°方向上,测得点D在北偏东21.34°方向上;在B处测得点C在北偏西21.34°方向上,测得点D在北偏东18.17°方向上,测得AB=100米.求长江口的宽度CD的值(结果精确到1米).(参考数据:sin18.17°≈0.31,cos18.17°≈0.95,tan18.17°≈0.33,sin21.34°≈0.36,cos21.34°≈0.93,tan21.34°≈0.39)
【分析】过点A作AE⊥CD,垂足为E,过点B作BF⊥CD,垂足为F,根据已知易得:AE=BF,AB=EF=100m,然后设AE=BF=x m,从而分别在Rt△ACE、Rt△BDF和Rt△AED中,利用锐角三角函数的定义求出CE、DF和DE的长,从而列出关于x的方程,进行计算即可解答.
【解答】解:过点A作AE⊥CD,垂足为E,过点B作BF⊥CD,垂足为F,
∵AB∥CD,
∴AE=BF,
由题意得:AB=EF=100m,
设AE=BF=x m,
在Rt△ACE中,∠CAE=18.17°,
∴CE=AE tan18.17°≈0.33x(m),
在Rt△BDF中,∠DBF=18.17°,
∴DF=BF tan18.17°≈0.33x(m),
在Rt△AED中,∠EAD=21.34°,
∴DE=AE tan21.34°≈0.39x(m),
∵DE=EF+DF,
∴0.39x=100+0.33x,
解得:x=,
∴CD=CE+DE=0.33x+0.39x=0.72x=1200(m),
∴长江口的宽度CD的值约为1200m.
【点评】本题考查了解直角三角形的应用﹣方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
13.(2024 广东)【知识技能】
(1)如图1,在△ABC中,DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A′DC′.当点E的对应点E′与点A重合时,求证:AB=BC.
【数学理解】
(2)如图2,在△ABC中(AB<BC),DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A′DC′,连接A′B,C′C,作△A′BD的中线DF.求证:2DF CD=BD CC′.
【拓展探索】
(3)如图3,在△ABC中,tanB=,点D在AB上,AD=.过点D作DE⊥BC,垂足为E,BE=3,CE=.在四边形ADEC内是否存在点G,使得∠AGD+∠CGE=180°?若存在,请给出证明;若不存在,请说明理由.
【分析】(1)利用等腰三角形+平行线证明∠DAE=∠BCA即可得证;
(2)先证△ADA′∽△CDC得到,再证AA'=2DF,代入变形即可得证;
(3)利用特殊点,∠AGD=90°,∠CGE=90°,则G就是以AD为直径的圆和以CE为直径的圆的交点,根据题意证G在内部即可.
【解答】(1)证明:∵△ADC绕点D按逆时针方向旋转,得到△A′DC',且E'与A重合,
∴AD=DE,
∴∠DAE=∠DEA,
∵DE是△ABC的中位线,
∴DE∥BC,
∴∠DEA=∠BCA,
∴∠DAE=∠BCA,
∴AB=BC.
(2)证明:连接AA',
∵旋转,
∴∠ADA′=∠CDC′,AD=A'D,CD=C'D,
∴,
∴△ADA′∽△CDC′,
∴,
∵DE是△ABC的中位线,DF是△A'BD的中线,
∴AD=BD,BF=A'F,
∴DF是△AA'B的中位线,
∴AA'=2DF,
∴,
∴2DF CD=BD CC'
(3)解:存在,理由如下,
解法一:取AD中点M,CE中点N,连接MN,
∵AD是⊙M直径,CE是⊙N直径,
∴∠AGD=90°,∠CGE=90°,
∴∠AGD+∠CGE=180°,
∵tanB=,BE=3,
∴BD=5,
∵CE=,
∴EN=CE=,
∴BN=BE+EN=,
∵DE⊥CE,
∴DE是⊙N的切线,即DE在⊙N外,
作NF⊥AB,
∵∠B=∠B,∠BED=∠BFN=90°,
∴△BDE∽△BNF,
∴,
∴NF=>,即NF>rn,
∴AB在⊙N外,
∴G点在四边形ADEC内部.
作MH⊥BC,
∵BM=,tanB=,
∴BH=,MH=,
∴NH=,
∴MN=≈7.4<AM+CN
∴⊙M和⊙N有交点.
故四边形ADEC内存在点G,使得∠AGD+∠CGE=180°.
解法二:相似互补弓形,
分别以AD,CE为弦作⊙O2和⊙O,使得△O2AD∽△OEC,两圆的交点即为所求.
作图步骤:①在四边形ADEC内任取一点F,作△EFC得外接圆,圆心为O,连接OE,OC,
②作AD的中垂线,
③以D为圆心,OC为半径画圆交AD中垂线于点O2,
④以O2为圆心,O2A为半径画圆,交⊙O于点G,点G即为所求.
证明:∵==,
∴△O2AD∽△OEC,
∴∠AO2D=∠EOC,
∵∠AGD=(360°﹣∠AO2D)=180°﹣∠AO2D,
∠EGC=∠EOC,
∴∠AGD+∠EGC=180°.
故四边形ADEC内存在点G,使得∠AGD+∠CGE=180°.
【点评】本题主要考查了相似三角形的判定和性质、中位线定理、圆周角定理、勾股定理等知识,熟练掌握相关知识是解题关键.
14.(2024 武汉)如图是由小正方形组成的3×4网格,每个小正方形的顶点叫做格点.△ABC三个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.
(1)在图(1)中,画射线AD交BC于点D,使AD平分△ABC的面积;
(2)在(1)的基础上,在射线AD上画点E,使∠ECB=∠ACB;
(3)在图(2)中,先画点F,使点A绕点F顺时针旋转90°到点C,再画射线AF交BC于点G;
(4)在(3)的基础上,将线段AB绕点G旋转180°,画对应线段MN(点A与点M对应,点B与点N对应).
【分析】(1)根据三角形中线的定义画出图形;
(2)作点A故BC的对称点A′,连接CA′交射线ADF于点E,点E即为所求;
(3)构造等腰直角三角形AFC即可;
(4)取格点P,Q,E,W,K,L,连接PQ,EW,KL,PQ交射线AF于点M,EW交KL于点J,连接MJ,延长MJ交BC一点N,线段MN即为所求(证明△ABG≌△MNG,可得结论).
【解答】解:(1)如图1中,线段AD即为所求;
(2)如图1中,点E即为所求;
(3)如图2中,点F,射线AF,点G即为所求;
(4)如图2中,线段MN即为所求.
【点评】本题考查作图﹣旋转变换,角平分线的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
15.(2024 临夏州)如图1,在矩形ABCD中,点E为AD边上不与端点重合的一动点,点F是对角线BD上一点,连接BE,AF交于点O,且∠ABE=∠DAF.
【模型建立】
(1)求证:AF⊥BE;
【模型应用】
(2)若AB=2,AD=3,DF=BF,求DE的长;
【模型迁移】
(3)如图2,若矩形ABCD是正方形,DF=BF,求的值.
【分析】(1)由矩形的性质得∠BAD=90°,而∠ABE=∠DAF,所以∠AOE=∠BAF+∠ABE=∠BAF+∠DAF=90°,则AF⊥BE;
(2)延长AF交CD于点G,由GD∥AB,证明△GDF∽△ABF,则==,求得GD=AB=1,由=tan∠ABE=tan∠DAG==,求得AE=AB=,则DE=AD﹣AE=;
(3)延长AF交CD于点H,由正方形的性质得AB=AD,∠ADH=90°,设AB=AD=2m,可证明△HDF∽△ABF,得===,则HD=AB=m,求得AH==m,则AF=AH=m,求得=.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵∠ABE=∠DAF,
∴∠AOE=∠BAF+∠ABE=∠BAF+∠DAF=∠BAD=90°,
∴AF⊥BE.
(2)解:如图1,延长AF交CD于点G,
∵GD∥AB,
∴△GDF∽△ABF,
∵DF=BF,AB=2,AD=3,
∴==,
∴GD=AB=×2=1,
∵∠BAE=∠ADG=90°,∠ABE=∠DAG,
∴=tan∠ABE=tan∠DAG==,
∴AE=AB=×2=,
∴DE=AD﹣AE=3﹣=,
∴DE的长是.
(3)解:如图2,延长AF交CD于点H,
∵四边形ABCD是正方形,
∴AB=AD,∠ADH=90°,
设AB=AD=2m,
∵HD∥AB,
∴△HDF∽△ABF,
∵DF=BF,
∴===,
∴HD=AB=×2m=m,
∴AH===m,
∴AF=AH=AH=×m=m,
∴==,
∴的值为.
【点评】此题重点考查矩形的性质,正方形的性质,三角形的一个外角等于与它不相邻的两个内角的和,相似三角形的判定与性质,锐角三角函数与解直角三角形,勾股定理等知识,此题综合性强,难度较大,正确地作出辅助线是解题的关键.
16.(2024 滨州)(1)如图1,△ABC中,点D,E,F分别在三边BC,CA,AB上,且满足DF∥AC,DE∥AB.
①求证:四边形AFDE为平行四边形;
②若,求证:四边形AFDE为菱形;
(2)把一块三角形余料MNH(如图2所示)加工成菱形零件,使它的一个顶点与△MNH的顶点M重合,另外三个顶点分别在三边MN,NH,HM上,请在图2上作出这个菱形.(用尺规作图,保留作图痕迹,不写作法)
【分析】(1)①根据DF∥AC,DE∥AB,点D,E,F分别在三边BC,CA,AB上,可以得到DF∥AE,DE∥AE,然后即可证明结论成立;
②延长BA到G,使得AG=AC,然后根据和∠ABD=∠GBC,可以得到△BAD∽△BGC,从而可以得到∠BAD=∠G,即可判断AD∥CG,然后根据平行线的性质和等腰三角形的性质,可以得到AD平分∠BAC,再根据平行线的性质,可以得到∠DAE=∠ADE,进而得到AE=DE,最后根据有一组邻边相等的平行四边形是菱形,即可证明结论成立;
(2)作∠NMH的角平分线,与NH交于点L,再作线段ML的垂直平分线,分别交MN、MH于点O,G,则四边形MGLO即为所求.
【解答】(1)①证明:∵DF∥AC,DE∥AB,点D,E,F分别在三边BC,CA,AB上,
∴DF∥AE,DE∥AE,
∴四边形AFDE为平行四边形;
②证明:延长BA到G,使得AG=AC,如图1所示,
则∠G=∠ACG,
∵,
∴,
∵∠ABD=∠GBC,
∴△BAD∽△BGC,
∴∠BAD=∠G,
∴AD∥GC,
∴∠DAC=∠ACG,
∴∠BAD=∠DAC,
又∵AB∥DE,
∴∠BAD=∠ADE,
∴∠DAE=∠ADE,
∴AE=DE,
∴四边形AFDE为菱形;
(2)解:作∠NMH的角平分线,与NH交于点L,再作线段ML的垂直平分线,分别交MN、MH于点O,G,如下图所示,
四边形MGLO即为所求.
【点评】本题是一道相似形综合题,主要考查平行四边形的判定、相似三角形的判定与性质、菱形的判定、角平分线的画法、线段垂直平分线的画法,解答本题的关键是明确题意,找出所求问题需要的条件.
17.(2024 齐齐哈尔)综合与实践
如图1,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”.如图2,在△ABC中,∠A=90°,将线段BC绕点B顺时针旋转90°得到线段BD,作DE⊥AB交AB的延长线于点E.
(1)【观察感知】如图2,通过观察,线段AB与DE的数量关系是 AB=DE ;
(2)【问题解决】如图3,连接CD并延长交AB的延长线于点F,若AB=2,AC=6,求△BDF的面积;
(3)【类比迁移】在(2)的条件下,连接CE交BD于点N,则= ;
(4)【拓展延伸】在(2)的条件下,在直线AB上找点P,使tan∠BCP=,请直接写出线段AP的长度.
【分析】(1)利用“一线三垂直“证△ABC≌△EBD(AAS)即可得证;
(2)证△DEF∽△CAF可求EF长度,然后即可求出△BDF的面积;
(3)要求的值,有两个方向,①把BN和BC的值求出来,这题BC很好求,但是BN不好求,可以建立坐标系求解析式,再求交点N坐标,最后利用两点距离公式求BN的长度;②根据题干给我们的思路建立一线三直角得相似进行转化即可,利用△EMN∽△EAC和△BMN∽△BED建立关于MN的方程,求出MN的长度,最后利用△BMN∽△CAB求值即可.
(4)由已知条件过P作BC垂线段,可得两个直角三角形,然后解这两个直角三角形即可求解.另外方法二的正切和差角公式可以作为课外拓展知识,在这种直接写答案的题型中可以用下,快速找出答案.
【解答】解:(1)∵线段BC绕点B逆时针旋转90°得到线段BD,
∴BC=BD,∠CBD=90°,
∴∠BCA=∠DBE=90°﹣∠ABC,
∵∠A=∠E=90°,
∴△ABC≌△EBD(AAS),
∴AB=DE;
故答案为:AB=DE.
(2)∵线段BC绕点B逆时针旋转90°得到线段BD,
∴BC=BD,∠CBD=90°,
∴∠BCA=∠DBE=90°﹣∠ABC,
∵∠A=∠E=90°,
∴△ABC≌△EBD(AAS),
∴DE=AB,BE=AC,
∵AB=2,AC=6,
∴DE=2,BE=6,
∴AE=AB+BE=8,
∵∠DEB+∠A=180°,
∴DE∥AC,
∴△DEF∽△CAF,
∴,即,
∴EF=4,
∴BF=BE+EF=10,
∴S△BDF=BF DE=10.
(3)方法一:如图,以AE所在直线为x轴,以AC所在直线为y轴建立坐标系,
由AC=6,AE=8,DE=2,BD=2,
∴C(0,6),B(2,0),E(8,0),D(8,2),
设直线BD解析式为y=kx+b,将B、D代入得,
,解得:,
∴直线BD解析式为y=x﹣,
同理可求直线CE解析式为:y=﹣x+6,
令x﹣=﹣x+6,解得x=,
∴y=,即N(,),
∴利用两点距离公式可得BN=,
∵BC==2,
∴==.
故答案为:.
方法二:如图,过N作NM⊥AE于点M,
由△EMN∽△EAC得,,即,
∴EM=MN,
由△BMN∽△BED得,,即,
解得MN=,
由△BMN∽△CAB得,=.
故答案为:.
(4)方法一:①当点P在点B左侧时,如图所示,过P作PQ⊥BC于点Q,
∵tan∠BCP==,tan∠ABC===3,
∴PQ=CQ,PQ=3BQ,
设BQ=2a,则PQ=6a,CQ=9a,
∴BC=BQ+CQ=11a,
∵BC==2=11a,
∴a=,
∴BP==2a=,
∴AP=BP﹣AB=;
②当点P在点B右侧时,如图所示,作PG⊥BC交BC延长线于点G,
tan∠BCP==,tan∠PBG=tan∠ABC,即,
剩下思路与第一种情况方法一致,求得AP=.
综上,AP的长度为或.
方法二:补充知识:正切和差角公式:tan(α+β)=,tan(α﹣β)=.
①当点P在点B左侧时,因为tan∠BCA=,tan∠BCP=,所以此时点P在A的左侧,如图所示,
tan∠BCP=tan(∠BCA+∠ACP)===,
解得tan∠ACP=,即=,
∵AC=6,
∴AP=.
②当点P在点B右侧时,如图所示,
tan∠ACP=tan(∠BCA+∠BCP)===,
即,
∵AC=6,
∴AP=.
综上,AP的长度为或.
【点评】本题主要考查了相似三角形的判定和性质、全等三角形的性质和判定、解直角三角形、勾股定理等知识,熟练掌握以上基础知识和添加合适的辅助线是解题关键.
18.(2024 湖北)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
【分析】(1)证明对应角相等,即可得到△EDP∽△PCH;
(2)根据△EDP∽△PCH,求得PH的长度,从而得出GH长度;
(3)延长AB,PG交于一点M,连接AP,先证明△MBH≌△PCH,得到相等的边,再根据△BMG∽△MAP,得出大小关系.
【解答】(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴DP=CP==1,
设EP=AP=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得x=,
∴EP=AP=x=,
∴ED=AD﹣AE=,
∵△EDP∽△PCH,
∴,即,
∴PH=,
∵PG=AB=2,
∴GH=PG﹣PH=.
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴HP=PM=y,
在Rt△PCH中,CH==y,
∴BC=2CH=y,
∴AD=BC=y,
在Rt△APD中,AP==y,
∵BG∥AP,
∴△BMG∽△AMP,
∴=,
∴BG=y,
∴=,
∴AB=BG.
【点评】本题考查了矩形与折叠、相似三角形的判定与性质、勾股定理、全等三角形的判定与性质等知识,熟练掌握以上基础知识是解题关键.
19.(2024 广西)如图1,△ABC中,∠B=90°,AB=6.AC的垂直平分线分别交AC,AB于点M,O,CO平分∠ACB.
(1)求证:△ABC∽△CBO;
(2)如图2,将△AOC绕点O逆时针旋转得到△A'OC',旋转角为α(0°<α<360°).连接A′M,C′M.
①求△A'MC'面积的最大值及此时旋转角α的度数,并说明理由;
②当△A'MC'是直角三角形时,请直接写出旋转角α的度数.
【分析】(1)从问题出发,证△ABC∽△CBO,两个三角形有一个公共角,所以只需证一角相等即可,由题干很容易得出∠ACO=∠BCO=∠A,即可得证;
(2)△A'MC'的底是定长,所以只要找到高的最大值就可求出面积最值,当N、H重合时MH取最大值,此时最大值为OM+ON=4,即可求解;
(3)首先有条件可知只有可能是∠A'MC'=90°,由特殊三角形和旋转的性质大胆猜测当点C'与A重合时和当A'与C重合时满足∠A'MC'=90°,进而求旋转角即可.
【解答】(1)证明:∵OM垂直平分AC,
∴OA=OC,∠A=∠ACO,
∵CO平分∠ACB,
∴∠ACO=∠BCO=∠A,
∵∠B=∠B,
∴△ABC∽△CBO.
(2)解:①∵∠ACO=∠BCO=∠A,∠B=90°,
∴:∠ACO=∠BCO=∠A=30°,
在Rt△ABC中,AB=6,
∴AC==4,
∴AM=2,
∴OM=AM tan30°=2,
如图3,作MH⊥A'C'于点H,ON⊥A'C'于点N,连接MN,
在△AOC旋转的过程中,对应边AC=A'C'=4,对应高OM=ON=2,
在Rt△MHN中,MH<MN,
在△OMN中,MN<OM+ON,
∴MH<MN<OM+ON,
如图4,当N、H重合时MH取最大值,此时最大值为OM+ON=4,
∴S△A'MC'=A'C' MH=8,即△A'MC'面积最大值是8,
此时M、O、N三点共线,α=∠MON=180°.
②在旋转得过程中,等腰三角形AOC的形状、大小不变,∠AOC=∠A'OC'=120°,
∵MC′≤MO+OC'=MO+OC=6<4=A'C',同理MA'≤6<A'C',
∴△A'MC'中只有可能∠A'MC'=90°,
∵OM垂直平分AC,
∴MA=MC,∠AMO=90°,
(Ⅰ)如图5,当点C'与A重合时,A'恰好在MO的延长线上,满足∠A'MC'=90°,此时α=120°;
(Ⅱ)如图6,当A'与C重合时,点C'恰好在MO的延长线上,满足∠A'MC'=90°,此时α=240°.
综上,当△A'MC'是直角三角形时,α为120°或240°.
【点评】本题主要考查了相似三角形的判定、含有30°的直角三角形、旋转的性质、几何动点问题等知识点,掌握相关基础知识是解题的关键,其中在最后一文中大胆的想象和猜测也是一种解题策略.
20.(2024 安徽)如图1, ABCD的对角线AC与BD交于点O,点M,N分别在边AD,BC上,且AM=CN.点E,F分别是BD与AN,CM的交点.
(1)求证:OE=OF;
(2)连接BM交AC于点H,连接HE,HF.
(ⅰ)如图2,若HE∥AB,求证:HF∥AD;
(ⅱ)如图3,若 ABCD为菱形,且MD=2AM,∠EHF=60°,求的值.
【分析】(1)证明△AOE≌△COF(ASA),即可得到OE=OF;
(2)(i)证明△HOF∽△AOD,即可得到HF∥AD;(ii)先求出OA=2OH,OB=5OE,即可得到的值.
【解答】(1)证明:∵ ABCD,
∴AD∥BC,OA=OC,
∴AM∥CN,
∵AM=CN,
∴四边形AMCN是平行四边形,
∴AN∥CM,
∴∠OAE=∠OCF,
在△AOE与△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF;
(2)(i)证明:∵HE∥AB,
∴,
∵OB=OD,OE=OF,
∴,
∵∠HOF=∠AOD,
∴△HOF∽△AOD,
∴∠OHF=∠OAD,
∴HF∥AD;
(ii)解:∵ ABCD为菱形,
∴AC⊥BD,
∵OE=OF,∠EHF=60°,
∴∠EHO=∠FHO=30°,
∴,
∵AM∥BC,MD=2AM,
∴=,即HC=3AH,
∴OA+OH=3(OA﹣OH),
∴OA=2OH,
∵BN∥AD,MD=2AM,AM=CN,
∴,即3BE=2ED,
∴3(OB﹣OE)=2(OB+OE),
∴OB=5OE,
∴,
∴的值是.
【点评】本题考查了平行四边形的性质与判定,相似三角形的性质与判定,全等三角形的性质与判定等,综合运用性质与判定方法是解题的关键.
21.(2024 江西)综合与实践
如图,在Rt△ABC中,点D是斜边AB上的动点(点D与点A不重合),连接CD,以CD为直角边在CD的右侧构造Rt△CDE,∠DCE=90°,连接BE,=m.
特例感知
(1)如图1,当m=1时,BE与AD之间的位置关系是 AD⊥BE ,数量关系是 AD=BE .
类比迁移
(2)如图2,当m≠1时,猜想BE与AD之间的位置关系和数量关系,并证明猜想.
拓展应用
(3)在(1)的条件下,点F与点C关于DE对称,连接DF,EF,BF,如图3.已知AC=6,设AD=x,四边形CDFE的面积为y.
①求y与x的函数表达式,并求出y的最小值;
②当BF=2时,请直接写出AD的长度.
【分析】(1)由=1,得到CE=CD,CB=CA,根据等腰直角三角形的性质得到∠A=∠ABC=45°,∠ACD=∠BAE,根据全等三角形的性质得到AD=BE,∠A=∠CBE=45°,根据垂直的定义得到AD⊥BE;
(2)根据相似三角形的判定定理得到△ADC∽△BEC,求得=m,∠CBE=∠A,得到BE=mAD,根据垂直的定义得到AD⊥BE;
(3)①连接CF交DE于O,由(1)知,AC=BC=6,∠ACB=90°,求得AB=6,得到BD=6﹣x,根据勾股定理得到DE2=BD2+BE2=(6﹣x)2+x2,根据线段垂直平分线的性质得到CE=EF,CD=DF,推出四边形CDFE是正方形,根据正方形的面积公式即可得到y=DE2=[(6﹣x)2+x2],根据二次函数的性质即可得到结论;
②过D作DH⊥AC于H,根据等腰直角三角形 到现在得到AH=DH=AD=x,求得CH=6﹣x,连接OB,推出OB=,得到∠CBF=90°,根据勾股定理得到结论.
【解答】解:(1)AD⊥BE,AD=BE,
理由:∵=1,
∴CE=CD,CB=CA,
∵∠ACB=∠DCE=90°,
∴∠A=∠ABC=45°,∠ACD=∠BAE,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠A=∠CBE=45°,
∴∠ABE=90°,
∴AD⊥BE;
故答案为:AD⊥BE,AD=BE;
(2)BE=mAD,AD⊥BE,
证明:∵∠ACB=∠DCE=90°,
∴∠ACD=∠BAE,
∵=m,
∴△ADC∽△BEC,
∴=m,∠CBE=∠A,
∴BE=mAD,
∵∠A+∠ABC=90°,
∴∠CBE+∠ABC=90°,
∴∠ABE=90°,
∴AD⊥BE;
(3)①连接CF交DE于O,
由(1)知,AC=BC=6,∠ACB=90°,
∴AB=6,
∴BD=6﹣x,
∵AD=BE=x,∠DBE=90°,
∴DE2=BD2+BE2=(6﹣x)2+x2,
∵点F与点C关于DE对称,
∴DE垂直平分CF,
∴CE=EF,CD=DF,
∵CD=CE,
∴CD=DF=EF=CE,
∵∠DCE=90°,
∴四边形CDFE是正方形,
∴y=DE2=[(6﹣x)2+x2],
∴y与x的函数表达式为y=x2﹣6+36(0<x≤6),
∵y=x2﹣6+36=(x﹣3)2+18,
∴y的最小值为18;
②过D作DH⊥AC于H,
则△ADH是等腰直角三角形,
∴AH=DH=AD=x,
∴CH=6﹣x,
连接OB,
∴OB=OE=OD=OC=OF,
∴OB=,
∴∠CBF=90°,
∵BC=6,BF=2,
∴CF==2
∴CD=CF=2,
∵CH2+DH2=CD2,
∴(6﹣x)2+(x)2=(2)2,
解得x=4或x=2,
∴AD=4或2.
【点评】本题是相似形的综合题,考查了等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,正方形的判定和性质.勾股定理,正确地作出辅助线是解题的关键.
22.(2024 凉山州)如图,在菱形ABCD中,∠ABC=60°,AB=2,E是BC边上一个动点,连接AE,AE的垂直平分线MN交AE于点M,交BD于点N,连接EN、CN.
(1)求证:EN=CN;
(2)求2EN+BN的最小值.
【分析】(1)利用线段垂直平分线的性质和菱形的性质即可证明出结论;
(2)过点N作NG⊥BC于点G,连接AN,AG,过点A作AH⊥BC于点H,证明出2EN+BN的最小值为2AH,再求出AH即可解决问题.
【解答】解:(1)连接AN,如图,
∵四边形ABCD是菱形,
∴点A,点C关于直线BD轴对称,
∴AN=CN,
∵AE的垂直平分线MN交AE于点M,交BD于点N,
∴AN=EN,
∴EN=CN;
(2)过点N作NG⊥BC于点G,连接AN,AG,过点A作AH⊥BC于点H,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠DBC=30°,
∴BN=2NG,
∵AE的垂直平分线MN交AE于点M,交BD于点N,
∴EN=AN,
∴2EN+BN=2AN+2NG=2(AN+NG)≥2AG≥2AH,
∴2EN+BN的最小值为2AH,
∵∠ABC=60°,AB=2,
∴AH=AB sin60°=,
∴2EN+BN的最小值为2.
【点评】本题考查菱形的性质,三角函数,含30°角直角三角形的性质,线段的垂直平分线的性质,通过作辅助线将所求线段和的最小值用一条线段表示是解题的关键.
23.(2024 辽宁)如图,在△ABC中,∠ABC=90°,∠ACB=α(0°<α<45°).将线段CA绕点C顺时针旋转90°得到线段CD,过点D作DE⊥BC,垂足为E.
(1)如图1,求证:△ABC≌△CED.
(2)如图2,∠ACD的平分线与AB的延长线相交于点F,连接DF,DF的延长线与CB的延长线相交于点P,猜想PC与PD的数量关系,并加以证明.
(3)如图3,在(2)的条件下,将△BFP沿AF折叠,在α变化过程中,当点P落在点E的位置时,连接EF.
①求证:点F是PD的中点;
②若CD=20,求△CEF的面积.
【分析】(1)可证得∠D+∠DCE=90°,∠DCE+∠ACB=90°,从而∠ACB=∠D,进而证得△ABC≌△CED;
(2)可证得△ACF≌△DCF,从而∠A=∠PDC,进而证得∠PDC=∠DCE,从而得出PC=PD;
(3)①由折叠得PF=EF,∠P=∠PEF,可证得∠PEF+∠DEF=90°,∠P+∠PDE=90°,从而∠PDE=∠DEF,从而得出EF=DF,进而得出PF=DF;
②设CE=a,BC=DE=b,从而BE=BC﹣CE=b﹣a,可证得△PBF∽△PED,
∴,从而得出PE=2BE=2(b﹣a),BF=DE=,从而S△CEF=,在Rt△PED中,根据勾股定理得出∠PED=90°,b2+[2(b﹣a)]2=(2b﹣a)2,从而得出b=3a,由∠DEC=90°得出a2+b2=202,从而得出a2+(3a)2=400,进一步得出结果.
【解答】(1)证明:∵DE⊥BC,
∴∠DEC=90°,
∴∠D+∠DCE=90°,
∵∠ABC=90°,
∴∠ABC=∠DEC,
∵线段CA绕点C顺时针旋转90°得到线段CD,
∴∠ACD=90°,AC=CD,
∴∠DCE+∠ACB=90°,
∴∠ACB=∠D,
∴△ABC≌△CED(AAS);
(2)PC=PD,理由如下:
∵CF是∠ACD的平分线,
∴∠ACF=∠DCF,
由(1)知,
AC=CD,△ABC≌△CED,
∴∠A=∠DCE,
∵CF=CF,
∴△ACF≌△DCF(SAS),
∴∠A=∠PDC,
∴∠PDC=∠DCE,
∴PC=PD;
(3)①∵△BFP沿AF折叠,点P落在点E,
∴PF=EF,∠P=∠PEF,
∵DE⊥BC,
∴∠PED=90°,
∴∠PEF+∠DEF=90°,∠P+∠PDE=90°,
∴∠PEF+∠PDE=90°,
∴∠PDE=∠DEF,
∴EF=DF,
∴PF=DF,
∴点F是PD的中点;
②解:设CE=a,BC=DE=b,
∴BE=BC﹣CE=b﹣a,
由①知,
点F是PD的中点,
∴PF=PD,
∵∠ABC=∠PED=90°,
∴BF∥DE,
∴△PBF∽△PED,
∴,
∴PE=2BE=2(b﹣a),BF=DE=b,
∴S△CEF==,
∵∠PED=90°,DE=b,PE=2(b﹣a),PD=PC=PE+CE=2(b﹣a)+a=2b﹣a,
∴b2+[2(b﹣a)]2=(2b﹣a)2,
化简得,
3a2﹣4ab+b2=0,
∴b=a或b=3a,
∵0°<α<45°,
∴a=b舍去,
∴b=3a,
∴S△CEF=ab=,
∵∠DEC=90°,
∴a2+b2=202,
∴a2+(3a)2=400,
∴a2=40,
∴S△CEF=,
∴△CEF的面积是30.
【点评】本题考查了等腰三角形的判定和性质,相似三角形的判定和性质,全等三角形的判定和性质,勾股定理等知识,解决问题的关键是熟练掌握有关基础知识.
24.(2024 牡丹江)数学老师在课堂上给出了一个问题,让同学们探究.在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.
(1)当点D在线段BC上时,如图①,求证:BD+EF=AB;
分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论:
推理证明:写出图①的证明过程:
探究问题:
(2)当点D在线段BC的延长线上时,如图②:当点D在线段CB的延长线上时,如图③,请判断并直接写出线段BD,EF,AB之间的数量关系;
拓展思考:
(3)在(1)(2)的条件下,若AC=6,CD=2BD,则EF= 10或18 .
【分析】(1)在AB边上截取AM=EF,连接DM,根据题意证明出△DAM≌△AEF(SAS),得到AF=DM,然后证明出△BMD是等边三角形,得到BD=BM=DM,进而求解即可;
(2)图②:在BD上取点H,使BH=AB,连接AH并延长到点G使AG=AF,连接DG,首先证明出△ABH是等边三角形,得到∠BAH=60°,然后求出∠BAH=∠DAE,然后证明出△FAE≌△GAD(SAS),得到EF=DG,∠AFE=∠G,然后证明出△DHG是等边三角形,得到DH=DG=EF,进而求解即可;
图③:在EF上取点H使AH=AF,同理证明出△EAH≌△ADB(AAS),得到BD=AH,AB=EH,进而求解即可;
(3)根据勾股定理和含30°角直角三角形的性质求出BC=6,AB=12,然后结合CD=2BD,分别(1)(2)的条件下求出BD的长度,进而求解即可.
【解答】(1)证明:在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.在AB边上截取AM=EF,连接DM.如图1,
∴∠B=90°﹣∠BAC=90°﹣30°=60°.
∵EF∥BC,
∴∠EFB=∠B=60°.
又∵∠EAD=60°,
∴∠EFB=∠EAD.
又∵∠BAD=∠EAD﹣∠EAF,∠AEF=∠EFB﹣∠EAF,
∴∠BAD=∠AEF.
又∵AD=AE,AM=EF,
∴△DAM≌△AEF(SAS).
∴AF=DM.
∴∠AMD=∠EFA=180°﹣∠EFB=180°﹣60°=120°.
∴∠BMD=180°﹣∠AMD=180°﹣120°=60°.
∵∠B=60°,
∴∠BMD=∠B=∠BDM.
∴△BMD是等边三角形.
∴BD=BM=DM,
∵AB=AM+BM,
∴AB=EF+BD;
(2)解:图②:AB=BD﹣EF,证明如下:
如图2.1所示,在BD上取点H,使BH=AB,连接AH并延长到点G使AG=AF,连接DG,
∵∠ABC=60°,
∴△ABH是等边三角形,
∴∠BAH=60°,
∵线段AD绕点A顺时针旋转60°得到线段AE,
∴∠DAE=60°,AE=AD,
∴∠BAH=∠DAE,
∴∠BAH﹣∠EAH=∠DAE﹣∠EAH,即∠BAE=∠HAD,
又∵AG=AF,
∴△FAE≌△GAD(SAS),
∴EF=DG,∠AFE=∠G,
∵BD∥EF,
∴∠ABC=∠F=∠G=60°,
∵∠DHG=∠AHB=60°,
∴△DHG是等边三角形,
∴DH=DG=EF,
∴AB=BH=BD﹣DH=BD﹣EF;
图③:AB=EF﹣BD,证明如下:
如图2.2所示,在EF上取点H使AH=AF,
∵EF∥BC,
∴∠F=∠ABC=60°,
∵AH=AF,
∴△AHF是等边三角形,
∴∠AHF=∠HAF=60°,
∴∠AHE=120°,
∵将线段AD绕点A顺时针旋转60°得到线段AE,
∴AD=AE,∠DAE=60°,
∴∠DAB+∠EAH=180°﹣∠EAD﹣∠HAF=60°,
∵∠D+∠DAB=∠ABC=60°,
∴∠D=∠EAH,
∵∠DBA=180°﹣∠ABC=120°=∠EHA,
又∵AD=AE,
∴△EAH≌△ADB(AAS),
∴BD=AH,AB=EH,
∵AH=FH,
∴BD=HF,
∴AB=EH=EF﹣FH=EF﹣BD;
(3)解:如图3.1所示,
∵∠BAC=30°,∠C=90°,
∴AB=2BC,AB2=BC2+AC2,
∴,
∴BC=6,
∴AB=2BC=12,
∵CD=2BD,BC=BD+CD,
∴,
由(1)可知,BD+EF=AB,
∴EF=AB﹣BD=12﹣2=10;
如图3.2所示,当点D在线段BC的延长线上时,
∵CD<BD,与CD=2BD矛盾,
∴不符合题意;
如图3.3所示,当点D在线段CB的延长线上时,
∵CD=2BD=BD+BC,BC=6,
∴BD=BC=6,
由(2)可知,AB=EF﹣BD,
∵AB=2BC=12,
∴EF=AB+BD=12+6=18.
综上所述,EF=10或18,
故答案为:10或18.
【点评】此题考查了全等三角形的性质和判定,勾股定理,等边三角形的性质和判定,含30°角直角三角形的性质,解题的关键是掌握以上知识点.
25.(2024 赤峰)数学课上,老师给出以下条件,请同学们经过小组讨论,提出探究问题.如图1,在△ABC中,AB=AC,点D是AC上的一个动点,过点D作DE⊥BC于点E,延长ED交BA延长线于点F.
请你解决下面各组提出的问题:
(1)求证:AD=AF;
(2)探究与的关系;
某小组探究发现,当时,;当时,.
请你继续探究:
①当时,直接写出的值;
②当时,猜想的值(用含m,n的式子表示),并证明;
(3)拓展应用:在图1中,过点F作FP⊥AC,垂足为点P,连接CF,得到图2,当点D运动到使∠ACF=∠ACB时,若,直接写出的值(用含m,n的式子表示).
【分析】(1)利用等角的余角相等即可得证;
(2)①过点A作AG∥CE,利用平行线分线段成比例+等腰三角形等线段转化即可得解;②与第①问思路一样;
(3)利用等线段转化得,在作平行线,利用平行线分线段成比例求解即可.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠BED=∠CED=90°,
∴∠B+∠F=∠C+∠EDC=90°,
∴∠F=∠EDC,
∵∠ADF=∠EDC,
∴∠F=∠ADF,
∴AD=AF.
(2)解:①如图,过点A作AG∥CE,则AG⊥DF,
∴△AGD∽△CED,
∴==,
∵AF=AD,
∴GF=GD,
∴=2 =.
②如图,过点A作AG∥CE,则AG⊥DF,
∴△AGD∽△CED,
∴==,
∵AF=AD,
∴GF=GD,
∴=2 =.
(3)解:设∠ABC=∠ACB=∠ACF=α,
在Rt△FAP中和Rt△FCE中,∠FAP=∠FCE=2α,
∴tan∠FAP=tan∠FCE,
∴=,
∵AD=AF,
∴.
则我们求出的值即可.
方法一:如图,过点F作FM∥BC交CA的延长线于点M,
∵∠ACB=∠ACF=∠M,
∴CF=MF,
同理AM=AF=AD,
∴.
∴.
方法二:如图,过点E作EN∥AC交FC延长线于点N,
同方法一CE=CN,
∴,
由(2)②得,
∴=,
∴.
方法三:如图,过D作DE'⊥CF于点E',
根据角平分线性质可得DE=DE',
△CED和△CDF可以看作等高三角形,同时也是等高三角形,
∴===,
∴.
【点评】本题主要考查了相似三角形的判定和性质、平行线分线段成比例、等腰三角形的判定和性质等知识,熟练掌握相关知识和添加合适的辅助线是解题关键.
26.(2024 绥化)综合与实践
问题情境
在一次综合与实践课上,老师让同学们以两个全等的等腰直角三角形纸片为操作对象.纸片△ABC和△DEF满足∠ACB=∠EDF=90°,AC=BC=DF=DE=2cm.
下面是创新小组的探究过程.
操作发现
(1)如图1,取AB的中点O,将两张纸片放置在同一平面内,使点O与点F重合.当旋转△DEF纸片交AC边于点H、交BC边于点G时,设AH=x(1<x<2),BG=y,请你探究出y与x的函数关系式,并写出解答过程.
问题解决
(2)如图2,在(1)的条件下连接GH,发现△CGH的周长是一个定值.请你写出这个定值,并说明理由.
拓展延伸
(3)如图3,当点F在AB边上运动(不包括端点A、B),且始终保持∠AFE=60°.请你直接写出△DEF纸片的斜边EF与△ABC纸片的直角边所夹锐角的正切值 2+或2﹣ (结果保留根号).
【分析】(1)证明△AFH∽△BGF,可得AH BG=AF BF,求出,可得,故,=2,从而y与x的函数关系式为;
(2)求出CH=2﹣x,CG=2﹣y,可得===,将xy=2代入得=,而1<x<2,1<y<2,知x+y>2,故GH=x+y﹣2,可得△CHG 的周长=CH+CG+GH=2﹣x+2﹣y+x+y﹣2=2;
(3)分两种情况:①过点F作 FN⊥AC于点N,作FH的垂直平分线交FN于点M,连接MH,求出∠AHF=75°,可得∠NMH=30°,设NH=k,则MH=MF=2k,从而FN=MF+MN=(2+)k,;②过点F作FN⊥BC于点N,作FG的垂直平分线交BG于点M,连接FM,同理可得GN=GM+MN=(2+)k,.
【解答】解:(1)如图:
∵∠ACB=∠EDF=90°,且 AC=BC=DF=DE=2cm,
∴∠A=∠B=∠DFE=45°,
∴∠AFH+∠BFG=∠BFG+∠FGB=135°,
∴∠AFH=∠FGB,
∴△AFH∽△BGF,
∴,
∴AH BG=AF BF,
在 Rt△ACB 中,AC=BC=2,
∴,
∵O是AB的中点,点O与点F重合,
∴,
∴,
∴,
∴y与x的函数关系式为;
(2)△CGH的周长定值为2,理由如下:
∵AC=BC=2,AH=x,BG=y,
∴CH=2﹣x,CG=2﹣y,
在Rt△HCG 中,
∴===,
将(1)中xy=2代入得:=,
∵1<x<2,y=,
∴1<y<2,
∴x+y>2,
∴GH=x+y﹣2,
∴△CHG 的周长=CH+CG+GH=2﹣x+2﹣y+x+y﹣2=2;
(3)①过点F作 FN⊥AC于点N,作FH的垂直平分线交FN于点M,连接MH,如图:
∵∠AFE=60°,∠A=45°,
∴∠AHF=75°,
∴FM=MH,
∵∠FNH=90°,
∴∠NFH=15°,
∵FM=MH,
∴∠NFH=∠MHF=15°,
∴∠NMH=30°,
在 Rt△MNH中,设NH=k,
∴MH=MF=2k,
∴MN==k,
∴FN=MF+MN=(2+)k,
在Rt△FNH中,
;
②过点F作FN⊥BC于点N,作FG的垂直平分线交BG于点M,连接FM,
∵∠AFE=60°,∠B=45°,
∴∠FGB=∠AFE﹣∠B=15°,
∵GM=MF,
∴∠FGB=∠GFM=15°,
∴∠FMB=30°,
在 Rt△FNM中,设FN=k,
∴GM=MF=2k,
由勾股定理得MN==k,
∴GN=GM+MN=(2+)k,
在 Rt△FNG 中,
,
综上所述,tan 或 ,
故答案为:2+或2﹣.
【点评】本题考查几何变换综合应用,涉及相似三角形判定与性质,等腰直角三角形性质及应用,锐角三角函数,勾股定理及应用等知识,解题的关键是作辅助线,构造直角三角形解决问题.
27.(2024 贵州)综合与探究:如图,∠AOB=90°,点P在∠AOB的平分线上,PA⊥OA于点A.
(1)【操作判断】
如图①,过点P作PC⊥OB于点C,根据题意在图①中画出PC,图中∠APC的度数为 90 度;
(2)【问题探究】
如图②,点M在线段AO上,连接PM,过点P作PN⊥PM交射线OB于点N,求证:OM+ON=2PA;
(3)【拓展延伸】
点M在射线AO上,连接PM,过点P作PN⊥PM交射线OB于点N,射线NM与射线PO相交于点F,若ON=3OM,求的值.
【分析】(1)依题意画出图形,证四边形OAPC是矩形即可求解;
(2)过P作PC⊥OB于点C,证矩形OAPC是正方形,得出OA=AP=PC=OC,再证△APM≌△CPN(ASA),得出AM=CN,然后利用线段的和差关系以及等量代换即可证明;
(3)分M在线段AO上和AO的延长线上讨论,利用相似三角形的判定和性质求解即可.
【解答】(1)解:如图,PC即为所求.
∵∠AOB=90°,PA⊥OA,PC⊥OB,
∴四边形OAPC是矩形,
∴∠APC=90°,
故答案为:90.
(2)证明:如图,过P作PC⊥OB于点C.
由(!)知四边形OAPC是矩形,
∵点P在∠AOB的平分线上,PA⊥OA,PC⊥OB,
∴PA=PC,
∴矩形OAPC是正方形,
∴OA=AP=PC=OC,∠APC=90°,
∵PN⊥PM,
∴∠APM=∠CPN=90°﹣∠MPC,
又∠MAP=∠CNP=90°,AP=CP,
∴△APM≌△CPN(ASA),
∴AM=CN,
∴OM+ON=OM+AC+CN=OM+AM+OC=OA+OC=2AP,
∴OM+ON=2PA.
(3)①当M在线段AO上时,如图,延长NM、PA交于点G.
由(2)知OM+ON=2AP,
设OM=x,则ON=3x,OA=AP=2x.
∴AM=AO﹣OM=x=OM,
∵∠MON=∠MAG=90°,∠OMN=∠AMG,
∴△MON≌△MAG(ASA),
∴AG=ON=3x,
∵AP∥OB,
∴△ONF∽△PGF,
∴=,
∴,
∴;
②当M在AO的延长线上时,如图,过P作PC⊥OB于C,并延长交MN于G.
由(2)知,四边形OAPC是正方形,
∴OA=AP=PC=OC,∠APC=90°,PC∥AO,
∵PN⊥PM,
∠APM=∠CPN=90°﹣∠MPC,
又∵∠A=∠PCN=90°,AP=CP,
∴△APM≌△CPN,
∴AM=CN,
∴ON﹣OM=OC+CN﹣OM=AO+AM﹣OM=2AO,
∵ON=3OM=x,
∴AO=x,CN=AM=2x,
∵PC∥AO,
∴△CGN∽△OMN,
∴,即,
∴CG=,
∵PC∥AO,
∴△OMF∽△PGF,
∴==,
∴=,
∴=;
综上,的值为或.
【点评】本题考查了四边形综合,同时考查了矩形的判定和性质、正方形的判定和性质、角平分线的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,明确题意,添加合适的辅助线,构造全等三角形、相似三角形,合理分类讨论是解题的关键.
28.(2024 重庆)在△ABC中,AB=AC,点D是BC边上一点(点D不与端点重合).点D关于直线AB的对称点为点E,连接AD,DE.在直线AD上取一点F,使∠EFD=∠BAC,直线EF与直线AC交于点G.
(1)如图1,若∠BAC=60°,BD<CD,∠BAD=α,求∠AGE的度数(用含α的代数式表示);
(2)如图1,若∠BAC=60°,BD<CD,用等式表示线段CG与DE之间的数量关系,并证明;
(3)如图2,若∠BAC=90°,点D从点B移动到点C的过程中,连接AE,当△AEG为等腰三角形时,请直接写出此时的值.
【分析】(1)由三角形内角和定理及外角定理结合∠EFD=∠BAC即可求解;
(2)在CG上截取CM=BD,连接BM,BE,BM交AD于点H,连接BE,AE,再证明四边形EBMG是平行四边形,可得CG=2BD,记AB 与DE的交点为点N,则由轴对称可知:DE⊥AB,NE=ND,再解Rt△BND即可;
(3)连接BE,记AB与DE的交点为点N,由轴对称知∠EAB=∠DAB,DE⊥AB,NE=ND,∠EBA=∠DBA=45°,当点G在边AC上时,由于∠EAG>90°,当△AEG为等腰三角形时,只能是AE=AG,∠BAD=α,∠AGE=α,解得α=30°,然后AF=x,解直角三角形,表示出AG=2x,CG=,即可求解;当点G在CA延长线上时,只能是GE=GA,设∠BAD=∠BAE=β,在Rt△AFE 中,90°﹣β+180°﹣2β=90°,解得β=60°,设GF=x,解直角三角形求出CG=,即可求解.
【解答】解:(1)如图1.1,
∵∠EFD=∠BAC,∠BAC=60°,
∴∠EFD=60°,
∵∠EFD=∠1+∠BAD=∠1+α,
∴∠1=60°﹣α,
∵∠AGE+∠1+∠BAC=180°,
∴∠AGE=180°﹣60°﹣∠1=120°﹣∠1,
∴∠AGE=120°﹣(60°﹣α)=60°+α;
(2)CG=;理由如下:
在CG上截取CM=BD,连接BM,BE,AE,BM交AD于点H,
∵AB=AC,∠BAC=60°,
∴△BCA为等边三角形,
∴∠ABC=∠C=60°,BC=AB,
∴△ABD≌△BCM(SAS),
∴∠3=∠4,
∵∠AHM=∠3+∠5,
∴∠AHM=∠4+∠5=60°,
∵∠EFD=∠BAC=60°,
∴∠AHM=∠EFD,
∴EG∥BM,
∵点D关于直线AB的对称点为点E,
∴AE=AD,BE=BD,∠ABE=∠ABC=60°,
∴∠EBC=120°,
∴∠EBC+∠C=180°,
∴EB∥AC,
∴四边形EBMG是平行四边形,
∴BE=GM,
∴BE=GM=BD=CM,
∴CG=2BD,记AB与DE的交点为点N,则由轴对称可知:DE⊥AB,NE=ND,
在Rt△DNB中,DN=BD sin∠ABC=BD,
∴DE=2DN=BD,
∴==,
∴CG=;
(3)连接BE,记AB与DE的交点为点N,如图2,
∵AB=AC,∠EFD=∠BAC=90°,
∴∠ABC=45°,
由轴对称知∠EAB=∠DAB=α,∠EBA=∠DBA=45°,DE⊥AB,NE=ND,
当点G在边AC上时,由于∠EAG>90°,
∴当△AEG为等腰三角形时,只能是AE=AG,
∵∠BAC=∠AFG=90°,
∴∠AGE=α,
∴∠AEG=α,
∵∠EAD=2α,
∵AE=AG,EG⊥AD,
∴∠FAG=∠EAD=2α,
在△AEG中,α+2α+2α+α=180°,
解得α=30°,
∴∠EAD=60°,
∵AE=AD,
∴△AED为等边三角形,
∴AE=ED,
设AF=x,
∵∠EAD=60°,
∴AG=AE=ED==2x,
∴DN=x,
在Rt△DAN中,AN==DN=,
∵DE⊥AB,∠ABC=45°,
∴BN==DN=x,
∴AC=AB=x+x,
∴CG=AC﹣AG=x+x﹣2x=,
∴=;
当点G在CA延长线上时,只能是GE=GA,如图3:
设∠BAD=∠BAE=β,
∴∠DAC=∠GAF=90﹣β,
∴∠EAF=180°﹣2β,
∴∠GAE=∠EAF﹣∠GAF
2024年中考数学解答题分类汇编——图形的变化
一.解答题(共30小题)
1.(2024 凉山州)为建设全城旅游西昌,加快旅游产业发展.2022年9月29日位于西昌主城区东部的历史风貌核心区唐园正式开园,坐落于唐园内的怀远塔乃唐园至高点,为七层密檐式八角砖混结构阁楼式塔楼,建筑面积为1845.4平方米,塔顶金碧辉煌,为“火珠垂莲”窣(sū)堵坡造型.某校为了让学生进一步了解怀远塔,组织九年级(2)班学生利用综合实践课测量怀远塔的高度.小江同学站在如图所示的怀远塔前的平地上A点处,测得塔顶C的仰角为30°,眼睛B距离地面1.8m,向塔前行67m,到达点D处,测得塔顶C的仰角为60°,求塔高CF. (参考数据:≈1.414,≈1.732,结果精确到0.01m)
2.(2024 烟台)根据收集的素材,探索完成任务.
探究太阳能热水器的安装
素材一 太阳能热水器是利用绿色能源造福人类的一项发明.某品牌热水器主要部件太阳能板需要安装在每天都可以有太阳光照射到的地方,才能保证使用效果,否则不予安装.
素材二 某市位于北半球,太阳光线与水平线的夹角为α,冬至日时,14°≤α≤29°;夏至日时,43°≤α≤76°. sin14°≈0.24,cos14°≈0.97,tan14°≈0.25 sin29°≈0.48,cos29°≈0.87,tan29°≈0.55 sin43°≈0.68,cos43°≈0.73,tan43°=0.94 sin76°≈0.97,cos76°≈0.24,tan76°≈4.01
素材三 如图,该市甲楼位于乙楼正南方向,两楼东西两侧都无法获得太阳光照射.现准备在乙楼南面墙上安装该品牌太阳能板.已知两楼间距为54米,甲楼AB共11层,乙楼CD共15层,一层从地面起,每层楼高皆为3.3米.AE为某时刻的太阳光线.
问题解决
任务一 确定使用数据 要判断乙楼哪些楼层不能安装该品牌太阳能板,应选择 日(填冬至或夏至)时,α为 (填14°,29°,43°,76°中的一个)进行计算.
任务二 探究安装范围 利用任务一中选择的数据进行计算,确定乙楼中哪些楼层不能安装该品牌太阳能热水器.
3.(2024 连云港)图1是古代数学家杨辉在《详解九章算法》中对“邑的计算”的相关研究.数学兴趣小组也类比进行了如下探究:如图2,正八边形游乐城A1A2A3A4A5A6A7A8的边长为km,南门O设立在A6A7边的正中央,游乐城南侧有一条东西走向的道路BM,A6A7在BM上(门宽及门与道路间距离忽略不计),东侧有一条南北走向的道路BC,C处有一座雕塑.在A1处测得雕塑在北偏东45°方向上,在A2处测得雕塑在北偏东59°方向上.
(1)∠CA1A2= °,∠CA2A1= °;
(2)求点A1到道路BC的距离;
(3)若该小组成员小李出南门O后沿道路MB向东行走,求她离B处不超过多少千米,才能确保观察雕塑不会受到游乐城的影响?
(结果精确到0.1km,参考数据,sin76°≈0.97,tan76°≈4.00,sin59°≈0.86,tan59°≈1.66)
4.(2024 重庆)在Rt△ABC中,∠ACB=90°,AC=BC,过点B作BD∥AC.
(1)如图1,若点D在点B的左侧,连接CD,过点A作AE⊥CD交BC于点E.若点E是BC的中点,求证:AC=2BD;
(2)如图2,若点D在点B的右侧,连接AD,点F是AD的中点,连接BF并延长交AC于点G,连接CF.过点F作FM⊥BG交AB于点M,CN平分∠ACB交BG于点N,求证:AM=CN+BD;
(3)若点D在点B的右侧,连接AD,点F是AD的中点,且AF=AC.点P是直线AC上一动点,连接FP,将FP绕点F逆时针旋转60°得到FQ,连接BQ,点R是直线AD上一动点,连接BR,QR.在点P的运动过程中,当BQ取得最小值时,在平面内将△BQR沿直线QR翻折得到△TQR,连接FT.在点R的运动过程中,直接写出的最大值.
5.(2024 自贡)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3m,据此可得旗杆高度为 m;
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5m,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16m.求旗杆高度;
(3)小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图6,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8m,DG=1.5m.将观测点D后移24m到D′处.采用同样方法,测得C′G′=1.2m,D′G′=2m.求雕塑高度(结果精确到1m).
6.(2024 烟台)在等腰直角△ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD.将线段AD绕点D按顺时针方向旋转90°得线段ED,连接BE.
【尝试发现】
(1)如图1,当点D在线段BC上时,线段BE与CD的数量关系为 ;
【类比探究】
(2)当点D在线段BC的延长线上时,先在图2中补全图形,再探究线段BE与CD的数量关系并证明;
【联系拓广】
(3)若AC=BC=1,CD=2,请直接写出sin∠ECD的值.
7.(2024 苏州)图①是某种可调节支撑架,BC为水平固定杆,竖直固定杆AB⊥BC,活动杆AD可绕点A旋转,CD为液压可伸缩支撑杆,已知AB=10cm,BC=20cm,AD=50cm.
(1)如图②,当活动杆AD处于水平状态时,求可伸缩支撑杆CD的长度(结果保留根号);
(2)如图③,当活动杆AD绕点A由水平状态按逆时针方向旋转角度α,且tanα=(α为锐角),求此时可伸缩支撑杆CD的长度(结果保留根号).
8.(2024 甘肃)习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富,风力发电发展迅速.某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒AH垂直于地面,测角仪CD,EF在AH两侧,CD=EF=1.6m,点C与点E相距182m(点C,H,E在同一条直线上),在D处测得筒尖顶点A的仰角为45°,在F处测得筒尖顶点A的仰角为53°.求风电塔简AH的高度.(参考数据:sin53°≈,cos53°≈,tan53°≈.)
9.(2024 江西)图1是世界第一“大碗”——景德镇昌南里文化艺术中心主体建筑,其造型灵感来自于宋代湖田窑影青斗笠碗,寓意“万瓷之母”.如图2,“大碗”的主视图由“大碗”主体ABCD和矩形碗底BEFC组成,已知AD∥EF,AM,DN是太阳光线,AM⊥MN,DN⊥MN,点M,E,F,N在同一条直线上.经测量ME=FN=20.0m,EF=40.0m,BE=2.4m,∠ABE=152°.(结果精确到0.1m)
(1)求“大碗”的口径AD的长;
(2)求“大碗”的高度AM的长.
(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
10.(2024 广安)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机,如图(1),某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图(2)为测量示意图(点A,B,C,D均在同一平面内,AB⊥BC).已知斜坡CD长为20米,斜坡CD的坡角为60°,在斜坡顶部D处测得风力发电机塔杆顶端A点的仰角为20°,坡底与塔杆底的距离BC=30米,求该风力发电机塔杆AB的高度.(结果精确到个位;参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,≈1.73)
11.(2024 重庆)如图,甲、乙两艘货轮同时从A港出发,分别向B,D两港运送物资,最后到达A港正东方向的C港装运新的物资.甲货轮沿A港的东南方向航行40海里后到达B港,再沿北偏东60°方向航行一定距离到达C港.乙货轮沿A港的北偏东60°方向航行一定距离到达D港,再沿南偏东30°方向航行一定距离到达C港.
(参考数据:≈1.41,≈1.73,≈2.45)
(1)求A,C两港之间的距离(结果保留小数点后一位);
(2)若甲、乙两艘货轮的速度相同(停靠B,D两港的时间相同),哪艘货轮先到达C港?请通过计算说明.
12.(2024 宜宾)宜宾地标广场位于三江汇合口(如图1,左侧是岷江,右侧是金沙江,正面是长江).某同学在数学实践中测量长江口的宽度,他在长江口的两岸选择两个标点C、D,在地标广场上选择两个观测点A、B(点A、B、C、D在同一水平面,且AB∥CD).如图2所示,在点A处测得点C在北偏西18.17°方向上,测得点D在北偏东21.34°方向上;在B处测得点C在北偏西21.34°方向上,测得点D在北偏东18.17°方向上,测得AB=100米.求长江口的宽度CD的值(结果精确到1米).(参考数据:sin18.17°≈0.31,cos18.17°≈0.95,tan18.17°≈0.33,sin21.34°≈0.36,cos21.34°≈0.93,tan21.34°≈0.39)
13.(2024 广东)【知识技能】
(1)如图1,在△ABC中,DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A′DC′.当点E的对应点E′与点A重合时,求证:AB=BC.
【数学理解】
(2)如图2,在△ABC中(AB<BC),DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A′DC′,连接A′B,C′C,作△A′BD的中线DF.求证:2DF CD=BD CC′.
【拓展探索】
(3)如图3,在△ABC中,tanB=,点D在AB上,AD=.过点D作DE⊥BC,垂足为E,BE=3,CE=.在四边形ADEC内是否存在点G,使得∠AGD+∠CGE=180°?若存在,请给出证明;若不存在,请说明理由.
14.(2024 武汉)如图是由小正方形组成的3×4网格,每个小正方形的顶点叫做格点.△ABC三个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.
(1)在图(1)中,画射线AD交BC于点D,使AD平分△ABC的面积;
(2)在(1)的基础上,在射线AD上画点E,使∠ECB=∠ACB;
(3)在图(2)中,先画点F,使点A绕点F顺时针旋转90°到点C,再画射线AF交BC于点G;
(4)在(3)的基础上,将线段AB绕点G旋转180°,画对应线段MN(点A与点M对应,点B与点N对应).
15.(2024 临夏州)如图1,在矩形ABCD中,点E为AD边上不与端点重合的一动点,点F是对角线BD上一点,连接BE,AF交于点O,且∠ABE=∠DAF.
【模型建立】
(1)求证:AF⊥BE;
【模型应用】
(2)若AB=2,AD=3,DF=BF,求DE的长;
【模型迁移】
(3)如图2,若矩形ABCD是正方形,DF=BF,求的值.
16.(2024 滨州)(1)如图1,△ABC中,点D,E,F分别在三边BC,CA,AB上,且满足DF∥AC,DE∥AB.
①求证:四边形AFDE为平行四边形;
②若,求证:四边形AFDE为菱形;
(2)把一块三角形余料MNH(如图2所示)加工成菱形零件,使它的一个顶点与△MNH的顶点M重合,另外三个顶点分别在三边MN,NH,HM上,请在图2上作出这个菱形.(用尺规作图,保留作图痕迹,不写作法)
17.(2024 齐齐哈尔)综合与实践
如图1,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”.如图2,在△ABC中,∠A=90°,将线段BC绕点B顺时针旋转90°得到线段BD,作DE⊥AB交AB的延长线于点E.
(1)【观察感知】如图2,通过观察,线段AB与DE的数量关系是 ;
(2)【问题解决】如图3,连接CD并延长交AB的延长线于点F,若AB=2,AC=6,求△BDF的面积;
(3)【类比迁移】在(2)的条件下,连接CE交BD于点N,则= ;
(4)【拓展延伸】在(2)的条件下,在直线AB上找点P,使tan∠BCP=,请直接写出线段AP的长度.
18.(2024 湖北)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
19.(2024 广西)如图1,△ABC中,∠B=90°,AB=6.AC的垂直平分线分别交AC,AB于点M,O,CO平分∠ACB.
(1)求证:△ABC∽△CBO;
(2)如图2,将△AOC绕点O逆时针旋转得到△A'OC',旋转角为α(0°<α<360°).连接A′M,C′M.
①求△A'MC'面积的最大值及此时旋转角α的度数,并说明理由;
②当△A'MC'是直角三角形时,请直接写出旋转角α的度数.
20.(2024 安徽)如图1, ABCD的对角线AC与BD交于点O,点M,N分别在边AD,BC上,且AM=CN.点E,F分别是BD与AN,CM的交点.
(1)求证:OE=OF;
(2)连接BM交AC于点H,连接HE,HF.
(ⅰ)如图2,若HE∥AB,求证:HF∥AD;
(ⅱ)如图3,若 ABCD为菱形,且MD=2AM,∠EHF=60°,求的值.
21.(2024 江西)综合与实践
如图,在Rt△ABC中,点D是斜边AB上的动点(点D与点A不重合),连接CD,以CD为直角边在CD的右侧构造Rt△CDE,∠DCE=90°,连接BE,=m.
特例感知
(1)如图1,当m=1时,BE与AD之间的位置关系是 ,数量关系是 .
类比迁移
(2)如图2,当m≠1时,猜想BE与AD之间的位置关系和数量关系,并证明猜想.
拓展应用
(3)在(1)的条件下,点F与点C关于DE对称,连接DF,EF,BF,如图3.已知AC=6,设AD=x,四边形CDFE的面积为y.
①求y与x的函数表达式,并求出y的最小值;
②当BF=2时,请直接写出AD的长度.
22.(2024 凉山州)如图,在菱形ABCD中,∠ABC=60°,AB=2,E是BC边上一个动点,连接AE,AE的垂直平分线MN交AE于点M,交BD于点N,连接EN、CN.
(1)求证:EN=CN;
(2)求2EN+BN的最小值.
23.(2024 辽宁)如图,在△ABC中,∠ABC=90°,∠ACB=α(0°<α<45°).将线段CA绕点C顺时针旋转90°得到线段CD,过点D作DE⊥BC,垂足为E.
(1)如图1,求证:△ABC≌△CED.
(2)如图2,∠ACD的平分线与AB的延长线相交于点F,连接DF,DF的延长线与CB的延长线相交于点P,猜想PC与PD的数量关系,并加以证明.
(3)如图3,在(2)的条件下,将△BFP沿AF折叠,在α变化过程中,当点P落在点E的位置时,连接EF.
①求证:点F是PD的中点;
②若CD=20,求△CEF的面积.
24.(2024 牡丹江)数学老师在课堂上给出了一个问题,让同学们探究.在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.
(1)当点D在线段BC上时,如图①,求证:BD+EF=AB;
分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论:
推理证明:写出图①的证明过程:
探究问题:
(2)当点D在线段BC的延长线上时,如图②:当点D在线段CB的延长线上时,如图③,请判断并直接写出线段BD,EF,AB之间的数量关系;
拓展思考:
(3)在(1)(2)的条件下,若AC=6,CD=2BD,则EF= .
25.(2024 赤峰)数学课上,老师给出以下条件,请同学们经过小组讨论,提出探究问题.如图1,在△ABC中,AB=AC,点D是AC上的一个动点,过点D作DE⊥BC于点E,延长ED交BA延长线于点F.
请你解决下面各组提出的问题:
(1)求证:AD=AF;
(2)探究与的关系;
某小组探究发现,当时,;当时,.
请你继续探究:
①当时,直接写出的值;
②当时,猜想的值(用含m,n的式子表示),并证明;
(3)拓展应用:在图1中,过点F作FP⊥AC,垂足为点P,连接CF,得到图2,当点D运动到使∠ACF=∠ACB时,若,直接写出的值(用含m,n的式子表示).
26.(2024 绥化)综合与实践
问题情境
在一次综合与实践课上,老师让同学们以两个全等的等腰直角三角形纸片为操作对象.纸片△ABC和△DEF满足∠ACB=∠EDF=90°,AC=BC=DF=DE=2cm.
下面是创新小组的探究过程.
操作发现
(1)如图1,取AB的中点O,将两张纸片放置在同一平面内,使点O与点F重合.当旋转△DEF纸片交AC边于点H、交BC边于点G时,设AH=x(1<x<2),BG=y,请你探究出y与x的函数关系式,并写出解答过程.
问题解决
(2)如图2,在(1)的条件下连接GH,发现△CGH的周长是一个定值.请你写出这个定值,并说明理由.
拓展延伸
(3)如图3,当点F在AB边上运动(不包括端点A、B),且始终保持∠AFE=60°.请你直接写出△DEF纸片的斜边EF与△ABC纸片的直角边所夹锐角的正切值 (结果保留根号).
27.(2024 贵州)综合与探究:如图,∠AOB=90°,点P在∠AOB的平分线上,PA⊥OA于点A.
(1)【操作判断】
如图①,过点P作PC⊥OB于点C,根据题意在图①中画出PC,图中∠APC的度数为 度;
(2)【问题探究】
如图②,点M在线段AO上,连接PM,过点P作PN⊥PM交射线OB于点N,求证:OM+ON=2PA;
(3)【拓展延伸】
点M在射线AO上,连接PM,过点P作PN⊥PM交射线OB于点N,射线NM与射线PO相交于点F,若ON=3OM,求的值.
28.(2024 重庆)在△ABC中,AB=AC,点D是BC边上一点(点D不与端点重合).点D关于直线AB的对称点为点E,连接AD,DE.在直线AD上取一点F,使∠EFD=∠BAC,直线EF与直线AC交于点G.
(1)如图1,若∠BAC=60°,BD<CD,∠BAD=α,求∠AGE的度数(用含α的代数式表示);
(2)如图1,若∠BAC=60°,BD<CD,用等式表示线段CG与DE之间的数量关系,并证明;
(3)如图2,若∠BAC=90°,点D从点B移动到点C的过程中,连接AE,当△AEG为等腰三角形时,请直接写出此时的值.
29.(2024 成都)数学活动课上,同学们将两个全等的三角形纸片完全重合放置,固定一个顶点,然后将其中一个纸片绕这个顶点旋转,来探究图形旋转的性质.已知三角形纸片ABC和ADE中,AB=AD=3,BC=DE=4,∠ABC=∠ADE=90°.
【初步感知】
(1)如图1,连接BD,CE,在纸片ADE绕点A旋转过程中,试探究的值.
【深入探究】
(2)如图2,在纸片ADE绕点A旋转过程中,当点D恰好落在△ABC的中线BM的延长线上时,延长ED交AC于点F,求CF的长.
【拓展延伸】
(3)在纸片ADE绕点A旋转过程中,试探究C,D,E三点能否构成直角三角形.若能,直接写出所有直角三角形CDE的面积;若不能,请说明理由.
30.(2024 南充)如图,正方形ABCD边长为6cm,点E为对角线AC上一点,CE=2AE,点P在AB边上以1cm/s的速度由点A向点B运动,同时点Q在BC边上以2cm/s的速度由点C向点B运动,设运动时间为t秒(0<t≤3).
(1)求证:△AEP∽△CEQ.
(2)当△EPQ是直角三角形时,求t的值.
(3)连接AQ,当tan∠AQE=时,求△AEQ的面积.
图形的变化
参考答案与试题解析
一.解答题(共30小题)
1.(2024 凉山州)为建设全城旅游西昌,加快旅游产业发展.2022年9月29日位于西昌主城区东部的历史风貌核心区唐园正式开园,坐落于唐园内的怀远塔乃唐园至高点,为七层密檐式八角砖混结构阁楼式塔楼,建筑面积为1845.4平方米,塔顶金碧辉煌,为“火珠垂莲”窣(sū)堵坡造型.某校为了让学生进一步了解怀远塔,组织九年级(2)班学生利用综合实践课测量怀远塔的高度.小江同学站在如图所示的怀远塔前的平地上A点处,测得塔顶C的仰角为30°,眼睛B距离地面1.8m,向塔前行67m,到达点D处,测得塔顶C的仰角为60°,求塔高CF. (参考数据:≈1.414,≈1.732,结果精确到0.01m)
【分析】先用CG表示EG,BG,再根据BG﹣EG=67m,列方程求出CG,进一步可求出CF,从而解决问题.
【解答】解:由题意,知∠CBG=30°,∠CEG=60°,∠CGB=∠CGE=90°,GF=ED=BA=1.8m,BE=67m,
在Rt△CBG中,
BG==CG,
在Rt△CEG中,
EG==CG,
∵BG﹣EG=BE,
∴CG﹣CG=67,
解得CG≈58.02(m),
∴CF=CG+GF=58.02+1.8=59.82(m),
答:塔高CF为59.82m.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,理解题意,熟练运用三角函数关系是解题的关键.
2.(2024 烟台)根据收集的素材,探索完成任务.
探究太阳能热水器的安装
素材一 太阳能热水器是利用绿色能源造福人类的一项发明.某品牌热水器主要部件太阳能板需要安装在每天都可以有太阳光照射到的地方,才能保证使用效果,否则不予安装.
素材二 某市位于北半球,太阳光线与水平线的夹角为α,冬至日时,14°≤α≤29°;夏至日时,43°≤α≤76°. sin14°≈0.24,cos14°≈0.97,tan14°≈0.25 sin29°≈0.48,cos29°≈0.87,tan29°≈0.55 sin43°≈0.68,cos43°≈0.73,tan43°=0.94 sin76°≈0.97,cos76°≈0.24,tan76°≈4.01
素材三 如图,该市甲楼位于乙楼正南方向,两楼东西两侧都无法获得太阳光照射.现准备在乙楼南面墙上安装该品牌太阳能板.已知两楼间距为54米,甲楼AB共11层,乙楼CD共15层,一层从地面起,每层楼高皆为3.3米.AE为某时刻的太阳光线.
问题解决
任务一 确定使用数据 要判断乙楼哪些楼层不能安装该品牌太阳能板,应选择 冬至 日(填冬至或夏至)时,α为 14° (填14°,29°,43°,76°中的一个)进行计算.
任务二 探究安装范围 利用任务一中选择的数据进行计算,确定乙楼中哪些楼层不能安装该品牌太阳能热水器.
【分析】任务一:根据题意直接求解即可;
任务二:过E作EF⊥AB于F,利用正切定义求得.
【解答】解:任务一:根据题意,要判断乙楼哪些楼层不能安装该品牌太阳能板,只需α为冬至日时的最小角度,即α=14°,
故答案为:冬至,14°;
任务二:过E作EF⊥AB于F,则∠AFE=90°,EF=54米,BF=DE,
在Rt△AFE中,,
∴AF=EF tan14°≈54×0.25=13.5(米),
∵AB=11×3.3=36.3(米),
∴DE=BF=AB﹣AF=36.3﹣13.5=22.8(米),
∴22.8÷3.3≈7(层),
答:乙楼中7层(含7层)以下不能安装该品牌太阳能热水器.
想法二:题干中说品牌热水器主要部件太阳能板需要安装在每天都可以有太阳光照射到的地方,才能保证使用效果,否则不予安装,而冬至日时,14°≤α≤29°,指一天当中的变化,所以任务一选择29°,任务二结果为一、二层不能照到.
【点评】本题考查了解直角三角形的应用,理解题意是解答的关键.
3.(2024 连云港)图1是古代数学家杨辉在《详解九章算法》中对“邑的计算”的相关研究.数学兴趣小组也类比进行了如下探究:如图2,正八边形游乐城A1A2A3A4A5A6A7A8的边长为km,南门O设立在A6A7边的正中央,游乐城南侧有一条东西走向的道路BM,A6A7在BM上(门宽及门与道路间距离忽略不计),东侧有一条南北走向的道路BC,C处有一座雕塑.在A1处测得雕塑在北偏东45°方向上,在A2处测得雕塑在北偏东59°方向上.
(1)∠CA1A2= 90 °,∠CA2A1= 76 °;
(2)求点A1到道路BC的距离;
(3)若该小组成员小李出南门O后沿道路MB向东行走,求她离B处不超过多少千米,才能确保观察雕塑不会受到游乐城的影响?
(结果精确到0.1km,参考数据,sin76°≈0.97,tan76°≈4.00,sin59°≈0.86,tan59°≈1.66)
【分析】(1)求出正八边形的一个外角的度数,再根据角的和差关系进行求解即可;
(2)过点A作AD⊥BC于点D,解Rt△CA2A1,求出(km),解Rt△CA1D,求出(km);
(3)连接CA8并延长交BM于点E,延长A1A8交BE于点G,过点A8作AF⊥BC,垂足为F,解Rt△A7A8G,求出A8G,证明△CA8F∽△CEB,列出比例式进行求解即可.
【解答】解:(1)∵正八边形A1A2A3A4A5A6A7A8,
∴外角=,
∴∠CA1A2=45°+45°=90°,∠CA2A1=45°+(90°﹣59°)=76°,
故答案为:90;76;
(2)过点A1作A1D⊥BC于点D,
在Rt△CA2A1中,,∠CA2A1=76°,
∴(km),
在Rt△CA1D中,易知∠CA1D=45°
∴,
答:点A1到道路BC的距离为2.0千米.
(3)连接CA8并延长交BM于点E,延长A1A8交BE于点G,过点A8作A8F⊥BC于点F,
∵正八边形的外角均为45°,
∴在Rt△A7A8G中,,
∴,
又∵A8F=A1D=CD=2,,
∴,
∵∠CFA8=∠B,∠FCA8=∠BCE,
∴△CA8F∽△CEB,
∴,
∴,
∵,
∴EB=2.4(km).
答:小李离点B不超过2.4km,才能确保观察雕塑不会受到游乐城的影响.
【点评】本题考查了正多边形的外角,解直角三角形,相似三角形的判定和性质,掌握综合推理能力是解题的关键.
4.(2024 重庆)在Rt△ABC中,∠ACB=90°,AC=BC,过点B作BD∥AC.
(1)如图1,若点D在点B的左侧,连接CD,过点A作AE⊥CD交BC于点E.若点E是BC的中点,求证:AC=2BD;
(2)如图2,若点D在点B的右侧,连接AD,点F是AD的中点,连接BF并延长交AC于点G,连接CF.过点F作FM⊥BG交AB于点M,CN平分∠ACB交BG于点N,求证:AM=CN+BD;
(3)若点D在点B的右侧,连接AD,点F是AD的中点,且AF=AC.点P是直线AC上一动点,连接FP,将FP绕点F逆时针旋转60°得到FQ,连接BQ,点R是直线AD上一动点,连接BR,QR.在点P的运动过程中,当BQ取得最小值时,在平面内将△BQR沿直线QR翻折得到△TQR,连接FT.在点R的运动过程中,直接写出的最大值.
【分析】(1)证明△ACE≌△CBD(ASA),得到BD=CE;
(2)作出辅助线证明△HFM≌△CFN(AAS),得到HM=CN;
(3)通过手拉手模型证明点Q的运动轨迹是直线,从而根据垂线段最短确定点Q的位置.
【解答】证明:(1)∵∠ACB=90°,BD∥AC,
∴∠CBD=180°﹣∠ACB=90°,
∵AE⊥CD,
∴∠ACD+∠CAE=90°,
∵∠ACD+∠BCD=90°,
∴∠CAE=∠BCD,
又∵AC=CB,∠CBD=∠ACE=90°,
∴△ACE≌△CBD(ASA),
∴BD=CE,
∵点E是BC的中点,
∴BC=2CE=2BD,
∴AC=2BD;
证明:(2)过点G作GH⊥AB于H,连接HF,
∵BD∥AC,
∴∠FBD=∠FGA,∠D=∠FAG,
∵点F是AD的中点,
∴AF=DF,
∴△AGF≌△DBF(AAS),
∴AG=BD,BF=GF,
∵AC=BC,∠ACB=90°,
∴∠CAB=∠ACB=45°,
∵GH⊥AH,
∴△AHG是等腰直角三角形,
∴,
∵∠BHG=∠BCG=90°,BF=GF,
∴,
∴∠FBH=∠FHB,∠FBC=∠FCB,
∴∠GFH=∠FBH+∠FHB=2∠FBH,∠GFC=∠FBC+∠FCB=2∠FBC,
∴∠HFC=∠GFH+∠GFC=2∠FBH+2∠FBC=2∠ABC=90°,
∵FM⊥BG,
∴∠BFM=90°,
∴∠HFM=∠CFN,
设∠CBG=x,则∠ABG=45°﹣x,∠CGB=90°﹣x,
∴∠HMF=∠BFM+∠FBM=135°﹣x,
∵CN平分∠ACB,
∴,
∴∠CNF=∠CGN+∠GCN=135°﹣x,
∴∠HMF=∠CNF,
∴△HFM≌△CFN(AAS),
∴HM=CN,
∵AM=AH+HM,
∴;
(3)解:过点D作DH⊥AC交AC延长线与H,连接FH,
∵BD∥AC,∠ACB=90°,
∴∠BCH=∠CBD=90°,
∵DH⊥AC,
∴四边形BCHD是矩形,
∴BC=DH=AC,
∵点F是AD的中点,且AF=AC,
∴AD=2AF=2DH=2FH=2DF,
∴△FDH是等边三角形,
∴∠DFH=∠FDH=60°,
∴∠BDA=∠DAH=30°,
∴∠FHA=∠FAH=30°,
由旋转的性质可得FQ=FP,∠PFQ=60°=∠DFH,
∴∠DFQ=∠HFP,
∴△DFQ≌△HFP(SAS),
∴∠FDQ=∠FHP=30°,
∴点Q在直线DQ上运动,
设直线DQ交FH于K,则DK⊥FH,,,
∴∠BDQ=60°,
由垂线段最短可知,当BQ⊥DQ时,BQ有最小值,
∴∠DBQ=30°,
设AC=DH=6a,则,
∴,
∴,
∴,
在Rt△DFK中,,
∴,
∴QK=DK﹣DQ=3a,
在Rt△FQK中,由勾股定理得,
∵△DFQ≌△HFP,
∴,
∴,
∴由折叠的性质可得:,
∵FT≤FQ+TQ,
∴,
∴当点Q在线段FT上时,此时有最大值,最大值为,
∴的最大值为.
【点评】本题主要考查了全等三角形的性质与判定,勾股定理,等边三角形的性质与判定,等腰直角三角形的性质与判定,旋转的性质,折叠的性质,垂线段最短,矩形的性质与判定等等,属于综合题,难度较大.
5.(2024 自贡)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3m,据此可得旗杆高度为 11.3 m;
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5m,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16m.求旗杆高度;
(3)小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图6,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8m,DG=1.5m.将观测点D后移24m到D′处.采用同样方法,测得C′G′=1.2m,D′G′=2m.求雕塑高度(结果精确到1m).
【分析】(1)由影长EF恰好等于自己的身高DE,知△DEF是等腰直角三角形,△ABC是等腰直角三角形,故AB=BC=11.3m,
(2)证明△DEC∽△ABC,可得=,故AB=12,即旗杆高度为12米;
(3)由△DCG∽△DAB,得=,设AB=x m,BD=y m,则=,知y=x,同理可得=,即得=,从而=,解出x即可得雕塑高度约为31m.
【解答】解:(1)∵影长EF恰好等于自己的身高DE,
∴△DEF是等腰直角三角形,
由平行投影性质可知,△ABC是等腰直角三角形,
∴AB=BC=11.3m,
故答案为:11.3;
(2)如图:
由反射定律可知,∠DCE=∠ACB,
又∠DEC=90°=∠ABC,
∴△DEC∽△ABC,
∴=,即=,
解得AB=12,
∴旗杆高度为12米;
(3)如图:
∵∠CDG=∠ADB,∠CGD=90°=∠ABD,
∴△DCG∽△DAB,
∴=,
设AB=x m,BD=y m,则=,
∴y=x,
同理可得=,
∴=,
∴=,
解得x=28.8;
经检验,x=28.8是原方程的解,
故AB≈29m,
∴雕塑高度AB约为29m.
【点评】本题考查解直角三角形应用,涉及相似三角形判定与性质,解题的关键是读懂题意,列出方程解决问题.
6.(2024 烟台)在等腰直角△ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD.将线段AD绕点D按顺时针方向旋转90°得线段ED,连接BE.
【尝试发现】
(1)如图1,当点D在线段BC上时,线段BE与CD的数量关系为 ;
【类比探究】
(2)当点D在线段BC的延长线上时,先在图2中补全图形,再探究线段BE与CD的数量关系并证明;
【联系拓广】
(3)若AC=BC=1,CD=2,请直接写出sin∠ECD的值.
【分析】(1)过点E作EM⊥CB延长线于点M,利用一线三垂直全等模型证明△ACD≌△DME,再证明BM=EM即可;
(2)同(1)中方法证明△ACD≌△DME,再证明BM=EM即可;
(3)过点E作EM⊥CB,求出EM,CE即可.
【解答】解:(1)如图,过点E作EM⊥CB延长线于点M,
由旋转得AD=DE,∠ADE=90°,
∴∠ADC+∠EDM=90°,
∵∠ACB=90°,
∴∠ACD=∠DME,∠ADC+∠CAD=90°,
∴∠CAD=∠EDM,
∴△ACD≌△DME(AAS),
∴CD=EM,AC=DM,
∵AC=BC,
∴BM=DM﹣BD=AC﹣BD=BC﹣BD=CD,
∴BM=EM,
∵EM⊥CB,
∴,
故答案为:;
(2)补全图形如图,,理由如下:
过点E作EM⊥BC于点M,
由旋转得AD=DE,∠ADE=90°,
∴∠ADC+∠EDM=90°,
∵∠ACB=90°,
∴∠ACD=∠DME,∠ADC+∠CAD=90°,
∴∠CAD=∠EDM,
∴△ACD≌△DME(AAS),
∴CD=EM,AC=DM,
∵AC=BC,
∴DM=BC,
∴DM﹣CM=BC﹣CM,
∴CD=BM,
∴EM=BM,
∵EM⊥CB,
∴;
(3)如图,当点D在CB延长线上时,过点E作EM⊥CB延长线于点M,
由(2)得DM=AC=1,EM=CD=2,
∴CM=CD+DM=3,
∴,
∴;
当点D在BC延长线上时,过点E作EM⊥CB于点M,
同理可得:△ACD≌△DME,
∴DM=AC=1,ME=CD=2,
∴CM=2﹣1=1,
∴CE=,
∴sin∠ECD=,
综上,sin∠ECD=或.
【点评】本题考查三角形全等的判定与性质,三角函数,掌握一线三垂直全等模型是解题的关键.
7.(2024 苏州)图①是某种可调节支撑架,BC为水平固定杆,竖直固定杆AB⊥BC,活动杆AD可绕点A旋转,CD为液压可伸缩支撑杆,已知AB=10cm,BC=20cm,AD=50cm.
(1)如图②,当活动杆AD处于水平状态时,求可伸缩支撑杆CD的长度(结果保留根号);
(2)如图③,当活动杆AD绕点A由水平状态按逆时针方向旋转角度α,且tanα=(α为锐角),求此时可伸缩支撑杆CD的长度(结果保留根号).
【分析】(1)过点C作CE⊥AD,垂足为E,根据题意可得:AB=CE=10cm,BC=AE=20cm,从而可得ED=30cm,然后在Rt△CED中,利用勾股定理进行计算,即可解答;
(2)过点D作DF⊥BC,交BC的延长线于点F,交AD′于点G,根据题意可得:AB=FG=10cm,AG=BF,∠AGD=90°,然后在Rt△ADG中,利用锐角三角函数的定义可设DG=3x cm,则AG=4x cm,从而利用勾股定理进行计算可求出AG和DG的长,进而可求出DF和CF的长,最后在Rt△CFD中,利用勾股定理进行计算,即可解答.
【解答】解:(1)过点C作CE⊥AD,垂足为E,
由题意得:AB=CE=10cm,BC=AE=20cm,
∵AD=50cm,
∴ED=AD﹣AE=50﹣20=30(cm),
在Rt△CED中,CD===10(cm),
∴可伸缩支撑杆CD的长度为10cm;
(2)过点D作DF⊥BC,交BC的延长线于点F,交AD′于点G,
由题意得:AB=FG=10cm,AG=BF,∠AGD=90°,
在Rt△ADG中,tanα==,
∴设DG=3x cm,则AG=4x cm,
∴AD===5x(cm),
∵AD=50cm,
∴5x=50,
解得:x=10,
∴AG=40cm,DG=30cm,
∴DF=DG+FG=30+10=40(cm),
∴BF=AG=40cm,
∵BC=20cm,
∴CF=BF﹣BC=40﹣20=20(cm),
在Rt△CFD中,CD===20(cm),
∴此时可伸缩支撑杆CD的长度为20cm.
【点评】本题考查了解直角三角形的应用,勾股定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
8.(2024 甘肃)习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富,风力发电发展迅速.某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒AH垂直于地面,测角仪CD,EF在AH两侧,CD=EF=1.6m,点C与点E相距182m(点C,H,E在同一条直线上),在D处测得筒尖顶点A的仰角为45°,在F处测得筒尖顶点A的仰角为53°.求风电塔简AH的高度.(参考数据:sin53°≈,cos53°≈,tan53°≈.)
【分析】连接DF交AH于点G,根据题意可得:CD=EF=GH=1.6m,DF=CE=182m,DF⊥AH,然后设DG=x m,则FG=(182﹣x)m,分别在Rt△ADG和Rt△AFG中,利用锐角三角函数的定义求出AG的长,从而列出关于x的方程,进行计算即可解答.
【解答】解:连接DF交AH于点G,
由题意得:CD=EF=GH=1.6m,DF=CE=182m,DF⊥AH,
设DG=x m,
∴FG=DF﹣DG=(182﹣x)m,
在Rt△ADG中,∠ADG=45°,
∴AG=DG tan45°=x(m),
在Rt△AFG中,∠AFG=53°,
∴AG=FG tan53°≈(182﹣x)m,
∴x=(182﹣x),
解得:x=104,
∴AG=104m,
∴AH=AG+GH=104+1.6=105.6(m),
∴风电塔简AH的高度约为105.6m.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
9.(2024 江西)图1是世界第一“大碗”——景德镇昌南里文化艺术中心主体建筑,其造型灵感来自于宋代湖田窑影青斗笠碗,寓意“万瓷之母”.如图2,“大碗”的主视图由“大碗”主体ABCD和矩形碗底BEFC组成,已知AD∥EF,AM,DN是太阳光线,AM⊥MN,DN⊥MN,点M,E,F,N在同一条直线上.经测量ME=FN=20.0m,EF=40.0m,BE=2.4m,∠ABE=152°.(结果精确到0.1m)
(1)求“大碗”的口径AD的长;
(2)求“大碗”的高度AM的长.
(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
【分析】(1)根据垂直定义可得∠AMN=∠DNM=90°,再利用平行线的性质可得∠DAM=90°,从而可得四边形AMND是矩形,然后利用矩形的性质可得AD=MN,从而利用线段的和差关系进行计算即可解答;
(2)延长CB交AM于点G,根据题意可得:BE=GM=2.4m,BG=ME=20.0m,BG⊥AM,∠EBG=90°,从而可得∠ABG=62°,然后在Rt△ABG中,利用锐角三角函数的定义求出AG的长,从而利用线段的和差关系进行计算,即可解答.
【解答】解:(1)∵AM⊥MN,DN⊥MN,
∴∠AMN=∠DNM=90°,
∵AD∥MN,
∴∠DAM=180°﹣∠AMN=90°,
∴四边形AMND是矩形,
∴AD=MN=ME+EF+FN=20.0+40.0+20.0=80.0(m),
∴“大碗”的口径AD的长为80.0m;
(2)延长CB交AM于点G,
由题意得:BE=GM=2.4m,BG=ME=20.0m,BG⊥AM,∠EBG=90°,
∵∠ABE=152°,
∴∠ABG=∠ABE﹣∠EBG=62°,
在Rt△ABG中,AG=BG tan62°≈20.0×1.88=37.6(m),
∴AM=AG+MG=37.6+2.4=40.0(m),
∴“大碗”的高度AM的长约为40.0m.
【点评】本题考查了解直角三角形的应用,矩形的判定与性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
10.(2024 广安)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机,如图(1),某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图(2)为测量示意图(点A,B,C,D均在同一平面内,AB⊥BC).已知斜坡CD长为20米,斜坡CD的坡角为60°,在斜坡顶部D处测得风力发电机塔杆顶端A点的仰角为20°,坡底与塔杆底的距离BC=30米,求该风力发电机塔杆AB的高度.(结果精确到个位;参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,≈1.73)
【分析】过点D作DF⊥AB于点F,作DH⊥BE于点H,由题意得:DC=20m,∠DCH=60°,根据三角函数的定义得到CH=CD cos60°=10m,D,根据矩形的性质得到BH=FD,BF=DH,求得FD=40m,根据三角函数的定义即可得到结论.
【解答】解:过点D作DF⊥AB于点F,作DH⊥BE于点H,
由题意得:DC=20m,∠DCH=60°,
在Rt△DCH中,
∵,,
∴CH=CD cos60°=10m,
∴D,
∵∠DFB=∠B=∠DHB=90°,
∴四边形DFBH为矩形,
∴BH=FD,BF=DH,
∵BH=BC+CH=(30+10)m=40m,
∴FD=40m,
在Rt△AFD中,,
∴AF=FD tan20°=40×0.36m=14.4m,
∴AB=AF+BF=(17.3+14.4)m=31.7m≈32m,
答:该风力发电机塔杆AB的高度为32m.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,解直角三角形的应用﹣坡度坡角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.
11.(2024 重庆)如图,甲、乙两艘货轮同时从A港出发,分别向B,D两港运送物资,最后到达A港正东方向的C港装运新的物资.甲货轮沿A港的东南方向航行40海里后到达B港,再沿北偏东60°方向航行一定距离到达C港.乙货轮沿A港的北偏东60°方向航行一定距离到达D港,再沿南偏东30°方向航行一定距离到达C港.
(参考数据:≈1.41,≈1.73,≈2.45)
(1)求A,C两港之间的距离(结果保留小数点后一位);
(2)若甲、乙两艘货轮的速度相同(停靠B,D两港的时间相同),哪艘货轮先到达C港?请通过计算说明.
【分析】(1)过点B作BE⊥AC,垂足为E,先在Rt△ABE中,利用锐角三角函数的定义求出AE和BE的长,再在Rt△BCE中,利用锐角三角函数的定义求出CE的长,从而利用线段的和差关系进行计算,即可解答;
(2)根据题意可得:∠CDF=30°,DF∥AG,从而可得∠GAD=∠ADF=60°,然后利用角的和差关系可得∠ADC=90°,从而在Rt△ACD中,利用含30度角的直角三角形的性质求出CD和AD的长,再在Rt△BCE中,利用锐角三角函数的定义求出BC的长,最后进行计算比较即可解答.
【解答】解:(1)过点B作BE⊥AC,垂足为E,
在Rt△ABE中,∠BAE=90°﹣45°=45°,AB=40海里,
∴AE=AB cos45°=40×=20(海里),
BE=AB sin45°=40×=20(海里),
在Rt△BCE中,∠CBE=60°,
∴CE=BE tan60°=20×=20(海里),
∴AC=AE+CE=20+20≈77.2(海里),
∴A,C两港之间的距离约为77.2海里;
(2)甲货轮先到达C港,
理由:如图:
由题意得:∠CDF=30°,DF∥AG,
∴∠GAD=∠ADF=60°,
∴∠ADC=∠ADF+∠CDF=90°,
在Rt△ACD中,∠CAD=90°﹣∠GAD=30°,
∴CD=AC=(10+10)海里,
AD=CD=(10+30)海里,
在Rt△BCE中,∠CBE=60°,BE=20海里,
∴BC===40(海里),
∴甲货轮航行的路程=AB+BC=40+40≈96.4(海里),
乙货轮航行的路程=AD+CD=10+30+10+10=20+40=105.4(海里),
∵96.4海里<105.4海里,
∴甲货轮先到达C港.
【点评】本题考查了解直角三角形的应用﹣方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
12.(2024 宜宾)宜宾地标广场位于三江汇合口(如图1,左侧是岷江,右侧是金沙江,正面是长江).某同学在数学实践中测量长江口的宽度,他在长江口的两岸选择两个标点C、D,在地标广场上选择两个观测点A、B(点A、B、C、D在同一水平面,且AB∥CD).如图2所示,在点A处测得点C在北偏西18.17°方向上,测得点D在北偏东21.34°方向上;在B处测得点C在北偏西21.34°方向上,测得点D在北偏东18.17°方向上,测得AB=100米.求长江口的宽度CD的值(结果精确到1米).(参考数据:sin18.17°≈0.31,cos18.17°≈0.95,tan18.17°≈0.33,sin21.34°≈0.36,cos21.34°≈0.93,tan21.34°≈0.39)
【分析】过点A作AE⊥CD,垂足为E,过点B作BF⊥CD,垂足为F,根据已知易得:AE=BF,AB=EF=100m,然后设AE=BF=x m,从而分别在Rt△ACE、Rt△BDF和Rt△AED中,利用锐角三角函数的定义求出CE、DF和DE的长,从而列出关于x的方程,进行计算即可解答.
【解答】解:过点A作AE⊥CD,垂足为E,过点B作BF⊥CD,垂足为F,
∵AB∥CD,
∴AE=BF,
由题意得:AB=EF=100m,
设AE=BF=x m,
在Rt△ACE中,∠CAE=18.17°,
∴CE=AE tan18.17°≈0.33x(m),
在Rt△BDF中,∠DBF=18.17°,
∴DF=BF tan18.17°≈0.33x(m),
在Rt△AED中,∠EAD=21.34°,
∴DE=AE tan21.34°≈0.39x(m),
∵DE=EF+DF,
∴0.39x=100+0.33x,
解得:x=,
∴CD=CE+DE=0.33x+0.39x=0.72x=1200(m),
∴长江口的宽度CD的值约为1200m.
【点评】本题考查了解直角三角形的应用﹣方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
13.(2024 广东)【知识技能】
(1)如图1,在△ABC中,DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A′DC′.当点E的对应点E′与点A重合时,求证:AB=BC.
【数学理解】
(2)如图2,在△ABC中(AB<BC),DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A′DC′,连接A′B,C′C,作△A′BD的中线DF.求证:2DF CD=BD CC′.
【拓展探索】
(3)如图3,在△ABC中,tanB=,点D在AB上,AD=.过点D作DE⊥BC,垂足为E,BE=3,CE=.在四边形ADEC内是否存在点G,使得∠AGD+∠CGE=180°?若存在,请给出证明;若不存在,请说明理由.
【分析】(1)利用等腰三角形+平行线证明∠DAE=∠BCA即可得证;
(2)先证△ADA′∽△CDC得到,再证AA'=2DF,代入变形即可得证;
(3)利用特殊点,∠AGD=90°,∠CGE=90°,则G就是以AD为直径的圆和以CE为直径的圆的交点,根据题意证G在内部即可.
【解答】(1)证明:∵△ADC绕点D按逆时针方向旋转,得到△A′DC',且E'与A重合,
∴AD=DE,
∴∠DAE=∠DEA,
∵DE是△ABC的中位线,
∴DE∥BC,
∴∠DEA=∠BCA,
∴∠DAE=∠BCA,
∴AB=BC.
(2)证明:连接AA',
∵旋转,
∴∠ADA′=∠CDC′,AD=A'D,CD=C'D,
∴,
∴△ADA′∽△CDC′,
∴,
∵DE是△ABC的中位线,DF是△A'BD的中线,
∴AD=BD,BF=A'F,
∴DF是△AA'B的中位线,
∴AA'=2DF,
∴,
∴2DF CD=BD CC'
(3)解:存在,理由如下,
解法一:取AD中点M,CE中点N,连接MN,
∵AD是⊙M直径,CE是⊙N直径,
∴∠AGD=90°,∠CGE=90°,
∴∠AGD+∠CGE=180°,
∵tanB=,BE=3,
∴BD=5,
∵CE=,
∴EN=CE=,
∴BN=BE+EN=,
∵DE⊥CE,
∴DE是⊙N的切线,即DE在⊙N外,
作NF⊥AB,
∵∠B=∠B,∠BED=∠BFN=90°,
∴△BDE∽△BNF,
∴,
∴NF=>,即NF>rn,
∴AB在⊙N外,
∴G点在四边形ADEC内部.
作MH⊥BC,
∵BM=,tanB=,
∴BH=,MH=,
∴NH=,
∴MN=≈7.4<AM+CN
∴⊙M和⊙N有交点.
故四边形ADEC内存在点G,使得∠AGD+∠CGE=180°.
解法二:相似互补弓形,
分别以AD,CE为弦作⊙O2和⊙O,使得△O2AD∽△OEC,两圆的交点即为所求.
作图步骤:①在四边形ADEC内任取一点F,作△EFC得外接圆,圆心为O,连接OE,OC,
②作AD的中垂线,
③以D为圆心,OC为半径画圆交AD中垂线于点O2,
④以O2为圆心,O2A为半径画圆,交⊙O于点G,点G即为所求.
证明:∵==,
∴△O2AD∽△OEC,
∴∠AO2D=∠EOC,
∵∠AGD=(360°﹣∠AO2D)=180°﹣∠AO2D,
∠EGC=∠EOC,
∴∠AGD+∠EGC=180°.
故四边形ADEC内存在点G,使得∠AGD+∠CGE=180°.
【点评】本题主要考查了相似三角形的判定和性质、中位线定理、圆周角定理、勾股定理等知识,熟练掌握相关知识是解题关键.
14.(2024 武汉)如图是由小正方形组成的3×4网格,每个小正方形的顶点叫做格点.△ABC三个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.
(1)在图(1)中,画射线AD交BC于点D,使AD平分△ABC的面积;
(2)在(1)的基础上,在射线AD上画点E,使∠ECB=∠ACB;
(3)在图(2)中,先画点F,使点A绕点F顺时针旋转90°到点C,再画射线AF交BC于点G;
(4)在(3)的基础上,将线段AB绕点G旋转180°,画对应线段MN(点A与点M对应,点B与点N对应).
【分析】(1)根据三角形中线的定义画出图形;
(2)作点A故BC的对称点A′,连接CA′交射线ADF于点E,点E即为所求;
(3)构造等腰直角三角形AFC即可;
(4)取格点P,Q,E,W,K,L,连接PQ,EW,KL,PQ交射线AF于点M,EW交KL于点J,连接MJ,延长MJ交BC一点N,线段MN即为所求(证明△ABG≌△MNG,可得结论).
【解答】解:(1)如图1中,线段AD即为所求;
(2)如图1中,点E即为所求;
(3)如图2中,点F,射线AF,点G即为所求;
(4)如图2中,线段MN即为所求.
【点评】本题考查作图﹣旋转变换,角平分线的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
15.(2024 临夏州)如图1,在矩形ABCD中,点E为AD边上不与端点重合的一动点,点F是对角线BD上一点,连接BE,AF交于点O,且∠ABE=∠DAF.
【模型建立】
(1)求证:AF⊥BE;
【模型应用】
(2)若AB=2,AD=3,DF=BF,求DE的长;
【模型迁移】
(3)如图2,若矩形ABCD是正方形,DF=BF,求的值.
【分析】(1)由矩形的性质得∠BAD=90°,而∠ABE=∠DAF,所以∠AOE=∠BAF+∠ABE=∠BAF+∠DAF=90°,则AF⊥BE;
(2)延长AF交CD于点G,由GD∥AB,证明△GDF∽△ABF,则==,求得GD=AB=1,由=tan∠ABE=tan∠DAG==,求得AE=AB=,则DE=AD﹣AE=;
(3)延长AF交CD于点H,由正方形的性质得AB=AD,∠ADH=90°,设AB=AD=2m,可证明△HDF∽△ABF,得===,则HD=AB=m,求得AH==m,则AF=AH=m,求得=.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵∠ABE=∠DAF,
∴∠AOE=∠BAF+∠ABE=∠BAF+∠DAF=∠BAD=90°,
∴AF⊥BE.
(2)解:如图1,延长AF交CD于点G,
∵GD∥AB,
∴△GDF∽△ABF,
∵DF=BF,AB=2,AD=3,
∴==,
∴GD=AB=×2=1,
∵∠BAE=∠ADG=90°,∠ABE=∠DAG,
∴=tan∠ABE=tan∠DAG==,
∴AE=AB=×2=,
∴DE=AD﹣AE=3﹣=,
∴DE的长是.
(3)解:如图2,延长AF交CD于点H,
∵四边形ABCD是正方形,
∴AB=AD,∠ADH=90°,
设AB=AD=2m,
∵HD∥AB,
∴△HDF∽△ABF,
∵DF=BF,
∴===,
∴HD=AB=×2m=m,
∴AH===m,
∴AF=AH=AH=×m=m,
∴==,
∴的值为.
【点评】此题重点考查矩形的性质,正方形的性质,三角形的一个外角等于与它不相邻的两个内角的和,相似三角形的判定与性质,锐角三角函数与解直角三角形,勾股定理等知识,此题综合性强,难度较大,正确地作出辅助线是解题的关键.
16.(2024 滨州)(1)如图1,△ABC中,点D,E,F分别在三边BC,CA,AB上,且满足DF∥AC,DE∥AB.
①求证:四边形AFDE为平行四边形;
②若,求证:四边形AFDE为菱形;
(2)把一块三角形余料MNH(如图2所示)加工成菱形零件,使它的一个顶点与△MNH的顶点M重合,另外三个顶点分别在三边MN,NH,HM上,请在图2上作出这个菱形.(用尺规作图,保留作图痕迹,不写作法)
【分析】(1)①根据DF∥AC,DE∥AB,点D,E,F分别在三边BC,CA,AB上,可以得到DF∥AE,DE∥AE,然后即可证明结论成立;
②延长BA到G,使得AG=AC,然后根据和∠ABD=∠GBC,可以得到△BAD∽△BGC,从而可以得到∠BAD=∠G,即可判断AD∥CG,然后根据平行线的性质和等腰三角形的性质,可以得到AD平分∠BAC,再根据平行线的性质,可以得到∠DAE=∠ADE,进而得到AE=DE,最后根据有一组邻边相等的平行四边形是菱形,即可证明结论成立;
(2)作∠NMH的角平分线,与NH交于点L,再作线段ML的垂直平分线,分别交MN、MH于点O,G,则四边形MGLO即为所求.
【解答】(1)①证明:∵DF∥AC,DE∥AB,点D,E,F分别在三边BC,CA,AB上,
∴DF∥AE,DE∥AE,
∴四边形AFDE为平行四边形;
②证明:延长BA到G,使得AG=AC,如图1所示,
则∠G=∠ACG,
∵,
∴,
∵∠ABD=∠GBC,
∴△BAD∽△BGC,
∴∠BAD=∠G,
∴AD∥GC,
∴∠DAC=∠ACG,
∴∠BAD=∠DAC,
又∵AB∥DE,
∴∠BAD=∠ADE,
∴∠DAE=∠ADE,
∴AE=DE,
∴四边形AFDE为菱形;
(2)解:作∠NMH的角平分线,与NH交于点L,再作线段ML的垂直平分线,分别交MN、MH于点O,G,如下图所示,
四边形MGLO即为所求.
【点评】本题是一道相似形综合题,主要考查平行四边形的判定、相似三角形的判定与性质、菱形的判定、角平分线的画法、线段垂直平分线的画法,解答本题的关键是明确题意,找出所求问题需要的条件.
17.(2024 齐齐哈尔)综合与实践
如图1,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”.如图2,在△ABC中,∠A=90°,将线段BC绕点B顺时针旋转90°得到线段BD,作DE⊥AB交AB的延长线于点E.
(1)【观察感知】如图2,通过观察,线段AB与DE的数量关系是 AB=DE ;
(2)【问题解决】如图3,连接CD并延长交AB的延长线于点F,若AB=2,AC=6,求△BDF的面积;
(3)【类比迁移】在(2)的条件下,连接CE交BD于点N,则= ;
(4)【拓展延伸】在(2)的条件下,在直线AB上找点P,使tan∠BCP=,请直接写出线段AP的长度.
【分析】(1)利用“一线三垂直“证△ABC≌△EBD(AAS)即可得证;
(2)证△DEF∽△CAF可求EF长度,然后即可求出△BDF的面积;
(3)要求的值,有两个方向,①把BN和BC的值求出来,这题BC很好求,但是BN不好求,可以建立坐标系求解析式,再求交点N坐标,最后利用两点距离公式求BN的长度;②根据题干给我们的思路建立一线三直角得相似进行转化即可,利用△EMN∽△EAC和△BMN∽△BED建立关于MN的方程,求出MN的长度,最后利用△BMN∽△CAB求值即可.
(4)由已知条件过P作BC垂线段,可得两个直角三角形,然后解这两个直角三角形即可求解.另外方法二的正切和差角公式可以作为课外拓展知识,在这种直接写答案的题型中可以用下,快速找出答案.
【解答】解:(1)∵线段BC绕点B逆时针旋转90°得到线段BD,
∴BC=BD,∠CBD=90°,
∴∠BCA=∠DBE=90°﹣∠ABC,
∵∠A=∠E=90°,
∴△ABC≌△EBD(AAS),
∴AB=DE;
故答案为:AB=DE.
(2)∵线段BC绕点B逆时针旋转90°得到线段BD,
∴BC=BD,∠CBD=90°,
∴∠BCA=∠DBE=90°﹣∠ABC,
∵∠A=∠E=90°,
∴△ABC≌△EBD(AAS),
∴DE=AB,BE=AC,
∵AB=2,AC=6,
∴DE=2,BE=6,
∴AE=AB+BE=8,
∵∠DEB+∠A=180°,
∴DE∥AC,
∴△DEF∽△CAF,
∴,即,
∴EF=4,
∴BF=BE+EF=10,
∴S△BDF=BF DE=10.
(3)方法一:如图,以AE所在直线为x轴,以AC所在直线为y轴建立坐标系,
由AC=6,AE=8,DE=2,BD=2,
∴C(0,6),B(2,0),E(8,0),D(8,2),
设直线BD解析式为y=kx+b,将B、D代入得,
,解得:,
∴直线BD解析式为y=x﹣,
同理可求直线CE解析式为:y=﹣x+6,
令x﹣=﹣x+6,解得x=,
∴y=,即N(,),
∴利用两点距离公式可得BN=,
∵BC==2,
∴==.
故答案为:.
方法二:如图,过N作NM⊥AE于点M,
由△EMN∽△EAC得,,即,
∴EM=MN,
由△BMN∽△BED得,,即,
解得MN=,
由△BMN∽△CAB得,=.
故答案为:.
(4)方法一:①当点P在点B左侧时,如图所示,过P作PQ⊥BC于点Q,
∵tan∠BCP==,tan∠ABC===3,
∴PQ=CQ,PQ=3BQ,
设BQ=2a,则PQ=6a,CQ=9a,
∴BC=BQ+CQ=11a,
∵BC==2=11a,
∴a=,
∴BP==2a=,
∴AP=BP﹣AB=;
②当点P在点B右侧时,如图所示,作PG⊥BC交BC延长线于点G,
tan∠BCP==,tan∠PBG=tan∠ABC,即,
剩下思路与第一种情况方法一致,求得AP=.
综上,AP的长度为或.
方法二:补充知识:正切和差角公式:tan(α+β)=,tan(α﹣β)=.
①当点P在点B左侧时,因为tan∠BCA=,tan∠BCP=,所以此时点P在A的左侧,如图所示,
tan∠BCP=tan(∠BCA+∠ACP)===,
解得tan∠ACP=,即=,
∵AC=6,
∴AP=.
②当点P在点B右侧时,如图所示,
tan∠ACP=tan(∠BCA+∠BCP)===,
即,
∵AC=6,
∴AP=.
综上,AP的长度为或.
【点评】本题主要考查了相似三角形的判定和性质、全等三角形的性质和判定、解直角三角形、勾股定理等知识,熟练掌握以上基础知识和添加合适的辅助线是解题关键.
18.(2024 湖北)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
【分析】(1)证明对应角相等,即可得到△EDP∽△PCH;
(2)根据△EDP∽△PCH,求得PH的长度,从而得出GH长度;
(3)延长AB,PG交于一点M,连接AP,先证明△MBH≌△PCH,得到相等的边,再根据△BMG∽△MAP,得出大小关系.
【解答】(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴DP=CP==1,
设EP=AP=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得x=,
∴EP=AP=x=,
∴ED=AD﹣AE=,
∵△EDP∽△PCH,
∴,即,
∴PH=,
∵PG=AB=2,
∴GH=PG﹣PH=.
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴HP=PM=y,
在Rt△PCH中,CH==y,
∴BC=2CH=y,
∴AD=BC=y,
在Rt△APD中,AP==y,
∵BG∥AP,
∴△BMG∽△AMP,
∴=,
∴BG=y,
∴=,
∴AB=BG.
【点评】本题考查了矩形与折叠、相似三角形的判定与性质、勾股定理、全等三角形的判定与性质等知识,熟练掌握以上基础知识是解题关键.
19.(2024 广西)如图1,△ABC中,∠B=90°,AB=6.AC的垂直平分线分别交AC,AB于点M,O,CO平分∠ACB.
(1)求证:△ABC∽△CBO;
(2)如图2,将△AOC绕点O逆时针旋转得到△A'OC',旋转角为α(0°<α<360°).连接A′M,C′M.
①求△A'MC'面积的最大值及此时旋转角α的度数,并说明理由;
②当△A'MC'是直角三角形时,请直接写出旋转角α的度数.
【分析】(1)从问题出发,证△ABC∽△CBO,两个三角形有一个公共角,所以只需证一角相等即可,由题干很容易得出∠ACO=∠BCO=∠A,即可得证;
(2)△A'MC'的底是定长,所以只要找到高的最大值就可求出面积最值,当N、H重合时MH取最大值,此时最大值为OM+ON=4,即可求解;
(3)首先有条件可知只有可能是∠A'MC'=90°,由特殊三角形和旋转的性质大胆猜测当点C'与A重合时和当A'与C重合时满足∠A'MC'=90°,进而求旋转角即可.
【解答】(1)证明:∵OM垂直平分AC,
∴OA=OC,∠A=∠ACO,
∵CO平分∠ACB,
∴∠ACO=∠BCO=∠A,
∵∠B=∠B,
∴△ABC∽△CBO.
(2)解:①∵∠ACO=∠BCO=∠A,∠B=90°,
∴:∠ACO=∠BCO=∠A=30°,
在Rt△ABC中,AB=6,
∴AC==4,
∴AM=2,
∴OM=AM tan30°=2,
如图3,作MH⊥A'C'于点H,ON⊥A'C'于点N,连接MN,
在△AOC旋转的过程中,对应边AC=A'C'=4,对应高OM=ON=2,
在Rt△MHN中,MH<MN,
在△OMN中,MN<OM+ON,
∴MH<MN<OM+ON,
如图4,当N、H重合时MH取最大值,此时最大值为OM+ON=4,
∴S△A'MC'=A'C' MH=8,即△A'MC'面积最大值是8,
此时M、O、N三点共线,α=∠MON=180°.
②在旋转得过程中,等腰三角形AOC的形状、大小不变,∠AOC=∠A'OC'=120°,
∵MC′≤MO+OC'=MO+OC=6<4=A'C',同理MA'≤6<A'C',
∴△A'MC'中只有可能∠A'MC'=90°,
∵OM垂直平分AC,
∴MA=MC,∠AMO=90°,
(Ⅰ)如图5,当点C'与A重合时,A'恰好在MO的延长线上,满足∠A'MC'=90°,此时α=120°;
(Ⅱ)如图6,当A'与C重合时,点C'恰好在MO的延长线上,满足∠A'MC'=90°,此时α=240°.
综上,当△A'MC'是直角三角形时,α为120°或240°.
【点评】本题主要考查了相似三角形的判定、含有30°的直角三角形、旋转的性质、几何动点问题等知识点,掌握相关基础知识是解题的关键,其中在最后一文中大胆的想象和猜测也是一种解题策略.
20.(2024 安徽)如图1, ABCD的对角线AC与BD交于点O,点M,N分别在边AD,BC上,且AM=CN.点E,F分别是BD与AN,CM的交点.
(1)求证:OE=OF;
(2)连接BM交AC于点H,连接HE,HF.
(ⅰ)如图2,若HE∥AB,求证:HF∥AD;
(ⅱ)如图3,若 ABCD为菱形,且MD=2AM,∠EHF=60°,求的值.
【分析】(1)证明△AOE≌△COF(ASA),即可得到OE=OF;
(2)(i)证明△HOF∽△AOD,即可得到HF∥AD;(ii)先求出OA=2OH,OB=5OE,即可得到的值.
【解答】(1)证明:∵ ABCD,
∴AD∥BC,OA=OC,
∴AM∥CN,
∵AM=CN,
∴四边形AMCN是平行四边形,
∴AN∥CM,
∴∠OAE=∠OCF,
在△AOE与△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF;
(2)(i)证明:∵HE∥AB,
∴,
∵OB=OD,OE=OF,
∴,
∵∠HOF=∠AOD,
∴△HOF∽△AOD,
∴∠OHF=∠OAD,
∴HF∥AD;
(ii)解:∵ ABCD为菱形,
∴AC⊥BD,
∵OE=OF,∠EHF=60°,
∴∠EHO=∠FHO=30°,
∴,
∵AM∥BC,MD=2AM,
∴=,即HC=3AH,
∴OA+OH=3(OA﹣OH),
∴OA=2OH,
∵BN∥AD,MD=2AM,AM=CN,
∴,即3BE=2ED,
∴3(OB﹣OE)=2(OB+OE),
∴OB=5OE,
∴,
∴的值是.
【点评】本题考查了平行四边形的性质与判定,相似三角形的性质与判定,全等三角形的性质与判定等,综合运用性质与判定方法是解题的关键.
21.(2024 江西)综合与实践
如图,在Rt△ABC中,点D是斜边AB上的动点(点D与点A不重合),连接CD,以CD为直角边在CD的右侧构造Rt△CDE,∠DCE=90°,连接BE,=m.
特例感知
(1)如图1,当m=1时,BE与AD之间的位置关系是 AD⊥BE ,数量关系是 AD=BE .
类比迁移
(2)如图2,当m≠1时,猜想BE与AD之间的位置关系和数量关系,并证明猜想.
拓展应用
(3)在(1)的条件下,点F与点C关于DE对称,连接DF,EF,BF,如图3.已知AC=6,设AD=x,四边形CDFE的面积为y.
①求y与x的函数表达式,并求出y的最小值;
②当BF=2时,请直接写出AD的长度.
【分析】(1)由=1,得到CE=CD,CB=CA,根据等腰直角三角形的性质得到∠A=∠ABC=45°,∠ACD=∠BAE,根据全等三角形的性质得到AD=BE,∠A=∠CBE=45°,根据垂直的定义得到AD⊥BE;
(2)根据相似三角形的判定定理得到△ADC∽△BEC,求得=m,∠CBE=∠A,得到BE=mAD,根据垂直的定义得到AD⊥BE;
(3)①连接CF交DE于O,由(1)知,AC=BC=6,∠ACB=90°,求得AB=6,得到BD=6﹣x,根据勾股定理得到DE2=BD2+BE2=(6﹣x)2+x2,根据线段垂直平分线的性质得到CE=EF,CD=DF,推出四边形CDFE是正方形,根据正方形的面积公式即可得到y=DE2=[(6﹣x)2+x2],根据二次函数的性质即可得到结论;
②过D作DH⊥AC于H,根据等腰直角三角形 到现在得到AH=DH=AD=x,求得CH=6﹣x,连接OB,推出OB=,得到∠CBF=90°,根据勾股定理得到结论.
【解答】解:(1)AD⊥BE,AD=BE,
理由:∵=1,
∴CE=CD,CB=CA,
∵∠ACB=∠DCE=90°,
∴∠A=∠ABC=45°,∠ACD=∠BAE,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠A=∠CBE=45°,
∴∠ABE=90°,
∴AD⊥BE;
故答案为:AD⊥BE,AD=BE;
(2)BE=mAD,AD⊥BE,
证明:∵∠ACB=∠DCE=90°,
∴∠ACD=∠BAE,
∵=m,
∴△ADC∽△BEC,
∴=m,∠CBE=∠A,
∴BE=mAD,
∵∠A+∠ABC=90°,
∴∠CBE+∠ABC=90°,
∴∠ABE=90°,
∴AD⊥BE;
(3)①连接CF交DE于O,
由(1)知,AC=BC=6,∠ACB=90°,
∴AB=6,
∴BD=6﹣x,
∵AD=BE=x,∠DBE=90°,
∴DE2=BD2+BE2=(6﹣x)2+x2,
∵点F与点C关于DE对称,
∴DE垂直平分CF,
∴CE=EF,CD=DF,
∵CD=CE,
∴CD=DF=EF=CE,
∵∠DCE=90°,
∴四边形CDFE是正方形,
∴y=DE2=[(6﹣x)2+x2],
∴y与x的函数表达式为y=x2﹣6+36(0<x≤6),
∵y=x2﹣6+36=(x﹣3)2+18,
∴y的最小值为18;
②过D作DH⊥AC于H,
则△ADH是等腰直角三角形,
∴AH=DH=AD=x,
∴CH=6﹣x,
连接OB,
∴OB=OE=OD=OC=OF,
∴OB=,
∴∠CBF=90°,
∵BC=6,BF=2,
∴CF==2
∴CD=CF=2,
∵CH2+DH2=CD2,
∴(6﹣x)2+(x)2=(2)2,
解得x=4或x=2,
∴AD=4或2.
【点评】本题是相似形的综合题,考查了等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,正方形的判定和性质.勾股定理,正确地作出辅助线是解题的关键.
22.(2024 凉山州)如图,在菱形ABCD中,∠ABC=60°,AB=2,E是BC边上一个动点,连接AE,AE的垂直平分线MN交AE于点M,交BD于点N,连接EN、CN.
(1)求证:EN=CN;
(2)求2EN+BN的最小值.
【分析】(1)利用线段垂直平分线的性质和菱形的性质即可证明出结论;
(2)过点N作NG⊥BC于点G,连接AN,AG,过点A作AH⊥BC于点H,证明出2EN+BN的最小值为2AH,再求出AH即可解决问题.
【解答】解:(1)连接AN,如图,
∵四边形ABCD是菱形,
∴点A,点C关于直线BD轴对称,
∴AN=CN,
∵AE的垂直平分线MN交AE于点M,交BD于点N,
∴AN=EN,
∴EN=CN;
(2)过点N作NG⊥BC于点G,连接AN,AG,过点A作AH⊥BC于点H,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠DBC=30°,
∴BN=2NG,
∵AE的垂直平分线MN交AE于点M,交BD于点N,
∴EN=AN,
∴2EN+BN=2AN+2NG=2(AN+NG)≥2AG≥2AH,
∴2EN+BN的最小值为2AH,
∵∠ABC=60°,AB=2,
∴AH=AB sin60°=,
∴2EN+BN的最小值为2.
【点评】本题考查菱形的性质,三角函数,含30°角直角三角形的性质,线段的垂直平分线的性质,通过作辅助线将所求线段和的最小值用一条线段表示是解题的关键.
23.(2024 辽宁)如图,在△ABC中,∠ABC=90°,∠ACB=α(0°<α<45°).将线段CA绕点C顺时针旋转90°得到线段CD,过点D作DE⊥BC,垂足为E.
(1)如图1,求证:△ABC≌△CED.
(2)如图2,∠ACD的平分线与AB的延长线相交于点F,连接DF,DF的延长线与CB的延长线相交于点P,猜想PC与PD的数量关系,并加以证明.
(3)如图3,在(2)的条件下,将△BFP沿AF折叠,在α变化过程中,当点P落在点E的位置时,连接EF.
①求证:点F是PD的中点;
②若CD=20,求△CEF的面积.
【分析】(1)可证得∠D+∠DCE=90°,∠DCE+∠ACB=90°,从而∠ACB=∠D,进而证得△ABC≌△CED;
(2)可证得△ACF≌△DCF,从而∠A=∠PDC,进而证得∠PDC=∠DCE,从而得出PC=PD;
(3)①由折叠得PF=EF,∠P=∠PEF,可证得∠PEF+∠DEF=90°,∠P+∠PDE=90°,从而∠PDE=∠DEF,从而得出EF=DF,进而得出PF=DF;
②设CE=a,BC=DE=b,从而BE=BC﹣CE=b﹣a,可证得△PBF∽△PED,
∴,从而得出PE=2BE=2(b﹣a),BF=DE=,从而S△CEF=,在Rt△PED中,根据勾股定理得出∠PED=90°,b2+[2(b﹣a)]2=(2b﹣a)2,从而得出b=3a,由∠DEC=90°得出a2+b2=202,从而得出a2+(3a)2=400,进一步得出结果.
【解答】(1)证明:∵DE⊥BC,
∴∠DEC=90°,
∴∠D+∠DCE=90°,
∵∠ABC=90°,
∴∠ABC=∠DEC,
∵线段CA绕点C顺时针旋转90°得到线段CD,
∴∠ACD=90°,AC=CD,
∴∠DCE+∠ACB=90°,
∴∠ACB=∠D,
∴△ABC≌△CED(AAS);
(2)PC=PD,理由如下:
∵CF是∠ACD的平分线,
∴∠ACF=∠DCF,
由(1)知,
AC=CD,△ABC≌△CED,
∴∠A=∠DCE,
∵CF=CF,
∴△ACF≌△DCF(SAS),
∴∠A=∠PDC,
∴∠PDC=∠DCE,
∴PC=PD;
(3)①∵△BFP沿AF折叠,点P落在点E,
∴PF=EF,∠P=∠PEF,
∵DE⊥BC,
∴∠PED=90°,
∴∠PEF+∠DEF=90°,∠P+∠PDE=90°,
∴∠PEF+∠PDE=90°,
∴∠PDE=∠DEF,
∴EF=DF,
∴PF=DF,
∴点F是PD的中点;
②解:设CE=a,BC=DE=b,
∴BE=BC﹣CE=b﹣a,
由①知,
点F是PD的中点,
∴PF=PD,
∵∠ABC=∠PED=90°,
∴BF∥DE,
∴△PBF∽△PED,
∴,
∴PE=2BE=2(b﹣a),BF=DE=b,
∴S△CEF==,
∵∠PED=90°,DE=b,PE=2(b﹣a),PD=PC=PE+CE=2(b﹣a)+a=2b﹣a,
∴b2+[2(b﹣a)]2=(2b﹣a)2,
化简得,
3a2﹣4ab+b2=0,
∴b=a或b=3a,
∵0°<α<45°,
∴a=b舍去,
∴b=3a,
∴S△CEF=ab=,
∵∠DEC=90°,
∴a2+b2=202,
∴a2+(3a)2=400,
∴a2=40,
∴S△CEF=,
∴△CEF的面积是30.
【点评】本题考查了等腰三角形的判定和性质,相似三角形的判定和性质,全等三角形的判定和性质,勾股定理等知识,解决问题的关键是熟练掌握有关基础知识.
24.(2024 牡丹江)数学老师在课堂上给出了一个问题,让同学们探究.在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.
(1)当点D在线段BC上时,如图①,求证:BD+EF=AB;
分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论:
推理证明:写出图①的证明过程:
探究问题:
(2)当点D在线段BC的延长线上时,如图②:当点D在线段CB的延长线上时,如图③,请判断并直接写出线段BD,EF,AB之间的数量关系;
拓展思考:
(3)在(1)(2)的条件下,若AC=6,CD=2BD,则EF= 10或18 .
【分析】(1)在AB边上截取AM=EF,连接DM,根据题意证明出△DAM≌△AEF(SAS),得到AF=DM,然后证明出△BMD是等边三角形,得到BD=BM=DM,进而求解即可;
(2)图②:在BD上取点H,使BH=AB,连接AH并延长到点G使AG=AF,连接DG,首先证明出△ABH是等边三角形,得到∠BAH=60°,然后求出∠BAH=∠DAE,然后证明出△FAE≌△GAD(SAS),得到EF=DG,∠AFE=∠G,然后证明出△DHG是等边三角形,得到DH=DG=EF,进而求解即可;
图③:在EF上取点H使AH=AF,同理证明出△EAH≌△ADB(AAS),得到BD=AH,AB=EH,进而求解即可;
(3)根据勾股定理和含30°角直角三角形的性质求出BC=6,AB=12,然后结合CD=2BD,分别(1)(2)的条件下求出BD的长度,进而求解即可.
【解答】(1)证明:在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.在AB边上截取AM=EF,连接DM.如图1,
∴∠B=90°﹣∠BAC=90°﹣30°=60°.
∵EF∥BC,
∴∠EFB=∠B=60°.
又∵∠EAD=60°,
∴∠EFB=∠EAD.
又∵∠BAD=∠EAD﹣∠EAF,∠AEF=∠EFB﹣∠EAF,
∴∠BAD=∠AEF.
又∵AD=AE,AM=EF,
∴△DAM≌△AEF(SAS).
∴AF=DM.
∴∠AMD=∠EFA=180°﹣∠EFB=180°﹣60°=120°.
∴∠BMD=180°﹣∠AMD=180°﹣120°=60°.
∵∠B=60°,
∴∠BMD=∠B=∠BDM.
∴△BMD是等边三角形.
∴BD=BM=DM,
∵AB=AM+BM,
∴AB=EF+BD;
(2)解:图②:AB=BD﹣EF,证明如下:
如图2.1所示,在BD上取点H,使BH=AB,连接AH并延长到点G使AG=AF,连接DG,
∵∠ABC=60°,
∴△ABH是等边三角形,
∴∠BAH=60°,
∵线段AD绕点A顺时针旋转60°得到线段AE,
∴∠DAE=60°,AE=AD,
∴∠BAH=∠DAE,
∴∠BAH﹣∠EAH=∠DAE﹣∠EAH,即∠BAE=∠HAD,
又∵AG=AF,
∴△FAE≌△GAD(SAS),
∴EF=DG,∠AFE=∠G,
∵BD∥EF,
∴∠ABC=∠F=∠G=60°,
∵∠DHG=∠AHB=60°,
∴△DHG是等边三角形,
∴DH=DG=EF,
∴AB=BH=BD﹣DH=BD﹣EF;
图③:AB=EF﹣BD,证明如下:
如图2.2所示,在EF上取点H使AH=AF,
∵EF∥BC,
∴∠F=∠ABC=60°,
∵AH=AF,
∴△AHF是等边三角形,
∴∠AHF=∠HAF=60°,
∴∠AHE=120°,
∵将线段AD绕点A顺时针旋转60°得到线段AE,
∴AD=AE,∠DAE=60°,
∴∠DAB+∠EAH=180°﹣∠EAD﹣∠HAF=60°,
∵∠D+∠DAB=∠ABC=60°,
∴∠D=∠EAH,
∵∠DBA=180°﹣∠ABC=120°=∠EHA,
又∵AD=AE,
∴△EAH≌△ADB(AAS),
∴BD=AH,AB=EH,
∵AH=FH,
∴BD=HF,
∴AB=EH=EF﹣FH=EF﹣BD;
(3)解:如图3.1所示,
∵∠BAC=30°,∠C=90°,
∴AB=2BC,AB2=BC2+AC2,
∴,
∴BC=6,
∴AB=2BC=12,
∵CD=2BD,BC=BD+CD,
∴,
由(1)可知,BD+EF=AB,
∴EF=AB﹣BD=12﹣2=10;
如图3.2所示,当点D在线段BC的延长线上时,
∵CD<BD,与CD=2BD矛盾,
∴不符合题意;
如图3.3所示,当点D在线段CB的延长线上时,
∵CD=2BD=BD+BC,BC=6,
∴BD=BC=6,
由(2)可知,AB=EF﹣BD,
∵AB=2BC=12,
∴EF=AB+BD=12+6=18.
综上所述,EF=10或18,
故答案为:10或18.
【点评】此题考查了全等三角形的性质和判定,勾股定理,等边三角形的性质和判定,含30°角直角三角形的性质,解题的关键是掌握以上知识点.
25.(2024 赤峰)数学课上,老师给出以下条件,请同学们经过小组讨论,提出探究问题.如图1,在△ABC中,AB=AC,点D是AC上的一个动点,过点D作DE⊥BC于点E,延长ED交BA延长线于点F.
请你解决下面各组提出的问题:
(1)求证:AD=AF;
(2)探究与的关系;
某小组探究发现,当时,;当时,.
请你继续探究:
①当时,直接写出的值;
②当时,猜想的值(用含m,n的式子表示),并证明;
(3)拓展应用:在图1中,过点F作FP⊥AC,垂足为点P,连接CF,得到图2,当点D运动到使∠ACF=∠ACB时,若,直接写出的值(用含m,n的式子表示).
【分析】(1)利用等角的余角相等即可得证;
(2)①过点A作AG∥CE,利用平行线分线段成比例+等腰三角形等线段转化即可得解;②与第①问思路一样;
(3)利用等线段转化得,在作平行线,利用平行线分线段成比例求解即可.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠BED=∠CED=90°,
∴∠B+∠F=∠C+∠EDC=90°,
∴∠F=∠EDC,
∵∠ADF=∠EDC,
∴∠F=∠ADF,
∴AD=AF.
(2)解:①如图,过点A作AG∥CE,则AG⊥DF,
∴△AGD∽△CED,
∴==,
∵AF=AD,
∴GF=GD,
∴=2 =.
②如图,过点A作AG∥CE,则AG⊥DF,
∴△AGD∽△CED,
∴==,
∵AF=AD,
∴GF=GD,
∴=2 =.
(3)解:设∠ABC=∠ACB=∠ACF=α,
在Rt△FAP中和Rt△FCE中,∠FAP=∠FCE=2α,
∴tan∠FAP=tan∠FCE,
∴=,
∵AD=AF,
∴.
则我们求出的值即可.
方法一:如图,过点F作FM∥BC交CA的延长线于点M,
∵∠ACB=∠ACF=∠M,
∴CF=MF,
同理AM=AF=AD,
∴.
∴.
方法二:如图,过点E作EN∥AC交FC延长线于点N,
同方法一CE=CN,
∴,
由(2)②得,
∴=,
∴.
方法三:如图,过D作DE'⊥CF于点E',
根据角平分线性质可得DE=DE',
△CED和△CDF可以看作等高三角形,同时也是等高三角形,
∴===,
∴.
【点评】本题主要考查了相似三角形的判定和性质、平行线分线段成比例、等腰三角形的判定和性质等知识,熟练掌握相关知识和添加合适的辅助线是解题关键.
26.(2024 绥化)综合与实践
问题情境
在一次综合与实践课上,老师让同学们以两个全等的等腰直角三角形纸片为操作对象.纸片△ABC和△DEF满足∠ACB=∠EDF=90°,AC=BC=DF=DE=2cm.
下面是创新小组的探究过程.
操作发现
(1)如图1,取AB的中点O,将两张纸片放置在同一平面内,使点O与点F重合.当旋转△DEF纸片交AC边于点H、交BC边于点G时,设AH=x(1<x<2),BG=y,请你探究出y与x的函数关系式,并写出解答过程.
问题解决
(2)如图2,在(1)的条件下连接GH,发现△CGH的周长是一个定值.请你写出这个定值,并说明理由.
拓展延伸
(3)如图3,当点F在AB边上运动(不包括端点A、B),且始终保持∠AFE=60°.请你直接写出△DEF纸片的斜边EF与△ABC纸片的直角边所夹锐角的正切值 2+或2﹣ (结果保留根号).
【分析】(1)证明△AFH∽△BGF,可得AH BG=AF BF,求出,可得,故,=2,从而y与x的函数关系式为;
(2)求出CH=2﹣x,CG=2﹣y,可得===,将xy=2代入得=,而1<x<2,1<y<2,知x+y>2,故GH=x+y﹣2,可得△CHG 的周长=CH+CG+GH=2﹣x+2﹣y+x+y﹣2=2;
(3)分两种情况:①过点F作 FN⊥AC于点N,作FH的垂直平分线交FN于点M,连接MH,求出∠AHF=75°,可得∠NMH=30°,设NH=k,则MH=MF=2k,从而FN=MF+MN=(2+)k,;②过点F作FN⊥BC于点N,作FG的垂直平分线交BG于点M,连接FM,同理可得GN=GM+MN=(2+)k,.
【解答】解:(1)如图:
∵∠ACB=∠EDF=90°,且 AC=BC=DF=DE=2cm,
∴∠A=∠B=∠DFE=45°,
∴∠AFH+∠BFG=∠BFG+∠FGB=135°,
∴∠AFH=∠FGB,
∴△AFH∽△BGF,
∴,
∴AH BG=AF BF,
在 Rt△ACB 中,AC=BC=2,
∴,
∵O是AB的中点,点O与点F重合,
∴,
∴,
∴,
∴y与x的函数关系式为;
(2)△CGH的周长定值为2,理由如下:
∵AC=BC=2,AH=x,BG=y,
∴CH=2﹣x,CG=2﹣y,
在Rt△HCG 中,
∴===,
将(1)中xy=2代入得:=,
∵1<x<2,y=,
∴1<y<2,
∴x+y>2,
∴GH=x+y﹣2,
∴△CHG 的周长=CH+CG+GH=2﹣x+2﹣y+x+y﹣2=2;
(3)①过点F作 FN⊥AC于点N,作FH的垂直平分线交FN于点M,连接MH,如图:
∵∠AFE=60°,∠A=45°,
∴∠AHF=75°,
∴FM=MH,
∵∠FNH=90°,
∴∠NFH=15°,
∵FM=MH,
∴∠NFH=∠MHF=15°,
∴∠NMH=30°,
在 Rt△MNH中,设NH=k,
∴MH=MF=2k,
∴MN==k,
∴FN=MF+MN=(2+)k,
在Rt△FNH中,
;
②过点F作FN⊥BC于点N,作FG的垂直平分线交BG于点M,连接FM,
∵∠AFE=60°,∠B=45°,
∴∠FGB=∠AFE﹣∠B=15°,
∵GM=MF,
∴∠FGB=∠GFM=15°,
∴∠FMB=30°,
在 Rt△FNM中,设FN=k,
∴GM=MF=2k,
由勾股定理得MN==k,
∴GN=GM+MN=(2+)k,
在 Rt△FNG 中,
,
综上所述,tan 或 ,
故答案为:2+或2﹣.
【点评】本题考查几何变换综合应用,涉及相似三角形判定与性质,等腰直角三角形性质及应用,锐角三角函数,勾股定理及应用等知识,解题的关键是作辅助线,构造直角三角形解决问题.
27.(2024 贵州)综合与探究:如图,∠AOB=90°,点P在∠AOB的平分线上,PA⊥OA于点A.
(1)【操作判断】
如图①,过点P作PC⊥OB于点C,根据题意在图①中画出PC,图中∠APC的度数为 90 度;
(2)【问题探究】
如图②,点M在线段AO上,连接PM,过点P作PN⊥PM交射线OB于点N,求证:OM+ON=2PA;
(3)【拓展延伸】
点M在射线AO上,连接PM,过点P作PN⊥PM交射线OB于点N,射线NM与射线PO相交于点F,若ON=3OM,求的值.
【分析】(1)依题意画出图形,证四边形OAPC是矩形即可求解;
(2)过P作PC⊥OB于点C,证矩形OAPC是正方形,得出OA=AP=PC=OC,再证△APM≌△CPN(ASA),得出AM=CN,然后利用线段的和差关系以及等量代换即可证明;
(3)分M在线段AO上和AO的延长线上讨论,利用相似三角形的判定和性质求解即可.
【解答】(1)解:如图,PC即为所求.
∵∠AOB=90°,PA⊥OA,PC⊥OB,
∴四边形OAPC是矩形,
∴∠APC=90°,
故答案为:90.
(2)证明:如图,过P作PC⊥OB于点C.
由(!)知四边形OAPC是矩形,
∵点P在∠AOB的平分线上,PA⊥OA,PC⊥OB,
∴PA=PC,
∴矩形OAPC是正方形,
∴OA=AP=PC=OC,∠APC=90°,
∵PN⊥PM,
∴∠APM=∠CPN=90°﹣∠MPC,
又∠MAP=∠CNP=90°,AP=CP,
∴△APM≌△CPN(ASA),
∴AM=CN,
∴OM+ON=OM+AC+CN=OM+AM+OC=OA+OC=2AP,
∴OM+ON=2PA.
(3)①当M在线段AO上时,如图,延长NM、PA交于点G.
由(2)知OM+ON=2AP,
设OM=x,则ON=3x,OA=AP=2x.
∴AM=AO﹣OM=x=OM,
∵∠MON=∠MAG=90°,∠OMN=∠AMG,
∴△MON≌△MAG(ASA),
∴AG=ON=3x,
∵AP∥OB,
∴△ONF∽△PGF,
∴=,
∴,
∴;
②当M在AO的延长线上时,如图,过P作PC⊥OB于C,并延长交MN于G.
由(2)知,四边形OAPC是正方形,
∴OA=AP=PC=OC,∠APC=90°,PC∥AO,
∵PN⊥PM,
∠APM=∠CPN=90°﹣∠MPC,
又∵∠A=∠PCN=90°,AP=CP,
∴△APM≌△CPN,
∴AM=CN,
∴ON﹣OM=OC+CN﹣OM=AO+AM﹣OM=2AO,
∵ON=3OM=x,
∴AO=x,CN=AM=2x,
∵PC∥AO,
∴△CGN∽△OMN,
∴,即,
∴CG=,
∵PC∥AO,
∴△OMF∽△PGF,
∴==,
∴=,
∴=;
综上,的值为或.
【点评】本题考查了四边形综合,同时考查了矩形的判定和性质、正方形的判定和性质、角平分线的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,明确题意,添加合适的辅助线,构造全等三角形、相似三角形,合理分类讨论是解题的关键.
28.(2024 重庆)在△ABC中,AB=AC,点D是BC边上一点(点D不与端点重合).点D关于直线AB的对称点为点E,连接AD,DE.在直线AD上取一点F,使∠EFD=∠BAC,直线EF与直线AC交于点G.
(1)如图1,若∠BAC=60°,BD<CD,∠BAD=α,求∠AGE的度数(用含α的代数式表示);
(2)如图1,若∠BAC=60°,BD<CD,用等式表示线段CG与DE之间的数量关系,并证明;
(3)如图2,若∠BAC=90°,点D从点B移动到点C的过程中,连接AE,当△AEG为等腰三角形时,请直接写出此时的值.
【分析】(1)由三角形内角和定理及外角定理结合∠EFD=∠BAC即可求解;
(2)在CG上截取CM=BD,连接BM,BE,BM交AD于点H,连接BE,AE,再证明四边形EBMG是平行四边形,可得CG=2BD,记AB 与DE的交点为点N,则由轴对称可知:DE⊥AB,NE=ND,再解Rt△BND即可;
(3)连接BE,记AB与DE的交点为点N,由轴对称知∠EAB=∠DAB,DE⊥AB,NE=ND,∠EBA=∠DBA=45°,当点G在边AC上时,由于∠EAG>90°,当△AEG为等腰三角形时,只能是AE=AG,∠BAD=α,∠AGE=α,解得α=30°,然后AF=x,解直角三角形,表示出AG=2x,CG=,即可求解;当点G在CA延长线上时,只能是GE=GA,设∠BAD=∠BAE=β,在Rt△AFE 中,90°﹣β+180°﹣2β=90°,解得β=60°,设GF=x,解直角三角形求出CG=,即可求解.
【解答】解:(1)如图1.1,
∵∠EFD=∠BAC,∠BAC=60°,
∴∠EFD=60°,
∵∠EFD=∠1+∠BAD=∠1+α,
∴∠1=60°﹣α,
∵∠AGE+∠1+∠BAC=180°,
∴∠AGE=180°﹣60°﹣∠1=120°﹣∠1,
∴∠AGE=120°﹣(60°﹣α)=60°+α;
(2)CG=;理由如下:
在CG上截取CM=BD,连接BM,BE,AE,BM交AD于点H,
∵AB=AC,∠BAC=60°,
∴△BCA为等边三角形,
∴∠ABC=∠C=60°,BC=AB,
∴△ABD≌△BCM(SAS),
∴∠3=∠4,
∵∠AHM=∠3+∠5,
∴∠AHM=∠4+∠5=60°,
∵∠EFD=∠BAC=60°,
∴∠AHM=∠EFD,
∴EG∥BM,
∵点D关于直线AB的对称点为点E,
∴AE=AD,BE=BD,∠ABE=∠ABC=60°,
∴∠EBC=120°,
∴∠EBC+∠C=180°,
∴EB∥AC,
∴四边形EBMG是平行四边形,
∴BE=GM,
∴BE=GM=BD=CM,
∴CG=2BD,记AB与DE的交点为点N,则由轴对称可知:DE⊥AB,NE=ND,
在Rt△DNB中,DN=BD sin∠ABC=BD,
∴DE=2DN=BD,
∴==,
∴CG=;
(3)连接BE,记AB与DE的交点为点N,如图2,
∵AB=AC,∠EFD=∠BAC=90°,
∴∠ABC=45°,
由轴对称知∠EAB=∠DAB=α,∠EBA=∠DBA=45°,DE⊥AB,NE=ND,
当点G在边AC上时,由于∠EAG>90°,
∴当△AEG为等腰三角形时,只能是AE=AG,
∵∠BAC=∠AFG=90°,
∴∠AGE=α,
∴∠AEG=α,
∵∠EAD=2α,
∵AE=AG,EG⊥AD,
∴∠FAG=∠EAD=2α,
在△AEG中,α+2α+2α+α=180°,
解得α=30°,
∴∠EAD=60°,
∵AE=AD,
∴△AED为等边三角形,
∴AE=ED,
设AF=x,
∵∠EAD=60°,
∴AG=AE=ED==2x,
∴DN=x,
在Rt△DAN中,AN==DN=,
∵DE⊥AB,∠ABC=45°,
∴BN==DN=x,
∴AC=AB=x+x,
∴CG=AC﹣AG=x+x﹣2x=,
∴=;
当点G在CA延长线上时,只能是GE=GA,如图3:
设∠BAD=∠BAE=β,
∴∠DAC=∠GAF=90﹣β,
∴∠EAF=180°﹣2β,
∴∠GAE=∠EAF﹣∠GAF
同课章节目录
