2024年中考数学填空题分类汇编——数与式(含解析)
文档属性
| 名称 | 2024年中考数学填空题分类汇编——数与式(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 285.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024年中考数学填空题分类汇编——函数数与式
一.填空题(共20小题)
1.(2024 兰州)因式分解:a2﹣2a+1= .
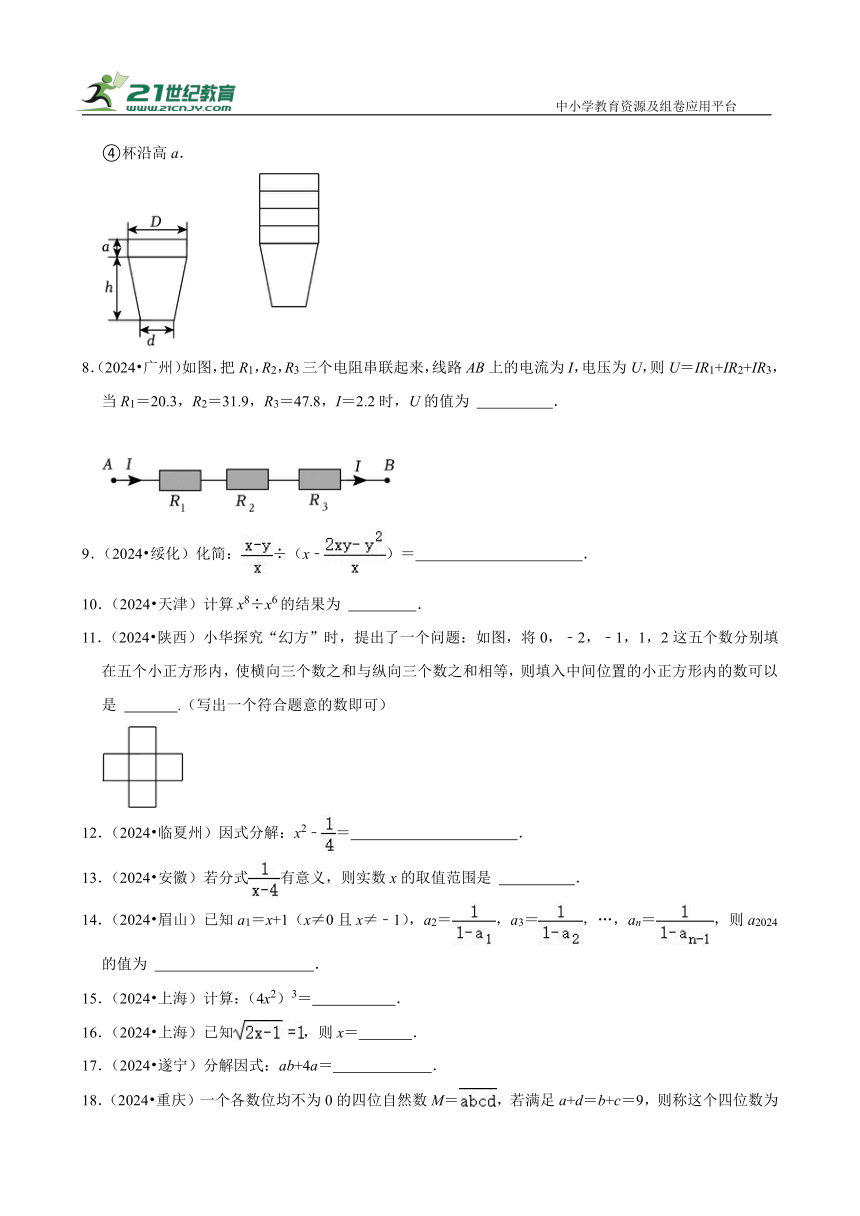
2.(2024 通辽)如图,根据机器零件的设计图纸,用不等式表示零件长度L的合格尺寸(L的取值范围) .
3.(2024 青海)如图是由火柴棒摆成的图案,按此规律摆放,第(7)个图案中有 个火柴棒.
4.(2024 广元)分解因式:(a+1)2﹣4a= .
5.(2024 内蒙古)分解因式:a+2ab+ab2= .
6.(2024 泰安)如图所示,是用图形“〇”和“●”按一定规律摆成的“小屋子”.
按照此规律继续摆下去,第 个“小屋子”中图形“〇”个数是图形“●”个数的3倍.
7.(2024 雅安)如图是1个纸杯和若干个叠放在一起的纸杯的示意图,在探究纸杯叠放在一起后的总高度H与杯子数量n的变化规律的活动中,我们可以获得以下数据(字母),请选用适当的字母表示H= .
①杯子底部到杯沿底边的高h;
②杯口直径D;
③杯底直径d;
④杯沿高a.
8.(2024 广州)如图,把R1,R2,R3三个电阻串联起来,线路AB上的电流为I,电压为U,则U=IR1+IR2+IR3,当R1=20.3,R2=31.9,R3=47.8,I=2.2时,U的值为 .
9.(2024 绥化)化简:÷(x﹣)= .
10.(2024 天津)计算x8÷x6的结果为 .
11.(2024 陕西)小华探究“幻方”时,提出了一个问题:如图,将0,﹣2,﹣1,1,2这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是 .(写出一个符合题意的数即可)
12.(2024 临夏州)因式分解:x2﹣= .
13.(2024 安徽)若分式有意义,则实数x的取值范围是 .
14.(2024 眉山)已知a1=x+1(x≠0且x≠﹣1),a2=,a3=,…,an=,则a2024的值为 .
15.(2024 上海)计算:(4x2)3= .
16.(2024 上海)已知,则x= .
17.(2024 遂宁)分解因式:ab+4a= .
18.(2024 重庆)一个各数位均不为0的四位自然数M=,若满足a+d=b+c=9,则称这个四位数为“友谊数”.例如:四位数1278,∵1+8=2+7=9,∴1278是“友谊数”.若是一个“友谊数”,且b﹣a=c﹣b=1,则这个数为 ;若M=是一个“友谊数”,设F(M)=,且是整数,则满足条件的M的最大值是 .
19.(2024 重庆)计算:|﹣2|+30= .
20.(2024 重庆)我们规定:若一个正整数A能写成m2﹣n,其中m与n都是两位数,且m与n的十位数字相同,个位数字之和为8,则称A为“方减数”,并把A分解成m2﹣n的过程,称为“方减分解”.例如:因为602=252﹣23,25与23的十位数字相同,个位数字5与3的和为8,所以602是“方减数”,602分解成602=252﹣23的过程就是“方减分解”.按照这个规定,最小的“方减数”是 .把一个“方减数”A进行“方减分解”,即A=m2﹣n,将m放在n的左边组成一个新的四位数B,若B除以19余数为1,且2m+n=k2(k为整数),则满足条件的正整数A为 .
数与式
参考答案与试题解析
一.填空题(共20小题)
1.(2024 兰州)因式分解:a2﹣2a+1= (a﹣1)2 .
【分析】本题直接利用完全平方公式进行因式分解即可.
【解答】解:a2﹣2a+1=(a﹣1)2,
故答案为:(a﹣1)2.
【点评】本题考查了因式分解,熟练掌握因式分解的方法是解题的关键.
2.(2024 通辽)如图,根据机器零件的设计图纸,用不等式表示零件长度L的合格尺寸(L的取值范围) 39.99≤L≤40.01. .
【分析】从图上可以看出:合格尺寸最小应是40﹣0.01=39.99;最大应是40+0.01=40.01.
【解答】解:根据题意,得.39.99≤L≤40.01.
故答案为:39.99≤L≤40.01.
【点评】本题考查了有理数的加减混合运算,理解40±0.01的意义是解题的关键.
3.(2024 青海)如图是由火柴棒摆成的图案,按此规律摆放,第(7)个图案中有 15 个火柴棒.
【分析】观察图形的变化即可得第1个图形火柴棒的个数;摆第2个图案要用的火柴棒;摆第3个图案要用的火柴棒;即可得第n个图形的火柴棒个数,从而可求解.
【解答】观察图形的变化可知:
摆第1个图案要用火柴棒的根数为:3;
摆第2个图案要用火柴棒的根数为:5=3+2=1+2×2;
摆第3个图案要用火柴棒的根数为:7=3+2+2=1+3×2;
…
则摆第n个图案要用火柴棒的根数为:1+2n×1=2n+1;
故第7个图案要用火柴棒的根数为:2×7+1=15.
故答案为:15.
【点评】本题主要考查规律型:图形的变化类,找出图形之间的联系,得出数字之间的运算规律,解题的关键是利用规律解决问题.
4.(2024 广元)分解因式:(a+1)2﹣4a= (a﹣1)2 .
【分析】首先利用完全平方把(a+1)2展开,然后再合并同类项,再利用完全平方公式进行分解即可.
【解答】解:(a+1)2﹣4a=a2+2a+1﹣4a=a2﹣2a+1=(a﹣1)2.
故答案为:(a﹣1)2.
【点评】此题主要考查了公式法分解因式,关键是掌握完全平方公式:a2±2ab+b2=(a±b)2.
5.(2024 内蒙古)分解因式:a+2ab+ab2= a(b+1)2 .
【分析】原式提取a,再利用完全平方公式分解即可.
【解答】解:原式=a(1+2b+b2)=a(b+1)2,
故答案为:a(b+1)2
【点评】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
6.(2024 泰安)如图所示,是用图形“〇”和“●”按一定规律摆成的“小屋子”.
按照此规律继续摆下去,第 12 个“小屋子”中图形“〇”个数是图形“●”个数的3倍.
【分析】根据所给图形,依次求出“〇”和“●”的个数,发现规律即可解决问题.
【解答】解:由所给图形可知,
第1个“小屋子”中图形“〇”的个数为:1=1,“●”的个数为:4=1×2+2;
第2个“小屋子”中图形“〇”的个数为:3=1+2,“●”的个数为:6=2×2+2;
第3个“小屋子”中图形“〇”的个数为:6=1+2+3,“●”的个数为:8=3×2+2;
第4个“小屋子”中图形“〇”的个数为:10=1+2+3+4,“●”的个数为:10=4×2+2;
…,
所以第n个“小屋子”中图形“〇”的个数为:1+2+3+…+n=,“●”的个数为:2n+2;
由题知,
,
解得n1=﹣1,n2=12,
又因为n为正整数,
所以n=12,
即第12个“小屋子”中图形“〇”个数是图形“●”个数的3倍.
故答案为:12.
【点评】本题主要考查了图形变化的规律,能根据所给图形发现“〇”和“●”的个数变化规律是解题的关键.
7.(2024 雅安)如图是1个纸杯和若干个叠放在一起的纸杯的示意图,在探究纸杯叠放在一起后的总高度H与杯子数量n的变化规律的活动中,我们可以获得以下数据(字母),请选用适当的字母表示H= h+an .
①杯子底部到杯沿底边的高h;
②杯口直径D;
③杯底直径d;
④杯沿高a.
【分析】如图可知,纸杯叠放在一起后的总高度H=杯子底部到杯沿底边的高h+杯子数量n×杯沿高a,列式即可.
【解答】解:如图可知,纸杯叠放在一起后的总高度H=杯子底部到杯沿底边的高h+杯子数量n×杯沿高a,
∴H=h+an,
故答案为:h+an.
【点评】本题考查的是数字的变化规律,熟练找出题目中字母间的变量关系是解题的关键.
8.(2024 广州)如图,把R1,R2,R3三个电阻串联起来,线路AB上的电流为I,电压为U,则U=IR1+IR2+IR3,当R1=20.3,R2=31.9,R3=47.8,I=2.2时,U的值为 220 .
【分析】根据题干条件代值即可.
【解答】解:由题意可得U=2.2×(20.3+31.9+47.8)=220.
故答案为:220.
【点评】本题主要考查有理数的混合运算,根据题意列出式子是解题关键.
9.(2024 绥化)化简:÷(x﹣)= .
【分析】先算括号内的减法,把除法变成乘法,再根据分式的乘法法则进行计算即可.
【解答】解:原式=÷
=
=,
故答案为:.
【点评】本题考查了分式的混合运算,能正确运用分式的运算法则进行化简是解此题的关键,注意运算顺序.
10.(2024 天津)计算x8÷x6的结果为 x2 .
【分析】运用同底数幂的除法法则进行求解.
【解答】解:x8÷x6=x8﹣6=x2,
故答案为:x2.
【点评】此题考查了同底数幂除法的运算能力,关键是能准确运用对应法则进行正确的计算.
11.(2024 陕西)小华探究“幻方”时,提出了一个问题:如图,将0,﹣2,﹣1,1,2这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是 0 .(写出一个符合题意的数即可)
【分析】根据题意,填写数字即可.
【解答】解:解法一:由题意,填写如下:
1+0+(﹣1)=0,2+0+(﹣2)=0,满足题意,
故答案为:0.
解法二:由题意,填写如下:
1+(﹣2)+0=﹣1,2+(﹣2)+(﹣1)=﹣1,满足题意,
故答案为:﹣2.
【点评】本题考查了有理数的运算,根据横向三个数之和与纵向三个数之和相等,进行填写即可得出结果.
12.(2024 临夏州)因式分解:x2﹣= (x+)(x﹣) .
【分析】原式利用平方差公式分解即可.
【解答】解:原式=(x+)(x﹣),
故答案为:(x+)(x﹣)
【点评】此题考查了因式分解﹣运用公式法,熟练掌握平方差公式是解本题的关键.
13.(2024 安徽)若分式有意义,则实数x的取值范围是 x≠4 .
【分析】根据分式分母不为0进行计算即可.
【解答】解:∵分式有意义,
∴x﹣4≠0,
∴x≠4,
故答案为:x≠4.
【点评】本题考查了分式有意义,分式有意义说明分母不为0.
14.(2024 眉山)已知a1=x+1(x≠0且x≠﹣1),a2=,a3=,…,an=,则a2024的值为 ﹣ .
【分析】先算出前几个式子的结果,然后根据求出的结果得出每三个数就循环一次,再根据得出的规律得出答案即可.
【解答】解:∵a1=x+1,
∴a2===﹣,
a3===,
∴a4====x+1,
∴a5=﹣,
a6=,
…,
由上可得,每三个为一个循环,
∵2024÷3=674 2,
∴a2024=﹣.
故答案为:﹣.
【点评】本题考查了分式的混合运算,数字的变化规律等知识点,能根据求出的结果得出规律是解此题的关键.
15.(2024 上海)计算:(4x2)3= 64x6 .
【分析】幂的乘方,底数不变指数相乘.
【解答】解:(4x2)3=64x6,
故答案为:64x6.
【点评】本题考查了幂的乘方,熟练掌握运算性质和法则是解题的关键.
16.(2024 上海)已知,则x= 1 .
【分析】根据算术平方根的定义,进行计算.
【解答】解:∵,
∴2x﹣1=1,
∴x=1,
故答案为:1.
【点评】本题考查了算术平方根的定义,利用两边平方进行解题即可.
17.(2024 遂宁)分解因式:ab+4a= a(b+4) .
【分析】提取a进行化简.
【解答】解:ab+4a=a(b+4),
故答案为:a(b+4).
【点评】本题考查了因式分解,重要的是找到公因式.
18.(2024 重庆)一个各数位均不为0的四位自然数M=,若满足a+d=b+c=9,则称这个四位数为“友谊数”.例如:四位数1278,∵1+8=2+7=9,∴1278是“友谊数”.若是一个“友谊数”,且b﹣a=c﹣b=1,则这个数为 3456 ;若M=是一个“友谊数”,设F(M)=,且是整数,则满足条件的M的最大值是 6273 .
【分析】根据新定义得到a+d=b+c=9,再由b﹣a=c﹣b=1可求出a、b、c、d的值,进而可得答案;先求出M=999a+90b+99,进而得到,根据是整数,得到是整数,即 是整数,则3a+b+6是13的倍数,求出a≤8,再按照a从大到小的范围讨论求解即可.
【解答】解:∵是一个“友谊数”,
∴a+d=b+c=9,
又∵b﹣a=c﹣b=1,
∴b=4,c=5,∴a=3,d=6,
∴这个数为3456;
∵是一个“友谊数”,
∴M=1000a+100b+10c+d=1000a+100b+10(9﹣b)+9﹣a=999a+90b+99,
∴,
∴====,
∵是整数,
∴是整数,即是整数,
∴3a+b+6是13的倍数,
∵a、b、c、d都是不为0的正整数,且a+d=b+c=9,
∴a≤8,
∴当a=8时,31≤3a+b+6≤38,此时不满足3a+b+6是13的倍数,不符合题意;
当a=7时,28≤3a+b+6≤35,此时不满足3a+b+6是13的倍数,不符合题意;
当a=6时,25≤3a+b+6≤32,此时可以满足3a+b+6是13的倍数,即此时b=2,则此时d=3,c=7,
∵要使M最大,则一定要满足a最大,
∴满足题意的M的最大值即为6273;
故答案为:3456;6273.
【点评】本题主要考查了新定义,理解新定义的内容是解题的关键.
19.(2024 重庆)计算:|﹣2|+30= 3 .
【分析】先化简绝对值和零指数幂,再计算.
【解答】解:|﹣2|+30=2+1=3,
故答案为:3.
【点评】本题考查了实数的计算,化简绝对值和零指数幂是解题的关键.
20.(2024 重庆)我们规定:若一个正整数A能写成m2﹣n,其中m与n都是两位数,且m与n的十位数字相同,个位数字之和为8,则称A为“方减数”,并把A分解成m2﹣n的过程,称为“方减分解”.例如:因为602=252﹣23,25与23的十位数字相同,个位数字5与3的和为8,所以602是“方减数”,602分解成602=252﹣23的过程就是“方减分解”.按照这个规定,最小的“方减数”是 82 .把一个“方减数”A进行“方减分解”,即A=m2﹣n,将m放在n的左边组成一个新的四位数B,若B除以19余数为1,且2m+n=k2(k为整数),则满足条件的正整数A为 4564 .
【分析】设m=10a+b,则n=10a+8﹣b(1≤a≤9,0≤b≤8),根据最小的“方减数”可得m=10,n=18,即可求解;根据B除以19余数为1,且2m+n=k2(k为整数),得出 为整数,30a+b+8是完全平方数,在1≤a≤9,0≤b≤8,逐个检验计算,即可求解.
【解答】解:①设m=10a+b,则n=10a+8﹣b(1≤a≤9,0≤b≤8),
由题意得:m2﹣n=(10a+b)2﹣(10a+8﹣b),
∵1≤a≤9,
∴要使“方减数”最小,需a=1,
∴m=10+b,n=18﹣b,
∴m2﹣n=(10+b)2﹣(18﹣b)=100+20b+b2﹣18+b=82+b2+21b,
当b=0时,m2﹣n 最小为82;
②设m=10a+b,则n=10a+8﹣b(1≤a≤9,0≤b≤8),
∴B=1000a+100b+10a+8﹣b=1010a+99b+8,
∵B除以19余数为1,
∴1010a+99b+7能被19整除,
∴=53a+5b+ 为整数,
又 2m+n=k2 (k为整数),
∴2(10a+b)+10a+8﹣b=30a+b+8是完全平方数,
∵1≤a≤9,0≤b≤8,
∴30a+b+8最小为49,最大为256,即7≤k≤16,
设3a+4b+7=19t,t为正整数,则1≤t≤3,
(Ⅰ) 当t=1时,3a+4b=12,则b=3﹣a,30a+b+8=30a+3﹣a+8是完全平方数,
又1≤a≤9,0≤b≤8,此时无整数解,
(Ⅱ)当t=2时,3a+4b=31,则b=,30a+b+8=30a++8是完全平方数,
又1≤a≤9,0≤b≤8,此时无整数解,
(Ⅲ)当t=3时,3a+4b=50,则, 是完全平方数,
若a=6,b=8,则3a+4b+7=57=19×3,30×6+8+8=196=142,
∴t=3,k=14,
此时m=10a+8=68,n=10a+8﹣a=60,
∴A=682﹣60=4564,
故答案为:82,4564.
【点评】本题考查因式分解的应用,涉及新定义,解题的关键是读懂题意,用含字母的式子表示相关的数.
2024年中考数学填空题分类汇编——函数数与式
一.填空题(共20小题)
1.(2024 兰州)因式分解:a2﹣2a+1= .
2.(2024 通辽)如图,根据机器零件的设计图纸,用不等式表示零件长度L的合格尺寸(L的取值范围) .
3.(2024 青海)如图是由火柴棒摆成的图案,按此规律摆放,第(7)个图案中有 个火柴棒.
4.(2024 广元)分解因式:(a+1)2﹣4a= .
5.(2024 内蒙古)分解因式:a+2ab+ab2= .
6.(2024 泰安)如图所示,是用图形“〇”和“●”按一定规律摆成的“小屋子”.
按照此规律继续摆下去,第 个“小屋子”中图形“〇”个数是图形“●”个数的3倍.
7.(2024 雅安)如图是1个纸杯和若干个叠放在一起的纸杯的示意图,在探究纸杯叠放在一起后的总高度H与杯子数量n的变化规律的活动中,我们可以获得以下数据(字母),请选用适当的字母表示H= .
①杯子底部到杯沿底边的高h;
②杯口直径D;
③杯底直径d;
④杯沿高a.
8.(2024 广州)如图,把R1,R2,R3三个电阻串联起来,线路AB上的电流为I,电压为U,则U=IR1+IR2+IR3,当R1=20.3,R2=31.9,R3=47.8,I=2.2时,U的值为 .
9.(2024 绥化)化简:÷(x﹣)= .
10.(2024 天津)计算x8÷x6的结果为 .
11.(2024 陕西)小华探究“幻方”时,提出了一个问题:如图,将0,﹣2,﹣1,1,2这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是 .(写出一个符合题意的数即可)
12.(2024 临夏州)因式分解:x2﹣= .
13.(2024 安徽)若分式有意义,则实数x的取值范围是 .
14.(2024 眉山)已知a1=x+1(x≠0且x≠﹣1),a2=,a3=,…,an=,则a2024的值为 .
15.(2024 上海)计算:(4x2)3= .
16.(2024 上海)已知,则x= .
17.(2024 遂宁)分解因式:ab+4a= .
18.(2024 重庆)一个各数位均不为0的四位自然数M=,若满足a+d=b+c=9,则称这个四位数为“友谊数”.例如:四位数1278,∵1+8=2+7=9,∴1278是“友谊数”.若是一个“友谊数”,且b﹣a=c﹣b=1,则这个数为 ;若M=是一个“友谊数”,设F(M)=,且是整数,则满足条件的M的最大值是 .
19.(2024 重庆)计算:|﹣2|+30= .
20.(2024 重庆)我们规定:若一个正整数A能写成m2﹣n,其中m与n都是两位数,且m与n的十位数字相同,个位数字之和为8,则称A为“方减数”,并把A分解成m2﹣n的过程,称为“方减分解”.例如:因为602=252﹣23,25与23的十位数字相同,个位数字5与3的和为8,所以602是“方减数”,602分解成602=252﹣23的过程就是“方减分解”.按照这个规定,最小的“方减数”是 .把一个“方减数”A进行“方减分解”,即A=m2﹣n,将m放在n的左边组成一个新的四位数B,若B除以19余数为1,且2m+n=k2(k为整数),则满足条件的正整数A为 .
数与式
参考答案与试题解析
一.填空题(共20小题)
1.(2024 兰州)因式分解:a2﹣2a+1= (a﹣1)2 .
【分析】本题直接利用完全平方公式进行因式分解即可.
【解答】解:a2﹣2a+1=(a﹣1)2,
故答案为:(a﹣1)2.
【点评】本题考查了因式分解,熟练掌握因式分解的方法是解题的关键.
2.(2024 通辽)如图,根据机器零件的设计图纸,用不等式表示零件长度L的合格尺寸(L的取值范围) 39.99≤L≤40.01. .
【分析】从图上可以看出:合格尺寸最小应是40﹣0.01=39.99;最大应是40+0.01=40.01.
【解答】解:根据题意,得.39.99≤L≤40.01.
故答案为:39.99≤L≤40.01.
【点评】本题考查了有理数的加减混合运算,理解40±0.01的意义是解题的关键.
3.(2024 青海)如图是由火柴棒摆成的图案,按此规律摆放,第(7)个图案中有 15 个火柴棒.
【分析】观察图形的变化即可得第1个图形火柴棒的个数;摆第2个图案要用的火柴棒;摆第3个图案要用的火柴棒;即可得第n个图形的火柴棒个数,从而可求解.
【解答】观察图形的变化可知:
摆第1个图案要用火柴棒的根数为:3;
摆第2个图案要用火柴棒的根数为:5=3+2=1+2×2;
摆第3个图案要用火柴棒的根数为:7=3+2+2=1+3×2;
…
则摆第n个图案要用火柴棒的根数为:1+2n×1=2n+1;
故第7个图案要用火柴棒的根数为:2×7+1=15.
故答案为:15.
【点评】本题主要考查规律型:图形的变化类,找出图形之间的联系,得出数字之间的运算规律,解题的关键是利用规律解决问题.
4.(2024 广元)分解因式:(a+1)2﹣4a= (a﹣1)2 .
【分析】首先利用完全平方把(a+1)2展开,然后再合并同类项,再利用完全平方公式进行分解即可.
【解答】解:(a+1)2﹣4a=a2+2a+1﹣4a=a2﹣2a+1=(a﹣1)2.
故答案为:(a﹣1)2.
【点评】此题主要考查了公式法分解因式,关键是掌握完全平方公式:a2±2ab+b2=(a±b)2.
5.(2024 内蒙古)分解因式:a+2ab+ab2= a(b+1)2 .
【分析】原式提取a,再利用完全平方公式分解即可.
【解答】解:原式=a(1+2b+b2)=a(b+1)2,
故答案为:a(b+1)2
【点评】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
6.(2024 泰安)如图所示,是用图形“〇”和“●”按一定规律摆成的“小屋子”.
按照此规律继续摆下去,第 12 个“小屋子”中图形“〇”个数是图形“●”个数的3倍.
【分析】根据所给图形,依次求出“〇”和“●”的个数,发现规律即可解决问题.
【解答】解:由所给图形可知,
第1个“小屋子”中图形“〇”的个数为:1=1,“●”的个数为:4=1×2+2;
第2个“小屋子”中图形“〇”的个数为:3=1+2,“●”的个数为:6=2×2+2;
第3个“小屋子”中图形“〇”的个数为:6=1+2+3,“●”的个数为:8=3×2+2;
第4个“小屋子”中图形“〇”的个数为:10=1+2+3+4,“●”的个数为:10=4×2+2;
…,
所以第n个“小屋子”中图形“〇”的个数为:1+2+3+…+n=,“●”的个数为:2n+2;
由题知,
,
解得n1=﹣1,n2=12,
又因为n为正整数,
所以n=12,
即第12个“小屋子”中图形“〇”个数是图形“●”个数的3倍.
故答案为:12.
【点评】本题主要考查了图形变化的规律,能根据所给图形发现“〇”和“●”的个数变化规律是解题的关键.
7.(2024 雅安)如图是1个纸杯和若干个叠放在一起的纸杯的示意图,在探究纸杯叠放在一起后的总高度H与杯子数量n的变化规律的活动中,我们可以获得以下数据(字母),请选用适当的字母表示H= h+an .
①杯子底部到杯沿底边的高h;
②杯口直径D;
③杯底直径d;
④杯沿高a.
【分析】如图可知,纸杯叠放在一起后的总高度H=杯子底部到杯沿底边的高h+杯子数量n×杯沿高a,列式即可.
【解答】解:如图可知,纸杯叠放在一起后的总高度H=杯子底部到杯沿底边的高h+杯子数量n×杯沿高a,
∴H=h+an,
故答案为:h+an.
【点评】本题考查的是数字的变化规律,熟练找出题目中字母间的变量关系是解题的关键.
8.(2024 广州)如图,把R1,R2,R3三个电阻串联起来,线路AB上的电流为I,电压为U,则U=IR1+IR2+IR3,当R1=20.3,R2=31.9,R3=47.8,I=2.2时,U的值为 220 .
【分析】根据题干条件代值即可.
【解答】解:由题意可得U=2.2×(20.3+31.9+47.8)=220.
故答案为:220.
【点评】本题主要考查有理数的混合运算,根据题意列出式子是解题关键.
9.(2024 绥化)化简:÷(x﹣)= .
【分析】先算括号内的减法,把除法变成乘法,再根据分式的乘法法则进行计算即可.
【解答】解:原式=÷
=
=,
故答案为:.
【点评】本题考查了分式的混合运算,能正确运用分式的运算法则进行化简是解此题的关键,注意运算顺序.
10.(2024 天津)计算x8÷x6的结果为 x2 .
【分析】运用同底数幂的除法法则进行求解.
【解答】解:x8÷x6=x8﹣6=x2,
故答案为:x2.
【点评】此题考查了同底数幂除法的运算能力,关键是能准确运用对应法则进行正确的计算.
11.(2024 陕西)小华探究“幻方”时,提出了一个问题:如图,将0,﹣2,﹣1,1,2这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是 0 .(写出一个符合题意的数即可)
【分析】根据题意,填写数字即可.
【解答】解:解法一:由题意,填写如下:
1+0+(﹣1)=0,2+0+(﹣2)=0,满足题意,
故答案为:0.
解法二:由题意,填写如下:
1+(﹣2)+0=﹣1,2+(﹣2)+(﹣1)=﹣1,满足题意,
故答案为:﹣2.
【点评】本题考查了有理数的运算,根据横向三个数之和与纵向三个数之和相等,进行填写即可得出结果.
12.(2024 临夏州)因式分解:x2﹣= (x+)(x﹣) .
【分析】原式利用平方差公式分解即可.
【解答】解:原式=(x+)(x﹣),
故答案为:(x+)(x﹣)
【点评】此题考查了因式分解﹣运用公式法,熟练掌握平方差公式是解本题的关键.
13.(2024 安徽)若分式有意义,则实数x的取值范围是 x≠4 .
【分析】根据分式分母不为0进行计算即可.
【解答】解:∵分式有意义,
∴x﹣4≠0,
∴x≠4,
故答案为:x≠4.
【点评】本题考查了分式有意义,分式有意义说明分母不为0.
14.(2024 眉山)已知a1=x+1(x≠0且x≠﹣1),a2=,a3=,…,an=,则a2024的值为 ﹣ .
【分析】先算出前几个式子的结果,然后根据求出的结果得出每三个数就循环一次,再根据得出的规律得出答案即可.
【解答】解:∵a1=x+1,
∴a2===﹣,
a3===,
∴a4====x+1,
∴a5=﹣,
a6=,
…,
由上可得,每三个为一个循环,
∵2024÷3=674 2,
∴a2024=﹣.
故答案为:﹣.
【点评】本题考查了分式的混合运算,数字的变化规律等知识点,能根据求出的结果得出规律是解此题的关键.
15.(2024 上海)计算:(4x2)3= 64x6 .
【分析】幂的乘方,底数不变指数相乘.
【解答】解:(4x2)3=64x6,
故答案为:64x6.
【点评】本题考查了幂的乘方,熟练掌握运算性质和法则是解题的关键.
16.(2024 上海)已知,则x= 1 .
【分析】根据算术平方根的定义,进行计算.
【解答】解:∵,
∴2x﹣1=1,
∴x=1,
故答案为:1.
【点评】本题考查了算术平方根的定义,利用两边平方进行解题即可.
17.(2024 遂宁)分解因式:ab+4a= a(b+4) .
【分析】提取a进行化简.
【解答】解:ab+4a=a(b+4),
故答案为:a(b+4).
【点评】本题考查了因式分解,重要的是找到公因式.
18.(2024 重庆)一个各数位均不为0的四位自然数M=,若满足a+d=b+c=9,则称这个四位数为“友谊数”.例如:四位数1278,∵1+8=2+7=9,∴1278是“友谊数”.若是一个“友谊数”,且b﹣a=c﹣b=1,则这个数为 3456 ;若M=是一个“友谊数”,设F(M)=,且是整数,则满足条件的M的最大值是 6273 .
【分析】根据新定义得到a+d=b+c=9,再由b﹣a=c﹣b=1可求出a、b、c、d的值,进而可得答案;先求出M=999a+90b+99,进而得到,根据是整数,得到是整数,即 是整数,则3a+b+6是13的倍数,求出a≤8,再按照a从大到小的范围讨论求解即可.
【解答】解:∵是一个“友谊数”,
∴a+d=b+c=9,
又∵b﹣a=c﹣b=1,
∴b=4,c=5,∴a=3,d=6,
∴这个数为3456;
∵是一个“友谊数”,
∴M=1000a+100b+10c+d=1000a+100b+10(9﹣b)+9﹣a=999a+90b+99,
∴,
∴====,
∵是整数,
∴是整数,即是整数,
∴3a+b+6是13的倍数,
∵a、b、c、d都是不为0的正整数,且a+d=b+c=9,
∴a≤8,
∴当a=8时,31≤3a+b+6≤38,此时不满足3a+b+6是13的倍数,不符合题意;
当a=7时,28≤3a+b+6≤35,此时不满足3a+b+6是13的倍数,不符合题意;
当a=6时,25≤3a+b+6≤32,此时可以满足3a+b+6是13的倍数,即此时b=2,则此时d=3,c=7,
∵要使M最大,则一定要满足a最大,
∴满足题意的M的最大值即为6273;
故答案为:3456;6273.
【点评】本题主要考查了新定义,理解新定义的内容是解题的关键.
19.(2024 重庆)计算:|﹣2|+30= 3 .
【分析】先化简绝对值和零指数幂,再计算.
【解答】解:|﹣2|+30=2+1=3,
故答案为:3.
【点评】本题考查了实数的计算,化简绝对值和零指数幂是解题的关键.
20.(2024 重庆)我们规定:若一个正整数A能写成m2﹣n,其中m与n都是两位数,且m与n的十位数字相同,个位数字之和为8,则称A为“方减数”,并把A分解成m2﹣n的过程,称为“方减分解”.例如:因为602=252﹣23,25与23的十位数字相同,个位数字5与3的和为8,所以602是“方减数”,602分解成602=252﹣23的过程就是“方减分解”.按照这个规定,最小的“方减数”是 82 .把一个“方减数”A进行“方减分解”,即A=m2﹣n,将m放在n的左边组成一个新的四位数B,若B除以19余数为1,且2m+n=k2(k为整数),则满足条件的正整数A为 4564 .
【分析】设m=10a+b,则n=10a+8﹣b(1≤a≤9,0≤b≤8),根据最小的“方减数”可得m=10,n=18,即可求解;根据B除以19余数为1,且2m+n=k2(k为整数),得出 为整数,30a+b+8是完全平方数,在1≤a≤9,0≤b≤8,逐个检验计算,即可求解.
【解答】解:①设m=10a+b,则n=10a+8﹣b(1≤a≤9,0≤b≤8),
由题意得:m2﹣n=(10a+b)2﹣(10a+8﹣b),
∵1≤a≤9,
∴要使“方减数”最小,需a=1,
∴m=10+b,n=18﹣b,
∴m2﹣n=(10+b)2﹣(18﹣b)=100+20b+b2﹣18+b=82+b2+21b,
当b=0时,m2﹣n 最小为82;
②设m=10a+b,则n=10a+8﹣b(1≤a≤9,0≤b≤8),
∴B=1000a+100b+10a+8﹣b=1010a+99b+8,
∵B除以19余数为1,
∴1010a+99b+7能被19整除,
∴=53a+5b+ 为整数,
又 2m+n=k2 (k为整数),
∴2(10a+b)+10a+8﹣b=30a+b+8是完全平方数,
∵1≤a≤9,0≤b≤8,
∴30a+b+8最小为49,最大为256,即7≤k≤16,
设3a+4b+7=19t,t为正整数,则1≤t≤3,
(Ⅰ) 当t=1时,3a+4b=12,则b=3﹣a,30a+b+8=30a+3﹣a+8是完全平方数,
又1≤a≤9,0≤b≤8,此时无整数解,
(Ⅱ)当t=2时,3a+4b=31,则b=,30a+b+8=30a++8是完全平方数,
又1≤a≤9,0≤b≤8,此时无整数解,
(Ⅲ)当t=3时,3a+4b=50,则, 是完全平方数,
若a=6,b=8,则3a+4b+7=57=19×3,30×6+8+8=196=142,
∴t=3,k=14,
此时m=10a+8=68,n=10a+8﹣a=60,
∴A=682﹣60=4564,
故答案为:82,4564.
【点评】本题考查因式分解的应用,涉及新定义,解题的关键是读懂题意,用含字母的式子表示相关的数.
同课章节目录
