2024年中考数学填空题分类汇编——图形的变化(含解析)
文档属性
| 名称 | 2024年中考数学填空题分类汇编——图形的变化(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 987.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 10:38:13 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024年中考数学填空题分类汇编——函数数与式图形的变化
一.填空题(共20小题)
1.(2024 遂宁)如图,在正方形纸片ABCD中,E是AB边的中点,将正方形纸片沿EC折叠,点B落在点P处,延长CP交AD于点Q,连结AP并延长交CD于点F.给出以下结论:①△AEP为等腰三角形;②F为CD的中点;②AP:PF=2:3;④cos∠DCQ=.其中正确结论是 (填序号).
2.(2024 烟台)如图,在 ABCD中,∠C=120°,AB=8,BC=10,E为边CD的中点,F为边AD上的一动点,将△DEF沿EF翻折得△D′EF,连接AD',BD',则△ABD′面积的最小值为 .
3.(2024 成都)如图,在Rt△ABC中,∠C=90°,AD是△ABC的一条角平分线,E为AD中点,连接BE.若BE=BC,CD=2,则BD= .
4.(2024 济宁)如图,△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.
(1)以点B为圆心,适当长为半径画弧,分别交BA,BC于点E,F.
(2)以点A为圆心,BE长为半径画弧,交AC于点G.
(3)以点G为圆心,EF长为半径画弧,与(2)中所画的弧相交于点H.
(4)画射线AH.
(5)以点B为圆心,BC长为半径画弧,交射线AH于点M.
(6)连接MC,MB.MB分别交AC,AD于点N,P.
根据以上信息,下面五个结论中正确的是 .(只填序号)
①BD=CD;②∠ABM=15°③∠APN=∠ANP;④;⑤MC2=MN MB.
5.(2024 牡丹江)如图,在正方形ABCD中,E是BC延长线上一点,AE分别交BD、CD于点F、M,过点F作NP⊥AE,分别交AD、BC于点N、P,连接MP.下列四个结论:①AM=PN;②DM+DN=DF;③若P是BC中点,AB=3,则EM=2;④BF NF=AF BP;⑤若PM∥BD,则CE=BC.其中正确的结论是 .
6.(2024 安徽)如图,现有正方形纸片ABCD,点E,F分别在边AB,BC上.沿垂直于EF的直线折叠得到折痕MN,点B,C分别落在正方形所在平面内的点B′,C′处,然后还原.
(1)若点N在边CD上,且∠BEF=α,则∠C′NM= (用含α的式子表示);
(2)再沿垂直于MN的直线折叠得到折痕GH,点G,H分别在边CD,AD上,点D落在正方形所在平面内的点D′处,然后还原.若点D′在线段B′C′上,且四边形EFGH是正方形,AE=4,EB=8,MN与GH的交点为P,则PH的长为 .
7.(2024 深圳)如图,在△ABC中,AB=BC,.D为BC上一点,且满足,过D作DE⊥AD交AC延长线于点E,则= .
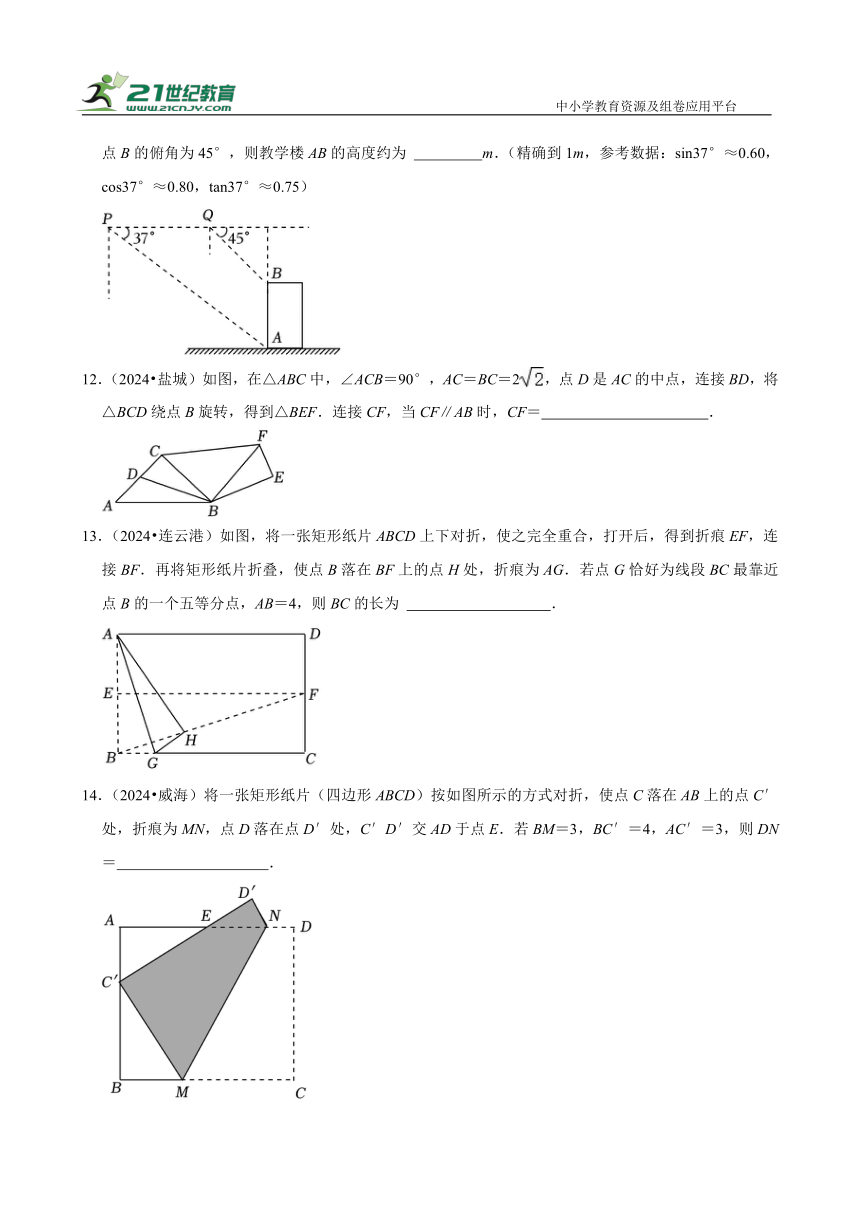
8.(2024 绥化)如图,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,测得底部点B的俯角为45°,点A与楼BC的水平距离AD=50m,则这栋楼的高度为 m(结果保留根号).
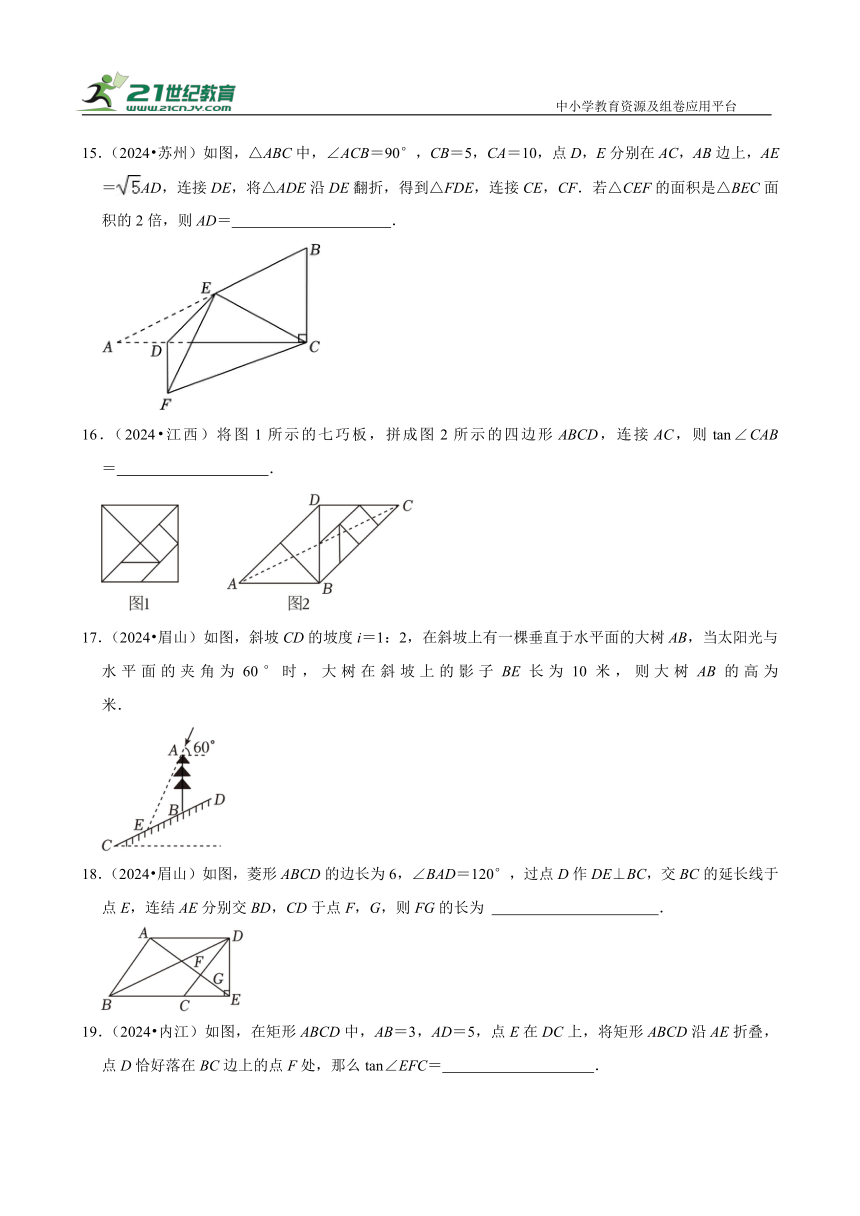
9.(2024 南充)如图,在矩形ABCD中,E为AD边上一点,∠ABE=30°,将△ABE沿BE折叠得△FBE,连接CF,DF,若CF平分∠BCD,AB=2,则DF的长为 .
10.(2024 泸州)定义:在平面直角坐标系中,将一个图形先向上平移a(a>0)个单位,再绕原点按逆时针方向旋转θ角度,这样的图形运动叫做图形的ρ(a,θ)变换.如:点A(2,0)按照ρ(1,90°)变换后得到点A'的坐标为(﹣1,2),则点B(,﹣1)按照ρ(2,105°)变换后得到点B'的坐标为 .
11.(2024 盐城)如图,小明用无人机测量教学楼的高度,将无人机垂直上升距地面30m的点P处,测得教学楼底端点A的俯角为37°,再将无人机沿教学楼方向水平飞行26.6m至点Q处,测得教学楼顶端点B的俯角为45°,则教学楼AB的高度约为 m.(精确到1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
12.(2024 盐城)如图,在△ABC中,∠ACB=90°,AC=BC=2,点D是AC的中点,连接BD,将△BCD绕点B旋转,得到△BEF.连接CF,当CF∥AB时,CF= .
13.(2024 连云港)如图,将一张矩形纸片ABCD上下对折,使之完全重合,打开后,得到折痕EF,连接BF.再将矩形纸片折叠,使点B落在BF上的点H处,折痕为AG.若点G恰好为线段BC最靠近点B的一个五等分点,AB=4,则BC的长为 .
14.(2024 威海)将一张矩形纸片(四边形ABCD)按如图所示的方式对折,使点C落在AB上的点C′处,折痕为MN,点D落在点D′处,C′D′交AD于点E.若BM=3,BC′=4,AC′=3,则DN= .
15.(2024 苏州)如图,△ABC中,∠ACB=90°,CB=5,CA=10,点D,E分别在AC,AB边上,AE=AD,连接DE,将△ADE沿DE翻折,得到△FDE,连接CE,CF.若△CEF的面积是△BEC面积的2倍,则AD= .
16.(2024 江西)将图1所示的七巧板,拼成图2所示的四边形ABCD,连接AC,则tan∠CAB= .
17.(2024 眉山)如图,斜坡CD的坡度i=1:2,在斜坡上有一棵垂直于水平面的大树AB,当太阳光与水平面的夹角为60°时,大树在斜坡上的影子BE长为10米,则大树AB的高为 米.
18.(2024 眉山)如图,菱形ABCD的边长为6,∠BAD=120°,过点D作DE⊥BC,交BC的延长线于点E,连结AE分别交BD,CD于点F,G,则FG的长为 .
19.(2024 内江)如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么tan∠EFC= .
20.(2024 武汉)黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼AB的高度.具体过程如下:如图,将无人机垂直上升至距水平地面102m的C处,测得黄鹤楼顶端A的俯角为45°,底端B的俯角为63°,则测得黄鹤楼的高度是 m.(参考数据:tan63°≈2)
图形的变化
参考答案与试题解析
一.填空题(共20小题)
1.(2024 遂宁)如图,在正方形纸片ABCD中,E是AB边的中点,将正方形纸片沿EC折叠,点B落在点P处,延长CP交AD于点Q,连结AP并延长交CD于点F.给出以下结论:①△AEP为等腰三角形;②F为CD的中点;②AP:PF=2:3;④cos∠DCQ=.其中正确结论是 ①②③ (填序号).
【分析】利用翻折的性质,证明EA=EP,即可判断①;利用AAS证明△BEC≌△DFA,即可判断②;过点P作PM⊥BC于点M,过点E作EN⊥AF于点N,设AE=BE=EP=DF=CF=a,然后求出AP,PF,再计算即可判断③;证明出AQ=PQ,再在Rt△CDQ中,利用勾股定理求出AQ,DQ,根据三角函数定义即可判断④.
【解答】解:∵E是AB边的中点,
∴EA=EB,
∵将正方形纸片沿EC折叠,点B落在点P处,
∴EB=EP,
∴EA=EP,
即△AEP为等腰三角形,故①正确;
∵EA=EP,
∴∠EAP=∠EPA,
∵将正方形纸片沿EC折叠,点B落在点P处,
∴∠BEC=∠PEC,
∵∠BEP=∠EAP+∠EPA,
∴∠BEC=∠EAP,
∵四边形ABCD是正方形,
∴∠CBE=∠ADF,AB∥CD,BC=AD,
∴∠EAP=∠DFA,
∴∠BEC=∠DFA,
∴△BEC≌△DFA(AAS),
∴DF=BE,
∴DF=AB=CD,
即F为CD的中点,故②正确;
过点P作PM⊥BC于点M,过点E作EN⊥AF于点N,
∵∠BEC=∠EAP,
∴EC∥AF,
∴EN=PM,
设AE=BE=EP=DF=CF=a,则BC=AD=PC=2a,
∴EC=AF==a,
∵S△PEC=EC PM=PE PC,
∴PM===,
∴EN=,
∴PN===,
∴AP=2PN=,
PF=AF﹣AP==,
∴AP:PF=:=2:3,故③正确;
∵∠EAP=∠EPA,∠EAD=∠EPQ=90°,
∴∠QAP=∠QPA,
∴AQ=PQ,
∵正方形的边长为2a,
∴AD=CD=CP=2a,QD=2a﹣AQ,CQ=2a+PQ=2a+AQ,
在Rt△CDQ中,
由勾股定理,得CD2+QD2=CQ2,
即(2a)2+(2a﹣AQ)2=(2a+AQ)2,
解得AQ=a,
∴DQ=2a﹣a=a,
∴CQ=2a+a=a,
∴cos∠DCQ===.故④不正确.
故答案为:①②③.
【点评】本题考查翻折变换,轴对称的性质,正方形的性质,等腰三角形的判定和性质,勾股定理,全等三角形的判定和性质,三角函数,能够熟练运用相关图形的判定和性质是解题的关键.
2.(2024 烟台)如图,在 ABCD中,∠C=120°,AB=8,BC=10,E为边CD的中点,F为边AD上的一动点,将△DEF沿EF翻折得△D′EF,连接AD',BD',则△ABD′面积的最小值为 20﹣16 .
【分析】先确定点D'是以E为圆心,CD为直径圆周上的一点,过点E作EH⊥AB交直线AB于点H,交⊙E于点G,过点D'作D'M⊥AB于点M,连接EM,推出△ABD′面积=4D'M,再求出D'M的最小值即可解决问题.
【解答】解:∵在 ABCD中,∠C=120°,AB=8,
∴∠ABC=60°,CD=8,
∵E为边CD的中点,F为边AD上的一动点,将△DEF沿EF翻折得△D′EF,
∴D'E=DE=CE=CD=4,
∴点D'是以E为圆心,CD为直径圆周上的一点,作出⊙E,如图,
过点E作EH⊥AB交直线AB于点H,交⊙E于点G,过点D'作D'M⊥AB于点M,连接EM,
∵△ABD′面积=AB D'M,AB=8,
∴△ABD′面积=4D'M,
要求△ABD′面积的最小值,只要求D'M的最小值即可,
∵D'M=D'M+D'E﹣4≥EM﹣4≥EH﹣4,
∴D'M的最小值为EH﹣4,
过点C作CN⊥AB于点N,
则EH=CN,
在Rt△BCN中,
∵BC=10,∠ABC=60°,
∴CN=BC sin60°=10×=5,
∴EH=5,
∴D'M的最小值为5﹣4,
∴△ABD′面积=4(5﹣4)=20﹣16,
故答案为:20﹣16.
【点评】本题考查翻折变换的性质,平行四边形的性质,平行线间的距离处处相等,圆的确定,直线与圆的位置关系,两点之间线段最短,垂线段最短,三角函数定义,找到△ABD′面积的最小值时,AB边上的高的位置是解题的关键.
3.(2024 成都)如图,在Rt△ABC中,∠C=90°,AD是△ABC的一条角平分线,E为AD中点,连接BE.若BE=BC,CD=2,则BD= .
【分析】连接CE,过E作EF⊥BC于F,设BD=x,则BC=x+2,由∠ACB=90°,E为AD中点,可得CE=AE=DE=AD,有∠CAE=∠ACE,∠ECD=∠EDC,证明△ECD∽△BCE,可得=,∠CED=∠CBE,故CE2=CD BC=2(x+2)=2x+4,再证△ABC∽△BEF,得=,而AC=2EF,即得2EF2=(x+1)(x+2),从而=(2x+4)﹣12,即可解得答案.
【解答】解:连接CE,过E作EF⊥BC于F,如图:
设BD=x,则BC=BD+CD=x+2,
∵∠ACB=90°,E为AD中点,
∴CE=AE=DE=AD,
∴∠CAE=∠ACE,∠ECD=∠EDC,
∴∠CED=2∠CAD,
∵BE=BC,
∴∠ECD=∠BEC,
∴∠BEC=∠EDC,
∵∠ECD=∠BCE,
∴△ECD∽△BCE,
∴=,∠CED=∠CBE,
∴CE2=CD BC=2(x+2)=2x+4,
∵AD平分∠CAB,
∴∠CAB=2∠CAD,
∴∠CAB=∠CED,
∴∠CAB=∠CBE,
∵∠ACB=90°=∠BFE,
∴△ABC∽△BEF,
∴=,
∵CE=DE,EF⊥BC,
∴CF=DF=CD=1,
∵E为AD中点,
∴AC=2EF,
∴=,
∴2EF2=(x+1)(x+2),
∵EF2=CE2﹣CF2,
∴=(2x+4)﹣12,
解得x=或x=(小于0,舍去),
∴BD=.
故答案为:.
【点评】本题考查相似三角形的判定与性质,涉及直角三角形斜边上的中线等于斜边的一半、等腰三角形的性质、三角形的中位线性质、三角形的外角性质、解一元二次方程等知识,有一定的难度,熟练掌握三角形相关知识是解答的关键.
4.(2024 济宁)如图,△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.
(1)以点B为圆心,适当长为半径画弧,分别交BA,BC于点E,F.
(2)以点A为圆心,BE长为半径画弧,交AC于点G.
(3)以点G为圆心,EF长为半径画弧,与(2)中所画的弧相交于点H.
(4)画射线AH.
(5)以点B为圆心,BC长为半径画弧,交射线AH于点M.
(6)连接MC,MB.MB分别交AC,AD于点N,P.
根据以上信息,下面五个结论中正确的是 ①②⑤ .(只填序号)
①BD=CD;②∠ABM=15°③∠APN=∠ANP;④;⑤MC2=MN MB.
【分析】根据等腰三角形的性质即可判断出①;过M作MK⊥BC于点K,证出四边形ADKM为矩形,即可通过边的比值关系求出∠MBK=30°,即可求出∠ABM判断②;利用三角形外角和分别求出两个角的值进行
比较即可判断③;设AP=x,则PD=AD﹣x,用含x的式子分别表达出AM和AD的长度后即可判断④;判定出△BMC∽△CMN即可判断⑤.
【解答】解:∵AB=AC,∠BAC=90°,
∴三角形ABC为等腰直角三角形,∠ABD=∠ACD=45°,
又∵AD是△ABC的角平分线,
∴∠BAD=∠CAD=∠BAC=×90°=45°,
∴∠ABD=∠ACD=∠BAD=∠CAD=45°,
∴BD=AD=DC,故①正确;
根据题意作图可得:∠MAC=∠ABD=45°,BM=BC,
过M作MK⊥BC于点K,则∠MKB=90°,如图:
∵AD是△ABC的角平分线,由三线合一可得:AD⊥BC,即∠ADC=90°,
∵∠DAM=∠DAC+∠MAC=45°+45°=90°,
∴∠DAM=∠MKB=∠ADC=90°,
∴四边形ADKM为矩形,
∴MK=AD=BC=BM,
∴∠MBK=30°,
∴∠ABM=∠ABD﹣∠MBK=45°﹣30°=15°,故②正确;
∵∠APN=∠ABM+∠BAD=15°+45°=60°,∠ANP=∠MBK+∠DAC=30°+45°=75°,
∴∠APN≠∠ANP,故③错误;
设AP=x,则PD=AD﹣x,
∵AM∥BC,
∴∠AMB=∠MBC=30°,
∴tan∠AMB=tan30°===,即AM=x,
tan∠MBC=tan30°===,即AD=,
∴==﹣1,故④错误;
∵∠BMC=∠BCM===75°,
∵∠MNC=∠ANP=75°,
∴∠MNC=∠BCM,
又∵∠BMC=∠CMN,
∴△BMC∽△CMN,
∴MC:MN=MB:MC,
∴MC2=MN MB,故⑤正确;
综上所述,正确的有:①②⑤;
故答案为:①②⑤.
【点评】本题为尺规作图几何综合题,涉及到了等腰三角形的性质即判定,矩形的判定,含30度角的直角三角形的定义,锐角三角函数的比值关系,相似三角形的判定及性质等知识点,灵活运用角的等量代换是解题的关键.
5.(2024 牡丹江)如图,在正方形ABCD中,E是BC延长线上一点,AE分别交BD、CD于点F、M,过点F作NP⊥AE,分别交AD、BC于点N、P,连接MP.下列四个结论:①AM=PN;②DM+DN=DF;③若P是BC中点,AB=3,则EM=2;④BF NF=AF BP;⑤若PM∥BD,则CE=BC.其中正确的结论是 ①②③⑤ .
【分析】如图1,作PG⊥AD于G,则四边形ABPG是矩形,证明△PGN≌△ADM(ASA),则AM=PN,可判断①的正误;如图2,作HF⊥DF交AD于H,连接CF,证明△ABF≌△CBF(SAS),则AF=CF,∠BAF=∠BCF,由∠BPF+∠BAF=360°﹣∠ABP﹣∠AFP=180°,∠BPF+∠FPC=180°,可得∠BAF=∠FPC,PF=CF=AF,FN=FM,证明△HFN≌△DFM(SAS),则HN=DM,由勾股定理得,,由DH=HN+DN=DM+DN,可得,可判断②的正误;如图3,连接AP,由勾股定理得,,,可求,设CE=x,则,BE=3+x,由勾股定理得,,由,可得,整理得,x2﹣2x﹣24=0,可求满足要求的解为x=6,则,BE=9,由,可得,可求,可判断③的正误;由题意知,∠BPF>90°,△BPF、△NFA不相似,BF NF≠AF BP,可判断④的正误;由设PC=CM=a,BC=CD=AD=AB=b,CE=c,则DM=b﹣a,BE=b+c,PE=a+c,,证明△AFN≌△PFM(SAS),则,证明△AMD∽△EDC,则,即,可求,同理,△ANF∽△EPF,则,即,同理,△DMF∽△BAF,则,即,可得,将代入得,,整理得,,可得,,则,可判断⑤的正误.
【解答】解:∵正方形ABCD,
∴∠ABC=∠BCD=∠CDA=∠DAB=90°,AB=BC=CD=AD,∠ADB=∠ABD=∠CBD=∠CDB=45°,
如图,作PG⊥AD于G,则四边形ABPG是矩形,
∴PG=AB=AD,
∵∠GPN+∠GNP=90°=∠GNP+∠DAM,
∴∠GPN=∠DAM,
又∵PG=AD,∠PGN=90°=∠ADM,
∴△PGN≌△ADM(ASA),
∴AM=PN,①正确,故符合要求;
如图,作HF⊥DF交AD于H,连接CF,
∴∠DHF=45°=∠ADB,
∴DF=HF,
∵AB=BC,∠ABF=∠CBF=45°,BF=BF,
∴△ABF≌△CBF(SAS),
∴AF=CF,∠BAF=∠BCF,
∵∠BPF+∠BAF=360°﹣∠ABP﹣∠AFP=180°,∠BPF+∠FPC=180°,
∴∠BAF=∠FPC,
∴∠BCF=∠FPC,
∴PF=CF=AF,
∴PN﹣PF=AM﹣AF,即FN=FM,
∵∠HFN+∠NFD=90°=∠DFM+∠NFD,
∴∠HFN=∠DFM,
∵HF=DF,∠HFN=∠DFM,FN=FM,
∴△HFN≌△DFM(SAS),
∴HN=DM,
由勾股定理得,,
∵DH=HN+DN=DM+DN,
∴,②正确,故符合要求;
∵P是BC中点,AB=3,
∴,
如图,连接AP,
由勾股定理得,,,
解得,,
设CE=x,则,BE=3+x,
由勾股定理得,,
∵,
∴,整理得,x2﹣2x﹣24=0,
解得,x=6或x=﹣4(舍去),
∴,BE=9,
∵,
∴,
解得,,③正确,故符合要求;
由题意知,∠BPF>90°,
∴△BPF、△NFA不相似,BF NF≠AF BP,④错误,故不符合要求;
∵PM∥BD,
∴∠CPM=∠CBD=45°,∠CMP=∠CDB=45°,
设PC=CM=a,BC=CD=AD=AB=b,CE=c,则DM=b﹣a,BE=b+c,PE=a+c,,
∵AF=PF,∠AFN=90°=∠PFM,FN=FM,
∴△AFN≌△PFM(SAS),
∴,
∵∠ADM=90°=∠ECM,∠AMD=∠EDC,
∴△AMD∽△EDC,
∴,即,
解得,,
同理,△ANF∽△EPF,
∴,即,
同理,△DMF∽△BAF,
∴,即,
∴,
将代入得,,整理得,,
解得,,
∴,⑤正确,故符合要求;
故答案为:①②③⑤.
【点评】本题考查了正方形的性质,全等三角形的判定与性质,等角对等边,勾股定理,正弦,余弦,相似三角形的判定与性质.熟练掌握正方形的性质,全等三角形的判定与性质,等角对等边,勾股定理,正弦,余弦,相似三角形的判定与性质是解题的关键.
6.(2024 安徽)如图,现有正方形纸片ABCD,点E,F分别在边AB,BC上.沿垂直于EF的直线折叠得到折痕MN,点B,C分别落在正方形所在平面内的点B′,C′处,然后还原.
(1)若点N在边CD上,且∠BEF=α,则∠C′NM= 90°﹣α (用含α的式子表示);
(2)再沿垂直于MN的直线折叠得到折痕GH,点G,H分别在边CD,AD上,点D落在正方形所在平面内的点D′处,然后还原.若点D′在线段B′C′上,且四边形EFGH是正方形,AE=4,EB=8,MN与GH的交点为P,则PH的长为 3 .
【分析】(1)根据已知条件推出∠EMN=90°﹣α,再利用折叠性质以及平行线即可求出答案,这也是折叠问题求角度常见处理方式;
(2)根据MN⊥GH和∠C′NM=∠CNM这一条件作为突破口,得到PG=PG'=GG'和NG=NG',从而得出C′G'=CG=4,再利用平行线分线段成比例求出G'也是GH中点即可求解.
【解答】解:(1)∵MN⊥EF,∠BEF=α,
∴∠EMN=90°﹣α,
∵CD∥AB,
∴∠CNM=∠EMN=90°﹣α,
∴∠C′NM=∠CNM=90°﹣α.
故答案为:90°﹣α.
(2)如图,设PH与NC'交于点G',
∵四边形ABCD和四边形EFGH是正方形,
∴∠A=∠D=∠GHE=90°,GH=EH,
∴∠AHE+∠GHD=∠AHE+∠AEH=90°
∴∠GHD=∠AEH,
∴△EAH≌△HDG(AAS)
同理可证△EAH≌△HDG≌△GCF≌△FBE,
∴DH=CG=AE=4,DG=EB=8,
∴GH==4,
∵MN⊥GH,且∠C′NM=∠CNM,
∴MN垂直平分GG',即PG=PG'=GG',且NG=NG',
∵四边形CBMN沿MN折叠,
∴CN=C'N,
∴CN﹣NG=C'N﹣NG',即C'G'=CG=4,
∵△GDH沿GH折叠得到△GD'H,
∴GD'=GD=8,
∵∠HC'G'=∠HD'G=90°,
∴C'G'∥D'G,
∴==,
∴HG'=GG'=HG=2,
又∵PG'=GG'=,
∴PH=PG'+HG'=3.
故答案为:3.
【点评】本题主要考查正方形的折叠问题,熟练掌握折叠和正方形的性质是解题的关键.
7.(2024 深圳)如图,在△ABC中,AB=BC,.D为BC上一点,且满足,过D作DE⊥AD交AC延长线于点E,则= .
【分析】根据问题分析:要求的值,可能需要构造相似或者平行线分线段成比例,所以作CM⊥AD于点M,从而将转化成,再根据题中条件去求解即可.
【解答】解:方法一:如图,过点A作AH⊥CB于点H,作CM⊥AD于点M,
∵AB=BC,,
设BD=8a,则CD=5a,
∴BC=AB=BD+CD=13a,
∵tanB=,
∴AH=5a,BH=12a,
∴DH=BH﹣BD=4a,CH=a,
在Rt△ACH中,AC==a,
在Rt△ADH中,AD==a,
∴cos∠ADC==,
∴DM=CD cos∠ADC=a,
∴AM=AD﹣DM=a,
∴.
故答案为:.
方法二:如图过A作AH⊥BC于点H,DM⊥AE于点M,
同方法一∵AB=BC,,
设BD=8a,则CD=5a,
∴BC=AB=BD+CD=13a,
∵tanB=,
∴AH=5a,BH=12a,
∴DH=BH﹣BD=4a,CH=a,
在Rt△ACH中,AC==a,
在Rt△ADH中,AD==a,
∵S△ADC=AH CD=AC DM
∴DM=a,AM==a,
有射影定理可知:AD2=AM ME,
∴AE=a,CE=AE﹣AC=a,
∴.
故答案为:.
方法三:如图所示建立直角坐标系,
由前述方法可得OA=5,0D=4,BD=8,OC=1,
∴A(0,5),C(1,0),D(﹣4,0),
∴AC解析式:y=﹣5x+5,
AD解析式为:y=x+5,
∵AD⊥DE,
∴DE解析式为:y=﹣x﹣,
联立AE和DE解析式得:E(,﹣)
∴==.
故答案为:.
【点评】本题主要考查了解直角三角形、平行线分线段成比例等知识点,作为填空压轴题有一定难度,其中熟练掌握相关知识和构造合适的辅助线是解题关键.
8.(2024 绥化)如图,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,测得底部点B的俯角为45°,点A与楼BC的水平距离AD=50m,则这栋楼的高度为 (50+50) m(结果保留根号).
【分析】根据题意可得:AD⊥BC,然后分别在Rt△ACD和Rt△ABD中,利用锐角三角函数的定义求出CD和BD的长,从而利用线段和差关系进行计算,即可解答.
【解答】解:由题意得:AD⊥BC,
在Rt△ACD中,∠CAD=60°,AD=50m,
∴CD=AD tan60°=50(m),
在Rt△ABD中,∠BAD=45°,
∴BD=AD tan45°=50(m),
∴BC=BD+CD=(50+50)m,
∴这栋楼的高度为(50+50)m,
故答案为:(50+50).
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
9.(2024 南充)如图,在矩形ABCD中,E为AD边上一点,∠ABE=30°,将△ABE沿BE折叠得△FBE,连接CF,DF,若CF平分∠BCD,AB=2,则DF的长为 .
【分析】过点F作FG⊥BC于点G,FH⊥CD于点H.由矩形的性质可得CD=AB=2,∠ABC=∠BCD=90°.由翻折得,BF=AB=2,∠ABE=∠FBE=30°,则∠FBG=30°,进而可得FG=BF=1,CH=FG=1,DH=CD﹣CH=1,结合角平分线的性质可得HF=FG=1,再利用勾股定理求DF的长即可.
【解答】解:过点F作FG⊥BC于点G,FH⊥CD于点H.
∵CF平分∠BCD,
∴HF=FG.
∵四边形ABCD为矩形,
∴CD=AB=2,∠ABC=∠BCD=90°.
由翻折得,BF=AB=2,∠ABE=∠FBE=30°,
∴∠FBG=30°,
∴FG=BF=1,
∴HF=1,CH=FG=1,
∴DH=CD﹣CH=1,
∴DF==.
故答案为:.
【点评】本题考查翻折变换(折叠问题)、矩形的性质、角平分线的性质,熟练掌握翻折的性质、矩形的性质、角平分线的性质是解答本题的关键.
10.(2024 泸州)定义:在平面直角坐标系中,将一个图形先向上平移a(a>0)个单位,再绕原点按逆时针方向旋转θ角度,这样的图形运动叫做图形的ρ(a,θ)变换.如:点A(2,0)按照ρ(1,90°)变换后得到点A'的坐标为(﹣1,2),则点B(,﹣1)按照ρ(2,105°)变换后得到点B'的坐标为 () .
【分析】根据题中的定义,画出示意图,结合图形旋转及平移的性质即可解决问题.
【解答】解:由题知,
将点B()向上平移2个单位所得点M的坐标为().
如图所示,
过点M作x轴的垂线,垂足为F,
则OF=,MF=1.
在Rt△MOF中,
tan∠MOF=,OM=,
所以∠MOF=30°.
由旋转可知,
B′O=MO=2,∠MOB′=105°,
所以∠B′OF=135°.
过点B′作y轴的垂线,垂足为E,
则∠B′OE=135°﹣90°=45°,
所以△B′OE是等腰直角三角形.
又因为B′O=2,
所以B′E=OE=,
所以点B′的坐标为().
故答案为:().
【点评】本题考查坐标与图形变化﹣平移及坐标与图形变化﹣旋转,能根据题意画出示意图及熟知图形平移和旋转的性质是解题的关键.
11.(2024 盐城)如图,小明用无人机测量教学楼的高度,将无人机垂直上升距地面30m的点P处,测得教学楼底端点A的俯角为37°,再将无人机沿教学楼方向水平飞行26.6m至点Q处,测得教学楼顶端点B的俯角为45°,则教学楼AB的高度约为 17 m.(精确到1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
【分析】令AB的延长线于PQ的延长线交于点C,先求出PC,从而得到QC,BC,再利用AB=AC﹣BC即可求出AB.
【解答】解:如图,令AB的延长线于PQ的延长线交于点C,
由题意,知AC=30m,PQ=26.6m,∠APC=37°,∠BQC=45°,
在Rt△APC中,
PC=≈=40(m),
∴QC=PC﹣PQ=40﹣26.6=13.4(m),
在Rt△BQC中,
BC=QC=13.4m,
∴AB=AC﹣BC=30﹣13.4=16.6≈17(m),
故答案为:17.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,理解题意,能熟练运用三角函数关系是解题的关键.
12.(2024 盐城)如图,在△ABC中,∠ACB=90°,AC=BC=2,点D是AC的中点,连接BD,将△BCD绕点B旋转,得到△BEF.连接CF,当CF∥AB时,CF= 2+或﹣2 .
【分析】根据旋转的性质可知:△DCB≌△FEB,根据勾股定理可以求得BD的值,然后再根据平行线的性质和勾股定理、锐角三角函数,可以求得CG和GF的值,从而可以求得CF的值;还有一种情况就是点F在点C的左侧时,同理可以求得CF的值.
【解答】解:作BG⊥CF于点G,如图所示,
∵∠ACB=90°,AC=BC=2,点D是AC的中点,
∴CD=,∠ABC=45°,
∴BD===,
由旋转的性质可知:△DCB≌△FEB,
∴BD=BF=,
∵CF∥AB,
∴∠ABC=∠BCG=45°,
∴CG=BC sin∠BCG=2×=2,
∴BG==2,
∴GF===,
∴CF=CG+GF=2+;
当点D运动点F′时,此时CF′∥AB,
同理可得,GF′=,CG=2,
∴CF′=﹣2;
故答案为:2+或﹣2.
【点评】本题考查旋转的性质、全等三角形的性质、勾股定理、锐角三角函数,解答本题的关键是明确题意,利用数形结合的思想解答.
13.(2024 连云港)如图,将一张矩形纸片ABCD上下对折,使之完全重合,打开后,得到折痕EF,连接BF.再将矩形纸片折叠,使点B落在BF上的点H处,折痕为AG.若点G恰好为线段BC最靠近点B的一个五等分点,AB=4,则BC的长为 .
【分析】设AG与BF交于点M,BG=a,则BC=5a,勾股定理求出AG,BF,根据等面积法求出BM,根据,列出方程进行求解即可.
【解答】解:方法一:设AG与BF交于点M,
∵四边形ABCD是矩形,
∴∠ABC=∠C=90°,AB=CD=4,
∵翻折,
∴,AG⊥BH,
设BG=a,则BC=5a,
∴,,
∵,
∴,
∵∠BMG=∠C=90°,
∴tan,
∴BM BF=BG BC,
∴,
∴,经检验是原方程的解,
∴,
方法二:∵△ABG∽△BCF,
∴,
∴,
∴,
∴,
故答案为:.
【点评】本题考查矩形折叠,勾股定理,解直角三角形,掌握性质和综合推理能力是解题的关键.
14.(2024 威海)将一张矩形纸片(四边形ABCD)按如图所示的方式对折,使点C落在AB上的点C′处,折痕为MN,点D落在点D′处,C′D′交AD于点E.若BM=3,BC′=4,AC′=3,则DN= .
【分析】本题考查矩形的折叠问题,全等三角形的判定和性质,勾股定理,先根据勾股定理求出 C′M=CM=5,然后证明△BC′M≌△AEC′,得到 BC'=AE=4,MC'=CE=5,即可得到DE=4,D′E=2,然后在Rt△D′EF 中,利用 NE2=D'E2+D'N2 解题即可.
【解答】解:在 RtΔC'BM 中,,
由折叠可得 C′M=CM=5,∠D'C'M=∠D'=∠D=∠C=90°,
又∵ABCD是矩形,
∴∠A=∠B=90°,
∴∠BC'M+∠AC'E=∠AEC'+∠AC'E=90°,
∴∠BC′M=∠AEC′,
又∵AC′=BM=3,
∴△BC'M≌△AEC'(AAS),
∴BC'=AE=4,MC'=CE=5,
∴AB=CD=C′D′=7,BC=AD=BM+CM=3+5=8,
∴DE=AD﹣AE=8﹣4=4,DE=C′D′﹣C′E=7﹣5=2,
设DN=DN=α,则EN=4﹣α,
在 Rt△D′EF 中,NE2=D'E2+D'N2,即 (4﹣a)2=a2+22,
解得:.
故答案为:
【点评】本题考查翻折变换,矩形的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
15.(2024 苏州)如图,△ABC中,∠ACB=90°,CB=5,CA=10,点D,E分别在AC,AB边上,AE=AD,连接DE,将△ADE沿DE翻折,得到△FDE,连接CE,CF.若△CEF的面积是△BEC面积的2倍,则AD= .
【分析】设AD=x,,根据折叠性质得DF=AD=x,∠ADE=∠FDE,过E作EH⊥AC于H,设EF与AC相交于M,证明△AHE∽△ACB,得到,进而得到EH=x,AH=2x,证明Rt△EHD是等腰直角三角形,得到∠HDE=∠HED=45°,可得∠FDM=90°,证明△FDM≌△EHM(AAS),得到,则,根据三角形的面积公式结合已知可得,然后解一元二次方程求解x的值即可.
【解答】解:∵,
∴设AD=x,,
∵△ADE沿DE翻折,得到△FDE,
∴DF=AD=x,∠ADE=∠FDE,
过E作EH⊥AC于H,设EF与AC相交于M,
则∠AHE=∠ACB=90°,
又∵∠A=∠A,
∴△AHE∽△ACB,
∴,
∵CB=5,CA=10,,
∴,
∴EH=x,,则DH=AH﹣AD=x=EH,
∴Rt△EHD是等腰直角三角形,
∴∠HDE=∠HED=45°,则∠ADE=∠EDF=135°,
∴∠FDM=135°﹣45°=90°,
在△FDM和△EHM中,
,
∴△FDM≌△EHM(AAS),
∴,,
∴,
=25﹣5x,
∵△CEF的面积是△BEC的面积的2倍,
∴,
则3x2﹣40x+100=0,
解得,x2=10(舍去),
则,
故答案为:.
【点评】本题考查了相似三角形的判定与性质、折叠性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、三角形的面积公式等知识,是综合性强的填空压轴题,熟练掌握相关知识的联系与运用是解 答的关键.
16.(2024 江西)将图1所示的七巧板,拼成图2所示的四边形ABCD,连接AC,则tan∠CAB= .
【分析】根据所给拼图,得出四边形ABCD是平行四边形,根据平行四边形的性质及正切的定义即可解决问题.
【解答】解:令AC与BD的交点为O,
∵∠ABD=∠CDB=90°,
∴CD∥AB,
又∵AB=CD,
∴四边形ABCD是平行四边形,
∴AC与BD互相平分,
∴OB=.
∵AB=BD,
∴OB=.
在Rt△AOB中,
tan∠CAB=.
故答案为:.
【点评】本题考查解直角三角形、七巧板及平行四边形的判定与性质,能根据所拼图形得出四边形ABCD是平行四边形及熟知正切的定义是解题的关键.
17.(2024 眉山)如图,斜坡CD的坡度i=1:2,在斜坡上有一棵垂直于水平面的大树AB,当太阳光与水平面的夹角为60°时,大树在斜坡上的影子BE长为10米,则大树AB的高为 (4﹣2) 米.
【分析】过点E作水平地面的平行线,交AB的延长线于点H,解直角三角形即可得到结论.
【解答】解:如图,过点E作水平地面的平行线,交AB的延长线于点H,
则∠BEH=∠DCF,
在Rt△BEH中,tan∠BEH=tan∠BCF==,
设BH=x米,EH=2x米,
∴BE==x=10,
∴x=2,
∴BH=2米,EH=4米,
∵∠EAH=180°﹣60°﹣90°=30°,
∴AH==4(米),
∴AB=AH﹣BH=(4﹣2)(米),
答:大树AB的高度为(4﹣2)米.
故答案为:(4﹣2).
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,熟记锐角三角函数的定义是解题的关键.
18.(2024 眉山)如图,菱形ABCD的边长为6,∠BAD=120°,过点D作DE⊥BC,交BC的延长线于点E,连结AE分别交BD,CD于点F,G,则FG的长为 .
【分析】先根据菱形的性质得到AD=BC=CD=6,AD∥BC,∠BCD=120°,则∠DCE=60°,再在Rt△DCE中利用含30度角的直角三角形三边的关系得到CE=3,DE=3,接着在Rt△ADE中利用勾股定理计算出AE=3,然后证明△AFD∽△EFB,利用相似比和比例的性质计算出AF=,同样方法计算出AG=2,最后计算AG﹣AF即可.
【解答】解:∵菱形ABCD的边长为6,∠BAD=120°,
∴AD=BC=CD=6,AD∥BC,∠BCD=120°,
∴∠DCE=60°,
∵DE⊥BC,
∴∠DEC=90°,
在Rt△DCE中,∵∠CDE=90°﹣∠DCE=30°,
∴CE=CD=3,
∴DE=CE=3,
∴BE=BC+CE=9,
∵AD∥BE,
∴∠ADE=180°﹣∠DEC=90°,
在Rt△ADE中,AE===3,
∵AD∥BE,
∴△AFD∽△EFB,
∴===,
∴AF=AE=×3=,
∵AD∥CE,
∴△AGD∽△EGC,
∴===2,
∴AG=AE=×3=2,
∴FG=AG﹣AF=2﹣=.
故答案为:.
【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用;灵活运用相似三角形的性质计算相应线段的长或表示线段之间的关系是解决问题的关键.也考查了菱形的性质.
19.(2024 内江)如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么tan∠EFC= .
【分析】先根据矩形的性质得BC=AD=5,CD=AB=3,再根据折叠的性质得AF=AD=5,EF=DE,在Rt△ABF中,利用勾股定理计算出BF=4,则CF=BC﹣BF=1,设CE=x,则DE=EF=3﹣x,然后在Rt△ECF中根据勾股定理得到x2+12=(3﹣x)2,解方程即可得到x,进一步得到EF的长,再根据正切数的定义即可求解.
【解答】解:∵四边形ABCD为矩形,
∴BC=AD=5,CD=AB=3,∠B=∠C=90°,
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=5,EF=DE,
∴在Rt△ABF中,,
∴CF=BC﹣BF=5﹣4=1,
设CE=x,则EF=DE=CD﹣CE=3﹣x,
∵在Rt△ECF中,CE2+FC2=EF2,
∴x2+12=(3﹣x)2,解得,
∴,
∴,
故答案为:.
【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理,正切的定义.
20.(2024 武汉)黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼AB的高度.具体过程如下:如图,将无人机垂直上升至距水平地面102m的C处,测得黄鹤楼顶端A的俯角为45°,底端B的俯角为63°,则测得黄鹤楼的高度是 51 m.(参考数据:tan63°≈2)
【分析】过点C作CH∥BD,延长BA交CH于H,在Rt△BCH中和Rt△ACH中,解直角三角形求出CH,AH,即可求出答案.
【解答】解:过点C作CH∥BD,延长BA交CH于H,
由题意得∠ABD=∠CDB=90°,
∴∠AHC=180°﹣90°=90°,
∴四边形BDCH是矩形,
∴BH=CD=102m,
在Rt△BCH中,∠BCH=63°,tan∠BCH=,
∴CH=≈=51(m),
在Rt△ACH中,∠ACH=45°,
∴∠CAH=45°=∠ACH,∴AH=CH=51m,
∴AB=BH﹣AH=51m.
答:黄鹤楼的高度约为51m.
故答案为:51.
【点评】本题主要考查了直角三角形的应用,把实际问题转换为直角三角形问题解决是解决问题的关键.
2024年中考数学填空题分类汇编——函数数与式图形的变化
一.填空题(共20小题)
1.(2024 遂宁)如图,在正方形纸片ABCD中,E是AB边的中点,将正方形纸片沿EC折叠,点B落在点P处,延长CP交AD于点Q,连结AP并延长交CD于点F.给出以下结论:①△AEP为等腰三角形;②F为CD的中点;②AP:PF=2:3;④cos∠DCQ=.其中正确结论是 (填序号).
2.(2024 烟台)如图,在 ABCD中,∠C=120°,AB=8,BC=10,E为边CD的中点,F为边AD上的一动点,将△DEF沿EF翻折得△D′EF,连接AD',BD',则△ABD′面积的最小值为 .
3.(2024 成都)如图,在Rt△ABC中,∠C=90°,AD是△ABC的一条角平分线,E为AD中点,连接BE.若BE=BC,CD=2,则BD= .
4.(2024 济宁)如图,△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.
(1)以点B为圆心,适当长为半径画弧,分别交BA,BC于点E,F.
(2)以点A为圆心,BE长为半径画弧,交AC于点G.
(3)以点G为圆心,EF长为半径画弧,与(2)中所画的弧相交于点H.
(4)画射线AH.
(5)以点B为圆心,BC长为半径画弧,交射线AH于点M.
(6)连接MC,MB.MB分别交AC,AD于点N,P.
根据以上信息,下面五个结论中正确的是 .(只填序号)
①BD=CD;②∠ABM=15°③∠APN=∠ANP;④;⑤MC2=MN MB.
5.(2024 牡丹江)如图,在正方形ABCD中,E是BC延长线上一点,AE分别交BD、CD于点F、M,过点F作NP⊥AE,分别交AD、BC于点N、P,连接MP.下列四个结论:①AM=PN;②DM+DN=DF;③若P是BC中点,AB=3,则EM=2;④BF NF=AF BP;⑤若PM∥BD,则CE=BC.其中正确的结论是 .
6.(2024 安徽)如图,现有正方形纸片ABCD,点E,F分别在边AB,BC上.沿垂直于EF的直线折叠得到折痕MN,点B,C分别落在正方形所在平面内的点B′,C′处,然后还原.
(1)若点N在边CD上,且∠BEF=α,则∠C′NM= (用含α的式子表示);
(2)再沿垂直于MN的直线折叠得到折痕GH,点G,H分别在边CD,AD上,点D落在正方形所在平面内的点D′处,然后还原.若点D′在线段B′C′上,且四边形EFGH是正方形,AE=4,EB=8,MN与GH的交点为P,则PH的长为 .
7.(2024 深圳)如图,在△ABC中,AB=BC,.D为BC上一点,且满足,过D作DE⊥AD交AC延长线于点E,则= .
8.(2024 绥化)如图,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,测得底部点B的俯角为45°,点A与楼BC的水平距离AD=50m,则这栋楼的高度为 m(结果保留根号).
9.(2024 南充)如图,在矩形ABCD中,E为AD边上一点,∠ABE=30°,将△ABE沿BE折叠得△FBE,连接CF,DF,若CF平分∠BCD,AB=2,则DF的长为 .
10.(2024 泸州)定义:在平面直角坐标系中,将一个图形先向上平移a(a>0)个单位,再绕原点按逆时针方向旋转θ角度,这样的图形运动叫做图形的ρ(a,θ)变换.如:点A(2,0)按照ρ(1,90°)变换后得到点A'的坐标为(﹣1,2),则点B(,﹣1)按照ρ(2,105°)变换后得到点B'的坐标为 .
11.(2024 盐城)如图,小明用无人机测量教学楼的高度,将无人机垂直上升距地面30m的点P处,测得教学楼底端点A的俯角为37°,再将无人机沿教学楼方向水平飞行26.6m至点Q处,测得教学楼顶端点B的俯角为45°,则教学楼AB的高度约为 m.(精确到1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
12.(2024 盐城)如图,在△ABC中,∠ACB=90°,AC=BC=2,点D是AC的中点,连接BD,将△BCD绕点B旋转,得到△BEF.连接CF,当CF∥AB时,CF= .
13.(2024 连云港)如图,将一张矩形纸片ABCD上下对折,使之完全重合,打开后,得到折痕EF,连接BF.再将矩形纸片折叠,使点B落在BF上的点H处,折痕为AG.若点G恰好为线段BC最靠近点B的一个五等分点,AB=4,则BC的长为 .
14.(2024 威海)将一张矩形纸片(四边形ABCD)按如图所示的方式对折,使点C落在AB上的点C′处,折痕为MN,点D落在点D′处,C′D′交AD于点E.若BM=3,BC′=4,AC′=3,则DN= .
15.(2024 苏州)如图,△ABC中,∠ACB=90°,CB=5,CA=10,点D,E分别在AC,AB边上,AE=AD,连接DE,将△ADE沿DE翻折,得到△FDE,连接CE,CF.若△CEF的面积是△BEC面积的2倍,则AD= .
16.(2024 江西)将图1所示的七巧板,拼成图2所示的四边形ABCD,连接AC,则tan∠CAB= .
17.(2024 眉山)如图,斜坡CD的坡度i=1:2,在斜坡上有一棵垂直于水平面的大树AB,当太阳光与水平面的夹角为60°时,大树在斜坡上的影子BE长为10米,则大树AB的高为 米.
18.(2024 眉山)如图,菱形ABCD的边长为6,∠BAD=120°,过点D作DE⊥BC,交BC的延长线于点E,连结AE分别交BD,CD于点F,G,则FG的长为 .
19.(2024 内江)如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么tan∠EFC= .
20.(2024 武汉)黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼AB的高度.具体过程如下:如图,将无人机垂直上升至距水平地面102m的C处,测得黄鹤楼顶端A的俯角为45°,底端B的俯角为63°,则测得黄鹤楼的高度是 m.(参考数据:tan63°≈2)
图形的变化
参考答案与试题解析
一.填空题(共20小题)
1.(2024 遂宁)如图,在正方形纸片ABCD中,E是AB边的中点,将正方形纸片沿EC折叠,点B落在点P处,延长CP交AD于点Q,连结AP并延长交CD于点F.给出以下结论:①△AEP为等腰三角形;②F为CD的中点;②AP:PF=2:3;④cos∠DCQ=.其中正确结论是 ①②③ (填序号).
【分析】利用翻折的性质,证明EA=EP,即可判断①;利用AAS证明△BEC≌△DFA,即可判断②;过点P作PM⊥BC于点M,过点E作EN⊥AF于点N,设AE=BE=EP=DF=CF=a,然后求出AP,PF,再计算即可判断③;证明出AQ=PQ,再在Rt△CDQ中,利用勾股定理求出AQ,DQ,根据三角函数定义即可判断④.
【解答】解:∵E是AB边的中点,
∴EA=EB,
∵将正方形纸片沿EC折叠,点B落在点P处,
∴EB=EP,
∴EA=EP,
即△AEP为等腰三角形,故①正确;
∵EA=EP,
∴∠EAP=∠EPA,
∵将正方形纸片沿EC折叠,点B落在点P处,
∴∠BEC=∠PEC,
∵∠BEP=∠EAP+∠EPA,
∴∠BEC=∠EAP,
∵四边形ABCD是正方形,
∴∠CBE=∠ADF,AB∥CD,BC=AD,
∴∠EAP=∠DFA,
∴∠BEC=∠DFA,
∴△BEC≌△DFA(AAS),
∴DF=BE,
∴DF=AB=CD,
即F为CD的中点,故②正确;
过点P作PM⊥BC于点M,过点E作EN⊥AF于点N,
∵∠BEC=∠EAP,
∴EC∥AF,
∴EN=PM,
设AE=BE=EP=DF=CF=a,则BC=AD=PC=2a,
∴EC=AF==a,
∵S△PEC=EC PM=PE PC,
∴PM===,
∴EN=,
∴PN===,
∴AP=2PN=,
PF=AF﹣AP==,
∴AP:PF=:=2:3,故③正确;
∵∠EAP=∠EPA,∠EAD=∠EPQ=90°,
∴∠QAP=∠QPA,
∴AQ=PQ,
∵正方形的边长为2a,
∴AD=CD=CP=2a,QD=2a﹣AQ,CQ=2a+PQ=2a+AQ,
在Rt△CDQ中,
由勾股定理,得CD2+QD2=CQ2,
即(2a)2+(2a﹣AQ)2=(2a+AQ)2,
解得AQ=a,
∴DQ=2a﹣a=a,
∴CQ=2a+a=a,
∴cos∠DCQ===.故④不正确.
故答案为:①②③.
【点评】本题考查翻折变换,轴对称的性质,正方形的性质,等腰三角形的判定和性质,勾股定理,全等三角形的判定和性质,三角函数,能够熟练运用相关图形的判定和性质是解题的关键.
2.(2024 烟台)如图,在 ABCD中,∠C=120°,AB=8,BC=10,E为边CD的中点,F为边AD上的一动点,将△DEF沿EF翻折得△D′EF,连接AD',BD',则△ABD′面积的最小值为 20﹣16 .
【分析】先确定点D'是以E为圆心,CD为直径圆周上的一点,过点E作EH⊥AB交直线AB于点H,交⊙E于点G,过点D'作D'M⊥AB于点M,连接EM,推出△ABD′面积=4D'M,再求出D'M的最小值即可解决问题.
【解答】解:∵在 ABCD中,∠C=120°,AB=8,
∴∠ABC=60°,CD=8,
∵E为边CD的中点,F为边AD上的一动点,将△DEF沿EF翻折得△D′EF,
∴D'E=DE=CE=CD=4,
∴点D'是以E为圆心,CD为直径圆周上的一点,作出⊙E,如图,
过点E作EH⊥AB交直线AB于点H,交⊙E于点G,过点D'作D'M⊥AB于点M,连接EM,
∵△ABD′面积=AB D'M,AB=8,
∴△ABD′面积=4D'M,
要求△ABD′面积的最小值,只要求D'M的最小值即可,
∵D'M=D'M+D'E﹣4≥EM﹣4≥EH﹣4,
∴D'M的最小值为EH﹣4,
过点C作CN⊥AB于点N,
则EH=CN,
在Rt△BCN中,
∵BC=10,∠ABC=60°,
∴CN=BC sin60°=10×=5,
∴EH=5,
∴D'M的最小值为5﹣4,
∴△ABD′面积=4(5﹣4)=20﹣16,
故答案为:20﹣16.
【点评】本题考查翻折变换的性质,平行四边形的性质,平行线间的距离处处相等,圆的确定,直线与圆的位置关系,两点之间线段最短,垂线段最短,三角函数定义,找到△ABD′面积的最小值时,AB边上的高的位置是解题的关键.
3.(2024 成都)如图,在Rt△ABC中,∠C=90°,AD是△ABC的一条角平分线,E为AD中点,连接BE.若BE=BC,CD=2,则BD= .
【分析】连接CE,过E作EF⊥BC于F,设BD=x,则BC=x+2,由∠ACB=90°,E为AD中点,可得CE=AE=DE=AD,有∠CAE=∠ACE,∠ECD=∠EDC,证明△ECD∽△BCE,可得=,∠CED=∠CBE,故CE2=CD BC=2(x+2)=2x+4,再证△ABC∽△BEF,得=,而AC=2EF,即得2EF2=(x+1)(x+2),从而=(2x+4)﹣12,即可解得答案.
【解答】解:连接CE,过E作EF⊥BC于F,如图:
设BD=x,则BC=BD+CD=x+2,
∵∠ACB=90°,E为AD中点,
∴CE=AE=DE=AD,
∴∠CAE=∠ACE,∠ECD=∠EDC,
∴∠CED=2∠CAD,
∵BE=BC,
∴∠ECD=∠BEC,
∴∠BEC=∠EDC,
∵∠ECD=∠BCE,
∴△ECD∽△BCE,
∴=,∠CED=∠CBE,
∴CE2=CD BC=2(x+2)=2x+4,
∵AD平分∠CAB,
∴∠CAB=2∠CAD,
∴∠CAB=∠CED,
∴∠CAB=∠CBE,
∵∠ACB=90°=∠BFE,
∴△ABC∽△BEF,
∴=,
∵CE=DE,EF⊥BC,
∴CF=DF=CD=1,
∵E为AD中点,
∴AC=2EF,
∴=,
∴2EF2=(x+1)(x+2),
∵EF2=CE2﹣CF2,
∴=(2x+4)﹣12,
解得x=或x=(小于0,舍去),
∴BD=.
故答案为:.
【点评】本题考查相似三角形的判定与性质,涉及直角三角形斜边上的中线等于斜边的一半、等腰三角形的性质、三角形的中位线性质、三角形的外角性质、解一元二次方程等知识,有一定的难度,熟练掌握三角形相关知识是解答的关键.
4.(2024 济宁)如图,△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.
(1)以点B为圆心,适当长为半径画弧,分别交BA,BC于点E,F.
(2)以点A为圆心,BE长为半径画弧,交AC于点G.
(3)以点G为圆心,EF长为半径画弧,与(2)中所画的弧相交于点H.
(4)画射线AH.
(5)以点B为圆心,BC长为半径画弧,交射线AH于点M.
(6)连接MC,MB.MB分别交AC,AD于点N,P.
根据以上信息,下面五个结论中正确的是 ①②⑤ .(只填序号)
①BD=CD;②∠ABM=15°③∠APN=∠ANP;④;⑤MC2=MN MB.
【分析】根据等腰三角形的性质即可判断出①;过M作MK⊥BC于点K,证出四边形ADKM为矩形,即可通过边的比值关系求出∠MBK=30°,即可求出∠ABM判断②;利用三角形外角和分别求出两个角的值进行
比较即可判断③;设AP=x,则PD=AD﹣x,用含x的式子分别表达出AM和AD的长度后即可判断④;判定出△BMC∽△CMN即可判断⑤.
【解答】解:∵AB=AC,∠BAC=90°,
∴三角形ABC为等腰直角三角形,∠ABD=∠ACD=45°,
又∵AD是△ABC的角平分线,
∴∠BAD=∠CAD=∠BAC=×90°=45°,
∴∠ABD=∠ACD=∠BAD=∠CAD=45°,
∴BD=AD=DC,故①正确;
根据题意作图可得:∠MAC=∠ABD=45°,BM=BC,
过M作MK⊥BC于点K,则∠MKB=90°,如图:
∵AD是△ABC的角平分线,由三线合一可得:AD⊥BC,即∠ADC=90°,
∵∠DAM=∠DAC+∠MAC=45°+45°=90°,
∴∠DAM=∠MKB=∠ADC=90°,
∴四边形ADKM为矩形,
∴MK=AD=BC=BM,
∴∠MBK=30°,
∴∠ABM=∠ABD﹣∠MBK=45°﹣30°=15°,故②正确;
∵∠APN=∠ABM+∠BAD=15°+45°=60°,∠ANP=∠MBK+∠DAC=30°+45°=75°,
∴∠APN≠∠ANP,故③错误;
设AP=x,则PD=AD﹣x,
∵AM∥BC,
∴∠AMB=∠MBC=30°,
∴tan∠AMB=tan30°===,即AM=x,
tan∠MBC=tan30°===,即AD=,
∴==﹣1,故④错误;
∵∠BMC=∠BCM===75°,
∵∠MNC=∠ANP=75°,
∴∠MNC=∠BCM,
又∵∠BMC=∠CMN,
∴△BMC∽△CMN,
∴MC:MN=MB:MC,
∴MC2=MN MB,故⑤正确;
综上所述,正确的有:①②⑤;
故答案为:①②⑤.
【点评】本题为尺规作图几何综合题,涉及到了等腰三角形的性质即判定,矩形的判定,含30度角的直角三角形的定义,锐角三角函数的比值关系,相似三角形的判定及性质等知识点,灵活运用角的等量代换是解题的关键.
5.(2024 牡丹江)如图,在正方形ABCD中,E是BC延长线上一点,AE分别交BD、CD于点F、M,过点F作NP⊥AE,分别交AD、BC于点N、P,连接MP.下列四个结论:①AM=PN;②DM+DN=DF;③若P是BC中点,AB=3,则EM=2;④BF NF=AF BP;⑤若PM∥BD,则CE=BC.其中正确的结论是 ①②③⑤ .
【分析】如图1,作PG⊥AD于G,则四边形ABPG是矩形,证明△PGN≌△ADM(ASA),则AM=PN,可判断①的正误;如图2,作HF⊥DF交AD于H,连接CF,证明△ABF≌△CBF(SAS),则AF=CF,∠BAF=∠BCF,由∠BPF+∠BAF=360°﹣∠ABP﹣∠AFP=180°,∠BPF+∠FPC=180°,可得∠BAF=∠FPC,PF=CF=AF,FN=FM,证明△HFN≌△DFM(SAS),则HN=DM,由勾股定理得,,由DH=HN+DN=DM+DN,可得,可判断②的正误;如图3,连接AP,由勾股定理得,,,可求,设CE=x,则,BE=3+x,由勾股定理得,,由,可得,整理得,x2﹣2x﹣24=0,可求满足要求的解为x=6,则,BE=9,由,可得,可求,可判断③的正误;由题意知,∠BPF>90°,△BPF、△NFA不相似,BF NF≠AF BP,可判断④的正误;由设PC=CM=a,BC=CD=AD=AB=b,CE=c,则DM=b﹣a,BE=b+c,PE=a+c,,证明△AFN≌△PFM(SAS),则,证明△AMD∽△EDC,则,即,可求,同理,△ANF∽△EPF,则,即,同理,△DMF∽△BAF,则,即,可得,将代入得,,整理得,,可得,,则,可判断⑤的正误.
【解答】解:∵正方形ABCD,
∴∠ABC=∠BCD=∠CDA=∠DAB=90°,AB=BC=CD=AD,∠ADB=∠ABD=∠CBD=∠CDB=45°,
如图,作PG⊥AD于G,则四边形ABPG是矩形,
∴PG=AB=AD,
∵∠GPN+∠GNP=90°=∠GNP+∠DAM,
∴∠GPN=∠DAM,
又∵PG=AD,∠PGN=90°=∠ADM,
∴△PGN≌△ADM(ASA),
∴AM=PN,①正确,故符合要求;
如图,作HF⊥DF交AD于H,连接CF,
∴∠DHF=45°=∠ADB,
∴DF=HF,
∵AB=BC,∠ABF=∠CBF=45°,BF=BF,
∴△ABF≌△CBF(SAS),
∴AF=CF,∠BAF=∠BCF,
∵∠BPF+∠BAF=360°﹣∠ABP﹣∠AFP=180°,∠BPF+∠FPC=180°,
∴∠BAF=∠FPC,
∴∠BCF=∠FPC,
∴PF=CF=AF,
∴PN﹣PF=AM﹣AF,即FN=FM,
∵∠HFN+∠NFD=90°=∠DFM+∠NFD,
∴∠HFN=∠DFM,
∵HF=DF,∠HFN=∠DFM,FN=FM,
∴△HFN≌△DFM(SAS),
∴HN=DM,
由勾股定理得,,
∵DH=HN+DN=DM+DN,
∴,②正确,故符合要求;
∵P是BC中点,AB=3,
∴,
如图,连接AP,
由勾股定理得,,,
解得,,
设CE=x,则,BE=3+x,
由勾股定理得,,
∵,
∴,整理得,x2﹣2x﹣24=0,
解得,x=6或x=﹣4(舍去),
∴,BE=9,
∵,
∴,
解得,,③正确,故符合要求;
由题意知,∠BPF>90°,
∴△BPF、△NFA不相似,BF NF≠AF BP,④错误,故不符合要求;
∵PM∥BD,
∴∠CPM=∠CBD=45°,∠CMP=∠CDB=45°,
设PC=CM=a,BC=CD=AD=AB=b,CE=c,则DM=b﹣a,BE=b+c,PE=a+c,,
∵AF=PF,∠AFN=90°=∠PFM,FN=FM,
∴△AFN≌△PFM(SAS),
∴,
∵∠ADM=90°=∠ECM,∠AMD=∠EDC,
∴△AMD∽△EDC,
∴,即,
解得,,
同理,△ANF∽△EPF,
∴,即,
同理,△DMF∽△BAF,
∴,即,
∴,
将代入得,,整理得,,
解得,,
∴,⑤正确,故符合要求;
故答案为:①②③⑤.
【点评】本题考查了正方形的性质,全等三角形的判定与性质,等角对等边,勾股定理,正弦,余弦,相似三角形的判定与性质.熟练掌握正方形的性质,全等三角形的判定与性质,等角对等边,勾股定理,正弦,余弦,相似三角形的判定与性质是解题的关键.
6.(2024 安徽)如图,现有正方形纸片ABCD,点E,F分别在边AB,BC上.沿垂直于EF的直线折叠得到折痕MN,点B,C分别落在正方形所在平面内的点B′,C′处,然后还原.
(1)若点N在边CD上,且∠BEF=α,则∠C′NM= 90°﹣α (用含α的式子表示);
(2)再沿垂直于MN的直线折叠得到折痕GH,点G,H分别在边CD,AD上,点D落在正方形所在平面内的点D′处,然后还原.若点D′在线段B′C′上,且四边形EFGH是正方形,AE=4,EB=8,MN与GH的交点为P,则PH的长为 3 .
【分析】(1)根据已知条件推出∠EMN=90°﹣α,再利用折叠性质以及平行线即可求出答案,这也是折叠问题求角度常见处理方式;
(2)根据MN⊥GH和∠C′NM=∠CNM这一条件作为突破口,得到PG=PG'=GG'和NG=NG',从而得出C′G'=CG=4,再利用平行线分线段成比例求出G'也是GH中点即可求解.
【解答】解:(1)∵MN⊥EF,∠BEF=α,
∴∠EMN=90°﹣α,
∵CD∥AB,
∴∠CNM=∠EMN=90°﹣α,
∴∠C′NM=∠CNM=90°﹣α.
故答案为:90°﹣α.
(2)如图,设PH与NC'交于点G',
∵四边形ABCD和四边形EFGH是正方形,
∴∠A=∠D=∠GHE=90°,GH=EH,
∴∠AHE+∠GHD=∠AHE+∠AEH=90°
∴∠GHD=∠AEH,
∴△EAH≌△HDG(AAS)
同理可证△EAH≌△HDG≌△GCF≌△FBE,
∴DH=CG=AE=4,DG=EB=8,
∴GH==4,
∵MN⊥GH,且∠C′NM=∠CNM,
∴MN垂直平分GG',即PG=PG'=GG',且NG=NG',
∵四边形CBMN沿MN折叠,
∴CN=C'N,
∴CN﹣NG=C'N﹣NG',即C'G'=CG=4,
∵△GDH沿GH折叠得到△GD'H,
∴GD'=GD=8,
∵∠HC'G'=∠HD'G=90°,
∴C'G'∥D'G,
∴==,
∴HG'=GG'=HG=2,
又∵PG'=GG'=,
∴PH=PG'+HG'=3.
故答案为:3.
【点评】本题主要考查正方形的折叠问题,熟练掌握折叠和正方形的性质是解题的关键.
7.(2024 深圳)如图,在△ABC中,AB=BC,.D为BC上一点,且满足,过D作DE⊥AD交AC延长线于点E,则= .
【分析】根据问题分析:要求的值,可能需要构造相似或者平行线分线段成比例,所以作CM⊥AD于点M,从而将转化成,再根据题中条件去求解即可.
【解答】解:方法一:如图,过点A作AH⊥CB于点H,作CM⊥AD于点M,
∵AB=BC,,
设BD=8a,则CD=5a,
∴BC=AB=BD+CD=13a,
∵tanB=,
∴AH=5a,BH=12a,
∴DH=BH﹣BD=4a,CH=a,
在Rt△ACH中,AC==a,
在Rt△ADH中,AD==a,
∴cos∠ADC==,
∴DM=CD cos∠ADC=a,
∴AM=AD﹣DM=a,
∴.
故答案为:.
方法二:如图过A作AH⊥BC于点H,DM⊥AE于点M,
同方法一∵AB=BC,,
设BD=8a,则CD=5a,
∴BC=AB=BD+CD=13a,
∵tanB=,
∴AH=5a,BH=12a,
∴DH=BH﹣BD=4a,CH=a,
在Rt△ACH中,AC==a,
在Rt△ADH中,AD==a,
∵S△ADC=AH CD=AC DM
∴DM=a,AM==a,
有射影定理可知:AD2=AM ME,
∴AE=a,CE=AE﹣AC=a,
∴.
故答案为:.
方法三:如图所示建立直角坐标系,
由前述方法可得OA=5,0D=4,BD=8,OC=1,
∴A(0,5),C(1,0),D(﹣4,0),
∴AC解析式:y=﹣5x+5,
AD解析式为:y=x+5,
∵AD⊥DE,
∴DE解析式为:y=﹣x﹣,
联立AE和DE解析式得:E(,﹣)
∴==.
故答案为:.
【点评】本题主要考查了解直角三角形、平行线分线段成比例等知识点,作为填空压轴题有一定难度,其中熟练掌握相关知识和构造合适的辅助线是解题关键.
8.(2024 绥化)如图,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,测得底部点B的俯角为45°,点A与楼BC的水平距离AD=50m,则这栋楼的高度为 (50+50) m(结果保留根号).
【分析】根据题意可得:AD⊥BC,然后分别在Rt△ACD和Rt△ABD中,利用锐角三角函数的定义求出CD和BD的长,从而利用线段和差关系进行计算,即可解答.
【解答】解:由题意得:AD⊥BC,
在Rt△ACD中,∠CAD=60°,AD=50m,
∴CD=AD tan60°=50(m),
在Rt△ABD中,∠BAD=45°,
∴BD=AD tan45°=50(m),
∴BC=BD+CD=(50+50)m,
∴这栋楼的高度为(50+50)m,
故答案为:(50+50).
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
9.(2024 南充)如图,在矩形ABCD中,E为AD边上一点,∠ABE=30°,将△ABE沿BE折叠得△FBE,连接CF,DF,若CF平分∠BCD,AB=2,则DF的长为 .
【分析】过点F作FG⊥BC于点G,FH⊥CD于点H.由矩形的性质可得CD=AB=2,∠ABC=∠BCD=90°.由翻折得,BF=AB=2,∠ABE=∠FBE=30°,则∠FBG=30°,进而可得FG=BF=1,CH=FG=1,DH=CD﹣CH=1,结合角平分线的性质可得HF=FG=1,再利用勾股定理求DF的长即可.
【解答】解:过点F作FG⊥BC于点G,FH⊥CD于点H.
∵CF平分∠BCD,
∴HF=FG.
∵四边形ABCD为矩形,
∴CD=AB=2,∠ABC=∠BCD=90°.
由翻折得,BF=AB=2,∠ABE=∠FBE=30°,
∴∠FBG=30°,
∴FG=BF=1,
∴HF=1,CH=FG=1,
∴DH=CD﹣CH=1,
∴DF==.
故答案为:.
【点评】本题考查翻折变换(折叠问题)、矩形的性质、角平分线的性质,熟练掌握翻折的性质、矩形的性质、角平分线的性质是解答本题的关键.
10.(2024 泸州)定义:在平面直角坐标系中,将一个图形先向上平移a(a>0)个单位,再绕原点按逆时针方向旋转θ角度,这样的图形运动叫做图形的ρ(a,θ)变换.如:点A(2,0)按照ρ(1,90°)变换后得到点A'的坐标为(﹣1,2),则点B(,﹣1)按照ρ(2,105°)变换后得到点B'的坐标为 () .
【分析】根据题中的定义,画出示意图,结合图形旋转及平移的性质即可解决问题.
【解答】解:由题知,
将点B()向上平移2个单位所得点M的坐标为().
如图所示,
过点M作x轴的垂线,垂足为F,
则OF=,MF=1.
在Rt△MOF中,
tan∠MOF=,OM=,
所以∠MOF=30°.
由旋转可知,
B′O=MO=2,∠MOB′=105°,
所以∠B′OF=135°.
过点B′作y轴的垂线,垂足为E,
则∠B′OE=135°﹣90°=45°,
所以△B′OE是等腰直角三角形.
又因为B′O=2,
所以B′E=OE=,
所以点B′的坐标为().
故答案为:().
【点评】本题考查坐标与图形变化﹣平移及坐标与图形变化﹣旋转,能根据题意画出示意图及熟知图形平移和旋转的性质是解题的关键.
11.(2024 盐城)如图,小明用无人机测量教学楼的高度,将无人机垂直上升距地面30m的点P处,测得教学楼底端点A的俯角为37°,再将无人机沿教学楼方向水平飞行26.6m至点Q处,测得教学楼顶端点B的俯角为45°,则教学楼AB的高度约为 17 m.(精确到1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
【分析】令AB的延长线于PQ的延长线交于点C,先求出PC,从而得到QC,BC,再利用AB=AC﹣BC即可求出AB.
【解答】解:如图,令AB的延长线于PQ的延长线交于点C,
由题意,知AC=30m,PQ=26.6m,∠APC=37°,∠BQC=45°,
在Rt△APC中,
PC=≈=40(m),
∴QC=PC﹣PQ=40﹣26.6=13.4(m),
在Rt△BQC中,
BC=QC=13.4m,
∴AB=AC﹣BC=30﹣13.4=16.6≈17(m),
故答案为:17.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,理解题意,能熟练运用三角函数关系是解题的关键.
12.(2024 盐城)如图,在△ABC中,∠ACB=90°,AC=BC=2,点D是AC的中点,连接BD,将△BCD绕点B旋转,得到△BEF.连接CF,当CF∥AB时,CF= 2+或﹣2 .
【分析】根据旋转的性质可知:△DCB≌△FEB,根据勾股定理可以求得BD的值,然后再根据平行线的性质和勾股定理、锐角三角函数,可以求得CG和GF的值,从而可以求得CF的值;还有一种情况就是点F在点C的左侧时,同理可以求得CF的值.
【解答】解:作BG⊥CF于点G,如图所示,
∵∠ACB=90°,AC=BC=2,点D是AC的中点,
∴CD=,∠ABC=45°,
∴BD===,
由旋转的性质可知:△DCB≌△FEB,
∴BD=BF=,
∵CF∥AB,
∴∠ABC=∠BCG=45°,
∴CG=BC sin∠BCG=2×=2,
∴BG==2,
∴GF===,
∴CF=CG+GF=2+;
当点D运动点F′时,此时CF′∥AB,
同理可得,GF′=,CG=2,
∴CF′=﹣2;
故答案为:2+或﹣2.
【点评】本题考查旋转的性质、全等三角形的性质、勾股定理、锐角三角函数,解答本题的关键是明确题意,利用数形结合的思想解答.
13.(2024 连云港)如图,将一张矩形纸片ABCD上下对折,使之完全重合,打开后,得到折痕EF,连接BF.再将矩形纸片折叠,使点B落在BF上的点H处,折痕为AG.若点G恰好为线段BC最靠近点B的一个五等分点,AB=4,则BC的长为 .
【分析】设AG与BF交于点M,BG=a,则BC=5a,勾股定理求出AG,BF,根据等面积法求出BM,根据,列出方程进行求解即可.
【解答】解:方法一:设AG与BF交于点M,
∵四边形ABCD是矩形,
∴∠ABC=∠C=90°,AB=CD=4,
∵翻折,
∴,AG⊥BH,
设BG=a,则BC=5a,
∴,,
∵,
∴,
∵∠BMG=∠C=90°,
∴tan,
∴BM BF=BG BC,
∴,
∴,经检验是原方程的解,
∴,
方法二:∵△ABG∽△BCF,
∴,
∴,
∴,
∴,
故答案为:.
【点评】本题考查矩形折叠,勾股定理,解直角三角形,掌握性质和综合推理能力是解题的关键.
14.(2024 威海)将一张矩形纸片(四边形ABCD)按如图所示的方式对折,使点C落在AB上的点C′处,折痕为MN,点D落在点D′处,C′D′交AD于点E.若BM=3,BC′=4,AC′=3,则DN= .
【分析】本题考查矩形的折叠问题,全等三角形的判定和性质,勾股定理,先根据勾股定理求出 C′M=CM=5,然后证明△BC′M≌△AEC′,得到 BC'=AE=4,MC'=CE=5,即可得到DE=4,D′E=2,然后在Rt△D′EF 中,利用 NE2=D'E2+D'N2 解题即可.
【解答】解:在 RtΔC'BM 中,,
由折叠可得 C′M=CM=5,∠D'C'M=∠D'=∠D=∠C=90°,
又∵ABCD是矩形,
∴∠A=∠B=90°,
∴∠BC'M+∠AC'E=∠AEC'+∠AC'E=90°,
∴∠BC′M=∠AEC′,
又∵AC′=BM=3,
∴△BC'M≌△AEC'(AAS),
∴BC'=AE=4,MC'=CE=5,
∴AB=CD=C′D′=7,BC=AD=BM+CM=3+5=8,
∴DE=AD﹣AE=8﹣4=4,DE=C′D′﹣C′E=7﹣5=2,
设DN=DN=α,则EN=4﹣α,
在 Rt△D′EF 中,NE2=D'E2+D'N2,即 (4﹣a)2=a2+22,
解得:.
故答案为:
【点评】本题考查翻折变换,矩形的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
15.(2024 苏州)如图,△ABC中,∠ACB=90°,CB=5,CA=10,点D,E分别在AC,AB边上,AE=AD,连接DE,将△ADE沿DE翻折,得到△FDE,连接CE,CF.若△CEF的面积是△BEC面积的2倍,则AD= .
【分析】设AD=x,,根据折叠性质得DF=AD=x,∠ADE=∠FDE,过E作EH⊥AC于H,设EF与AC相交于M,证明△AHE∽△ACB,得到,进而得到EH=x,AH=2x,证明Rt△EHD是等腰直角三角形,得到∠HDE=∠HED=45°,可得∠FDM=90°,证明△FDM≌△EHM(AAS),得到,则,根据三角形的面积公式结合已知可得,然后解一元二次方程求解x的值即可.
【解答】解:∵,
∴设AD=x,,
∵△ADE沿DE翻折,得到△FDE,
∴DF=AD=x,∠ADE=∠FDE,
过E作EH⊥AC于H,设EF与AC相交于M,
则∠AHE=∠ACB=90°,
又∵∠A=∠A,
∴△AHE∽△ACB,
∴,
∵CB=5,CA=10,,
∴,
∴EH=x,,则DH=AH﹣AD=x=EH,
∴Rt△EHD是等腰直角三角形,
∴∠HDE=∠HED=45°,则∠ADE=∠EDF=135°,
∴∠FDM=135°﹣45°=90°,
在△FDM和△EHM中,
,
∴△FDM≌△EHM(AAS),
∴,,
∴,
=25﹣5x,
∵△CEF的面积是△BEC的面积的2倍,
∴,
则3x2﹣40x+100=0,
解得,x2=10(舍去),
则,
故答案为:.
【点评】本题考查了相似三角形的判定与性质、折叠性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、三角形的面积公式等知识,是综合性强的填空压轴题,熟练掌握相关知识的联系与运用是解 答的关键.
16.(2024 江西)将图1所示的七巧板,拼成图2所示的四边形ABCD,连接AC,则tan∠CAB= .
【分析】根据所给拼图,得出四边形ABCD是平行四边形,根据平行四边形的性质及正切的定义即可解决问题.
【解答】解:令AC与BD的交点为O,
∵∠ABD=∠CDB=90°,
∴CD∥AB,
又∵AB=CD,
∴四边形ABCD是平行四边形,
∴AC与BD互相平分,
∴OB=.
∵AB=BD,
∴OB=.
在Rt△AOB中,
tan∠CAB=.
故答案为:.
【点评】本题考查解直角三角形、七巧板及平行四边形的判定与性质,能根据所拼图形得出四边形ABCD是平行四边形及熟知正切的定义是解题的关键.
17.(2024 眉山)如图,斜坡CD的坡度i=1:2,在斜坡上有一棵垂直于水平面的大树AB,当太阳光与水平面的夹角为60°时,大树在斜坡上的影子BE长为10米,则大树AB的高为 (4﹣2) 米.
【分析】过点E作水平地面的平行线,交AB的延长线于点H,解直角三角形即可得到结论.
【解答】解:如图,过点E作水平地面的平行线,交AB的延长线于点H,
则∠BEH=∠DCF,
在Rt△BEH中,tan∠BEH=tan∠BCF==,
设BH=x米,EH=2x米,
∴BE==x=10,
∴x=2,
∴BH=2米,EH=4米,
∵∠EAH=180°﹣60°﹣90°=30°,
∴AH==4(米),
∴AB=AH﹣BH=(4﹣2)(米),
答:大树AB的高度为(4﹣2)米.
故答案为:(4﹣2).
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,熟记锐角三角函数的定义是解题的关键.
18.(2024 眉山)如图,菱形ABCD的边长为6,∠BAD=120°,过点D作DE⊥BC,交BC的延长线于点E,连结AE分别交BD,CD于点F,G,则FG的长为 .
【分析】先根据菱形的性质得到AD=BC=CD=6,AD∥BC,∠BCD=120°,则∠DCE=60°,再在Rt△DCE中利用含30度角的直角三角形三边的关系得到CE=3,DE=3,接着在Rt△ADE中利用勾股定理计算出AE=3,然后证明△AFD∽△EFB,利用相似比和比例的性质计算出AF=,同样方法计算出AG=2,最后计算AG﹣AF即可.
【解答】解:∵菱形ABCD的边长为6,∠BAD=120°,
∴AD=BC=CD=6,AD∥BC,∠BCD=120°,
∴∠DCE=60°,
∵DE⊥BC,
∴∠DEC=90°,
在Rt△DCE中,∵∠CDE=90°﹣∠DCE=30°,
∴CE=CD=3,
∴DE=CE=3,
∴BE=BC+CE=9,
∵AD∥BE,
∴∠ADE=180°﹣∠DEC=90°,
在Rt△ADE中,AE===3,
∵AD∥BE,
∴△AFD∽△EFB,
∴===,
∴AF=AE=×3=,
∵AD∥CE,
∴△AGD∽△EGC,
∴===2,
∴AG=AE=×3=2,
∴FG=AG﹣AF=2﹣=.
故答案为:.
【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用;灵活运用相似三角形的性质计算相应线段的长或表示线段之间的关系是解决问题的关键.也考查了菱形的性质.
19.(2024 内江)如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么tan∠EFC= .
【分析】先根据矩形的性质得BC=AD=5,CD=AB=3,再根据折叠的性质得AF=AD=5,EF=DE,在Rt△ABF中,利用勾股定理计算出BF=4,则CF=BC﹣BF=1,设CE=x,则DE=EF=3﹣x,然后在Rt△ECF中根据勾股定理得到x2+12=(3﹣x)2,解方程即可得到x,进一步得到EF的长,再根据正切数的定义即可求解.
【解答】解:∵四边形ABCD为矩形,
∴BC=AD=5,CD=AB=3,∠B=∠C=90°,
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=5,EF=DE,
∴在Rt△ABF中,,
∴CF=BC﹣BF=5﹣4=1,
设CE=x,则EF=DE=CD﹣CE=3﹣x,
∵在Rt△ECF中,CE2+FC2=EF2,
∴x2+12=(3﹣x)2,解得,
∴,
∴,
故答案为:.
【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理,正切的定义.
20.(2024 武汉)黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼AB的高度.具体过程如下:如图,将无人机垂直上升至距水平地面102m的C处,测得黄鹤楼顶端A的俯角为45°,底端B的俯角为63°,则测得黄鹤楼的高度是 51 m.(参考数据:tan63°≈2)
【分析】过点C作CH∥BD,延长BA交CH于H,在Rt△BCH中和Rt△ACH中,解直角三角形求出CH,AH,即可求出答案.
【解答】解:过点C作CH∥BD,延长BA交CH于H,
由题意得∠ABD=∠CDB=90°,
∴∠AHC=180°﹣90°=90°,
∴四边形BDCH是矩形,
∴BH=CD=102m,
在Rt△BCH中,∠BCH=63°,tan∠BCH=,
∴CH=≈=51(m),
在Rt△ACH中,∠ACH=45°,
∴∠CAH=45°=∠ACH,∴AH=CH=51m,
∴AB=BH﹣AH=51m.
答:黄鹤楼的高度约为51m.
故答案为:51.
【点评】本题主要考查了直角三角形的应用,把实际问题转换为直角三角形问题解决是解决问题的关键.
同课章节目录
