2024年中考数学填空题分类汇编——图形的性质(含解析)
文档属性
| 名称 | 2024年中考数学填空题分类汇编——图形的性质(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 10:54:01 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024年中考数学填空题分类汇编——函数数与式图形的性质
一.填空题(共30小题)
1.(2024 资阳)如图,在矩形ABCD中,AB=4,AD=2.以点A为圆心,AD长为半径作弧交AB于点E,再以AB为直径作半圆,与交于点F,则图中阴影部分的面积为 .
2.(2024 兰州)“轮动发石车”是我国古代的一种投石工具,在春秋战国时期被广泛应用,图1是陈列在展览馆的仿真模型.图2是模型驱动部分的示意图,其中⊙M,⊙N的半径分别是1cm和10cm,当⊙M顺时针转动3周时,⊙N上的点P随之旋转n°,则n= .
3.(2024 甘孜州)如图,在△ABC中,AB=AC,∠A=40°,按如下步骤作图:①以点B为圆心,适当长为半径画弧,分别交BA,BC于点D,E;②分别以点D,E为圆心,大于DE长为半径画弧,两弧在∠ABC的内部相交于点F,作射线BF交AC于点G.则∠ABG的大小为 度.
4.(2024 长春)一块含30°角的直角三角板ABC按如图所示的方式摆放,边AB与直线l重合,AB=12cm.现将该三角板绕点B顺时针旋转,使点C的对应点C′落在直线l上,则点A经过的路径长至少为 cm.(结果保留π)
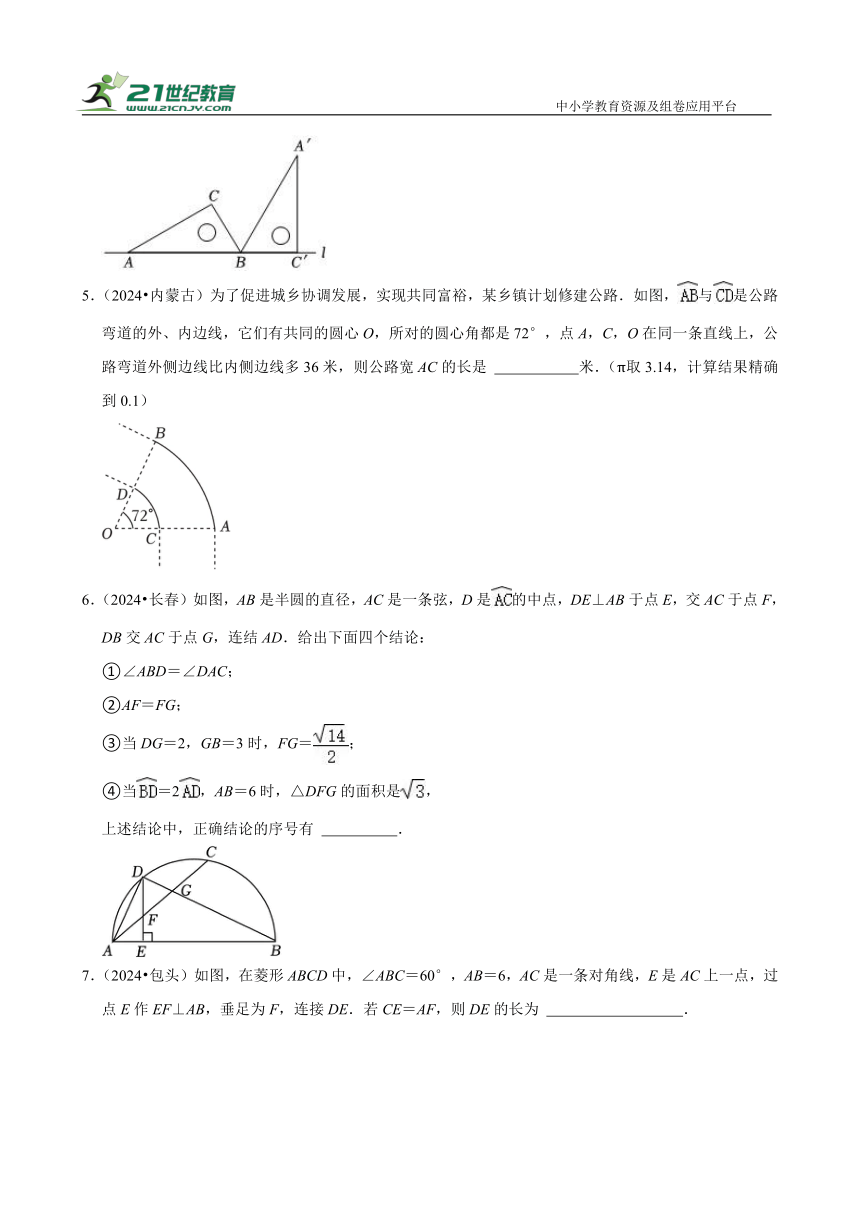
5.(2024 内蒙古)为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,与是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是72°,点A,C,O在同一条直线上,公路弯道外侧边线比内侧边线多36米,则公路宽AC的长是 米.(π取3.14,计算结果精确到0.1)
6.(2024 长春)如图,AB是半圆的直径,AC是一条弦,D是的中点,DE⊥AB于点E,交AC于点F,DB交AC于点G,连结AD.给出下面四个结论:
①∠ABD=∠DAC;
②AF=FG;
③当DG=2,GB=3时,FG=;
④当=2,AB=6时,△DFG的面积是,
上述结论中,正确结论的序号有 .
7.(2024 包头)如图,在菱形ABCD中,∠ABC=60°,AB=6,AC是一条对角线,E是AC上一点,过点E作EF⊥AB,垂足为F,连接DE.若CE=AF,则DE的长为 .
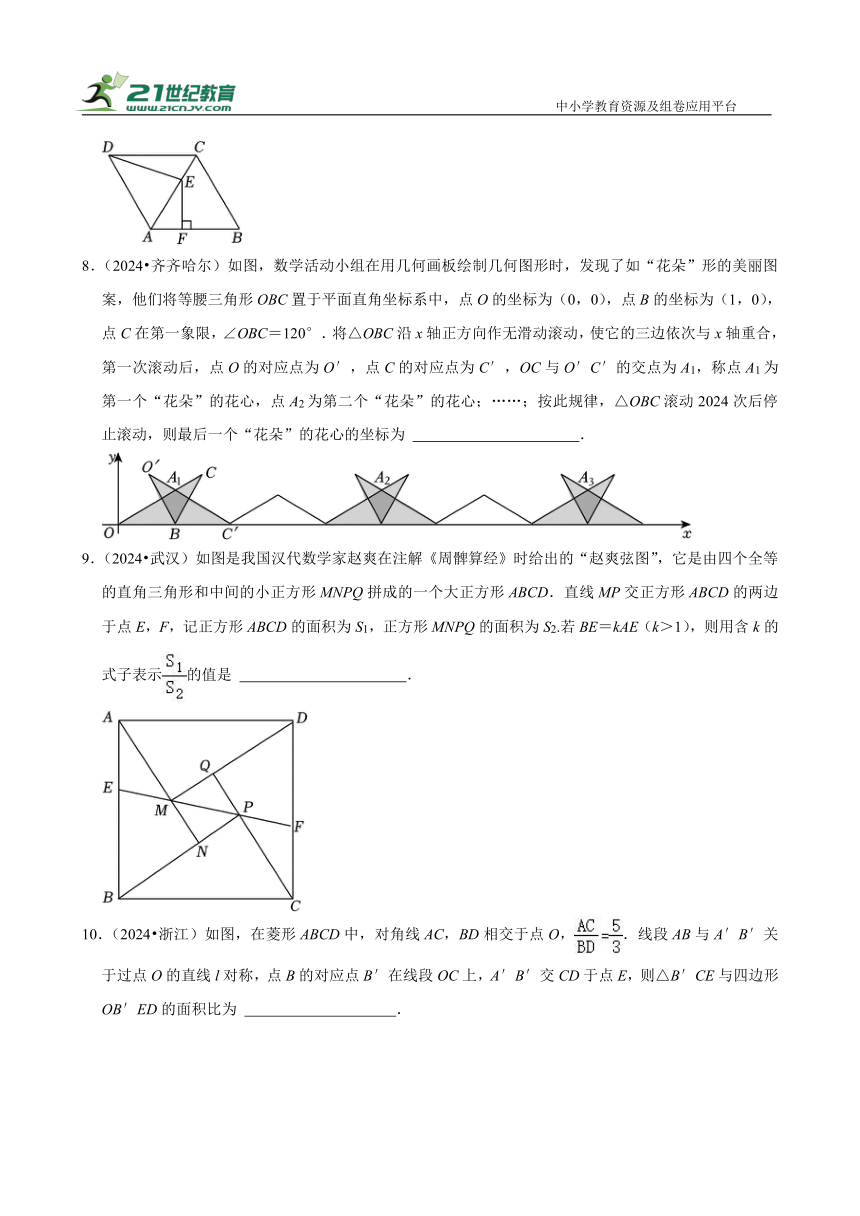
8.(2024 齐齐哈尔)如图,数学活动小组在用几何画板绘制几何图形时,发现了如“花朵”形的美丽图案,他们将等腰三角形OBC置于平面直角坐标系中,点O的坐标为(0,0),点B的坐标为(1,0),点C在第一象限,∠OBC=120°.将△OBC沿x轴正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后,点O的对应点为O′,点C的对应点为C′,OC与O′C′的交点为A1,称点A1为第一个“花朵”的花心,点A2为第二个“花朵”的花心;……;按此规律,△OBC滚动2024次后停止滚动,则最后一个“花朵”的花心的坐标为 .
9.(2024 武汉)如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形和中间的小正方形MNPQ拼成的一个大正方形ABCD.直线MP交正方形ABCD的两边于点E,F,记正方形ABCD的面积为S1,正方形MNPQ的面积为S2.若BE=kAE(k>1),则用含k的式子表示的值是 .
10.(2024 浙江)如图,在菱形ABCD中,对角线AC,BD相交于点O,.线段AB与A′B′关于过点O的直线l对称,点B的对应点B′在线段OC上,A′B′交CD于点E,则△B′CE与四边形OB′ED的面积比为 .
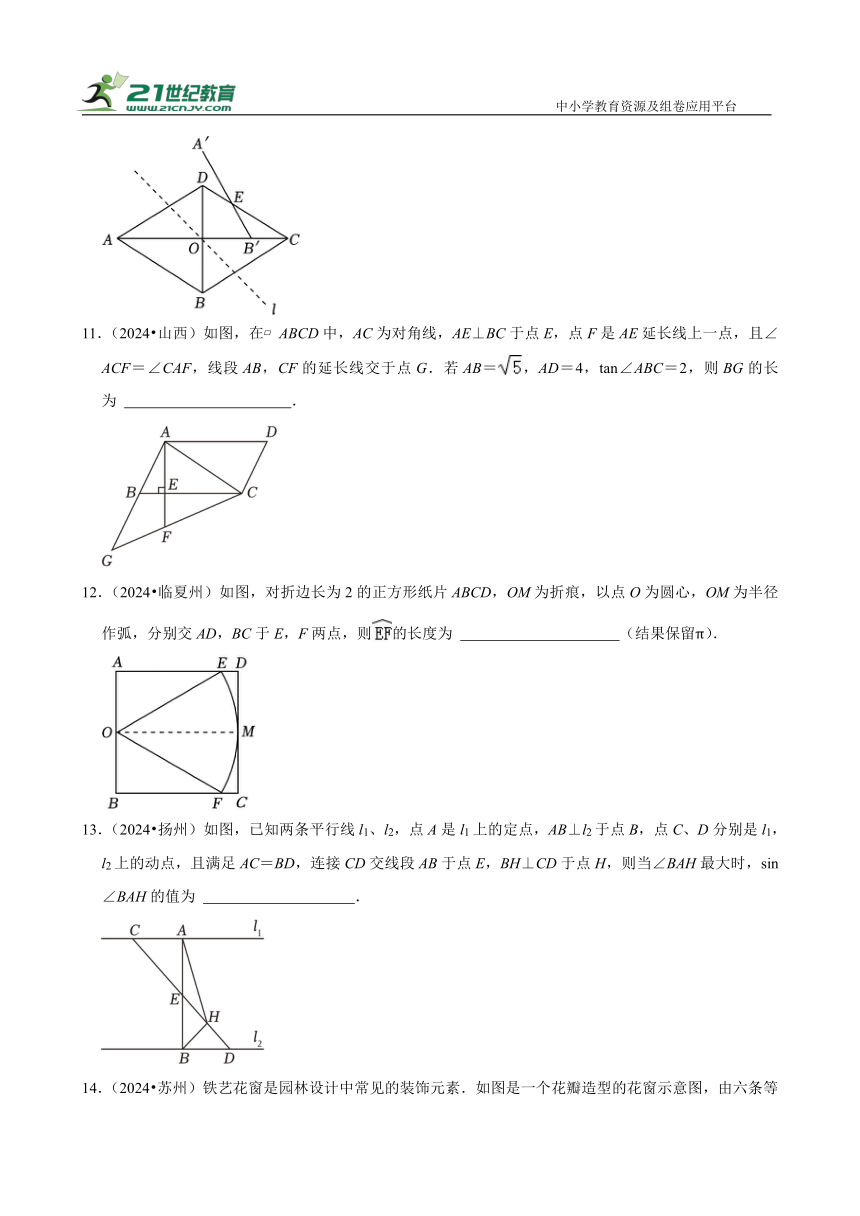
11.(2024 山西)如图,在 ABCD中,AC为对角线,AE⊥BC于点E,点F是AE延长线上一点,且∠ACF=∠CAF,线段AB,CF的延长线交于点G.若AB=,AD=4,tan∠ABC=2,则BG的长为 .
12.(2024 临夏州)如图,对折边长为2的正方形纸片ABCD,OM为折痕,以点O为圆心,OM为半径作弧,分别交AD,BC于E,F两点,则的长度为 (结果保留π).
13.(2024 扬州)如图,已知两条平行线l1、l2,点A是l1上的定点,AB⊥l2于点B,点C、D分别是l1,l2上的动点,且满足AC=BD,连接CD交线段AB于点E,BH⊥CD于点H,则当∠BAH最大时,sin∠BAH的值为 .
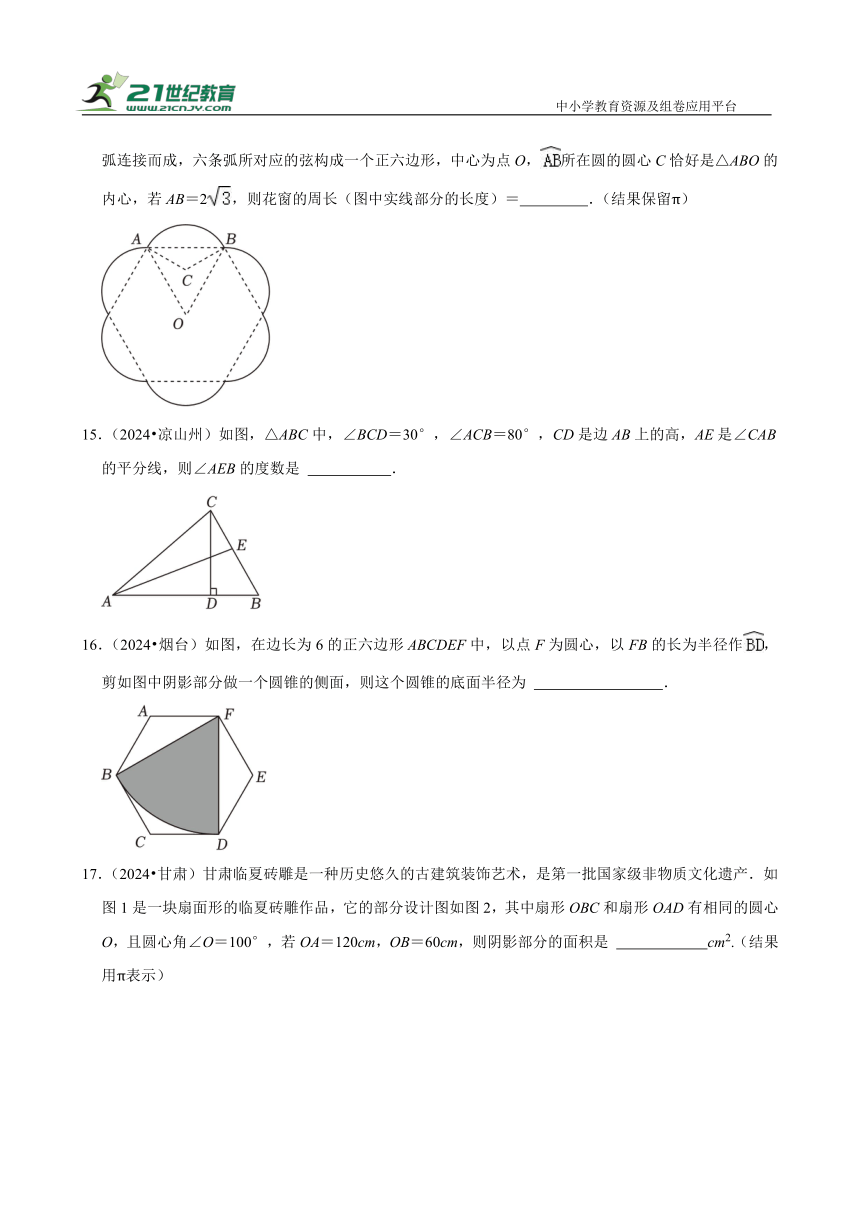
14.(2024 苏州)铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,所在圆的圆心C恰好是△ABO的内心,若AB=2,则花窗的周长(图中实线部分的长度)= .(结果保留π)
15.(2024 凉山州)如图,△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 .
16.(2024 烟台)如图,在边长为6的正六边形ABCDEF中,以点F为圆心,以FB的长为半径作,剪如图中阴影部分做一个圆锥的侧面,则这个圆锥的底面半径为 .
17.(2024 甘肃)甘肃临夏砖雕是一种历史悠久的古建筑装饰艺术,是第一批国家级非物质文化遗产.如图1是一块扇面形的临夏砖雕作品,它的部分设计图如图2,其中扇形OBC和扇形OAD有相同的圆心O,且圆心角∠O=100°,若OA=120cm,OB=60cm,则阴影部分的面积是 cm2.(结果用π表示)
18.(2024 眉山)如图,△ABC内接于⊙O,点O在AB上,AD平分∠BAC交⊙O于D,连结BD.若AB=10,BD=2,则BC的长为 .
19.(2024 内江)如图,在△ABC中,∠ABC=60°,BC=8,E是BC边上一点,且BE=2,点I是△ABC的内心,BI的延长线交AC于点D,P是BD上一动点,连接PE、PC,则PE+PC的最小值为 .
20.(2024 滨州)如图,在边长为1的正方形网格中,点A,B均在格点上.
(1)AB的长为 ;
(2)请只用无刻度的直尺,在如图所示的网格中,画出以AB为边的矩形ABCD,使其面积为,并简要说明点C,D的位置是如何找到的(不用证明): .
21.(2024 连云港)如图,AB是圆的直径,∠1、∠2、∠3、∠4的顶点均在AB上方的圆弧上,∠1、∠4的一边分别经过点A、B,则∠1+∠2+∠3+∠4= °.
22.(2024 达州)如图,在△ABC中,AE1,BE1分别是内角∠CAB,外角∠CBD的三等分线,且∠E1AD=∠CAB,∠E1BD=∠CBD,在△ABE1中,AE2,BE2分别是内角∠E1AB,外角∠E1BD的三等分线,且∠E2AD=∠E1AB,∠E2BD=∠E1BD,…,以此规律作下去,若∠C=m°,则∠En= 度.
23.(2024 自贡)龚扇是自贡“小三绝”之一,为弘扬民族传统文化,某校手工兴趣小组将一个废弃的大纸杯侧面剪开直接当作扇面,制作了一个龚扇模型(如图),扇形外侧两竹条AB,AC夹角为120°,AB长30cm,扇面的BD边长为18cm,则扇面面积为 cm2(结果保留π).
24.(2024 山东)如图,已知∠MAN,以点A为圆心,以适当长为半径作弧,分别与AM、AN相交于点B,C;分别以B,C为圆心,以大于BC的长为半径作弧,两弧在∠MAN内部相交于点P,作射线AP.分别以A,B为圆心,以大于AB的长为半径作弧,两弧相交于点D,E,作直线DE分别与AB,AP相交于点F,Q.若AB=4,∠PQE=67.5°,则F到AN的距离为 .
25.(2024 连云港)如图,在△ABC中,∠C=90°,∠B=30°,AC=2.点P在边AC上,过点P作PD⊥AB,垂足为D,过点D作DF⊥BC,垂足为F.连接PF,取PF的中点E.在点P从点A到点C的运动过程中,点E所经过的路径长为 .
26.(2024 宜宾)如图,一个圆柱体容器,其底部有三个完全相同的小孔槽,分别命名为甲槽、乙槽、丙槽.有大小质地完全相同的三个小球,每个小球标有从1至9中选取的一个数字,且每个小球所标数字互不相同.作如下操作:将这三个小球放入容器中,摇动容器使这三个小球全部落入不同的小孔槽(每个小孔槽只能容下一个小球),取出小球记录下各小孔槽的计分(分数为落入该小孔槽小球上所标的数字),完成第一次操作.再重复以上操作两次.已知甲槽、乙槽、丙槽三次操作计分之和分别为20分、10分、9分,其中第一次操作计分最高的是乙槽,则第二次操作计分最低的是 (从“甲槽”、“乙槽”、“丙槽”中选填).
27.(2024 遂宁)在等边△ABC三边上分别取点D、E、F,使得AD=BE=CF,连结三点得到△DEF,易得△ADF≌△BED≌△CFE,设S△ABC=1,则S△DEF=1﹣3S△ADF.
如图①当=时,S△DEF=1﹣3×=;
如图②当=时,S△DEF=1﹣3×=;
如图③当=时,S△DEF=1﹣3×=;
…
直接写出,当=时,S△DEF= .
28.(2024 重庆)如图,AB是⊙O的直径,BC是⊙O的切线,点B为切点.连接AC交⊙O于点D,点E是⊙O上一点,连接BE,DE,过点A作AF∥BE交BD的延长线于点F.若BC=5,CD=3,∠F=∠ADE,则AB的长度是 ;DF的长度是 .
29.(2024 湖北)如图,由三个全等的三角形(△ABE,△BCF,△CAD)与中间的小等边三角形DEF拼成一个大等边三角形ABC.连接BD并延长交AC于点G.若AE=ED=2.则(1)∠FDB的度数是 ;(2)DG的长是 .
30.(2024 湖北)△DEF为等边三角形,分别延长FD,DE,EF,到点A,B,C,使DA=EB=FC,连接AB,AC,BC,连接BF并延长交AC于点G.若AD=DF=2,则∠DBF= ,FG= .
图形的性质
参考答案与试题解析
一.填空题(共30小题)
1.(2024 资阳)如图,在矩形ABCD中,AB=4,AD=2.以点A为圆心,AD长为半径作弧交AB于点E,再以AB为直径作半圆,与交于点F,则图中阴影部分的面积为 .
【分析】如图,连接AF、EF、由题意易知△AEF是等边三角形,根据S阴=S半圆﹣S扇形AEF﹣S弓形AF计算即可解决问题.
【解答】解:如图,连接AF、EF.
由题意易知△AEF是等边三角形,
S阴=S半圆﹣S扇形AEF﹣S弓形AF
=2π﹣﹣(﹣)
=.
故答案为:.
【点评】本题考查扇形的面积的计算、矩形的性质,等边三角形的判定和性质,解题的关键是学会利用分割法求阴影部分的面积,属于中考常考题型.
2.(2024 兰州)“轮动发石车”是我国古代的一种投石工具,在春秋战国时期被广泛应用,图1是陈列在展览馆的仿真模型.图2是模型驱动部分的示意图,其中⊙M,⊙N的半径分别是1cm和10cm,当⊙M顺时针转动3周时,⊙N上的点P随之旋转n°,则n= 108 .
【分析】利用弧长公式根据点P移动的弧长=3个⊙M周长,列出关于n的方程,解方程即可.
【解答】解:∵⊙M的周长为2π cm,
∴⊙M顺时针转动3周时,点P移动的弧长为6π cm,
∴6π=,
解得n=108,
故答案为:108.
【点评】本题考查了弧长的计算,掌握弧长公式是解题的关键.
3.(2024 甘孜州)如图,在△ABC中,AB=AC,∠A=40°,按如下步骤作图:①以点B为圆心,适当长为半径画弧,分别交BA,BC于点D,E;②分别以点D,E为圆心,大于DE长为半径画弧,两弧在∠ABC的内部相交于点F,作射线BF交AC于点G.则∠ABG的大小为 35 度.
【分析】利用等腰三角形的性质求出∠ABC的度数,再根据角平分线的定义求解.
【解答】解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=(180°﹣40°)=70°,
由作图可知BG平分∠ABC,
∴∠ABG=∠ABC=35°.
故答案为:35.
【点评】本题考查作图﹣基本作图,等腰三角形的性质,角平分线的定义等知识,解题的关键是读懂图象信息.
4.(2024 长春)一块含30°角的直角三角板ABC按如图所示的方式摆放,边AB与直线l重合,AB=12cm.现将该三角板绕点B顺时针旋转,使点C的对应点C′落在直线l上,则点A经过的路径长至少为 8π cm.(结果保留π)
【分析】根据很容易得出点A的运动轨迹是弧AA',再用弧长公式求解即可.
【解答】解:有题可知点A经过的轨迹是以B为圆心的弧AA'.
∵∠A=30°,
∴∠ABC=60°
∴∠CBC'=120°,
∴∠ABA'=120°,
弧AA'得长度为:=8π.
故答案为:8π.
【点评】本题主要考查点的运动轨迹、弧长公式,识别出点的运动轨迹和熟练掌握弧长公式是解题关键.
5.(2024 内蒙古)为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,与是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是72°,点A,C,O在同一条直线上,公路弯道外侧边线比内侧边线多36米,则公路宽AC的长是 28.7 米.(π取3.14,计算结果精确到0.1)
【分析】利用弧长公式构建关系式,可得结论.
【解答】解:由题意﹣=36,
∴OA﹣OC=≈28.7(米).
∴AC=OA﹣OC=28.7米.
故答案为:28.7.
【点评】本题考查弧长公式,解题的关键是记住弧长公式l=.
6.(2024 长春)如图,AB是半圆的直径,AC是一条弦,D是的中点,DE⊥AB于点E,交AC于点F,DB交AC于点G,连结AD.给出下面四个结论:
①∠ABD=∠DAC;
②AF=FG;
③当DG=2,GB=3时,FG=;
④当=2,AB=6时,△DFG的面积是,
上述结论中,正确结论的序号有 ①②③ .
【分析】①根据点D是AC弧的中点得AD弧=CD弧,由此可对结论①进行判断;
②先证明∠ADE=∠DAC得AF=FD,再证明∠BDE=∠AGD得FD=FG,由此可对结论②进行判断;
③在Rt△ADG中tan∠DAC=,在Rt△ABD中tan∠ABD=,再根据∠ABD=∠DAC得AD2=10,然后由勾股定理得AG=,再由结论②正确可对结论③进行判断;
④先证明点D,C为半圆弧上的三等分点,则∠ABD=∠DAC=30°,由此得AD=3,DG=,进而得S△ADG=AD DG=,然后根据AF=FG得S△DFG=S△ADG=,由此可对结论④进行判断,综上所述即可得出答案.
【解答】解:①∵点D是的中点,
∴,
∴∠ABD=∠DAC,
故结论①正确;
②∵AB是半圆的直径,
∴∠ADB=90°,
∴∠ADE+∠BDE=90°,
∵DE⊥AB,
∴∠BDE+∠ABD=90°,
∴∠ADE=∠ABD,
∴∠ADE=∠DAC,
∴AF=FD,
∵∠ADB=90°,
∴∠ADE+∠BDE=90°,∠AGD+∠DAC=90°,
又∵∠ADE=∠DAC,
∴∠BDE=∠AGD,
∴FD=FG,
∴AF=FG,
故结论②正确;
③∵DG=2,GB=3,
∴BD=DG+GB=5,
在Rt△ADG中,tan∠DAC=,
在Rt△ABD中,tan∠ABD=,
∵∠ABD=∠DAC,
∴,
∴AD2=10,
在Rt△ADG中,由勾股定理得:AG==,
∴AF=FG=AG=,
故结论③正确;
④∵点D是的中点,=2,
∴,
即点D,C为半圆弧上的三等分点,
∴∠ABD=∠DAC=30°,
在Rt△ABD中,AB=6,sin∠ABD=,
∴AD=AB sin∠ABD=6×sin30°=3,
在Rt△ADG中,tan∠DAC=,
∴DG=AD tan∠DAC=3×tan30°=√3,
∴S△ADG=AD DG=×3×=,
∵AF=FG,
∴S△DFG=S△ADG=,
故结论④不正确,
综上所述:正确的结论是①②③.
故答案为:①②③.
【点评】此题主要考查了圆周角定理,圆心角,弧,弦的关系,解直角三角形的应用,熟练掌握圆周角定理,圆心角,弧,弦的关系,灵活运用锐角三角函数进行计算是解决问题的关键.
7.(2024 包头)如图,在菱形ABCD中,∠ABC=60°,AB=6,AC是一条对角线,E是AC上一点,过点E作EF⊥AB,垂足为F,连接DE.若CE=AF,则DE的长为 2 .
【分析】如图,连接BD交AC于点O.求出OD,OE,再利用勾股定理求解.
【解答】解:如图,连接BD交AC于点O.
∵四边形ABCD是菱形,
∴AC⊥BD,∠ADC=∠ABC=60°,AB=BC=CD=AD=6,
∴△ABC,△ADC都是等边三角形,
∴∠CAB=60°,
∵EF⊥AF,
∴∠AFE=90°,∠AEF=30°,
∴AE=2AF,
∵CE=AF,
∴AC=3EC,
∴AE=4,EC=2,
∴OA=OC=3,OD=AO=3,
∴OE=AE﹣OA=4﹣3=1,
∴DE===2.
故答案为:2.
【点评】本题考查菱形的性质,等边三角形的判定与性质,解直角三角形,勾股定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
8.(2024 齐齐哈尔)如图,数学活动小组在用几何画板绘制几何图形时,发现了如“花朵”形的美丽图案,他们将等腰三角形OBC置于平面直角坐标系中,点O的坐标为(0,0),点B的坐标为(1,0),点C在第一象限,∠OBC=120°.将△OBC沿x轴正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后,点O的对应点为O′,点C的对应点为C′,OC与O′C′的交点为A1,称点A1为第一个“花朵”的花心,点A2为第二个“花朵”的花心;……;按此规律,△OBC滚动2024次后停止滚动,则最后一个“花朵”的花心的坐标为 (1349+674,) .
【分析】根据所给滚动方式,发现每滚动三次,出现一个花心,再根据点An坐标变化的规律即可解决问题.
【解答】解:由题知,
∠COB=∠O′C′B=30°,BO=BC′,
∴A1O=A1C′,
∴点A1在OC′的垂直平分线上.
∵点B的坐标为(1,0),
∴OB=1,
在Rt△A1OB中,
tan30°=,
∴A1B=,
∴点A1的坐标为(1,).
依次类推,
点A2的坐标为(),
点A3的坐标为(),
…,
∴点An的坐标为()(n为正整数).
又∵每滚动三次,出现下一个花心,
∴2024÷3=674于2,
则674+1=675,
∴滚动2024次后停止滚动,最后一个“花朵”的花心对应的点为点A675.
当n=675时,
点A675的坐标为(1349+,),
即滚动2024次后停止滚动,最后一个“花朵”的花心的坐标为(1349+674,).
故答案为:(1349+674,).
【点评】本题主要考查了点的坐标变化规律及等腰三角形的性质,熟知等腰三角形的性质及能根据所给滚动方式发现点An坐标变化的规律是解题的关键.
9.(2024 武汉)如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形和中间的小正方形MNPQ拼成的一个大正方形ABCD.直线MP交正方形ABCD的两边于点E,F,记正方形ABCD的面积为S1,正方形MNPQ的面积为S2.若BE=kAE(k>1),则用含k的式子表示的值是 .
【分析】方法一:由BE=kAE可想到构造8字型相似,再利用比例线段求解即可;方法二:见到45°可构造等腰直角三角形,再利用手拉手全等和一个角平分线比例定理即可求解.
【解答】解:方法一:如图,过A作AG∥BP交FE延长线于点G,
∵AG∥BP,
∴∠GAE=∠PBE,∠AGE=∠BPE,
∴△AGE∽△PBE,
∴=,
设AG=1,则BP=k,
∵∠NMP=45°,
∴∠AMG=45°,AM=AG=1,
∵AN=BP=k,
∴MN=k﹣1,
∵S1=AD2=AM2+MD2=k2+1,S2=MN2=(k﹣1)2,
∴=;
方法二:如图,过B作BG⊥BP交FE延长线于点G,则△GBP是等腰直角三角形,
易证△GBA≌△PBC,
∴∠BGP=∠AGP=45°,
根据角平分线比例定理得:,
设AG=1,则BG=k,
∴AM=1,MD=k=AN,
∴MN=k﹣1,
∵S1=AD2=AM2+MD2=k2+1,S2=MN2=(k﹣1)2,
∴=;
故答案为:.
【点评】本题主要考查勾股定理得证明及正方形得性质、相似的判定和性质等知识点,熟练掌握以上知识和添加合适辅助线是解题关键.
10.(2024 浙江)如图,在菱形ABCD中,对角线AC,BD相交于点O,.线段AB与A′B′关于过点O的直线l对称,点B的对应点B′在线段OC上,A′B′交CD于点E,则△B′CE与四边形OB′ED的面积比为 .
【分析】根据轴对称可得到等线段等角,再结合菱形的性质可得到△A'ED≌△CEB'(AAS),再证△DOE≌△B'OE(SSS),由B'C:B'O=2:3即可求出答案.
【解答】解:如图连接OE、A'D,
∵AB关于过O的直线对称,
∴A'在BD延长线上,
∵,
∴设AC=10k,BD=6k,
在菱形ABCD中,OA=OC=5k,CB=OD=3k,
∵AB与A'B'关于过O的直线对称,
∴OA=OA'=5k,OB=OB'=3k,∠A'=∠DAC=∠DCA,
∴A'D=B'C=2k,
∵∠A'ED=∠B'CE,
∴△A'ED≌△CEB'(AAS),
∴DE=B'E,
∵OE=OE,OD=OB',
∴△DOE≌△B'OE(SSS),
∴S△DOE=S△B′OE,
∵==,
∴==.
故答案为:.
【点评】本题主要考查了轴对称的性质和菱形的性质、全等三角形的判定和性质,熟练掌握以上基础知识和线段之间的转化是解题关键.
11.(2024 山西)如图,在 ABCD中,AC为对角线,AE⊥BC于点E,点F是AE延长线上一点,且∠ACF=∠CAF,线段AB,CF的延长线交于点G.若AB=,AD=4,tan∠ABC=2,则BG的长为 .
【分析】方法一:过点F作FH⊥AC于H,延长AD与GC的延长线交于K,由tan∠ABC==2得AE=2BE,进而得BE=1,AE=2,则CE=3,AC=,再由∠ACF=∠CAF得FA=FC,则AH=CH=,由S△FAC=AC FH=AF CE,得FH=,在Rt△AFH中由勾股定理得AF=,则EF=AF﹣AE=,证明△FCE∽△FKA得AK=,则DK=AK﹣AD=,再证明△KDC∽△KAG得AG=,由此可得BG的长.
方法二:过点G作GH⊥BC,交CB的延长线于H,先求出BE=1,AE=2,CE=3,设EF=a,则AF=CF=2+a,由勾股定理求出a=,根据∠GBH=∠ABC得GH=2HB,设HB=b,则GH=2b,CH=BC+HB=4+b,GB=,证明△CEF∽△CHG得b=,由此可得GH的长.
【解答】解法一:过点F作FH⊥AC于H,延长AD与GC的延长线交于K,如下图所示:
∵四边形ABCD为平行四边形,
∴AB=CD=,BC=AD=4,AB∥CD,BC∥AD,
又∵AE⊥BC,
在Rt△ABE中,tan∠ABC==2,
∴AE=2BE,
由勾股定理得:AE2+BE2=AB2,
即(2BE)2+BE2=()2,
∴BE=1,
∴AE=2BE=2,
∴CE=BC﹣BE=3,
在Rt△ACE中,由勾股定理得:AC==,
∵∠ACF=∠CAF,
∴FA=FC,
∵FH⊥AC,
∴AH=CH=AC=,
∵S△FAC=AC FH=AF CE,
∴FH=,
在Rt△AFH中,由勾股定理得:AF2﹣FH2=AH2,
即,
∴AF=,
∴EF=AF﹣AE=,
∵BC∥AD,
∴△FCE∽△FKA,
∴EF:AF=CE:AK,
即,
∴AK=,
∴DK=AK﹣AD=,
∵AB∥CD,
∴△KDC∽△KAG,
∴DK:AK=CD:AG,
即,
∴AG=,
∴BG=AG﹣AB=.
故答案为:.
解法二:过点G作GH⊥BC,交CB的延长线于H,如下图所示:
∵四边形ABCD为平行四边形,
∴AB=CD=,BC=AD=4,AB∥CD,BC∥AD,
又∵AE⊥BC
在Rt△ABE中,tan∠ABC==,
∴AE=2BE,
由勾股定理得:AE2+BE2=AB2,
即(2BE)2+BE2=()2,
∴BE=1,
∴AE=2BE=2,
∴CE=BC﹣BE=3,
设EF=a,则AF=AE+EF=2+a,
∵∠ACF=∠CAF,
∴AF=CF=2+a,
在Rt△CEF中,由勾股定理得:CF2=CE2+EF2,
即(2+a)2=32+a2,
解得:a=,
∵∠GBH=∠ABC,
∴在Rt△GBH中,tan∠GBH=,
∴GH=2HB,
设HB=b,则GH=2b,CH=BC+HB=4+b,
在Rt△GBH中,由勾股定理得:GB=,
∵GH⊥BC,AF⊥BC,
∴EF∥GH,
∴△CEF∽△CHG,
∴CE:CH=EF:GH,
即3:(4+b)=:2b,
解得:b=,
∴GH==,
故答案为:.
【点评】此题主要考查了平行四边形的性质,解直角三角形的应用,相似三角形的判定和性质,熟练掌握平行四边形的性质,锐角三角函数的定义是解决问题的关键,正确地添加辅助线构造相似三角形,并利用相似三角形的性质进行计算是解决问题的难点.
12.(2024 临夏州)如图,对折边长为2的正方形纸片ABCD,OM为折痕,以点O为圆心,OM为半径作弧,分别交AD,BC于E,F两点,则的长度为 (结果保留π).
【分析】由对折可知,∠EOM=∠FOM,过点E作OM的垂线,进而可求出∠EOM的度数,则可得出∠EOF的度数,最后根据弧长公式即可解决问题.
【解答】解:由对折可知,
四边形AOMD是矩形,∠EOM=∠FOM,
则OM=AD,DM=.
过点E作OM的垂线,垂足为P,
则EP=DM=.
因为OE=OM=AD,CD=AD,
所以EP=.
在Rt△EOP中,
sin∠EOP==,
所以∠EOP=30°,
则∠EOF=30°×2=60°,
所以的长度为:.
故答案为:.
【点评】本题主要考查了弧长的计算、正方形的性质及翻折变换(折叠问题),熟知正方形的性质、图形翻折的性质及弧长的计算公式是解题的关键.
13.(2024 扬州)如图,已知两条平行线l1、l2,点A是l1上的定点,AB⊥l2于点B,点C、D分别是l1,l2上的动点,且满足AC=BD,连接CD交线段AB于点E,BH⊥CD于点H,则当∠BAH最大时,sin∠BAH的值为 .
【分析】由题易得四边形ACBD是平行四边形,从而得到BE是定长,又由∠BHE=90°,得出直角对直角的隐圆模型,再根据最大张角问题(相切时)求解即可.
【解答】解:∵AC∥BD,
∴四边形ACBD是平行四边形,
∴AE=BE=AB,
∵A为定点,且AB⊥l2,
∴AE为定值,
∵BH⊥CD,
∴∠BHE=90°,
∴点H在以BE为直径的圆上运动(如图,O为圆心),
此时OE=BE=OA,
∵当AH与⊙O相切时∠BAH最大,
∴sin∠BAH==.
故答案为:.
【点评】本题主要考查了切线的性质,熟练掌握切线的性质、圆周角定理是解题的关键,其中识别出隐圆模型至关重要.
14.(2024 苏州)铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,所在圆的圆心C恰好是△ABO的内心,若AB=2,则花窗的周长(图中实线部分的长度)= 8π .(结果保留π)
【分析】根据正六边形的性质,三角形内心的性质以及直角三角形的边角关系求出所对应的圆心角的度数及半径,由弧长公式求出弧的长,再计算长的6倍即可.
【解答】解:如图,过点C作CM⊥AB于点M,则AM=BM=AB=,
∵六条等弧所对应的弦构成一个正六边形,中心为点O,
∴∠AOB==60°,
∵OA=OB,
∴△AOB是正三角形,
∵点O是△AOB的内心,
∴∠CAB=∠CBA=×60°=30°,∠ACB=2∠AOB=120°,
在Rt△ACM中,AM=,∠CAM=30°,
∴AC==2,
∴的长为=π,
∴花窗的周长为π×6=8π.
故答案为:8π.
【点评】本题考查正多边形和圆,弧长的计算,掌握正六边形的性质,三角形的内心的性质以及直角三角形的边角关系,弧长的计算方法是正确解答的关键.
15.(2024 凉山州)如图,△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 100° .
【分析】由CD是边AB上的高,∠BCD=30°,∠ACB=80°,可求得∠CAB、∠CBA的度数,因为AE是∠CAB的平分线,可得∠EAB的度数,根据三角形内角和定理,可得∠AEB的度数.
【解答】解:∵CD是边AB上的高,
∴∠CDB=∠CDA=90°,
∵∠BCD=30°,∠ACB=80°,
∴∠ACD=∠ACB﹣∠BCD=50°,∠CBD=90°﹣∠BCD=60°,
∴∠CAB=90°﹣∠ACD=40°,
∵AE是∠CAB的平分线,
∴∠EAB=∠CAB=20°,
∴∠AEB=180°﹣∠EAB﹣∠EBA=100°,
故答案为:100°.
【点评】本题考查了三角形内角和定理,角平分线的定义,关键是掌握三角形内角和定理,角平分线的定义.
16.(2024 烟台)如图,在边长为6的正六边形ABCDEF中,以点F为圆心,以FB的长为半径作,剪如图中阴影部分做一个圆锥的侧面,则这个圆锥的底面半径为 .
【分析】根据正六边形的性质求出阴影部分扇形的圆心角度数,再根据直角三角形的边角关系求出半径,由弧长的计算方法进行计算即可.
【解答】解:如图,过点A作AM⊥BF,垂足为M,则BM=FM,
∵六边形ABCDEF是正六边形,
∴∠BAF=∠E==120°,AB=AF=EF=DE=6,
∴∠ABF=∠AFB=∠DFE==30°,
∴∠BFD=120°﹣30°﹣30°=60°,
在Rt△ABM中,AB=6,∠ABM=30°,
∴BM=AB=3,
∴BF=2BM=6,
设这个圆锥的底面半径为r,由题意可得,
2πr=,
解得r=.
故答案为:.
【点评】本题考查正多边形和圆,弧长的计算,掌握正六边形的性质,等腰三角形的性质以及弧长的计算方法是正确解答的关键.
17.(2024 甘肃)甘肃临夏砖雕是一种历史悠久的古建筑装饰艺术,是第一批国家级非物质文化遗产.如图1是一块扇面形的临夏砖雕作品,它的部分设计图如图2,其中扇形OBC和扇形OAD有相同的圆心O,且圆心角∠O=100°,若OA=120cm,OB=60cm,则阴影部分的面积是 3000π cm2.(结果用π表示)
【分析】利用扇形面积公式,根据S阴影=S扇形AOD﹣S扇形BOC即可求解.
【解答】解:S阴影=S扇形AOD﹣S扇形BOC
=
=
=3000π(cm2),
故答案为:3000π.
【点评】本题考查了求扇形面积,熟练掌握扇形面积公式是解题的关键.
18.(2024 眉山)如图,△ABC内接于⊙O,点O在AB上,AD平分∠BAC交⊙O于D,连结BD.若AB=10,BD=2,则BC的长为 8 .
【分析】延长AC,BD交于E,根据圆周角定理得到BD⊥AD,求得∠ADB=∠ADE=90°,根据角平分线的定义得到∠BAD=∠DAE,根据全等三角形的性质得到BD=DE=2,根据勾股定理得到AD,根据相似三角形的判定和性质即可得到结论.
【解答】解:延长AC,BD交于E,
∵AB是⊙O的直径,
∴BD⊥AD,
∴∠ADB=∠ADE=90°,
∵AD平分∠BAC,
∴∠BAD=∠DAE,
∵AD=AD,
∴△BAD≌△EAD(ASA),
∴BD=DE=2,
∴BE=4,
∵AB=10,BD=2,
∴AD==4,
∵∠DAC=∠CBD,
∵∠ADB=∠BCE=90°,
∴△ABD∽△BEC,
∴,
∴=,
∴BC=8.
故答案为:8.
【点评】本题考查了三角形的外接圆与外心,全等三角形的判定和性质,勾股定理,相似三角形的判定和性质,正确地作出辅助线是解题的关键.
19.(2024 内江)如图,在△ABC中,∠ABC=60°,BC=8,E是BC边上一点,且BE=2,点I是△ABC的内心,BI的延长线交AC于点D,P是BD上一动点,连接PE、PC,则PE+PC的最小值为 .
【分析】在AB取点F,使BF=BE=2,连接PF,CF,过点F作FH⊥BC于H,利用三角形内心的定义可得出∠ABD=∠CBD,利用SAS证明△BFP≌△BEP,得出PF=PE,则 PE+PC=PF+PC≥CF,当C、P、F三点共线时,PE+PC最小,最小值为CF,利用含 30° 的直 角三角形的性质求出BH,利用勾股定理求出FH,CF即可.
【解答】解:在AB取点F,使 BF=BE=2,连接PF,CF,过点F作FH⊥BC于H,
∵是△ABC 的内心,
∴BI平分∠ABC,
∴∠ABD=∠CBD,
又 BP=BP,
∴△BFP≌△BEP(SAS),
∴PF=PE,
∴PE+PC=PF+PC≥CF,
当C、P、F三点共线时,PE+PC最小,最小值为CF,
∵FH⊥BC,∠ABC=60°,
∴∠BFH=30°,
∴,
∴,CH=BC﹣BH=7,
∴,
∴PE+PC 的最小值为 ,
故答案为:.
【点评】本题考查了三角形的内心,全等三角形的判定与性质,含30°的直角三角形的性质,勾股定理等知识,明确题意,添加合适辅助线,构造全等三角形和含30°的直角三角形是解题的关键.
20.(2024 滨州)如图,在边长为1的正方形网格中,点A,B均在格点上.
(1)AB的长为 ;
(2)请只用无刻度的直尺,在如图所示的网格中,画出以AB为边的矩形ABCD,使其面积为,并简要说明点C,D的位置是如何找到的(不用证明): 根据相似三角形的性质和矩形的面积,可以得到AD与AB的乘积为,从而可以得到点C和点D .
【分析】(1)根据题意和勾股定理,可以求得AB的长;
(2)根据相似三角形的性质和矩形的面积,可以得到AD与AB的乘积为,从而可以得到点C和点D,然后画出这个矩形即可.
【解答】解:(1)由图可得,
AB==,
故答案为:;
(2)如图所示,四边形ABCD即为所求,理由:根据相似三角形的性质和矩形的面积,可以得到AD与AB的乘积为,从而可以得到点C和点D,
具体的计算过程:由图可知:△ABF∽ADE,
则,
即,
解得AD=,
∴AD AB=×=,
这样找到点D,同理可以找到点C,
即图中ABCD即为所求,
故答案为:根据相似三角形的性质和矩形的面积,可以得到AD与AB的乘积为,从而可以得到点C和点D.
【点评】本题考查作图—复杂作图、勾股定理、矩形的判定,解答本题的关键是明确题意,利用数形结合的思想解答.
21.(2024 连云港)如图,AB是圆的直径,∠1、∠2、∠3、∠4的顶点均在AB上方的圆弧上,∠1、∠4的一边分别经过点A、B,则∠1+∠2+∠3+∠4= 90 °.
【分析】根据半圆的度数为 180°,同弧所对的圆周角是圆心角的一半,即可得出结果.
【解答】∵AB是圆的直径,
∴AB所对的弧是半圆,所对圆心角的度数为180°,
∵∠1、∠2、∠3、∠4所对的弧的和为半圆,
∴,
故答案为:90.
【点评】本题考查圆周角定理,根据半圆的度数为 180°,同弧所对的圆周角是圆心角的一半,进行求解即可.
22.(2024 达州)如图,在△ABC中,AE1,BE1分别是内角∠CAB,外角∠CBD的三等分线,且∠E1AD=∠CAB,∠E1BD=∠CBD,在△ABE1中,AE2,BE2分别是内角∠E1AB,外角∠E1BD的三等分线,且∠E2AD=∠E1AB,∠E2BD=∠E1BD,…,以此规律作下去,若∠C=m°,则∠En= 度.
【分析】本题考查了三角形的外角定理,等式性质,熟练掌握知识点是解题的关键.先分别对△ABC.△E1AB 运用三角形的外角定理,设∠E1AD=α,则∠CAB=3α,∠E1BD=β,则∠CBD=3β,得到 β=α+∠E1,3β=3a+∠C,同建可求:,所以可得 .
【解答】解:由题意,,
∴设∠E1AD=α,∠E1BD=β,则∠CAB=3α,∠CBD=3β,
由三角形的外角的性质得:β=α+∠E1,3β=3α+∠C,,
同理可求:, ……,,
即 ,
故答案为:.
【点评】本题考查三角形的外角性质,三角形内角和定理,规律型:图形变化类等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.
23.(2024 自贡)龚扇是自贡“小三绝”之一,为弘扬民族传统文化,某校手工兴趣小组将一个废弃的大纸杯侧面剪开直接当作扇面,制作了一个龚扇模型(如图),扇形外侧两竹条AB,AC夹角为120°,AB长30cm,扇面的BD边长为18cm,则扇面面积为 252π cm2(结果保留π).
【分析】根据扇形公式进行计算即可.
【解答】解:扇面面积=扇形BAC的面积﹣扇形DAE的面积
=﹣
=252π(cm2),
故答案为:252π.
【点评】本题考查了扇面面积计算,掌握扇面面积等于两个扇形面积相减是解题的关键.
24.(2024 山东)如图,已知∠MAN,以点A为圆心,以适当长为半径作弧,分别与AM、AN相交于点B,C;分别以B,C为圆心,以大于BC的长为半径作弧,两弧在∠MAN内部相交于点P,作射线AP.分别以A,B为圆心,以大于AB的长为半径作弧,两弧相交于点D,E,作直线DE分别与AB,AP相交于点F,Q.若AB=4,∠PQE=67.5°,则F到AN的距离为 .
【分析】如图,过F作FH⊥AC于H,证明∠BAP=∠CAP,DE⊥AB,,再证明∠FAH=45°,再结合勾股定理可得答案.
【解答】解:如图,过F作FH⊥AC于H,
由作图可得:∠BAP=∠CAP,DE⊥AB,,
∵∠PQE=67.5°,
∴∠AQF=67.5°,
∴∠BAP=∠CAP=90°﹣67.5°=22.5°,
∴∠FAH=45°,
∴,
∴F到AN的距离为;
故答案为:.
【点评】本题考查了作图 复杂作图:基本作图,三角形的内角和定理的应用,勾股定理的应用,等腰三角形的判定,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质,逐步操作.
25.(2024 连云港)如图,在△ABC中,∠C=90°,∠B=30°,AC=2.点P在边AC上,过点P作PD⊥AB,垂足为D,过点D作DF⊥BC,垂足为F.连接PF,取PF的中点E.在点P从点A到点C的运动过程中,点E所经过的路径长为 .
【分析】以C为原点,建立坐标系,设AP=a,则CP=2﹣a,利用含30度角的直角三角形的性质,求出点E的坐标,得到点E在直线上运动,求出点P分别与A,C重合时点E的坐标,利用两点间的距离公式进行求解即可.
【解答】解:方法一:以C为原点,建立坐标系,过点D作DG⊥AC
设AP=a,则CP=2﹣a,
∴P(0,2﹣a),
∵∠B=30°,
∴∠A=60°,
∵PD⊥AB,
∴∠PDA=90°,
∴∠APD=30°,
∴,
∵DG⊥AC,
∴∠AGD=90°,
∴,,
∵DF⊥BC,DG⊥AC,∠ACB=90°,
∴四边形DGCF为矩形,
∴DG=CF,
∴,
∵E为P,F的中点,
∴,
令,
∴,
∴点E在直线上运动,
当点P与A重合时,a=0,此时E(0,1),
当点P与C重合时,a=2,此时,
∴点E所经过的路径长为:,
方法二:∵P在AC上运动,运动路径为线段,E为PF中点,
∴E的运动路径亦为线段,
∵当P与A重合时,CE=1,当P与C重合时,CE=,
∴点E所经过的路径长为:,
故答案为:.
【点评】本题考查含30度角的直角三角形,一次函数与几何的综合应用,矩形的判定和性质,两点间的距离,综合运用这些性质是解题的关键.
26.(2024 宜宾)如图,一个圆柱体容器,其底部有三个完全相同的小孔槽,分别命名为甲槽、乙槽、丙槽.有大小质地完全相同的三个小球,每个小球标有从1至9中选取的一个数字,且每个小球所标数字互不相同.作如下操作:将这三个小球放入容器中,摇动容器使这三个小球全部落入不同的小孔槽(每个小孔槽只能容下一个小球),取出小球记录下各小孔槽的计分(分数为落入该小孔槽小球上所标的数字),完成第一次操作.再重复以上操作两次.已知甲槽、乙槽、丙槽三次操作计分之和分别为20分、10分、9分,其中第一次操作计分最高的是乙槽,则第二次操作计分最低的是 乙槽 (从“甲槽”、“乙槽”、“丙槽”中选填).
【分析】由三次操作三个槽总分是20+10+9=39分,所以一次操作得总分就是13分,再根据三个球得数不相同可以列举出综合为13得所有情况.,然后再根据各自得分去一一分析比较即可.
【解答】方法一:∵三次操作相同,且总得分是20+10+9=39分.
∴一次操作的总分,即三个球数字之后为39÷3=13,
则有以下情况:
,
其中只有1,4,8这一组能同时满足三个数组合相加得20,10,9;
,
∴第一次操作甲槽乙槽丙槽分数分别为4,8,1;
第二次操作甲槽乙槽丙槽分数分别为8,1,1;
第三次操作甲槽乙槽丙槽分数分别为8,1,1;
∴第二次操作计分最低的是乙槽.
方法二:设乙第一,第二,第三次操作计分分别为x、y、z.
则x+y+z=10,
x不可能为9,否则yz出现为0的情况,与题意矛盾.
所以x最大为8,此时8+1+1=10,
1已经是最小了,所以第二次操作计分最小的是乙槽.
故答案为:乙槽.
【点评】本题主要考查了推理与论证,题型比较活,属于现在比较多的考查形式,要求学生具备一定的数学思维.
27.(2024 遂宁)在等边△ABC三边上分别取点D、E、F,使得AD=BE=CF,连结三点得到△DEF,易得△ADF≌△BED≌△CFE,设S△ABC=1,则S△DEF=1﹣3S△ADF.
如图①当=时,S△DEF=1﹣3×=;
如图②当=时,S△DEF=1﹣3×=;
如图③当=时,S△DEF=1﹣3×=;
…
直接写出,当=时,S△DEF= .
【分析】探究规律,利用规律解决问题.
【解答】解:如图①当=时,S△DEF=1﹣3×=1﹣3×=;
如图②当=时,S△DEF=1﹣3×=1﹣3×=;
如图③当=时,S△DEF=1﹣3×=1﹣3×=;
…
当=时,S△DEF=1﹣3×;
故当=时,S△DEF=1﹣3×=.
【点评】本题考查全等三角形的判定和性质,等边三角形的性质,规律型﹣图形变化等知识,解题的关键是学会探究规律,利用规律解决问题.
28.(2024 重庆)如图,AB是⊙O的直径,BC是⊙O的切线,点B为切点.连接AC交⊙O于点D,点E是⊙O上一点,连接BE,DE,过点A作AF∥BE交BD的延长线于点F.若BC=5,CD=3,∠F=∠ADE,则AB的长度是 ;DF的长度是 .
【分析】由圆周角定理得到∠BDC=90°,由勾股定理求出BD==4,由△CDB∽△CBA,推出DB:BA=CD:CB,得到AB=,由平行线的性质,圆周角定理推出∠F=∠BAF,得到BF=AB=,即可求出FD的值.
【解答】解:∵AB是圆的直径,
∴∠ADB=90°,
∴∠BDC=90°,
∵BC=5,CD=3,
∴BD==4,
∵BC切圆于B,
∴直径AB⊥BC,
∴∠ABC=90°,
∵∠BCD=∠ACB,∠CDB=∠ABC=90°,
∴△CDB∽△CBA,
∴DB:BA=CD:CB,
∴4:AB=3:5,
∴AB=,
∵AF∥BE,
∴∠BAF=∠ABE,
∵∠ABE=∠ADE,∠F=∠ADE,
∴∠F=∠BAF,
∴BF=AB=,
∴FD=BF﹣BD=﹣4=.
故答案为:,.
【点评】本题考查切线的性质,勾股定理,相似三角形的判定和性质,圆周角定理,平行线的性质,关键是判定△CDB∽△CBA,推出DB:BA=CD:CB,由圆周角定理,平行线的性质推出∠F=∠BAF.
29.(2024 湖北)如图,由三个全等的三角形(△ABE,△BCF,△CAD)与中间的小等边三角形DEF拼成一个大等边三角形ABC.连接BD并延长交AC于点G.若AE=ED=2.则(1)∠FDB的度数是 30° ;(2)DG的长是 .
【分析】(1)利用三角形相似及AE=DE可得BF=DF,再利用三角形的外角性质结合可求得∠DBF=30°;
(2)作CH⊥BG交BG的延长线于点H,利用直角三角形的性质求得CH=1,FH=,证明△ADG∽△CHG,利用相似三角形的性质列式计算即可求解.
【解答】解:∵△ABE≌△BCF≌△CAD(已知),
∴AD=BE=CF,AE=BF=DC,
∵AE=ED=2,
∴AD=BE=4,
∵△DEF为等边三角形,
∴EF=DF=DE=2,∠EFD=∠EDF=60°,
∴BF=DF=DC=2,
∴∠FDB=∠FBD=∠EFD=30°,∠ADB=∠EDF+∠FDB=90°,
如图,过点C作CH⊥BG的延长线于点H,
∵∠CDH=30°,
∴CH=CD×sin30°=2×=1,
DH=CD×cos30°=2×=,
∵∠ADG=∠CHG,∠AGD=∠CGH,
∴△ADG∽△CHG,
∴,
∴DG==.
【点评】本题考查了相似三角形的判定和性质,等边三角形的判定和性质,勾股定理等知识.
30.(2024 湖北)△DEF为等边三角形,分别延长FD,DE,EF,到点A,B,C,使DA=EB=FC,连接AB,AC,BC,连接BF并延长交AC于点G.若AD=DF=2,则∠DBF= 30° ,FG= .
【分析】根据题干可得EB=EF=ED,∠DEF=60°,利用外角性质和一个等腰三角形可得∠DBF=30°;作CH⊥BG,交BG的延长线于点H,易证△AFG∽△CHG,根据相似比易求FG的长度.
【解答】解:∵△DEF为等边三角形,且DE=EB,
∴DE=BE=EF,∠DEF=∠DFE=∠EDF=60°,
∴∠DBF=∠EFB=30°,
∴∠AFB=90°,
作CH⊥BG,交BG的延长线于点H,
∵∠CFH=∠BFE=30°,AD=DF=CF=2,
∴CH=CF=1,
∴FH=,
∵∠AFG=∠CHG=90°,∠AGF=∠CGH,
∴△AFG∽△CHG,
∴===4,
∴FG=FH=.
故答案为:30°;.
【点评】本题主要考查相似三角形的判定和性质,熟练掌握相似三角形的判定和性质以及等边三角形的性质等相关知识是解题关键.
2024年中考数学填空题分类汇编——函数数与式图形的性质
一.填空题(共30小题)
1.(2024 资阳)如图,在矩形ABCD中,AB=4,AD=2.以点A为圆心,AD长为半径作弧交AB于点E,再以AB为直径作半圆,与交于点F,则图中阴影部分的面积为 .
2.(2024 兰州)“轮动发石车”是我国古代的一种投石工具,在春秋战国时期被广泛应用,图1是陈列在展览馆的仿真模型.图2是模型驱动部分的示意图,其中⊙M,⊙N的半径分别是1cm和10cm,当⊙M顺时针转动3周时,⊙N上的点P随之旋转n°,则n= .
3.(2024 甘孜州)如图,在△ABC中,AB=AC,∠A=40°,按如下步骤作图:①以点B为圆心,适当长为半径画弧,分别交BA,BC于点D,E;②分别以点D,E为圆心,大于DE长为半径画弧,两弧在∠ABC的内部相交于点F,作射线BF交AC于点G.则∠ABG的大小为 度.
4.(2024 长春)一块含30°角的直角三角板ABC按如图所示的方式摆放,边AB与直线l重合,AB=12cm.现将该三角板绕点B顺时针旋转,使点C的对应点C′落在直线l上,则点A经过的路径长至少为 cm.(结果保留π)
5.(2024 内蒙古)为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,与是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是72°,点A,C,O在同一条直线上,公路弯道外侧边线比内侧边线多36米,则公路宽AC的长是 米.(π取3.14,计算结果精确到0.1)
6.(2024 长春)如图,AB是半圆的直径,AC是一条弦,D是的中点,DE⊥AB于点E,交AC于点F,DB交AC于点G,连结AD.给出下面四个结论:
①∠ABD=∠DAC;
②AF=FG;
③当DG=2,GB=3时,FG=;
④当=2,AB=6时,△DFG的面积是,
上述结论中,正确结论的序号有 .
7.(2024 包头)如图,在菱形ABCD中,∠ABC=60°,AB=6,AC是一条对角线,E是AC上一点,过点E作EF⊥AB,垂足为F,连接DE.若CE=AF,则DE的长为 .
8.(2024 齐齐哈尔)如图,数学活动小组在用几何画板绘制几何图形时,发现了如“花朵”形的美丽图案,他们将等腰三角形OBC置于平面直角坐标系中,点O的坐标为(0,0),点B的坐标为(1,0),点C在第一象限,∠OBC=120°.将△OBC沿x轴正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后,点O的对应点为O′,点C的对应点为C′,OC与O′C′的交点为A1,称点A1为第一个“花朵”的花心,点A2为第二个“花朵”的花心;……;按此规律,△OBC滚动2024次后停止滚动,则最后一个“花朵”的花心的坐标为 .
9.(2024 武汉)如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形和中间的小正方形MNPQ拼成的一个大正方形ABCD.直线MP交正方形ABCD的两边于点E,F,记正方形ABCD的面积为S1,正方形MNPQ的面积为S2.若BE=kAE(k>1),则用含k的式子表示的值是 .
10.(2024 浙江)如图,在菱形ABCD中,对角线AC,BD相交于点O,.线段AB与A′B′关于过点O的直线l对称,点B的对应点B′在线段OC上,A′B′交CD于点E,则△B′CE与四边形OB′ED的面积比为 .
11.(2024 山西)如图,在 ABCD中,AC为对角线,AE⊥BC于点E,点F是AE延长线上一点,且∠ACF=∠CAF,线段AB,CF的延长线交于点G.若AB=,AD=4,tan∠ABC=2,则BG的长为 .
12.(2024 临夏州)如图,对折边长为2的正方形纸片ABCD,OM为折痕,以点O为圆心,OM为半径作弧,分别交AD,BC于E,F两点,则的长度为 (结果保留π).
13.(2024 扬州)如图,已知两条平行线l1、l2,点A是l1上的定点,AB⊥l2于点B,点C、D分别是l1,l2上的动点,且满足AC=BD,连接CD交线段AB于点E,BH⊥CD于点H,则当∠BAH最大时,sin∠BAH的值为 .
14.(2024 苏州)铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,所在圆的圆心C恰好是△ABO的内心,若AB=2,则花窗的周长(图中实线部分的长度)= .(结果保留π)
15.(2024 凉山州)如图,△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 .
16.(2024 烟台)如图,在边长为6的正六边形ABCDEF中,以点F为圆心,以FB的长为半径作,剪如图中阴影部分做一个圆锥的侧面,则这个圆锥的底面半径为 .
17.(2024 甘肃)甘肃临夏砖雕是一种历史悠久的古建筑装饰艺术,是第一批国家级非物质文化遗产.如图1是一块扇面形的临夏砖雕作品,它的部分设计图如图2,其中扇形OBC和扇形OAD有相同的圆心O,且圆心角∠O=100°,若OA=120cm,OB=60cm,则阴影部分的面积是 cm2.(结果用π表示)
18.(2024 眉山)如图,△ABC内接于⊙O,点O在AB上,AD平分∠BAC交⊙O于D,连结BD.若AB=10,BD=2,则BC的长为 .
19.(2024 内江)如图,在△ABC中,∠ABC=60°,BC=8,E是BC边上一点,且BE=2,点I是△ABC的内心,BI的延长线交AC于点D,P是BD上一动点,连接PE、PC,则PE+PC的最小值为 .
20.(2024 滨州)如图,在边长为1的正方形网格中,点A,B均在格点上.
(1)AB的长为 ;
(2)请只用无刻度的直尺,在如图所示的网格中,画出以AB为边的矩形ABCD,使其面积为,并简要说明点C,D的位置是如何找到的(不用证明): .
21.(2024 连云港)如图,AB是圆的直径,∠1、∠2、∠3、∠4的顶点均在AB上方的圆弧上,∠1、∠4的一边分别经过点A、B,则∠1+∠2+∠3+∠4= °.
22.(2024 达州)如图,在△ABC中,AE1,BE1分别是内角∠CAB,外角∠CBD的三等分线,且∠E1AD=∠CAB,∠E1BD=∠CBD,在△ABE1中,AE2,BE2分别是内角∠E1AB,外角∠E1BD的三等分线,且∠E2AD=∠E1AB,∠E2BD=∠E1BD,…,以此规律作下去,若∠C=m°,则∠En= 度.
23.(2024 自贡)龚扇是自贡“小三绝”之一,为弘扬民族传统文化,某校手工兴趣小组将一个废弃的大纸杯侧面剪开直接当作扇面,制作了一个龚扇模型(如图),扇形外侧两竹条AB,AC夹角为120°,AB长30cm,扇面的BD边长为18cm,则扇面面积为 cm2(结果保留π).
24.(2024 山东)如图,已知∠MAN,以点A为圆心,以适当长为半径作弧,分别与AM、AN相交于点B,C;分别以B,C为圆心,以大于BC的长为半径作弧,两弧在∠MAN内部相交于点P,作射线AP.分别以A,B为圆心,以大于AB的长为半径作弧,两弧相交于点D,E,作直线DE分别与AB,AP相交于点F,Q.若AB=4,∠PQE=67.5°,则F到AN的距离为 .
25.(2024 连云港)如图,在△ABC中,∠C=90°,∠B=30°,AC=2.点P在边AC上,过点P作PD⊥AB,垂足为D,过点D作DF⊥BC,垂足为F.连接PF,取PF的中点E.在点P从点A到点C的运动过程中,点E所经过的路径长为 .
26.(2024 宜宾)如图,一个圆柱体容器,其底部有三个完全相同的小孔槽,分别命名为甲槽、乙槽、丙槽.有大小质地完全相同的三个小球,每个小球标有从1至9中选取的一个数字,且每个小球所标数字互不相同.作如下操作:将这三个小球放入容器中,摇动容器使这三个小球全部落入不同的小孔槽(每个小孔槽只能容下一个小球),取出小球记录下各小孔槽的计分(分数为落入该小孔槽小球上所标的数字),完成第一次操作.再重复以上操作两次.已知甲槽、乙槽、丙槽三次操作计分之和分别为20分、10分、9分,其中第一次操作计分最高的是乙槽,则第二次操作计分最低的是 (从“甲槽”、“乙槽”、“丙槽”中选填).
27.(2024 遂宁)在等边△ABC三边上分别取点D、E、F,使得AD=BE=CF,连结三点得到△DEF,易得△ADF≌△BED≌△CFE,设S△ABC=1,则S△DEF=1﹣3S△ADF.
如图①当=时,S△DEF=1﹣3×=;
如图②当=时,S△DEF=1﹣3×=;
如图③当=时,S△DEF=1﹣3×=;
…
直接写出,当=时,S△DEF= .
28.(2024 重庆)如图,AB是⊙O的直径,BC是⊙O的切线,点B为切点.连接AC交⊙O于点D,点E是⊙O上一点,连接BE,DE,过点A作AF∥BE交BD的延长线于点F.若BC=5,CD=3,∠F=∠ADE,则AB的长度是 ;DF的长度是 .
29.(2024 湖北)如图,由三个全等的三角形(△ABE,△BCF,△CAD)与中间的小等边三角形DEF拼成一个大等边三角形ABC.连接BD并延长交AC于点G.若AE=ED=2.则(1)∠FDB的度数是 ;(2)DG的长是 .
30.(2024 湖北)△DEF为等边三角形,分别延长FD,DE,EF,到点A,B,C,使DA=EB=FC,连接AB,AC,BC,连接BF并延长交AC于点G.若AD=DF=2,则∠DBF= ,FG= .
图形的性质
参考答案与试题解析
一.填空题(共30小题)
1.(2024 资阳)如图,在矩形ABCD中,AB=4,AD=2.以点A为圆心,AD长为半径作弧交AB于点E,再以AB为直径作半圆,与交于点F,则图中阴影部分的面积为 .
【分析】如图,连接AF、EF、由题意易知△AEF是等边三角形,根据S阴=S半圆﹣S扇形AEF﹣S弓形AF计算即可解决问题.
【解答】解:如图,连接AF、EF.
由题意易知△AEF是等边三角形,
S阴=S半圆﹣S扇形AEF﹣S弓形AF
=2π﹣﹣(﹣)
=.
故答案为:.
【点评】本题考查扇形的面积的计算、矩形的性质,等边三角形的判定和性质,解题的关键是学会利用分割法求阴影部分的面积,属于中考常考题型.
2.(2024 兰州)“轮动发石车”是我国古代的一种投石工具,在春秋战国时期被广泛应用,图1是陈列在展览馆的仿真模型.图2是模型驱动部分的示意图,其中⊙M,⊙N的半径分别是1cm和10cm,当⊙M顺时针转动3周时,⊙N上的点P随之旋转n°,则n= 108 .
【分析】利用弧长公式根据点P移动的弧长=3个⊙M周长,列出关于n的方程,解方程即可.
【解答】解:∵⊙M的周长为2π cm,
∴⊙M顺时针转动3周时,点P移动的弧长为6π cm,
∴6π=,
解得n=108,
故答案为:108.
【点评】本题考查了弧长的计算,掌握弧长公式是解题的关键.
3.(2024 甘孜州)如图,在△ABC中,AB=AC,∠A=40°,按如下步骤作图:①以点B为圆心,适当长为半径画弧,分别交BA,BC于点D,E;②分别以点D,E为圆心,大于DE长为半径画弧,两弧在∠ABC的内部相交于点F,作射线BF交AC于点G.则∠ABG的大小为 35 度.
【分析】利用等腰三角形的性质求出∠ABC的度数,再根据角平分线的定义求解.
【解答】解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=(180°﹣40°)=70°,
由作图可知BG平分∠ABC,
∴∠ABG=∠ABC=35°.
故答案为:35.
【点评】本题考查作图﹣基本作图,等腰三角形的性质,角平分线的定义等知识,解题的关键是读懂图象信息.
4.(2024 长春)一块含30°角的直角三角板ABC按如图所示的方式摆放,边AB与直线l重合,AB=12cm.现将该三角板绕点B顺时针旋转,使点C的对应点C′落在直线l上,则点A经过的路径长至少为 8π cm.(结果保留π)
【分析】根据很容易得出点A的运动轨迹是弧AA',再用弧长公式求解即可.
【解答】解:有题可知点A经过的轨迹是以B为圆心的弧AA'.
∵∠A=30°,
∴∠ABC=60°
∴∠CBC'=120°,
∴∠ABA'=120°,
弧AA'得长度为:=8π.
故答案为:8π.
【点评】本题主要考查点的运动轨迹、弧长公式,识别出点的运动轨迹和熟练掌握弧长公式是解题关键.
5.(2024 内蒙古)为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,与是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是72°,点A,C,O在同一条直线上,公路弯道外侧边线比内侧边线多36米,则公路宽AC的长是 28.7 米.(π取3.14,计算结果精确到0.1)
【分析】利用弧长公式构建关系式,可得结论.
【解答】解:由题意﹣=36,
∴OA﹣OC=≈28.7(米).
∴AC=OA﹣OC=28.7米.
故答案为:28.7.
【点评】本题考查弧长公式,解题的关键是记住弧长公式l=.
6.(2024 长春)如图,AB是半圆的直径,AC是一条弦,D是的中点,DE⊥AB于点E,交AC于点F,DB交AC于点G,连结AD.给出下面四个结论:
①∠ABD=∠DAC;
②AF=FG;
③当DG=2,GB=3时,FG=;
④当=2,AB=6时,△DFG的面积是,
上述结论中,正确结论的序号有 ①②③ .
【分析】①根据点D是AC弧的中点得AD弧=CD弧,由此可对结论①进行判断;
②先证明∠ADE=∠DAC得AF=FD,再证明∠BDE=∠AGD得FD=FG,由此可对结论②进行判断;
③在Rt△ADG中tan∠DAC=,在Rt△ABD中tan∠ABD=,再根据∠ABD=∠DAC得AD2=10,然后由勾股定理得AG=,再由结论②正确可对结论③进行判断;
④先证明点D,C为半圆弧上的三等分点,则∠ABD=∠DAC=30°,由此得AD=3,DG=,进而得S△ADG=AD DG=,然后根据AF=FG得S△DFG=S△ADG=,由此可对结论④进行判断,综上所述即可得出答案.
【解答】解:①∵点D是的中点,
∴,
∴∠ABD=∠DAC,
故结论①正确;
②∵AB是半圆的直径,
∴∠ADB=90°,
∴∠ADE+∠BDE=90°,
∵DE⊥AB,
∴∠BDE+∠ABD=90°,
∴∠ADE=∠ABD,
∴∠ADE=∠DAC,
∴AF=FD,
∵∠ADB=90°,
∴∠ADE+∠BDE=90°,∠AGD+∠DAC=90°,
又∵∠ADE=∠DAC,
∴∠BDE=∠AGD,
∴FD=FG,
∴AF=FG,
故结论②正确;
③∵DG=2,GB=3,
∴BD=DG+GB=5,
在Rt△ADG中,tan∠DAC=,
在Rt△ABD中,tan∠ABD=,
∵∠ABD=∠DAC,
∴,
∴AD2=10,
在Rt△ADG中,由勾股定理得:AG==,
∴AF=FG=AG=,
故结论③正确;
④∵点D是的中点,=2,
∴,
即点D,C为半圆弧上的三等分点,
∴∠ABD=∠DAC=30°,
在Rt△ABD中,AB=6,sin∠ABD=,
∴AD=AB sin∠ABD=6×sin30°=3,
在Rt△ADG中,tan∠DAC=,
∴DG=AD tan∠DAC=3×tan30°=√3,
∴S△ADG=AD DG=×3×=,
∵AF=FG,
∴S△DFG=S△ADG=,
故结论④不正确,
综上所述:正确的结论是①②③.
故答案为:①②③.
【点评】此题主要考查了圆周角定理,圆心角,弧,弦的关系,解直角三角形的应用,熟练掌握圆周角定理,圆心角,弧,弦的关系,灵活运用锐角三角函数进行计算是解决问题的关键.
7.(2024 包头)如图,在菱形ABCD中,∠ABC=60°,AB=6,AC是一条对角线,E是AC上一点,过点E作EF⊥AB,垂足为F,连接DE.若CE=AF,则DE的长为 2 .
【分析】如图,连接BD交AC于点O.求出OD,OE,再利用勾股定理求解.
【解答】解:如图,连接BD交AC于点O.
∵四边形ABCD是菱形,
∴AC⊥BD,∠ADC=∠ABC=60°,AB=BC=CD=AD=6,
∴△ABC,△ADC都是等边三角形,
∴∠CAB=60°,
∵EF⊥AF,
∴∠AFE=90°,∠AEF=30°,
∴AE=2AF,
∵CE=AF,
∴AC=3EC,
∴AE=4,EC=2,
∴OA=OC=3,OD=AO=3,
∴OE=AE﹣OA=4﹣3=1,
∴DE===2.
故答案为:2.
【点评】本题考查菱形的性质,等边三角形的判定与性质,解直角三角形,勾股定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
8.(2024 齐齐哈尔)如图,数学活动小组在用几何画板绘制几何图形时,发现了如“花朵”形的美丽图案,他们将等腰三角形OBC置于平面直角坐标系中,点O的坐标为(0,0),点B的坐标为(1,0),点C在第一象限,∠OBC=120°.将△OBC沿x轴正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后,点O的对应点为O′,点C的对应点为C′,OC与O′C′的交点为A1,称点A1为第一个“花朵”的花心,点A2为第二个“花朵”的花心;……;按此规律,△OBC滚动2024次后停止滚动,则最后一个“花朵”的花心的坐标为 (1349+674,) .
【分析】根据所给滚动方式,发现每滚动三次,出现一个花心,再根据点An坐标变化的规律即可解决问题.
【解答】解:由题知,
∠COB=∠O′C′B=30°,BO=BC′,
∴A1O=A1C′,
∴点A1在OC′的垂直平分线上.
∵点B的坐标为(1,0),
∴OB=1,
在Rt△A1OB中,
tan30°=,
∴A1B=,
∴点A1的坐标为(1,).
依次类推,
点A2的坐标为(),
点A3的坐标为(),
…,
∴点An的坐标为()(n为正整数).
又∵每滚动三次,出现下一个花心,
∴2024÷3=674于2,
则674+1=675,
∴滚动2024次后停止滚动,最后一个“花朵”的花心对应的点为点A675.
当n=675时,
点A675的坐标为(1349+,),
即滚动2024次后停止滚动,最后一个“花朵”的花心的坐标为(1349+674,).
故答案为:(1349+674,).
【点评】本题主要考查了点的坐标变化规律及等腰三角形的性质,熟知等腰三角形的性质及能根据所给滚动方式发现点An坐标变化的规律是解题的关键.
9.(2024 武汉)如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形和中间的小正方形MNPQ拼成的一个大正方形ABCD.直线MP交正方形ABCD的两边于点E,F,记正方形ABCD的面积为S1,正方形MNPQ的面积为S2.若BE=kAE(k>1),则用含k的式子表示的值是 .
【分析】方法一:由BE=kAE可想到构造8字型相似,再利用比例线段求解即可;方法二:见到45°可构造等腰直角三角形,再利用手拉手全等和一个角平分线比例定理即可求解.
【解答】解:方法一:如图,过A作AG∥BP交FE延长线于点G,
∵AG∥BP,
∴∠GAE=∠PBE,∠AGE=∠BPE,
∴△AGE∽△PBE,
∴=,
设AG=1,则BP=k,
∵∠NMP=45°,
∴∠AMG=45°,AM=AG=1,
∵AN=BP=k,
∴MN=k﹣1,
∵S1=AD2=AM2+MD2=k2+1,S2=MN2=(k﹣1)2,
∴=;
方法二:如图,过B作BG⊥BP交FE延长线于点G,则△GBP是等腰直角三角形,
易证△GBA≌△PBC,
∴∠BGP=∠AGP=45°,
根据角平分线比例定理得:,
设AG=1,则BG=k,
∴AM=1,MD=k=AN,
∴MN=k﹣1,
∵S1=AD2=AM2+MD2=k2+1,S2=MN2=(k﹣1)2,
∴=;
故答案为:.
【点评】本题主要考查勾股定理得证明及正方形得性质、相似的判定和性质等知识点,熟练掌握以上知识和添加合适辅助线是解题关键.
10.(2024 浙江)如图,在菱形ABCD中,对角线AC,BD相交于点O,.线段AB与A′B′关于过点O的直线l对称,点B的对应点B′在线段OC上,A′B′交CD于点E,则△B′CE与四边形OB′ED的面积比为 .
【分析】根据轴对称可得到等线段等角,再结合菱形的性质可得到△A'ED≌△CEB'(AAS),再证△DOE≌△B'OE(SSS),由B'C:B'O=2:3即可求出答案.
【解答】解:如图连接OE、A'D,
∵AB关于过O的直线对称,
∴A'在BD延长线上,
∵,
∴设AC=10k,BD=6k,
在菱形ABCD中,OA=OC=5k,CB=OD=3k,
∵AB与A'B'关于过O的直线对称,
∴OA=OA'=5k,OB=OB'=3k,∠A'=∠DAC=∠DCA,
∴A'D=B'C=2k,
∵∠A'ED=∠B'CE,
∴△A'ED≌△CEB'(AAS),
∴DE=B'E,
∵OE=OE,OD=OB',
∴△DOE≌△B'OE(SSS),
∴S△DOE=S△B′OE,
∵==,
∴==.
故答案为:.
【点评】本题主要考查了轴对称的性质和菱形的性质、全等三角形的判定和性质,熟练掌握以上基础知识和线段之间的转化是解题关键.
11.(2024 山西)如图,在 ABCD中,AC为对角线,AE⊥BC于点E,点F是AE延长线上一点,且∠ACF=∠CAF,线段AB,CF的延长线交于点G.若AB=,AD=4,tan∠ABC=2,则BG的长为 .
【分析】方法一:过点F作FH⊥AC于H,延长AD与GC的延长线交于K,由tan∠ABC==2得AE=2BE,进而得BE=1,AE=2,则CE=3,AC=,再由∠ACF=∠CAF得FA=FC,则AH=CH=,由S△FAC=AC FH=AF CE,得FH=,在Rt△AFH中由勾股定理得AF=,则EF=AF﹣AE=,证明△FCE∽△FKA得AK=,则DK=AK﹣AD=,再证明△KDC∽△KAG得AG=,由此可得BG的长.
方法二:过点G作GH⊥BC,交CB的延长线于H,先求出BE=1,AE=2,CE=3,设EF=a,则AF=CF=2+a,由勾股定理求出a=,根据∠GBH=∠ABC得GH=2HB,设HB=b,则GH=2b,CH=BC+HB=4+b,GB=,证明△CEF∽△CHG得b=,由此可得GH的长.
【解答】解法一:过点F作FH⊥AC于H,延长AD与GC的延长线交于K,如下图所示:
∵四边形ABCD为平行四边形,
∴AB=CD=,BC=AD=4,AB∥CD,BC∥AD,
又∵AE⊥BC,
在Rt△ABE中,tan∠ABC==2,
∴AE=2BE,
由勾股定理得:AE2+BE2=AB2,
即(2BE)2+BE2=()2,
∴BE=1,
∴AE=2BE=2,
∴CE=BC﹣BE=3,
在Rt△ACE中,由勾股定理得:AC==,
∵∠ACF=∠CAF,
∴FA=FC,
∵FH⊥AC,
∴AH=CH=AC=,
∵S△FAC=AC FH=AF CE,
∴FH=,
在Rt△AFH中,由勾股定理得:AF2﹣FH2=AH2,
即,
∴AF=,
∴EF=AF﹣AE=,
∵BC∥AD,
∴△FCE∽△FKA,
∴EF:AF=CE:AK,
即,
∴AK=,
∴DK=AK﹣AD=,
∵AB∥CD,
∴△KDC∽△KAG,
∴DK:AK=CD:AG,
即,
∴AG=,
∴BG=AG﹣AB=.
故答案为:.
解法二:过点G作GH⊥BC,交CB的延长线于H,如下图所示:
∵四边形ABCD为平行四边形,
∴AB=CD=,BC=AD=4,AB∥CD,BC∥AD,
又∵AE⊥BC
在Rt△ABE中,tan∠ABC==,
∴AE=2BE,
由勾股定理得:AE2+BE2=AB2,
即(2BE)2+BE2=()2,
∴BE=1,
∴AE=2BE=2,
∴CE=BC﹣BE=3,
设EF=a,则AF=AE+EF=2+a,
∵∠ACF=∠CAF,
∴AF=CF=2+a,
在Rt△CEF中,由勾股定理得:CF2=CE2+EF2,
即(2+a)2=32+a2,
解得:a=,
∵∠GBH=∠ABC,
∴在Rt△GBH中,tan∠GBH=,
∴GH=2HB,
设HB=b,则GH=2b,CH=BC+HB=4+b,
在Rt△GBH中,由勾股定理得:GB=,
∵GH⊥BC,AF⊥BC,
∴EF∥GH,
∴△CEF∽△CHG,
∴CE:CH=EF:GH,
即3:(4+b)=:2b,
解得:b=,
∴GH==,
故答案为:.
【点评】此题主要考查了平行四边形的性质,解直角三角形的应用,相似三角形的判定和性质,熟练掌握平行四边形的性质,锐角三角函数的定义是解决问题的关键,正确地添加辅助线构造相似三角形,并利用相似三角形的性质进行计算是解决问题的难点.
12.(2024 临夏州)如图,对折边长为2的正方形纸片ABCD,OM为折痕,以点O为圆心,OM为半径作弧,分别交AD,BC于E,F两点,则的长度为 (结果保留π).
【分析】由对折可知,∠EOM=∠FOM,过点E作OM的垂线,进而可求出∠EOM的度数,则可得出∠EOF的度数,最后根据弧长公式即可解决问题.
【解答】解:由对折可知,
四边形AOMD是矩形,∠EOM=∠FOM,
则OM=AD,DM=.
过点E作OM的垂线,垂足为P,
则EP=DM=.
因为OE=OM=AD,CD=AD,
所以EP=.
在Rt△EOP中,
sin∠EOP==,
所以∠EOP=30°,
则∠EOF=30°×2=60°,
所以的长度为:.
故答案为:.
【点评】本题主要考查了弧长的计算、正方形的性质及翻折变换(折叠问题),熟知正方形的性质、图形翻折的性质及弧长的计算公式是解题的关键.
13.(2024 扬州)如图,已知两条平行线l1、l2,点A是l1上的定点,AB⊥l2于点B,点C、D分别是l1,l2上的动点,且满足AC=BD,连接CD交线段AB于点E,BH⊥CD于点H,则当∠BAH最大时,sin∠BAH的值为 .
【分析】由题易得四边形ACBD是平行四边形,从而得到BE是定长,又由∠BHE=90°,得出直角对直角的隐圆模型,再根据最大张角问题(相切时)求解即可.
【解答】解:∵AC∥BD,
∴四边形ACBD是平行四边形,
∴AE=BE=AB,
∵A为定点,且AB⊥l2,
∴AE为定值,
∵BH⊥CD,
∴∠BHE=90°,
∴点H在以BE为直径的圆上运动(如图,O为圆心),
此时OE=BE=OA,
∵当AH与⊙O相切时∠BAH最大,
∴sin∠BAH==.
故答案为:.
【点评】本题主要考查了切线的性质,熟练掌握切线的性质、圆周角定理是解题的关键,其中识别出隐圆模型至关重要.
14.(2024 苏州)铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,所在圆的圆心C恰好是△ABO的内心,若AB=2,则花窗的周长(图中实线部分的长度)= 8π .(结果保留π)
【分析】根据正六边形的性质,三角形内心的性质以及直角三角形的边角关系求出所对应的圆心角的度数及半径,由弧长公式求出弧的长,再计算长的6倍即可.
【解答】解:如图,过点C作CM⊥AB于点M,则AM=BM=AB=,
∵六条等弧所对应的弦构成一个正六边形,中心为点O,
∴∠AOB==60°,
∵OA=OB,
∴△AOB是正三角形,
∵点O是△AOB的内心,
∴∠CAB=∠CBA=×60°=30°,∠ACB=2∠AOB=120°,
在Rt△ACM中,AM=,∠CAM=30°,
∴AC==2,
∴的长为=π,
∴花窗的周长为π×6=8π.
故答案为:8π.
【点评】本题考查正多边形和圆,弧长的计算,掌握正六边形的性质,三角形的内心的性质以及直角三角形的边角关系,弧长的计算方法是正确解答的关键.
15.(2024 凉山州)如图,△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 100° .
【分析】由CD是边AB上的高,∠BCD=30°,∠ACB=80°,可求得∠CAB、∠CBA的度数,因为AE是∠CAB的平分线,可得∠EAB的度数,根据三角形内角和定理,可得∠AEB的度数.
【解答】解:∵CD是边AB上的高,
∴∠CDB=∠CDA=90°,
∵∠BCD=30°,∠ACB=80°,
∴∠ACD=∠ACB﹣∠BCD=50°,∠CBD=90°﹣∠BCD=60°,
∴∠CAB=90°﹣∠ACD=40°,
∵AE是∠CAB的平分线,
∴∠EAB=∠CAB=20°,
∴∠AEB=180°﹣∠EAB﹣∠EBA=100°,
故答案为:100°.
【点评】本题考查了三角形内角和定理,角平分线的定义,关键是掌握三角形内角和定理,角平分线的定义.
16.(2024 烟台)如图,在边长为6的正六边形ABCDEF中,以点F为圆心,以FB的长为半径作,剪如图中阴影部分做一个圆锥的侧面,则这个圆锥的底面半径为 .
【分析】根据正六边形的性质求出阴影部分扇形的圆心角度数,再根据直角三角形的边角关系求出半径,由弧长的计算方法进行计算即可.
【解答】解:如图,过点A作AM⊥BF,垂足为M,则BM=FM,
∵六边形ABCDEF是正六边形,
∴∠BAF=∠E==120°,AB=AF=EF=DE=6,
∴∠ABF=∠AFB=∠DFE==30°,
∴∠BFD=120°﹣30°﹣30°=60°,
在Rt△ABM中,AB=6,∠ABM=30°,
∴BM=AB=3,
∴BF=2BM=6,
设这个圆锥的底面半径为r,由题意可得,
2πr=,
解得r=.
故答案为:.
【点评】本题考查正多边形和圆,弧长的计算,掌握正六边形的性质,等腰三角形的性质以及弧长的计算方法是正确解答的关键.
17.(2024 甘肃)甘肃临夏砖雕是一种历史悠久的古建筑装饰艺术,是第一批国家级非物质文化遗产.如图1是一块扇面形的临夏砖雕作品,它的部分设计图如图2,其中扇形OBC和扇形OAD有相同的圆心O,且圆心角∠O=100°,若OA=120cm,OB=60cm,则阴影部分的面积是 3000π cm2.(结果用π表示)
【分析】利用扇形面积公式,根据S阴影=S扇形AOD﹣S扇形BOC即可求解.
【解答】解:S阴影=S扇形AOD﹣S扇形BOC
=
=
=3000π(cm2),
故答案为:3000π.
【点评】本题考查了求扇形面积,熟练掌握扇形面积公式是解题的关键.
18.(2024 眉山)如图,△ABC内接于⊙O,点O在AB上,AD平分∠BAC交⊙O于D,连结BD.若AB=10,BD=2,则BC的长为 8 .
【分析】延长AC,BD交于E,根据圆周角定理得到BD⊥AD,求得∠ADB=∠ADE=90°,根据角平分线的定义得到∠BAD=∠DAE,根据全等三角形的性质得到BD=DE=2,根据勾股定理得到AD,根据相似三角形的判定和性质即可得到结论.
【解答】解:延长AC,BD交于E,
∵AB是⊙O的直径,
∴BD⊥AD,
∴∠ADB=∠ADE=90°,
∵AD平分∠BAC,
∴∠BAD=∠DAE,
∵AD=AD,
∴△BAD≌△EAD(ASA),
∴BD=DE=2,
∴BE=4,
∵AB=10,BD=2,
∴AD==4,
∵∠DAC=∠CBD,
∵∠ADB=∠BCE=90°,
∴△ABD∽△BEC,
∴,
∴=,
∴BC=8.
故答案为:8.
【点评】本题考查了三角形的外接圆与外心,全等三角形的判定和性质,勾股定理,相似三角形的判定和性质,正确地作出辅助线是解题的关键.
19.(2024 内江)如图,在△ABC中,∠ABC=60°,BC=8,E是BC边上一点,且BE=2,点I是△ABC的内心,BI的延长线交AC于点D,P是BD上一动点,连接PE、PC,则PE+PC的最小值为 .
【分析】在AB取点F,使BF=BE=2,连接PF,CF,过点F作FH⊥BC于H,利用三角形内心的定义可得出∠ABD=∠CBD,利用SAS证明△BFP≌△BEP,得出PF=PE,则 PE+PC=PF+PC≥CF,当C、P、F三点共线时,PE+PC最小,最小值为CF,利用含 30° 的直 角三角形的性质求出BH,利用勾股定理求出FH,CF即可.
【解答】解:在AB取点F,使 BF=BE=2,连接PF,CF,过点F作FH⊥BC于H,
∵是△ABC 的内心,
∴BI平分∠ABC,
∴∠ABD=∠CBD,
又 BP=BP,
∴△BFP≌△BEP(SAS),
∴PF=PE,
∴PE+PC=PF+PC≥CF,
当C、P、F三点共线时,PE+PC最小,最小值为CF,
∵FH⊥BC,∠ABC=60°,
∴∠BFH=30°,
∴,
∴,CH=BC﹣BH=7,
∴,
∴PE+PC 的最小值为 ,
故答案为:.
【点评】本题考查了三角形的内心,全等三角形的判定与性质,含30°的直角三角形的性质,勾股定理等知识,明确题意,添加合适辅助线,构造全等三角形和含30°的直角三角形是解题的关键.
20.(2024 滨州)如图,在边长为1的正方形网格中,点A,B均在格点上.
(1)AB的长为 ;
(2)请只用无刻度的直尺,在如图所示的网格中,画出以AB为边的矩形ABCD,使其面积为,并简要说明点C,D的位置是如何找到的(不用证明): 根据相似三角形的性质和矩形的面积,可以得到AD与AB的乘积为,从而可以得到点C和点D .
【分析】(1)根据题意和勾股定理,可以求得AB的长;
(2)根据相似三角形的性质和矩形的面积,可以得到AD与AB的乘积为,从而可以得到点C和点D,然后画出这个矩形即可.
【解答】解:(1)由图可得,
AB==,
故答案为:;
(2)如图所示,四边形ABCD即为所求,理由:根据相似三角形的性质和矩形的面积,可以得到AD与AB的乘积为,从而可以得到点C和点D,
具体的计算过程:由图可知:△ABF∽ADE,
则,
即,
解得AD=,
∴AD AB=×=,
这样找到点D,同理可以找到点C,
即图中ABCD即为所求,
故答案为:根据相似三角形的性质和矩形的面积,可以得到AD与AB的乘积为,从而可以得到点C和点D.
【点评】本题考查作图—复杂作图、勾股定理、矩形的判定,解答本题的关键是明确题意,利用数形结合的思想解答.
21.(2024 连云港)如图,AB是圆的直径,∠1、∠2、∠3、∠4的顶点均在AB上方的圆弧上,∠1、∠4的一边分别经过点A、B,则∠1+∠2+∠3+∠4= 90 °.
【分析】根据半圆的度数为 180°,同弧所对的圆周角是圆心角的一半,即可得出结果.
【解答】∵AB是圆的直径,
∴AB所对的弧是半圆,所对圆心角的度数为180°,
∵∠1、∠2、∠3、∠4所对的弧的和为半圆,
∴,
故答案为:90.
【点评】本题考查圆周角定理,根据半圆的度数为 180°,同弧所对的圆周角是圆心角的一半,进行求解即可.
22.(2024 达州)如图,在△ABC中,AE1,BE1分别是内角∠CAB,外角∠CBD的三等分线,且∠E1AD=∠CAB,∠E1BD=∠CBD,在△ABE1中,AE2,BE2分别是内角∠E1AB,外角∠E1BD的三等分线,且∠E2AD=∠E1AB,∠E2BD=∠E1BD,…,以此规律作下去,若∠C=m°,则∠En= 度.
【分析】本题考查了三角形的外角定理,等式性质,熟练掌握知识点是解题的关键.先分别对△ABC.△E1AB 运用三角形的外角定理,设∠E1AD=α,则∠CAB=3α,∠E1BD=β,则∠CBD=3β,得到 β=α+∠E1,3β=3a+∠C,同建可求:,所以可得 .
【解答】解:由题意,,
∴设∠E1AD=α,∠E1BD=β,则∠CAB=3α,∠CBD=3β,
由三角形的外角的性质得:β=α+∠E1,3β=3α+∠C,,
同理可求:, ……,,
即 ,
故答案为:.
【点评】本题考查三角形的外角性质,三角形内角和定理,规律型:图形变化类等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.
23.(2024 自贡)龚扇是自贡“小三绝”之一,为弘扬民族传统文化,某校手工兴趣小组将一个废弃的大纸杯侧面剪开直接当作扇面,制作了一个龚扇模型(如图),扇形外侧两竹条AB,AC夹角为120°,AB长30cm,扇面的BD边长为18cm,则扇面面积为 252π cm2(结果保留π).
【分析】根据扇形公式进行计算即可.
【解答】解:扇面面积=扇形BAC的面积﹣扇形DAE的面积
=﹣
=252π(cm2),
故答案为:252π.
【点评】本题考查了扇面面积计算,掌握扇面面积等于两个扇形面积相减是解题的关键.
24.(2024 山东)如图,已知∠MAN,以点A为圆心,以适当长为半径作弧,分别与AM、AN相交于点B,C;分别以B,C为圆心,以大于BC的长为半径作弧,两弧在∠MAN内部相交于点P,作射线AP.分别以A,B为圆心,以大于AB的长为半径作弧,两弧相交于点D,E,作直线DE分别与AB,AP相交于点F,Q.若AB=4,∠PQE=67.5°,则F到AN的距离为 .
【分析】如图,过F作FH⊥AC于H,证明∠BAP=∠CAP,DE⊥AB,,再证明∠FAH=45°,再结合勾股定理可得答案.
【解答】解:如图,过F作FH⊥AC于H,
由作图可得:∠BAP=∠CAP,DE⊥AB,,
∵∠PQE=67.5°,
∴∠AQF=67.5°,
∴∠BAP=∠CAP=90°﹣67.5°=22.5°,
∴∠FAH=45°,
∴,
∴F到AN的距离为;
故答案为:.
【点评】本题考查了作图 复杂作图:基本作图,三角形的内角和定理的应用,勾股定理的应用,等腰三角形的判定,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质,逐步操作.
25.(2024 连云港)如图,在△ABC中,∠C=90°,∠B=30°,AC=2.点P在边AC上,过点P作PD⊥AB,垂足为D,过点D作DF⊥BC,垂足为F.连接PF,取PF的中点E.在点P从点A到点C的运动过程中,点E所经过的路径长为 .
【分析】以C为原点,建立坐标系,设AP=a,则CP=2﹣a,利用含30度角的直角三角形的性质,求出点E的坐标,得到点E在直线上运动,求出点P分别与A,C重合时点E的坐标,利用两点间的距离公式进行求解即可.
【解答】解:方法一:以C为原点,建立坐标系,过点D作DG⊥AC
设AP=a,则CP=2﹣a,
∴P(0,2﹣a),
∵∠B=30°,
∴∠A=60°,
∵PD⊥AB,
∴∠PDA=90°,
∴∠APD=30°,
∴,
∵DG⊥AC,
∴∠AGD=90°,
∴,,
∵DF⊥BC,DG⊥AC,∠ACB=90°,
∴四边形DGCF为矩形,
∴DG=CF,
∴,
∵E为P,F的中点,
∴,
令,
∴,
∴点E在直线上运动,
当点P与A重合时,a=0,此时E(0,1),
当点P与C重合时,a=2,此时,
∴点E所经过的路径长为:,
方法二:∵P在AC上运动,运动路径为线段,E为PF中点,
∴E的运动路径亦为线段,
∵当P与A重合时,CE=1,当P与C重合时,CE=,
∴点E所经过的路径长为:,
故答案为:.
【点评】本题考查含30度角的直角三角形,一次函数与几何的综合应用,矩形的判定和性质,两点间的距离,综合运用这些性质是解题的关键.
26.(2024 宜宾)如图,一个圆柱体容器,其底部有三个完全相同的小孔槽,分别命名为甲槽、乙槽、丙槽.有大小质地完全相同的三个小球,每个小球标有从1至9中选取的一个数字,且每个小球所标数字互不相同.作如下操作:将这三个小球放入容器中,摇动容器使这三个小球全部落入不同的小孔槽(每个小孔槽只能容下一个小球),取出小球记录下各小孔槽的计分(分数为落入该小孔槽小球上所标的数字),完成第一次操作.再重复以上操作两次.已知甲槽、乙槽、丙槽三次操作计分之和分别为20分、10分、9分,其中第一次操作计分最高的是乙槽,则第二次操作计分最低的是 乙槽 (从“甲槽”、“乙槽”、“丙槽”中选填).
【分析】由三次操作三个槽总分是20+10+9=39分,所以一次操作得总分就是13分,再根据三个球得数不相同可以列举出综合为13得所有情况.,然后再根据各自得分去一一分析比较即可.
【解答】方法一:∵三次操作相同,且总得分是20+10+9=39分.
∴一次操作的总分,即三个球数字之后为39÷3=13,
则有以下情况:
,
其中只有1,4,8这一组能同时满足三个数组合相加得20,10,9;
,
∴第一次操作甲槽乙槽丙槽分数分别为4,8,1;
第二次操作甲槽乙槽丙槽分数分别为8,1,1;
第三次操作甲槽乙槽丙槽分数分别为8,1,1;
∴第二次操作计分最低的是乙槽.
方法二:设乙第一,第二,第三次操作计分分别为x、y、z.
则x+y+z=10,
x不可能为9,否则yz出现为0的情况,与题意矛盾.
所以x最大为8,此时8+1+1=10,
1已经是最小了,所以第二次操作计分最小的是乙槽.
故答案为:乙槽.
【点评】本题主要考查了推理与论证,题型比较活,属于现在比较多的考查形式,要求学生具备一定的数学思维.
27.(2024 遂宁)在等边△ABC三边上分别取点D、E、F,使得AD=BE=CF,连结三点得到△DEF,易得△ADF≌△BED≌△CFE,设S△ABC=1,则S△DEF=1﹣3S△ADF.
如图①当=时,S△DEF=1﹣3×=;
如图②当=时,S△DEF=1﹣3×=;
如图③当=时,S△DEF=1﹣3×=;
…
直接写出,当=时,S△DEF= .
【分析】探究规律,利用规律解决问题.
【解答】解:如图①当=时,S△DEF=1﹣3×=1﹣3×=;
如图②当=时,S△DEF=1﹣3×=1﹣3×=;
如图③当=时,S△DEF=1﹣3×=1﹣3×=;
…
当=时,S△DEF=1﹣3×;
故当=时,S△DEF=1﹣3×=.
【点评】本题考查全等三角形的判定和性质,等边三角形的性质,规律型﹣图形变化等知识,解题的关键是学会探究规律,利用规律解决问题.
28.(2024 重庆)如图,AB是⊙O的直径,BC是⊙O的切线,点B为切点.连接AC交⊙O于点D,点E是⊙O上一点,连接BE,DE,过点A作AF∥BE交BD的延长线于点F.若BC=5,CD=3,∠F=∠ADE,则AB的长度是 ;DF的长度是 .
【分析】由圆周角定理得到∠BDC=90°,由勾股定理求出BD==4,由△CDB∽△CBA,推出DB:BA=CD:CB,得到AB=,由平行线的性质,圆周角定理推出∠F=∠BAF,得到BF=AB=,即可求出FD的值.
【解答】解:∵AB是圆的直径,
∴∠ADB=90°,
∴∠BDC=90°,
∵BC=5,CD=3,
∴BD==4,
∵BC切圆于B,
∴直径AB⊥BC,
∴∠ABC=90°,
∵∠BCD=∠ACB,∠CDB=∠ABC=90°,
∴△CDB∽△CBA,
∴DB:BA=CD:CB,
∴4:AB=3:5,
∴AB=,
∵AF∥BE,
∴∠BAF=∠ABE,
∵∠ABE=∠ADE,∠F=∠ADE,
∴∠F=∠BAF,
∴BF=AB=,
∴FD=BF﹣BD=﹣4=.
故答案为:,.
【点评】本题考查切线的性质,勾股定理,相似三角形的判定和性质,圆周角定理,平行线的性质,关键是判定△CDB∽△CBA,推出DB:BA=CD:CB,由圆周角定理,平行线的性质推出∠F=∠BAF.
29.(2024 湖北)如图,由三个全等的三角形(△ABE,△BCF,△CAD)与中间的小等边三角形DEF拼成一个大等边三角形ABC.连接BD并延长交AC于点G.若AE=ED=2.则(1)∠FDB的度数是 30° ;(2)DG的长是 .
【分析】(1)利用三角形相似及AE=DE可得BF=DF,再利用三角形的外角性质结合可求得∠DBF=30°;
(2)作CH⊥BG交BG的延长线于点H,利用直角三角形的性质求得CH=1,FH=,证明△ADG∽△CHG,利用相似三角形的性质列式计算即可求解.
【解答】解:∵△ABE≌△BCF≌△CAD(已知),
∴AD=BE=CF,AE=BF=DC,
∵AE=ED=2,
∴AD=BE=4,
∵△DEF为等边三角形,
∴EF=DF=DE=2,∠EFD=∠EDF=60°,
∴BF=DF=DC=2,
∴∠FDB=∠FBD=∠EFD=30°,∠ADB=∠EDF+∠FDB=90°,
如图,过点C作CH⊥BG的延长线于点H,
∵∠CDH=30°,
∴CH=CD×sin30°=2×=1,
DH=CD×cos30°=2×=,
∵∠ADG=∠CHG,∠AGD=∠CGH,
∴△ADG∽△CHG,
∴,
∴DG==.
【点评】本题考查了相似三角形的判定和性质,等边三角形的判定和性质,勾股定理等知识.
30.(2024 湖北)△DEF为等边三角形,分别延长FD,DE,EF,到点A,B,C,使DA=EB=FC,连接AB,AC,BC,连接BF并延长交AC于点G.若AD=DF=2,则∠DBF= 30° ,FG= .
【分析】根据题干可得EB=EF=ED,∠DEF=60°,利用外角性质和一个等腰三角形可得∠DBF=30°;作CH⊥BG,交BG的延长线于点H,易证△AFG∽△CHG,根据相似比易求FG的长度.
【解答】解:∵△DEF为等边三角形,且DE=EB,
∴DE=BE=EF,∠DEF=∠DFE=∠EDF=60°,
∴∠DBF=∠EFB=30°,
∴∠AFB=90°,
作CH⊥BG,交BG的延长线于点H,
∵∠CFH=∠BFE=30°,AD=DF=CF=2,
∴CH=CF=1,
∴FH=,
∵∠AFG=∠CHG=90°,∠AGF=∠CGH,
∴△AFG∽△CHG,
∴===4,
∴FG=FH=.
故答案为:30°;.
【点评】本题主要考查相似三角形的判定和性质,熟练掌握相似三角形的判定和性质以及等边三角形的性质等相关知识是解题关键.
同课章节目录
