2024年中考数学选择题题分类汇编——数与式(含解析)
文档属性
| 名称 | 2024年中考数学选择题题分类汇编——数与式(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 499.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024年中考数学选择题题分类汇编——数与式
一.选择题(共30小题)
1.(2024 齐齐哈尔)下列计算正确的是( )
A.4a2+2a2=6a4 B.5a 2a=10a
C.a6÷a2=a3 D.(﹣a2)2=a4
2.(2024 包头)计算所得结果是( )
A.3 B. C.3 D.±3
3.(2024 广州)若a≠0,则下列运算正确的是( )
A.+= B.a3 a2=a5 C. = D.a3÷a2=1
4.(2024 内蒙古)下列计算正确的是( )
A.(﹣2a4)3=﹣6a12
B.a﹣2+a5=a3
C.
D.(a+b)(a2﹣ab+b2)=a3+b3
5.(2024 甘孜州)祖国江山美丽如画,川西风光多姿多彩.据四川省某州相关部门通报,“五一”期间,全国各地众多游客前往旅游,共接待游客约1665000人次.将1665000用科学记数法表示应为( )
A.0.1665×107 B.1.665×106
C.16.65×105 D.166.5×104
6.(2024 广元)将﹣1在数轴上对应的点向右平移2个单位,则此时该点对应的数是( )
A.﹣1 B.1 C.﹣3 D.3
7.(2024 长春)根据有理数加法法则,计算2+(﹣3)过程正确的是( )
A.+(3+2) B.+(3﹣2) C.﹣(3+2) D.﹣(3﹣2)
8.(2024 兰州)计算:2a(a﹣1)﹣2a2=( )
A.a B.﹣a C.2a D.﹣2a
9.(2024 济宁)如图,用大小相等的小正方形按照一定规律拼正方形.第一幅图有1个正方形,第二幅图有5个正方形,第三幅图有14个正方形……按照此规律,第六幅图中正方形的个数为( )
A.90 B.91 C.92 D.93
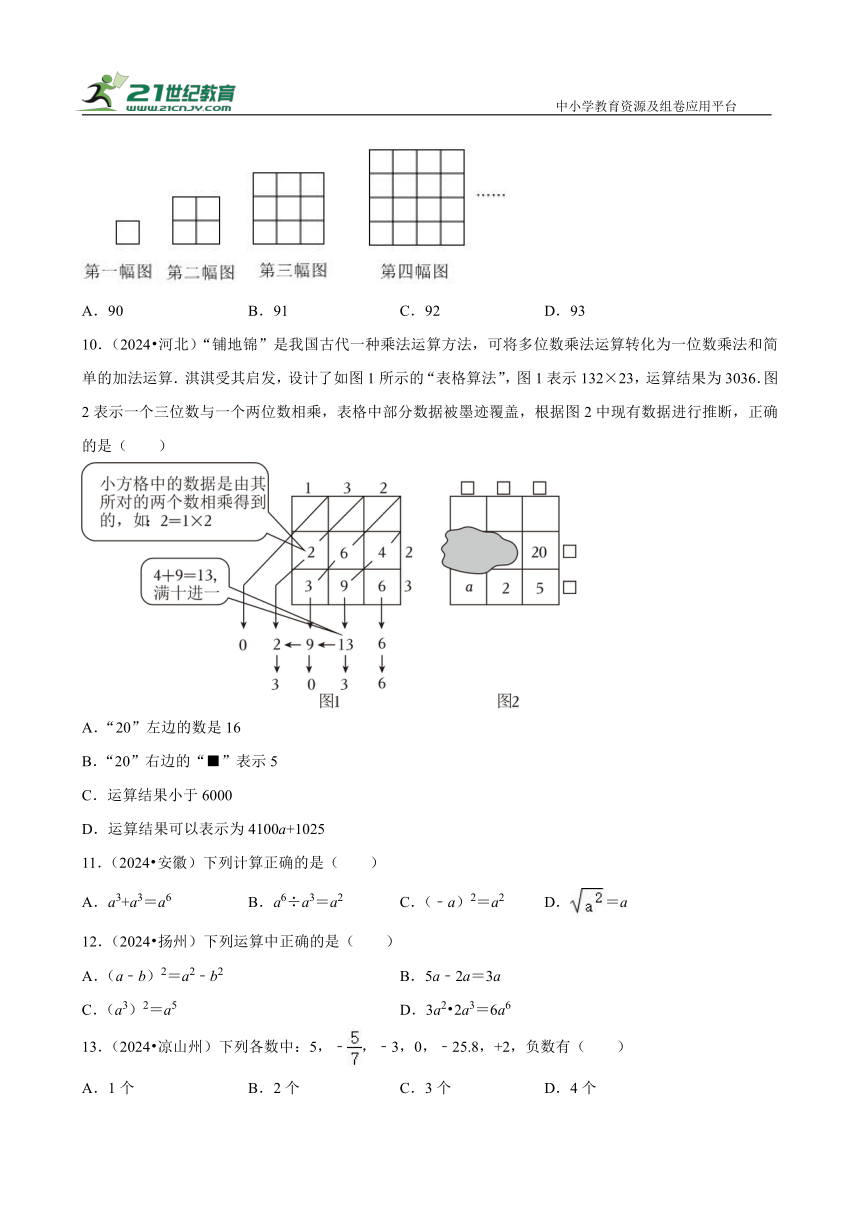
10.(2024 河北)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1表示132×23,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,正确的是( )
A.“20”左边的数是16
B.“20”右边的“■”表示5
C.运算结果小于6000
D.运算结果可以表示为4100a+1025
11.(2024 安徽)下列计算正确的是( )
A.a3+a3=a6 B.a6÷a3=a2 C.(﹣a)2=a2 D.=a
12.(2024 扬州)下列运算中正确的是( )
A.(a﹣b)2=a2﹣b2 B.5a﹣2a=3a
C.(a3)2=a5 D.3a2 2a3=6a6
13.(2024 凉山州)下列各数中:5,﹣,﹣3,0,﹣25.8,+2,负数有( )
A.1个 B.2个 C.3个 D.4个
14.(2024 眉山)下列四个数中,无理数是( )
A.﹣3.14 B.﹣2 C. D.
15.(2024 烟台)实数a,b,c在数轴上的位置如图所示,下列结论正确的是( )
A.b+c>3 B.a﹣c<0 C.|a|>|c| D.﹣2a<﹣2b
16.(2024 云南)下列计算正确的是( )
A.x3+5x3=6x4 B.x6÷x3=x5
C.(a2)3=a7 D.(ab)3=a3b3
17.(2024 云南)中国是最早使用正负数表示具有相反意义的量的国家.若向北运动100米记作+100米,则向南运动100米可记作( )
A.100米 B.﹣100米 C.200米 D.﹣200米
18.(2024 云南)按一定规律排列的代数式:2x,3x2,4x3,5x4,6x5, ,第n个代数式是( )
A.2xn B.(n﹣1)xn C.nxn+1 D.(n+1)xn
19.(2024 连云港)如图,正方形中有一个由若干个长方形组成的对称图案,其中正方形边长是80cm,则图中阴影图形的周长是( )
A.440cm B.320cm C.280cm D.160cm
20.(2024 达州)下列计算正确的是( )
A.a2+a3=a5 B.(a+2)2=a2+2a+4
C.(﹣2a2b3)3=﹣8a6b9 D.a12÷a6=a2
21.(2024 山东)下列实数中,平方最大的数是( )
A.3 B. C.﹣1 D.﹣2
22.(2024 德阳)将一组数,2,,2,,2,…,,…,按以下方式进行排列:则第八行左起第1个数是( )
A.7 B.8 C. D.4
23.(2024 重庆)烷烃是一类由碳、氢元素组成的有机化合物质,如图是这类物质前四种化合物的分子结构模型图,其中灰球代表碳原子,白球代表氢原子.第1种如图①有4个氢原子,第2种如图②有6个氢原子,第3种如图③有8个氢原子,……按照这一规律,第10种化合物的分子结构模型中氢原子的个数是( )
A.20 B.22 C.24 D.26
24.(2024 重庆)已知整式M:anxn+an﹣1xn﹣1+ +a1x+a0,其中n,an﹣1,…,a0为自然数,an为正整数,且n+an+an﹣1+ +a1+a0=5.下列说法:
①满足条件的整式M中有5个单项式;
②不存在任何一个n,使得满足条件的整式M有且仅有3个;
③满足条件的整式M共有16个.
其中正确的个数是( )
A.0 B.1 C.2 D.3
25.(2024 宜宾)如果一个数等于它的全部真因数(含单位1,不含它本身)的和,那么这个数称为完美数.例如:6的真因数是1、2、3,且6=1+2+3,则称6为完美数.下列数中为完美数的是( )
A.8 B.18 C.28 D.32
26.(2024 重庆)估计的值应在( )
A.8和9之间 B.9和10之间
C.10和11之间 D.11和12之间
27.(2024 重庆)已知整式M:anxn+an﹣1xn﹣1+ +a1x+a0,其中n,an﹣1,…,a0为自然数,an为正整数,且n+an+an﹣1+ +a1+a0=5.下列说法:
①满足条件的整式M中有5个单项式;
②不存在任何一个n,使得满足条件的整式M有且只有3个;
③满足条件的整式M共有16个.
其中正确的个数是( )
A.0 B.1 C.2 D.3
28.(2024 重庆)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,…,按此规律,则第⑧个图案中,菱形的个数是( )
A.20 B.21 C.23 D.26
29.(2024 台湾)有研究报告指出,1880年至2020年全球平均气温上升趋势约为每十年上升0.08℃.已知2020年全球平均气温为14.88℃,假设未来的全球平均气温上升趋势与上述趋势相同,且每年上升的度数相同,则预估2020年之后第x年的全球平均气温为多少℃?(以x表示)( )
A.14.88+0.08x
B.14.88+0.008x
C.14.88+0.08[x+(2020 1880)]
D.14.88+0.008[x+(2020 1880)]
30.(2024 台湾)如图的数在线有A( 2)、O(0)、B(2)三点.今打算在此数在线标示P(p)、Q(q)两点,且p、q互为倒数,若P在A的左侧,则下列叙述何者正确?( )
A.Q在AO上,且AQ<QO B.Q在AO上,且AQ>QO
C.Q在OB上,且OQ<QB D.Q在OB上,且OQ>QB
数与式
参考答案与试题解析
一.选择题(共30小题)
1.(2024 齐齐哈尔)下列计算正确的是( )
A.4a2+2a2=6a4 B.5a 2a=10a
C.a6÷a2=a3 D.(﹣a2)2=a4
【分析】根据合并同类项、单项式乘单项式、同底数幂相除及幂的乘方与积的乘方进行计算,逐一判断即可.
【解答】解:A.4a2+2a2=6a2,故本选项不符合题意;
B.5a 2a=10a2,故本选项不符合题意;
C.a6÷a2=a4,故本选项不符合题意;
D.(﹣a2)2=a4,故本选项符合题意;
故选:D.
【点评】本题主要考查合并同类项、单项式乘单项式、同底数幂相除及幂的乘方与积的乘方,熟练掌握以上知识点是解题的关键.
2.(2024 包头)计算所得结果是( )
A.3 B. C.3 D.±3
【分析】先计算,再化简二次根式.
【解答】解:
=
=
=,
故答案为:C.
【点评】本题考查了二次根式的计算,掌握计算法则是解题的关键.
3.(2024 广州)若a≠0,则下列运算正确的是( )
A.+= B.a3 a2=a5 C. = D.a3÷a2=1
【分析】利用合并同类项法则,同底数幂乘法及除法法则,分式的乘法法则计算即可.
【解答】解:+==,则A不符合题意;
a3 a2=a5,则B符合题意;
=,则C不符合题意;
a3÷a2=a,则D不符合题意;
故选:B.
【点评】本题考查合并同类项,同底数幂乘法及除法,分式的乘法,熟练掌握相关运算法则是解题的关键.
4.(2024 内蒙古)下列计算正确的是( )
A.(﹣2a4)3=﹣6a12
B.a﹣2+a5=a3
C.
D.(a+b)(a2﹣ab+b2)=a3+b3
【分析】A.根据积的乘方法则和幂的乘方法则进行计算,然后判断即可;
B.根据同底数幂相乘法则进行计算,然后判断即可;
C.根据同分母的分式加减法则进行计算,然后判断即可;
D.根据多项式乘多项式法则进行计算,然后判断即可.
【解答】解:A.∵(﹣2a4)3=﹣8a12,∴此选项的计算错误,故此选项不符合题意;
B.∵,∴此选项的计算错误,故此选项不符合题意;
C.∵,∴此选项的计算错误,故此选项不符合题意;
D.∵(a+b)(a2﹣ab+b2)=a3﹣a2b+ab2+a2b﹣ab2+b3=a3+b3,∴此选项的计算正确,故此选项符合题意;
故选:D.
【点评】本题主要考查了整式和分式的混合运算,解题关键是熟练掌握积的乘方法则、幂的乘方法则和多项式乘多项式法则.
5.(2024 甘孜州)祖国江山美丽如画,川西风光多姿多彩.据四川省某州相关部门通报,“五一”期间,全国各地众多游客前往旅游,共接待游客约1665000人次.将1665000用科学记数法表示应为( )
A.0.1665×107 B.1.665×106
C.16.65×105 D.166.5×104
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:1665000=1.665×106,
故选:B.
【点评】此题考查科学记数法的表示方法,科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
6.(2024 广元)将﹣1在数轴上对应的点向右平移2个单位,则此时该点对应的数是( )
A.﹣1 B.1 C.﹣3 D.3
【分析】将﹣1在数轴上对应的点向右平移2个单位,可列算式﹣1+2,求得此时该点对应的数是1,于是得到问题的答案.
【解答】解:由题意得﹣1+2=1,
所以﹣1在数轴上对应的点向右平移2个单位,此时该点对应的数是1,
故选:B.
【点评】此题重点考查数轴、有理数的运算等知识,根据题意正确地列出算式是解题的关键.
7.(2024 长春)根据有理数加法法则,计算2+(﹣3)过程正确的是( )
A.+(3+2) B.+(3﹣2) C.﹣(3+2) D.﹣(3﹣2)
【分析】有理数加法法则:
1、同号两数相加,取相同符号,并把绝对值相加.
2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
3、一个数同0相加,仍得这个数.
【解答】根据有理数加法法则第2条:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
2+(﹣3)
=﹣(3﹣2)
故答案为D.
【点评】本题考查有理数加法法则,熟练法则非常重要.
8.(2024 兰州)计算:2a(a﹣1)﹣2a2=( )
A.a B.﹣a C.2a D.﹣2a
【分析】根据单项式乘多项式去括号,再用整式的加减法则计算即可.
【解答】解:2a(a﹣1)﹣2a2=2a2﹣2a﹣2a2=﹣2a.
故选:D.
【点评】本题主要考查了单项式乘多项式、整式的加减,熟练掌握相关知识是解题的关键.
9.(2024 济宁)如图,用大小相等的小正方形按照一定规律拼正方形.第一幅图有1个正方形,第二幅图有5个正方形,第三幅图有14个正方形……按照此规律,第六幅图中正方形的个数为( )
A.90 B.91 C.92 D.93
【分析】根据所给图形,依次求出图形中正方形的个数,发现规律即可解决问题.
【解答】解:由所给图形可知,
第一幅图中正方形的个数为:1=12;
第二幅图中正方形的个数为:5=12+22;
第三幅图中正方形的个数为:14=12+22+32;
第四幅图中正方形的个数为:30=12+22+32+42;
…,
所以第n幅图中正方形的个数为:12+22+32+…+n2,
当n=6时,
12+22+32+…+62=91(个),
即第六幅图中正方形的个数为91个.
故选:B.
【点评】本题主要考查了图形变化的规律,能根据所给图形发现正方形个数变化的规律是解题的关键.
10.(2024 河北)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1表示132×23,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,正确的是( )
A.“20”左边的数是16
B.“20”右边的“■”表示5
C.运算结果小于6000
D.运算结果可以表示为4100a+1025
【分析】设一个三位数与一个两位数分别为100x+10y+z和10m+n,则mz=20,nz=5,ny=2,nx=a,即m=4n,可确定n=1,y=2时,则m=4,z=5,x=a,由题意可判断A、B选项,根据题意可得运算结果可以表示为:1000(4a+1)+100a+25=4100a+1025,故可判断C、D选项.
【解答】解:设一个三位数与一个两位数分别为100x+10y+z和10m+n,如图2:
则由题意得:mz=20,nz=5,ny=2,nx=a,
∴,即m=4n,
∴当n=2,y=1 时,z=2.5不是正整数,不符合题意,故舍去;
当n=1,y=2时,则m=4,z=5,x=a,如图3:
∴A、“20”左边的数是2×4=8,故本选项不符合题意;
B、“20”右边的“□”表示4,故本选项不符合题意;
∴a上面的数应为4a,如图4:
∴运算结果可以表示为:1000(4a+1)+100a+25=4100a+1025,
∴D选项符合题意,
当a=2时,计算的结果大于6000,
故C选项不符合题意,
故选:D.
【点评】本题考查了整式的加法运算,整式的乘法运算,理解题意,正确的逻辑推理时解决本题的关键.
11.(2024 安徽)下列计算正确的是( )
A.a3+a3=a6 B.a6÷a3=a2 C.(﹣a)2=a2 D.=a
【分析】利用合并同类项法则,同底数幂除法法则,幂的乘方,二次根式逐项判断即可.
【解答】解:A、a3+a3=2a3,故A选项错误;
B、a6÷a3=a3,故B选项错误;
C、(﹣a)2=a2,故C选项正确;
D、,故D选项错误;
故选:C.
【点评】本题考查合并同类项,同底数幂除法法则,幂的乘方,二次根式,熟练掌握相关运算法则是解题的关键.
12.(2024 扬州)下列运算中正确的是( )
A.(a﹣b)2=a2﹣b2 B.5a﹣2a=3a
C.(a3)2=a5 D.3a2 2a3=6a6
【分析】根据单项式乘单项式、合并同类项法则、完全平方公式、幂的乘方法则,逐项计算,即可得出正确答案.
【解答】解:A、(a﹣b)2=a2﹣2ab+b2,故A选项错误;
B、5a﹣2a=3a,故B选项正确;
C、(a3)2=a6,故C选项错误;
D、3a2 2a3=6a5,故D选项错误;
故选:B.
【点评】本题考查了整式的混合运算,掌握整式的运算法则并正确计算是解题的关键.
13.(2024 凉山州)下列各数中:5,﹣,﹣3,0,﹣25.8,+2,负数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据正数和负数的定义判断即可,注意:0既不是负数也不是正数.
【解答】解:5>0,是正数;
,是负数;
﹣3<0,是负数;
0既不是正数,也不是负数;
﹣25.8<0,是负数;
+2>0,是正数;
∴负数有,﹣3,﹣25.8,共3个.
故选:C.
【点评】本题考查了对正数和负数定义的理解,难度不大,注意0既不是正数也不是负数.
14.(2024 眉山)下列四个数中,无理数是( )
A.﹣3.14 B.﹣2 C. D.
【分析】根据无理数、有理数的定义即可判定选择项.
【解答】解:﹣3.14,﹣2,是有理数,是无理数,
故选:D.
【点评】此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,,0.8080080008…(每两个8之间依次多1个0)等形式.
15.(2024 烟台)实数a,b,c在数轴上的位置如图所示,下列结论正确的是( )
A.b+c>3 B.a﹣c<0 C.|a|>|c| D.﹣2a<﹣2b
【分析】如图所示,﹣3<a<﹣2<b<﹣1<3<c<4,|c|>|a|>|b|,所以b+c<3,a﹣c<0,﹣2a>﹣2b.
【解答】解:如图所示,﹣3<a<﹣2<b<﹣1<3<c<4,|c|>|a|>|b|,故C不符合题意,
∴b+c<3,故A不符合题意,
a﹣c<0,故B符合题意,
﹣2a>﹣2b,故D不符合题意,
故选:B.
【点评】本题考查了实数与数轴,关键是从数轴上提取数学信息.
16.(2024 云南)下列计算正确的是( )
A.x3+5x3=6x4 B.x6÷x3=x5
C.(a2)3=a7 D.(ab)3=a3b3
【分析】根据合并同类项法则,幂的乘方,底数不变指数相乘;同底数幂相除,底数不变指数相减,对各选项分析判断后利用排除法求解.
【解答】解:A、x3+5x3=6x3,故A选项错误;
B、x6÷x3=x3,故B选项错误;
C、(a2)3=a6,故C选项错误;
D、(ab)3=a3b3,故D选项正确;
故选:D.
【点评】本题考查合并同类项、幂的乘方、同底数幂的除法,熟练掌握运算性质和法则是解题的关键.
17.(2024 云南)中国是最早使用正负数表示具有相反意义的量的国家.若向北运动100米记作+100米,则向南运动100米可记作( )
A.100米 B.﹣100米 C.200米 D.﹣200米
【分析】正和负具有相对性,向北运动用“+”表示,那么向南运动就用“﹣”表示,据此求解即可.
【解答】解:∵向北运动100米记作+100米,
∴向南运动100米可记作﹣100米,
故选:B.
【点评】本题主要考查了正负数的实际应用,掌握正和负具有相对性,向北运动用“+”表示,那么向南运动就用“﹣”表示是关键.
18.(2024 云南)按一定规律排列的代数式:2x,3x2,4x3,5x4,6x5, ,第n个代数式是( )
A.2xn B.(n﹣1)xn C.nxn+1 D.(n+1)xn
【分析】根据题目给出的式子的特点,可以发现第n的代数式的系数应该是n+1,而x的次数为n,然后即可写出第n个代数式.
【解答】解:∵按一定规律排列的代数式:2x,3x2,4x3,5x4,6x5, ,
∴第n个代数式为(n+1)xn,
故选:D.
【点评】本题考查数字的变换类、单项式,解答本题的关键是发现式子的变化特点,写出第n个代数式.
19.(2024 连云港)如图,正方形中有一个由若干个长方形组成的对称图案,其中正方形边长是80cm,则图中阴影图形的周长是( )
A.440cm B.320cm C.280cm D.160cm
【分析】利用平移的性质将阴影部分的周长转化为边长是80cm的正方形的周长,加上边长是80cm的正方形的两条边长,再减去2×20cm,即可得出结果.
【解答】解:阴影图形的周长=4×80+2×80﹣2×20=440(cm),
故选:A.
【点评】本题考查平移的性质,利用平移的性质将阴影部分的周长进行转化是解题的关键.
20.(2024 达州)下列计算正确的是( )
A.a2+a3=a5 B.(a+2)2=a2+2a+4
C.(﹣2a2b3)3=﹣8a6b9 D.a12÷a6=a2
【分析】根据公式化简代数式即可.
【解答】解:a2+a3不能化简,故A选项错误;
(a+2)2=a2+4a+4,故B选项错误;
(﹣2a2b3)3=﹣8a6b9,故C选项正确;
a12÷a6=a6,故D选项错误;
故选:C.
【点评】本题考查了代数式的化简,掌握幂的乘方与积的乘方,同底数幂的除法是解题的关键.
21.(2024 山东)下列实数中,平方最大的数是( )
A.3 B. C.﹣1 D.﹣2
【分析】本题考查的是实数的大小比较,乘方运算,先分别计算各数的乘方,再比较大小即可.
【解答】解:∵32=9,()2=,(﹣1)2=1,(﹣2)2=4,
∵<1<4<9,
∴最大的数是:9,
∴平方最大的数是3.
故选:A.
【点评】本题主要考查了实数的大小比较和有理数的乘方,掌握正数都大于零,负数都小于零,正数大于负数,两个正数比较大小,绝对值大的数大,两个负数比较大小,绝对值大的数反而小是本题的关键.
22.(2024 德阳)将一组数,2,,2,,2,…,,…,按以下方式进行排列:则第八行左起第1个数是( )
A.7 B.8 C. D.4
【分析】根据题意求得第八行左起第1个数是第几个数后即可求得答案.
【解答】解:由题意可得前七行所有的数的总个数为1+2+3+4+5+6+7=28,
则第八行左起第1个数是第29个数,即=,
故选:C.
【点评】本题考查算术平方根及规律探索问题,结合已知条件求得前七行所有的数的总个数是解题的关键.
23.(2024 重庆)烷烃是一类由碳、氢元素组成的有机化合物质,如图是这类物质前四种化合物的分子结构模型图,其中灰球代表碳原子,白球代表氢原子.第1种如图①有4个氢原子,第2种如图②有6个氢原子,第3种如图③有8个氢原子,……按照这一规律,第10种化合物的分子结构模型中氢原子的个数是( )
A.20 B.22 C.24 D.26
【分析】根据所给图形,依次求出模型中氢原子的个数,发现规律即可解决问题.
【解答】解:由所给图形可知,
第1种化合物的分子结构模型中氢原子的个数为:4=1×2+2;
第2种化合物的分子结构模型中氢原子的个数为:6=2×2+2;
第3种化合物的分子结构模型中氢原子的个数为:8=3×2+2;
第4种化合物的分子结构模型中氢原子的个数为:10=4×2+2;
…,
所以第n种化合物的分子结构模型中氢原子的个数为(2n+2)个,
当n=10时,
2n+2=22(个),
即第10种化合物的分子结构模型中氢原子的个数为22个.
故选:B.
【点评】本题考查图形变化的规律,能根据所给图形发现氢原子的个数依次增加2是解题的关键.
24.(2024 重庆)已知整式M:anxn+an﹣1xn﹣1+ +a1x+a0,其中n,an﹣1,…,a0为自然数,an为正整数,且n+an+an﹣1+ +a1+a0=5.下列说法:
①满足条件的整式M中有5个单项式;
②不存在任何一个n,使得满足条件的整式M有且仅有3个;
③满足条件的整式M共有16个.
其中正确的个数是( )
A.0 B.1 C.2 D.3
【分析】根据题意,对n进行分类讨论即可.
【解答】解:∵n,an﹣1,…,a0为自然数,an为正整数,且n+an+an﹣1+ +a1+a0=5,
∴0≤n≤4,
当n=4时,则4+a4+a3+a2+a1+a0=5,
∴a4=1,a3=a2=a1=a0=0,
满足条件的整式有x4,
当n=3时,则3+a3+a2+a1+a0=5,
∴(a3,a2,a1,a0)=(2,0,0,0),(1,1,0,0),(1,0,1,0),(1,0,0,1),
满足条件的整式有:2x3,x3+x2,x3+x,x3+1,
当n=2时,则2+a2+a1+a0=5,
∴(a2,a1,a0)=(3,0,0),(2,1,0),(2,0,1),(1,2,0),(1,0,2),(1,1,1),
满足条件的整式有:3x2,2x2+x,2x2+1,x2+2x,x2+2,x2+x+1;
当n=1时,则1+a1+a0=5,
∴(a1,a0)=(4,0),(3,1),(1,3),(2,2),
满足条件的整式有:4x,3x+1,x+3,2x+2;
当n=0时,0+a0=5,
满足条件的整式有:5;
∴满足条件的单项式有:x4,2x3,3x2,4x,5,故①符合题意;
不存在任何一个n,使得满足条件的整式M有且只有3个,故②符合题意;
满足条件的整式M共有1+4+6+4+1=16个,故③符合题意;
故选:D.
【点评】本题考查的是整式的规律探究,单项式,分类讨论思想的应用,由条件可得0≤n≤4,再分类讨论得到答案即可.
25.(2024 宜宾)如果一个数等于它的全部真因数(含单位1,不含它本身)的和,那么这个数称为完美数.例如:6的真因数是1、2、3,且6=1+2+3,则称6为完美数.下列数中为完美数的是( )
A.8 B.18 C.28 D.32
【分析】根据“完美数”的定义,先找出各个数的因数,再按完美数的要求相加,和与这个数相等的,就是“完美数”.
【解答】解:A.8的因数有:1,2,4,8;1+2+4=7,8不是“完美数”,故A错误;
B.18的因数有1,2,3,6,9,18;1+2+3+6+9=21,18不是“完美数”,故B错误;
C.28的因数有:1,2,4,7,14,28;1+2+4+7+14=28,28是“完美数”,故C正确;
D.32的因数有:1,2,4,8,16,32,1+2+4+8+16=31,32不是“完美数”,故D错误;
故选:C.
【点评】理解“完美数”的定义,掌握求一个数的因数的方法是解题的关键.
26.(2024 重庆)估计的值应在( )
A.8和9之间 B.9和10之间
C.10和11之间 D.11和12之间
【分析】先将式子化简,再根据2.4<<2.5,得出式子的值的范围.
【解答】解:
=
=,
∵5.76<6<6.25,
∴,
∴2.4<<2.5,
∴10.8<<11,
故选:C.
【点评】本题考查了无理数的大小估算,二次根式的混合运算,利用平方法估算无理数是解题的关键.
27.(2024 重庆)已知整式M:anxn+an﹣1xn﹣1+ +a1x+a0,其中n,an﹣1,…,a0为自然数,an为正整数,且n+an+an﹣1+ +a1+a0=5.下列说法:
①满足条件的整式M中有5个单项式;
②不存在任何一个n,使得满足条件的整式M有且只有3个;
③满足条件的整式M共有16个.
其中正确的个数是( )
A.0 B.1 C.2 D.3
【分析】根据题意,对n进行分类讨论即可.
【解答】解:∵n,an﹣1,…a0为自然数,an为正整数,且n+an+an﹣1+ +a1+a0=5,
∴0≤n≤4,
当n=4时,则4+a4+a3+a2+a1+a0=5,
∴a4=1,a3=a2=a1=a0=0,
满足条件的整式有x4,
当n=3时,则3+a3+a2+a1+a0=5,
∴(a3,a2,a1,a0)=(2,0,0,0),(1,1,0,0),(1,0,1,0),(1,0,0,1),
满足条件的整式有:2x3,x3+x2,x3+x,x3+1,
当n=2时,则2+a2+a1+a0=5,
∴(a2,a1,a0)=(3,0,0),(2,1,0),(2,0,1),(1,2,0),(1,0,2),(1,1,1),
满足条件的整式有:3x2,2x2+x,2x2+1,x2+2x,x2+2,x2+x+1;
当n=1时,则1+a1+a0=5,
∴(a1,a0)=(4,0),(3,1),(1,3),(2,2),
满足条件的整式有:4x,3x+1,x+3,2x+2;
当n=0时,0+a0=5,
满足条件的整式有:5;
∴满足条件的单项式有:x4,2x3,3x2,4x,5,故①符合题意;
不存在任何一个n,使得满足条件的整式M有且只有3个,故②符合题意;
满足条件的整式M共有1+4+6+4+1=16个,故③符合题意;
故选:D.
【点评】本题考查的是整式的规律探究,分类讨论思想的应用,由条件可得0≤n≤4,再分类讨论得到答案即可.
28.(2024 重庆)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,…,按此规律,则第⑧个图案中,菱形的个数是( )
A.20 B.21 C.23 D.26
【分析】根据所给图形,依次求出菱形的个数,发现规律即可解决问题.
【解答】解:由所给图形可知,
第①个图案中,菱形的个数为:2=1×3﹣1;
第②个图案中,菱形的个数为:5=2×3﹣1;
第③个图案中,菱形的个数为:8=3×3﹣1;
第④个图案中,菱形的个数为:11=4×3﹣1;
…,
所以第n个图案中,菱形的个数为(3n﹣1)个,
当n=8时,
3n﹣1=23(个),
即第⑧个图案中,菱形的个数为23个.
故选:C.
【点评】本题考查图形变化的规律,能根据所给图形发现菱形的个数依次增加3是解题的关键.
29.(2024 台湾)有研究报告指出,1880年至2020年全球平均气温上升趋势约为每十年上升0.08℃.已知2020年全球平均气温为14.88℃,假设未来的全球平均气温上升趋势与上述趋势相同,且每年上升的度数相同,则预估2020年之后第x年的全球平均气温为多少℃?(以x表示)( )
A.14.88+0.08x
B.14.88+0.008x
C.14.88+0.08[x+(2020 1880)]
D.14.88+0.008[x+(2020 1880)]
【分析】先求出每年平均气温约上升多少度;再表示出x年平均气温上升多少度;最后加上2020年全球平均气温即可.
【解答】解:14.88+x(0.08÷10)=14.88+0.008x,
故选:B.
【点评】本题考查了列代数式,解题的关键根据题中的数量关系来解答.
30.(2024 台湾)如图的数在线有A( 2)、O(0)、B(2)三点.今打算在此数在线标示P(p)、Q(q)两点,且p、q互为倒数,若P在A的左侧,则下列叙述何者正确?( )
A.Q在AO上,且AQ<QO B.Q在AO上,且AQ>QO
C.Q在OB上,且OQ<QB D.Q在OB上,且OQ>QB
【分析】取特殊值法排除A选项,再用倒数的性质排除C、D选项.
【解答】解:取P(﹣3),则Q(),则AQ=,OQ=,故A错误;
∵p为负数,p、q互为倒数,
∴q为负数,
∴点Q不可能在OB上,
故C、D错误.
故选:B.
【点评】本题考查利用特殊值和倒数的性质解题.
2024年中考数学选择题题分类汇编——数与式
一.选择题(共30小题)
1.(2024 齐齐哈尔)下列计算正确的是( )
A.4a2+2a2=6a4 B.5a 2a=10a
C.a6÷a2=a3 D.(﹣a2)2=a4
2.(2024 包头)计算所得结果是( )
A.3 B. C.3 D.±3
3.(2024 广州)若a≠0,则下列运算正确的是( )
A.+= B.a3 a2=a5 C. = D.a3÷a2=1
4.(2024 内蒙古)下列计算正确的是( )
A.(﹣2a4)3=﹣6a12
B.a﹣2+a5=a3
C.
D.(a+b)(a2﹣ab+b2)=a3+b3
5.(2024 甘孜州)祖国江山美丽如画,川西风光多姿多彩.据四川省某州相关部门通报,“五一”期间,全国各地众多游客前往旅游,共接待游客约1665000人次.将1665000用科学记数法表示应为( )
A.0.1665×107 B.1.665×106
C.16.65×105 D.166.5×104
6.(2024 广元)将﹣1在数轴上对应的点向右平移2个单位,则此时该点对应的数是( )
A.﹣1 B.1 C.﹣3 D.3
7.(2024 长春)根据有理数加法法则,计算2+(﹣3)过程正确的是( )
A.+(3+2) B.+(3﹣2) C.﹣(3+2) D.﹣(3﹣2)
8.(2024 兰州)计算:2a(a﹣1)﹣2a2=( )
A.a B.﹣a C.2a D.﹣2a
9.(2024 济宁)如图,用大小相等的小正方形按照一定规律拼正方形.第一幅图有1个正方形,第二幅图有5个正方形,第三幅图有14个正方形……按照此规律,第六幅图中正方形的个数为( )
A.90 B.91 C.92 D.93
10.(2024 河北)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1表示132×23,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,正确的是( )
A.“20”左边的数是16
B.“20”右边的“■”表示5
C.运算结果小于6000
D.运算结果可以表示为4100a+1025
11.(2024 安徽)下列计算正确的是( )
A.a3+a3=a6 B.a6÷a3=a2 C.(﹣a)2=a2 D.=a
12.(2024 扬州)下列运算中正确的是( )
A.(a﹣b)2=a2﹣b2 B.5a﹣2a=3a
C.(a3)2=a5 D.3a2 2a3=6a6
13.(2024 凉山州)下列各数中:5,﹣,﹣3,0,﹣25.8,+2,负数有( )
A.1个 B.2个 C.3个 D.4个
14.(2024 眉山)下列四个数中,无理数是( )
A.﹣3.14 B.﹣2 C. D.
15.(2024 烟台)实数a,b,c在数轴上的位置如图所示,下列结论正确的是( )
A.b+c>3 B.a﹣c<0 C.|a|>|c| D.﹣2a<﹣2b
16.(2024 云南)下列计算正确的是( )
A.x3+5x3=6x4 B.x6÷x3=x5
C.(a2)3=a7 D.(ab)3=a3b3
17.(2024 云南)中国是最早使用正负数表示具有相反意义的量的国家.若向北运动100米记作+100米,则向南运动100米可记作( )
A.100米 B.﹣100米 C.200米 D.﹣200米
18.(2024 云南)按一定规律排列的代数式:2x,3x2,4x3,5x4,6x5, ,第n个代数式是( )
A.2xn B.(n﹣1)xn C.nxn+1 D.(n+1)xn
19.(2024 连云港)如图,正方形中有一个由若干个长方形组成的对称图案,其中正方形边长是80cm,则图中阴影图形的周长是( )
A.440cm B.320cm C.280cm D.160cm
20.(2024 达州)下列计算正确的是( )
A.a2+a3=a5 B.(a+2)2=a2+2a+4
C.(﹣2a2b3)3=﹣8a6b9 D.a12÷a6=a2
21.(2024 山东)下列实数中,平方最大的数是( )
A.3 B. C.﹣1 D.﹣2
22.(2024 德阳)将一组数,2,,2,,2,…,,…,按以下方式进行排列:则第八行左起第1个数是( )
A.7 B.8 C. D.4
23.(2024 重庆)烷烃是一类由碳、氢元素组成的有机化合物质,如图是这类物质前四种化合物的分子结构模型图,其中灰球代表碳原子,白球代表氢原子.第1种如图①有4个氢原子,第2种如图②有6个氢原子,第3种如图③有8个氢原子,……按照这一规律,第10种化合物的分子结构模型中氢原子的个数是( )
A.20 B.22 C.24 D.26
24.(2024 重庆)已知整式M:anxn+an﹣1xn﹣1+ +a1x+a0,其中n,an﹣1,…,a0为自然数,an为正整数,且n+an+an﹣1+ +a1+a0=5.下列说法:
①满足条件的整式M中有5个单项式;
②不存在任何一个n,使得满足条件的整式M有且仅有3个;
③满足条件的整式M共有16个.
其中正确的个数是( )
A.0 B.1 C.2 D.3
25.(2024 宜宾)如果一个数等于它的全部真因数(含单位1,不含它本身)的和,那么这个数称为完美数.例如:6的真因数是1、2、3,且6=1+2+3,则称6为完美数.下列数中为完美数的是( )
A.8 B.18 C.28 D.32
26.(2024 重庆)估计的值应在( )
A.8和9之间 B.9和10之间
C.10和11之间 D.11和12之间
27.(2024 重庆)已知整式M:anxn+an﹣1xn﹣1+ +a1x+a0,其中n,an﹣1,…,a0为自然数,an为正整数,且n+an+an﹣1+ +a1+a0=5.下列说法:
①满足条件的整式M中有5个单项式;
②不存在任何一个n,使得满足条件的整式M有且只有3个;
③满足条件的整式M共有16个.
其中正确的个数是( )
A.0 B.1 C.2 D.3
28.(2024 重庆)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,…,按此规律,则第⑧个图案中,菱形的个数是( )
A.20 B.21 C.23 D.26
29.(2024 台湾)有研究报告指出,1880年至2020年全球平均气温上升趋势约为每十年上升0.08℃.已知2020年全球平均气温为14.88℃,假设未来的全球平均气温上升趋势与上述趋势相同,且每年上升的度数相同,则预估2020年之后第x年的全球平均气温为多少℃?(以x表示)( )
A.14.88+0.08x
B.14.88+0.008x
C.14.88+0.08[x+(2020 1880)]
D.14.88+0.008[x+(2020 1880)]
30.(2024 台湾)如图的数在线有A( 2)、O(0)、B(2)三点.今打算在此数在线标示P(p)、Q(q)两点,且p、q互为倒数,若P在A的左侧,则下列叙述何者正确?( )
A.Q在AO上,且AQ<QO B.Q在AO上,且AQ>QO
C.Q在OB上,且OQ<QB D.Q在OB上,且OQ>QB
数与式
参考答案与试题解析
一.选择题(共30小题)
1.(2024 齐齐哈尔)下列计算正确的是( )
A.4a2+2a2=6a4 B.5a 2a=10a
C.a6÷a2=a3 D.(﹣a2)2=a4
【分析】根据合并同类项、单项式乘单项式、同底数幂相除及幂的乘方与积的乘方进行计算,逐一判断即可.
【解答】解:A.4a2+2a2=6a2,故本选项不符合题意;
B.5a 2a=10a2,故本选项不符合题意;
C.a6÷a2=a4,故本选项不符合题意;
D.(﹣a2)2=a4,故本选项符合题意;
故选:D.
【点评】本题主要考查合并同类项、单项式乘单项式、同底数幂相除及幂的乘方与积的乘方,熟练掌握以上知识点是解题的关键.
2.(2024 包头)计算所得结果是( )
A.3 B. C.3 D.±3
【分析】先计算,再化简二次根式.
【解答】解:
=
=
=,
故答案为:C.
【点评】本题考查了二次根式的计算,掌握计算法则是解题的关键.
3.(2024 广州)若a≠0,则下列运算正确的是( )
A.+= B.a3 a2=a5 C. = D.a3÷a2=1
【分析】利用合并同类项法则,同底数幂乘法及除法法则,分式的乘法法则计算即可.
【解答】解:+==,则A不符合题意;
a3 a2=a5,则B符合题意;
=,则C不符合题意;
a3÷a2=a,则D不符合题意;
故选:B.
【点评】本题考查合并同类项,同底数幂乘法及除法,分式的乘法,熟练掌握相关运算法则是解题的关键.
4.(2024 内蒙古)下列计算正确的是( )
A.(﹣2a4)3=﹣6a12
B.a﹣2+a5=a3
C.
D.(a+b)(a2﹣ab+b2)=a3+b3
【分析】A.根据积的乘方法则和幂的乘方法则进行计算,然后判断即可;
B.根据同底数幂相乘法则进行计算,然后判断即可;
C.根据同分母的分式加减法则进行计算,然后判断即可;
D.根据多项式乘多项式法则进行计算,然后判断即可.
【解答】解:A.∵(﹣2a4)3=﹣8a12,∴此选项的计算错误,故此选项不符合题意;
B.∵,∴此选项的计算错误,故此选项不符合题意;
C.∵,∴此选项的计算错误,故此选项不符合题意;
D.∵(a+b)(a2﹣ab+b2)=a3﹣a2b+ab2+a2b﹣ab2+b3=a3+b3,∴此选项的计算正确,故此选项符合题意;
故选:D.
【点评】本题主要考查了整式和分式的混合运算,解题关键是熟练掌握积的乘方法则、幂的乘方法则和多项式乘多项式法则.
5.(2024 甘孜州)祖国江山美丽如画,川西风光多姿多彩.据四川省某州相关部门通报,“五一”期间,全国各地众多游客前往旅游,共接待游客约1665000人次.将1665000用科学记数法表示应为( )
A.0.1665×107 B.1.665×106
C.16.65×105 D.166.5×104
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:1665000=1.665×106,
故选:B.
【点评】此题考查科学记数法的表示方法,科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
6.(2024 广元)将﹣1在数轴上对应的点向右平移2个单位,则此时该点对应的数是( )
A.﹣1 B.1 C.﹣3 D.3
【分析】将﹣1在数轴上对应的点向右平移2个单位,可列算式﹣1+2,求得此时该点对应的数是1,于是得到问题的答案.
【解答】解:由题意得﹣1+2=1,
所以﹣1在数轴上对应的点向右平移2个单位,此时该点对应的数是1,
故选:B.
【点评】此题重点考查数轴、有理数的运算等知识,根据题意正确地列出算式是解题的关键.
7.(2024 长春)根据有理数加法法则,计算2+(﹣3)过程正确的是( )
A.+(3+2) B.+(3﹣2) C.﹣(3+2) D.﹣(3﹣2)
【分析】有理数加法法则:
1、同号两数相加,取相同符号,并把绝对值相加.
2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
3、一个数同0相加,仍得这个数.
【解答】根据有理数加法法则第2条:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
2+(﹣3)
=﹣(3﹣2)
故答案为D.
【点评】本题考查有理数加法法则,熟练法则非常重要.
8.(2024 兰州)计算:2a(a﹣1)﹣2a2=( )
A.a B.﹣a C.2a D.﹣2a
【分析】根据单项式乘多项式去括号,再用整式的加减法则计算即可.
【解答】解:2a(a﹣1)﹣2a2=2a2﹣2a﹣2a2=﹣2a.
故选:D.
【点评】本题主要考查了单项式乘多项式、整式的加减,熟练掌握相关知识是解题的关键.
9.(2024 济宁)如图,用大小相等的小正方形按照一定规律拼正方形.第一幅图有1个正方形,第二幅图有5个正方形,第三幅图有14个正方形……按照此规律,第六幅图中正方形的个数为( )
A.90 B.91 C.92 D.93
【分析】根据所给图形,依次求出图形中正方形的个数,发现规律即可解决问题.
【解答】解:由所给图形可知,
第一幅图中正方形的个数为:1=12;
第二幅图中正方形的个数为:5=12+22;
第三幅图中正方形的个数为:14=12+22+32;
第四幅图中正方形的个数为:30=12+22+32+42;
…,
所以第n幅图中正方形的个数为:12+22+32+…+n2,
当n=6时,
12+22+32+…+62=91(个),
即第六幅图中正方形的个数为91个.
故选:B.
【点评】本题主要考查了图形变化的规律,能根据所给图形发现正方形个数变化的规律是解题的关键.
10.(2024 河北)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1表示132×23,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,正确的是( )
A.“20”左边的数是16
B.“20”右边的“■”表示5
C.运算结果小于6000
D.运算结果可以表示为4100a+1025
【分析】设一个三位数与一个两位数分别为100x+10y+z和10m+n,则mz=20,nz=5,ny=2,nx=a,即m=4n,可确定n=1,y=2时,则m=4,z=5,x=a,由题意可判断A、B选项,根据题意可得运算结果可以表示为:1000(4a+1)+100a+25=4100a+1025,故可判断C、D选项.
【解答】解:设一个三位数与一个两位数分别为100x+10y+z和10m+n,如图2:
则由题意得:mz=20,nz=5,ny=2,nx=a,
∴,即m=4n,
∴当n=2,y=1 时,z=2.5不是正整数,不符合题意,故舍去;
当n=1,y=2时,则m=4,z=5,x=a,如图3:
∴A、“20”左边的数是2×4=8,故本选项不符合题意;
B、“20”右边的“□”表示4,故本选项不符合题意;
∴a上面的数应为4a,如图4:
∴运算结果可以表示为:1000(4a+1)+100a+25=4100a+1025,
∴D选项符合题意,
当a=2时,计算的结果大于6000,
故C选项不符合题意,
故选:D.
【点评】本题考查了整式的加法运算,整式的乘法运算,理解题意,正确的逻辑推理时解决本题的关键.
11.(2024 安徽)下列计算正确的是( )
A.a3+a3=a6 B.a6÷a3=a2 C.(﹣a)2=a2 D.=a
【分析】利用合并同类项法则,同底数幂除法法则,幂的乘方,二次根式逐项判断即可.
【解答】解:A、a3+a3=2a3,故A选项错误;
B、a6÷a3=a3,故B选项错误;
C、(﹣a)2=a2,故C选项正确;
D、,故D选项错误;
故选:C.
【点评】本题考查合并同类项,同底数幂除法法则,幂的乘方,二次根式,熟练掌握相关运算法则是解题的关键.
12.(2024 扬州)下列运算中正确的是( )
A.(a﹣b)2=a2﹣b2 B.5a﹣2a=3a
C.(a3)2=a5 D.3a2 2a3=6a6
【分析】根据单项式乘单项式、合并同类项法则、完全平方公式、幂的乘方法则,逐项计算,即可得出正确答案.
【解答】解:A、(a﹣b)2=a2﹣2ab+b2,故A选项错误;
B、5a﹣2a=3a,故B选项正确;
C、(a3)2=a6,故C选项错误;
D、3a2 2a3=6a5,故D选项错误;
故选:B.
【点评】本题考查了整式的混合运算,掌握整式的运算法则并正确计算是解题的关键.
13.(2024 凉山州)下列各数中:5,﹣,﹣3,0,﹣25.8,+2,负数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据正数和负数的定义判断即可,注意:0既不是负数也不是正数.
【解答】解:5>0,是正数;
,是负数;
﹣3<0,是负数;
0既不是正数,也不是负数;
﹣25.8<0,是负数;
+2>0,是正数;
∴负数有,﹣3,﹣25.8,共3个.
故选:C.
【点评】本题考查了对正数和负数定义的理解,难度不大,注意0既不是正数也不是负数.
14.(2024 眉山)下列四个数中,无理数是( )
A.﹣3.14 B.﹣2 C. D.
【分析】根据无理数、有理数的定义即可判定选择项.
【解答】解:﹣3.14,﹣2,是有理数,是无理数,
故选:D.
【点评】此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,,0.8080080008…(每两个8之间依次多1个0)等形式.
15.(2024 烟台)实数a,b,c在数轴上的位置如图所示,下列结论正确的是( )
A.b+c>3 B.a﹣c<0 C.|a|>|c| D.﹣2a<﹣2b
【分析】如图所示,﹣3<a<﹣2<b<﹣1<3<c<4,|c|>|a|>|b|,所以b+c<3,a﹣c<0,﹣2a>﹣2b.
【解答】解:如图所示,﹣3<a<﹣2<b<﹣1<3<c<4,|c|>|a|>|b|,故C不符合题意,
∴b+c<3,故A不符合题意,
a﹣c<0,故B符合题意,
﹣2a>﹣2b,故D不符合题意,
故选:B.
【点评】本题考查了实数与数轴,关键是从数轴上提取数学信息.
16.(2024 云南)下列计算正确的是( )
A.x3+5x3=6x4 B.x6÷x3=x5
C.(a2)3=a7 D.(ab)3=a3b3
【分析】根据合并同类项法则,幂的乘方,底数不变指数相乘;同底数幂相除,底数不变指数相减,对各选项分析判断后利用排除法求解.
【解答】解:A、x3+5x3=6x3,故A选项错误;
B、x6÷x3=x3,故B选项错误;
C、(a2)3=a6,故C选项错误;
D、(ab)3=a3b3,故D选项正确;
故选:D.
【点评】本题考查合并同类项、幂的乘方、同底数幂的除法,熟练掌握运算性质和法则是解题的关键.
17.(2024 云南)中国是最早使用正负数表示具有相反意义的量的国家.若向北运动100米记作+100米,则向南运动100米可记作( )
A.100米 B.﹣100米 C.200米 D.﹣200米
【分析】正和负具有相对性,向北运动用“+”表示,那么向南运动就用“﹣”表示,据此求解即可.
【解答】解:∵向北运动100米记作+100米,
∴向南运动100米可记作﹣100米,
故选:B.
【点评】本题主要考查了正负数的实际应用,掌握正和负具有相对性,向北运动用“+”表示,那么向南运动就用“﹣”表示是关键.
18.(2024 云南)按一定规律排列的代数式:2x,3x2,4x3,5x4,6x5, ,第n个代数式是( )
A.2xn B.(n﹣1)xn C.nxn+1 D.(n+1)xn
【分析】根据题目给出的式子的特点,可以发现第n的代数式的系数应该是n+1,而x的次数为n,然后即可写出第n个代数式.
【解答】解:∵按一定规律排列的代数式:2x,3x2,4x3,5x4,6x5, ,
∴第n个代数式为(n+1)xn,
故选:D.
【点评】本题考查数字的变换类、单项式,解答本题的关键是发现式子的变化特点,写出第n个代数式.
19.(2024 连云港)如图,正方形中有一个由若干个长方形组成的对称图案,其中正方形边长是80cm,则图中阴影图形的周长是( )
A.440cm B.320cm C.280cm D.160cm
【分析】利用平移的性质将阴影部分的周长转化为边长是80cm的正方形的周长,加上边长是80cm的正方形的两条边长,再减去2×20cm,即可得出结果.
【解答】解:阴影图形的周长=4×80+2×80﹣2×20=440(cm),
故选:A.
【点评】本题考查平移的性质,利用平移的性质将阴影部分的周长进行转化是解题的关键.
20.(2024 达州)下列计算正确的是( )
A.a2+a3=a5 B.(a+2)2=a2+2a+4
C.(﹣2a2b3)3=﹣8a6b9 D.a12÷a6=a2
【分析】根据公式化简代数式即可.
【解答】解:a2+a3不能化简,故A选项错误;
(a+2)2=a2+4a+4,故B选项错误;
(﹣2a2b3)3=﹣8a6b9,故C选项正确;
a12÷a6=a6,故D选项错误;
故选:C.
【点评】本题考查了代数式的化简,掌握幂的乘方与积的乘方,同底数幂的除法是解题的关键.
21.(2024 山东)下列实数中,平方最大的数是( )
A.3 B. C.﹣1 D.﹣2
【分析】本题考查的是实数的大小比较,乘方运算,先分别计算各数的乘方,再比较大小即可.
【解答】解:∵32=9,()2=,(﹣1)2=1,(﹣2)2=4,
∵<1<4<9,
∴最大的数是:9,
∴平方最大的数是3.
故选:A.
【点评】本题主要考查了实数的大小比较和有理数的乘方,掌握正数都大于零,负数都小于零,正数大于负数,两个正数比较大小,绝对值大的数大,两个负数比较大小,绝对值大的数反而小是本题的关键.
22.(2024 德阳)将一组数,2,,2,,2,…,,…,按以下方式进行排列:则第八行左起第1个数是( )
A.7 B.8 C. D.4
【分析】根据题意求得第八行左起第1个数是第几个数后即可求得答案.
【解答】解:由题意可得前七行所有的数的总个数为1+2+3+4+5+6+7=28,
则第八行左起第1个数是第29个数,即=,
故选:C.
【点评】本题考查算术平方根及规律探索问题,结合已知条件求得前七行所有的数的总个数是解题的关键.
23.(2024 重庆)烷烃是一类由碳、氢元素组成的有机化合物质,如图是这类物质前四种化合物的分子结构模型图,其中灰球代表碳原子,白球代表氢原子.第1种如图①有4个氢原子,第2种如图②有6个氢原子,第3种如图③有8个氢原子,……按照这一规律,第10种化合物的分子结构模型中氢原子的个数是( )
A.20 B.22 C.24 D.26
【分析】根据所给图形,依次求出模型中氢原子的个数,发现规律即可解决问题.
【解答】解:由所给图形可知,
第1种化合物的分子结构模型中氢原子的个数为:4=1×2+2;
第2种化合物的分子结构模型中氢原子的个数为:6=2×2+2;
第3种化合物的分子结构模型中氢原子的个数为:8=3×2+2;
第4种化合物的分子结构模型中氢原子的个数为:10=4×2+2;
…,
所以第n种化合物的分子结构模型中氢原子的个数为(2n+2)个,
当n=10时,
2n+2=22(个),
即第10种化合物的分子结构模型中氢原子的个数为22个.
故选:B.
【点评】本题考查图形变化的规律,能根据所给图形发现氢原子的个数依次增加2是解题的关键.
24.(2024 重庆)已知整式M:anxn+an﹣1xn﹣1+ +a1x+a0,其中n,an﹣1,…,a0为自然数,an为正整数,且n+an+an﹣1+ +a1+a0=5.下列说法:
①满足条件的整式M中有5个单项式;
②不存在任何一个n,使得满足条件的整式M有且仅有3个;
③满足条件的整式M共有16个.
其中正确的个数是( )
A.0 B.1 C.2 D.3
【分析】根据题意,对n进行分类讨论即可.
【解答】解:∵n,an﹣1,…,a0为自然数,an为正整数,且n+an+an﹣1+ +a1+a0=5,
∴0≤n≤4,
当n=4时,则4+a4+a3+a2+a1+a0=5,
∴a4=1,a3=a2=a1=a0=0,
满足条件的整式有x4,
当n=3时,则3+a3+a2+a1+a0=5,
∴(a3,a2,a1,a0)=(2,0,0,0),(1,1,0,0),(1,0,1,0),(1,0,0,1),
满足条件的整式有:2x3,x3+x2,x3+x,x3+1,
当n=2时,则2+a2+a1+a0=5,
∴(a2,a1,a0)=(3,0,0),(2,1,0),(2,0,1),(1,2,0),(1,0,2),(1,1,1),
满足条件的整式有:3x2,2x2+x,2x2+1,x2+2x,x2+2,x2+x+1;
当n=1时,则1+a1+a0=5,
∴(a1,a0)=(4,0),(3,1),(1,3),(2,2),
满足条件的整式有:4x,3x+1,x+3,2x+2;
当n=0时,0+a0=5,
满足条件的整式有:5;
∴满足条件的单项式有:x4,2x3,3x2,4x,5,故①符合题意;
不存在任何一个n,使得满足条件的整式M有且只有3个,故②符合题意;
满足条件的整式M共有1+4+6+4+1=16个,故③符合题意;
故选:D.
【点评】本题考查的是整式的规律探究,单项式,分类讨论思想的应用,由条件可得0≤n≤4,再分类讨论得到答案即可.
25.(2024 宜宾)如果一个数等于它的全部真因数(含单位1,不含它本身)的和,那么这个数称为完美数.例如:6的真因数是1、2、3,且6=1+2+3,则称6为完美数.下列数中为完美数的是( )
A.8 B.18 C.28 D.32
【分析】根据“完美数”的定义,先找出各个数的因数,再按完美数的要求相加,和与这个数相等的,就是“完美数”.
【解答】解:A.8的因数有:1,2,4,8;1+2+4=7,8不是“完美数”,故A错误;
B.18的因数有1,2,3,6,9,18;1+2+3+6+9=21,18不是“完美数”,故B错误;
C.28的因数有:1,2,4,7,14,28;1+2+4+7+14=28,28是“完美数”,故C正确;
D.32的因数有:1,2,4,8,16,32,1+2+4+8+16=31,32不是“完美数”,故D错误;
故选:C.
【点评】理解“完美数”的定义,掌握求一个数的因数的方法是解题的关键.
26.(2024 重庆)估计的值应在( )
A.8和9之间 B.9和10之间
C.10和11之间 D.11和12之间
【分析】先将式子化简,再根据2.4<<2.5,得出式子的值的范围.
【解答】解:
=
=,
∵5.76<6<6.25,
∴,
∴2.4<<2.5,
∴10.8<<11,
故选:C.
【点评】本题考查了无理数的大小估算,二次根式的混合运算,利用平方法估算无理数是解题的关键.
27.(2024 重庆)已知整式M:anxn+an﹣1xn﹣1+ +a1x+a0,其中n,an﹣1,…,a0为自然数,an为正整数,且n+an+an﹣1+ +a1+a0=5.下列说法:
①满足条件的整式M中有5个单项式;
②不存在任何一个n,使得满足条件的整式M有且只有3个;
③满足条件的整式M共有16个.
其中正确的个数是( )
A.0 B.1 C.2 D.3
【分析】根据题意,对n进行分类讨论即可.
【解答】解:∵n,an﹣1,…a0为自然数,an为正整数,且n+an+an﹣1+ +a1+a0=5,
∴0≤n≤4,
当n=4时,则4+a4+a3+a2+a1+a0=5,
∴a4=1,a3=a2=a1=a0=0,
满足条件的整式有x4,
当n=3时,则3+a3+a2+a1+a0=5,
∴(a3,a2,a1,a0)=(2,0,0,0),(1,1,0,0),(1,0,1,0),(1,0,0,1),
满足条件的整式有:2x3,x3+x2,x3+x,x3+1,
当n=2时,则2+a2+a1+a0=5,
∴(a2,a1,a0)=(3,0,0),(2,1,0),(2,0,1),(1,2,0),(1,0,2),(1,1,1),
满足条件的整式有:3x2,2x2+x,2x2+1,x2+2x,x2+2,x2+x+1;
当n=1时,则1+a1+a0=5,
∴(a1,a0)=(4,0),(3,1),(1,3),(2,2),
满足条件的整式有:4x,3x+1,x+3,2x+2;
当n=0时,0+a0=5,
满足条件的整式有:5;
∴满足条件的单项式有:x4,2x3,3x2,4x,5,故①符合题意;
不存在任何一个n,使得满足条件的整式M有且只有3个,故②符合题意;
满足条件的整式M共有1+4+6+4+1=16个,故③符合题意;
故选:D.
【点评】本题考查的是整式的规律探究,分类讨论思想的应用,由条件可得0≤n≤4,再分类讨论得到答案即可.
28.(2024 重庆)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,…,按此规律,则第⑧个图案中,菱形的个数是( )
A.20 B.21 C.23 D.26
【分析】根据所给图形,依次求出菱形的个数,发现规律即可解决问题.
【解答】解:由所给图形可知,
第①个图案中,菱形的个数为:2=1×3﹣1;
第②个图案中,菱形的个数为:5=2×3﹣1;
第③个图案中,菱形的个数为:8=3×3﹣1;
第④个图案中,菱形的个数为:11=4×3﹣1;
…,
所以第n个图案中,菱形的个数为(3n﹣1)个,
当n=8时,
3n﹣1=23(个),
即第⑧个图案中,菱形的个数为23个.
故选:C.
【点评】本题考查图形变化的规律,能根据所给图形发现菱形的个数依次增加3是解题的关键.
29.(2024 台湾)有研究报告指出,1880年至2020年全球平均气温上升趋势约为每十年上升0.08℃.已知2020年全球平均气温为14.88℃,假设未来的全球平均气温上升趋势与上述趋势相同,且每年上升的度数相同,则预估2020年之后第x年的全球平均气温为多少℃?(以x表示)( )
A.14.88+0.08x
B.14.88+0.008x
C.14.88+0.08[x+(2020 1880)]
D.14.88+0.008[x+(2020 1880)]
【分析】先求出每年平均气温约上升多少度;再表示出x年平均气温上升多少度;最后加上2020年全球平均气温即可.
【解答】解:14.88+x(0.08÷10)=14.88+0.008x,
故选:B.
【点评】本题考查了列代数式,解题的关键根据题中的数量关系来解答.
30.(2024 台湾)如图的数在线有A( 2)、O(0)、B(2)三点.今打算在此数在线标示P(p)、Q(q)两点,且p、q互为倒数,若P在A的左侧,则下列叙述何者正确?( )
A.Q在AO上,且AQ<QO B.Q在AO上,且AQ>QO
C.Q在OB上,且OQ<QB D.Q在OB上,且OQ>QB
【分析】取特殊值法排除A选项,再用倒数的性质排除C、D选项.
【解答】解:取P(﹣3),则Q(),则AQ=,OQ=,故A错误;
∵p为负数,p、q互为倒数,
∴q为负数,
∴点Q不可能在OB上,
故C、D错误.
故选:B.
【点评】本题考查利用特殊值和倒数的性质解题.
同课章节目录
