2024年中考数学选择题题分类汇编——图形的性质(含解析)
文档属性
| 名称 | 2024年中考数学选择题题分类汇编——图形的性质(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 841.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 11:04:24 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024年中考数学选择题题分类汇编——图形的性质
一.选择题(共30小题)
1.(2024 辽宁)如图,在矩形ABCD中,点E在AD上,当△EBC是等边三角形时,∠AEB为( )
A.30° B.45° C.60° D.120°
2.(2024 南充)如图,两个平面镜平行放置,光线经过平面镜反射时,∠1=∠2=40°,则∠3的度数为( )
A.80° B.90° C.100° D.120°
3.(2024 通辽)如图, ABCD的对角线AC,BD交于点O,以下条件不能证明 ABCD是菱形的是( )
A.∠BAC=∠BCA B.∠ABD=∠CBD
C.OA2+OB2=AD2 D.AD2+OA2=OD2
4.(2024 长春)如图,在△ABC中,O是边AB的中点.按下列要求作图:①以点B为圆心、适当长为半径画弧,交线段BO于点D,交BC于点E;②以点O为圆心、BD长为半径画弧,交线段OA于点F;③以点F为圆心、DE长为半径画弧,交前一条弧于点G,点G与点C在直线AB同侧;④作直线OG,交AC于点M.下列结论不一定成立的是( )
A.∠AOM=∠B B.∠OMC+∠C=180°
C.AM=CM D.OM=AB
5.(2024 长沙)如图,在菱形ABCD中,AB=6,∠B=30°,点E是BC边上的动点,连接AE,DE,过点A作AF⊥DE于点F.设DE=x,AF=y,则y与x之间的函数解析式为(不考虑自变量x的取值范围)( )
A.y= B.y= C.y= D.y=
6.(2024 长沙)如图,在⊙O中,弦AB的长为8,圆心O到AB的距离OE=4,则⊙O的半径长为( )
A.4 B. C.5 D.
7.(2024 内蒙古)如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,适当长为半径画弧分别交AB,AC于点M和点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D.若△ACD的面积为8,则△ABD的面积是( )
A.8 B.16 C.12 D.24
8.(2024 泰安)如图,菱形ABCD中,∠B=60°,点E是AB边上的点,AE=4,BE=8,点F是BC上的一点,△EGF是以点G为直角顶点,∠EFG为30°角的直角三角形,连结AG.当点F在直线BC上运动时,线段AG的最小值是( )
A.2 B. C. D.4
9.(2024 泰安)如图,AB是⊙O的直径,C,D是⊙O上两点,BA平分∠CBD,若∠AOD=50°,则∠A的度数为( )
A.65° B.55° C.50° D.75°
10.(2024 泰安)两个半径相等的半圆按如图方式放置,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为2,则阴影部分的面积是( )
A. B. C. D.
11.(2024 泰安)如图,Rt△ABC中,∠ABC=90°,分别以顶点A,C为圆心,大于的长为半径画弧,两弧分别相交于点M和点N,作直线MN分别与BC,AC交于点E和点F;以点A为圆心,任意长为半径画弧,分别交AB,AC于点H和点G,再分别以点H,点G为圆心,大于HG的长为半径画弧,两弧交于点P,作射线AP,若射线AP恰好经过点E,则下列四个结论:
①∠C=30°;
②AP垂直平分线段BF;
③CE=2BE;
④.
其中,正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
12.(2024 赤峰)如图,△ABC中,AB=BC=1,∠C=72°.将△ABC绕点A顺时针旋转得到△AB′C′,点B′与点B是对应点,点C′与点C是对应点.若点C′恰好落在BC边上,下列结论:①点B在旋转过程中经过的路径长是π;②B′A∥BC;③BD=C′D;④.其中正确的结论是( )
A.①②③④ B.①②③ C.①③④ D.②④
13.(2024 广州)如图,在△ABC中,∠A=90°,AB=AC=6,D为边BC的中点,点E,F分别在边AB,AC上,AE=CF,则四边形AEDF的面积为( )
A.18 B.9 C.9 D.6
14.(2024 赤峰)如图,AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是( )
A.61° B.63° C.65° D.67°
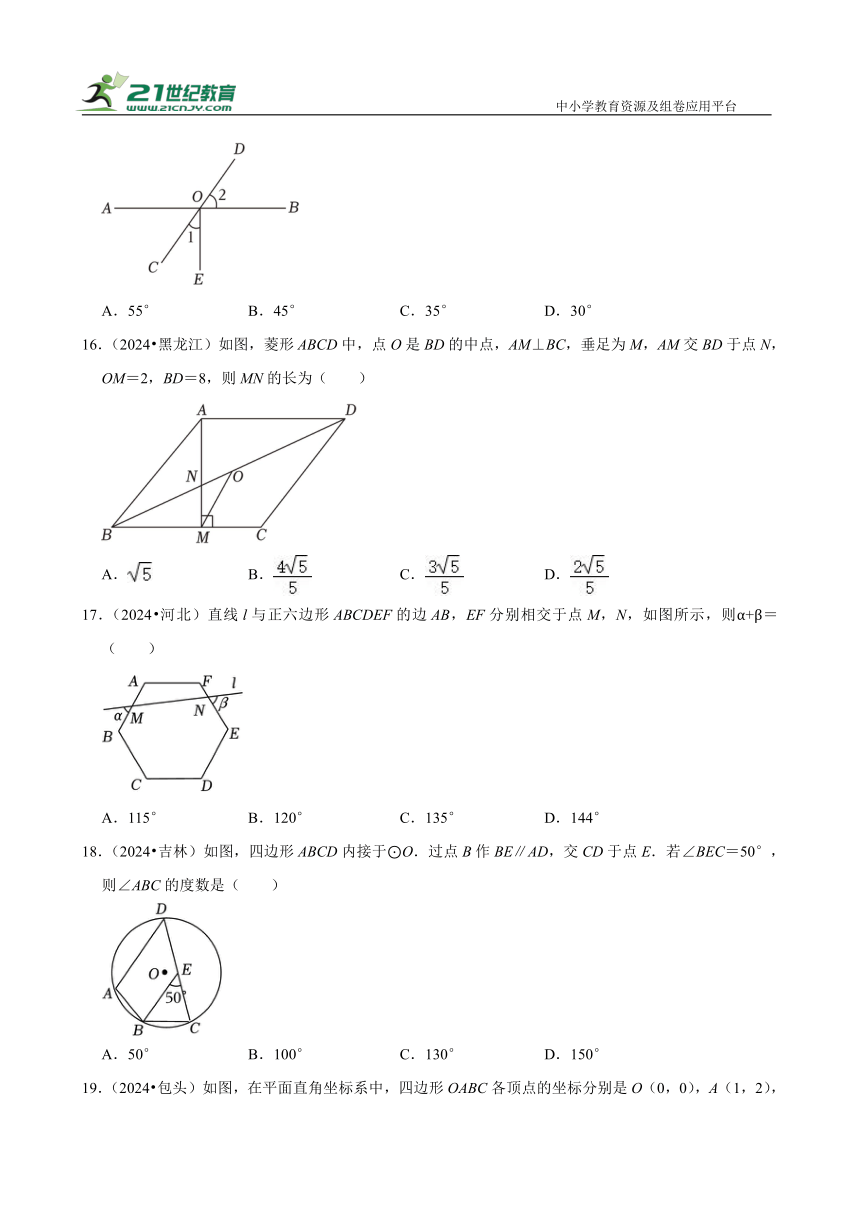
15.(2024 雅安)如图,直线AB,CD交于点O,OE⊥AB于O,若∠1=35°,则∠2的度数是( )
A.55° B.45° C.35° D.30°
16.(2024 黑龙江)如图,菱形ABCD中,点O是BD的中点,AM⊥BC,垂足为M,AM交BD于点N,OM=2,BD=8,则MN的长为( )
A. B. C. D.
17.(2024 河北)直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,如图所示,则α+β=( )
A.115° B.120° C.135° D.144°
18.(2024 吉林)如图,四边形ABCD内接于⊙O.过点B作BE∥AD,交CD于点E.若∠BEC=50°,则∠ABC的度数是( )
A.50° B.100° C.130° D.150°
19.(2024 包头)如图,在平面直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(1,2),B(3,3),C(5,0),则四边形OABC的面积为( )
A.14 B.11 C.10 D.9
20.(2024 武汉)如图,四边形ABCD内接于⊙O,∠ABC=60°,∠BAC=∠CAD=45°,AB+AD=2,则⊙O的半径是( )
A. B. C. D.
21.(2024 武汉)小美同学按如下步骤作四边形ABCD;(1)画∠MAN;(2)以点A为圆心,1个单位长为半径画弧,分别交AM,AN于点B,D;(3)分别以点B,D为圆心,1个单位长为半径画弧,两弧交于点C;(4)连接BC,CD,BD.若∠A=44°,则∠CBD的大小是( )
A.64° B.66° C.68° D.70°
22.(2024 绥化)如图,四边形ABCD是菱形,CD=5,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
23.(2024 浙江)如图,正方形ABCD由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和中间一个小正方形EFGH组成,连接DE.若AE=4,BE=3,则DE=( )
A.5 B. C. D.4
24.(2024 浙江)如图,在 ABCD中,AC,BD相交于点O,AC=2,.过点A作AE⊥BC的垂线交BC于点E,记BE长为x,BC长为y.当x,y的值发生变化时,下列代数式的值不变的是( )
A.x+y B.x﹣y C.xy D.x2+y2
25.(2024 湖北)如图,AB是半圆O的直径,C为半圆O上一点,以点B为圆心,适当长为半径画弧,交BA于点M,交BC于点N,分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠ABC的内部相交于点D,画射线BD,连接AC.若∠CAB=50°,则∠CBD的度数是( )
A.30° B.25° C.20° D.15°
26.(2024 广西)如图,边长为5的正方形ABCD,E,F,G,H分别为各边中点.连接AG,BH,CE,DF,交点分别为M,N,P,Q,那么四边形MNPQ的面积为( )
A.1 B.2 C.5 D.10
27.(2024 重庆)如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M.若BE=DF=1,则DM的长度为( )
A.2 B. C. D.
28.(2024 天津)如图,Rt△ABC中,∠C=90°,∠B=40°,以点A为圆心,适当长为半径画弧,交AB于点E,交AC于点F;再分别以点E,F为圆心,大于的长为半径画弧,两弧(所在圆的半径相等)在∠BAC的内部相交于点P;画射线AP,与BC相交于点D,则∠ADC的大小为( )
A.60° B.65° C.70° D.75°
29.(2024 黑龙江)如图,在正方形ABCD中,点H在AD边上(不与点A、D重合),∠BHF=90°,HF交正方形外角的平分线DF于点F,连接AC交BH于点M,连接BF交AC于点G,交CD于点N,连接BD.则下列结论:
①∠HBF=45°;②点G是BF的中点;③若点H是AD的中点,则sin∠NBC=;④BN=BM;⑤若AH=HD,则S△BND=S△AHM.其中正确的结论是( )
A.①②③④ B.①③⑤ C.①②④⑤ D.①②③④⑤
30.(2024 达州)如图,△ABC是等腰直角三角形,∠ABC=90°,AB=4,点D,E分别在AC,BC边上运动,连结AE,BD交于点F,且始终满足AD=CE,则下列结论:①=;②∠DFE=135°;③△ABF面积的最大值是4﹣4;④CF的最小值是2﹣2.其中正确的是( )
A.①③ B.①②④ C.②③④ D.①②③④
图形的性质
参考答案与试题解析
一.选择题(共30小题)
1.(2024 辽宁)如图,在矩形ABCD中,点E在AD上,当△EBC是等边三角形时,∠AEB为( )
A.30° B.45° C.60° D.120°
【分析】根据平行线的性质和等边三角形的性质即可解答.
【解答】证明:∵△EBC是等边三角形,
∴∠CBE=60°,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠AEB=∠CBE=60°.
故选:C.
【点评】本题考查矩形的性质,等边三角形的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.
2.(2024 南充)如图,两个平面镜平行放置,光线经过平面镜反射时,∠1=∠2=40°,则∠3的度数为( )
A.80° B.90° C.100° D.120°
【分析】根据经过两次反射后的光线与入射光线平行,得出∠3=∠4即可.
【解答】解:如图:∵∠1=∠2=40°,
∴∠4=180°﹣∠1﹣∠2=100°,
∵两个平面镜平行放置,
∴经过两次反射后的光线与入射光线平行,
∴∠3=∠4=100°,
故选:C.
【点评】本题考查平行线的性质,关键是掌握经过两次反射后的光线与入射光线平行.
3.(2024 通辽)如图, ABCD的对角线AC,BD交于点O,以下条件不能证明 ABCD是菱形的是( )
A.∠BAC=∠BCA B.∠ABD=∠CBD
C.OA2+OB2=AD2 D.AD2+OA2=OD2
【分析】由菱形的判定、矩形的判定分别对各个选项进行判断即可.
【解答】解:A、∵∠BAC=∠BCA,
∴AB=BC,
∴ ABCD是菱形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∴ ABCD是菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴OB=OD,
∵OA2+OB2=AD2,
∴OA2+OD2=AD2,
∴∠AOD=90°,
∴AC⊥BD,
∴ ABCD是菱形,故选项C不符合题意,
D、∵AD2+OA2=OD2,
∴∠OAD=90°,
∴OA⊥AD,
∴不能证得 ABCD是菱形,故选项D符合题意;
故选:D.
【点评】本题考查了菱形的判定、平行四边形的性质,熟练掌握菱形的判定方法是解题的关键.
4.(2024 长春)如图,在△ABC中,O是边AB的中点.按下列要求作图:①以点B为圆心、适当长为半径画弧,交线段BO于点D,交BC于点E;②以点O为圆心、BD长为半径画弧,交线段OA于点F;③以点F为圆心、DE长为半径画弧,交前一条弧于点G,点G与点C在直线AB同侧;④作直线OG,交AC于点M.下列结论不一定成立的是( )
A.∠AOM=∠B B.∠OMC+∠C=180°
C.AM=CM D.OM=AB
【分析】由作图过程可知,∠AOM=∠B,则OM∥BC,根据平行线的性质可得∠OMC+∠C=180°.根据O是边AB的中点,OM∥BC,可得点M为AC的中点,即AM=CM,进而可得答案.
【解答】解:由作图过程可知,∠AOM=∠B,
故A选项正确,不符合题意;
∵∠AOM=∠B,
∴OM∥BC,
∴∠OMC+∠C=180°,
故B选项正确,不符合题意;
∵O是边AB的中点,OM∥BC,
∴点M为AC的中点,
∴AM=CM,
故C选项正确,不符合题意;
根据已知条件不能得出OM=AB,
故D选项不正确,符合题意.
故选:D.
【点评】本题考查作图—复杂作图、平行线的判定与性质,解题的关键是理解题意,灵活运用所学知识解决问题.
5.(2024 长沙)如图,在菱形ABCD中,AB=6,∠B=30°,点E是BC边上的动点,连接AE,DE,过点A作AF⊥DE于点F.设DE=x,AF=y,则y与x之间的函数解析式为(不考虑自变量x的取值范围)( )
A.y= B.y= C.y= D.y=
【分析】过D作DH⊥BC交BC的延长线于H,在菱形ABCD中,AB=6,AB∥CD,AB=CD=AD=6,AD∥BC,根据平行线的性质得到∠DCH=∠B=30°,∠ADF=∠DEH,根据直角三角形 到现在得到DH=,根据相似三角形的判定和性质定理即可得到结论.
【解答】解:过D作DH⊥BC交BC的延长线于H,
在菱形ABCD中,AB=6,AB∥CD,AB=CD=AD=6,AD∥BC,
∴∠DCH=∠B=30°,∠ADF=∠DEH,
∴DH=,
∵AF⊥DE,
∴∠AFD=∠EHD=90°,
∴△ADF∽△DEH,
∴,
∴=,
∴y=,
故选:C.
【点评】本题考查了菱形的性质,含30°直角三角形的性质,相似三角形的判定和性质,正确地作出辅助线是解题的关键.
6.(2024 长沙)如图,在⊙O中,弦AB的长为8,圆心O到AB的距离OE=4,则⊙O的半径长为( )
A.4 B. C.5 D.
【分析】利用垂径定理,勾股定理求解即可.
【解答】解:∵OE⊥AB,
∴AE=EB=4,
∴OA===4.
故选:B.
【点评】本题考查垂径定理,勾股定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
7.(2024 内蒙古)如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,适当长为半径画弧分别交AB,AC于点M和点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D.若△ACD的面积为8,则△ABD的面积是( )
A.8 B.16 C.12 D.24
【分析】过点D作DE⊥AB于点E,由作图过程可知,AD平分∠BAC,可得CD=ED,证明Rt△ACD≌Rt△AED,可得S△ADE=S△ACD=8.由题意可得∠EAD=∠B,则AD=BD,即△ABD为等腰三角形,则S△ADE=S△BDE=8,进而可得答案.
【解答】解:过点D作DE⊥AB于点E,
由作图过程可知,AD平分∠BAC,
∴CD=ED.
∵AD=AD,
∴Rt△ACD≌Rt△AED(AAS),
∴S△ADE=S△ACD=8.
∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD平分∠BAC,
∴∠CAD=∠EAD=30°,
∴∠EAD=∠B,
∴AD=BD,
即△ABD为等腰三角形,
∴S△ADE=S△BDE=8,
∴△ABD的面积为S△ADE+S△BDE=16.
故选:B.
【点评】本题考查作图—基本作图、角平分线的性质、全等三角形的判定与性质、等腰三角形的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
8.(2024 泰安)如图,菱形ABCD中,∠B=60°,点E是AB边上的点,AE=4,BE=8,点F是BC上的一点,△EGF是以点G为直角顶点,∠EFG为30°角的直角三角形,连结AG.当点F在直线BC上运动时,线段AG的最小值是( )
A.2 B. C. D.4
【分析】E作EM⊥BC,则点E、M、F、G四点共圆,从而得到AF=MH,因为AG≥GF,所以求出MH的值即可得解.
【解答】解:如图,过E作EM⊥BC于点M,作MH⊥AB于点H,作AF⊥GM于点F,
∵∠EMF+∠EGF=180°,
∴点E、M、F、G四点共圆,
∴∠EMG=∠EFG=30°,
∵∠B=60°,
∴∠BEM=30°=∠EMG,
∴MG∥AB,
∴四边形MHAF是矩形,
∴MH=AF,
∵BE=8,
∴EM=BE cos30°=4,
∴MH=EM=2=AF,
∴AG≥AF=2,
∴AG最小值是2.
故选:C.
【点评】本题主要考查了菱形的性质、解直角三角形、垂线段最短、圆内接四边形对角互补等知识,熟练掌握相关知识点和添加合适的辅助线是解题关键.
9.(2024 泰安)如图,AB是⊙O的直径,C,D是⊙O上两点,BA平分∠CBD,若∠AOD=50°,则∠A的度数为( )
A.65° B.55° C.50° D.75°
【分析】先利用圆周角定理可得:∠ABD=25°,然后利用平角定义得∠ABC=25°,根据圆周角定理得∠C=90°,再根据三角形内角和定理进行计算即可解答.
【解答】解:∵∠AOD=50°,
∴∠ABD=∠AOD=25°,
∵BA平分∠CBD,
∴∠ABC=∠ABD=25°,
∵AB是⊙O的直径,
∴∠C=90°,
∴∠A=180°﹣90°﹣25°=65°.
故选:A.
【点评】本题考查了圆周角定理,圆心角、弧、弦的关系,熟练掌握圆周角定理是解题的关键.
10.(2024 泰安)两个半径相等的半圆按如图方式放置,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为2,则阴影部分的面积是( )
A. B. C. D.
【分析】连接OA,AO′,作AB⊥OO′于点B,得三角形AOO′是等边三角形,求出AB=,S弓形AO′=S扇形AOO′﹣S△AOO′=﹣,再根据S阴影=S弓形AO′+S扇形AO′O,即可得出答案.
【解答】解:如图,连接OA,AO′,作AB⊥OO′于点B,
∵OA=OO′=AO′=2,
∴三角形AOO′是等边三角形,
∴∠AOO′=60°,OB=OO′=1,
∴AB==,
∴S弓形AO′=S扇形AOO′﹣S△AOO′
=﹣2××
=﹣,
∴S阴影=S弓形AO′+S扇形AO′O
=﹣+
=﹣.
故选:A.
【点评】本题考查了扇形的面积公式的运用、三角形的面积公式的运用,熟练掌握扇形的面积公式是关键.
11.(2024 泰安)如图,Rt△ABC中,∠ABC=90°,分别以顶点A,C为圆心,大于的长为半径画弧,两弧分别相交于点M和点N,作直线MN分别与BC,AC交于点E和点F;以点A为圆心,任意长为半径画弧,分别交AB,AC于点H和点G,再分别以点H,点G为圆心,大于HG的长为半径画弧,两弧交于点P,作射线AP,若射线AP恰好经过点E,则下列四个结论:
①∠C=30°;
②AP垂直平分线段BF;
③CE=2BE;
④.
其中,正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】首先证明∠C=∠EAC=∠BAE=30°,推出AC=2AB,AE=2BE,可得①②③④正确.
【解答】解:由作图可知MN垂直平分线段AC,
∴EA=EC,
∴∠EAC=∠C,
由作图可知AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠ABC=90°,
∴∠C=∠CAE=∠BAE=30°,故①正确,
∴AC=2AB,
∵AF=FC,
∴AB=AF,
∴AP垂直平分线段BF,故②正确,
∵AE=2BE,EA=EC,
∴EC=2BE,故③正确,
∴S△BEF=S△BCF,
∵AF=FC,
∴S△BFC=S△ABC,
∴S△BEF=S△ABC,故④正确.
故选:D.
【点评】本题考查作图﹣复杂作图,角平分线的性质,线段的垂直平分线的性质等知识,解题的关键是读懂图象信息,灵活运用所学知识解决问题.
12.(2024 赤峰)如图,△ABC中,AB=BC=1,∠C=72°.将△ABC绕点A顺时针旋转得到△AB′C′,点B′与点B是对应点,点C′与点C是对应点.若点C′恰好落在BC边上,下列结论:①点B在旋转过程中经过的路径长是π;②B′A∥BC;③BD=C′D;④.其中正确的结论是( )
A.①②③④ B.①②③ C.①③④ D.②④
【分析】①先求出点B旋转的角度为36°,半径为1,即可求出路径长;②∠B′AB=∠ABC=36°,所以B′A∥BC;③∠DC′B=∠ABC=36°,所以BD=C′D;④△B′BD∽△BAC,所以.
【解答】解:∵AB=BC,∠C=72°,
∴∠BAC=∠C=72°,∠ABC=180°﹣2∠C=36°,
由旋转的性质得∠AB′C=∠ABC=36°,∠B'AC'=∠BAC=72°,∠AC′B′=∠C=72°,∠AC′B′=∠ADC=72°,AC′=AC,
∴∠AC′C=∠C=72°,
∴∠CAC'=36°,
∴∠CAC′=∠BAC′=36°,
∴∠B′AB=72°﹣36°=36°,
由旋转的性质得AB′=AB,
∴,
①点B在旋转过程中经过的路径长是,①说法正确;
②∵∠B′AB=∠ABC=36°,∴B′A∥BC,②说法正确;
③∵∠DC′B=180°﹣2×72°=36°,
∴∠DC′B=∠ABC=36°,
∴BD=C′D,③说法正确;
④∵∠BB′D=∠ABC=36°,∠B′BD=∠BAC=72°,
∴△B′BD∽△BAC,
∴,④说法正确;
综上,①②③④都是正确的,
故选:A.
【点评】本题考查了平行四边形的性质与判定,旋转的性质等,掌握平行四边形的性质与判定是解题的关键.
13.(2024 广州)如图,在△ABC中,∠A=90°,AB=AC=6,D为边BC的中点,点E,F分别在边AB,AC上,AE=CF,则四边形AEDF的面积为( )
A.18 B.9 C.9 D.6
【分析】由等腰直角三角形的性质可得AD=BD=CD,∠BAD=∠C=45°,S△ABC=×6×6=18,由“SAS”可证△ADE≌△CDF,可得S△ADE=S△CDF,即可求解.
【解答】解:如图,连接AD,
∵∠BAC=90°,AB=AC=6,D为边BC的中点,
∴AD=BD=CD,∠BAD=∠C=45°,S△ABC=×6×6=18,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴S△ADE=S△CDF,
∴四边形AEDF的面积=S△ADC=S△ABC=9,
故选:C.
【点评】本题主要考查了全等三角形的判定和性质,等腰直角三角形的性质,证明三角形全等是解题的关键.
14.(2024 赤峰)如图,AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是( )
A.61° B.63° C.65° D.67°
【分析】根据垂径定理得=,所以∠AOC=∠BOC=42°,根据圆周角定理得∠D=∠AOC=21°,再根据OC=OD,∠C=∠D=21°,最后根据三角形的外角的性质即可得出答案.
【解答】解:∵半径OC⊥AB,
∴=,
∴∠AOC=∠BOC=42°,
∴∠D=∠AOC=21°,
∵OC=OD,
∴∠C=∠D=21°,
∴∠OED=∠C+∠BOC=21°+42°=63°.
故选:B.
【点评】本题主要考查了圆周角定理,垂径定理,圆心角、弧、弦的关系,熟练掌握圆周角定理和垂径定理是解题的关键.
15.(2024 雅安)如图,直线AB,CD交于点O,OE⊥AB于O,若∠1=35°,则∠2的度数是( )
A.55° B.45° C.35° D.30°
【分析】已知OE⊥AB,∠1=35°,可得∠AOC的度数,因为对顶角∠2=∠AOC,即得∠2的度数.
【解答】解:∵OE⊥AB,∠1=35°,
∴∠AOC=55°,
∴∠2=∠AOC=55°,
故选:A.
【点评】本题考查了垂线、对顶角的性质,关键是掌握垂线、对顶角的性质.
16.(2024 黑龙江)如图,菱形ABCD中,点O是BD的中点,AM⊥BC,垂足为M,AM交BD于点N,OM=2,BD=8,则MN的长为( )
A. B. C. D.
【分析】先由菱形性质可得对角线AC与BD交于点O,由直角三角形斜边中线等于斜边一半可得OA=OC=OM=2,进而由菱形对角线求出边长,由sin∠MAC=sin∠OBC=解三角形即可求出MC=ACsin∠MAC=,MN=BMtan∠OBC=.
【解答】解:连接AC,如图,
∵菱形ABCD中,AC与BD互相垂直平分,
又∵点O是BD的中点,
∴A、O、C三点在同一直线上,
∴OA=OC,
∵OM=2,AM⊥BC,
∴OA=OC=OM=2,
∵BD=8,
∴OB=OD=BD=4,
∴BC===2,tan∠OBC===,
∵∠ACM+∠MAC=90°,∠ACM+∠OBC=90°,
∴∠MAC=∠OBC
∴sin∠MAC=sin∠OBC===,
∴MC=ACsin∠MAC=,
∴BM=BC MC=2 =,
∴MN=BMtan∠OBC=×=,
故选:C.
【点评】本题考查了解直角三角形,菱形的性质、直角三角形斜边中线等于斜边一半.熟练掌握各知识点是解题的关键.
17.(2024 河北)直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,如图所示,则α+β=( )
A.115° B.120° C.135° D.144°
【分析】先求出正六边形的每个内角为120°,再根据六边形MBCDEN的内角和为720°即可求解∠ENM+∠NMB的度数,最后根据邻补角的意义即可求解.
【解答】解:正六边形每个内角为:,
而六边形MBCDEN的内角和也为(6﹣2)×180°=720°,
∴∠B+∠C+∠D+∠E+∠ENM+∠NMB=720°,
∴∠ENM+∠NMB=720°﹣4×120°=240°,
∵β+∠ENM+α+∠NMB=180°×2=360°,
∴α+β=360°﹣240°=120°,
故选:B.
【点评】本题考查了多边形的内角和,正多边形的每个内角,邻补角,熟练掌握知识点是解决本题的关键.
18.(2024 吉林)如图,四边形ABCD内接于⊙O.过点B作BE∥AD,交CD于点E.若∠BEC=50°,则∠ABC的度数是( )
A.50° B.100° C.130° D.150°
【分析】根据BE∥AD,得出∠ADC=∠BEC=50°,再根据圆内接四边形的性质即可得出答案.
【解答】解:∵BE∥AD,
∴∠ADC=∠BEC=50°,
∵四边形ABCD内接于⊙O,
∴∠ABC=180°﹣∠ADC=130°.
故选:C.
【点评】本题主要考查圆内接四边形的性质,平行线的性质,熟练掌握圆内接四边形的性质是解题的关键.
19.(2024 包头)如图,在平面直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(1,2),B(3,3),C(5,0),则四边形OABC的面积为( )
A.14 B.11 C.10 D.9
【分析】过A点作AE⊥x轴于E,作BF⊥x轴于F,如图,利用三角形面积公式和梯形的面积公式,利用四边形OABC的面积=S△BCF+S梯形ABFE+S△AOE进行计算.
【解答】解:过A点作AE⊥x轴于E,作BF⊥x轴于F,如图,
∵O(0,0),A(1,2),B(3,3),C(5,0),
∴OE=1,AE=2,BF=3,CF=2,EF=2,
∴四边形OABC的面积=S△AOE+S△BCF+S梯形ABFE
=×1×2+×3×2+
=9,
故选:D.
【点评】本题主要考查了梯形的面积、三角形的面积:三角形的面积等于底边长与高线乘积的一半,即S△=×底×高.也考查了坐标与图形性质.
20.(2024 武汉)如图,四边形ABCD内接于⊙O,∠ABC=60°,∠BAC=∠CAD=45°,AB+AD=2,则⊙O的半径是( )
A. B. C. D.
【分析】过C作CM⊥AB于M,CN⊥AD交AD延长线于N,过O作OH⊥AC于H,连接OA,OC,由角平分线的性质推出MC=CN,判定四边形AMCN是正方形,得到AM=AN,由圆周角定理得到=,推出CD=BC,即可证明Rt△CDN≌Rt△CBM(HL),得到ND=MB,推出AB+AD=2AM=2,求出AM=1,判定△ACM是等腰直角三角形,求出AC=AM=,由圆周角定理得到∠AOC=2∠B=120°,由等腰三角形的性质推出AH=AC=,∠AOH=∠AOC=60°,由sin∠AOH==,求出OA=,得到⊙O的半径是.
【解答】解:过C作CM⊥AB于M,CN⊥AD交AD延长线于N,过O作OH⊥AC于H,连接OA,OC,
∵∠BAC=∠CAD=45°,
∴AC平分∠BAN,
∴MC=CN,
∵∠MAN=∠BAC+∠CAD=90°,∠AMC=∠ANC=90°,
∴四边形AMCN是正方形,
∴AM=AN,
∵∠BAC=∠CAD,
∴=,
∴CD=BC,
∵CN=CM,
∴Rt△CDN≌Rt△CBM(HL),
∴ND=MB,
∵AB+AD=AM+MB+AD=AM+DN+AD=AM+AN=2AM=2,
∴AM=1,
∵∠BAC=45°,∠AMC=90°,
∴△ACM是等腰直角三角形,
∴AC=AM=,
∵∠B=60°,
∴∠AOC=2∠B=120°,
∵OA=OC,OH⊥AC,
∴AH=AC=,∠AOH=∠AOC=60°,
∵sin∠AOH=sin60°==,
∴OA=,
∴⊙O的半径是.
故选:A.
【点评】本题考查全等三角形的判定和性质,正方形的判定和性质,圆周角定理,角平分线的性质,等腰三角形的性质,解直角三角形,关键是由Rt△CDN≌Rt△CBM(HL),推出ND=MB,得到AB+AD=2AM.
21.(2024 武汉)小美同学按如下步骤作四边形ABCD;(1)画∠MAN;(2)以点A为圆心,1个单位长为半径画弧,分别交AM,AN于点B,D;(3)分别以点B,D为圆心,1个单位长为半径画弧,两弧交于点C;(4)连接BC,CD,BD.若∠A=44°,则∠CBD的大小是( )
A.64° B.66° C.68° D.70°
【分析】由(1)(2)(3)可知四边形ABCD是菱形,然后根据菱形的性质和三角形内角和定理求出答案即可.
【解答】解:由(1)(2)(3)可知四边形ABCD是菱形,
∴AB=AD,BC∥AD,
∴∠ABD=∠ADB=∠CBD,
∵∠A=44°,
∴∠ABD+∠ADB=180°﹣∠A=180°﹣44°=136°,
∴∠ABD=∠ADB=∠CBD=68°,
故选:C.
【点评】本题主要考查了多边形的内角与外角和菱形的判定与性质,解题关键是根据已知条件中的作图判定四边形ABCD的形状.
22.(2024 绥化)如图,四边形ABCD是菱形,CD=5,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
【分析】由菱形的性质和勾股定理求出AC=6,再由菱形的面积求出AE即可.
【解答】解:∵四边形ABCD是菱形,CD=5,BD=8,
∴BC=CD=5,BO=DO=4,OA=OC,AC⊥BD,
∴∠BOC=90°,
在Rt△OBC中,由勾股定理得:OC===3,
∴AC=2OC=6,
∵菱形ABCD的面积=AE BC=BD×AC=OB AC,
∴AE===,
故选:A.
【点评】此题考查了菱形的性质以及勾股定理等知识,熟练掌握菱形的性质和勾股定理是解题的关键.
23.(2024 浙江)如图,正方形ABCD由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和中间一个小正方形EFGH组成,连接DE.若AE=4,BE=3,则DE=( )
A.5 B. C. D.4
【分析】由全等三角形的性质得DH=AE=4,AH=BE=3,则EH=AE﹣AH=1,而∠DHE=90°,所以DE==,于是得到问题的答案.
【解答】解:∵Rt△DAH≌Rt△ABE,
∴DH=AE=4,AH=BE=3,
∴EH=AE﹣AH=4﹣3=1,
∵四边形形EFGH是正方形,
∴∠DHE=90°,
∴DE===,
故选:C.
【点评】此题重点考查全等三角形的性质、正方形的性质、勾股定理等知识,求得DH=4,EH=1,并且证明∠DHE=90°是解题的关键.
24.(2024 浙江)如图,在 ABCD中,AC,BD相交于点O,AC=2,.过点A作AE⊥BC的垂线交BC于点E,记BE长为x,BC长为y.当x,y的值发生变化时,下列代数式的值不变的是( )
A.x+y B.x﹣y C.xy D.x2+y2
【分析】过D作DH⊥BC,交BC延长线于H,由平行四边形当性质推出AB=DC,AD∥BC,得到AE=DH,判定Rt△DCH≌Rt△ABE(HL),得到CH=BE=x,由勾股定理得到22﹣(y﹣x)2=﹣(y+x)2,得到xy=2.
【解答】解:过D作DH⊥BC,交BC延长线于H,
∵四边形ABCD是平行四边形,
∴AB=DC,AD∥BC,
∵AE⊥BC,DH⊥BC,
∴AE=DH,
∴Rt△DCH≌Rt△ABE(HL),
∴CH=BE=x,
∵BC=y,
∴EC=BC﹣BE=y﹣x,BH=BC+CH=y+x,
∵AE2=AC2﹣EC2,DH2=BD2﹣BH2,
∴22﹣(y﹣x)2=﹣(y+x)2,
∴xy=2.
故选:C.
【点评】本题考查平行四边形的性质,全等三角形的判定和性质,勾股定理,关键是由Rt△DCH≌Rt△ABE(HL),得到CH=BE,由勾股定理得到22﹣(y﹣x)2=﹣(y+x)2.
25.(2024 湖北)如图,AB是半圆O的直径,C为半圆O上一点,以点B为圆心,适当长为半径画弧,交BA于点M,交BC于点N,分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠ABC的内部相交于点D,画射线BD,连接AC.若∠CAB=50°,则∠CBD的度数是( )
A.30° B.25° C.20° D.15°
【分析】由圆周角定理得到∠ACB=90°,由直角三角形的性质得到∠ABC=40°,根据角平分线的定义即可求得答案.
【解答】解:∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠CAB=50°,
∴∠ABC=90°﹣50°=40°,
由题意得,BD为∠ABC的平分线,
∴∠CBD=∠ABD=∠ABC=20°.
故选:C.
【点评】本题主要考查尺规作图,圆周角定理,熟练掌握角平分线的作图步骤以及圆周角定理是解答本题的关键.
26.(2024 广西)如图,边长为5的正方形ABCD,E,F,G,H分别为各边中点.连接AG,BH,CE,DF,交点分别为M,N,P,Q,那么四边形MNPQ的面积为( )
A.1 B.2 C.5 D.10
【分析】根据正方形的性质及相似三角形的性质求得四边形MNPQ的边长,从而即可求得四边形MNPQ的面积.
点评
【解答】解:正方形的边长为5,则CD=5,CF=2.5,
由勾股定理得,DF=,
由题意得△DQG∽△DFC,
:.DQ:QG=CD:CF=2:1,得
DQ=2QG=,
∵E,F,G,H分别为各边中点.
∴DQ=PQ=
∴四边形MNPQ的面积=,
故选:C.
【点评】本题利用了正方形的性质,相似三角形的判定和性质,勾股定理求解.
27.(2024 重庆)如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M.若BE=DF=1,则DM的长度为( )
A.2 B. C. D.
【分析】根据正方形的性质及三角形全等的判定及性质,证明AE=AF;利用角平分线的定义及三角形全等的判定及性质,证明EM=FM;设DM=x,将EM、MC和CE分别表示出来,在Rt△MCE中根据勾股定理列关于x的方程并求解即可.
【解答】解:∵四边形ABCD是正方形,
∴AB=AD,∠ABE=∠ADF=90°,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(SAS),
∴AE=AF;
∵AM平分∠EAF,
∴∠EAM=∠FAM,
在△AEM和△AFM中,
,
∴△AEM≌△AFM(SAS),
∴EM=FM;
∵四边形ABCD是正方形,
∴BC=CD=4,∠BCD=90°,
设DM=x,则MC=CD﹣DM=4﹣x,CE=BC﹣BE=4﹣1=3,EM=FM=FD+DM=1+x,
在Rt△MCE中,根据勾股定理,得EM2=MC2+CE2,即(1+x)2=(4﹣x)2+32,
解得x=.
故选:D.
【点评】本题考查正方形的性质、三角形全等的判定及性质等,掌握正方形的性质、三角形全等的判定及性质和角平分线的定义、勾股定理是解题的关键.
28.(2024 天津)如图,Rt△ABC中,∠C=90°,∠B=40°,以点A为圆心,适当长为半径画弧,交AB于点E,交AC于点F;再分别以点E,F为圆心,大于的长为半径画弧,两弧(所在圆的半径相等)在∠BAC的内部相交于点P;画射线AP,与BC相交于点D,则∠ADC的大小为( )
A.60° B.65° C.70° D.75°
【分析】由直角三角形两锐角互余可求出∠BAC=50°,由作图得∠BAD=25°,由三角形的外角的性质可得∠ADC=65°,故可得答案.
【解答】解:∵∠C=90°,∠B=40°,
∴∠BAC=90°﹣∠B=90°﹣40°=50°,
由作图知,AP平分∠BAC,
∴,
∵∠ADC=∠B+∠BAD,
∴∠ADC=40°+25°=65°,
故选:B.
【点评】本题主要考查基本作图,直角三角形两锐角互余以及三角形外角的性质,掌握尺规作图的方法是解题的关键.
29.(2024 黑龙江)如图,在正方形ABCD中,点H在AD边上(不与点A、D重合),∠BHF=90°,HF交正方形外角的平分线DF于点F,连接AC交BH于点M,连接BF交AC于点G,交CD于点N,连接BD.则下列结论:
①∠HBF=45°;②点G是BF的中点;③若点H是AD的中点,则sin∠NBC=;④BN=BM;⑤若AH=HD,则S△BND=S△AHM.其中正确的结论是( )
A.①②③④ B.①③⑤ C.①②④⑤ D.①②③④⑤
【分析】连接DG,可得,AC垂直平分BD,先证明点B、H、D、F四点共圆,即可判断①;根据AC垂直平分BD,结合互余可证明DG=FG,即有DG=FG=BG,则可判断②正确;证明△ABM∽△DBN,即有,可判断④;根据相似有 ,根据 可得3AH=AD,再证明△AHM﹣△CBM,可得,即可判断⑤;根据点H是AD的中点,设AD=2,即求出 ,同理可证明△AHM∽△CBM,可得 ,即可得 ,进而可判断③.
【解答】解:连接DG,如图,
∵四边形ABCD是正方形,∠BDC=∠BAC=∠ADB=45°,,∠BAD=∠ADC=90°,AC垂直平分BD,
∴∠CDP=90°,
∵DF平分∠CDP,
∴,
∴∠BDF=∠CDF+∠CDB=90°,∠BHF=90°=∠BDF,
∴点B、H、D、F四点共圆,
∴∠HFB=∠HDB=45°,∠DHF=∠DBF,
∴∠HBF=180°﹣∠HFB﹣∠FHB=45°,故①正确,
∵AC垂直平分BD,
∴BG=DG,
∴∠BDG=∠DBG,
∵∠BDF=90°,
∴∠BDG+∠GDF=90°=∠DBG+∠DFG,
∴∠GDF=∠DFG,
∴DG=FG,
∴DG=FG=BG,
∴点G是BF的中点,故②正确,
∵∠BHF=90°=∠BAH,
∴∠AHB+∠DHF=90°=∠AHB+∠ABH,
∴∠DHF=∠ABH,
∵∠DHF=∠DBF,
∴∠ABH=∠DBF,
又∵∠BAC=∠DBC=45°,AD∥BC,
∴△ABM∽△DBN,
∴,
∴,故④正确,
∴,
若,则,
∴3AH=AD,
∴,即,
∵AD∥DC,
∴△AHM∽△CBM,
∴,
∵,
∴S△ABM=3S△AHM,
∴,
∴S△BND=2S△ABM=6S△AHM,故⑤错误,
如图,③若点H是AD的中点,
设AD=2,即AB=BC=AD=2,
∴,
∴,
同理可证明△AHM∽△CBM,
∴, ,
∵,
∴,
∵BC=2,
在Rt△BNC 中, ,故③正确,则正确的有:①②③④,
故选:A.
【点评】本题考查了正方形的性质,相似三角形的判定与性质,正弦,圆周角定理以及勾股定理等知识,证明点B、H、D、F四点共圆,△ABM∽△DBN,是解答本题的关键.
30.(2024 达州)如图,△ABC是等腰直角三角形,∠ABC=90°,AB=4,点D,E分别在AC,BC边上运动,连结AE,BD交于点F,且始终满足AD=CE,则下列结论:①=;②∠DFE=135°;③△ABF面积的最大值是4﹣4;④CF的最小值是2﹣2.其中正确的是( )
A.①③ B.①②④ C.②③④ D.①②③④
【分析】①先求出,,则,由此可证△CAE∽△ABD,然后根据相似三角形性质可对结论①进行判断确;
②根据△CAE∽△ABD得∠CAE=∠ABD,再根据三角形外角性质得∠BFE=45°,由此可对结论②进行判断确;
③以AB为斜边在△ABC外侧构造等腰Rt△OAB,作△OAB的外接圆⊙O,过点O作OK⊥AB于K,OK的延长线交⊙O于H,连接AH,BH,过点O作OM⊥CB交CB的延长线于M,连接OC交⊙O于P,证明点F在弧AB上运动,则当点F与点H重合时,△ABF的面积为最大,最大值为△ABH的面积,然后求出△ABH的面积即可对结论③进行判断确;
④根据点F在弧AB上运动,得当点F与点P重合时,CF为最小,最小值为线段CP的长,然后求出线段CP的长即可对结论④进行判断确,综上所述即可得出答案.
【解答】解:①∵△ABC是等腰直角三角形,∠ABC=90°,AB=4,
∴∠BCA=∠BAC=45°,AB=BC=4,
由勾股定理得:AC==,
∴,
∵AD=CE,
∴,
∴,
又∵∠ECA=∠DAB=45°,
∴△CAE∽△ABD,
∴,
故结论①正确;
②∵△CAE∽△ABD,
∴∠CAE=∠ABD,
∴∠BFE=∠BAF+∠ABD=∠BAF+∠CAE=∠BAC=45°,
∴∠DFE=180°﹣∠BFE=180°﹣45°=135°,
故结论②正确;
③以AB为斜边在△ABC外侧构造等腰Rt△OAB,作△OAB的外接圆⊙O,过点O作OK⊥AB于K,OK的延长线交⊙O于H,连接AH,BH,过点O作OM⊥CB交CB的延长线于M,连接OC交⊙O于P,如下图所示:
∴∠AOB=90°,
∴∠AHB=180°﹣∠AOB=180°﹣×90°=135°,
∵∠DFE=135°,
∴点F在上运动,
∵AB=4,
∴当点F与点H重合时,△ABF的面积为最大,最大值为△ABH的面积,
根据等腰直角三角形的性质得:AK=BK=AB=2,∠AOH=45°,
∴AK=OK=2,
在Rt△AOK中,由勾股定理得:OA==,
∴OA=OH=OB=OP=,
∴KH=OH﹣OK=,
∴S△ABH=AB KH==,
故结论③正确;
④∵点F在上运动,
∴当点F与点P重合时,CF为最小,最小值为线段CP的长,
∵OM⊥CB,OK⊥AB,∠ABM=∠ABC=90°,
∴四边形OMBK为矩形,
∴OM=BK=2,BM=OK=2,
∴CM=BC+BM=4+2=6,
在Rt△COM中,由勾股定理得:CO==,
∴CP=CO﹣OP=,
即CF的最小值是,
故结论④正确,
综上所述:正确的结论是①②③④.
故选:D.
【点评】此题主要考查了等腰三角形的性质,相似三角形的判定和性质,点与圆的位置关系,熟练掌握等腰三角形的性质,相似三角形的判定和性质是解决问题的关键,构造辅助圆,证明点F在上运动,利用点与圆的位置关系求出△ABF面积的最大值和线段CF的最小值是解决问题的难点.
2024年中考数学选择题题分类汇编——图形的性质
一.选择题(共30小题)
1.(2024 辽宁)如图,在矩形ABCD中,点E在AD上,当△EBC是等边三角形时,∠AEB为( )
A.30° B.45° C.60° D.120°
2.(2024 南充)如图,两个平面镜平行放置,光线经过平面镜反射时,∠1=∠2=40°,则∠3的度数为( )
A.80° B.90° C.100° D.120°
3.(2024 通辽)如图, ABCD的对角线AC,BD交于点O,以下条件不能证明 ABCD是菱形的是( )
A.∠BAC=∠BCA B.∠ABD=∠CBD
C.OA2+OB2=AD2 D.AD2+OA2=OD2
4.(2024 长春)如图,在△ABC中,O是边AB的中点.按下列要求作图:①以点B为圆心、适当长为半径画弧,交线段BO于点D,交BC于点E;②以点O为圆心、BD长为半径画弧,交线段OA于点F;③以点F为圆心、DE长为半径画弧,交前一条弧于点G,点G与点C在直线AB同侧;④作直线OG,交AC于点M.下列结论不一定成立的是( )
A.∠AOM=∠B B.∠OMC+∠C=180°
C.AM=CM D.OM=AB
5.(2024 长沙)如图,在菱形ABCD中,AB=6,∠B=30°,点E是BC边上的动点,连接AE,DE,过点A作AF⊥DE于点F.设DE=x,AF=y,则y与x之间的函数解析式为(不考虑自变量x的取值范围)( )
A.y= B.y= C.y= D.y=
6.(2024 长沙)如图,在⊙O中,弦AB的长为8,圆心O到AB的距离OE=4,则⊙O的半径长为( )
A.4 B. C.5 D.
7.(2024 内蒙古)如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,适当长为半径画弧分别交AB,AC于点M和点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D.若△ACD的面积为8,则△ABD的面积是( )
A.8 B.16 C.12 D.24
8.(2024 泰安)如图,菱形ABCD中,∠B=60°,点E是AB边上的点,AE=4,BE=8,点F是BC上的一点,△EGF是以点G为直角顶点,∠EFG为30°角的直角三角形,连结AG.当点F在直线BC上运动时,线段AG的最小值是( )
A.2 B. C. D.4
9.(2024 泰安)如图,AB是⊙O的直径,C,D是⊙O上两点,BA平分∠CBD,若∠AOD=50°,则∠A的度数为( )
A.65° B.55° C.50° D.75°
10.(2024 泰安)两个半径相等的半圆按如图方式放置,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为2,则阴影部分的面积是( )
A. B. C. D.
11.(2024 泰安)如图,Rt△ABC中,∠ABC=90°,分别以顶点A,C为圆心,大于的长为半径画弧,两弧分别相交于点M和点N,作直线MN分别与BC,AC交于点E和点F;以点A为圆心,任意长为半径画弧,分别交AB,AC于点H和点G,再分别以点H,点G为圆心,大于HG的长为半径画弧,两弧交于点P,作射线AP,若射线AP恰好经过点E,则下列四个结论:
①∠C=30°;
②AP垂直平分线段BF;
③CE=2BE;
④.
其中,正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
12.(2024 赤峰)如图,△ABC中,AB=BC=1,∠C=72°.将△ABC绕点A顺时针旋转得到△AB′C′,点B′与点B是对应点,点C′与点C是对应点.若点C′恰好落在BC边上,下列结论:①点B在旋转过程中经过的路径长是π;②B′A∥BC;③BD=C′D;④.其中正确的结论是( )
A.①②③④ B.①②③ C.①③④ D.②④
13.(2024 广州)如图,在△ABC中,∠A=90°,AB=AC=6,D为边BC的中点,点E,F分别在边AB,AC上,AE=CF,则四边形AEDF的面积为( )
A.18 B.9 C.9 D.6
14.(2024 赤峰)如图,AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是( )
A.61° B.63° C.65° D.67°
15.(2024 雅安)如图,直线AB,CD交于点O,OE⊥AB于O,若∠1=35°,则∠2的度数是( )
A.55° B.45° C.35° D.30°
16.(2024 黑龙江)如图,菱形ABCD中,点O是BD的中点,AM⊥BC,垂足为M,AM交BD于点N,OM=2,BD=8,则MN的长为( )
A. B. C. D.
17.(2024 河北)直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,如图所示,则α+β=( )
A.115° B.120° C.135° D.144°
18.(2024 吉林)如图,四边形ABCD内接于⊙O.过点B作BE∥AD,交CD于点E.若∠BEC=50°,则∠ABC的度数是( )
A.50° B.100° C.130° D.150°
19.(2024 包头)如图,在平面直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(1,2),B(3,3),C(5,0),则四边形OABC的面积为( )
A.14 B.11 C.10 D.9
20.(2024 武汉)如图,四边形ABCD内接于⊙O,∠ABC=60°,∠BAC=∠CAD=45°,AB+AD=2,则⊙O的半径是( )
A. B. C. D.
21.(2024 武汉)小美同学按如下步骤作四边形ABCD;(1)画∠MAN;(2)以点A为圆心,1个单位长为半径画弧,分别交AM,AN于点B,D;(3)分别以点B,D为圆心,1个单位长为半径画弧,两弧交于点C;(4)连接BC,CD,BD.若∠A=44°,则∠CBD的大小是( )
A.64° B.66° C.68° D.70°
22.(2024 绥化)如图,四边形ABCD是菱形,CD=5,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
23.(2024 浙江)如图,正方形ABCD由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和中间一个小正方形EFGH组成,连接DE.若AE=4,BE=3,则DE=( )
A.5 B. C. D.4
24.(2024 浙江)如图,在 ABCD中,AC,BD相交于点O,AC=2,.过点A作AE⊥BC的垂线交BC于点E,记BE长为x,BC长为y.当x,y的值发生变化时,下列代数式的值不变的是( )
A.x+y B.x﹣y C.xy D.x2+y2
25.(2024 湖北)如图,AB是半圆O的直径,C为半圆O上一点,以点B为圆心,适当长为半径画弧,交BA于点M,交BC于点N,分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠ABC的内部相交于点D,画射线BD,连接AC.若∠CAB=50°,则∠CBD的度数是( )
A.30° B.25° C.20° D.15°
26.(2024 广西)如图,边长为5的正方形ABCD,E,F,G,H分别为各边中点.连接AG,BH,CE,DF,交点分别为M,N,P,Q,那么四边形MNPQ的面积为( )
A.1 B.2 C.5 D.10
27.(2024 重庆)如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M.若BE=DF=1,则DM的长度为( )
A.2 B. C. D.
28.(2024 天津)如图,Rt△ABC中,∠C=90°,∠B=40°,以点A为圆心,适当长为半径画弧,交AB于点E,交AC于点F;再分别以点E,F为圆心,大于的长为半径画弧,两弧(所在圆的半径相等)在∠BAC的内部相交于点P;画射线AP,与BC相交于点D,则∠ADC的大小为( )
A.60° B.65° C.70° D.75°
29.(2024 黑龙江)如图,在正方形ABCD中,点H在AD边上(不与点A、D重合),∠BHF=90°,HF交正方形外角的平分线DF于点F,连接AC交BH于点M,连接BF交AC于点G,交CD于点N,连接BD.则下列结论:
①∠HBF=45°;②点G是BF的中点;③若点H是AD的中点,则sin∠NBC=;④BN=BM;⑤若AH=HD,则S△BND=S△AHM.其中正确的结论是( )
A.①②③④ B.①③⑤ C.①②④⑤ D.①②③④⑤
30.(2024 达州)如图,△ABC是等腰直角三角形,∠ABC=90°,AB=4,点D,E分别在AC,BC边上运动,连结AE,BD交于点F,且始终满足AD=CE,则下列结论:①=;②∠DFE=135°;③△ABF面积的最大值是4﹣4;④CF的最小值是2﹣2.其中正确的是( )
A.①③ B.①②④ C.②③④ D.①②③④
图形的性质
参考答案与试题解析
一.选择题(共30小题)
1.(2024 辽宁)如图,在矩形ABCD中,点E在AD上,当△EBC是等边三角形时,∠AEB为( )
A.30° B.45° C.60° D.120°
【分析】根据平行线的性质和等边三角形的性质即可解答.
【解答】证明:∵△EBC是等边三角形,
∴∠CBE=60°,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠AEB=∠CBE=60°.
故选:C.
【点评】本题考查矩形的性质,等边三角形的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.
2.(2024 南充)如图,两个平面镜平行放置,光线经过平面镜反射时,∠1=∠2=40°,则∠3的度数为( )
A.80° B.90° C.100° D.120°
【分析】根据经过两次反射后的光线与入射光线平行,得出∠3=∠4即可.
【解答】解:如图:∵∠1=∠2=40°,
∴∠4=180°﹣∠1﹣∠2=100°,
∵两个平面镜平行放置,
∴经过两次反射后的光线与入射光线平行,
∴∠3=∠4=100°,
故选:C.
【点评】本题考查平行线的性质,关键是掌握经过两次反射后的光线与入射光线平行.
3.(2024 通辽)如图, ABCD的对角线AC,BD交于点O,以下条件不能证明 ABCD是菱形的是( )
A.∠BAC=∠BCA B.∠ABD=∠CBD
C.OA2+OB2=AD2 D.AD2+OA2=OD2
【分析】由菱形的判定、矩形的判定分别对各个选项进行判断即可.
【解答】解:A、∵∠BAC=∠BCA,
∴AB=BC,
∴ ABCD是菱形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∴ ABCD是菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴OB=OD,
∵OA2+OB2=AD2,
∴OA2+OD2=AD2,
∴∠AOD=90°,
∴AC⊥BD,
∴ ABCD是菱形,故选项C不符合题意,
D、∵AD2+OA2=OD2,
∴∠OAD=90°,
∴OA⊥AD,
∴不能证得 ABCD是菱形,故选项D符合题意;
故选:D.
【点评】本题考查了菱形的判定、平行四边形的性质,熟练掌握菱形的判定方法是解题的关键.
4.(2024 长春)如图,在△ABC中,O是边AB的中点.按下列要求作图:①以点B为圆心、适当长为半径画弧,交线段BO于点D,交BC于点E;②以点O为圆心、BD长为半径画弧,交线段OA于点F;③以点F为圆心、DE长为半径画弧,交前一条弧于点G,点G与点C在直线AB同侧;④作直线OG,交AC于点M.下列结论不一定成立的是( )
A.∠AOM=∠B B.∠OMC+∠C=180°
C.AM=CM D.OM=AB
【分析】由作图过程可知,∠AOM=∠B,则OM∥BC,根据平行线的性质可得∠OMC+∠C=180°.根据O是边AB的中点,OM∥BC,可得点M为AC的中点,即AM=CM,进而可得答案.
【解答】解:由作图过程可知,∠AOM=∠B,
故A选项正确,不符合题意;
∵∠AOM=∠B,
∴OM∥BC,
∴∠OMC+∠C=180°,
故B选项正确,不符合题意;
∵O是边AB的中点,OM∥BC,
∴点M为AC的中点,
∴AM=CM,
故C选项正确,不符合题意;
根据已知条件不能得出OM=AB,
故D选项不正确,符合题意.
故选:D.
【点评】本题考查作图—复杂作图、平行线的判定与性质,解题的关键是理解题意,灵活运用所学知识解决问题.
5.(2024 长沙)如图,在菱形ABCD中,AB=6,∠B=30°,点E是BC边上的动点,连接AE,DE,过点A作AF⊥DE于点F.设DE=x,AF=y,则y与x之间的函数解析式为(不考虑自变量x的取值范围)( )
A.y= B.y= C.y= D.y=
【分析】过D作DH⊥BC交BC的延长线于H,在菱形ABCD中,AB=6,AB∥CD,AB=CD=AD=6,AD∥BC,根据平行线的性质得到∠DCH=∠B=30°,∠ADF=∠DEH,根据直角三角形 到现在得到DH=,根据相似三角形的判定和性质定理即可得到结论.
【解答】解:过D作DH⊥BC交BC的延长线于H,
在菱形ABCD中,AB=6,AB∥CD,AB=CD=AD=6,AD∥BC,
∴∠DCH=∠B=30°,∠ADF=∠DEH,
∴DH=,
∵AF⊥DE,
∴∠AFD=∠EHD=90°,
∴△ADF∽△DEH,
∴,
∴=,
∴y=,
故选:C.
【点评】本题考查了菱形的性质,含30°直角三角形的性质,相似三角形的判定和性质,正确地作出辅助线是解题的关键.
6.(2024 长沙)如图,在⊙O中,弦AB的长为8,圆心O到AB的距离OE=4,则⊙O的半径长为( )
A.4 B. C.5 D.
【分析】利用垂径定理,勾股定理求解即可.
【解答】解:∵OE⊥AB,
∴AE=EB=4,
∴OA===4.
故选:B.
【点评】本题考查垂径定理,勾股定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
7.(2024 内蒙古)如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,适当长为半径画弧分别交AB,AC于点M和点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D.若△ACD的面积为8,则△ABD的面积是( )
A.8 B.16 C.12 D.24
【分析】过点D作DE⊥AB于点E,由作图过程可知,AD平分∠BAC,可得CD=ED,证明Rt△ACD≌Rt△AED,可得S△ADE=S△ACD=8.由题意可得∠EAD=∠B,则AD=BD,即△ABD为等腰三角形,则S△ADE=S△BDE=8,进而可得答案.
【解答】解:过点D作DE⊥AB于点E,
由作图过程可知,AD平分∠BAC,
∴CD=ED.
∵AD=AD,
∴Rt△ACD≌Rt△AED(AAS),
∴S△ADE=S△ACD=8.
∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD平分∠BAC,
∴∠CAD=∠EAD=30°,
∴∠EAD=∠B,
∴AD=BD,
即△ABD为等腰三角形,
∴S△ADE=S△BDE=8,
∴△ABD的面积为S△ADE+S△BDE=16.
故选:B.
【点评】本题考查作图—基本作图、角平分线的性质、全等三角形的判定与性质、等腰三角形的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
8.(2024 泰安)如图,菱形ABCD中,∠B=60°,点E是AB边上的点,AE=4,BE=8,点F是BC上的一点,△EGF是以点G为直角顶点,∠EFG为30°角的直角三角形,连结AG.当点F在直线BC上运动时,线段AG的最小值是( )
A.2 B. C. D.4
【分析】E作EM⊥BC,则点E、M、F、G四点共圆,从而得到AF=MH,因为AG≥GF,所以求出MH的值即可得解.
【解答】解:如图,过E作EM⊥BC于点M,作MH⊥AB于点H,作AF⊥GM于点F,
∵∠EMF+∠EGF=180°,
∴点E、M、F、G四点共圆,
∴∠EMG=∠EFG=30°,
∵∠B=60°,
∴∠BEM=30°=∠EMG,
∴MG∥AB,
∴四边形MHAF是矩形,
∴MH=AF,
∵BE=8,
∴EM=BE cos30°=4,
∴MH=EM=2=AF,
∴AG≥AF=2,
∴AG最小值是2.
故选:C.
【点评】本题主要考查了菱形的性质、解直角三角形、垂线段最短、圆内接四边形对角互补等知识,熟练掌握相关知识点和添加合适的辅助线是解题关键.
9.(2024 泰安)如图,AB是⊙O的直径,C,D是⊙O上两点,BA平分∠CBD,若∠AOD=50°,则∠A的度数为( )
A.65° B.55° C.50° D.75°
【分析】先利用圆周角定理可得:∠ABD=25°,然后利用平角定义得∠ABC=25°,根据圆周角定理得∠C=90°,再根据三角形内角和定理进行计算即可解答.
【解答】解:∵∠AOD=50°,
∴∠ABD=∠AOD=25°,
∵BA平分∠CBD,
∴∠ABC=∠ABD=25°,
∵AB是⊙O的直径,
∴∠C=90°,
∴∠A=180°﹣90°﹣25°=65°.
故选:A.
【点评】本题考查了圆周角定理,圆心角、弧、弦的关系,熟练掌握圆周角定理是解题的关键.
10.(2024 泰安)两个半径相等的半圆按如图方式放置,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为2,则阴影部分的面积是( )
A. B. C. D.
【分析】连接OA,AO′,作AB⊥OO′于点B,得三角形AOO′是等边三角形,求出AB=,S弓形AO′=S扇形AOO′﹣S△AOO′=﹣,再根据S阴影=S弓形AO′+S扇形AO′O,即可得出答案.
【解答】解:如图,连接OA,AO′,作AB⊥OO′于点B,
∵OA=OO′=AO′=2,
∴三角形AOO′是等边三角形,
∴∠AOO′=60°,OB=OO′=1,
∴AB==,
∴S弓形AO′=S扇形AOO′﹣S△AOO′
=﹣2××
=﹣,
∴S阴影=S弓形AO′+S扇形AO′O
=﹣+
=﹣.
故选:A.
【点评】本题考查了扇形的面积公式的运用、三角形的面积公式的运用,熟练掌握扇形的面积公式是关键.
11.(2024 泰安)如图,Rt△ABC中,∠ABC=90°,分别以顶点A,C为圆心,大于的长为半径画弧,两弧分别相交于点M和点N,作直线MN分别与BC,AC交于点E和点F;以点A为圆心,任意长为半径画弧,分别交AB,AC于点H和点G,再分别以点H,点G为圆心,大于HG的长为半径画弧,两弧交于点P,作射线AP,若射线AP恰好经过点E,则下列四个结论:
①∠C=30°;
②AP垂直平分线段BF;
③CE=2BE;
④.
其中,正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】首先证明∠C=∠EAC=∠BAE=30°,推出AC=2AB,AE=2BE,可得①②③④正确.
【解答】解:由作图可知MN垂直平分线段AC,
∴EA=EC,
∴∠EAC=∠C,
由作图可知AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠ABC=90°,
∴∠C=∠CAE=∠BAE=30°,故①正确,
∴AC=2AB,
∵AF=FC,
∴AB=AF,
∴AP垂直平分线段BF,故②正确,
∵AE=2BE,EA=EC,
∴EC=2BE,故③正确,
∴S△BEF=S△BCF,
∵AF=FC,
∴S△BFC=S△ABC,
∴S△BEF=S△ABC,故④正确.
故选:D.
【点评】本题考查作图﹣复杂作图,角平分线的性质,线段的垂直平分线的性质等知识,解题的关键是读懂图象信息,灵活运用所学知识解决问题.
12.(2024 赤峰)如图,△ABC中,AB=BC=1,∠C=72°.将△ABC绕点A顺时针旋转得到△AB′C′,点B′与点B是对应点,点C′与点C是对应点.若点C′恰好落在BC边上,下列结论:①点B在旋转过程中经过的路径长是π;②B′A∥BC;③BD=C′D;④.其中正确的结论是( )
A.①②③④ B.①②③ C.①③④ D.②④
【分析】①先求出点B旋转的角度为36°,半径为1,即可求出路径长;②∠B′AB=∠ABC=36°,所以B′A∥BC;③∠DC′B=∠ABC=36°,所以BD=C′D;④△B′BD∽△BAC,所以.
【解答】解:∵AB=BC,∠C=72°,
∴∠BAC=∠C=72°,∠ABC=180°﹣2∠C=36°,
由旋转的性质得∠AB′C=∠ABC=36°,∠B'AC'=∠BAC=72°,∠AC′B′=∠C=72°,∠AC′B′=∠ADC=72°,AC′=AC,
∴∠AC′C=∠C=72°,
∴∠CAC'=36°,
∴∠CAC′=∠BAC′=36°,
∴∠B′AB=72°﹣36°=36°,
由旋转的性质得AB′=AB,
∴,
①点B在旋转过程中经过的路径长是,①说法正确;
②∵∠B′AB=∠ABC=36°,∴B′A∥BC,②说法正确;
③∵∠DC′B=180°﹣2×72°=36°,
∴∠DC′B=∠ABC=36°,
∴BD=C′D,③说法正确;
④∵∠BB′D=∠ABC=36°,∠B′BD=∠BAC=72°,
∴△B′BD∽△BAC,
∴,④说法正确;
综上,①②③④都是正确的,
故选:A.
【点评】本题考查了平行四边形的性质与判定,旋转的性质等,掌握平行四边形的性质与判定是解题的关键.
13.(2024 广州)如图,在△ABC中,∠A=90°,AB=AC=6,D为边BC的中点,点E,F分别在边AB,AC上,AE=CF,则四边形AEDF的面积为( )
A.18 B.9 C.9 D.6
【分析】由等腰直角三角形的性质可得AD=BD=CD,∠BAD=∠C=45°,S△ABC=×6×6=18,由“SAS”可证△ADE≌△CDF,可得S△ADE=S△CDF,即可求解.
【解答】解:如图,连接AD,
∵∠BAC=90°,AB=AC=6,D为边BC的中点,
∴AD=BD=CD,∠BAD=∠C=45°,S△ABC=×6×6=18,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴S△ADE=S△CDF,
∴四边形AEDF的面积=S△ADC=S△ABC=9,
故选:C.
【点评】本题主要考查了全等三角形的判定和性质,等腰直角三角形的性质,证明三角形全等是解题的关键.
14.(2024 赤峰)如图,AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是( )
A.61° B.63° C.65° D.67°
【分析】根据垂径定理得=,所以∠AOC=∠BOC=42°,根据圆周角定理得∠D=∠AOC=21°,再根据OC=OD,∠C=∠D=21°,最后根据三角形的外角的性质即可得出答案.
【解答】解:∵半径OC⊥AB,
∴=,
∴∠AOC=∠BOC=42°,
∴∠D=∠AOC=21°,
∵OC=OD,
∴∠C=∠D=21°,
∴∠OED=∠C+∠BOC=21°+42°=63°.
故选:B.
【点评】本题主要考查了圆周角定理,垂径定理,圆心角、弧、弦的关系,熟练掌握圆周角定理和垂径定理是解题的关键.
15.(2024 雅安)如图,直线AB,CD交于点O,OE⊥AB于O,若∠1=35°,则∠2的度数是( )
A.55° B.45° C.35° D.30°
【分析】已知OE⊥AB,∠1=35°,可得∠AOC的度数,因为对顶角∠2=∠AOC,即得∠2的度数.
【解答】解:∵OE⊥AB,∠1=35°,
∴∠AOC=55°,
∴∠2=∠AOC=55°,
故选:A.
【点评】本题考查了垂线、对顶角的性质,关键是掌握垂线、对顶角的性质.
16.(2024 黑龙江)如图,菱形ABCD中,点O是BD的中点,AM⊥BC,垂足为M,AM交BD于点N,OM=2,BD=8,则MN的长为( )
A. B. C. D.
【分析】先由菱形性质可得对角线AC与BD交于点O,由直角三角形斜边中线等于斜边一半可得OA=OC=OM=2,进而由菱形对角线求出边长,由sin∠MAC=sin∠OBC=解三角形即可求出MC=ACsin∠MAC=,MN=BMtan∠OBC=.
【解答】解:连接AC,如图,
∵菱形ABCD中,AC与BD互相垂直平分,
又∵点O是BD的中点,
∴A、O、C三点在同一直线上,
∴OA=OC,
∵OM=2,AM⊥BC,
∴OA=OC=OM=2,
∵BD=8,
∴OB=OD=BD=4,
∴BC===2,tan∠OBC===,
∵∠ACM+∠MAC=90°,∠ACM+∠OBC=90°,
∴∠MAC=∠OBC
∴sin∠MAC=sin∠OBC===,
∴MC=ACsin∠MAC=,
∴BM=BC MC=2 =,
∴MN=BMtan∠OBC=×=,
故选:C.
【点评】本题考查了解直角三角形,菱形的性质、直角三角形斜边中线等于斜边一半.熟练掌握各知识点是解题的关键.
17.(2024 河北)直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,如图所示,则α+β=( )
A.115° B.120° C.135° D.144°
【分析】先求出正六边形的每个内角为120°,再根据六边形MBCDEN的内角和为720°即可求解∠ENM+∠NMB的度数,最后根据邻补角的意义即可求解.
【解答】解:正六边形每个内角为:,
而六边形MBCDEN的内角和也为(6﹣2)×180°=720°,
∴∠B+∠C+∠D+∠E+∠ENM+∠NMB=720°,
∴∠ENM+∠NMB=720°﹣4×120°=240°,
∵β+∠ENM+α+∠NMB=180°×2=360°,
∴α+β=360°﹣240°=120°,
故选:B.
【点评】本题考查了多边形的内角和,正多边形的每个内角,邻补角,熟练掌握知识点是解决本题的关键.
18.(2024 吉林)如图,四边形ABCD内接于⊙O.过点B作BE∥AD,交CD于点E.若∠BEC=50°,则∠ABC的度数是( )
A.50° B.100° C.130° D.150°
【分析】根据BE∥AD,得出∠ADC=∠BEC=50°,再根据圆内接四边形的性质即可得出答案.
【解答】解:∵BE∥AD,
∴∠ADC=∠BEC=50°,
∵四边形ABCD内接于⊙O,
∴∠ABC=180°﹣∠ADC=130°.
故选:C.
【点评】本题主要考查圆内接四边形的性质,平行线的性质,熟练掌握圆内接四边形的性质是解题的关键.
19.(2024 包头)如图,在平面直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(1,2),B(3,3),C(5,0),则四边形OABC的面积为( )
A.14 B.11 C.10 D.9
【分析】过A点作AE⊥x轴于E,作BF⊥x轴于F,如图,利用三角形面积公式和梯形的面积公式,利用四边形OABC的面积=S△BCF+S梯形ABFE+S△AOE进行计算.
【解答】解:过A点作AE⊥x轴于E,作BF⊥x轴于F,如图,
∵O(0,0),A(1,2),B(3,3),C(5,0),
∴OE=1,AE=2,BF=3,CF=2,EF=2,
∴四边形OABC的面积=S△AOE+S△BCF+S梯形ABFE
=×1×2+×3×2+
=9,
故选:D.
【点评】本题主要考查了梯形的面积、三角形的面积:三角形的面积等于底边长与高线乘积的一半,即S△=×底×高.也考查了坐标与图形性质.
20.(2024 武汉)如图,四边形ABCD内接于⊙O,∠ABC=60°,∠BAC=∠CAD=45°,AB+AD=2,则⊙O的半径是( )
A. B. C. D.
【分析】过C作CM⊥AB于M,CN⊥AD交AD延长线于N,过O作OH⊥AC于H,连接OA,OC,由角平分线的性质推出MC=CN,判定四边形AMCN是正方形,得到AM=AN,由圆周角定理得到=,推出CD=BC,即可证明Rt△CDN≌Rt△CBM(HL),得到ND=MB,推出AB+AD=2AM=2,求出AM=1,判定△ACM是等腰直角三角形,求出AC=AM=,由圆周角定理得到∠AOC=2∠B=120°,由等腰三角形的性质推出AH=AC=,∠AOH=∠AOC=60°,由sin∠AOH==,求出OA=,得到⊙O的半径是.
【解答】解:过C作CM⊥AB于M,CN⊥AD交AD延长线于N,过O作OH⊥AC于H,连接OA,OC,
∵∠BAC=∠CAD=45°,
∴AC平分∠BAN,
∴MC=CN,
∵∠MAN=∠BAC+∠CAD=90°,∠AMC=∠ANC=90°,
∴四边形AMCN是正方形,
∴AM=AN,
∵∠BAC=∠CAD,
∴=,
∴CD=BC,
∵CN=CM,
∴Rt△CDN≌Rt△CBM(HL),
∴ND=MB,
∵AB+AD=AM+MB+AD=AM+DN+AD=AM+AN=2AM=2,
∴AM=1,
∵∠BAC=45°,∠AMC=90°,
∴△ACM是等腰直角三角形,
∴AC=AM=,
∵∠B=60°,
∴∠AOC=2∠B=120°,
∵OA=OC,OH⊥AC,
∴AH=AC=,∠AOH=∠AOC=60°,
∵sin∠AOH=sin60°==,
∴OA=,
∴⊙O的半径是.
故选:A.
【点评】本题考查全等三角形的判定和性质,正方形的判定和性质,圆周角定理,角平分线的性质,等腰三角形的性质,解直角三角形,关键是由Rt△CDN≌Rt△CBM(HL),推出ND=MB,得到AB+AD=2AM.
21.(2024 武汉)小美同学按如下步骤作四边形ABCD;(1)画∠MAN;(2)以点A为圆心,1个单位长为半径画弧,分别交AM,AN于点B,D;(3)分别以点B,D为圆心,1个单位长为半径画弧,两弧交于点C;(4)连接BC,CD,BD.若∠A=44°,则∠CBD的大小是( )
A.64° B.66° C.68° D.70°
【分析】由(1)(2)(3)可知四边形ABCD是菱形,然后根据菱形的性质和三角形内角和定理求出答案即可.
【解答】解:由(1)(2)(3)可知四边形ABCD是菱形,
∴AB=AD,BC∥AD,
∴∠ABD=∠ADB=∠CBD,
∵∠A=44°,
∴∠ABD+∠ADB=180°﹣∠A=180°﹣44°=136°,
∴∠ABD=∠ADB=∠CBD=68°,
故选:C.
【点评】本题主要考查了多边形的内角与外角和菱形的判定与性质,解题关键是根据已知条件中的作图判定四边形ABCD的形状.
22.(2024 绥化)如图,四边形ABCD是菱形,CD=5,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
【分析】由菱形的性质和勾股定理求出AC=6,再由菱形的面积求出AE即可.
【解答】解:∵四边形ABCD是菱形,CD=5,BD=8,
∴BC=CD=5,BO=DO=4,OA=OC,AC⊥BD,
∴∠BOC=90°,
在Rt△OBC中,由勾股定理得:OC===3,
∴AC=2OC=6,
∵菱形ABCD的面积=AE BC=BD×AC=OB AC,
∴AE===,
故选:A.
【点评】此题考查了菱形的性质以及勾股定理等知识,熟练掌握菱形的性质和勾股定理是解题的关键.
23.(2024 浙江)如图,正方形ABCD由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和中间一个小正方形EFGH组成,连接DE.若AE=4,BE=3,则DE=( )
A.5 B. C. D.4
【分析】由全等三角形的性质得DH=AE=4,AH=BE=3,则EH=AE﹣AH=1,而∠DHE=90°,所以DE==,于是得到问题的答案.
【解答】解:∵Rt△DAH≌Rt△ABE,
∴DH=AE=4,AH=BE=3,
∴EH=AE﹣AH=4﹣3=1,
∵四边形形EFGH是正方形,
∴∠DHE=90°,
∴DE===,
故选:C.
【点评】此题重点考查全等三角形的性质、正方形的性质、勾股定理等知识,求得DH=4,EH=1,并且证明∠DHE=90°是解题的关键.
24.(2024 浙江)如图,在 ABCD中,AC,BD相交于点O,AC=2,.过点A作AE⊥BC的垂线交BC于点E,记BE长为x,BC长为y.当x,y的值发生变化时,下列代数式的值不变的是( )
A.x+y B.x﹣y C.xy D.x2+y2
【分析】过D作DH⊥BC,交BC延长线于H,由平行四边形当性质推出AB=DC,AD∥BC,得到AE=DH,判定Rt△DCH≌Rt△ABE(HL),得到CH=BE=x,由勾股定理得到22﹣(y﹣x)2=﹣(y+x)2,得到xy=2.
【解答】解:过D作DH⊥BC,交BC延长线于H,
∵四边形ABCD是平行四边形,
∴AB=DC,AD∥BC,
∵AE⊥BC,DH⊥BC,
∴AE=DH,
∴Rt△DCH≌Rt△ABE(HL),
∴CH=BE=x,
∵BC=y,
∴EC=BC﹣BE=y﹣x,BH=BC+CH=y+x,
∵AE2=AC2﹣EC2,DH2=BD2﹣BH2,
∴22﹣(y﹣x)2=﹣(y+x)2,
∴xy=2.
故选:C.
【点评】本题考查平行四边形的性质,全等三角形的判定和性质,勾股定理,关键是由Rt△DCH≌Rt△ABE(HL),得到CH=BE,由勾股定理得到22﹣(y﹣x)2=﹣(y+x)2.
25.(2024 湖北)如图,AB是半圆O的直径,C为半圆O上一点,以点B为圆心,适当长为半径画弧,交BA于点M,交BC于点N,分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠ABC的内部相交于点D,画射线BD,连接AC.若∠CAB=50°,则∠CBD的度数是( )
A.30° B.25° C.20° D.15°
【分析】由圆周角定理得到∠ACB=90°,由直角三角形的性质得到∠ABC=40°,根据角平分线的定义即可求得答案.
【解答】解:∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠CAB=50°,
∴∠ABC=90°﹣50°=40°,
由题意得,BD为∠ABC的平分线,
∴∠CBD=∠ABD=∠ABC=20°.
故选:C.
【点评】本题主要考查尺规作图,圆周角定理,熟练掌握角平分线的作图步骤以及圆周角定理是解答本题的关键.
26.(2024 广西)如图,边长为5的正方形ABCD,E,F,G,H分别为各边中点.连接AG,BH,CE,DF,交点分别为M,N,P,Q,那么四边形MNPQ的面积为( )
A.1 B.2 C.5 D.10
【分析】根据正方形的性质及相似三角形的性质求得四边形MNPQ的边长,从而即可求得四边形MNPQ的面积.
点评
【解答】解:正方形的边长为5,则CD=5,CF=2.5,
由勾股定理得,DF=,
由题意得△DQG∽△DFC,
:.DQ:QG=CD:CF=2:1,得
DQ=2QG=,
∵E,F,G,H分别为各边中点.
∴DQ=PQ=
∴四边形MNPQ的面积=,
故选:C.
【点评】本题利用了正方形的性质,相似三角形的判定和性质,勾股定理求解.
27.(2024 重庆)如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M.若BE=DF=1,则DM的长度为( )
A.2 B. C. D.
【分析】根据正方形的性质及三角形全等的判定及性质,证明AE=AF;利用角平分线的定义及三角形全等的判定及性质,证明EM=FM;设DM=x,将EM、MC和CE分别表示出来,在Rt△MCE中根据勾股定理列关于x的方程并求解即可.
【解答】解:∵四边形ABCD是正方形,
∴AB=AD,∠ABE=∠ADF=90°,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(SAS),
∴AE=AF;
∵AM平分∠EAF,
∴∠EAM=∠FAM,
在△AEM和△AFM中,
,
∴△AEM≌△AFM(SAS),
∴EM=FM;
∵四边形ABCD是正方形,
∴BC=CD=4,∠BCD=90°,
设DM=x,则MC=CD﹣DM=4﹣x,CE=BC﹣BE=4﹣1=3,EM=FM=FD+DM=1+x,
在Rt△MCE中,根据勾股定理,得EM2=MC2+CE2,即(1+x)2=(4﹣x)2+32,
解得x=.
故选:D.
【点评】本题考查正方形的性质、三角形全等的判定及性质等,掌握正方形的性质、三角形全等的判定及性质和角平分线的定义、勾股定理是解题的关键.
28.(2024 天津)如图,Rt△ABC中,∠C=90°,∠B=40°,以点A为圆心,适当长为半径画弧,交AB于点E,交AC于点F;再分别以点E,F为圆心,大于的长为半径画弧,两弧(所在圆的半径相等)在∠BAC的内部相交于点P;画射线AP,与BC相交于点D,则∠ADC的大小为( )
A.60° B.65° C.70° D.75°
【分析】由直角三角形两锐角互余可求出∠BAC=50°,由作图得∠BAD=25°,由三角形的外角的性质可得∠ADC=65°,故可得答案.
【解答】解:∵∠C=90°,∠B=40°,
∴∠BAC=90°﹣∠B=90°﹣40°=50°,
由作图知,AP平分∠BAC,
∴,
∵∠ADC=∠B+∠BAD,
∴∠ADC=40°+25°=65°,
故选:B.
【点评】本题主要考查基本作图,直角三角形两锐角互余以及三角形外角的性质,掌握尺规作图的方法是解题的关键.
29.(2024 黑龙江)如图,在正方形ABCD中,点H在AD边上(不与点A、D重合),∠BHF=90°,HF交正方形外角的平分线DF于点F,连接AC交BH于点M,连接BF交AC于点G,交CD于点N,连接BD.则下列结论:
①∠HBF=45°;②点G是BF的中点;③若点H是AD的中点,则sin∠NBC=;④BN=BM;⑤若AH=HD,则S△BND=S△AHM.其中正确的结论是( )
A.①②③④ B.①③⑤ C.①②④⑤ D.①②③④⑤
【分析】连接DG,可得,AC垂直平分BD,先证明点B、H、D、F四点共圆,即可判断①;根据AC垂直平分BD,结合互余可证明DG=FG,即有DG=FG=BG,则可判断②正确;证明△ABM∽△DBN,即有,可判断④;根据相似有 ,根据 可得3AH=AD,再证明△AHM﹣△CBM,可得,即可判断⑤;根据点H是AD的中点,设AD=2,即求出 ,同理可证明△AHM∽△CBM,可得 ,即可得 ,进而可判断③.
【解答】解:连接DG,如图,
∵四边形ABCD是正方形,∠BDC=∠BAC=∠ADB=45°,,∠BAD=∠ADC=90°,AC垂直平分BD,
∴∠CDP=90°,
∵DF平分∠CDP,
∴,
∴∠BDF=∠CDF+∠CDB=90°,∠BHF=90°=∠BDF,
∴点B、H、D、F四点共圆,
∴∠HFB=∠HDB=45°,∠DHF=∠DBF,
∴∠HBF=180°﹣∠HFB﹣∠FHB=45°,故①正确,
∵AC垂直平分BD,
∴BG=DG,
∴∠BDG=∠DBG,
∵∠BDF=90°,
∴∠BDG+∠GDF=90°=∠DBG+∠DFG,
∴∠GDF=∠DFG,
∴DG=FG,
∴DG=FG=BG,
∴点G是BF的中点,故②正确,
∵∠BHF=90°=∠BAH,
∴∠AHB+∠DHF=90°=∠AHB+∠ABH,
∴∠DHF=∠ABH,
∵∠DHF=∠DBF,
∴∠ABH=∠DBF,
又∵∠BAC=∠DBC=45°,AD∥BC,
∴△ABM∽△DBN,
∴,
∴,故④正确,
∴,
若,则,
∴3AH=AD,
∴,即,
∵AD∥DC,
∴△AHM∽△CBM,
∴,
∵,
∴S△ABM=3S△AHM,
∴,
∴S△BND=2S△ABM=6S△AHM,故⑤错误,
如图,③若点H是AD的中点,
设AD=2,即AB=BC=AD=2,
∴,
∴,
同理可证明△AHM∽△CBM,
∴, ,
∵,
∴,
∵BC=2,
在Rt△BNC 中, ,故③正确,则正确的有:①②③④,
故选:A.
【点评】本题考查了正方形的性质,相似三角形的判定与性质,正弦,圆周角定理以及勾股定理等知识,证明点B、H、D、F四点共圆,△ABM∽△DBN,是解答本题的关键.
30.(2024 达州)如图,△ABC是等腰直角三角形,∠ABC=90°,AB=4,点D,E分别在AC,BC边上运动,连结AE,BD交于点F,且始终满足AD=CE,则下列结论:①=;②∠DFE=135°;③△ABF面积的最大值是4﹣4;④CF的最小值是2﹣2.其中正确的是( )
A.①③ B.①②④ C.②③④ D.①②③④
【分析】①先求出,,则,由此可证△CAE∽△ABD,然后根据相似三角形性质可对结论①进行判断确;
②根据△CAE∽△ABD得∠CAE=∠ABD,再根据三角形外角性质得∠BFE=45°,由此可对结论②进行判断确;
③以AB为斜边在△ABC外侧构造等腰Rt△OAB,作△OAB的外接圆⊙O,过点O作OK⊥AB于K,OK的延长线交⊙O于H,连接AH,BH,过点O作OM⊥CB交CB的延长线于M,连接OC交⊙O于P,证明点F在弧AB上运动,则当点F与点H重合时,△ABF的面积为最大,最大值为△ABH的面积,然后求出△ABH的面积即可对结论③进行判断确;
④根据点F在弧AB上运动,得当点F与点P重合时,CF为最小,最小值为线段CP的长,然后求出线段CP的长即可对结论④进行判断确,综上所述即可得出答案.
【解答】解:①∵△ABC是等腰直角三角形,∠ABC=90°,AB=4,
∴∠BCA=∠BAC=45°,AB=BC=4,
由勾股定理得:AC==,
∴,
∵AD=CE,
∴,
∴,
又∵∠ECA=∠DAB=45°,
∴△CAE∽△ABD,
∴,
故结论①正确;
②∵△CAE∽△ABD,
∴∠CAE=∠ABD,
∴∠BFE=∠BAF+∠ABD=∠BAF+∠CAE=∠BAC=45°,
∴∠DFE=180°﹣∠BFE=180°﹣45°=135°,
故结论②正确;
③以AB为斜边在△ABC外侧构造等腰Rt△OAB,作△OAB的外接圆⊙O,过点O作OK⊥AB于K,OK的延长线交⊙O于H,连接AH,BH,过点O作OM⊥CB交CB的延长线于M,连接OC交⊙O于P,如下图所示:
∴∠AOB=90°,
∴∠AHB=180°﹣∠AOB=180°﹣×90°=135°,
∵∠DFE=135°,
∴点F在上运动,
∵AB=4,
∴当点F与点H重合时,△ABF的面积为最大,最大值为△ABH的面积,
根据等腰直角三角形的性质得:AK=BK=AB=2,∠AOH=45°,
∴AK=OK=2,
在Rt△AOK中,由勾股定理得:OA==,
∴OA=OH=OB=OP=,
∴KH=OH﹣OK=,
∴S△ABH=AB KH==,
故结论③正确;
④∵点F在上运动,
∴当点F与点P重合时,CF为最小,最小值为线段CP的长,
∵OM⊥CB,OK⊥AB,∠ABM=∠ABC=90°,
∴四边形OMBK为矩形,
∴OM=BK=2,BM=OK=2,
∴CM=BC+BM=4+2=6,
在Rt△COM中,由勾股定理得:CO==,
∴CP=CO﹣OP=,
即CF的最小值是,
故结论④正确,
综上所述:正确的结论是①②③④.
故选:D.
【点评】此题主要考查了等腰三角形的性质,相似三角形的判定和性质,点与圆的位置关系,熟练掌握等腰三角形的性质,相似三角形的判定和性质是解决问题的关键,构造辅助圆,证明点F在上运动,利用点与圆的位置关系求出△ABF面积的最大值和线段CF的最小值是解决问题的难点.
同课章节目录
