1.2 数轴、相反数和绝对值 3课时 课件(共54张PPT)2024-2025学年七年级数学上册 沪科版
文档属性
| 名称 | 1.2 数轴、相反数和绝对值 3课时 课件(共54张PPT)2024-2025学年七年级数学上册 沪科版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 592.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-19 00:00:00 | ||
图片预览









文档简介
(共54张PPT)
1.2 数轴、相反数和绝对值
第1课时 数轴
1.知道数轴的三要素,能正确地画出数轴.
2.能说出数轴上的点所表示的数,能将有理数用数轴上的点表示出来.
3.探索数轴上的点与有理数的对应关系,初步体会数形结合的数学思想.
◎重点:数轴上的点与有理数的对应关系.
◎难点:数形结合的数学思想.
激趣导入
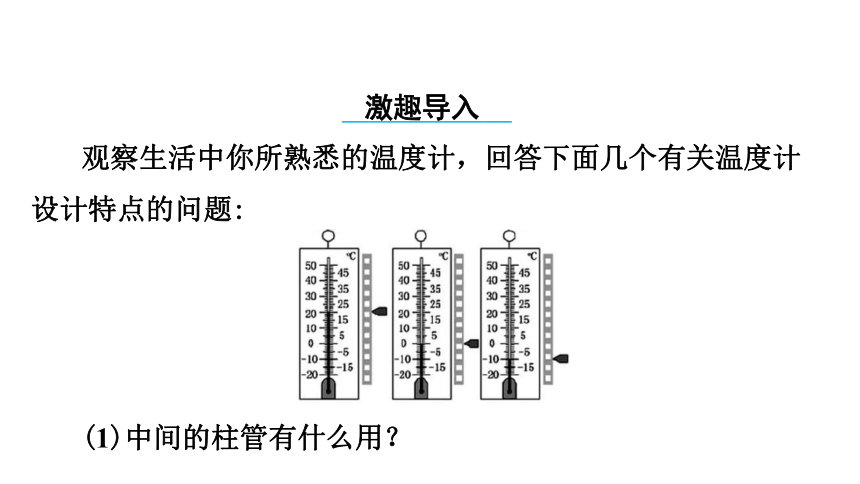
观察生活中你所熟悉的温度计,回答下面几个有关温度计设计特点的问题:
(1)中间的柱管有什么用?
激趣导入
(2)温度计刻度的正负是怎样规定的?以什么为基准?基准刻度线表示多少摄氏度?
(3)每相邻两条刻度线之间的距离有什么特点?
温度计就是一种由数字构成的轴,我们这节课将学习数轴.
数轴的概念
1.原点表示数 0 ,当直线水平放置时,一般取从左到右的方向为 正方向 .
2.规定了 原点 、 正方向 、 单位长度 的直线叫做数轴.
0
正方向
原点
正方向
单位长度
数轴上的点与有理数的对应关系
1.正有理数可用原点 右边 的点来表示,负有理数可用原点 左边 的点来表示,零用 原点 表示.
2.任何一个有理数都可以用 数轴上的一个点 来表示.
右边
左边
原点
数轴上的一个点
1.下列说法中,错误的是( C )
A.所有的有理数都可以用数轴上的点表示
B.数轴上的原点表示0
C.在数轴上表示-3的点与表示-1的点的距离是-2
D.数轴上表示-3的点在原点左边第3个单位长度上
2.在数轴上,M点表示-5,N点表示-3,则这两点中, N 点离原点较近.
C
N
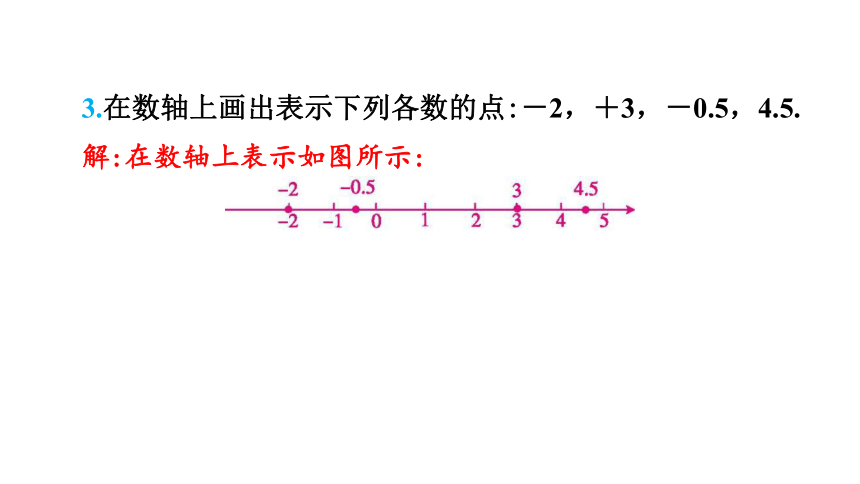
3.在数轴上画出表示下列各数的点:-2,+3,-0.5,4.5.
解:在数轴上表示如图所示:
数轴的概念
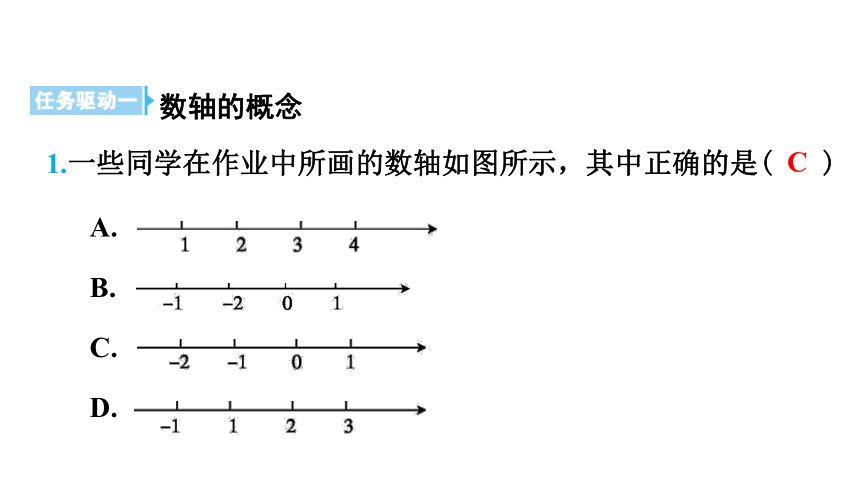
1.一些同学在作业中所画的数轴如图所示,其中正确的是( C)
A.
B.
C.
D.
C
数轴上的点与有理数的关系
2.指出如图所示的数轴上A、B、C、D四个点分别表示的数.
解:点A表示的数是-2.5;点B表示的数是-0.5;点C表示的数是1;点D表示的数是3.5.
方法归纳交流 如何读出数轴上的点所表示的数?
首先要看点在原点的左侧还是右侧,从而确定符号,然后再看距离原点几个单位长度,从而确定数.
解:点A表示的数是-2.5;点B表示的数是-0.5;点C表示的
数是1;点D表示的数是3.5.
首先要看点在原点的左侧还是右侧,从而确定符号,然后
再看距离原点几个单位长度,从而确定数.
3.在数轴上表示下列各数.
-11,-2,1,2.5,3,4.
解:在数轴上表示各数如图所示.
方法归纳交流 一般地,设a是一个正数,则数轴上表示a的点在原点的 右 边,与原点的距离是 a 个单位长度;表示-a的点在原点的 左 边,与原点的距离是 a 个单位长度.
解:在数轴上表示各数如图所示.
右
a
左
a
1.数轴上A,B两点对应的有理数分别是-,,则A,B两点之间的整数有( C )
A.4个 B.5个 C.6个 D.7个
2.在数轴上,表示-4的点与表示-6的点之间的距离是 2 个单位长度.
C
2
3.A点与数轴上表示-2的点相距3个单位长度,则A点表示的数是 -5或1 .
-5或1
4.某市一条自西向东的道路旁依次有人民公园、新华书店、实验中学、科技馆、花园小区五个地点,相邻两个地点的距离依次为3 km,1.5 km,2 km,3.5 km.如果以新华书店为原点,规定向东方向为正,向西方向为负,设图上0.5 cm长的线段表示实际距离1 km,请画出数轴,将五个地点在数轴上表示出来.
解:五个地点在数轴上表示如图所示.
1.2 数轴、相反数和绝对值
第2课时 相反数
1.能借助数轴知道只有符号不同的两个数互为相反数,知道互为相反数的一对数在数轴上位于原点的两侧,且到原点的距离相等.
2.能够利用相反数的概念求出一个数的相反数,会进行简单的简化符号.
3.知道相反数的几何意义和代数意义,培养学生的归纳能力以及数形结合思想.
◎重点:相反数的意义以及双重符号的化简.
◎难点:相反数的概念以及“-a”的理解.
激趣导入
拔河与相反数
学校运动会开始啦,两支队伍开始拔河,中间地面上的白线为起始点.当绳子上的红色布条向左移动1米,记为-1米,则左边的队伍获胜;当红色布条向右移动1米,记为+1米,则右边的队伍获胜.-1米与+1米有什么特殊的地方吗?它们就是一对相反数.
激趣导入
相反数的意义
揭示概念:像2与-2,4与-4,与-这样只有 符号不同 的两个数互为相反数.
符号不同
求一个数的相反数
1.正数的相反数是 负数 ,负数的相反数是 正数 ,0的相反数仍是 0 .
2.思考:当a表示任意一个有理数时,a的相反数是 -a .
3.要求一个数的相反数,只需要在该数的前面添加 负11 号.
负数
正数
0
-a
负
4.-(+3)表示 +3 的相反数;-(-3)表示 -3 的相反数,所以-(+3)= -3 ,-(-3)= 3 .
+3
-3
-3
3
1.-5的相反数是( B )
A. B.5 C.- D.-5
2.下列各数互为相反数的是( A )
A.-(-2)与-2 B.-(-2)与2
C.-2与- D.-2与
B
A
3.给出下列说法:①若两个数互为相反数,则它们的相反数也互为相反数;②在任何一个数前面添加一个“-”号,就变成原数的相反数;③+与-2.4互为相反数;④-与0.1互为相反数.其中错误说法的序号是 ④ .
④
相反数的定义
1.下列各对数:①3.3与-3;②与4;③-(-)与-;④0与0;⑤-与0.75.其中互为相反数的是( A )
A.③④⑤ B.②③④
C.②③ D.②③④⑤
A
相反数的求法
2.分别写出下列各数的相反数.
(1)+;(2)-3;(3)0;(4)0.15;(5)-1.
解:(1)+的相反数是-;
(2)-3的相反数是3;
(3)0的相反数是0;
(4)0.15的相反数是-0.15;
(5)-1的相反数是1.
[变式演练]若a=-13,则-a= 13 ;若-a=-8,则a= 8 ;若a是负数,则-a是 正数 ;若-a是负数,则a是 正数 .
讨论:-a一定表示一个负数吗?
不一定,-a表示a的相反数,当a表示正数时,-a表示负数;当a表示负数时,-a表示正数;当a表示0时,-a仍表示0.
13
8
正数
正数
多重符号的化简
3.化简下列各数的符号.
(1)-(+5);(2)-(-5);(3)+(+5);
(4)+(-5);(5)-[-(+5)];(6)+[-(-5)].
解:(1)-(+5)=-5;
(2)-(-5)=5;
(3)+(+5)=5;
(4)+(-5)=-5;
(5)-[-(+5)]=5;
(6)+[-(-5)]=5.
方法归纳交流 多重符号的化简有如下规律:“+”的个数 不影响 化简的结果,若一个数的前面有偶数个“-”,其结果为 正 ;若一个数的前面有奇数个“-”,其结果为 负 .
不影响
正
负
1.如图,表示互为相反数的两个点是( C )
A.M与Q B.N与P
C.M与P D.N与Q
2.下列各对数:+(-3)与-3;-(-3)与+(-3);-(+3)与+(-3);+3与+(-3)中,互为相反数的有( B )
A.1对 B.2对 C.3对 D.4对
3.相反数等于本身的数是 0 .
C
B
0
4.在数轴上,点A,B表示的数互为相反数,且两点间的距离是10,点A在点B的左边,则点A表示的数为 -5 ,点B表示的数为 5 .
-5
5
5.写出下列各数的相反数,并将这些数连同它们的相反数在数轴上表示出来.
-4,+2,-1.5,0,.
解:-4,+2,-1.5,0,的相反数分别是4,-2,1.5,0,-.
这些数在数轴上表示如图所示.
1.2 数轴、相反数和绝对值
第3课时 绝对值
1.知道绝对值的概念,用数轴体会绝对值的实际意义.
2.会求一个数的绝对值,能解决与绝对值相关的问题.
◎重点:求一个数的绝对值.
◎难点:绝对值的实际意义.
激趣导入
激趣导入
绝对值的定义
1.在数轴上,表示数a的点到原点的距离叫做数a的 绝对值 .
2.数a的绝对值可记作 |a| ,读作 a的绝对值 .
绝对
值
|a|
a的绝对值
3.讨论:你能用绝对值的定义求出0的绝对值吗?
数轴上表示0的点与原点的距离是0,即|0|=0.
【学法指导】对于绝对值的代数意义这个知识点,0是一个比较特殊的数,0的绝对值既可以理解是它的本身,也可以理解为它的相反数.
绝对值的性质
1.若a>0,则|a|= a ;若a<0,则|a|= -a ;若a=0,则|a|= 0 .
2.思考:一个有理数的绝对值有可能是负数吗?
不可能,任何有理数的绝对值都是正数或0.
a
-a
0
1.3的绝对值是( B )
A.-3 B.3 C. D.
2.|-2|的相反数是( B )
A.- B.-2 C. D.2
B
B
3.下列各式不成立的是( D )
A.|-2|=2 B.|+2|=|-2|
C.-|-3|=-3 D.-|2|=|-2|
4.一个数的绝对值是4,则这个数是 ±4 .
D
±4
绝对值的几何意义
1.到原点距离为4的数是 4或-4 ,|-5|的相反数是 -5 .
4或-4
-
5
[变式演练]已知数轴上的A点到原点的距离是2,那么数轴上到点A的距离是3的点所表示的数有( D )
A.1个 B.2个 C.3个 D.4个
D
绝对值的代数意义
2.求下列各数的绝对值.
(1)-17;(2)-(-3.5);(3)-;(4)-.
解:(1)|-17|=17;
(2)|-(-3.5)|=|3.5|=3.5;
(3)
(4)因为-=-,所以-的绝对值是.
[变式演练]已知|a|=5,求a的值.
解:因为|a|=5,而|5|=5,|-5|=5,所以a=5或-5.
绝对值的实际应用
3.某车间生产一批圆形机器零件,从中抽取6件进行检验,比规定直径长的毫米数记作正数,比规定直径短的毫米数记作负数.
检查记录如下表:
1 2 3 4 5 6
+0.2 -0.3 -0.2 +0.3 +0.4 -0.1
请指出第几个零件好些,并用学过的绝对值知识来说明什么样的零件好些.
解:因为|+0.2|=0.2,|-0.3|=0.3,|-0.2|=0.2,|+0.3|=0.3,|+0.4|=0.4,|-0.1|=0.1,显然|-0.1|最小,第6个零件好些.因为根据绝对值的意义,绝对值越小,说明它与零件规定的直径越接近,所以在表中绝对值最小的那个零件好.
1.若|a|=-a,则a的值不可以是( A )
A.2 B.-5 C.0 D.-0.5
2.若|a|=|b|,则a,b的关系是( D )
A.a=b B.a=-b
C.a=0且b=0 D.a=b或a=-b
A
D
3.若|a+2|+|b-7|=0,则a,b的值为( C )
A.2,7 B.2,-7 C.-2,7 D.-2,-7
4.如图,若数轴上a的绝对值是b的绝对值的3倍,则数轴的原点在点 C 或点 D .(填“A”、“B”、“C”或“D”)
C
C
D
5.已知|a-2|=0,求a的值.
解:因为|a-2|=0,而|0|=0,所以a-2=0,a的值为2.
6.已知某零件的标准直径是100 mm,超过标准直径长度的数量(mm)记作正数,不足标准直径长度的数量(mm)记作负数,检验员某次抽查了五件样品,检查结果如下表:
序号 1 2 3 4 5
直径长度 (mm) +0.1 -0.15 +0.2 -0.05 +0.25
(1)哪件样品的大小最符合要求?
(2)如果规定误差的绝对值在0.18 mm之内是正品,误差的绝对值在0.18~0.22 mm之间是次品,误差的绝对值超过0.22 mm是废品,那么这五件样品分别属于哪类产品?
解:(1)第4件样品的大小最符合要求.
(2)因为|+0.1|=0.1<0.18,|-0.15|=0.15<0.18,|-0.05|=0.05<0.18,所以第1、2、4件样品是正品;
因为|0.2|=0.2,0.18<0.2<0.22,所以第3件样品为次品;
因为|+0.25|=0.25>0.22,所以第5件样品为废品.
1.2 数轴、相反数和绝对值
第1课时 数轴
1.知道数轴的三要素,能正确地画出数轴.
2.能说出数轴上的点所表示的数,能将有理数用数轴上的点表示出来.
3.探索数轴上的点与有理数的对应关系,初步体会数形结合的数学思想.
◎重点:数轴上的点与有理数的对应关系.
◎难点:数形结合的数学思想.
激趣导入
观察生活中你所熟悉的温度计,回答下面几个有关温度计设计特点的问题:
(1)中间的柱管有什么用?
激趣导入
(2)温度计刻度的正负是怎样规定的?以什么为基准?基准刻度线表示多少摄氏度?
(3)每相邻两条刻度线之间的距离有什么特点?
温度计就是一种由数字构成的轴,我们这节课将学习数轴.
数轴的概念
1.原点表示数 0 ,当直线水平放置时,一般取从左到右的方向为 正方向 .
2.规定了 原点 、 正方向 、 单位长度 的直线叫做数轴.
0
正方向
原点
正方向
单位长度
数轴上的点与有理数的对应关系
1.正有理数可用原点 右边 的点来表示,负有理数可用原点 左边 的点来表示,零用 原点 表示.
2.任何一个有理数都可以用 数轴上的一个点 来表示.
右边
左边
原点
数轴上的一个点
1.下列说法中,错误的是( C )
A.所有的有理数都可以用数轴上的点表示
B.数轴上的原点表示0
C.在数轴上表示-3的点与表示-1的点的距离是-2
D.数轴上表示-3的点在原点左边第3个单位长度上
2.在数轴上,M点表示-5,N点表示-3,则这两点中, N 点离原点较近.
C
N
3.在数轴上画出表示下列各数的点:-2,+3,-0.5,4.5.
解:在数轴上表示如图所示:
数轴的概念
1.一些同学在作业中所画的数轴如图所示,其中正确的是( C)
A.
B.
C.
D.
C
数轴上的点与有理数的关系
2.指出如图所示的数轴上A、B、C、D四个点分别表示的数.
解:点A表示的数是-2.5;点B表示的数是-0.5;点C表示的数是1;点D表示的数是3.5.
方法归纳交流 如何读出数轴上的点所表示的数?
首先要看点在原点的左侧还是右侧,从而确定符号,然后再看距离原点几个单位长度,从而确定数.
解:点A表示的数是-2.5;点B表示的数是-0.5;点C表示的
数是1;点D表示的数是3.5.
首先要看点在原点的左侧还是右侧,从而确定符号,然后
再看距离原点几个单位长度,从而确定数.
3.在数轴上表示下列各数.
-11,-2,1,2.5,3,4.
解:在数轴上表示各数如图所示.
方法归纳交流 一般地,设a是一个正数,则数轴上表示a的点在原点的 右 边,与原点的距离是 a 个单位长度;表示-a的点在原点的 左 边,与原点的距离是 a 个单位长度.
解:在数轴上表示各数如图所示.
右
a
左
a
1.数轴上A,B两点对应的有理数分别是-,,则A,B两点之间的整数有( C )
A.4个 B.5个 C.6个 D.7个
2.在数轴上,表示-4的点与表示-6的点之间的距离是 2 个单位长度.
C
2
3.A点与数轴上表示-2的点相距3个单位长度,则A点表示的数是 -5或1 .
-5或1
4.某市一条自西向东的道路旁依次有人民公园、新华书店、实验中学、科技馆、花园小区五个地点,相邻两个地点的距离依次为3 km,1.5 km,2 km,3.5 km.如果以新华书店为原点,规定向东方向为正,向西方向为负,设图上0.5 cm长的线段表示实际距离1 km,请画出数轴,将五个地点在数轴上表示出来.
解:五个地点在数轴上表示如图所示.
1.2 数轴、相反数和绝对值
第2课时 相反数
1.能借助数轴知道只有符号不同的两个数互为相反数,知道互为相反数的一对数在数轴上位于原点的两侧,且到原点的距离相等.
2.能够利用相反数的概念求出一个数的相反数,会进行简单的简化符号.
3.知道相反数的几何意义和代数意义,培养学生的归纳能力以及数形结合思想.
◎重点:相反数的意义以及双重符号的化简.
◎难点:相反数的概念以及“-a”的理解.
激趣导入
拔河与相反数
学校运动会开始啦,两支队伍开始拔河,中间地面上的白线为起始点.当绳子上的红色布条向左移动1米,记为-1米,则左边的队伍获胜;当红色布条向右移动1米,记为+1米,则右边的队伍获胜.-1米与+1米有什么特殊的地方吗?它们就是一对相反数.
激趣导入
相反数的意义
揭示概念:像2与-2,4与-4,与-这样只有 符号不同 的两个数互为相反数.
符号不同
求一个数的相反数
1.正数的相反数是 负数 ,负数的相反数是 正数 ,0的相反数仍是 0 .
2.思考:当a表示任意一个有理数时,a的相反数是 -a .
3.要求一个数的相反数,只需要在该数的前面添加 负11 号.
负数
正数
0
-a
负
4.-(+3)表示 +3 的相反数;-(-3)表示 -3 的相反数,所以-(+3)= -3 ,-(-3)= 3 .
+3
-3
-3
3
1.-5的相反数是( B )
A. B.5 C.- D.-5
2.下列各数互为相反数的是( A )
A.-(-2)与-2 B.-(-2)与2
C.-2与- D.-2与
B
A
3.给出下列说法:①若两个数互为相反数,则它们的相反数也互为相反数;②在任何一个数前面添加一个“-”号,就变成原数的相反数;③+与-2.4互为相反数;④-与0.1互为相反数.其中错误说法的序号是 ④ .
④
相反数的定义
1.下列各对数:①3.3与-3;②与4;③-(-)与-;④0与0;⑤-与0.75.其中互为相反数的是( A )
A.③④⑤ B.②③④
C.②③ D.②③④⑤
A
相反数的求法
2.分别写出下列各数的相反数.
(1)+;(2)-3;(3)0;(4)0.15;(5)-1.
解:(1)+的相反数是-;
(2)-3的相反数是3;
(3)0的相反数是0;
(4)0.15的相反数是-0.15;
(5)-1的相反数是1.
[变式演练]若a=-13,则-a= 13 ;若-a=-8,则a= 8 ;若a是负数,则-a是 正数 ;若-a是负数,则a是 正数 .
讨论:-a一定表示一个负数吗?
不一定,-a表示a的相反数,当a表示正数时,-a表示负数;当a表示负数时,-a表示正数;当a表示0时,-a仍表示0.
13
8
正数
正数
多重符号的化简
3.化简下列各数的符号.
(1)-(+5);(2)-(-5);(3)+(+5);
(4)+(-5);(5)-[-(+5)];(6)+[-(-5)].
解:(1)-(+5)=-5;
(2)-(-5)=5;
(3)+(+5)=5;
(4)+(-5)=-5;
(5)-[-(+5)]=5;
(6)+[-(-5)]=5.
方法归纳交流 多重符号的化简有如下规律:“+”的个数 不影响 化简的结果,若一个数的前面有偶数个“-”,其结果为 正 ;若一个数的前面有奇数个“-”,其结果为 负 .
不影响
正
负
1.如图,表示互为相反数的两个点是( C )
A.M与Q B.N与P
C.M与P D.N与Q
2.下列各对数:+(-3)与-3;-(-3)与+(-3);-(+3)与+(-3);+3与+(-3)中,互为相反数的有( B )
A.1对 B.2对 C.3对 D.4对
3.相反数等于本身的数是 0 .
C
B
0
4.在数轴上,点A,B表示的数互为相反数,且两点间的距离是10,点A在点B的左边,则点A表示的数为 -5 ,点B表示的数为 5 .
-5
5
5.写出下列各数的相反数,并将这些数连同它们的相反数在数轴上表示出来.
-4,+2,-1.5,0,.
解:-4,+2,-1.5,0,的相反数分别是4,-2,1.5,0,-.
这些数在数轴上表示如图所示.
1.2 数轴、相反数和绝对值
第3课时 绝对值
1.知道绝对值的概念,用数轴体会绝对值的实际意义.
2.会求一个数的绝对值,能解决与绝对值相关的问题.
◎重点:求一个数的绝对值.
◎难点:绝对值的实际意义.
激趣导入
激趣导入
绝对值的定义
1.在数轴上,表示数a的点到原点的距离叫做数a的 绝对值 .
2.数a的绝对值可记作 |a| ,读作 a的绝对值 .
绝对
值
|a|
a的绝对值
3.讨论:你能用绝对值的定义求出0的绝对值吗?
数轴上表示0的点与原点的距离是0,即|0|=0.
【学法指导】对于绝对值的代数意义这个知识点,0是一个比较特殊的数,0的绝对值既可以理解是它的本身,也可以理解为它的相反数.
绝对值的性质
1.若a>0,则|a|= a ;若a<0,则|a|= -a ;若a=0,则|a|= 0 .
2.思考:一个有理数的绝对值有可能是负数吗?
不可能,任何有理数的绝对值都是正数或0.
a
-a
0
1.3的绝对值是( B )
A.-3 B.3 C. D.
2.|-2|的相反数是( B )
A.- B.-2 C. D.2
B
B
3.下列各式不成立的是( D )
A.|-2|=2 B.|+2|=|-2|
C.-|-3|=-3 D.-|2|=|-2|
4.一个数的绝对值是4,则这个数是 ±4 .
D
±4
绝对值的几何意义
1.到原点距离为4的数是 4或-4 ,|-5|的相反数是 -5 .
4或-4
-
5
[变式演练]已知数轴上的A点到原点的距离是2,那么数轴上到点A的距离是3的点所表示的数有( D )
A.1个 B.2个 C.3个 D.4个
D
绝对值的代数意义
2.求下列各数的绝对值.
(1)-17;(2)-(-3.5);(3)-;(4)-.
解:(1)|-17|=17;
(2)|-(-3.5)|=|3.5|=3.5;
(3)
(4)因为-=-,所以-的绝对值是.
[变式演练]已知|a|=5,求a的值.
解:因为|a|=5,而|5|=5,|-5|=5,所以a=5或-5.
绝对值的实际应用
3.某车间生产一批圆形机器零件,从中抽取6件进行检验,比规定直径长的毫米数记作正数,比规定直径短的毫米数记作负数.
检查记录如下表:
1 2 3 4 5 6
+0.2 -0.3 -0.2 +0.3 +0.4 -0.1
请指出第几个零件好些,并用学过的绝对值知识来说明什么样的零件好些.
解:因为|+0.2|=0.2,|-0.3|=0.3,|-0.2|=0.2,|+0.3|=0.3,|+0.4|=0.4,|-0.1|=0.1,显然|-0.1|最小,第6个零件好些.因为根据绝对值的意义,绝对值越小,说明它与零件规定的直径越接近,所以在表中绝对值最小的那个零件好.
1.若|a|=-a,则a的值不可以是( A )
A.2 B.-5 C.0 D.-0.5
2.若|a|=|b|,则a,b的关系是( D )
A.a=b B.a=-b
C.a=0且b=0 D.a=b或a=-b
A
D
3.若|a+2|+|b-7|=0,则a,b的值为( C )
A.2,7 B.2,-7 C.-2,7 D.-2,-7
4.如图,若数轴上a的绝对值是b的绝对值的3倍,则数轴的原点在点 C 或点 D .(填“A”、“B”、“C”或“D”)
C
C
D
5.已知|a-2|=0,求a的值.
解:因为|a-2|=0,而|0|=0,所以a-2=0,a的值为2.
6.已知某零件的标准直径是100 mm,超过标准直径长度的数量(mm)记作正数,不足标准直径长度的数量(mm)记作负数,检验员某次抽查了五件样品,检查结果如下表:
序号 1 2 3 4 5
直径长度 (mm) +0.1 -0.15 +0.2 -0.05 +0.25
(1)哪件样品的大小最符合要求?
(2)如果规定误差的绝对值在0.18 mm之内是正品,误差的绝对值在0.18~0.22 mm之间是次品,误差的绝对值超过0.22 mm是废品,那么这五件样品分别属于哪类产品?
解:(1)第4件样品的大小最符合要求.
(2)因为|+0.1|=0.1<0.18,|-0.15|=0.15<0.18,|-0.05|=0.05<0.18,所以第1、2、4件样品是正品;
因为|0.2|=0.2,0.18<0.2<0.22,所以第3件样品为次品;
因为|+0.25|=0.25>0.22,所以第5件样品为废品.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
