十八章 勾股定理
图片预览

文档简介
第十八章 勾股定理
GSZX
广顺中学简明学案
学科:数学 设计人: 时间:2009.4 班级: 姓名:
18.1 勾股定理(1)
【课时目标】1、了解勾股定理的由来,经历探索勾股定理的过程.
理解并能用不同的方法证明勾股定理,并能简单的运用.
提高推理意识与探究习惯,感受我国古代数学的伟大成就.
【重点难点】重点:勾股定理及及其应用.
难点:用面积法(拼图法)证明勾股定理.
【学具】4个全等的直角三角形
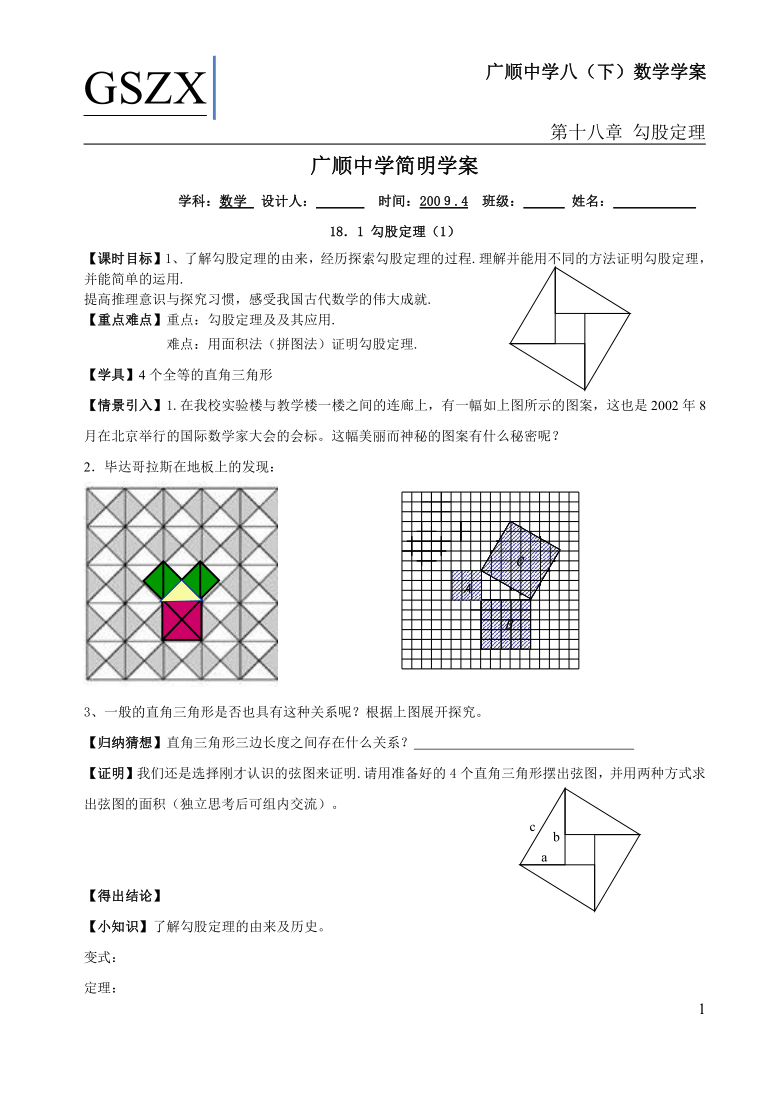
【情景引入】1.在我校实验楼与教学楼一楼之间的连廊上,有一幅如上图所示的图案,这也是2002年8月在北京举行的国际数学家大会的会标。这幅美丽而神秘的图案有什么秘密呢?
2.毕达哥拉斯在地板上的发现:
(
A
B
C
A
B
C
)
3、一般的直角三角形是否也具有这种关系呢?根据上图展开探究。
【归纳猜想】直角三角形三边长度之间存在什么关系?
(
a
b
c
)【证明】我们还是选择刚才认识的弦图来证明.请用准备好的4个直角三角形摆出弦图,并用两种方式求出弦图的面积(独立思考后可组内交流)。
【得出结论】
【小知识】了解勾股定理的由来及历史。
变式:
定理:
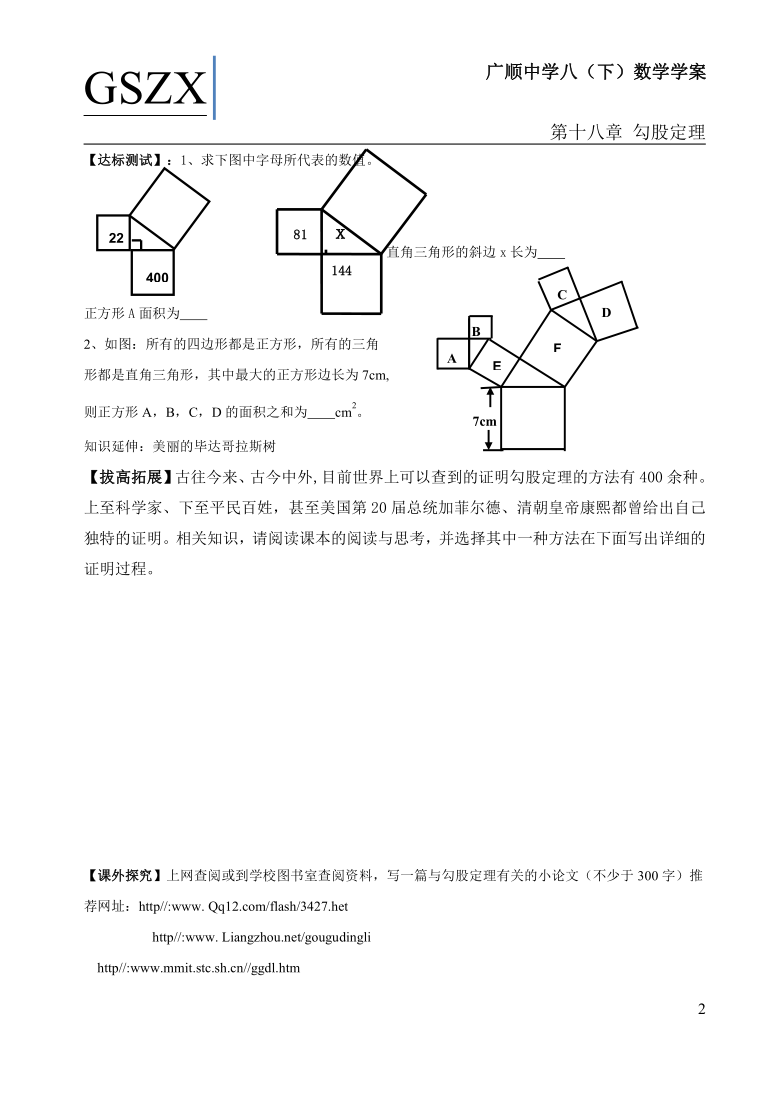
【达标测试】:1、求下图中字母所代表的数值。
(
144
x
)
(
225
400
A
)
(
81
)
直角三角形的斜边x长为
(
A
B
C
D
7
cm
F
E
)
正方形A面积为
2、如图:所有的四边形都是正方形,所有的三角
形都是直角三角形,其中最大的正方形边长为7cm,
则正方形A,B,C,D的面积之和为 cm2。
知识延伸:美丽的毕达哥拉斯树
【拔高拓展】古往今来、古今中外,目前世界上可以查到的证明勾股定理的方法有400余种。上至科学家、下至平民百姓,甚至美国第20届总统加菲尔德、清朝皇帝康熙都曾给出自己独特的证明。相关知识,请阅读课本的阅读与思考,并选择其中一种方法在下面写出详细的证明过程。
【课外探究】上网查阅或到学校图书室查阅资料,写一篇与勾股定理有关的小论文(不少于300字)
推荐网址:http//:www. Qq12.com/flash/3427.het
http//:www. /gougudingli
http//:www.mmit.stc.//ggdl.htm
广顺中学简明学案
学科:数学 设计人: 时间:2009.4 班级: 姓名:
18.1 勾股定理(2)
【课时目标】1.能运用勾股定理解决简单的实际问题.
2.通过本节学习,使学生真正体会数学来源于生活,又应用于生活,增强如何在日常生活中用数学知识解决问题的经验和感受.
【重点难点】重点难点:运用勾股定理及方程的思想解决简单的实际问题.
【温故知新】回忆勾股定理的内容:
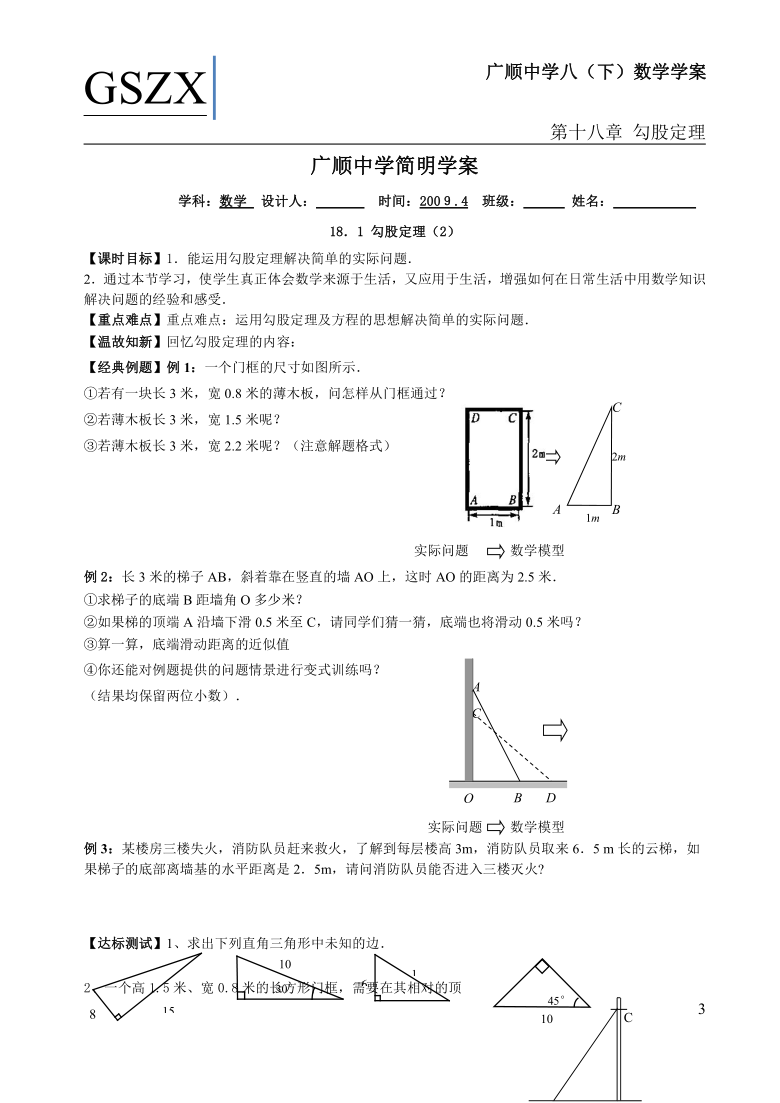
【经典例题】例1:一个门框的尺寸如图所示.
(
B
C
1
m
2
m
A
)①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?(注意解题格式)
实际问题 数学模型
例2:长3米的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.
①求梯子的底端B距墙角O多少米?
②如果梯的顶端A沿墙下滑0.5米至C,请同学们猜一猜,底端也将滑动0.5米吗?
③算一算,底端滑动距离的近似值
(
O
B
D
C
C
A
)④你还能对例题提供的问题情景进行变式训练吗?
(结果均保留两位小数).
实际问题 数学模型
例3:某楼房三楼失火,消防队员赶来救火,了解到每层楼高3m,消防队员取来6.5 m长的云梯,如果梯子的底部离墙基的水平距离是2.5m,请问消防队员能否进入三楼灭火
(
6
10
) (
10
30
°
) (
15
8
)【达标测试】1、求出下列直角三角形中未知的边.
(
10
45
°
)
(
B
A
C
)2、一个高1.5米、宽0.8米的长方形门框,需要在其相对的顶
点间用一条木条加固,则需木条长为 。
3、从电杆离地面5m处向地面拉一条长为7m的钢缆,则地面
钢缆A到电线杆底部B的距离为 。
4、有一个边长为50dm的正方形洞口,想用一个圆盖盖住这个洞口,
圆的直径至少为 (结果保留整数)
5、一旗杆离地面6m处折断,其顶部落在离旗杆底部8m处,则旗杆折断前高
(
A
E
B
D
C
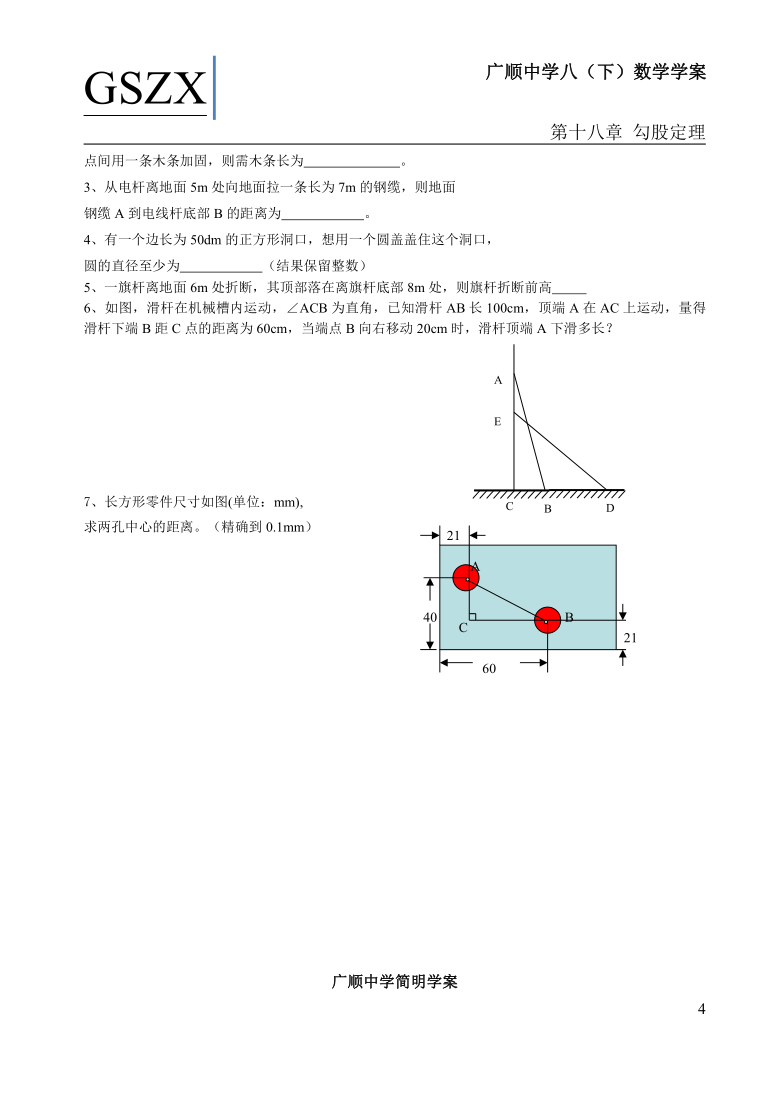
)6、如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长100cm,顶端A在AC上运动,量得滑杆下端B距C点的距离为60cm,当端点B向右移动20cm时,滑杆顶端A下滑多长?
7、长方形零件尺寸如图(单位:mm),
(
21
40
21
60
A
B
C
)求两孔中心的距离。(精确到0.1mm)
广顺中学简明学案
学科:数学 设计人: 时间:2009.4 班级: 姓名:
18.1 勾股定理(3)
【课时目标】1、掌握勾股定理,能运用勾股定理在数轴上画出表示无理数的点,进一步领会数形结合的思想.
2、通过学生实践操作,培养学生的探究能力、画图能力和解决问题的能力.
【重点难点】重点难点:运用勾股定理解决数学和实际问题.
【学具】圆规、刻度尺
【问题引入】1、你能画出长为cm的线段吗?在小组内说说你的办法,和同伴一起确定切实可行的方案。
2、你能在数轴上找出表示的点吗?请作图说明。
3、在数轴上表示、、……的点又如何表示?
4、你能找到,,,…,在数轴上更简便的画法吗?
【经典例题】例1:用上述方法在数轴上作出表示的点,并补充完整课本76页的作图方法。
练习:课本第77页练习第l题.
【达标测试】1.在Rt△ABC中,∠C=90°,①若a=5,b=12,则c=______;
②若a=15,c=25,则b=_____; ③若c=61,b=60,则a=_____。
2.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ,面积为 。
3.等边三角形的边长为a,则其面积为 。
4.一个圆柱状的杯子,由内部测得其底面半径为4cm,高为6cm,现有一支11cm的吸管任意斜放于杯中,则吸管露出杯口至少________cm.
5.一轮船以16海里/时的速度从港口A出发向西北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东北方向航行,
离开港口3小时后,则两船相距_______海里.
6.如图,每个小正方形的边长是1,在图中画出一个
三角形,使三角形的三边长分别是,,。
7.在数轴上作出表示的点。
(
A
B
C
D
L
)【拔高拓展】8.如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
广顺中学简明学案
学科:数学 设计人: 时间:2009.4 班级: 姓名:
18.1 勾股定理的逆定理(2)
【课时目标】1、能运用勾股定理的逆定理解决简单的实际问题.
2、经历将实际问题转化为数学模型的过程,体会用勾股定理的逆定理解决实际问题的方法,发展学生的应用意识.
【重点难点】重点:运用勾股定理的逆定理解决实际问题.
难点:将实际问题转化成用勾股定理的逆定理解决的数学问题.
【温故知新】说说你对勾股定理及其逆定理的理解。
【问题引入】A、B、C三地两两距离如下图所示,A地在B地的正东方向,C地在B地的什么方向?
【经典例题】例2:“远航”号,“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里,如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
练习:课本第84页练习第3题、习题第3题.
补例:如下图所示是一尊雕塑的底座的正面,李叔叔想要检测正面的AD边和BC边是否垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想想办法完成任务吗?
(
C
B
D
A
)(2)李叔叔量得AD的的长是30厘米,AB的长是40厘米,BD的长是50厘米,AD边垂直于AB边吗?
(3)小明随身只有一个长度为20厘米的刻度尺,他能有
办法检验AD边是否垂直于AB边吗?BC边与AB边呢?
【达标测试】1.△ABC中,AB=13,BC=10,BC边上的中线AD=12,则AC=
2.如图,△ABC中,D是BC上的一点, 若AB=10,BD=6
AD=8,AC=17,则△ABC的面积为 。
3.已知△ABC,在下列条件:①
②∠A=∠B-∠C;③∠A:∠B:∠C=3:4:5;;;④(m、n为正整数,且m>n)中,使△ABC成为直角三角形的选法有( )
(
A
B
C
)A. 2种 B. 3种 C. 4种 D. 5种
4.如图,正方形小方格边长为1,则网格中的△ABC是 ( )
A.直角三角形B.锐角三角形C.钝角三角形D.以上答案都不对
5.小明向东走80m后,沿另一方向又走了60m,再沿第三方向走
100米回到原地。小明向东走80m后又向哪个方向走的?
6.如图,在正方形ABCD中,E是BC的中点,F为CD上一点,
且CF=CD.求证:△AEF是直角三角形.
【拔高拓展】7.小红和小军周日去郊外放风筝,风筝飞得又高又远,他俩很想知道风筝离地面到底有多高,你能帮助他们吗?
8.学习了勾股定理以后,有同学提出“在直角三角形中,三边满足,或许其他的三角形三边也有这样的关系”.让我们来做一个实验!
(1)画出任意的一个锐角三角形,如图2,量出各边的长度(精确到1毫米),较短的两条边长分别是______mm;______mm;较长的一条边长_______mm。
比较(填写“>”,“<”,或“=”);
(2)画出任意的一个钝角三角形,如图3,量出各边的长度(精确到1毫米),较短的两条边长分别是______mm;_______mm;较长的一条边长_______mm。
比较(填写“>”,“<”,或“=”);
(3)根据以上的操作和结果,对这位同学提出的问题, 你猜想的结论是:
。
(4)对你猜想与的两个关系,任选其中一个结论利用勾股定理证明。
4
GSZX
广顺中学简明学案
学科:数学 设计人: 时间:2009.4 班级: 姓名:
18.1 勾股定理(1)
【课时目标】1、了解勾股定理的由来,经历探索勾股定理的过程.
理解并能用不同的方法证明勾股定理,并能简单的运用.
提高推理意识与探究习惯,感受我国古代数学的伟大成就.
【重点难点】重点:勾股定理及及其应用.
难点:用面积法(拼图法)证明勾股定理.
【学具】4个全等的直角三角形
【情景引入】1.在我校实验楼与教学楼一楼之间的连廊上,有一幅如上图所示的图案,这也是2002年8月在北京举行的国际数学家大会的会标。这幅美丽而神秘的图案有什么秘密呢?
2.毕达哥拉斯在地板上的发现:
(
A
B
C
A
B
C
)
3、一般的直角三角形是否也具有这种关系呢?根据上图展开探究。
【归纳猜想】直角三角形三边长度之间存在什么关系?
(
a
b
c
)【证明】我们还是选择刚才认识的弦图来证明.请用准备好的4个直角三角形摆出弦图,并用两种方式求出弦图的面积(独立思考后可组内交流)。
【得出结论】
【小知识】了解勾股定理的由来及历史。
变式:
定理:
【达标测试】:1、求下图中字母所代表的数值。
(
144
x
)
(
225
400
A
)
(
81
)
直角三角形的斜边x长为
(
A
B
C
D
7
cm
F
E
)
正方形A面积为
2、如图:所有的四边形都是正方形,所有的三角
形都是直角三角形,其中最大的正方形边长为7cm,
则正方形A,B,C,D的面积之和为 cm2。
知识延伸:美丽的毕达哥拉斯树
【拔高拓展】古往今来、古今中外,目前世界上可以查到的证明勾股定理的方法有400余种。上至科学家、下至平民百姓,甚至美国第20届总统加菲尔德、清朝皇帝康熙都曾给出自己独特的证明。相关知识,请阅读课本的阅读与思考,并选择其中一种方法在下面写出详细的证明过程。
【课外探究】上网查阅或到学校图书室查阅资料,写一篇与勾股定理有关的小论文(不少于300字)
推荐网址:http//:www. Qq12.com/flash/3427.het
http//:www. /gougudingli
http//:www.mmit.stc.//ggdl.htm
广顺中学简明学案
学科:数学 设计人: 时间:2009.4 班级: 姓名:
18.1 勾股定理(2)
【课时目标】1.能运用勾股定理解决简单的实际问题.
2.通过本节学习,使学生真正体会数学来源于生活,又应用于生活,增强如何在日常生活中用数学知识解决问题的经验和感受.
【重点难点】重点难点:运用勾股定理及方程的思想解决简单的实际问题.
【温故知新】回忆勾股定理的内容:
【经典例题】例1:一个门框的尺寸如图所示.
(
B
C
1
m
2
m
A
)①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?(注意解题格式)
实际问题 数学模型
例2:长3米的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.
①求梯子的底端B距墙角O多少米?
②如果梯的顶端A沿墙下滑0.5米至C,请同学们猜一猜,底端也将滑动0.5米吗?
③算一算,底端滑动距离的近似值
(
O
B
D
C
C
A
)④你还能对例题提供的问题情景进行变式训练吗?
(结果均保留两位小数).
实际问题 数学模型
例3:某楼房三楼失火,消防队员赶来救火,了解到每层楼高3m,消防队员取来6.5 m长的云梯,如果梯子的底部离墙基的水平距离是2.5m,请问消防队员能否进入三楼灭火
(
6
10
) (
10
30
°
) (
15
8
)【达标测试】1、求出下列直角三角形中未知的边.
(
10
45
°
)
(
B
A
C
)2、一个高1.5米、宽0.8米的长方形门框,需要在其相对的顶
点间用一条木条加固,则需木条长为 。
3、从电杆离地面5m处向地面拉一条长为7m的钢缆,则地面
钢缆A到电线杆底部B的距离为 。
4、有一个边长为50dm的正方形洞口,想用一个圆盖盖住这个洞口,
圆的直径至少为 (结果保留整数)
5、一旗杆离地面6m处折断,其顶部落在离旗杆底部8m处,则旗杆折断前高
(
A
E
B
D
C
)6、如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长100cm,顶端A在AC上运动,量得滑杆下端B距C点的距离为60cm,当端点B向右移动20cm时,滑杆顶端A下滑多长?
7、长方形零件尺寸如图(单位:mm),
(
21
40
21
60
A
B
C
)求两孔中心的距离。(精确到0.1mm)
广顺中学简明学案
学科:数学 设计人: 时间:2009.4 班级: 姓名:
18.1 勾股定理(3)
【课时目标】1、掌握勾股定理,能运用勾股定理在数轴上画出表示无理数的点,进一步领会数形结合的思想.
2、通过学生实践操作,培养学生的探究能力、画图能力和解决问题的能力.
【重点难点】重点难点:运用勾股定理解决数学和实际问题.
【学具】圆规、刻度尺
【问题引入】1、你能画出长为cm的线段吗?在小组内说说你的办法,和同伴一起确定切实可行的方案。
2、你能在数轴上找出表示的点吗?请作图说明。
3、在数轴上表示、、……的点又如何表示?
4、你能找到,,,…,在数轴上更简便的画法吗?
【经典例题】例1:用上述方法在数轴上作出表示的点,并补充完整课本76页的作图方法。
练习:课本第77页练习第l题.
【达标测试】1.在Rt△ABC中,∠C=90°,①若a=5,b=12,则c=______;
②若a=15,c=25,则b=_____; ③若c=61,b=60,则a=_____。
2.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ,面积为 。
3.等边三角形的边长为a,则其面积为 。
4.一个圆柱状的杯子,由内部测得其底面半径为4cm,高为6cm,现有一支11cm的吸管任意斜放于杯中,则吸管露出杯口至少________cm.
5.一轮船以16海里/时的速度从港口A出发向西北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东北方向航行,
离开港口3小时后,则两船相距_______海里.
6.如图,每个小正方形的边长是1,在图中画出一个
三角形,使三角形的三边长分别是,,。
7.在数轴上作出表示的点。
(
A
B
C
D
L
)【拔高拓展】8.如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
广顺中学简明学案
学科:数学 设计人: 时间:2009.4 班级: 姓名:
18.1 勾股定理的逆定理(2)
【课时目标】1、能运用勾股定理的逆定理解决简单的实际问题.
2、经历将实际问题转化为数学模型的过程,体会用勾股定理的逆定理解决实际问题的方法,发展学生的应用意识.
【重点难点】重点:运用勾股定理的逆定理解决实际问题.
难点:将实际问题转化成用勾股定理的逆定理解决的数学问题.
【温故知新】说说你对勾股定理及其逆定理的理解。
【问题引入】A、B、C三地两两距离如下图所示,A地在B地的正东方向,C地在B地的什么方向?
【经典例题】例2:“远航”号,“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里,如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
练习:课本第84页练习第3题、习题第3题.
补例:如下图所示是一尊雕塑的底座的正面,李叔叔想要检测正面的AD边和BC边是否垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想想办法完成任务吗?
(
C
B
D
A
)(2)李叔叔量得AD的的长是30厘米,AB的长是40厘米,BD的长是50厘米,AD边垂直于AB边吗?
(3)小明随身只有一个长度为20厘米的刻度尺,他能有
办法检验AD边是否垂直于AB边吗?BC边与AB边呢?
【达标测试】1.△ABC中,AB=13,BC=10,BC边上的中线AD=12,则AC=
2.如图,△ABC中,D是BC上的一点, 若AB=10,BD=6
AD=8,AC=17,则△ABC的面积为 。
3.已知△ABC,在下列条件:①
②∠A=∠B-∠C;③∠A:∠B:∠C=3:4:5;;;④(m、n为正整数,且m>n)中,使△ABC成为直角三角形的选法有( )
(
A
B
C
)A. 2种 B. 3种 C. 4种 D. 5种
4.如图,正方形小方格边长为1,则网格中的△ABC是 ( )
A.直角三角形B.锐角三角形C.钝角三角形D.以上答案都不对
5.小明向东走80m后,沿另一方向又走了60m,再沿第三方向走
100米回到原地。小明向东走80m后又向哪个方向走的?
6.如图,在正方形ABCD中,E是BC的中点,F为CD上一点,
且CF=CD.求证:△AEF是直角三角形.
【拔高拓展】7.小红和小军周日去郊外放风筝,风筝飞得又高又远,他俩很想知道风筝离地面到底有多高,你能帮助他们吗?
8.学习了勾股定理以后,有同学提出“在直角三角形中,三边满足,或许其他的三角形三边也有这样的关系”.让我们来做一个实验!
(1)画出任意的一个锐角三角形,如图2,量出各边的长度(精确到1毫米),较短的两条边长分别是______mm;______mm;较长的一条边长_______mm。
比较(填写“>”,“<”,或“=”);
(2)画出任意的一个钝角三角形,如图3,量出各边的长度(精确到1毫米),较短的两条边长分别是______mm;_______mm;较长的一条边长_______mm。
比较(填写“>”,“<”,或“=”);
(3)根据以上的操作和结果,对这位同学提出的问题, 你猜想的结论是:
。
(4)对你猜想与的两个关系,任选其中一个结论利用勾股定理证明。
4
