华师大版七年级下册(新)6.2.1 等式的性质与方程的简单变形课件(53张PPT)
文档属性
| 名称 | 华师大版七年级下册(新)6.2.1 等式的性质与方程的简单变形课件(53张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-29 14:04:52 | ||
图片预览

文档简介
课件53张PPT。6.2 解一元一次方程
1.等式的性质与方程的简单变形
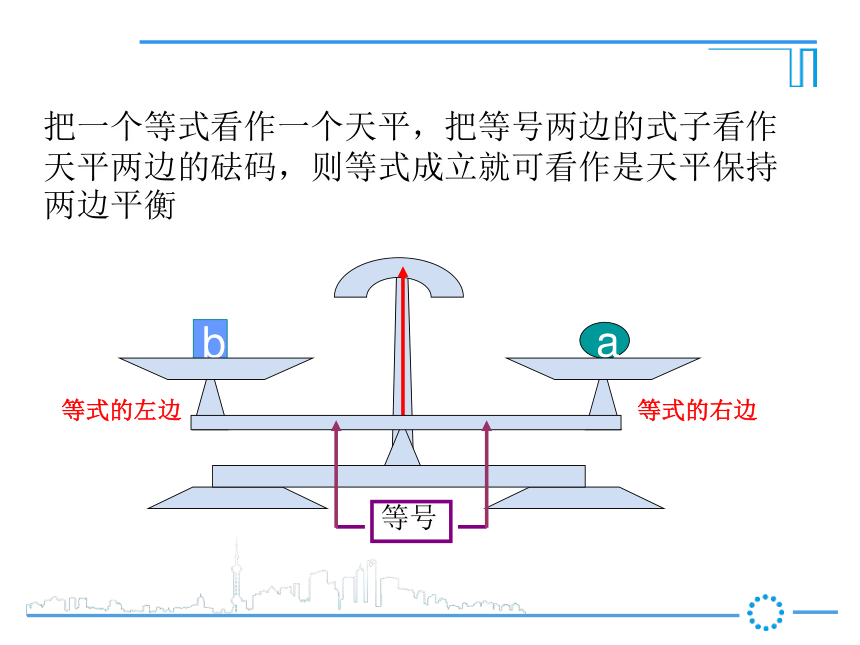
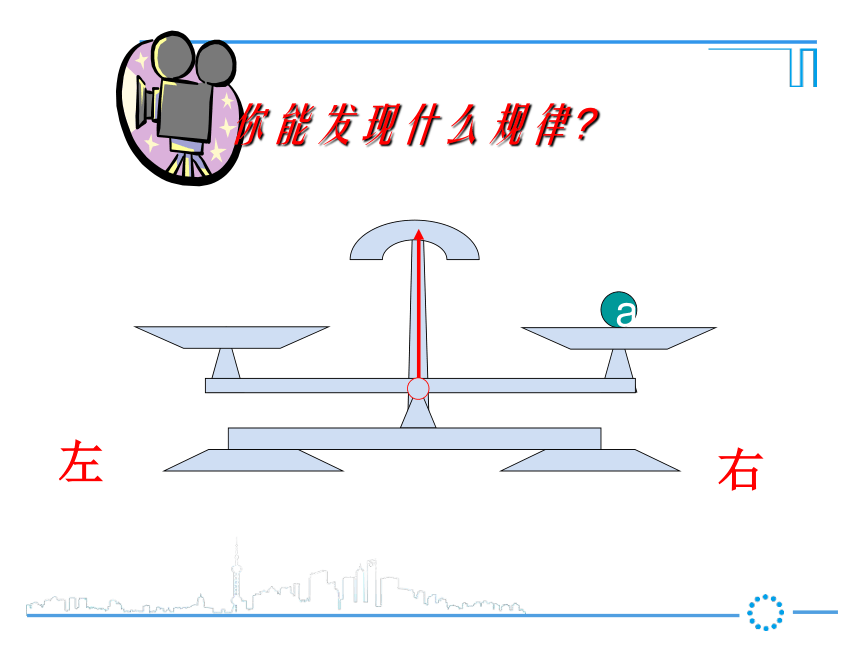
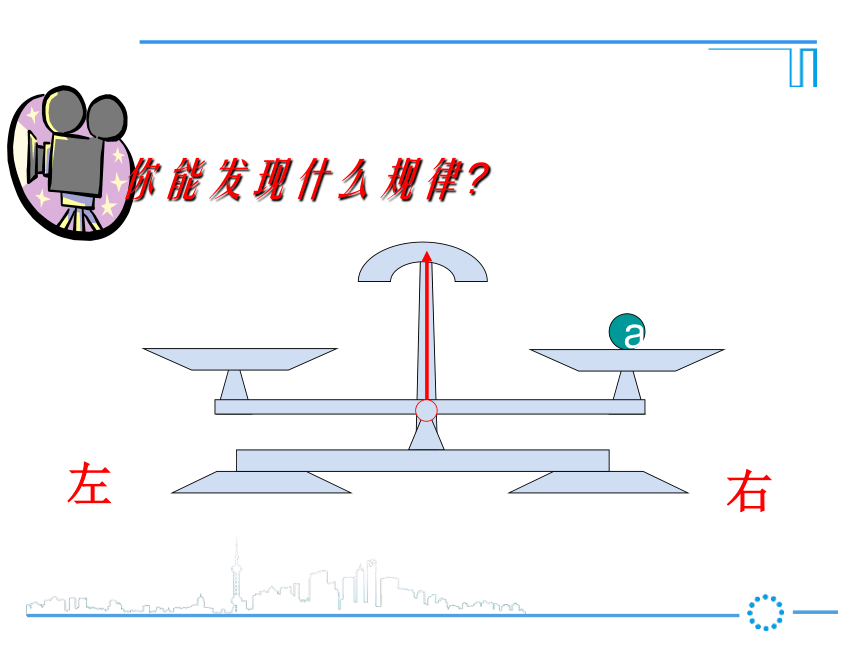
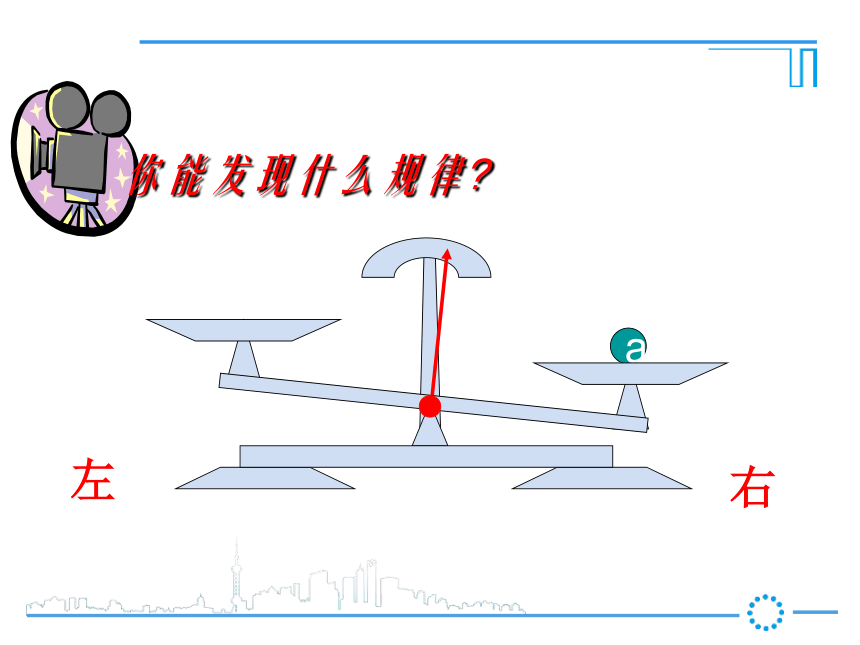
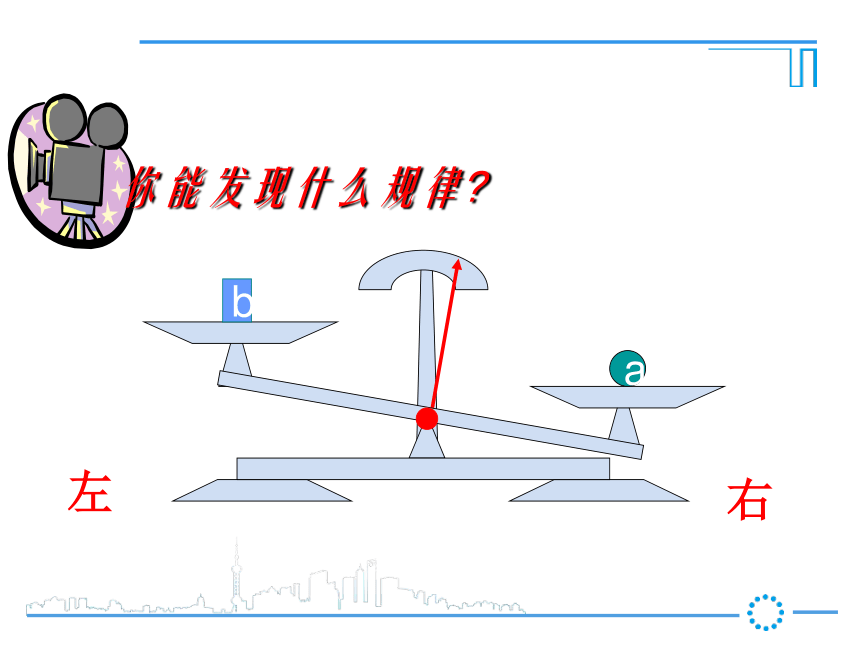
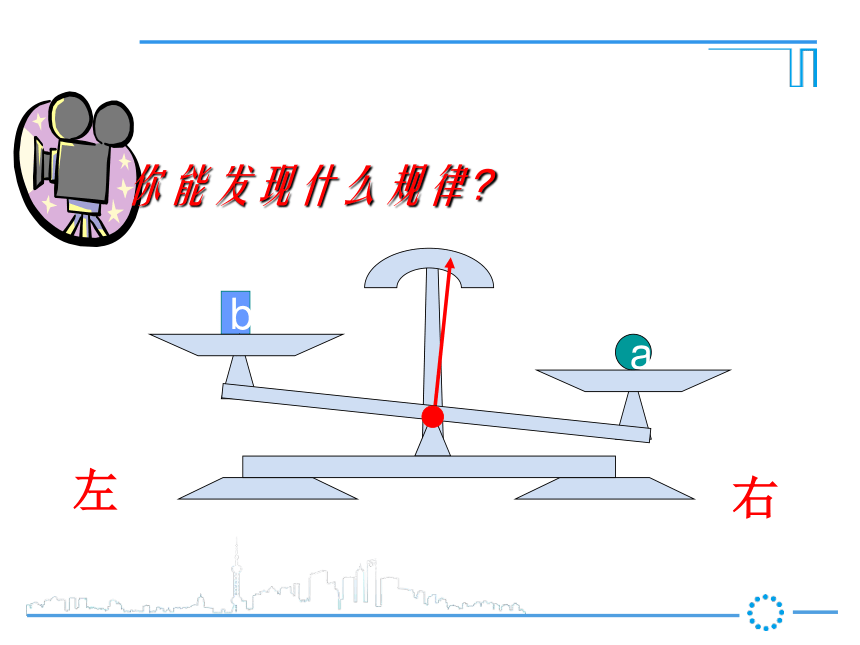
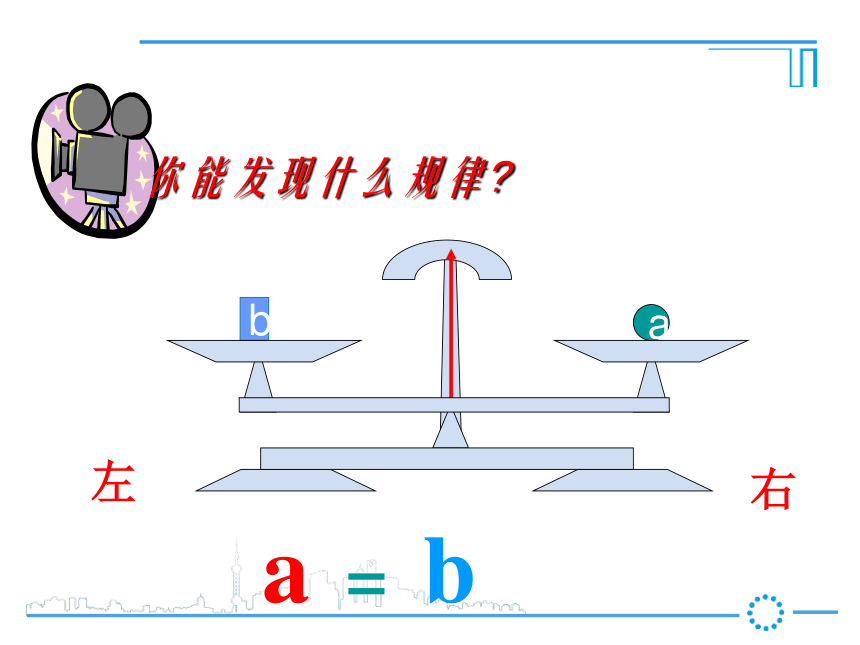
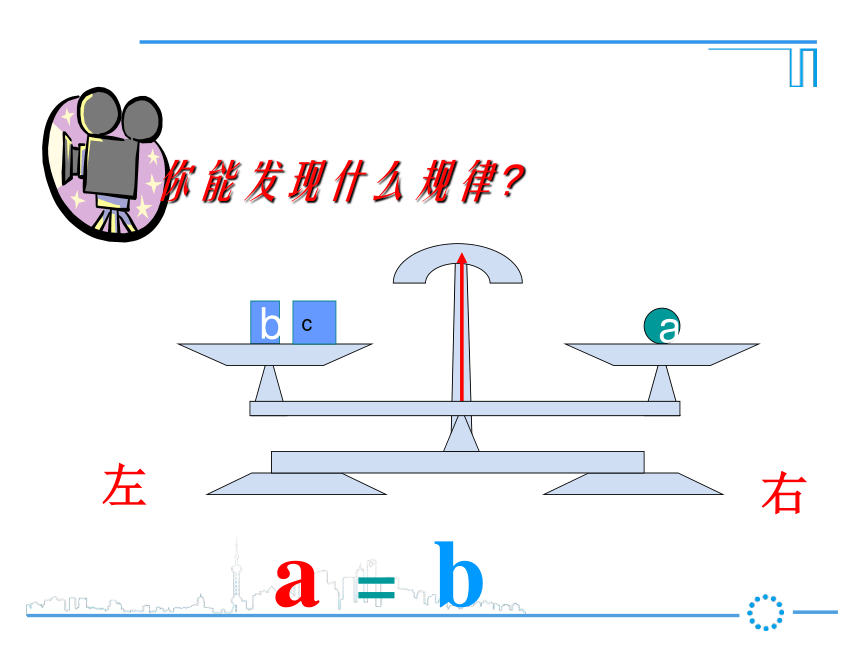
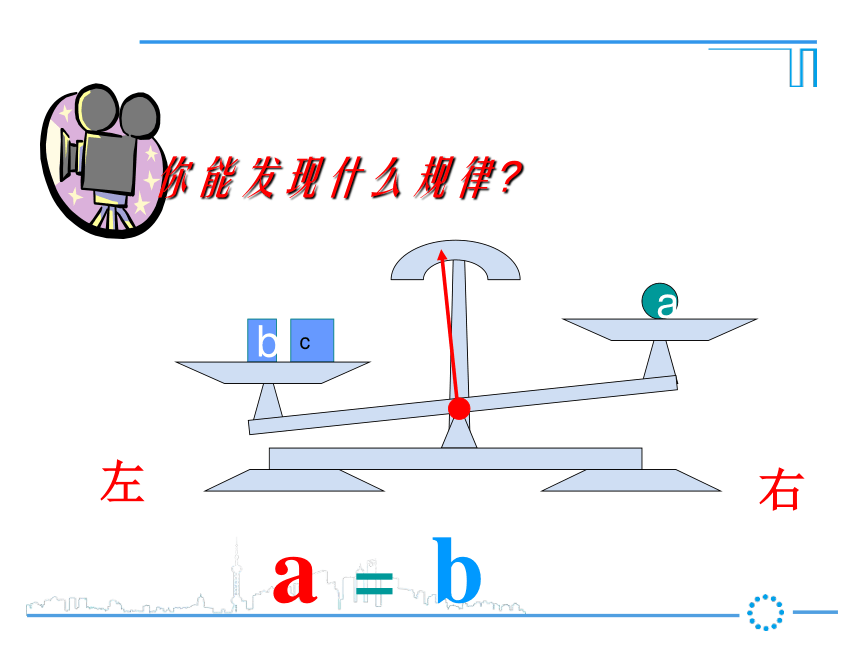
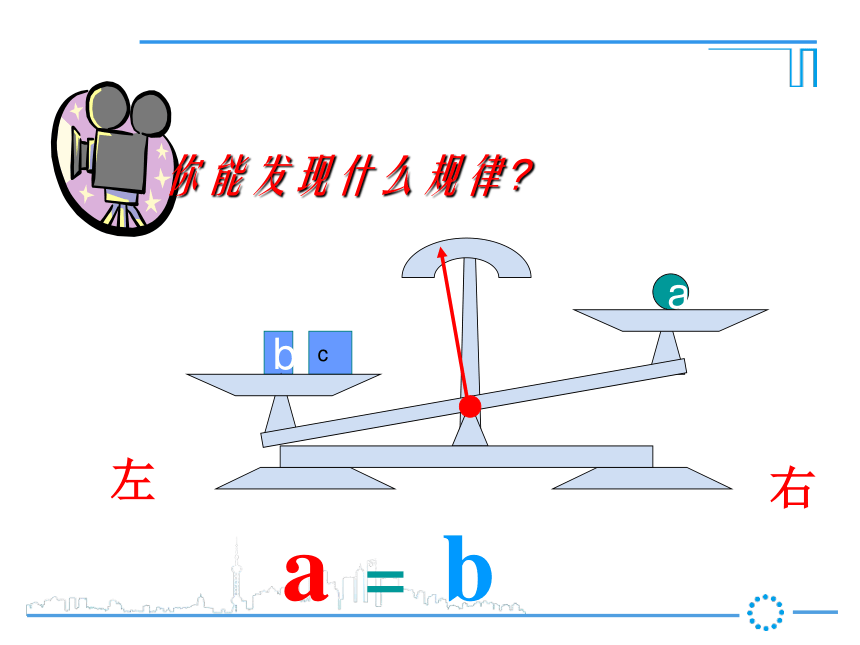
第1课时 等式的性质新课导入ba把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡等式的左边等式的右边a你能发现什么规律?右左a你能发现什么规律?右左a你能发现什么规律?右左ab你能发现什么规律?右左ba你能发现什么规律?右左ba你能发现什么规律?a = b右左ba你能发现什么规律?a = bc右左cba你能发现什么规律?a = b右左acb你能发现什么规律?a = b右左cbca你能发现什么规律?a = b右左cbca你能发现什么规律?a = ba+c b+c=右左cc你能发现什么规律?a = b右左c你能发现什么规律?a = b右左c你能发现什么规律?a = b右左你能发现什么规律?a = b右左你能发现什么规律?a = ba-c b-c=右左ba你能发现什么规律?a = b右左ba你能发现什么规律?a = b右左ab2a = 2bba你能发现什么规律?a = b右左bbaa3a = 3bba你能发现什么规律?a = b右左bbbbbbaaaaaaC个 C个ac = bcba你能发现什么规律?a = b右左 【等式性质2】【等式性质1】推进新课2一、我会应用 (3)、如果4x=-12y,那么x= , 根据 。 (4)、如果-0.2x=6,那么x= , 根据 。(2)、如果x-3=2,那么x-3+3= ,2×0.5等式性质2,在等式两边同时乘2等式性质1,在等式两边同加32+3-3y等式性质2,在等式两边同时除以4-30等式性质2,在等式两边同除-0.2或乘-51 、3、依据等式性质进行变形,用得不正确的是( )D D .(因为x可能等于0)(等量代换)(对称性)用等式的性质解方程解:(1)两边减7得(2)两边同时除以-5得(3)两边加5,得化简得:两边同乘-3,得 经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的 式:
x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项。两边同时减4,得【等式性质 2】【等式性质1】课后小结1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业6.2 解一元一次方程
1.等式的性质与方程的简单变形第2课时 方程的简单变形方程的变形规则1方程的两边都加上或减去同一个整式,方程的解不变。在运用这一规则进行变形时,只有在方程的两边都加上或减去同一个整式时,才能保证方程的解不变,否则,就会破坏原来的相等关系。例如:若在方程7-3x=4左边加上3,右边加上5,那么新方程7-3x+3=4+5的解就不是原方程的解了。新课导入例如下面的方程(两边都减去2)(两边都减去4x)关于“移项”概括将方程中的某些项改变符号后,从方程的一边移到另一边的变形叫做移项.注意:3、移项要变号!1、移动的项的位置发生了变化,同时符号也发生了改变。2、移项是从“=”的一边移动到另一边。推进新课例1解下列方程:解下列方程:方程的变形规则2方程的两边都乘以或除以同一个不为零的数,方程的解不变。在运用这一规则进行变形时,除了要注意方程两边都乘以或除以同一个数才能保证方程的解不变外,还必须注意方程两边不能都除以0,因为0不能作除数。(如何变形?)(两边都除以2)将未知数的系数化为1两边都除以-5,得例2解下列方程:利用方程的变形求方程 的解请说出每一步的变形( )( )移项将x的系数化为1解下列方程:(将未知数的系数化为1)(移项)例3:1.找出错误并改正在横线上。课堂演练2.解方程。3.解方程:44 x+64=328解:44 x=328-6444 x=26444 x 264=4444x=6.1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业劳动教养了身体,
学习教养了心灵。
—— 史密斯
1.等式的性质与方程的简单变形
第1课时 等式的性质新课导入ba把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡等式的左边等式的右边a你能发现什么规律?右左a你能发现什么规律?右左a你能发现什么规律?右左ab你能发现什么规律?右左ba你能发现什么规律?右左ba你能发现什么规律?a = b右左ba你能发现什么规律?a = bc右左cba你能发现什么规律?a = b右左acb你能发现什么规律?a = b右左cbca你能发现什么规律?a = b右左cbca你能发现什么规律?a = ba+c b+c=右左cc你能发现什么规律?a = b右左c你能发现什么规律?a = b右左c你能发现什么规律?a = b右左你能发现什么规律?a = b右左你能发现什么规律?a = ba-c b-c=右左ba你能发现什么规律?a = b右左ba你能发现什么规律?a = b右左ab2a = 2bba你能发现什么规律?a = b右左bbaa3a = 3bba你能发现什么规律?a = b右左bbbbbbaaaaaaC个 C个ac = bcba你能发现什么规律?a = b右左 【等式性质2】【等式性质1】推进新课2一、我会应用 (3)、如果4x=-12y,那么x= , 根据 。 (4)、如果-0.2x=6,那么x= , 根据 。(2)、如果x-3=2,那么x-3+3= ,2×0.5等式性质2,在等式两边同时乘2等式性质1,在等式两边同加32+3-3y等式性质2,在等式两边同时除以4-30等式性质2,在等式两边同除-0.2或乘-51 、3、依据等式性质进行变形,用得不正确的是( )D D .(因为x可能等于0)(等量代换)(对称性)用等式的性质解方程解:(1)两边减7得(2)两边同时除以-5得(3)两边加5,得化简得:两边同乘-3,得 经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的 式:
x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项。两边同时减4,得【等式性质 2】【等式性质1】课后小结1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业6.2 解一元一次方程
1.等式的性质与方程的简单变形第2课时 方程的简单变形方程的变形规则1方程的两边都加上或减去同一个整式,方程的解不变。在运用这一规则进行变形时,只有在方程的两边都加上或减去同一个整式时,才能保证方程的解不变,否则,就会破坏原来的相等关系。例如:若在方程7-3x=4左边加上3,右边加上5,那么新方程7-3x+3=4+5的解就不是原方程的解了。新课导入例如下面的方程(两边都减去2)(两边都减去4x)关于“移项”概括将方程中的某些项改变符号后,从方程的一边移到另一边的变形叫做移项.注意:3、移项要变号!1、移动的项的位置发生了变化,同时符号也发生了改变。2、移项是从“=”的一边移动到另一边。推进新课例1解下列方程:解下列方程:方程的变形规则2方程的两边都乘以或除以同一个不为零的数,方程的解不变。在运用这一规则进行变形时,除了要注意方程两边都乘以或除以同一个数才能保证方程的解不变外,还必须注意方程两边不能都除以0,因为0不能作除数。(如何变形?)(两边都除以2)将未知数的系数化为1两边都除以-5,得例2解下列方程:利用方程的变形求方程 的解请说出每一步的变形( )( )移项将x的系数化为1解下列方程:(将未知数的系数化为1)(移项)例3:1.找出错误并改正在横线上。课堂演练2.解方程。3.解方程:44 x+64=328解:44 x=328-6444 x=26444 x 264=4444x=6.1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业劳动教养了身体,
学习教养了心灵。
—— 史密斯
