华师大版七年级下册(新)6.2.2 解一元一次方程课件(43张PPT)
文档属性
| 名称 | 华师大版七年级下册(新)6.2.2 解一元一次方程课件(43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-29 00:00:00 | ||
图片预览









文档简介
课件43张PPT。2.解一元一次方程
第1课时 一元一次方程的解法(1) 1.等式的两边都加上或减去同一个数或式, 等式仍然成立.
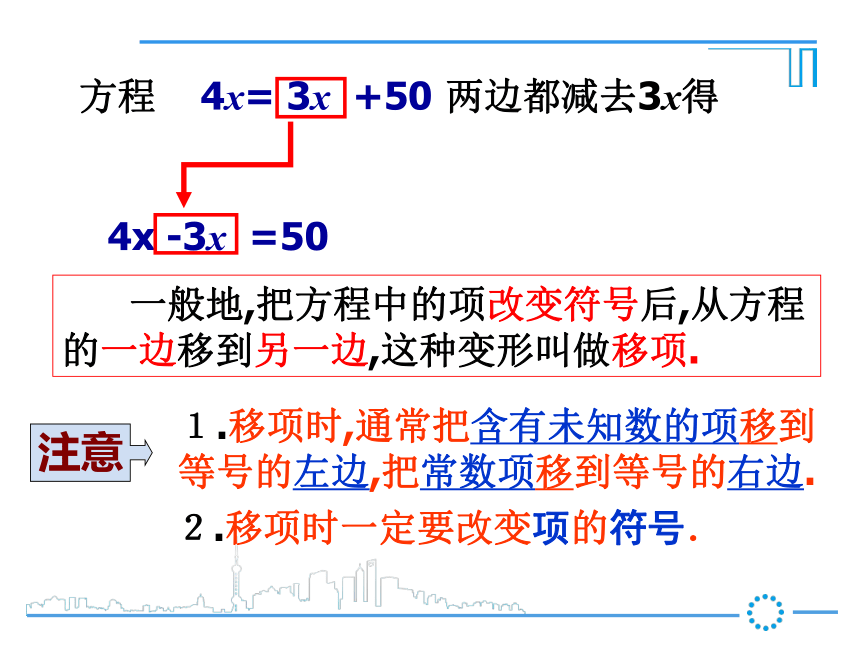
2.等式的两边都乘以或除以同一个的数或式(零不能作除数),等式仍然成立.复习导入xxx50xxx4x=3x+504x-3x=3x+50-3x 天平两边承载物体的质量相等时,天平保持平衡.x即 4x-3x=50方程 4x= 3x +50两边都减去3x得 4x -3x =50 一般地,把方程中的项改变符号后,从方程的一边移到另一边,这种变形叫做移项.注意1.移项时,通常把含有未知数的项移到等号的左边,把常数项移到等号的右边.2.移项时一定要改变项的符号. (1)6+x=8,移项得 x =8+6
(2)3x=8-2x,移项得3x+2x=-8
(3)5x-2=3x+7,移项得5x+3x=7+2错 x=8-6 错3x+2x=8错5x-3x=7+21、下列方程变形是否正确?注意:移项要变号!
不移不变号!推进新课将含未知数的项放在方程的左边,
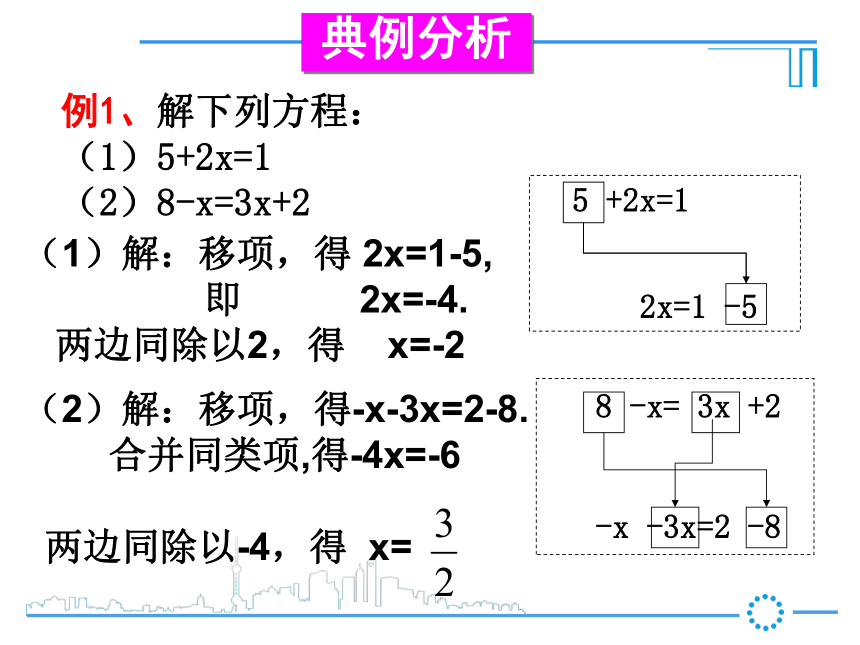
常数项放在方程的右边,对方程进行移项变形。做一做⑴ 3x-5=13⑵ 5x=3x⑶ 5=3x-1⑷ 3y-2=y-13x =13+55x-3x =0-3x =-1-53y-y =-1+2例1、解下列方程:
(1)5+2x=1
(2)8-x=3x+2(1)解:移项,得 2x=1-5,
即 2x=-4.
两边同除以2,得 x=-2(2)解:移项,得-x-3x=2-8.
合并同类项,得-4x=-6
两边同除以-4,得 x=
5 +2x=1
2x=1 -5 8 -x= 3x +2
-x -3x=2 -8典例分析例2解下列方程:
(1)3-(4x-3)=7,
(2)x- = 2(x+1)(结果精确到0.01)方程中有括号,怎么办?先去括号去括号法则:
括号前是”+“号,把括号和它前面的”+“号去掉,括号里各项都不变号;
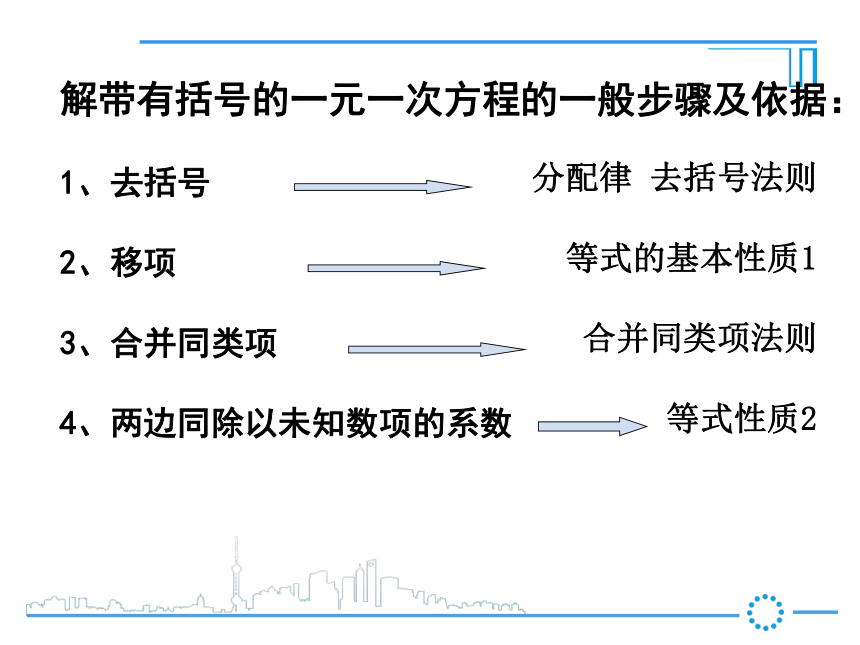
括号前是”-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号。你还记得去括号法则吗?解(1)去括号,得移项,得 合并同类项,得 两边同除以-4,得 解(2)去括号,得移项,得合并同类项得 即 ∴解带有括号的一元一次方程的一般步骤及依据:
1、去括号
2、移项
3、合并同类项
4、两边同除以未知数项的系数
分配律 去括号法则
等式的基本性质1
合并同类项法则
等式性质21、解下列方程,并口算检验:
(1)
(2)
(3)
(4)x=5 x=-1 x=2 x=1 随堂演练2、下列变形对吗?若不对,请说明理由,并改正:
解方程
去括号,得
移项,得
合并同类项,得
两边同除以-0.2得去括号变形错,有一项
没变号,改正如下:3、解下列方程:
(1)
(2)
(3)
(4)
x=0 x=3 比一比1.解方程:2.根据下列条件列方程,并求出方程的解:
一个数的2倍与3的和等于这个数与7的差.3.如果关于m的方程2m+b=m-1的解是-4,则b的值是( )
A. 3 B. 5 C . -3 D. -5A2、移项时要注意改变项符号。3、解一元一次方程的步骤:
(1)去括号;
(2)移项;
(3)合并同类项;
(4)两边同除以未知数项的系数。1、通过移项和合并同类项将简单方程变形,从而得到方程的解。课后小结1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业2.解一元一次方程
第2课时 一元一次方程的解法(2)例1、解方程:新课导入例2、 解下列方程解:方程的两边都乘以6,得即 2(3y+1)=7+y去括号,得 6y+2=7+y移项,得 6y-y=7-2合并同类项,得 5y=5两边同除以5,得 y=1推进新课例3 解下列方程: 解:方程的两边同乘以10,得 去括号,得移项,得合并同类项,得两边同除以2,得从前面的例题中我们看到,去分母、去括号、移项、合并同类项等都是方程变形的常用方法,但必须注意,移项和去分母的依据是等式的性质,而去括号和合并同类项的依据是代数式的运算法则。一般地,解一元一次方程的基本程序是: 想一想:解一元一次方程有哪些步骤?解一元一次方程的步骤是:(1)去分母。
(2)去括号。
(3)移项。
(4)合并同类项
(5)等式两边除以未知数前面的系数(未知数的系数化为1),化成X=a的形式。例4 解方程 分析:当分母中含有小数时,可以应用分数的基本性质把它们先化为整数,如 解:将原方程化为 去分母,得 去括号,得 移项,合并同类项,得 ∴ 解方程 解:去分母,得 去括号,得 移项,得 ∴ 2、下面方程的解法对吗?若不对,请改正 。不对在下式的空格内填入同一个适当的数,使等式成立:
12×46□=□64×21(46□和□64都是三位数)。
你可按以下步骤考虑:
1)设这个数为x,怎样把三位数46 x和x64转化为关于x的
代数式表示;
2)列出满足条件的关于x 的方程;
3)解这个方程,求出x的值;
4)对所求得的x值进行检验。探究活动
1)46x=460+x,
x64=100x+64;
2)4(460+x)=7(100x+64);
3)x=2;
4)∵462×12=5544
∴ 264 ×21=5544
∴462×12=264×21
通过这结课的学习,
你学到了什么?课后小结1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业2.解一元一次方程
第3课时 一元一次方程的实际应用新课导入在小学算术中,我们学习了用算术方法解决实际问题的有关知识,那么,一个实际问题能否用一元一次方程来解决,若能解决,怎样解?
用一元一次方程解应用题与用算术方法解应用题相比较它有什么优越性?新课导入某数的3倍减2等于它与4的和,求某数.解:(4+2)÷(3-1)=3
答:某数为3.如果设某数为x,根据题意,其数学表达式为
3x-2=x+4
此式恰是关于x的一元一次方程.
解之得x=3.上述两种解法,很明显算术方法不易思考,而应用设未知数,列出方程并通过解一元一次方程求得应用题的解有化难为易之感,这就是我们学习运用一元一次方程解应用题的目的之一.
我们知道方程是一个含有未知数的等式,而等式表示了一个相等的关系.对于任何一个应用题中所提供的条件应首先找出一个相等的关系,然后再将这个相等的关系表示成方程.1.如图,天平的两个盘内分别盛有51g、45g盐,问应该从盘A内拿出多少盐放到盘B内,才能使两者所盛盐的质量相等?推进新课分析:设应从盘A内拿出盐xg,可列出下表.
?
等量关系:盘A中现有的盐=盘B中现有的盐.解:设应从盘A内拿出盐x g,放到盘B内,则根据题意,得
51-x=45+x
解这个方程,得
x=3.
经检验,符合题意.
答:应从盘A内拿出盐3g放到盘B内.2.学校团委组织65名团员为学校建花坛搬砖.女同学每人搬6块,男同学每人搬8块,每人各搬4次,总共搬了1800块.问有多少名男同学?
分析:设男同学有x人,可列出下表.(完成下表)解:设男同学有x人,根据题意,得
32x+24(65-x)=1800
解这个方程得
x=30
经检验的,符合题意.
答:这些团员中有30名男同学.课后小结用一元一次方程解答实际问题,关键在于抓住问题中有关数量的相等关系,列出方程.求得方程的解后,经过检验,就可得到实际问题的解答.
这一过程也可以简单地表述为:其中分析和抽象的过程通常包括:
(1)弄清题意和其中的数量关系,用字母表示适当的未知数;
(2)找出能表示问题含义的一个主要的等量关系;
(3)对这个等量关系中涉及的量,列出所需的表达式,根据等量关系,得到方程.在设未知数和解答时,应注意量的单位要统一.1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业学习要有三心,
一信心,二决心,三恒心。
—— 陈景润
第1课时 一元一次方程的解法(1) 1.等式的两边都加上或减去同一个数或式, 等式仍然成立.
2.等式的两边都乘以或除以同一个的数或式(零不能作除数),等式仍然成立.复习导入xxx50xxx4x=3x+504x-3x=3x+50-3x 天平两边承载物体的质量相等时,天平保持平衡.x即 4x-3x=50方程 4x= 3x +50两边都减去3x得 4x -3x =50 一般地,把方程中的项改变符号后,从方程的一边移到另一边,这种变形叫做移项.注意1.移项时,通常把含有未知数的项移到等号的左边,把常数项移到等号的右边.2.移项时一定要改变项的符号. (1)6+x=8,移项得 x =8+6
(2)3x=8-2x,移项得3x+2x=-8
(3)5x-2=3x+7,移项得5x+3x=7+2错 x=8-6 错3x+2x=8错5x-3x=7+21、下列方程变形是否正确?注意:移项要变号!
不移不变号!推进新课将含未知数的项放在方程的左边,
常数项放在方程的右边,对方程进行移项变形。做一做⑴ 3x-5=13⑵ 5x=3x⑶ 5=3x-1⑷ 3y-2=y-13x =13+55x-3x =0-3x =-1-53y-y =-1+2例1、解下列方程:
(1)5+2x=1
(2)8-x=3x+2(1)解:移项,得 2x=1-5,
即 2x=-4.
两边同除以2,得 x=-2(2)解:移项,得-x-3x=2-8.
合并同类项,得-4x=-6
两边同除以-4,得 x=
5 +2x=1
2x=1 -5 8 -x= 3x +2
-x -3x=2 -8典例分析例2解下列方程:
(1)3-(4x-3)=7,
(2)x- = 2(x+1)(结果精确到0.01)方程中有括号,怎么办?先去括号去括号法则:
括号前是”+“号,把括号和它前面的”+“号去掉,括号里各项都不变号;
括号前是”-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号。你还记得去括号法则吗?解(1)去括号,得移项,得 合并同类项,得 两边同除以-4,得 解(2)去括号,得移项,得合并同类项得 即 ∴解带有括号的一元一次方程的一般步骤及依据:
1、去括号
2、移项
3、合并同类项
4、两边同除以未知数项的系数
分配律 去括号法则
等式的基本性质1
合并同类项法则
等式性质21、解下列方程,并口算检验:
(1)
(2)
(3)
(4)x=5 x=-1 x=2 x=1 随堂演练2、下列变形对吗?若不对,请说明理由,并改正:
解方程
去括号,得
移项,得
合并同类项,得
两边同除以-0.2得去括号变形错,有一项
没变号,改正如下:3、解下列方程:
(1)
(2)
(3)
(4)
x=0 x=3 比一比1.解方程:2.根据下列条件列方程,并求出方程的解:
一个数的2倍与3的和等于这个数与7的差.3.如果关于m的方程2m+b=m-1的解是-4,则b的值是( )
A. 3 B. 5 C . -3 D. -5A2、移项时要注意改变项符号。3、解一元一次方程的步骤:
(1)去括号;
(2)移项;
(3)合并同类项;
(4)两边同除以未知数项的系数。1、通过移项和合并同类项将简单方程变形,从而得到方程的解。课后小结1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业2.解一元一次方程
第2课时 一元一次方程的解法(2)例1、解方程:新课导入例2、 解下列方程解:方程的两边都乘以6,得即 2(3y+1)=7+y去括号,得 6y+2=7+y移项,得 6y-y=7-2合并同类项,得 5y=5两边同除以5,得 y=1推进新课例3 解下列方程: 解:方程的两边同乘以10,得 去括号,得移项,得合并同类项,得两边同除以2,得从前面的例题中我们看到,去分母、去括号、移项、合并同类项等都是方程变形的常用方法,但必须注意,移项和去分母的依据是等式的性质,而去括号和合并同类项的依据是代数式的运算法则。一般地,解一元一次方程的基本程序是: 想一想:解一元一次方程有哪些步骤?解一元一次方程的步骤是:(1)去分母。
(2)去括号。
(3)移项。
(4)合并同类项
(5)等式两边除以未知数前面的系数(未知数的系数化为1),化成X=a的形式。例4 解方程 分析:当分母中含有小数时,可以应用分数的基本性质把它们先化为整数,如 解:将原方程化为 去分母,得 去括号,得 移项,合并同类项,得 ∴ 解方程 解:去分母,得 去括号,得 移项,得 ∴ 2、下面方程的解法对吗?若不对,请改正 。不对在下式的空格内填入同一个适当的数,使等式成立:
12×46□=□64×21(46□和□64都是三位数)。
你可按以下步骤考虑:
1)设这个数为x,怎样把三位数46 x和x64转化为关于x的
代数式表示;
2)列出满足条件的关于x 的方程;
3)解这个方程,求出x的值;
4)对所求得的x值进行检验。探究活动
1)46x=460+x,
x64=100x+64;
2)4(460+x)=7(100x+64);
3)x=2;
4)∵462×12=5544
∴ 264 ×21=5544
∴462×12=264×21
通过这结课的学习,
你学到了什么?课后小结1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业2.解一元一次方程
第3课时 一元一次方程的实际应用新课导入在小学算术中,我们学习了用算术方法解决实际问题的有关知识,那么,一个实际问题能否用一元一次方程来解决,若能解决,怎样解?
用一元一次方程解应用题与用算术方法解应用题相比较它有什么优越性?新课导入某数的3倍减2等于它与4的和,求某数.解:(4+2)÷(3-1)=3
答:某数为3.如果设某数为x,根据题意,其数学表达式为
3x-2=x+4
此式恰是关于x的一元一次方程.
解之得x=3.上述两种解法,很明显算术方法不易思考,而应用设未知数,列出方程并通过解一元一次方程求得应用题的解有化难为易之感,这就是我们学习运用一元一次方程解应用题的目的之一.
我们知道方程是一个含有未知数的等式,而等式表示了一个相等的关系.对于任何一个应用题中所提供的条件应首先找出一个相等的关系,然后再将这个相等的关系表示成方程.1.如图,天平的两个盘内分别盛有51g、45g盐,问应该从盘A内拿出多少盐放到盘B内,才能使两者所盛盐的质量相等?推进新课分析:设应从盘A内拿出盐xg,可列出下表.
?
等量关系:盘A中现有的盐=盘B中现有的盐.解:设应从盘A内拿出盐x g,放到盘B内,则根据题意,得
51-x=45+x
解这个方程,得
x=3.
经检验,符合题意.
答:应从盘A内拿出盐3g放到盘B内.2.学校团委组织65名团员为学校建花坛搬砖.女同学每人搬6块,男同学每人搬8块,每人各搬4次,总共搬了1800块.问有多少名男同学?
分析:设男同学有x人,可列出下表.(完成下表)解:设男同学有x人,根据题意,得
32x+24(65-x)=1800
解这个方程得
x=30
经检验的,符合题意.
答:这些团员中有30名男同学.课后小结用一元一次方程解答实际问题,关键在于抓住问题中有关数量的相等关系,列出方程.求得方程的解后,经过检验,就可得到实际问题的解答.
这一过程也可以简单地表述为:其中分析和抽象的过程通常包括:
(1)弄清题意和其中的数量关系,用字母表示适当的未知数;
(2)找出能表示问题含义的一个主要的等量关系;
(3)对这个等量关系中涉及的量,列出所需的表达式,根据等量关系,得到方程.在设未知数和解答时,应注意量的单位要统一.1.从教材习题中选取,
2.完成练习册本课时的习题.课后作业学习要有三心,
一信心,二决心,三恒心。
—— 陈景润
