华师大八年级下册一次函数的性质
图片预览



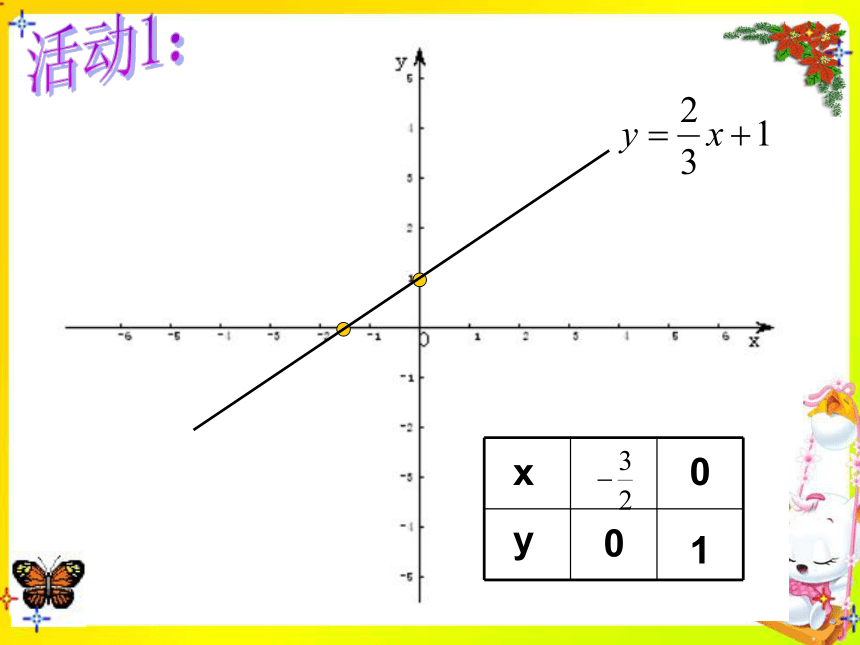



文档简介
课件21张PPT。欢迎各位老师光临指导2009年3月13日问题1: 小明暑假从石狮去深圳,在车上他发现汽车的平均速度是100千米/时。已知石狮到深圳全程约为700千米,小明想知道汽车从石狮驶出后,距深圳的路程s(千米)和汽车行驶的时间t(小时)有什么关系,以便根据时间估计自己和深圳的距离。S=700 – 100t(0≤ t ≤7)-6o-4246246-2-2-4xy一次函数的性质xy100活动1:一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
?
(2) 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____. 概括减小下降例1、已知一次函数y=(m+1)x-3
(1)当m取何值时,y随x的增大而增大?
(2)当 m取何值时,y随x的增大而减小?解:(1)当m+1>0即m>-1时,y随x的增大而增大;(2)当m+1<0即m<-1时,y随x的增大而减小。 1、下列一次函数中,y的值随x的增大而减小
的有________
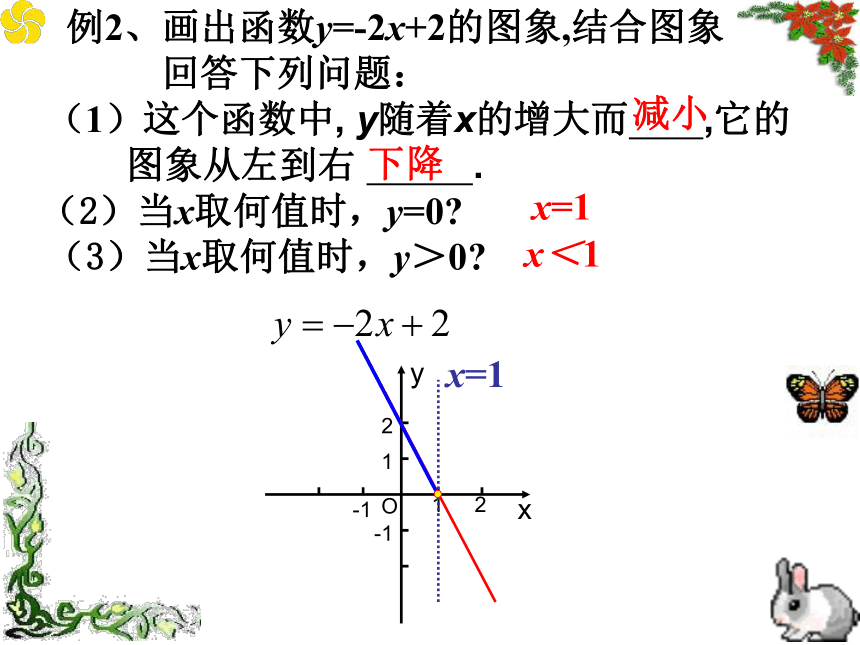
(1)、(3)试一试 例2、画出函数y=-2x+2的图象,结合图象
回答下列问题:
(1)这个函数中, y随着x的增大而 ,它的
图象从左到右 .
(2)当x取何值时,y=0?
(3)当x取何值时,y>0?x=1x<1减小下降x=1
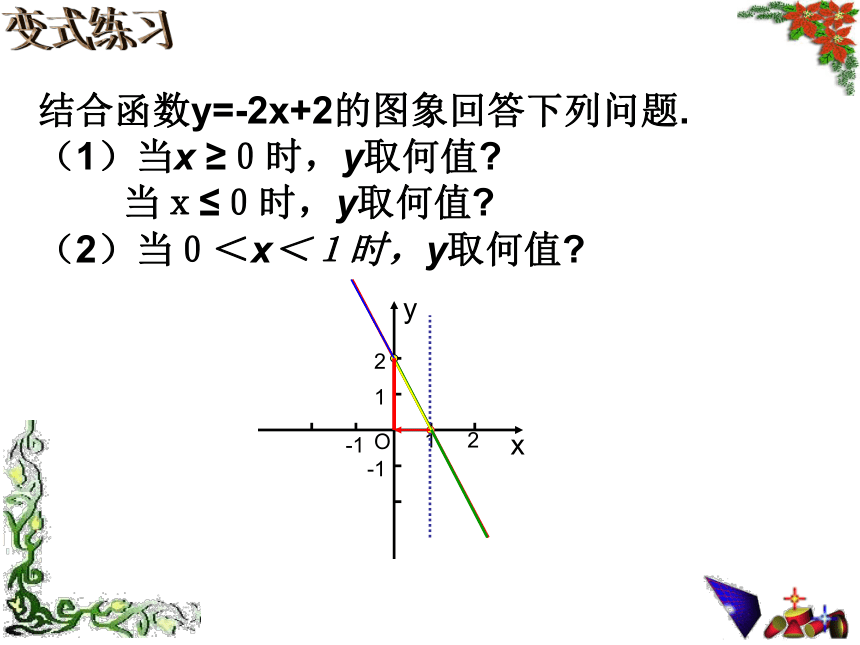
结合函数y=-2x+2的图象回答下列问题.
(1)当x ≥0时,y取何值?
当x≤0时,y取何值?(2)当0<x<1时,y取何值?变式练习实战演练1、已知一次函数y=(m-2)x+5,y随x的增大而减小,则m的取值范围为 。 2、已知点(2,m) 、(-3,n)都在直线 上,
试比较m、n的大小。m<2 所以函数y随x增大而增大。解:方法一: 把两点的坐标代入函数关系式当 x=2 时, m= ; 当 x= -3 时, n=
所以 m > n。方法二:因为 K=>0,由 2 > -3得 m > n。已知一次函数若函数y随x的增大而减小并且函数的图像经过二、三、四象限,求
M的取值范围?解:由题意得:1-2m﹤0,m-1﹤0得﹤m﹤13、一次函数y=x+2的图象如图所示,观察图象可知,
①当x 时,y=0;
②当x 时,y ≥ 2;实战演练= - 2≥0 4、如图,l1反映了某公司产品的销售收入与销售量的关系, l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:(1)当销售量为 时,销售收入等于销售成本;4吨(3)当销售量为6吨时,销售收入 销售成本;大于(2)当销售量为2吨时,销售收入 销售成本;小于(4)当销售量 时,该公司赢利(收入大于成本);
当销售量 时,该公司亏损(收入小于成本);大于4吨0≤x <4知识回顾 1、一次函数y=kx+b有下列性质:
(1)当k>0时,y随x的增大而 ,这时函数的图象从
左到右 ;
(2)当k<0时,y随x的增大而 ,这时函数的图象从
左到右 。 2、利用函数图象归纳函数的性质或解决简单的实际问题是我们经常使用的方法,是数形结合的具体体现.增大上升减小下降 经过本节课的学习,你有哪些收获?作业:练习卷“一次函数的性质” 已知一次函数y=kx+b的图象经过点(0,2), 且y随x的增大而减小,请写出一个符合条件的一次函数______。开放性试题谢谢指导!一次函数的性质 1.在y=kx+b中:经过_________的一条直线;
当k>0,y随x的增大而______;当k<0,y随x的增大而______.正比例函数的性质1.正比例函数y=kx的图象是经过_________的一条直线;2.在直线y=k1x+b1与直线y=k2x+b2中,
如果______________,那么这两条直线平行。2. 1)当 k >0,y=kx经过______象限
2)当 k <0,y=kx经过______象限.k1 = k2 , b1≠b2增大减小原点(0,0)一、三二、四3.y=kx+b(k≠0)所经过的象限:k>0,b>0→___ ___ ___k>0,b<0→___ ___ ___k<0,b>0→___ ___ ___ k<0,b<0→___ ___ ___一、三、二一、三、四一、二、四二、三、四小 结点(0,b)完成下表并画出函数(1) ;(2)y= -x + 2的图象,探究当x增大时,y的值如何变化?… -3 -2 -1 0 1 2 3 … -3 -2 -1 0 1 2 3 5 4 3 2 1 0 -1活动1:… -1 1 3 …
?
(1) 当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
?
(2) 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____. 概括减小下降例1、已知一次函数y=(m+1)x-3
(1)当m取何值时,y随x的增大而增大?
(2)当 m取何值时,y随x的增大而减小?解:(1)当m+1>0即m>-1时,y随x的增大而增大;(2)当m+1<0即m<-1时,y随x的增大而减小。 1、下列一次函数中,y的值随x的增大而减小
的有________
(1)、(3)试一试 例2、画出函数y=-2x+2的图象,结合图象
回答下列问题:
(1)这个函数中, y随着x的增大而 ,它的
图象从左到右 .
(2)当x取何值时,y=0?
(3)当x取何值时,y>0?x=1x<1减小下降x=1
结合函数y=-2x+2的图象回答下列问题.
(1)当x ≥0时,y取何值?
当x≤0时,y取何值?(2)当0<x<1时,y取何值?变式练习实战演练1、已知一次函数y=(m-2)x+5,y随x的增大而减小,则m的取值范围为 。 2、已知点(2,m) 、(-3,n)都在直线 上,
试比较m、n的大小。m<2 所以函数y随x增大而增大。解:方法一: 把两点的坐标代入函数关系式当 x=2 时, m= ; 当 x= -3 时, n=
所以 m > n。方法二:因为 K=>0,由 2 > -3得 m > n。已知一次函数若函数y随x的增大而减小并且函数的图像经过二、三、四象限,求
M的取值范围?解:由题意得:1-2m﹤0,m-1﹤0得﹤m﹤13、一次函数y=x+2的图象如图所示,观察图象可知,
①当x 时,y=0;
②当x 时,y ≥ 2;实战演练= - 2≥0 4、如图,l1反映了某公司产品的销售收入与销售量的关系, l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:(1)当销售量为 时,销售收入等于销售成本;4吨(3)当销售量为6吨时,销售收入 销售成本;大于(2)当销售量为2吨时,销售收入 销售成本;小于(4)当销售量 时,该公司赢利(收入大于成本);
当销售量 时,该公司亏损(收入小于成本);大于4吨0≤x <4知识回顾 1、一次函数y=kx+b有下列性质:
(1)当k>0时,y随x的增大而 ,这时函数的图象从
左到右 ;
(2)当k<0时,y随x的增大而 ,这时函数的图象从
左到右 。 2、利用函数图象归纳函数的性质或解决简单的实际问题是我们经常使用的方法,是数形结合的具体体现.增大上升减小下降 经过本节课的学习,你有哪些收获?作业:练习卷“一次函数的性质” 已知一次函数y=kx+b的图象经过点(0,2), 且y随x的增大而减小,请写出一个符合条件的一次函数______。开放性试题谢谢指导!一次函数的性质 1.在y=kx+b中:经过_________的一条直线;
当k>0,y随x的增大而______;当k<0,y随x的增大而______.正比例函数的性质1.正比例函数y=kx的图象是经过_________的一条直线;2.在直线y=k1x+b1与直线y=k2x+b2中,
如果______________,那么这两条直线平行。2. 1)当 k >0,y=kx经过______象限
2)当 k <0,y=kx经过______象限.k1 = k2 , b1≠b2增大减小原点(0,0)一、三二、四3.y=kx+b(k≠0)所经过的象限:k>0,b>0→___ ___ ___k>0,b<0→___ ___ ___k<0,b>0→___ ___ ___ k<0,b<0→___ ___ ___一、三、二一、三、四一、二、四二、三、四小 结点(0,b)完成下表并画出函数(1) ;(2)y= -x + 2的图象,探究当x增大时,y的值如何变化?… -3 -2 -1 0 1 2 3 … -3 -2 -1 0 1 2 3 5 4 3 2 1 0 -1活动1:… -1 1 3 …
