湘教版八年级下册(新)第1章《1.2 直角三角形的性质和判定(II)》同步练习
文档属性
| 名称 | 湘教版八年级下册(新)第1章《1.2 直角三角形的性质和判定(II)》同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 196.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-30 00:00:00 | ||
图片预览


文档简介
1.2 直角三角形的性质和判定(Ⅱ)
第1课时 勾股定理
要点感知 直角三角形的性质定理(勾股定理):直角三角形两直角边a、b的平方和等于__________的平方.即a2+b2=c2.
预习练习 △ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边.
(1)若a=5,b=12,则c=__________;
(2)若c=41,a=40,则b=__________.
知识点 勾股定理
1.在△ABC中,∠C=90°,如果AB=10,BC∶AC=3∶4,那么BC=( )
A.6 B.8 C.10 D.以上都不对
2.一个直角三角形的三边长为三个连续偶数,则它的斜边长为( )
A.6 B.8 C.10 D.12
3.已知一个三角形三个内角的比是1∶2∶1,则它的三条边的比是( )
A.1∶∶1 B.1∶2∶1 C.1∶∶ D.1∶4∶1
4.如图,长方形OABC的边OA长为2, ( http: / / www.21cnjy.com )边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A.2.5 B.2 C. D.
( http: / / www.21cnjy.com )
5.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重合.若BC=5,CD=3,则BD的长为( )
A.1 B.2 C.3 D.4
( http: / / www.21cnjy.com )
6.在△ABC中,∠C=90°,AB=7,BC=5,则边AC的长为__________.
7.等腰△ABC中,AB=AC=10 cm,BC=12 cm,则BC边上的高是__________cm.
8.一个直角三角形的斜边长比直角长边大2,另一直角边长为6,则斜边长为__________.
9.如图,△ABC中,AB=AC=20,BC=32,D是BC上一点,AD=15,且AD⊥AC,求BD长.
( http: / / www.21cnjy.com )
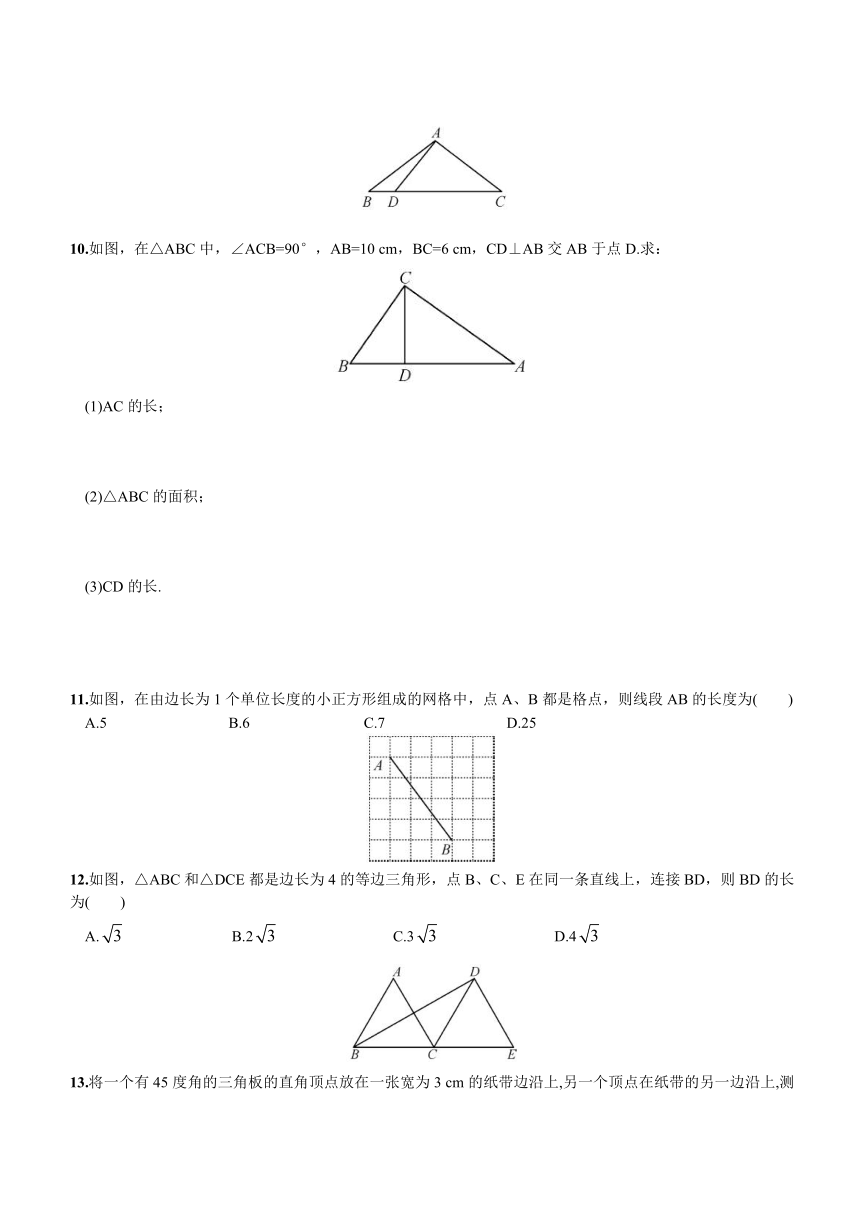
10.如图,在△ABC中,∠ACB=90°,AB=10 cm,BC=6 cm,CD⊥AB交AB于点D.求:
( http: / / www.21cnjy.com )
(1)AC的长;
(2)△ABC的面积;
(3)CD的长.
11.如图,在由边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
( http: / / www.21cnjy.com )
12.如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为( )
A. B.2 C.3 D.4
( http: / / www.21cnjy.com )
13.将一个有45度角的三角板的直角顶点放 ( http: / / www.21cnjy.com )在一张宽为3 cm的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30度角,如图,则三角板的最大边的长为( )
A.3 cm B.6 cm C.3 cm D.6 cm
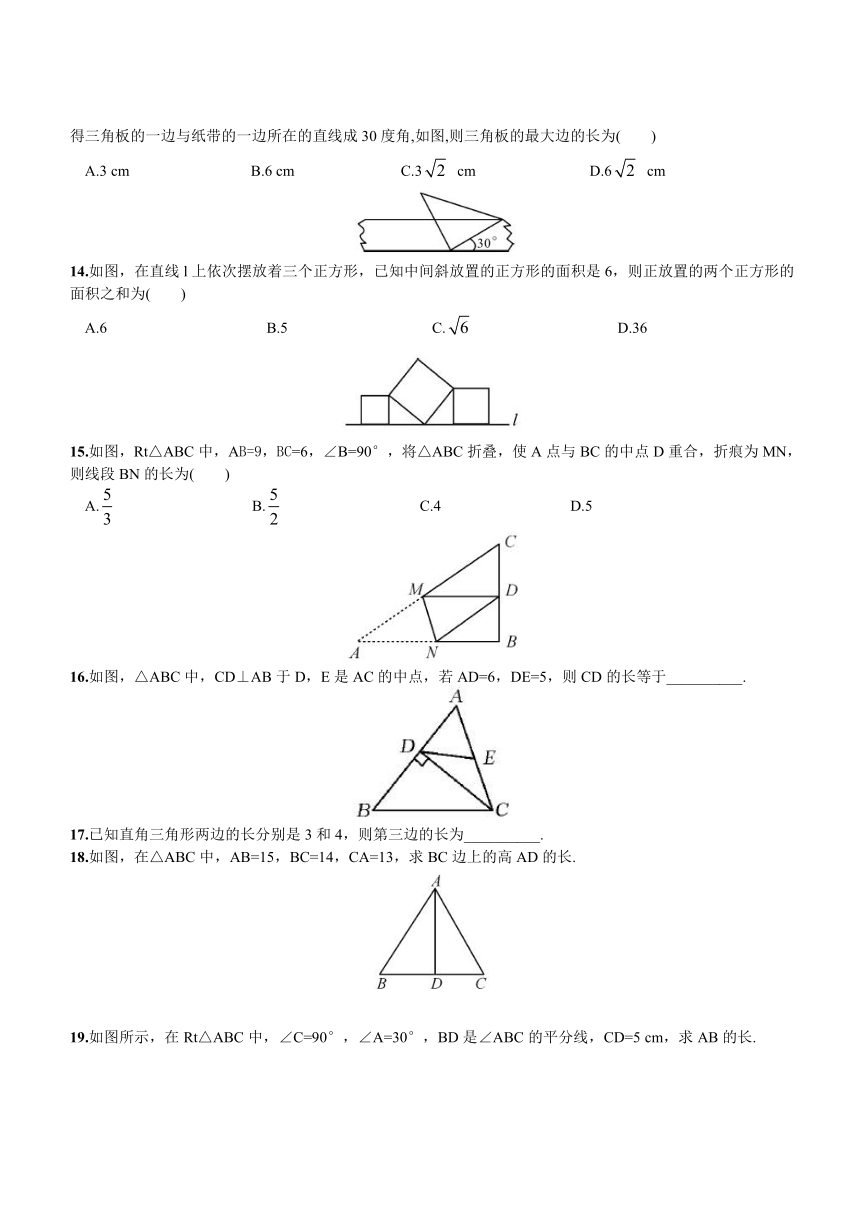
14.如图,在直线l上依次摆放着三个正方形,已知中间斜放置的正方形的面积是6,则正放置的两个正方形的面积之和为( )
A.6 B.5 C. D.36
( http: / / www.21cnjy.com )
15.如图,Rt△ABC中,AB=9,BC ( http: / / www.21cnjy.com )=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A. B. C.4 D.5
( http: / / www.21cnjy.com )
16.如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=6,DE=5,则CD的长等于__________.
( http: / / www.21cnjy.com )
17.已知直角三角形两边的长分别是3和4,则第三边的长为__________.
18.如图,在△ABC中,AB=15,BC=14,CA=13,求BC边上的高AD的长.
( http: / / www.21cnjy.com )
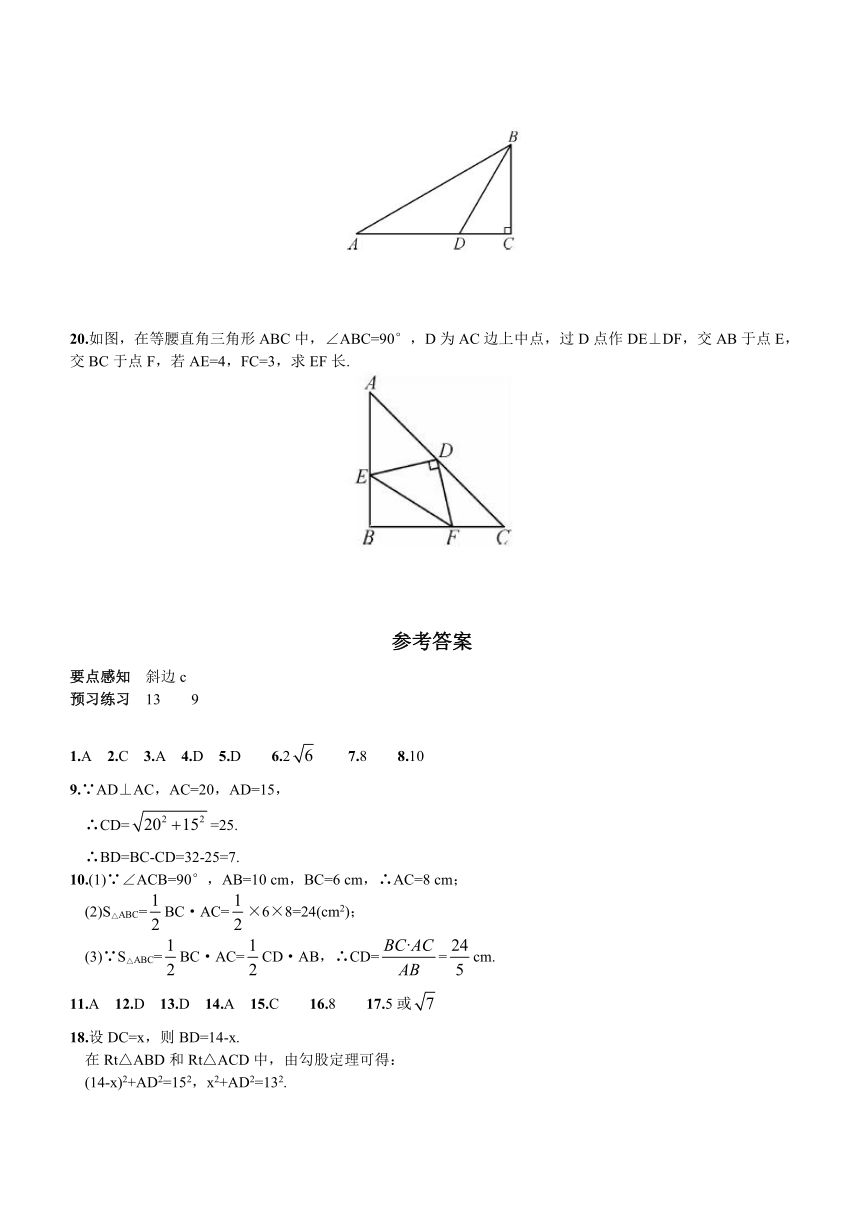
19.如图所示,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5 cm,求AB的长.
( http: / / www.21cnjy.com )
20.如图,在等腰直角三角 ( http: / / www.21cnjy.com )形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于点E,交BC于点F,若AE=4,FC=3,求EF长.
( http: / / www.21cnjy.com )
参考答案
要点感知 斜边c
预习练习 13 9
1.A 2.C 3.A 4.D 5.D 6.2 7.8 8.10
9.∵AD⊥AC,AC=20,AD=15,
∴CD==25.
∴BD=BC-CD=32-25=7.
10.(1)∵∠ACB=90°,AB=10 cm,BC=6 cm,∴AC=8 cm;
(2)S△ABC=BC·AC=×6×8=24(cm2);
(3)∵S△ABC=BC·AC=CD·AB,∴CD==cm.
11.A 12.D 13.D 14.A 15.C 16.8 17.5或
18.设DC=x,则BD=14-x.
在Rt△ABD和Rt△ACD中,由勾股定理可得:
(14-x)2+AD2=152,x2+AD2=132.
两式相减得(14-x)2-x2=56.解得x=5.
在Rt△ACD中,由勾股定理得AD=12.
19.∵在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,
∴∠ABD=∠CBD=30°.
∴AD=DB.
又∵Rt△CBD中,CD=5 cm,
∴BD=10 cm.
∴BC===5(cm).
∴AB=2BC=10 cm.
20.连接BD,
∵等腰直角三角形ABC中,D为AC边上中点,
∴BD⊥AC,BD=CD=AD,∠ABD=∠C=45°.
∵DE⊥DF,
∴∠FDC=∠EDB.
在△EDB与△FDC中,
∴△EDB≌△FDC.
∴BE=FC=3.
∴AB=7,则BC=7.
∴BF=4.
在Rt△EBF中,EF2=BE2+BF2=32+42,
∴EF=5.
第2课时 勾股定理的实际应用
要点感知 应用勾股定理解决实际问题时 ( http: / / www.21cnjy.com ),应先根据题意画出几何图形,分析图形中各线段之间的数量关系,正确运用勾股定理求解.求边长时,一般有两种情况:一是直接运用勾股定理通过计算求解,二是借助勾股定理列方程求解.
预习练习 (2014·东营)如图 ( http: / / www.21cnjy.com ),有两棵树,一棵高12米,另一棵高6米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行__________米.
( http: / / www.21cnjy.com )
知识点1 直接利用勾股定理
1.一座建筑物发生了火灾,消防车到 ( http: / / www.21cnjy.com )达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以到达该建筑物的最大高度是( )
A.12米 B.13米 C.14米 D.15米
2.如图,一个高1.5米,宽3.6米的大门,需要在相对的顶点间用一条木板加固,则这条木板的长度是( )
A.3.8米 B.3.9米 C.4米 D.4.4米
( http: / / www.21cnjy.com )
3.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为( )
A.米 B.米 C.(+1)米 D.3米
( http: / / www.21cnjy.com )
4.假期中,小华与同学去玩探宝游戏,按照探宝 ( http: / / www.21cnjy.com )图,他们从门口A处出发先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东拐,仅走了1千米,就找到了宝藏,则门口A到藏宝点B的直线距离是( )
A.20千米 B.14千米 C.11千米 D.10千米
( http: / / www.21cnjy.com )
5.如图,某人欲横渡一条河 ( http: / / www.21cnjy.com ),由于水流的影响,实际上岸地点C偏离欲到达点B200 m,结果他在水中实际游了520 m,该河流的宽度为__________m.
( http: / / www.21cnjy.com )
知识点2 利用勾股定理列方程求解
6.小明准备测量一段河水 ( http: / / www.21cnjy.com )的深度,他把一根竹竿竖直插到离岸边1.5 m远的水底,竹竿高出水面0.5 m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A.2 m B.2.5 m C.2.25 m D.3 m
7.在一次课外社会实践中,王强想知道学 ( http: / / www.21cnjy.com )校旗杆的高,但不能爬上旗杆也不能把绳子解下来,可是他发现旗杆上的绳子垂到地面上还多1 m,当他把绳子的下端拉开5 m后,发现下端刚好接触地面,则旗杆的高为( )
A.13 m B.12 m C.4 m D.10 m
8.如图所示,某风景名胜区为了方便游人参 ( http: / / www.21cnjy.com )观,计划从主峰A处架设一条缆车线路到另一山峰C处,若在A处测得∠EAC=30°,两山峰的底部BD相距900米,则缆车线路AC的长为__________米.
( http: / / www.21cnjy.com )
9.如图,在一棵树的10米高B处有两 ( http: / / www.21cnjy.com )只猴子,其中一只爬下树走向离树20米的池塘C,而另一只爬到树顶D后直扑池塘C,结果两只猴子经过的距离相等,问这棵树有多高?
( http: / / www.21cnjy.com )
10.为迎接新年的到来,同学们做了许多 ( http: / / www.21cnjy.com )拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为( )
A.0.7米 B.0.8米 C.0.9米 D.1.0米
11.如图,沿AC方向开山修路,为加快 ( http: / / www.21cnjy.com )施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=120°,BD=210 m,∠D=30°,要正好能使A、C、E成一直线,那么E、D两点的距离等于( )
A.105 m B.210 m C.70 m D.105 m
( http: / / www.21cnjy.com )
12.在长、宽、高分别为12 cm、4 cm、3 cm的木箱中,放一根木棒,能放进去的木棒的最大长度为( )
A.5 cm B.12 cm C.13 cm D. cm
13.如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离为__________mm.
( http: / / www.21cnjy.com )
14.如图,一辆小汽车在一条东西走向的城市 ( http: / / www.21cnjy.com )公路上直道行驶,某一时刻刚好行驶到路边的车速检测仪的正前方30 m处,过了2 s后,测得小汽车与车速检测仪的距离为50 m,问这辆小汽车是否超速了?(中华人民共和国交通管理条例规定:小汽车在城市公路上行驶时的速度不得超过70 km/h)
( http: / / www.21cnjy.com )
15.为了丰富居民的业余生活 ( http: / / www.21cnjy.com ),某社区要在如图所示AB所在的直线上建一图书室,本社区有两所学校,所在的位置在点C和点D处,CA⊥AB于点A,DB⊥AB于点B,已知AB=25 km,CA=15 km,DB=10 km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
( http: / / www.21cnjy.com )
16.两条公路OM、ON相交成30度角 ( http: / / www.21cnjy.com ),在公路OM上,距O点80米的A处有一所小学,当拖拉机沿公路ON方向行驶时,路两旁50米以内会受到噪音的影响,已知拖拉机的速度为18千米/时,那么拖拉机沿ON方向行驶时,是否会给小学带来噪声影响?若受影响,计算影响的时间.
( http: / / www.21cnjy.com )
参考答案
预习练习 10
1.A 2.B 3.C 4.D 5.480 6.A 7.B 8.600
9.设BD=x米,则AD=(10+x)米,CD=(30-x)米,根据题意得
(30-x)2-(x+10)2=202.解得x=5.
即树的高度是10+5=15(米).
10.A 11.A 12.C 13.150
14.小汽车超速了.
理由:在Rt△ABC中,AC=30 m,AB=50 m,
根据勾股定理得:BC==40 m.
小汽车的速度是40÷2=20(m/s)=72(km/h).
而规定速度为70 km/h,72>70,
∴小汽车超速了.
15.设AE=x km,则BE=(25-x)km.
在Rt△ACE中,由勾股定理得:CE2=AE2+AC2=x2+152.
同理可得:DE2=(25-x)2+102.
若CE=DE,则
x2+152=(25-x)2+102.解得x=10.
答:图书室E应该建在距A点10 km处,才能使它到两所学校的距离相等.
16.过点A作AD⊥ON于点D,即点A ( http: / / www.21cnjy.com )到ON的最短距离为AD,已知在Rt△OAD中,∠O=30°,OA=80,可得AD=40<50,故学校会受到拖拉机的影响;
在D点两侧分别取两点E、F,使得AE=AF=50,在Rt△ADE中,AE=50,AD=40,可得DE=30,
又易证Rt△ADE≌Rt△ADF,即DE=DF=30,即EF=60.
又拖拉机的速度为18千米/时,
故拖拉机经过EF段所用的时间t=×3 600=12(s).
答:拖拉机会给小学带来噪声影响,影响时间为12秒.
第3课时 勾股定理的逆定理
要点感知 直角三角形的判定定理(勾股定 ( http: / / www.21cnjy.com )理的逆定理):如果一个三角形的三边长a、b、c有下面的关系:a2+b2=c2,那么这个三角形是__________三角形.
预习练习1-1 三角形的三边长满足(a+b)2=c2+2ab,则这个三角形是( )
A.等边三角形 B.钝角三角形 C.直角三角形 D.锐角三角形
1-2 以下列数组为三角形的边长:①5,1 ( http: / / www.21cnjy.com )2,13;②10,12,13;③7,24,25;④6,8,10,其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
知识点 勾股定理的逆定理
1.下列四组线段中,可以构成直角三角形的是( )
A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1,,3
2.已知三角形的三边长之比为1∶1∶,则此三角形一定是( )
A.等腰三角形 B.钝角三角形 C.直角三角形 D.等腰直角三角形
3.已知两条线段的长分别为 cm、 cm,那么能与它们组成直角三角形的第三条线段的长是( )
A.1 cm B.5 cm C. cm D.1 cm与cm
4.如图,正方形小方格边长为1,则网格中的△ABC是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上答案都不对
( http: / / www.21cnjy.com )
5.若a、b、c表示△ABC的三边,且满足+|a-8|+(b-15)2=0,则△ABC的形状是( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等边三角形
6.在Rt△ABC中,若AC=,BC=,AB=3,则下列结论中正确的是( )
A.∠C=90° B.∠B=90° C.△ABC是锐角三角形 D.△ABC是钝角三角形
7.在△ABC中,a=,b=,c=2,则最大边上的中线长为( )
A. B. C.2 D.以上都不对
8.三角形三边长分别为4、8、4,则该三角形最小角与最大角依次是( )
A.30°,60° B.30°,90° C.60°,90° D.45°,90°
9.若在△ABC中,AB=5 cm,BC=6 cm,BC边上的中线AD=4 cm,则∠ADC的度数是__________度.
10.如图,一根电线杆高8 m.为了安 ( http: / / www.21cnjy.com )全起见,在电线杆顶部到与电线杆底部水平距离6 m处加一拉线.拉线工人发现所用线长为10.2 m(不计捆缚部分),则电线杆与地面__________(填“垂直”或“不垂直”).
( http: / / www.21cnjy.com )
11.如图,在△ABC中,AB=2,BC=4,AC=2,∠C=30°,求∠B的大小.
( http: / / www.21cnjy.com )
12.如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是( )
A.CD、EF、GH B.AB、EF、GH C.AB、CF、EF D.GH、AB、CD
( http: / / www.21cnjy.com )
13.已知一个三角形的三边长分别为n+1,n+2,n+3,则当n=__________时,这个三角形是直角三角形.
14.如图所示,是一个零件的形状, ( http: / / www.21cnjy.com )按规定这个零件中的AD与CD必须互相垂直,工人师傅通过测量得到A到C的距离是10 cm,AD=8 cm,CD=6 cm.问这个零件是否合格?
( http: / / www.21cnjy.com )
15.如图,在四边形ABCD中,∠ABC=90°,BC=3,AB=4,AD=12,CD=13.求四边形ABCD的面积.
( http: / / www.21cnjy.com )
16.已知:如图,在△ABC中,CD是AB边上的高,且CD2=AD·BD.求证:△ABC是直角三角形.
( http: / / www.21cnjy.com )
17.如图,点D是△ABC内一点,把△ABD绕点B顺时针方向旋转60°得到△CBE,若AD=4,BD=3,CD=5.
( http: / / www.21cnjy.com )
(1)判断△DEC的形状,并说明理由;
(2)求∠ADB的度数.
参考答案
要点感知 直角
预习练习1-1 C
1-2 B
1.B 2.D 3.D 4.A 5.B 6.A 7.A 8.B 9.90 10.不垂直
11.∵△ABC中,AB=2,BC=4,AC=2,
∴AB2+AC2=4+12=16=BC2.
∴∠A=90°.
∴∠B+∠C=90°.
又∵∠C=30°,
∴∠B=60°.
12.B 13.2
14.合格.
连接AC.
∵AD2+CD2=82+62=102=AC2,
根据勾股定理的逆定理得△ACD是直角三角形,且∠ADC=90°,
∴零件合格.
15.连接AC.
∵∠ABC=90°,在Rt△ABC中,BC=3,AB=4,
∴AC===5.
在△ACD中,∵AC2+AD2=52+122=132=CD2,
∴△ACD是直角三角形.
∴S四边形ABCD=S△ABC+S△ACD=×3×4+×5×12=36.
16.证明:∵CD是AB边上的高,
∴△ADC和△BCD都是直角三角形.
∴AC2=AD2+CD2,BC2=BD2+CD2.
∴AC2+BC2=AD2+CD2+BD2+CD2=AD2+2CD2+BD2=AD2+2AD·BD+BD2=(AD+BD)2=AB2.
∴△ABC是直角三角形.
17.(1)根据旋转的性质,得AD=EC=4,BD=BE=3,AB=BC,∠DBE=∠ABC=60°,∠ADB=∠BEC.
∴△ABC和△DBE均为等边三角形.
∴DE=BD=3.
∵CD=5,
∴DE2+EC2=32+42=52=CD2.
故△DEC为直角三角形.
(2)∵△DEC为直角三角形,
∴∠DEC=90°.
又∵△BDE为等边三角形,
∴∠BED=60°.
故∠BEC=90°+60°=150°,
即∠ADB=150°.
第1课时 勾股定理
要点感知 直角三角形的性质定理(勾股定理):直角三角形两直角边a、b的平方和等于__________的平方.即a2+b2=c2.
预习练习 △ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边.
(1)若a=5,b=12,则c=__________;
(2)若c=41,a=40,则b=__________.
知识点 勾股定理
1.在△ABC中,∠C=90°,如果AB=10,BC∶AC=3∶4,那么BC=( )
A.6 B.8 C.10 D.以上都不对
2.一个直角三角形的三边长为三个连续偶数,则它的斜边长为( )
A.6 B.8 C.10 D.12
3.已知一个三角形三个内角的比是1∶2∶1,则它的三条边的比是( )
A.1∶∶1 B.1∶2∶1 C.1∶∶ D.1∶4∶1
4.如图,长方形OABC的边OA长为2, ( http: / / www.21cnjy.com )边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A.2.5 B.2 C. D.
( http: / / www.21cnjy.com )
5.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重合.若BC=5,CD=3,则BD的长为( )
A.1 B.2 C.3 D.4
( http: / / www.21cnjy.com )
6.在△ABC中,∠C=90°,AB=7,BC=5,则边AC的长为__________.
7.等腰△ABC中,AB=AC=10 cm,BC=12 cm,则BC边上的高是__________cm.
8.一个直角三角形的斜边长比直角长边大2,另一直角边长为6,则斜边长为__________.
9.如图,△ABC中,AB=AC=20,BC=32,D是BC上一点,AD=15,且AD⊥AC,求BD长.
( http: / / www.21cnjy.com )
10.如图,在△ABC中,∠ACB=90°,AB=10 cm,BC=6 cm,CD⊥AB交AB于点D.求:
( http: / / www.21cnjy.com )
(1)AC的长;
(2)△ABC的面积;
(3)CD的长.
11.如图,在由边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
( http: / / www.21cnjy.com )
12.如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为( )
A. B.2 C.3 D.4
( http: / / www.21cnjy.com )
13.将一个有45度角的三角板的直角顶点放 ( http: / / www.21cnjy.com )在一张宽为3 cm的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30度角,如图,则三角板的最大边的长为( )
A.3 cm B.6 cm C.3 cm D.6 cm
14.如图,在直线l上依次摆放着三个正方形,已知中间斜放置的正方形的面积是6,则正放置的两个正方形的面积之和为( )
A.6 B.5 C. D.36
( http: / / www.21cnjy.com )
15.如图,Rt△ABC中,AB=9,BC ( http: / / www.21cnjy.com )=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A. B. C.4 D.5
( http: / / www.21cnjy.com )
16.如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=6,DE=5,则CD的长等于__________.
( http: / / www.21cnjy.com )
17.已知直角三角形两边的长分别是3和4,则第三边的长为__________.
18.如图,在△ABC中,AB=15,BC=14,CA=13,求BC边上的高AD的长.
( http: / / www.21cnjy.com )
19.如图所示,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5 cm,求AB的长.
( http: / / www.21cnjy.com )
20.如图,在等腰直角三角 ( http: / / www.21cnjy.com )形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于点E,交BC于点F,若AE=4,FC=3,求EF长.
( http: / / www.21cnjy.com )
参考答案
要点感知 斜边c
预习练习 13 9
1.A 2.C 3.A 4.D 5.D 6.2 7.8 8.10
9.∵AD⊥AC,AC=20,AD=15,
∴CD==25.
∴BD=BC-CD=32-25=7.
10.(1)∵∠ACB=90°,AB=10 cm,BC=6 cm,∴AC=8 cm;
(2)S△ABC=BC·AC=×6×8=24(cm2);
(3)∵S△ABC=BC·AC=CD·AB,∴CD==cm.
11.A 12.D 13.D 14.A 15.C 16.8 17.5或
18.设DC=x,则BD=14-x.
在Rt△ABD和Rt△ACD中,由勾股定理可得:
(14-x)2+AD2=152,x2+AD2=132.
两式相减得(14-x)2-x2=56.解得x=5.
在Rt△ACD中,由勾股定理得AD=12.
19.∵在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,
∴∠ABD=∠CBD=30°.
∴AD=DB.
又∵Rt△CBD中,CD=5 cm,
∴BD=10 cm.
∴BC===5(cm).
∴AB=2BC=10 cm.
20.连接BD,
∵等腰直角三角形ABC中,D为AC边上中点,
∴BD⊥AC,BD=CD=AD,∠ABD=∠C=45°.
∵DE⊥DF,
∴∠FDC=∠EDB.
在△EDB与△FDC中,
∴△EDB≌△FDC.
∴BE=FC=3.
∴AB=7,则BC=7.
∴BF=4.
在Rt△EBF中,EF2=BE2+BF2=32+42,
∴EF=5.
第2课时 勾股定理的实际应用
要点感知 应用勾股定理解决实际问题时 ( http: / / www.21cnjy.com ),应先根据题意画出几何图形,分析图形中各线段之间的数量关系,正确运用勾股定理求解.求边长时,一般有两种情况:一是直接运用勾股定理通过计算求解,二是借助勾股定理列方程求解.
预习练习 (2014·东营)如图 ( http: / / www.21cnjy.com ),有两棵树,一棵高12米,另一棵高6米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行__________米.
( http: / / www.21cnjy.com )
知识点1 直接利用勾股定理
1.一座建筑物发生了火灾,消防车到 ( http: / / www.21cnjy.com )达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以到达该建筑物的最大高度是( )
A.12米 B.13米 C.14米 D.15米
2.如图,一个高1.5米,宽3.6米的大门,需要在相对的顶点间用一条木板加固,则这条木板的长度是( )
A.3.8米 B.3.9米 C.4米 D.4.4米
( http: / / www.21cnjy.com )
3.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为( )
A.米 B.米 C.(+1)米 D.3米
( http: / / www.21cnjy.com )
4.假期中,小华与同学去玩探宝游戏,按照探宝 ( http: / / www.21cnjy.com )图,他们从门口A处出发先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东拐,仅走了1千米,就找到了宝藏,则门口A到藏宝点B的直线距离是( )
A.20千米 B.14千米 C.11千米 D.10千米
( http: / / www.21cnjy.com )
5.如图,某人欲横渡一条河 ( http: / / www.21cnjy.com ),由于水流的影响,实际上岸地点C偏离欲到达点B200 m,结果他在水中实际游了520 m,该河流的宽度为__________m.
( http: / / www.21cnjy.com )
知识点2 利用勾股定理列方程求解
6.小明准备测量一段河水 ( http: / / www.21cnjy.com )的深度,他把一根竹竿竖直插到离岸边1.5 m远的水底,竹竿高出水面0.5 m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A.2 m B.2.5 m C.2.25 m D.3 m
7.在一次课外社会实践中,王强想知道学 ( http: / / www.21cnjy.com )校旗杆的高,但不能爬上旗杆也不能把绳子解下来,可是他发现旗杆上的绳子垂到地面上还多1 m,当他把绳子的下端拉开5 m后,发现下端刚好接触地面,则旗杆的高为( )
A.13 m B.12 m C.4 m D.10 m
8.如图所示,某风景名胜区为了方便游人参 ( http: / / www.21cnjy.com )观,计划从主峰A处架设一条缆车线路到另一山峰C处,若在A处测得∠EAC=30°,两山峰的底部BD相距900米,则缆车线路AC的长为__________米.
( http: / / www.21cnjy.com )
9.如图,在一棵树的10米高B处有两 ( http: / / www.21cnjy.com )只猴子,其中一只爬下树走向离树20米的池塘C,而另一只爬到树顶D后直扑池塘C,结果两只猴子经过的距离相等,问这棵树有多高?
( http: / / www.21cnjy.com )
10.为迎接新年的到来,同学们做了许多 ( http: / / www.21cnjy.com )拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为( )
A.0.7米 B.0.8米 C.0.9米 D.1.0米
11.如图,沿AC方向开山修路,为加快 ( http: / / www.21cnjy.com )施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=120°,BD=210 m,∠D=30°,要正好能使A、C、E成一直线,那么E、D两点的距离等于( )
A.105 m B.210 m C.70 m D.105 m
( http: / / www.21cnjy.com )
12.在长、宽、高分别为12 cm、4 cm、3 cm的木箱中,放一根木棒,能放进去的木棒的最大长度为( )
A.5 cm B.12 cm C.13 cm D. cm
13.如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B的距离为__________mm.
( http: / / www.21cnjy.com )
14.如图,一辆小汽车在一条东西走向的城市 ( http: / / www.21cnjy.com )公路上直道行驶,某一时刻刚好行驶到路边的车速检测仪的正前方30 m处,过了2 s后,测得小汽车与车速检测仪的距离为50 m,问这辆小汽车是否超速了?(中华人民共和国交通管理条例规定:小汽车在城市公路上行驶时的速度不得超过70 km/h)
( http: / / www.21cnjy.com )
15.为了丰富居民的业余生活 ( http: / / www.21cnjy.com ),某社区要在如图所示AB所在的直线上建一图书室,本社区有两所学校,所在的位置在点C和点D处,CA⊥AB于点A,DB⊥AB于点B,已知AB=25 km,CA=15 km,DB=10 km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
( http: / / www.21cnjy.com )
16.两条公路OM、ON相交成30度角 ( http: / / www.21cnjy.com ),在公路OM上,距O点80米的A处有一所小学,当拖拉机沿公路ON方向行驶时,路两旁50米以内会受到噪音的影响,已知拖拉机的速度为18千米/时,那么拖拉机沿ON方向行驶时,是否会给小学带来噪声影响?若受影响,计算影响的时间.
( http: / / www.21cnjy.com )
参考答案
预习练习 10
1.A 2.B 3.C 4.D 5.480 6.A 7.B 8.600
9.设BD=x米,则AD=(10+x)米,CD=(30-x)米,根据题意得
(30-x)2-(x+10)2=202.解得x=5.
即树的高度是10+5=15(米).
10.A 11.A 12.C 13.150
14.小汽车超速了.
理由:在Rt△ABC中,AC=30 m,AB=50 m,
根据勾股定理得:BC==40 m.
小汽车的速度是40÷2=20(m/s)=72(km/h).
而规定速度为70 km/h,72>70,
∴小汽车超速了.
15.设AE=x km,则BE=(25-x)km.
在Rt△ACE中,由勾股定理得:CE2=AE2+AC2=x2+152.
同理可得:DE2=(25-x)2+102.
若CE=DE,则
x2+152=(25-x)2+102.解得x=10.
答:图书室E应该建在距A点10 km处,才能使它到两所学校的距离相等.
16.过点A作AD⊥ON于点D,即点A ( http: / / www.21cnjy.com )到ON的最短距离为AD,已知在Rt△OAD中,∠O=30°,OA=80,可得AD=40<50,故学校会受到拖拉机的影响;
在D点两侧分别取两点E、F,使得AE=AF=50,在Rt△ADE中,AE=50,AD=40,可得DE=30,
又易证Rt△ADE≌Rt△ADF,即DE=DF=30,即EF=60.
又拖拉机的速度为18千米/时,
故拖拉机经过EF段所用的时间t=×3 600=12(s).
答:拖拉机会给小学带来噪声影响,影响时间为12秒.
第3课时 勾股定理的逆定理
要点感知 直角三角形的判定定理(勾股定 ( http: / / www.21cnjy.com )理的逆定理):如果一个三角形的三边长a、b、c有下面的关系:a2+b2=c2,那么这个三角形是__________三角形.
预习练习1-1 三角形的三边长满足(a+b)2=c2+2ab,则这个三角形是( )
A.等边三角形 B.钝角三角形 C.直角三角形 D.锐角三角形
1-2 以下列数组为三角形的边长:①5,1 ( http: / / www.21cnjy.com )2,13;②10,12,13;③7,24,25;④6,8,10,其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
知识点 勾股定理的逆定理
1.下列四组线段中,可以构成直角三角形的是( )
A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1,,3
2.已知三角形的三边长之比为1∶1∶,则此三角形一定是( )
A.等腰三角形 B.钝角三角形 C.直角三角形 D.等腰直角三角形
3.已知两条线段的长分别为 cm、 cm,那么能与它们组成直角三角形的第三条线段的长是( )
A.1 cm B.5 cm C. cm D.1 cm与cm
4.如图,正方形小方格边长为1,则网格中的△ABC是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上答案都不对
( http: / / www.21cnjy.com )
5.若a、b、c表示△ABC的三边,且满足+|a-8|+(b-15)2=0,则△ABC的形状是( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等边三角形
6.在Rt△ABC中,若AC=,BC=,AB=3,则下列结论中正确的是( )
A.∠C=90° B.∠B=90° C.△ABC是锐角三角形 D.△ABC是钝角三角形
7.在△ABC中,a=,b=,c=2,则最大边上的中线长为( )
A. B. C.2 D.以上都不对
8.三角形三边长分别为4、8、4,则该三角形最小角与最大角依次是( )
A.30°,60° B.30°,90° C.60°,90° D.45°,90°
9.若在△ABC中,AB=5 cm,BC=6 cm,BC边上的中线AD=4 cm,则∠ADC的度数是__________度.
10.如图,一根电线杆高8 m.为了安 ( http: / / www.21cnjy.com )全起见,在电线杆顶部到与电线杆底部水平距离6 m处加一拉线.拉线工人发现所用线长为10.2 m(不计捆缚部分),则电线杆与地面__________(填“垂直”或“不垂直”).
( http: / / www.21cnjy.com )
11.如图,在△ABC中,AB=2,BC=4,AC=2,∠C=30°,求∠B的大小.
( http: / / www.21cnjy.com )
12.如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是( )
A.CD、EF、GH B.AB、EF、GH C.AB、CF、EF D.GH、AB、CD
( http: / / www.21cnjy.com )
13.已知一个三角形的三边长分别为n+1,n+2,n+3,则当n=__________时,这个三角形是直角三角形.
14.如图所示,是一个零件的形状, ( http: / / www.21cnjy.com )按规定这个零件中的AD与CD必须互相垂直,工人师傅通过测量得到A到C的距离是10 cm,AD=8 cm,CD=6 cm.问这个零件是否合格?
( http: / / www.21cnjy.com )
15.如图,在四边形ABCD中,∠ABC=90°,BC=3,AB=4,AD=12,CD=13.求四边形ABCD的面积.
( http: / / www.21cnjy.com )
16.已知:如图,在△ABC中,CD是AB边上的高,且CD2=AD·BD.求证:△ABC是直角三角形.
( http: / / www.21cnjy.com )
17.如图,点D是△ABC内一点,把△ABD绕点B顺时针方向旋转60°得到△CBE,若AD=4,BD=3,CD=5.
( http: / / www.21cnjy.com )
(1)判断△DEC的形状,并说明理由;
(2)求∠ADB的度数.
参考答案
要点感知 直角
预习练习1-1 C
1-2 B
1.B 2.D 3.D 4.A 5.B 6.A 7.A 8.B 9.90 10.不垂直
11.∵△ABC中,AB=2,BC=4,AC=2,
∴AB2+AC2=4+12=16=BC2.
∴∠A=90°.
∴∠B+∠C=90°.
又∵∠C=30°,
∴∠B=60°.
12.B 13.2
14.合格.
连接AC.
∵AD2+CD2=82+62=102=AC2,
根据勾股定理的逆定理得△ACD是直角三角形,且∠ADC=90°,
∴零件合格.
15.连接AC.
∵∠ABC=90°,在Rt△ABC中,BC=3,AB=4,
∴AC===5.
在△ACD中,∵AC2+AD2=52+122=132=CD2,
∴△ACD是直角三角形.
∴S四边形ABCD=S△ABC+S△ACD=×3×4+×5×12=36.
16.证明:∵CD是AB边上的高,
∴△ADC和△BCD都是直角三角形.
∴AC2=AD2+CD2,BC2=BD2+CD2.
∴AC2+BC2=AD2+CD2+BD2+CD2=AD2+2CD2+BD2=AD2+2AD·BD+BD2=(AD+BD)2=AB2.
∴△ABC是直角三角形.
17.(1)根据旋转的性质,得AD=EC=4,BD=BE=3,AB=BC,∠DBE=∠ABC=60°,∠ADB=∠BEC.
∴△ABC和△DBE均为等边三角形.
∴DE=BD=3.
∵CD=5,
∴DE2+EC2=32+42=52=CD2.
故△DEC为直角三角形.
(2)∵△DEC为直角三角形,
∴∠DEC=90°.
又∵△BDE为等边三角形,
∴∠BED=60°.
故∠BEC=90°+60°=150°,
即∠ADB=150°.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
