湘教版七年级下册(新)第4章平行线的性质与判定综合练习
文档属性
| 名称 | 湘教版七年级下册(新)第4章平行线的性质与判定综合练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 72.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-29 00:00:00 | ||
图片预览

文档简介
综合练行线的性质与判定
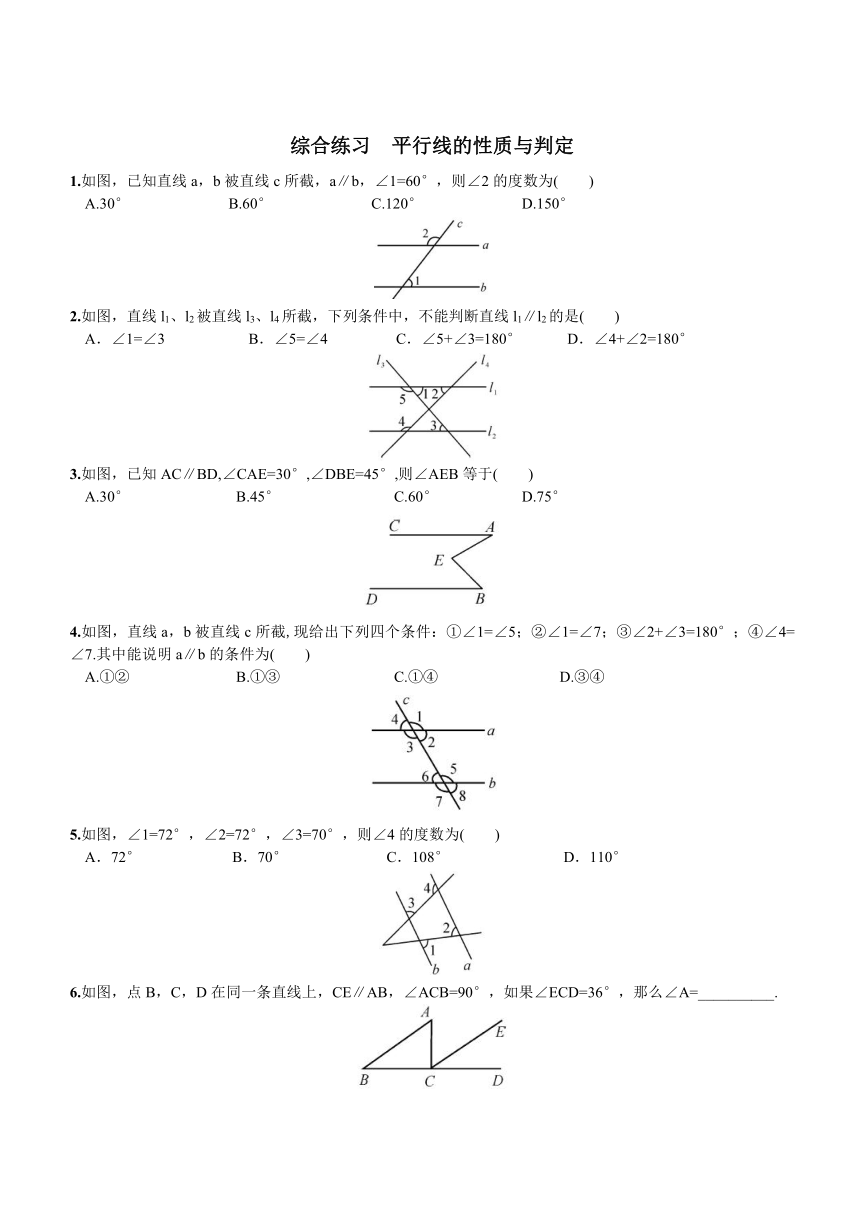
1.如图,已知直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数为( )
A.30° B.60° C.120° D.150°
( http: / / www.21cnjy.com )
2.如图,直线l1、l2被直线l3、l4所截,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠5=∠4 C.∠5+∠3=180° D.∠4+∠2=180°
( http: / / www.21cnjy.com )
3.如图,已知AC∥BD,∠CAE=30°,∠DBE=45°,则∠AEB等于( )
A.30° B.45° C.60° D.75°
( http: / / www.21cnjy.com )
4.如图,直线a,b被直线c所截,现给出 ( http: / / www.21cnjy.com )下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a∥b的条件为( )
A.①② B.①③ C.①④ D.③④
( http: / / www.21cnjy.com )
5.如图,∠1=72°,∠2=72°,∠3=70°,则∠4的度数为( )
A.72° B.70° C.108° D.110°
( http: / / www.21cnjy.com )
6.如图,点B,C,D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD=36°,那么∠A=__________.
( http: / / www.21cnjy.com )
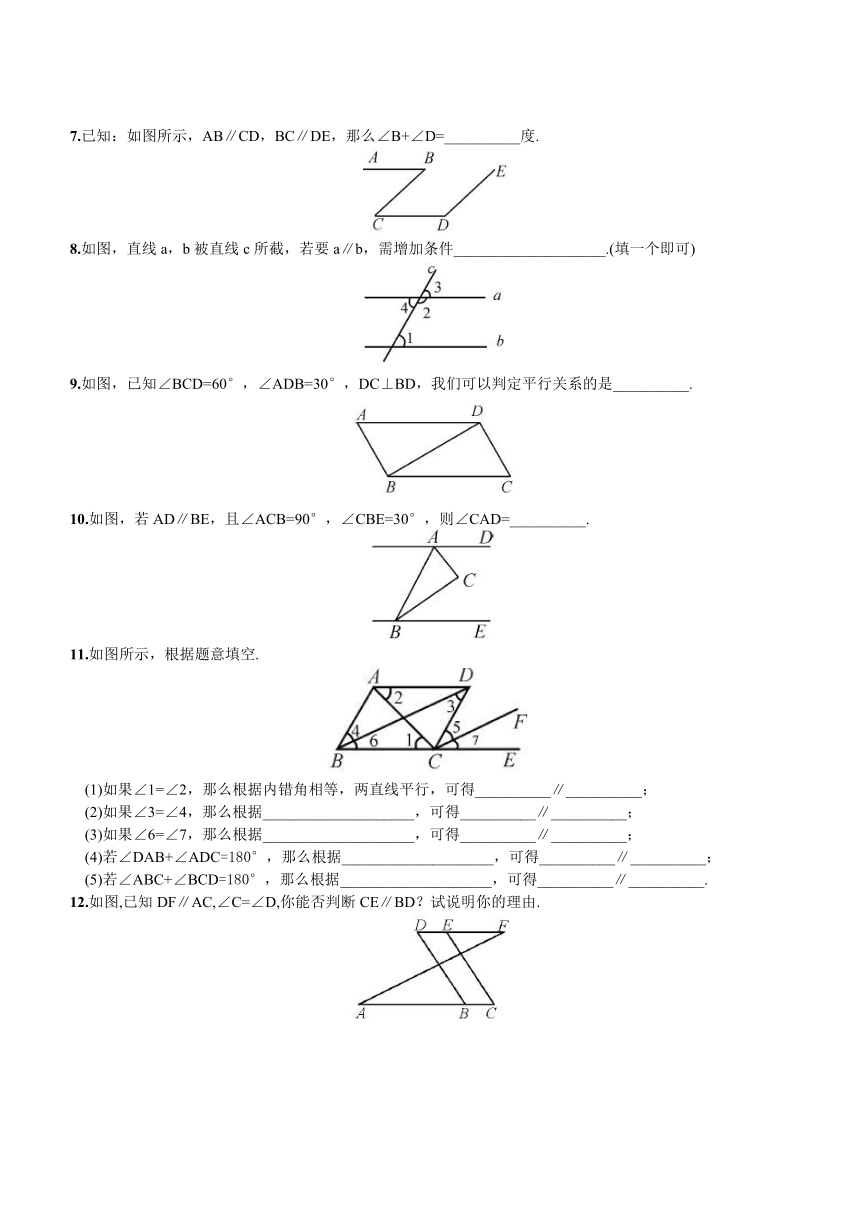
7.已知:如图所示,AB∥CD,BC∥DE,那么∠B+∠D=__________度.
( http: / / www.21cnjy.com )
8.如图,直线a,b被直线c所截,若要a∥b,需增加条件____________________.(填一个即可)
( http: / / www.21cnjy.com )
9.如图,已知∠BCD=60°,∠ADB=30°,DC⊥BD,我们可以判定平行关系的是__________.
( http: / / www.21cnjy.com )
10.如图,若AD∥BE,且∠ACB=90°,∠CBE=30°,则∠CAD=__________.
( http: / / www.21cnjy.com )
11.如图所示,根据题意填空.
( http: / / www.21cnjy.com )
(1)如果∠1=∠2,那么根据内错角相等,两直线平行,可得__________∥__________;
(2)如果∠3=∠4,那么根据____________________,可得__________∥__________;
(3)如果∠6=∠7,那么根据____________________,可得__________∥__________;
(4)若∠DAB+∠ADC=180°, ( http: / / www.21cnjy.com )那么根据____________________,可得__________∥__________;
(5)若∠ABC+∠BCD=180°, ( http: / / www.21cnjy.com )那么根据____________________,可得__________∥__________.
12.如图,已知DF∥AC,∠C=∠D,你能否判断CE∥BD?试说明你的理由.
( http: / / www.21cnjy.com )
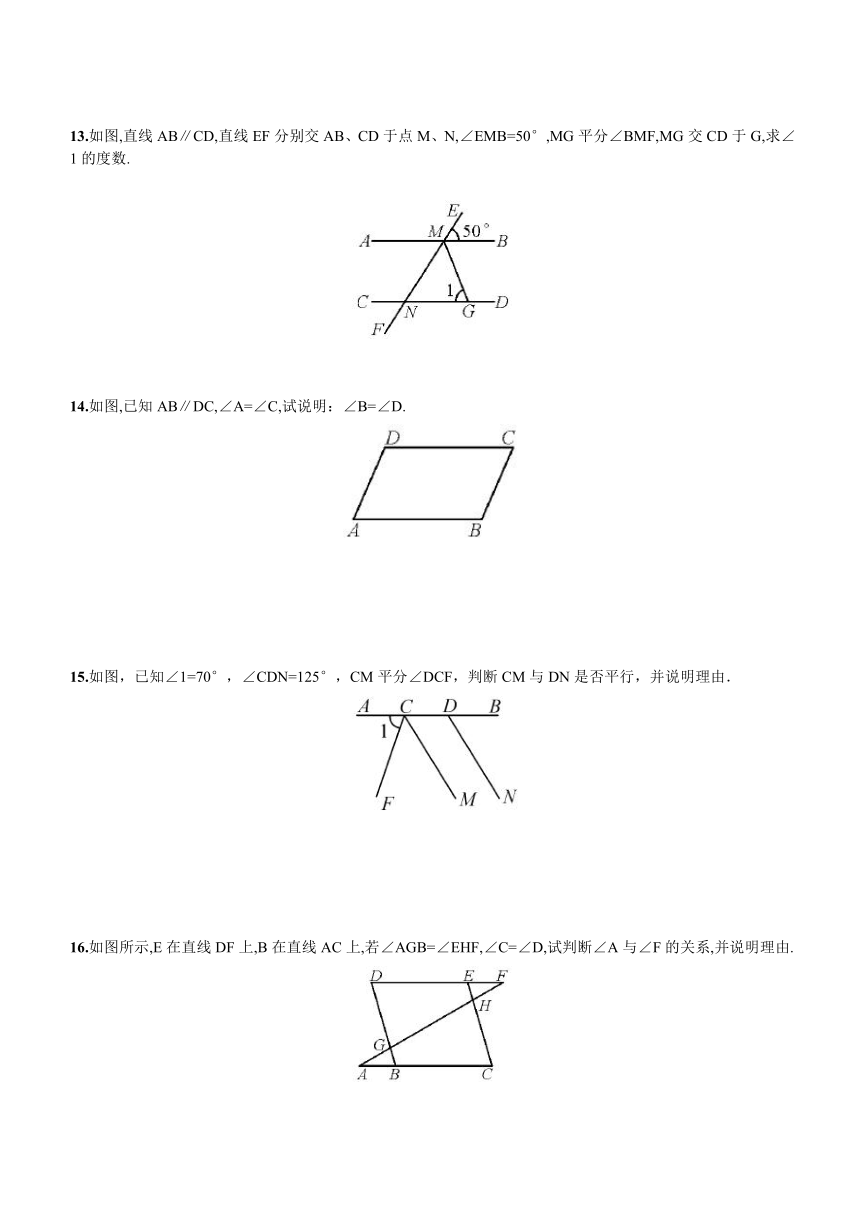
13.如图,直线AB∥CD,直线EF分别交AB、CD于点M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.
( http: / / www.21cnjy.com )
14.如图,已知AB∥DC,∠A=∠C,试说明:∠B=∠D.
( http: / / www.21cnjy.com )
15.如图,已知∠1=70°,∠CDN=125°,CM平分∠DCF,判断CM与DN是否平行,并说明理由.
( http: / / www.21cnjy.com )
16.如图所示,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D,试判断∠A与∠F的关系,并说明理由.
( http: / / www.21cnjy.com )
17.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由.
( http: / / www.21cnjy.com )
18.如图,已知直线CB∥OA,∠C=∠OAB=100°,E,F在BC上,满足∠FOB=∠AOB,OE平分∠COF.
( http: / / www.21cnjy.com )
(1)求∠EOB的度数;
(2)若平行移动AB,则∠OBC∶∠OFC的值是否发生变化?若变化找出变化规律,若不变求其比值.
参考答案
1.C 2.B 3.D 4.A 5.D 6.54° 7.180
8.答案不唯一,如∠1=∠4或∠1=∠3或∠1+∠2=180° 9.AD∥BC 10.60°
11.(1)AD BC
(2)内错角相等,两直线平行 AB CD
(3)同位角相等,两直线平行 BD CF
(4)同旁内角互补,两直线平行 AB CD
(5)同旁内角互补,两直线平行 AB CD
12.CE∥BD.
理由:因为DF∥AC(已知),
所以∠C=∠FEC(两直线平行,内错角相等).
又因为∠C=∠D(已知),
所以∠D=∠FEC(等量代换).
所以CE∥BD(同位角相等,两直线平行).
13.因为∠EMB=50°,
所以∠BMF=180°-∠EMB=130°.
因为MG平分∠BMF,
所以∠BMG=∠BMF=65°.
因为AB∥CD,
所以∠1=∠BMG=65°.
14.因为AB∥DC(已知),
所以∠B+∠C=180°(两直线平行,同旁内角互补).
又因为∠A=∠C(已知),
所以∠B+∠A=180°(等量代换).
所以AD∥BC(同旁内角互补,两直线平行).
所以∠C+∠D=180°(两直线平行,同旁内角互补).
所以∠B=∠D(等量代换).
15.CM与DN平行.
理由:因为∠1=70°,
所以∠BCF=180°-70°=110°.
因为CM平分∠DCF,
所以∠DCM=55°.
因为∠CDN=125°,
所以∠DCM+∠CDN=180°,
所以CM∥DN.
16.∠A=∠F.
理由:因为∠AGB=∠DGF,∠AGB=∠EHF,
所以∠DGF=∠EHF.
所以BD∥CE.
所以∠C=∠ABD.
又因为∠C=∠D,
所以∠D=∠ABD.
所以DF∥AC.
所以∠A=∠F.
17.∠AED=∠ACB.
理由:因为∠1+∠4=180°,∠1+∠2=180°,
所以∠2=∠4.
所以EF∥AB.
所以∠3=∠ADE.
因为∠3=∠B,
所以∠B=∠ADE.
所以DE∥BC.
所以∠AED=∠ACB.
18.(1)因为CB∥OA,∠C=∠OAB=100°,
所以∠COA=180°-∠C=180°-100°=80°,∠FBO=∠AOB.
又因为∠FOB=∠AOB,
所以∠FBO=∠FOB.
所以OB平分∠AOF.
又因为OE平分∠COF,
所以∠EOB=∠EOF+∠FOB=∠COA=×80°=40°.
(2)不变.
因为CB∥OA,
所以∠OBC=∠BOA,∠OFC=∠FOA.
所以∠OBC∶∠OFC=∠AOB∶∠FOA.
又因为∠FOA=∠FOB+∠AOB=2∠AOB,
所以∠OBC∶∠OFC=∠AOB∶∠FOA=∠AOB∶2∠AOB=1∶2.
1.如图,已知直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数为( )
A.30° B.60° C.120° D.150°
( http: / / www.21cnjy.com )
2.如图,直线l1、l2被直线l3、l4所截,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠5=∠4 C.∠5+∠3=180° D.∠4+∠2=180°
( http: / / www.21cnjy.com )
3.如图,已知AC∥BD,∠CAE=30°,∠DBE=45°,则∠AEB等于( )
A.30° B.45° C.60° D.75°
( http: / / www.21cnjy.com )
4.如图,直线a,b被直线c所截,现给出 ( http: / / www.21cnjy.com )下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a∥b的条件为( )
A.①② B.①③ C.①④ D.③④
( http: / / www.21cnjy.com )
5.如图,∠1=72°,∠2=72°,∠3=70°,则∠4的度数为( )
A.72° B.70° C.108° D.110°
( http: / / www.21cnjy.com )
6.如图,点B,C,D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD=36°,那么∠A=__________.
( http: / / www.21cnjy.com )
7.已知:如图所示,AB∥CD,BC∥DE,那么∠B+∠D=__________度.
( http: / / www.21cnjy.com )
8.如图,直线a,b被直线c所截,若要a∥b,需增加条件____________________.(填一个即可)
( http: / / www.21cnjy.com )
9.如图,已知∠BCD=60°,∠ADB=30°,DC⊥BD,我们可以判定平行关系的是__________.
( http: / / www.21cnjy.com )
10.如图,若AD∥BE,且∠ACB=90°,∠CBE=30°,则∠CAD=__________.
( http: / / www.21cnjy.com )
11.如图所示,根据题意填空.
( http: / / www.21cnjy.com )
(1)如果∠1=∠2,那么根据内错角相等,两直线平行,可得__________∥__________;
(2)如果∠3=∠4,那么根据____________________,可得__________∥__________;
(3)如果∠6=∠7,那么根据____________________,可得__________∥__________;
(4)若∠DAB+∠ADC=180°, ( http: / / www.21cnjy.com )那么根据____________________,可得__________∥__________;
(5)若∠ABC+∠BCD=180°, ( http: / / www.21cnjy.com )那么根据____________________,可得__________∥__________.
12.如图,已知DF∥AC,∠C=∠D,你能否判断CE∥BD?试说明你的理由.
( http: / / www.21cnjy.com )
13.如图,直线AB∥CD,直线EF分别交AB、CD于点M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.
( http: / / www.21cnjy.com )
14.如图,已知AB∥DC,∠A=∠C,试说明:∠B=∠D.
( http: / / www.21cnjy.com )
15.如图,已知∠1=70°,∠CDN=125°,CM平分∠DCF,判断CM与DN是否平行,并说明理由.
( http: / / www.21cnjy.com )
16.如图所示,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D,试判断∠A与∠F的关系,并说明理由.
( http: / / www.21cnjy.com )
17.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由.
( http: / / www.21cnjy.com )
18.如图,已知直线CB∥OA,∠C=∠OAB=100°,E,F在BC上,满足∠FOB=∠AOB,OE平分∠COF.
( http: / / www.21cnjy.com )
(1)求∠EOB的度数;
(2)若平行移动AB,则∠OBC∶∠OFC的值是否发生变化?若变化找出变化规律,若不变求其比值.
参考答案
1.C 2.B 3.D 4.A 5.D 6.54° 7.180
8.答案不唯一,如∠1=∠4或∠1=∠3或∠1+∠2=180° 9.AD∥BC 10.60°
11.(1)AD BC
(2)内错角相等,两直线平行 AB CD
(3)同位角相等,两直线平行 BD CF
(4)同旁内角互补,两直线平行 AB CD
(5)同旁内角互补,两直线平行 AB CD
12.CE∥BD.
理由:因为DF∥AC(已知),
所以∠C=∠FEC(两直线平行,内错角相等).
又因为∠C=∠D(已知),
所以∠D=∠FEC(等量代换).
所以CE∥BD(同位角相等,两直线平行).
13.因为∠EMB=50°,
所以∠BMF=180°-∠EMB=130°.
因为MG平分∠BMF,
所以∠BMG=∠BMF=65°.
因为AB∥CD,
所以∠1=∠BMG=65°.
14.因为AB∥DC(已知),
所以∠B+∠C=180°(两直线平行,同旁内角互补).
又因为∠A=∠C(已知),
所以∠B+∠A=180°(等量代换).
所以AD∥BC(同旁内角互补,两直线平行).
所以∠C+∠D=180°(两直线平行,同旁内角互补).
所以∠B=∠D(等量代换).
15.CM与DN平行.
理由:因为∠1=70°,
所以∠BCF=180°-70°=110°.
因为CM平分∠DCF,
所以∠DCM=55°.
因为∠CDN=125°,
所以∠DCM+∠CDN=180°,
所以CM∥DN.
16.∠A=∠F.
理由:因为∠AGB=∠DGF,∠AGB=∠EHF,
所以∠DGF=∠EHF.
所以BD∥CE.
所以∠C=∠ABD.
又因为∠C=∠D,
所以∠D=∠ABD.
所以DF∥AC.
所以∠A=∠F.
17.∠AED=∠ACB.
理由:因为∠1+∠4=180°,∠1+∠2=180°,
所以∠2=∠4.
所以EF∥AB.
所以∠3=∠ADE.
因为∠3=∠B,
所以∠B=∠ADE.
所以DE∥BC.
所以∠AED=∠ACB.
18.(1)因为CB∥OA,∠C=∠OAB=100°,
所以∠COA=180°-∠C=180°-100°=80°,∠FBO=∠AOB.
又因为∠FOB=∠AOB,
所以∠FBO=∠FOB.
所以OB平分∠AOF.
又因为OE平分∠COF,
所以∠EOB=∠EOF+∠FOB=∠COA=×80°=40°.
(2)不变.
因为CB∥OA,
所以∠OBC=∠BOA,∠OFC=∠FOA.
所以∠OBC∶∠OFC=∠AOB∶∠FOA.
又因为∠FOA=∠FOB+∠AOB=2∠AOB,
所以∠OBC∶∠OFC=∠AOB∶∠FOA=∠AOB∶2∠AOB=1∶2.
