湘教版七年级下册(新)第4章《4.3 平行线的性质》同步练习
文档属性
| 名称 | 湘教版七年级下册(新)第4章《4.3 平行线的性质》同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 91.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-29 00:00:00 | ||
图片预览

文档简介
4.3 平行线的性质
要点感知1 两条平行直线被第三条直线所截,同位角__________.
预习练习1-1 (2012·玉林)如图,a∥b,c与a,b都相交,∠1=50°,则∠2=( )
A.40° B.50° C.100° D.130°
( http: / / www.21cnjy.com )
要点感知2 两条平行直线被第三条直线所截,内错角__________.
预习练习2-1 如图,AB∥CD,如果∠B=20°,那么∠C为( )
A.40° B.20° C.60° D.70°
( http: / / www.21cnjy.com )
要点感知3 两条平行线被第三条直线所截,同旁内角__________.
预习练习3-1 如图,直线AB∥CD,直线EF分别交AB、CD于点E、F,若∠AEF=50°,则∠EFC的大小是( )
A.40° B.50° C.120° D.130°
( http: / / www.21cnjy.com )
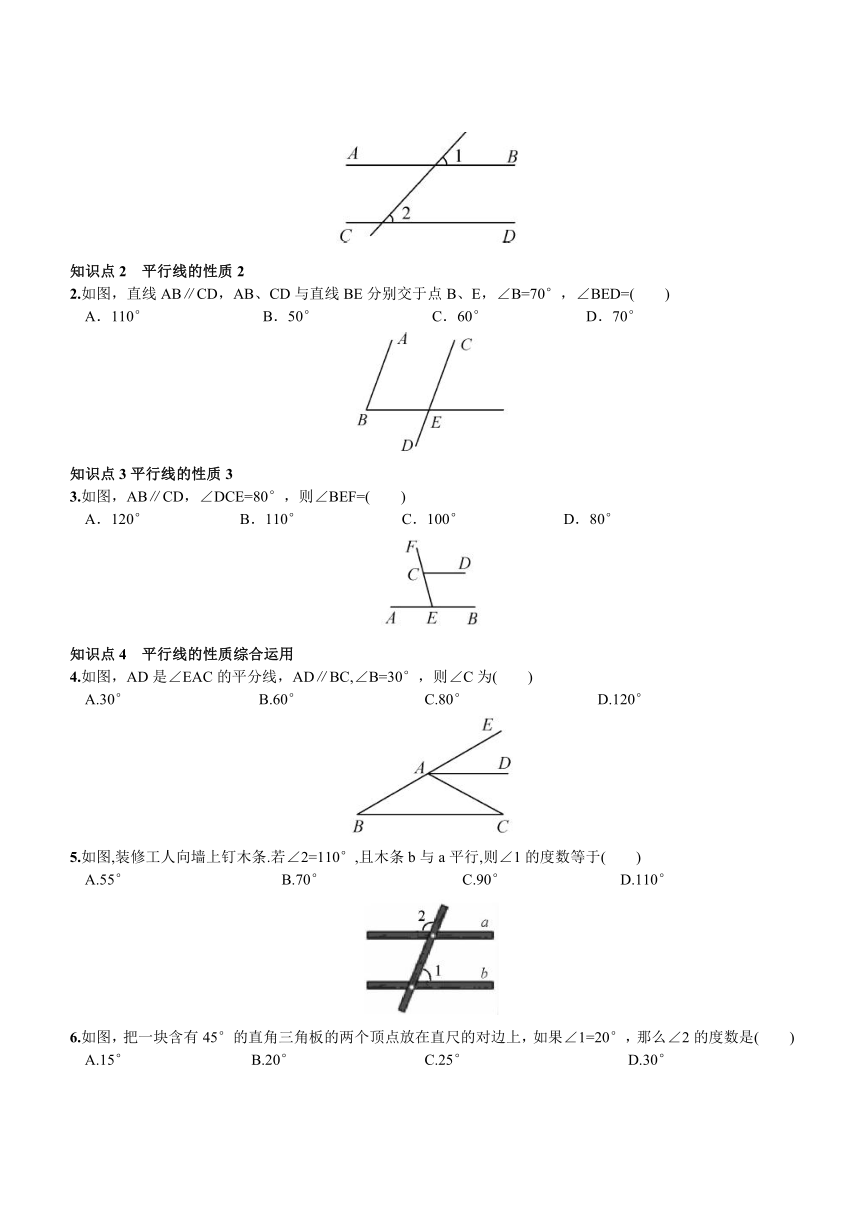
知识点1 平行线的性质1
1.如图,已知AB∥CD,∠1=56°,则∠2的度数是( )
A.34° B.56° C.65° D.124°
( http: / / www.21cnjy.com )
知识点2 平行线的性质2
2.如图,直线AB∥CD,AB、CD与直线BE分别交于点B、E,∠B=70°,∠BED=( )
A.110° B.50° C.60° D.70°
( http: / / www.21cnjy.com )
知识点3平行线的性质3
3.如图,AB∥CD,∠DCE=80°,则∠BEF=( )
A.120° B.110° C.100° D.80°
( http: / / www.21cnjy.com )
知识点4 平行线的性质综合运用
4.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30° B.60° C.80° D.120°
( http: / / www.21cnjy.com )
5.如图,装修工人向墙上钉木条.若∠2=110°,且木条b与a平行,则∠1的度数等于( )
A.55° B.70° C.90° D.110°
( http: / / www.21cnjy.com )
6.如图,把一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是( )
A.15° B.20° C.25° D.30°
( http: / / www.21cnjy.com )
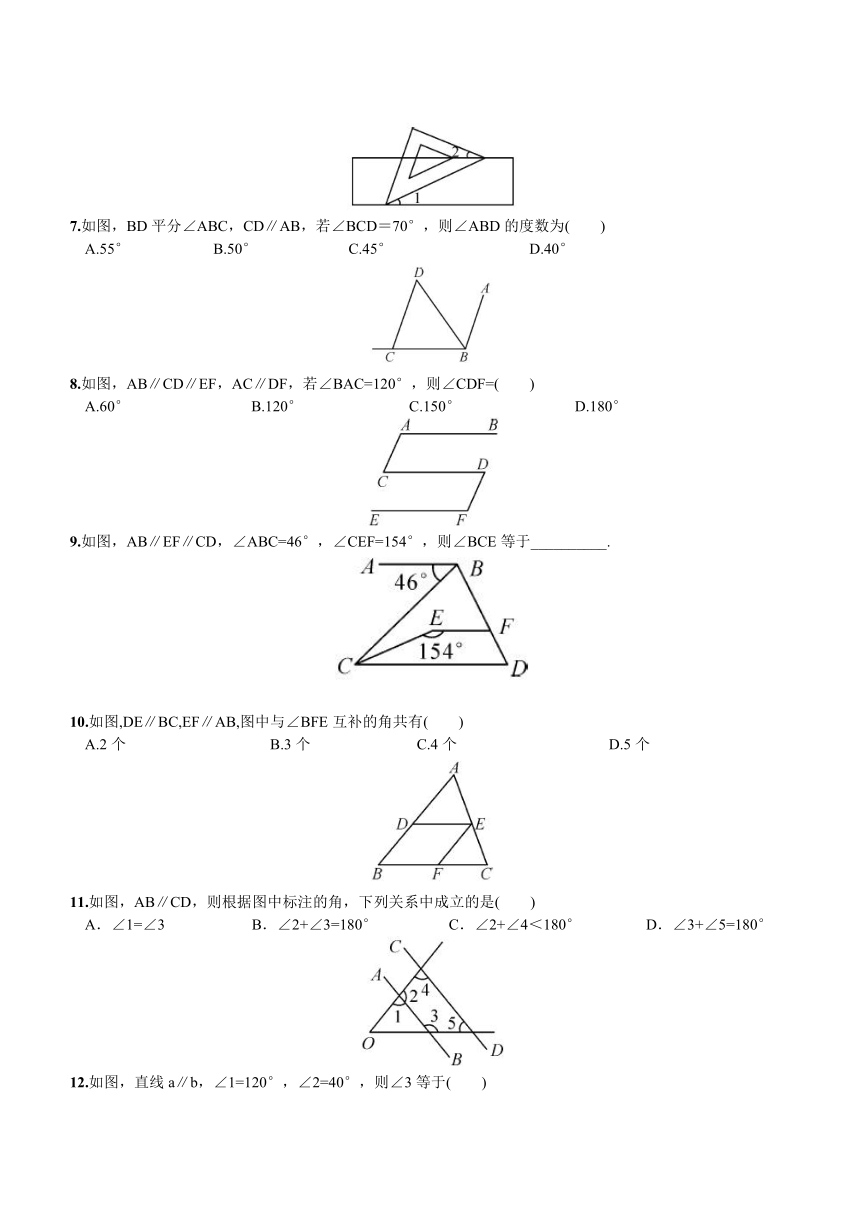
7.如图,BD平分∠ABC,CD∥AB,若∠BCD=70°,则∠ABD的度数为( )
A.55° B.50° C.45° D.40°
( http: / / www.21cnjy.com )
8.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=( )
A.60° B.120° C.150° D.180°
( http: / / www.21cnjy.com )
9.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于__________.
( http: / / www.21cnjy.com )
10.如图,DE∥BC,EF∥AB,图中与∠BFE互补的角共有( )
A.2个 B.3个 C.4个 D.5个
( http: / / www.21cnjy.com )
11.如图,AB∥CD,则根据图中标注的角,下列关系中成立的是( )
A.∠1=∠3 B.∠2+∠3=180° C.∠2+∠4<180° D.∠3+∠5=180°
( http: / / www.21cnjy.com )
12.如图,直线a∥b,∠1=120°,∠2=40°,则∠3等于( )
A.60° B.70° C.80° D.90°
( http: / / www.21cnjy.com )
13.如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
A.17° B.34° C.56° D.68°
( http: / / www.21cnjy.com )
14.如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
A.70° B.100° C.140° D.170°
( http: / / www.21cnjy.com )
15.如图,a∥b,∠1+∠2=75°,则∠3+∠4=__________ .
( http: / / www.21cnjy.com )
16.如图,CD平分∠ACB,DE∥BC,∠AED=70°,求∠EDC的度数.
( http: / / www.21cnjy.com )
17.如图,AB∥DE,BC∥FG,∠1=56°,∠2=104°,求∠ABF的度数.
( http: / / www.21cnjy.com )
18.如图,DB∥FG∥EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD的度数.
( http: / / www.21cnjy.com )
19.(1)如图,已知AB∥CD,EF∥MN,∠1=115°,求∠2和∠4的度数;
( http: / / www.21cnjy.com )
(2)本题隐含着一个规律,请你根据(1)的结果进行归纳,试着用文字表述出来;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一个角是另一个角的两倍,求这两个角的大小.
参考答案
要点感知1 相等
预习练习1-1 B
要点感知2 相等
预习练习2-1 B
要点感知3 互补
预习练习3-1 D
1.B 2.D 3.C 4.A 5.B 6.C 7.A 8.A 9.20°
10.C 11.D 12.C 13.D 14.C 15.105°
16.因为DE∥BC,∠AED=70°,
所以∠ACB=∠AED=70°.
因为CD平分∠ACB,
所以∠BCD=∠ACB=35°.
因为DE∥BC,
所以∠EDC=∠BCD=35°.
17.因为BC∥FG,
所以∠BCG=∠1=56°,∠FBC+∠2=180°.
因为∠2=104°,
所以∠FBC=180°-104°=76°.
因为AB∥DE,
所以∠ABC=∠BCG=56°.
所以∠ABF=∠ABC+∠FBC =56°+76°=132°.
18.因为FG∥EC,∠ACE=36°,
所以∠CAG=∠ACE=36°.
因为∠PAG=12°,
所以∠PAC=∠CAG+∠PAG=48°.
因为AP平分∠BAC,
所以∠BAP=∠PAC=48°.
所以∠BAG=∠BAP+∠PAG=60°.
又因为DB∥FG,
所以∠ABD=∠BAG=60°.
19.(1)∠2=115°,∠4=65°;
(2)如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补;
(3)根据(2),设其中一个角为x°,则另一个角为(2x)°,则
x+2x=180.解得x=60.
故这两个角分别为60°,120°.
要点感知1 两条平行直线被第三条直线所截,同位角__________.
预习练习1-1 (2012·玉林)如图,a∥b,c与a,b都相交,∠1=50°,则∠2=( )
A.40° B.50° C.100° D.130°
( http: / / www.21cnjy.com )
要点感知2 两条平行直线被第三条直线所截,内错角__________.
预习练习2-1 如图,AB∥CD,如果∠B=20°,那么∠C为( )
A.40° B.20° C.60° D.70°
( http: / / www.21cnjy.com )
要点感知3 两条平行线被第三条直线所截,同旁内角__________.
预习练习3-1 如图,直线AB∥CD,直线EF分别交AB、CD于点E、F,若∠AEF=50°,则∠EFC的大小是( )
A.40° B.50° C.120° D.130°
( http: / / www.21cnjy.com )
知识点1 平行线的性质1
1.如图,已知AB∥CD,∠1=56°,则∠2的度数是( )
A.34° B.56° C.65° D.124°
( http: / / www.21cnjy.com )
知识点2 平行线的性质2
2.如图,直线AB∥CD,AB、CD与直线BE分别交于点B、E,∠B=70°,∠BED=( )
A.110° B.50° C.60° D.70°
( http: / / www.21cnjy.com )
知识点3平行线的性质3
3.如图,AB∥CD,∠DCE=80°,则∠BEF=( )
A.120° B.110° C.100° D.80°
( http: / / www.21cnjy.com )
知识点4 平行线的性质综合运用
4.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30° B.60° C.80° D.120°
( http: / / www.21cnjy.com )
5.如图,装修工人向墙上钉木条.若∠2=110°,且木条b与a平行,则∠1的度数等于( )
A.55° B.70° C.90° D.110°
( http: / / www.21cnjy.com )
6.如图,把一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是( )
A.15° B.20° C.25° D.30°
( http: / / www.21cnjy.com )
7.如图,BD平分∠ABC,CD∥AB,若∠BCD=70°,则∠ABD的度数为( )
A.55° B.50° C.45° D.40°
( http: / / www.21cnjy.com )
8.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=( )
A.60° B.120° C.150° D.180°
( http: / / www.21cnjy.com )
9.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于__________.
( http: / / www.21cnjy.com )
10.如图,DE∥BC,EF∥AB,图中与∠BFE互补的角共有( )
A.2个 B.3个 C.4个 D.5个
( http: / / www.21cnjy.com )
11.如图,AB∥CD,则根据图中标注的角,下列关系中成立的是( )
A.∠1=∠3 B.∠2+∠3=180° C.∠2+∠4<180° D.∠3+∠5=180°
( http: / / www.21cnjy.com )
12.如图,直线a∥b,∠1=120°,∠2=40°,则∠3等于( )
A.60° B.70° C.80° D.90°
( http: / / www.21cnjy.com )
13.如图,已知AB∥CD,BC平分∠ABE,∠C=34°,则∠BED的度数是( )
A.17° B.34° C.56° D.68°
( http: / / www.21cnjy.com )
14.如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
A.70° B.100° C.140° D.170°
( http: / / www.21cnjy.com )
15.如图,a∥b,∠1+∠2=75°,则∠3+∠4=__________ .
( http: / / www.21cnjy.com )
16.如图,CD平分∠ACB,DE∥BC,∠AED=70°,求∠EDC的度数.
( http: / / www.21cnjy.com )
17.如图,AB∥DE,BC∥FG,∠1=56°,∠2=104°,求∠ABF的度数.
( http: / / www.21cnjy.com )
18.如图,DB∥FG∥EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD的度数.
( http: / / www.21cnjy.com )
19.(1)如图,已知AB∥CD,EF∥MN,∠1=115°,求∠2和∠4的度数;
( http: / / www.21cnjy.com )
(2)本题隐含着一个规律,请你根据(1)的结果进行归纳,试着用文字表述出来;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一个角是另一个角的两倍,求这两个角的大小.
参考答案
要点感知1 相等
预习练习1-1 B
要点感知2 相等
预习练习2-1 B
要点感知3 互补
预习练习3-1 D
1.B 2.D 3.C 4.A 5.B 6.C 7.A 8.A 9.20°
10.C 11.D 12.C 13.D 14.C 15.105°
16.因为DE∥BC,∠AED=70°,
所以∠ACB=∠AED=70°.
因为CD平分∠ACB,
所以∠BCD=∠ACB=35°.
因为DE∥BC,
所以∠EDC=∠BCD=35°.
17.因为BC∥FG,
所以∠BCG=∠1=56°,∠FBC+∠2=180°.
因为∠2=104°,
所以∠FBC=180°-104°=76°.
因为AB∥DE,
所以∠ABC=∠BCG=56°.
所以∠ABF=∠ABC+∠FBC =56°+76°=132°.
18.因为FG∥EC,∠ACE=36°,
所以∠CAG=∠ACE=36°.
因为∠PAG=12°,
所以∠PAC=∠CAG+∠PAG=48°.
因为AP平分∠BAC,
所以∠BAP=∠PAC=48°.
所以∠BAG=∠BAP+∠PAG=60°.
又因为DB∥FG,
所以∠ABD=∠BAG=60°.
19.(1)∠2=115°,∠4=65°;
(2)如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补;
(3)根据(2),设其中一个角为x°,则另一个角为(2x)°,则
x+2x=180.解得x=60.
故这两个角分别为60°,120°.
