湘教版七年级下册(新)第4章《4.4 平行线的判定》同步练习
文档属性
| 名称 | 湘教版七年级下册(新)第4章《4.4 平行线的判定》同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 142.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-29 00:00:00 | ||
图片预览





文档简介
4.4 平行线的判定
第1课时 平行线的判定方法1
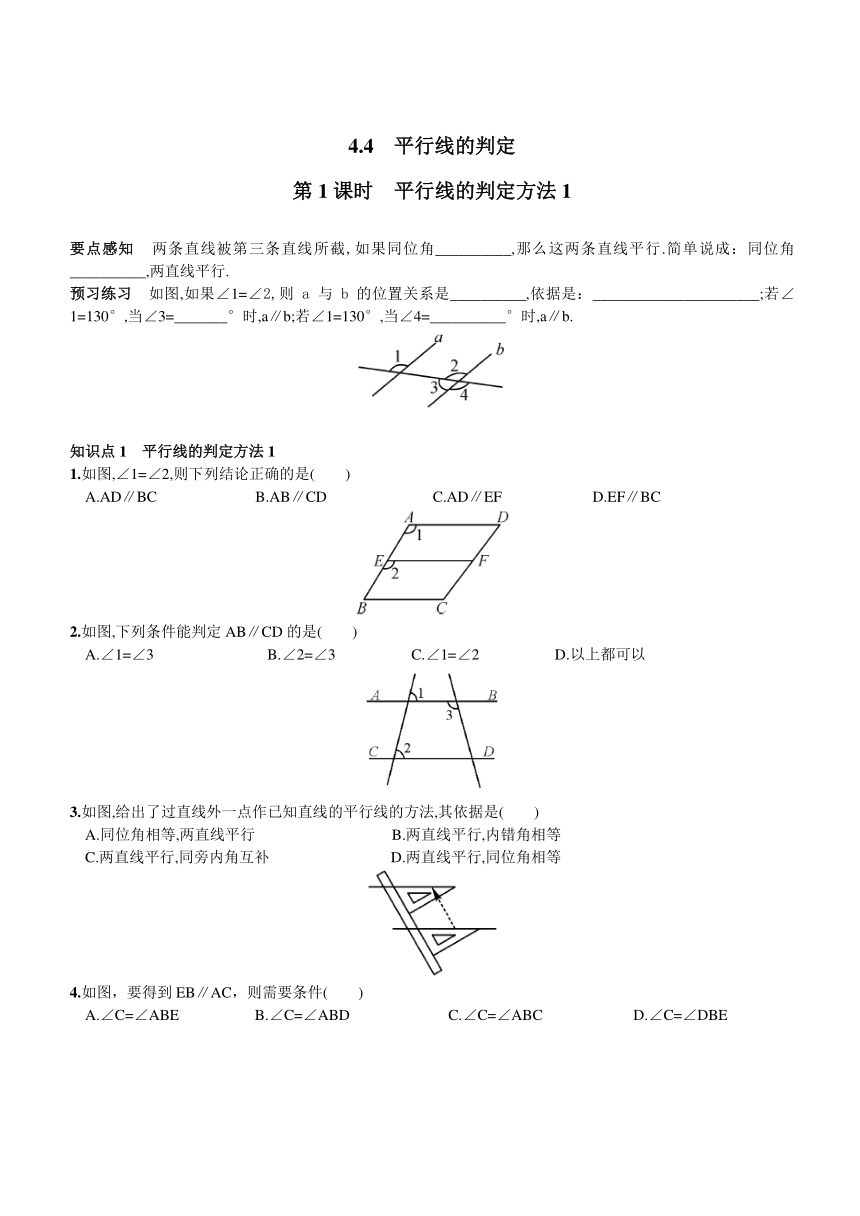
要点感知 两条直线被第三条直线所截,如 ( http: / / www.21cnjy.com )果同位角__________,那么这两条直线平行.简单说成:同位角__________,两直线平行.
预习练习 如图,如果∠1=∠2,则a与b ( http: / / www.21cnjy.com )的位置关系是__________,依据是:______________________;若∠1=130°,当∠3=_______°时,a∥b;若∠1=130°,当∠4=__________°时,a∥b.
( http: / / www.21cnjy.com )
知识点1 平行线的判定方法1
1.如图,∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD C.AD∥EF D.EF∥BC
( http: / / www.21cnjy.com )
2.如图,下列条件能判定AB∥CD的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠2 D.以上都可以
( http: / / www.21cnjy.com )
3.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.两直线平行,内错角相等
C.两直线平行,同旁内角互补 D.两直线平行,同位角相等
( http: / / www.21cnjy.com )
4.如图,要得到EB∥AC,则需要条件( )
A.∠C=∠ABE B.∠C=∠ABD C.∠C=∠ABC D.∠C=∠DBE
( http: / / www.21cnjy.com )
5.如图,∠1=60°,∠2=60°,则直线a与b的位置关系是__________.
( http: / / www.21cnjy.com )
知识点2平行线的判定与性质的综合运用
6.如图,已知∠1=∠2,∠3=80°,则∠4=( )
A.80° B.70° C.60° D.50°
( http: / / www.21cnjy.com )
7.如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
A.35° B.70° C.90° D.110°
( http: / / www.21cnjy.com )
8.如图,请你添加一个条件__________,使AD∥BC.
( http: / / www.21cnjy.com )
9.如图,∠EAD=∠B,∠D=75°,则∠C=__________.
( http: / / www.21cnjy.com )
10.如图,已知AB∥DE,且有∠1=∠2,∠3=∠4,试说明:BC∥EF.
( http: / / www.21cnjy.com )
11.如图,直线a,b被c所截,下面能判定a∥b的是( )
A.∠1=∠2 ( http: / / www.21cnjy.com ) B.∠1=∠4 C.∠3=∠1 D.∠3=∠2
( http: / / www.21cnjy.com )
12.如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有____________________.
( http: / / www.21cnjy.com )
13.(1)如图,因为∠4=∠2(已知),所以__________∥__________(同位角相等,两直线平行);
(2)因为∠3=∠1(已知),所以__________∥__________(同位角相等,两直线平行).
( http: / / www.21cnjy.com )
14.如图,已知:∠1=120°,∠C=60°,说明AB∥CD的理由.
( http: / / www.21cnjy.com )
15.如图,已知∠1=∠2,∠3=∠4,试说明:a∥c.
( http: / / www.21cnjy.com )
16.如图,∠ABC=∠DEF,AB∥DE,AB,EF相交于M,试判断BC,EF是否平行,并说明理由.
( http: / / www.21cnjy.com )
17.如图,AD平分∠BAC,EF平分∠DEC,且∠1=∠2,试说明DE与AB的位置关系.
( http: / / www.21cnjy.com )
18.如图,已知AB∥DC,∠D=125°,∠CBE=55°,AD与BC平行吗?为什么?
( http: / / www.21cnjy.com )
19.如图,已知∠1=∠B,∠2=∠3,问:CD平分∠ACB吗?为什么?
( http: / / www.21cnjy.com )
20.如图,已知直线AB,CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,那么MQ∥NP,试写出推理.
( http: / / www.21cnjy.com )
参考答案
要点感知 相等 相等
预习练习 a∥b 同位角相等,两直线平行 50 130
1.C 2.C 3.A 4.D 5.平行 6.A 7.D 8.∠B=∠EAD 9.105°
10.因为AB∥DE(已知),
所以∠1=∠3(两直线平行,同位角相等).
因为∠1=∠2,∠3=∠4(已知),
所以∠2=∠4(等量代换).
所以BC∥EF(同位角相等,两直线平行).
11.B 12.AB∥CD,EF∥CG
13.(1)BC AD (2)BE CD
14.因为∠1+∠BEF=180°(平角的定义),∠1=120°(已知),
所以∠BEF=60°.
又因为∠C=60°(已知),
所以∠BEF=∠C(等量代换).
所以AB∥CD(同位角相等,两直线平行).
15.因为∠1=∠2,
所以a∥b.
因为∠3=∠4,
所以b∥c.
所以a∥c.
16.BC∥EF.
理由:因为AB∥ED,
所以∠DEF=∠AMF.
又因为∠ABC=∠DEF,
所以∠ABC=∠AMF.
所以BC∥EF.
17.DE∥AB,
因为AD平分∠BAC,
所以∠BAC=2∠1.
因为EF平分∠DEC,
所以∠DEC=2∠2.
因为∠1=∠2,
所以∠BAC=∠DEC,
所以DE∥AB.
18.AD∥BC.
因为AB∥DC(已知),
所以∠A+∠D=180°(两直线平行,同旁内角互补).
因为∠D=125°(已知),
所以∠A=180°-∠D=55°.
因为∠CBE=55°(已知),
所以∠A=∠CBE.
所以AD∥BC(同位角相等,两直线平行).
19.CD平分∠ACB.
理由:因为∠1=∠B,
所以DE∥BC.
所以∠2=∠DCB.
又因为∠2=∠3,
所以∠DCB=∠3.
所以CD平分∠ACB.
20.因为∠BMN=∠DNF,∠1=∠2,
所以∠BMN+∠1=∠DNF+∠2,即∠QMN=∠PNF.
所以MQ∥NP.
第2课时 平行线的判定方法2、3
要点感知1 两条直线被第三条直线所截 ( http: / / www.21cnjy.com ),如果内错角__________,那么这两条直线平行.简单说成:内错角__________,两直线平行.
预习练习1-1 如图,∠1=60°,∠2=60°,则直线a与b的位置关系是__________.
( http: / / www.21cnjy.com )
要点感知2 两条直线被第三条直线 ( http: / / www.21cnjy.com )所截,如果同旁内角__________,那么这两条直线平行.简单说成:同旁内角__________,两直线平行.
预习练习2-1 如图,若∠ABC+∠__________=180°,则AB∥CD.
( http: / / www.21cnjy.com )
知识点1 平行线的判定方法2、3
1.如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180° C.∠ABD=∠BDC D.∠BAC=∠ACD
( http: / / www.21cnjy.com )
2.如图,下列条件中能判断直线l1∥l2的是( )
A.∠1=∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
( http: / / www.21cnjy.com )
3.如图,两直线AB,CD被第三条直线EF所截,∠1=70°,下列说法中,不正确的是( )
A.若∠5=70°,则AB∥CD B.若∠3=70°,则AB∥CD
C.若∠4=70°,则AB∥CD D.若∠4=110°,则AB∥CD
( http: / / www.21cnjy.com )
4.如图,点E是AB上一点,点F是DC上一点,点G是BC延长线上一点.
( http: / / www.21cnjy.com )
(1)如果∠B=∠DCG,可以判断哪两条直线平行?请说明理由;
(2)如果∠DCG=∠D,可以判断哪两条直线平行?请说明理由;
(3)如果∠DFE+∠D=180°,可以判断哪两条直线平行?请说明理由.
知识点2 平行线的判定与性质的综合运用
5.如图,若∠DAC=∠ECA,∠ADB=35°,B在CE上,则∠DBE=( )
A.35° B.135° C.145° D.大小不能确定
( http: / / www.21cnjy.com )
6.如图,∠1=60°,∠2=∠3,则∠ADC=__________.
( http: / / www.21cnjy.com )
7.如图,BD平分∠ABC,∠D=∠1=35°,则∠A=__________°.
( http: / / www.21cnjy.com )
8.如图,已知AB∥CD,∠1=∠2,试说明:BE∥CF.
( http: / / www.21cnjy.com )
9.如图,下列条件:①∠1 ( http: / / www.21cnjy.com )=∠5;②∠2=∠C;③∠3=∠4;④∠3=∠5;⑤∠4+∠5+∠BDE=180°中,能判断DE∥BC的是( )
A.只有②④ B.只有①② C.只有②④⑤ D.只有②
( http: / / www.21cnjy.com )
10.如图,∠1+∠2=180°,∠3=100°,则∠4等于( )
A.70° B.80° C.90° D.100°
( http: / / www.21cnjy.com )
11.如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=__________.
( http: / / www.21cnjy.com )
12.如图,一个弯曲管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD对吗?为什么?
( http: / / www.21cnjy.com )
13.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.试说明:AB∥CD.
( http: / / www.21cnjy.com )
14.如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗 为什么
( http: / / www.21cnjy.com )
15.如图,为了确定一条 ( http: / / www.21cnjy.com )经过点D且与直线AB平行的直线,小明同学在直线AB上取一点C,在直线AB外取一点E,恰好量得∠2=80°,∠D=50°,∠1=∠3,这时,小明说AB与DE平行了,他说得对吗?为什么?
( http: / / www.21cnjy.com )
16.如图,已知∠A=∠F,∠C=∠D.试问BD是否与CE平行?为什么?
( http: / / www.21cnjy.com )
17.如图,∠1=60°,∠2=60°,∠3=100°.要使AB∥EF,∠4应为多少度?说明理由.
( http: / / www.21cnjy.com )
参考答案
要点感知1 相等 相等
预习练习1-1 平行
要点感知2 互补 互补
预习练习2-1 BCD
1.A 2.C 3.C
4.(1)因为∠B=∠DCG,
所以AB∥CD(同位角相等,两直线平行).
(2)因为∠DCG=∠D,
所以AD∥BC(内错角相等,两直线平行).
(3)因为∠DFE+∠D=180°,
所以AD∥EF(同旁内角互补,两直线平行).
5.C 6.60° 7.110
8.因为AB∥CD,
所以∠ABC=∠BCD.
因为∠1=∠2,
所以∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF.
所以BE∥CF.
9.C 10.D 11.63°30′
12.对.
因为AB,CD可以看作两条线段,由 ( http: / / www.21cnjy.com )于∠ABC和∠BCD是同旁内角,且∠ABC+∠BCD=120°+60°=180°,根据“同旁内角互补,两直线平行”可知AB∥CD.
13.因为∠ACD=70°,∠ACB=60°,
所以∠BCD=130°.
又因为∠ABC=50°,
所以∠BCD+∠ABC=180°.
所以AB∥CD.
14.平行.
理由:因为∠1=∠2,
所以a∥b.
又因为∠3+∠4=180°,
所以b∥c.
所以a∥c.
15.对.
理由:因为∠2=80°,∠1=∠3,
所以2∠1+∠2=180°.
所以∠1=∠3=50°.
又因为∠D=50°,
所以∠1=∠D.
所以AB∥DE.
16.BD∥CE.
理由:因为∠A=∠F,
所以DF∥AC.
所以∠D=∠DBA.
又因为∠C=∠D,
所以∠DBA=∠C.
所以BD∥CE.
17.∠4应为100°.
理由是:因为∠1=∠2=60°,
所以AB∥CD.
当∠4=100°时,
因为∠3=100°,
所以∠4=∠3=100°,
所以CD∥EF.
又因为AB∥CD,
所以AB∥EF.
第1课时 平行线的判定方法1
要点感知 两条直线被第三条直线所截,如 ( http: / / www.21cnjy.com )果同位角__________,那么这两条直线平行.简单说成:同位角__________,两直线平行.
预习练习 如图,如果∠1=∠2,则a与b ( http: / / www.21cnjy.com )的位置关系是__________,依据是:______________________;若∠1=130°,当∠3=_______°时,a∥b;若∠1=130°,当∠4=__________°时,a∥b.
( http: / / www.21cnjy.com )
知识点1 平行线的判定方法1
1.如图,∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD C.AD∥EF D.EF∥BC
( http: / / www.21cnjy.com )
2.如图,下列条件能判定AB∥CD的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠2 D.以上都可以
( http: / / www.21cnjy.com )
3.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.两直线平行,内错角相等
C.两直线平行,同旁内角互补 D.两直线平行,同位角相等
( http: / / www.21cnjy.com )
4.如图,要得到EB∥AC,则需要条件( )
A.∠C=∠ABE B.∠C=∠ABD C.∠C=∠ABC D.∠C=∠DBE
( http: / / www.21cnjy.com )
5.如图,∠1=60°,∠2=60°,则直线a与b的位置关系是__________.
( http: / / www.21cnjy.com )
知识点2平行线的判定与性质的综合运用
6.如图,已知∠1=∠2,∠3=80°,则∠4=( )
A.80° B.70° C.60° D.50°
( http: / / www.21cnjy.com )
7.如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
A.35° B.70° C.90° D.110°
( http: / / www.21cnjy.com )
8.如图,请你添加一个条件__________,使AD∥BC.
( http: / / www.21cnjy.com )
9.如图,∠EAD=∠B,∠D=75°,则∠C=__________.
( http: / / www.21cnjy.com )
10.如图,已知AB∥DE,且有∠1=∠2,∠3=∠4,试说明:BC∥EF.
( http: / / www.21cnjy.com )
11.如图,直线a,b被c所截,下面能判定a∥b的是( )
A.∠1=∠2 ( http: / / www.21cnjy.com ) B.∠1=∠4 C.∠3=∠1 D.∠3=∠2
( http: / / www.21cnjy.com )
12.如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有____________________.
( http: / / www.21cnjy.com )
13.(1)如图,因为∠4=∠2(已知),所以__________∥__________(同位角相等,两直线平行);
(2)因为∠3=∠1(已知),所以__________∥__________(同位角相等,两直线平行).
( http: / / www.21cnjy.com )
14.如图,已知:∠1=120°,∠C=60°,说明AB∥CD的理由.
( http: / / www.21cnjy.com )
15.如图,已知∠1=∠2,∠3=∠4,试说明:a∥c.
( http: / / www.21cnjy.com )
16.如图,∠ABC=∠DEF,AB∥DE,AB,EF相交于M,试判断BC,EF是否平行,并说明理由.
( http: / / www.21cnjy.com )
17.如图,AD平分∠BAC,EF平分∠DEC,且∠1=∠2,试说明DE与AB的位置关系.
( http: / / www.21cnjy.com )
18.如图,已知AB∥DC,∠D=125°,∠CBE=55°,AD与BC平行吗?为什么?
( http: / / www.21cnjy.com )
19.如图,已知∠1=∠B,∠2=∠3,问:CD平分∠ACB吗?为什么?
( http: / / www.21cnjy.com )
20.如图,已知直线AB,CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,那么MQ∥NP,试写出推理.
( http: / / www.21cnjy.com )
参考答案
要点感知 相等 相等
预习练习 a∥b 同位角相等,两直线平行 50 130
1.C 2.C 3.A 4.D 5.平行 6.A 7.D 8.∠B=∠EAD 9.105°
10.因为AB∥DE(已知),
所以∠1=∠3(两直线平行,同位角相等).
因为∠1=∠2,∠3=∠4(已知),
所以∠2=∠4(等量代换).
所以BC∥EF(同位角相等,两直线平行).
11.B 12.AB∥CD,EF∥CG
13.(1)BC AD (2)BE CD
14.因为∠1+∠BEF=180°(平角的定义),∠1=120°(已知),
所以∠BEF=60°.
又因为∠C=60°(已知),
所以∠BEF=∠C(等量代换).
所以AB∥CD(同位角相等,两直线平行).
15.因为∠1=∠2,
所以a∥b.
因为∠3=∠4,
所以b∥c.
所以a∥c.
16.BC∥EF.
理由:因为AB∥ED,
所以∠DEF=∠AMF.
又因为∠ABC=∠DEF,
所以∠ABC=∠AMF.
所以BC∥EF.
17.DE∥AB,
因为AD平分∠BAC,
所以∠BAC=2∠1.
因为EF平分∠DEC,
所以∠DEC=2∠2.
因为∠1=∠2,
所以∠BAC=∠DEC,
所以DE∥AB.
18.AD∥BC.
因为AB∥DC(已知),
所以∠A+∠D=180°(两直线平行,同旁内角互补).
因为∠D=125°(已知),
所以∠A=180°-∠D=55°.
因为∠CBE=55°(已知),
所以∠A=∠CBE.
所以AD∥BC(同位角相等,两直线平行).
19.CD平分∠ACB.
理由:因为∠1=∠B,
所以DE∥BC.
所以∠2=∠DCB.
又因为∠2=∠3,
所以∠DCB=∠3.
所以CD平分∠ACB.
20.因为∠BMN=∠DNF,∠1=∠2,
所以∠BMN+∠1=∠DNF+∠2,即∠QMN=∠PNF.
所以MQ∥NP.
第2课时 平行线的判定方法2、3
要点感知1 两条直线被第三条直线所截 ( http: / / www.21cnjy.com ),如果内错角__________,那么这两条直线平行.简单说成:内错角__________,两直线平行.
预习练习1-1 如图,∠1=60°,∠2=60°,则直线a与b的位置关系是__________.
( http: / / www.21cnjy.com )
要点感知2 两条直线被第三条直线 ( http: / / www.21cnjy.com )所截,如果同旁内角__________,那么这两条直线平行.简单说成:同旁内角__________,两直线平行.
预习练习2-1 如图,若∠ABC+∠__________=180°,则AB∥CD.
( http: / / www.21cnjy.com )
知识点1 平行线的判定方法2、3
1.如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180° C.∠ABD=∠BDC D.∠BAC=∠ACD
( http: / / www.21cnjy.com )
2.如图,下列条件中能判断直线l1∥l2的是( )
A.∠1=∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
( http: / / www.21cnjy.com )
3.如图,两直线AB,CD被第三条直线EF所截,∠1=70°,下列说法中,不正确的是( )
A.若∠5=70°,则AB∥CD B.若∠3=70°,则AB∥CD
C.若∠4=70°,则AB∥CD D.若∠4=110°,则AB∥CD
( http: / / www.21cnjy.com )
4.如图,点E是AB上一点,点F是DC上一点,点G是BC延长线上一点.
( http: / / www.21cnjy.com )
(1)如果∠B=∠DCG,可以判断哪两条直线平行?请说明理由;
(2)如果∠DCG=∠D,可以判断哪两条直线平行?请说明理由;
(3)如果∠DFE+∠D=180°,可以判断哪两条直线平行?请说明理由.
知识点2 平行线的判定与性质的综合运用
5.如图,若∠DAC=∠ECA,∠ADB=35°,B在CE上,则∠DBE=( )
A.35° B.135° C.145° D.大小不能确定
( http: / / www.21cnjy.com )
6.如图,∠1=60°,∠2=∠3,则∠ADC=__________.
( http: / / www.21cnjy.com )
7.如图,BD平分∠ABC,∠D=∠1=35°,则∠A=__________°.
( http: / / www.21cnjy.com )
8.如图,已知AB∥CD,∠1=∠2,试说明:BE∥CF.
( http: / / www.21cnjy.com )
9.如图,下列条件:①∠1 ( http: / / www.21cnjy.com )=∠5;②∠2=∠C;③∠3=∠4;④∠3=∠5;⑤∠4+∠5+∠BDE=180°中,能判断DE∥BC的是( )
A.只有②④ B.只有①② C.只有②④⑤ D.只有②
( http: / / www.21cnjy.com )
10.如图,∠1+∠2=180°,∠3=100°,则∠4等于( )
A.70° B.80° C.90° D.100°
( http: / / www.21cnjy.com )
11.如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=__________.
( http: / / www.21cnjy.com )
12.如图,一个弯曲管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD对吗?为什么?
( http: / / www.21cnjy.com )
13.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.试说明:AB∥CD.
( http: / / www.21cnjy.com )
14.如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗 为什么
( http: / / www.21cnjy.com )
15.如图,为了确定一条 ( http: / / www.21cnjy.com )经过点D且与直线AB平行的直线,小明同学在直线AB上取一点C,在直线AB外取一点E,恰好量得∠2=80°,∠D=50°,∠1=∠3,这时,小明说AB与DE平行了,他说得对吗?为什么?
( http: / / www.21cnjy.com )
16.如图,已知∠A=∠F,∠C=∠D.试问BD是否与CE平行?为什么?
( http: / / www.21cnjy.com )
17.如图,∠1=60°,∠2=60°,∠3=100°.要使AB∥EF,∠4应为多少度?说明理由.
( http: / / www.21cnjy.com )
参考答案
要点感知1 相等 相等
预习练习1-1 平行
要点感知2 互补 互补
预习练习2-1 BCD
1.A 2.C 3.C
4.(1)因为∠B=∠DCG,
所以AB∥CD(同位角相等,两直线平行).
(2)因为∠DCG=∠D,
所以AD∥BC(内错角相等,两直线平行).
(3)因为∠DFE+∠D=180°,
所以AD∥EF(同旁内角互补,两直线平行).
5.C 6.60° 7.110
8.因为AB∥CD,
所以∠ABC=∠BCD.
因为∠1=∠2,
所以∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF.
所以BE∥CF.
9.C 10.D 11.63°30′
12.对.
因为AB,CD可以看作两条线段,由 ( http: / / www.21cnjy.com )于∠ABC和∠BCD是同旁内角,且∠ABC+∠BCD=120°+60°=180°,根据“同旁内角互补,两直线平行”可知AB∥CD.
13.因为∠ACD=70°,∠ACB=60°,
所以∠BCD=130°.
又因为∠ABC=50°,
所以∠BCD+∠ABC=180°.
所以AB∥CD.
14.平行.
理由:因为∠1=∠2,
所以a∥b.
又因为∠3+∠4=180°,
所以b∥c.
所以a∥c.
15.对.
理由:因为∠2=80°,∠1=∠3,
所以2∠1+∠2=180°.
所以∠1=∠3=50°.
又因为∠D=50°,
所以∠1=∠D.
所以AB∥DE.
16.BD∥CE.
理由:因为∠A=∠F,
所以DF∥AC.
所以∠D=∠DBA.
又因为∠C=∠D,
所以∠DBA=∠C.
所以BD∥CE.
17.∠4应为100°.
理由是:因为∠1=∠2=60°,
所以AB∥CD.
当∠4=100°时,
因为∠3=100°,
所以∠4=∠3=100°,
所以CD∥EF.
又因为AB∥CD,
所以AB∥EF.
