湘教版七年级下册(新)第4章《4.5 垂线》同步练习
文档属性
| 名称 | 湘教版七年级下册(新)第4章《4.5 垂线》同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 152.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-29 00:00:00 | ||
图片预览

文档简介
4.5 垂线
第1课时 垂线
要点感知1 两条直线相交所成的四个角中 ( http: / / www.21cnjy.com ),如果有一个是__________角时,这两条直线叫做互相垂直.其中一条直线叫做另一条的__________,它们的交点叫__________.
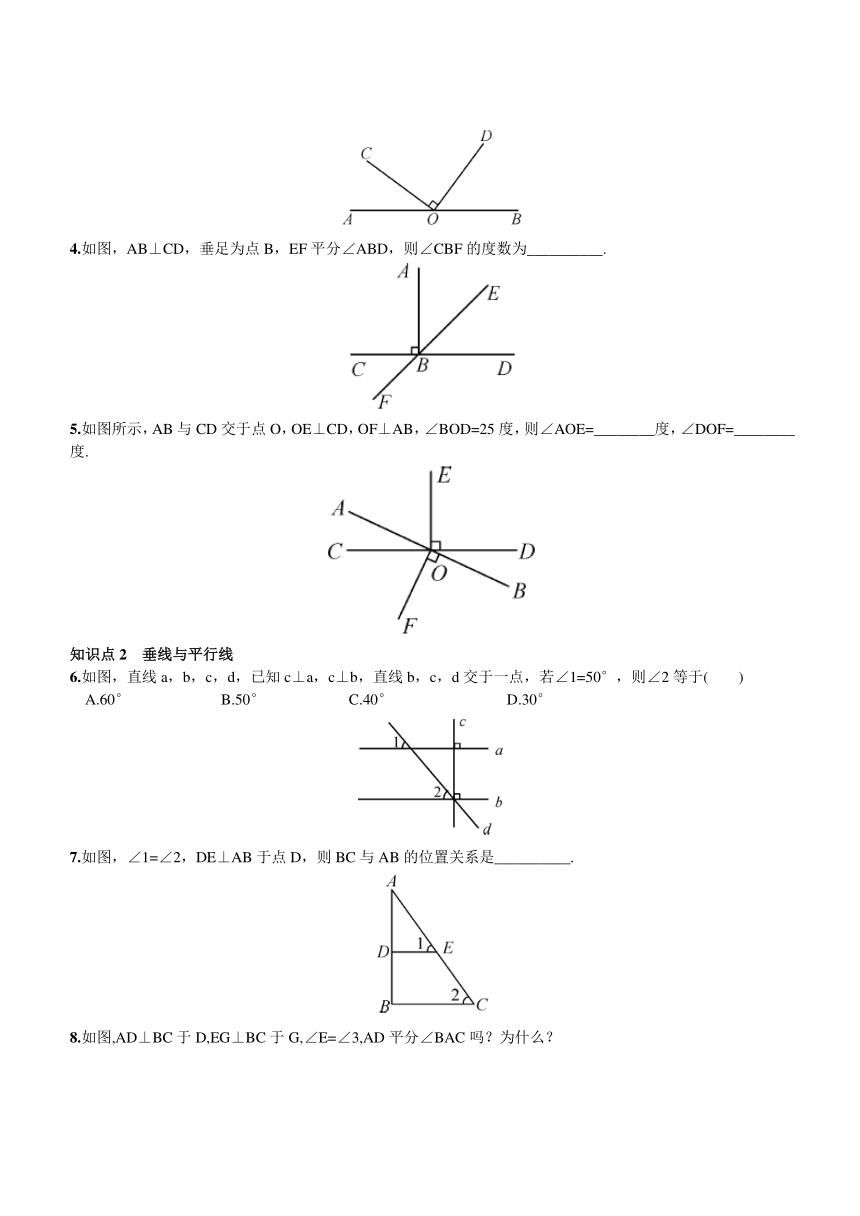
预习练习1-1 如图,∠PQR等于138°,SQ⊥QR,QT⊥PQ,则∠SQT等于__________.
( http: / / www.21cnjy.com )
要点感知2 在同一平面内,垂直于同一条直线的两条直线__________.
预习练习2-1 在同一平面内,若a⊥b,c⊥b,d∥c,则a与d的位置关系是__________.
要点感知3 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线____________________.
预习练习3-1 直线a,b,c中,若a⊥b,b∥c,则a,c的位置关系是__________.
知识点1 垂线的概念
1.如图,OA⊥OB,若∠1=40°,则∠2的度数是( )
A.20° B.40° C.50° D.60°
( http: / / www.21cnjy.com )
2.如图,平面内三条直线交于点O,∠1=30°,∠2=60°,AB与CD的关系是( )
A.平行 B.垂直 C.重合 D.以上均有可能
( http: / / www.21cnjy.com )
3.如图,点O在直线AB上,且OC⊥OD.若∠COA=36°,则∠DOB的大小为( )
A.36° B.54° C.64° D.72°
( http: / / www.21cnjy.com )
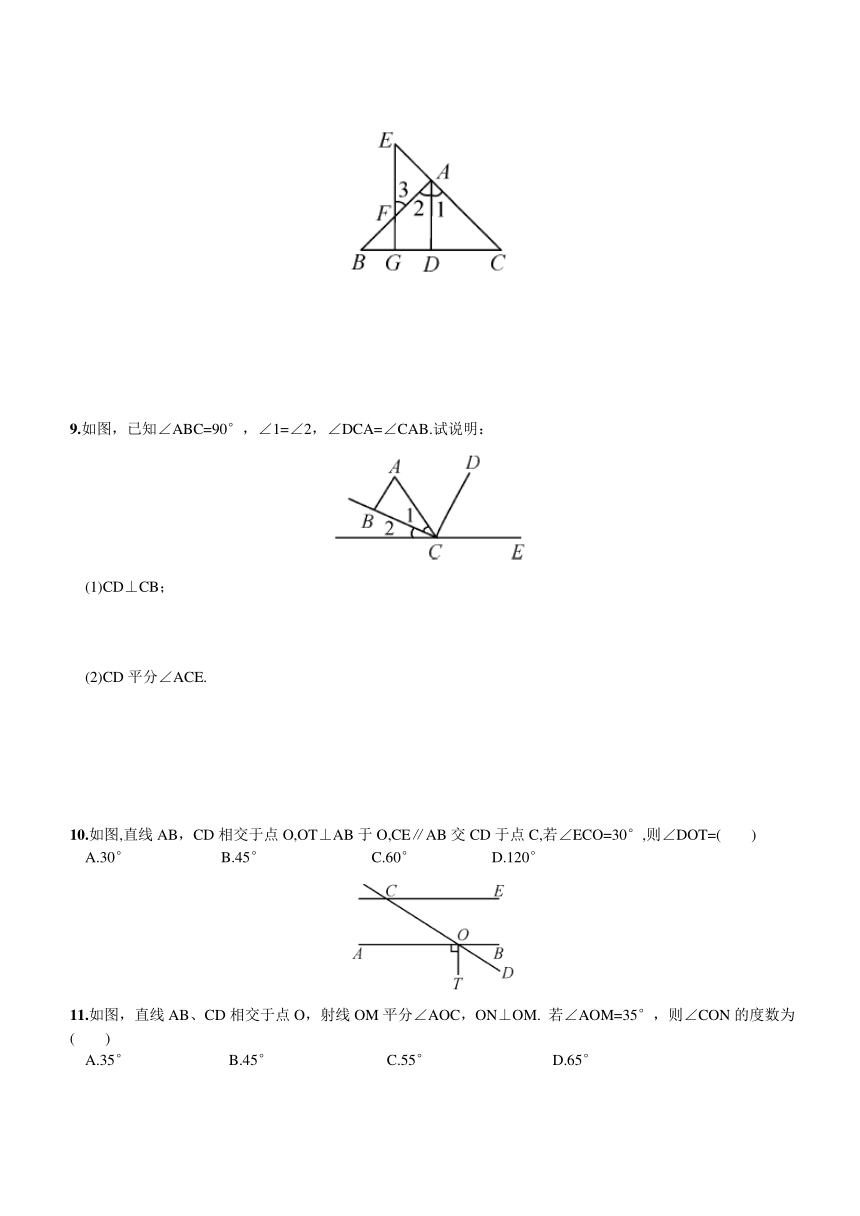
4.如图,AB⊥CD,垂足为点B,EF平分∠ABD,则∠CBF的度数为__________.
( http: / / www.21cnjy.com )
5.如图所示,AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25度,则∠AOE=________度,∠DOF=________度.
( http: / / www.21cnjy.com )
知识点2 垂线与平行线
6.如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2等于( )
A.60° B.50° C.40° D.30°
( http: / / www.21cnjy.com )
7.如图,∠1=∠2,DE⊥AB于点D,则BC与AB的位置关系是__________.
( http: / / www.21cnjy.com )
8.如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,AD平分∠BAC吗?为什么?
( http: / / www.21cnjy.com )
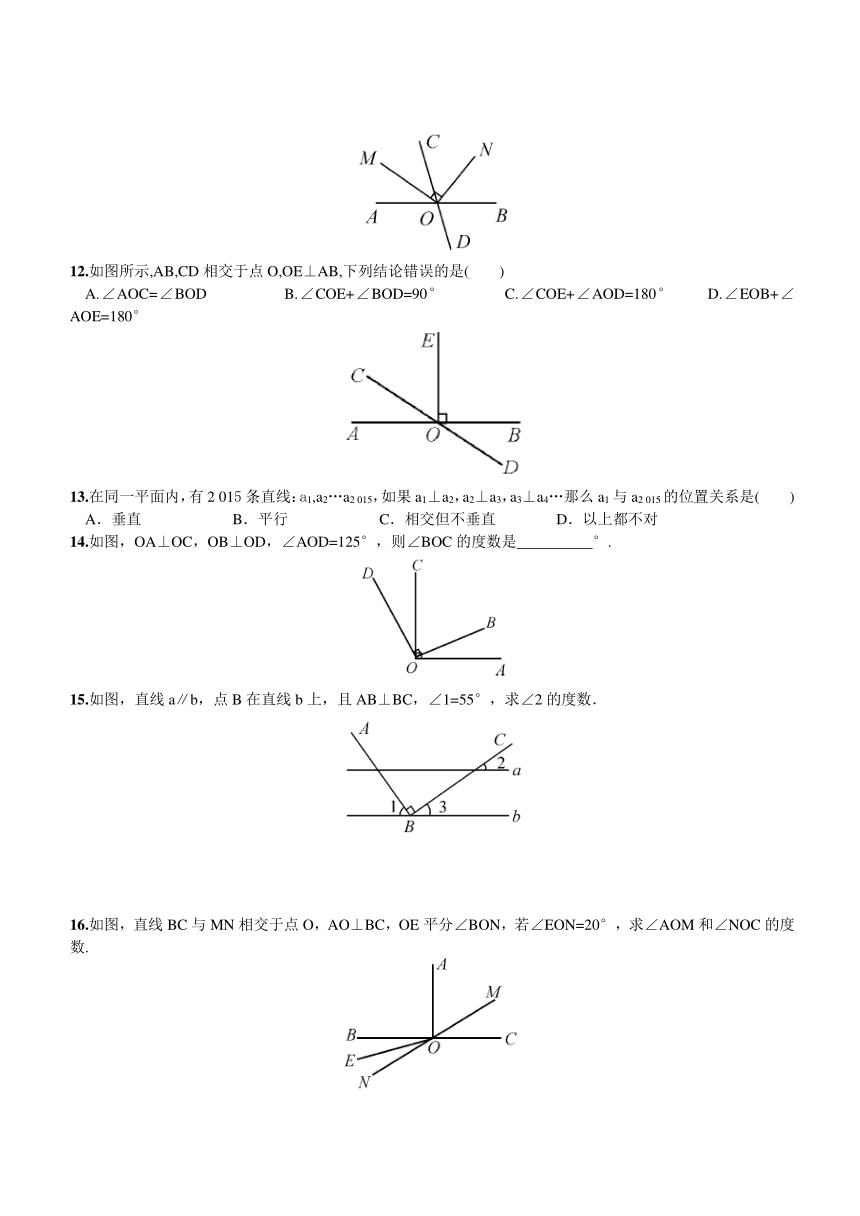
9.如图,已知∠ABC=90°,∠1=∠2,∠DCA=∠CAB.试说明:
( http: / / www.21cnjy.com )
(1)CD⊥CB;
(2)CD平分∠ACE.
10.如图,直线AB,CD相交于点O,OT⊥AB于O,CE∥AB交CD于点C,若∠ECO=30°,则∠DOT=( )
A.30° B.45° C.60° D.120°
( http: / / www.21cnjy.com )
11.如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM. 若∠AOM=35°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
( http: / / www.21cnjy.com )
12.如图所示,AB,CD相交于点O,OE⊥AB,下列结论错误的是( )
A.∠AOC=∠BOD B.∠COE+∠BOD=90° C.∠COE+∠AOD=180° D.∠EOB+∠AOE=180°
( http: / / www.21cnjy.com )
13.在同一平面内,有2 015条直线:a ( http: / / www.21cnjy.com )1,a2…a2 015,如果a1⊥a2,a2⊥a3,a3⊥a4…那么a1与a2 015的位置关系是( )
A.垂直 B.平行 C.相交但不垂直 D.以上都不对
14.如图,OA⊥OC,OB⊥OD,∠AOD=125°,则∠BOC的度数是__________°.
( http: / / www.21cnjy.com )
15.如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,求∠2的度数.
( http: / / www.21cnjy.com )
16.如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20°,求∠AOM和∠NOC的度数.
( http: / / www.21cnjy.com )
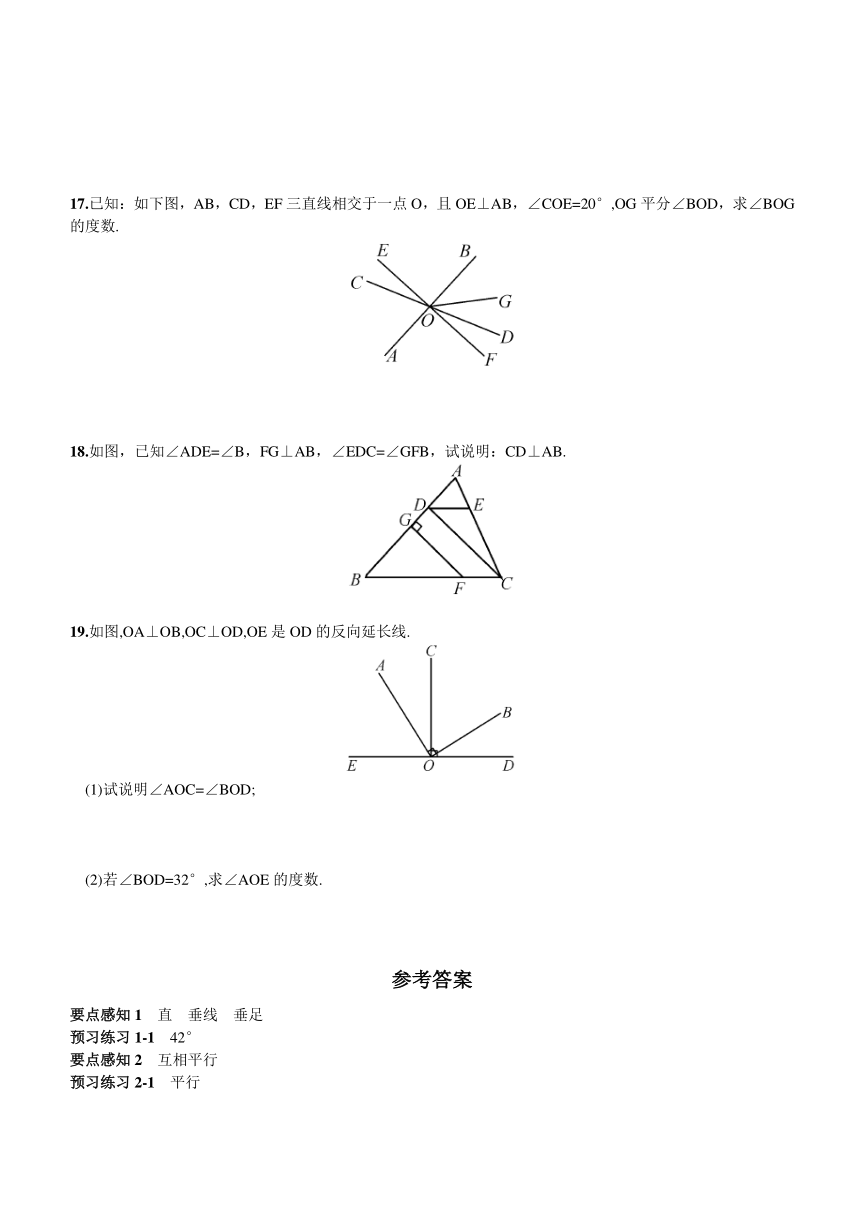
17.已知:如下图,AB,CD,EF三直线相交于一点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,求∠BOG的度数.
( http: / / www.21cnjy.com )
18.如图,已知∠ADE=∠B,FG⊥AB,∠EDC=∠GFB,试说明:CD⊥AB.
( http: / / www.21cnjy.com )
19.如图,OA⊥OB,OC⊥OD,OE是OD的反向延长线.
( http: / / www.21cnjy.com )
(1)试说明∠AOC=∠BOD;
(2)若∠BOD=32°,求∠AOE的度数.
参考答案
要点感知1 直 垂线 垂足
预习练习1-1 42°
要点感知2 互相平行
预习练习2-1 平行
要点感知3 垂直于另一条直线
预习练习3-1 垂直
1.C 2.B 3.B 4.45° 5.65 115 6.B 7.垂直
8.AD平分∠BAC.
因为AD⊥BC,EG⊥BC,
所以AD∥EG.
所以∠1=∠E,∠2=∠3.
因为∠3=∠E,
所以∠1=∠2.
所以AD平分∠BAC.
9.(1)因为∠DCA=∠CAB,
所以AB∥CD.
又因为∠ABC=90°,
所以AB⊥CB.
所以CD⊥CB.
(2)因为∠DCA+∠1=90°,
所以∠DCE+∠2=90°.
又因为∠1=∠2,
所以∠DCA=∠DCE.
所以CD平分∠ACE.
10.C 11.C 12.C 13.B 14.55
15.因为AB⊥BC,
所以∠1+∠3=90°.
因为∠1=55°,
所以∠3=35°.
因为a∥b,
所以∠2=∠3=35°.
16.因为OE平分∠BON,∠EON=20°,
所以∠BON=2∠EON=40°.
所以∠NOC=180°-∠BON=140°,∠MOC=∠BON=40°.
又因为AO⊥BC,
所以∠AOC=90°.
所以∠AOM=∠AOC-∠MOC=50°.
即∠NOC=140°,∠AOM=50°.
17.因为OE⊥AB,
所以∠AOE=90°.
因为∠COE=20°,
所以∠AOC=90°-20°=70°.
所以∠BOD=∠AOC=70°.
因为OG平分∠BOD,
所以∠BOG=∠BOD=35°.
18.因为∠ADE=∠B,
所以DE∥BC.
所以∠EDC=∠DCB.
因为∠EDC=∠GFB,
所以∠DCB=∠GFB.
所以FG∥CD.
因为FG⊥AB,
所以CD⊥AB.
19.(1)因为OA⊥OB,OC⊥OD,
所以∠AOC+∠BOC=90°,∠BOD+∠BOC=90°.
所以∠AOC=∠BOD(同角的余角相等).
(2)因为OA⊥OB,
所以∠AOB=90°.
所以∠AOE=180°-∠AOB-∠BOD=180°-90°-32°=58°.
第2课时 垂线段与点到直线的距离
要点感知1 在同一平面内,过一点__________直线与已知直线垂直.
预习练习1-1 过直线AB上一点P,在同一平面内画AB的垂线,可以画的条数是( )
A.0 B.1 C.2 D.无数条
要点感知2 直线外一点与直线上各点连接的所有线段中,__________最短.简单说成:__________最短.
预习练习2-1 如图,计 ( http: / / www.21cnjy.com )划把河AB中的水引到水池C中,可以先作CD⊥AB,垂足为D,然后沿CD开渠,则能使所打开的水渠最短,这种方案的设计根据是____________________.
( http: / / www.21cnjy.com )
要点感知3 从直线外一点到这条直线的__________的长度,叫做点到直线的距离.
预习练习3-1 点到直线的距离是指( )
A.从直线外一点到这条直线的连线
B.从直线外一点到这条直线的垂线段
C.从直线外一点到这条直线的垂线的长
D.从直线外一点到这条直线的垂线段的长
3-2 如图,三角形ABC中,CD⊥AC,CE⊥AB,垂足分别是C,E,那么点C到线段AB的距离是线段__________的长度.
( http: / / www.21cnjy.com )
知识点1 垂线、垂线段及其性质
1.如图,已知ON⊥a,OM⊥a,可以推断出OM与ON重合的理由是( )
( http: / / www.21cnjy.com )
A.两点确定一条直线
B.过一点只能作一条直线
C.垂线段最短
D.在平面内,过一点有且只有一条直线与已知直线垂直
2.如图,三角形ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP的长不可能是( )
A.2.5 B.3 C.4 D.5
( http: / / www.21cnjy.com )
3.如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是PB,理由是____________________.
( http: / / www.21cnjy.com )
4.如图,某人站在马路的左侧A点处,要到路的右侧,怎样走最近?为什么?如果他要到马路对面的B点处,怎样走最近?为什么?
( http: / / www.21cnjy.com )
知识点2 点到直线的距离
5.P为直线l外一点,A,B,C为l上三点,且PB⊥l,那么下列说法正确的是( )
A.线段PA的长度是点P到直线l的距离
B.线段PB的长度是点P到直线l的距离
C.线段PC的长度是点P到直线l的距离
D.线段AC的长度是点A到PC的距离
6.如图,AB⊥BC,BD⊥AC,能表示点到直线的距离的线段共有( )
A.2条 B.3条 C.4条 D.5条
( http: / / www.21cnjy.com )
7.如图,A,D是直线l1上两点, ( http: / / www.21cnjy.com )B,C是直线l2上两点,且AB⊥BC,CD⊥AD,点A到直线l2的距离是线段______的长,点C与l1的距离是线段__________的长.
( http: / / www.21cnjy.com )
8.如图,AC⊥BC,C为垂足,CD⊥AB, ( http: / / www.21cnjy.com )D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC=6,那么点C到AB的距离是,点A到BC的距离是__________,点B到CD的距离是__________.
( http: / / www.21cnjy.com )
9.已知直线AB,CB ,l 在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
( http: / / www.21cnjy.com )
10.下列说法正确的有( )
①在平面内,过直线上一 ( http: / / www.21cnjy.com )点有且只有一条直线垂直于已知直线;②在平面内,过直线外一点有且只有一条直线垂直于已知直线;③在平面内,过一点任意画一条直线垂直于已知直线;④在平面内,有且只有一条直线垂直于已知直线.
A.1个 B.2个 C.3个 D.4个
11.如图,这是一条马路上的人行横道线,即斑马线的示意图,请你根据图示判断,在过马路时三条线路AC、AB、AD中最短的是( )
A.AC B.AB C.AD D.不确定
( http: / / www.21cnjy.com )
12.下列说法中正确的是( )
A.有且只有一条直线垂直于已知直线
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
C.互相垂直的两条线段一定相交
D.直线c外一点A与直线c上各点连接而成的所有线段中最短线段的长是3 cm,则点A到直线c的距离是3 cm
13.点P为直线l外一点,点A、B、C在直线l上,若PA=3 cm,PB=4 cm,PC=6 cm,则点P到直线l的距离是( )
A.3 cm B.小于3 cm C.小于或等于3 cm D.4 cm
14.如图所示,AD⊥BD,BC⊥CD,AB=5 cm,BC=3 cm,则BD的长度的取值范围是( )
A.大于3 cm B.小于5 cm C.大于3 cm或小于5 cm D.大于3 cm且小于5 cm
( http: / / www.21cnjy.com )
15.如图,从学校到公路最近的是__________号路线,数学道理是____________________.
( http: / / www.21cnjy.com )
16.如图,从B村经A村到河边修一条道路,怎样修使道路最短?并说明道理.
( http: / / www.21cnjy.com )
17.如图,分别画出点A到BC的垂线段,并量出点A到BC的距离.
( http: / / www.21cnjy.com )
18.如图:在三角形ABC中,∠BCA=90°,CD⊥AB于点D,线段AB,BC,CD的大小顺序如何,并说明理由.
( http: / / www.21cnjy.com )
19.如图,DE⊥EF,EF=8,DE=15,DF=17.
( http: / / www.21cnjy.com )
(1)试说出点F到直线DE的距离,点D到直线EF的距离;
(2)点E到直线DF的距离是多少?你是怎样求得的?
参考答案
要点感知1 有且只有一条
预习练习1-1 B
要点感知2 垂线段 垂线段
预习练习2-1 垂线段最短
要点感知3 垂线段
预习练习3-1 D
3-2 CE
1.D 2.A 3.垂线段最短
4.此人要走到马路的右侧,可沿A点到马 ( http: / / www.21cnjy.com )路右侧的垂线段走,因为直线外一点到直线的垂线段最短.要到B点处,可沿线段AB走,因为两点之间线段最短.
5.B 6.D 7.AB CD 8.4.8 6 6.4
9.C 10.B 11.B 12.D 13.C 14.D 15.② 垂线段最短
16.连接AB,过点A作AC垂直于河岸线于点C.
理由:两点之间,线段最短;
直线外一点与直线上各点连接的所有线段中,垂线段最短.
17.作图略.
18.因为CD⊥AB于点D,
所以BC>CD.
因为∠BCA=90°,
所以BC⊥AC.
所以AB>BC.
所以AB>BC>CD.
19.(1)因为DE⊥EF,EF=8,DE=15,
所以点F到直线DE的距离,点D到直线EF的距离分别是:8,15.
(2)设点E到直线DF的距离为h,三角形DEF的面积=DE·EF=DF·h,
所以17h=8×15,
所以h=.
所以点E到直线DF的距离为.
第1课时 垂线
要点感知1 两条直线相交所成的四个角中 ( http: / / www.21cnjy.com ),如果有一个是__________角时,这两条直线叫做互相垂直.其中一条直线叫做另一条的__________,它们的交点叫__________.
预习练习1-1 如图,∠PQR等于138°,SQ⊥QR,QT⊥PQ,则∠SQT等于__________.
( http: / / www.21cnjy.com )
要点感知2 在同一平面内,垂直于同一条直线的两条直线__________.
预习练习2-1 在同一平面内,若a⊥b,c⊥b,d∥c,则a与d的位置关系是__________.
要点感知3 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线____________________.
预习练习3-1 直线a,b,c中,若a⊥b,b∥c,则a,c的位置关系是__________.
知识点1 垂线的概念
1.如图,OA⊥OB,若∠1=40°,则∠2的度数是( )
A.20° B.40° C.50° D.60°
( http: / / www.21cnjy.com )
2.如图,平面内三条直线交于点O,∠1=30°,∠2=60°,AB与CD的关系是( )
A.平行 B.垂直 C.重合 D.以上均有可能
( http: / / www.21cnjy.com )
3.如图,点O在直线AB上,且OC⊥OD.若∠COA=36°,则∠DOB的大小为( )
A.36° B.54° C.64° D.72°
( http: / / www.21cnjy.com )
4.如图,AB⊥CD,垂足为点B,EF平分∠ABD,则∠CBF的度数为__________.
( http: / / www.21cnjy.com )
5.如图所示,AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25度,则∠AOE=________度,∠DOF=________度.
( http: / / www.21cnjy.com )
知识点2 垂线与平行线
6.如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2等于( )
A.60° B.50° C.40° D.30°
( http: / / www.21cnjy.com )
7.如图,∠1=∠2,DE⊥AB于点D,则BC与AB的位置关系是__________.
( http: / / www.21cnjy.com )
8.如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,AD平分∠BAC吗?为什么?
( http: / / www.21cnjy.com )
9.如图,已知∠ABC=90°,∠1=∠2,∠DCA=∠CAB.试说明:
( http: / / www.21cnjy.com )
(1)CD⊥CB;
(2)CD平分∠ACE.
10.如图,直线AB,CD相交于点O,OT⊥AB于O,CE∥AB交CD于点C,若∠ECO=30°,则∠DOT=( )
A.30° B.45° C.60° D.120°
( http: / / www.21cnjy.com )
11.如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM. 若∠AOM=35°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
( http: / / www.21cnjy.com )
12.如图所示,AB,CD相交于点O,OE⊥AB,下列结论错误的是( )
A.∠AOC=∠BOD B.∠COE+∠BOD=90° C.∠COE+∠AOD=180° D.∠EOB+∠AOE=180°
( http: / / www.21cnjy.com )
13.在同一平面内,有2 015条直线:a ( http: / / www.21cnjy.com )1,a2…a2 015,如果a1⊥a2,a2⊥a3,a3⊥a4…那么a1与a2 015的位置关系是( )
A.垂直 B.平行 C.相交但不垂直 D.以上都不对
14.如图,OA⊥OC,OB⊥OD,∠AOD=125°,则∠BOC的度数是__________°.
( http: / / www.21cnjy.com )
15.如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,求∠2的度数.
( http: / / www.21cnjy.com )
16.如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20°,求∠AOM和∠NOC的度数.
( http: / / www.21cnjy.com )
17.已知:如下图,AB,CD,EF三直线相交于一点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,求∠BOG的度数.
( http: / / www.21cnjy.com )
18.如图,已知∠ADE=∠B,FG⊥AB,∠EDC=∠GFB,试说明:CD⊥AB.
( http: / / www.21cnjy.com )
19.如图,OA⊥OB,OC⊥OD,OE是OD的反向延长线.
( http: / / www.21cnjy.com )
(1)试说明∠AOC=∠BOD;
(2)若∠BOD=32°,求∠AOE的度数.
参考答案
要点感知1 直 垂线 垂足
预习练习1-1 42°
要点感知2 互相平行
预习练习2-1 平行
要点感知3 垂直于另一条直线
预习练习3-1 垂直
1.C 2.B 3.B 4.45° 5.65 115 6.B 7.垂直
8.AD平分∠BAC.
因为AD⊥BC,EG⊥BC,
所以AD∥EG.
所以∠1=∠E,∠2=∠3.
因为∠3=∠E,
所以∠1=∠2.
所以AD平分∠BAC.
9.(1)因为∠DCA=∠CAB,
所以AB∥CD.
又因为∠ABC=90°,
所以AB⊥CB.
所以CD⊥CB.
(2)因为∠DCA+∠1=90°,
所以∠DCE+∠2=90°.
又因为∠1=∠2,
所以∠DCA=∠DCE.
所以CD平分∠ACE.
10.C 11.C 12.C 13.B 14.55
15.因为AB⊥BC,
所以∠1+∠3=90°.
因为∠1=55°,
所以∠3=35°.
因为a∥b,
所以∠2=∠3=35°.
16.因为OE平分∠BON,∠EON=20°,
所以∠BON=2∠EON=40°.
所以∠NOC=180°-∠BON=140°,∠MOC=∠BON=40°.
又因为AO⊥BC,
所以∠AOC=90°.
所以∠AOM=∠AOC-∠MOC=50°.
即∠NOC=140°,∠AOM=50°.
17.因为OE⊥AB,
所以∠AOE=90°.
因为∠COE=20°,
所以∠AOC=90°-20°=70°.
所以∠BOD=∠AOC=70°.
因为OG平分∠BOD,
所以∠BOG=∠BOD=35°.
18.因为∠ADE=∠B,
所以DE∥BC.
所以∠EDC=∠DCB.
因为∠EDC=∠GFB,
所以∠DCB=∠GFB.
所以FG∥CD.
因为FG⊥AB,
所以CD⊥AB.
19.(1)因为OA⊥OB,OC⊥OD,
所以∠AOC+∠BOC=90°,∠BOD+∠BOC=90°.
所以∠AOC=∠BOD(同角的余角相等).
(2)因为OA⊥OB,
所以∠AOB=90°.
所以∠AOE=180°-∠AOB-∠BOD=180°-90°-32°=58°.
第2课时 垂线段与点到直线的距离
要点感知1 在同一平面内,过一点__________直线与已知直线垂直.
预习练习1-1 过直线AB上一点P,在同一平面内画AB的垂线,可以画的条数是( )
A.0 B.1 C.2 D.无数条
要点感知2 直线外一点与直线上各点连接的所有线段中,__________最短.简单说成:__________最短.
预习练习2-1 如图,计 ( http: / / www.21cnjy.com )划把河AB中的水引到水池C中,可以先作CD⊥AB,垂足为D,然后沿CD开渠,则能使所打开的水渠最短,这种方案的设计根据是____________________.
( http: / / www.21cnjy.com )
要点感知3 从直线外一点到这条直线的__________的长度,叫做点到直线的距离.
预习练习3-1 点到直线的距离是指( )
A.从直线外一点到这条直线的连线
B.从直线外一点到这条直线的垂线段
C.从直线外一点到这条直线的垂线的长
D.从直线外一点到这条直线的垂线段的长
3-2 如图,三角形ABC中,CD⊥AC,CE⊥AB,垂足分别是C,E,那么点C到线段AB的距离是线段__________的长度.
( http: / / www.21cnjy.com )
知识点1 垂线、垂线段及其性质
1.如图,已知ON⊥a,OM⊥a,可以推断出OM与ON重合的理由是( )
( http: / / www.21cnjy.com )
A.两点确定一条直线
B.过一点只能作一条直线
C.垂线段最短
D.在平面内,过一点有且只有一条直线与已知直线垂直
2.如图,三角形ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP的长不可能是( )
A.2.5 B.3 C.4 D.5
( http: / / www.21cnjy.com )
3.如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是PB,理由是____________________.
( http: / / www.21cnjy.com )
4.如图,某人站在马路的左侧A点处,要到路的右侧,怎样走最近?为什么?如果他要到马路对面的B点处,怎样走最近?为什么?
( http: / / www.21cnjy.com )
知识点2 点到直线的距离
5.P为直线l外一点,A,B,C为l上三点,且PB⊥l,那么下列说法正确的是( )
A.线段PA的长度是点P到直线l的距离
B.线段PB的长度是点P到直线l的距离
C.线段PC的长度是点P到直线l的距离
D.线段AC的长度是点A到PC的距离
6.如图,AB⊥BC,BD⊥AC,能表示点到直线的距离的线段共有( )
A.2条 B.3条 C.4条 D.5条
( http: / / www.21cnjy.com )
7.如图,A,D是直线l1上两点, ( http: / / www.21cnjy.com )B,C是直线l2上两点,且AB⊥BC,CD⊥AD,点A到直线l2的距离是线段______的长,点C与l1的距离是线段__________的长.
( http: / / www.21cnjy.com )
8.如图,AC⊥BC,C为垂足,CD⊥AB, ( http: / / www.21cnjy.com )D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC=6,那么点C到AB的距离是,点A到BC的距离是__________,点B到CD的距离是__________.
( http: / / www.21cnjy.com )
9.已知直线AB,CB ,l 在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
( http: / / www.21cnjy.com )
10.下列说法正确的有( )
①在平面内,过直线上一 ( http: / / www.21cnjy.com )点有且只有一条直线垂直于已知直线;②在平面内,过直线外一点有且只有一条直线垂直于已知直线;③在平面内,过一点任意画一条直线垂直于已知直线;④在平面内,有且只有一条直线垂直于已知直线.
A.1个 B.2个 C.3个 D.4个
11.如图,这是一条马路上的人行横道线,即斑马线的示意图,请你根据图示判断,在过马路时三条线路AC、AB、AD中最短的是( )
A.AC B.AB C.AD D.不确定
( http: / / www.21cnjy.com )
12.下列说法中正确的是( )
A.有且只有一条直线垂直于已知直线
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
C.互相垂直的两条线段一定相交
D.直线c外一点A与直线c上各点连接而成的所有线段中最短线段的长是3 cm,则点A到直线c的距离是3 cm
13.点P为直线l外一点,点A、B、C在直线l上,若PA=3 cm,PB=4 cm,PC=6 cm,则点P到直线l的距离是( )
A.3 cm B.小于3 cm C.小于或等于3 cm D.4 cm
14.如图所示,AD⊥BD,BC⊥CD,AB=5 cm,BC=3 cm,则BD的长度的取值范围是( )
A.大于3 cm B.小于5 cm C.大于3 cm或小于5 cm D.大于3 cm且小于5 cm
( http: / / www.21cnjy.com )
15.如图,从学校到公路最近的是__________号路线,数学道理是____________________.
( http: / / www.21cnjy.com )
16.如图,从B村经A村到河边修一条道路,怎样修使道路最短?并说明道理.
( http: / / www.21cnjy.com )
17.如图,分别画出点A到BC的垂线段,并量出点A到BC的距离.
( http: / / www.21cnjy.com )
18.如图:在三角形ABC中,∠BCA=90°,CD⊥AB于点D,线段AB,BC,CD的大小顺序如何,并说明理由.
( http: / / www.21cnjy.com )
19.如图,DE⊥EF,EF=8,DE=15,DF=17.
( http: / / www.21cnjy.com )
(1)试说出点F到直线DE的距离,点D到直线EF的距离;
(2)点E到直线DF的距离是多少?你是怎样求得的?
参考答案
要点感知1 有且只有一条
预习练习1-1 B
要点感知2 垂线段 垂线段
预习练习2-1 垂线段最短
要点感知3 垂线段
预习练习3-1 D
3-2 CE
1.D 2.A 3.垂线段最短
4.此人要走到马路的右侧,可沿A点到马 ( http: / / www.21cnjy.com )路右侧的垂线段走,因为直线外一点到直线的垂线段最短.要到B点处,可沿线段AB走,因为两点之间线段最短.
5.B 6.D 7.AB CD 8.4.8 6 6.4
9.C 10.B 11.B 12.D 13.C 14.D 15.② 垂线段最短
16.连接AB,过点A作AC垂直于河岸线于点C.
理由:两点之间,线段最短;
直线外一点与直线上各点连接的所有线段中,垂线段最短.
17.作图略.
18.因为CD⊥AB于点D,
所以BC>CD.
因为∠BCA=90°,
所以BC⊥AC.
所以AB>BC.
所以AB>BC>CD.
19.(1)因为DE⊥EF,EF=8,DE=15,
所以点F到直线DE的距离,点D到直线EF的距离分别是:8,15.
(2)设点E到直线DF的距离为h,三角形DEF的面积=DE·EF=DF·h,
所以17h=8×15,
所以h=.
所以点E到直线DF的距离为.
