2023-2024学年福建省福州十八中七年级(下)期末数学试卷(无答案)
文档属性
| 名称 | 2023-2024学年福建省福州十八中七年级(下)期末数学试卷(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 374.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-19 00:00:00 | ||
图片预览

文档简介
2023-2024学年福建省福州十八中七年级(下)期末数学试卷
一、选择题:(本题共10小题,每小题4分,共40分)
1.(4分)下列选项中,显示部分在总体中所占百分比的统计图是( )
A.扇形图 B.条形图 C.折线图 D.直方图
2.(4分)下列说法正确的是( )
A.9的平方根是3 B.
C.0的立方根是0 D.1的立方根是±1
3.(4分)下列长度的三条线段能组成三角形的是( )
A.4,5,10 B.5,6,11 C.4,4,8 D.8,8,8
4.(4分)已知是二元一次方程ax+3y=0的解,则点(a,a﹣3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(4分)已知AB∥x轴,且点A的坐标为(m,2m﹣1),点B的坐标为(2,4),则点A的坐标为( )
A.(2,3) B. C.(﹣2,﹣4) D.
6.(4分)若x>y,则下列不等式中不一定成立的是( )
A.x+1>y+1 B.x2>y2 C. D.2x>2y
7.(4分)茶叶作为浙江省农业十大主导产业之一,是助力乡村振兴的民生产业.某村有土地60公顷,计划将其中10%的土地种植蔬菜,其余的土地开辟为茶园和种植粮食,已知茶园的面积比种粮食面积的2倍少3公顷,问茶园和种粮食的面积各多少公顷?设茶园的面积为x公顷,种粮食的面积为y公顷,可列方程组为( )
A. B.
C. D.
8.(4分)如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为( )
A.3 B.4 C.5 D.6
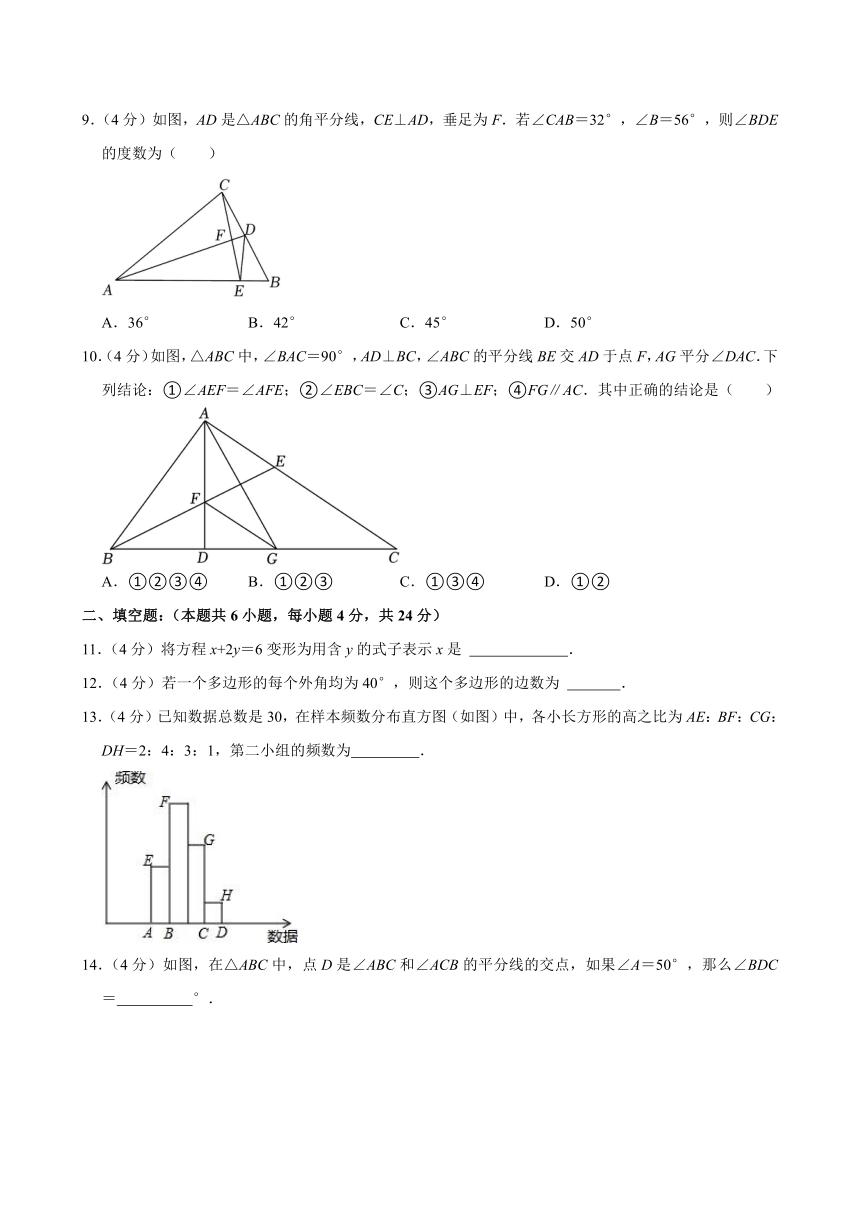
9.(4分)如图,AD是△ABC的角平分线,CE⊥AD,垂足为F.若∠CAB=32°,∠B=56°,则∠BDE的度数为( )
A.36° B.42° C.45° D.50°
10.(4分)如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.下列结论:①∠AEF=∠AFE;②∠EBC=∠C;③AG⊥EF;④FG∥AC.其中正确的结论是( )
A.①②③④ B.①②③ C.①③④ D.①②
二、填空题:(本题共6小题,每小题4分,共24分)
11.(4分)将方程x+2y=6变形为用含y的式子表示x是 .
12.(4分)若一个多边形的每个外角均为40°,则这个多边形的边数为 .
13.(4分)已知数据总数是30,在样本频数分布直方图(如图)中,各小长方形的高之比为AE:BF:CG:DH=2:4:3:1,第二小组的频数为 .
14.(4分)如图,在△ABC中,点D是∠ABC和∠ACB的平分线的交点,如果∠A=50°,那么∠BDC= °.
15.(4分)若关于x的不等式组的解集是2<x≤5,则a的值为 .
16.(4分)如图,AO⊥OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为 .
三、解答题:(本大题共9小题,共86分)
17.(8分)(1)计算:.
(2)求式中x的值:4x2﹣3=6.
18.(8分)解方程组:
(1);
(2).
19.(8分)(1)解不等式,并把它的解集在数轴上表示出来.
(2)解不等式组.
20.(8分)已知,如图,△ABC.
(1)用尺规作△ABC的一条角平分线BD(保留作图痕迹,不写作法,写出结论);
(2)若∠A=80°,∠C=30°,则∠ADB= .
21.(8分)某校积极开展中学生社会实践活动,决定成立文明宣传、环境保护、交通监督三个志愿者队伍,每名学生最多选择一个队伍.为了了解学生的选择意向,随机抽取A,B,C,D四个班,共200名学生进行调查.将调查得到的数据进行整理,绘制成如下统计图.
(1)求扇形统计图中交通监督所在扇形的圆心角度数;
(2)求D班选择环境保护的学生人数,并补全折线统计图;
(3)若该校共有学生2500人,试估计该校选择文明宣传的学生人数.
22.(10分)已知△ABN和△ACM位置如图所示,∠B=∠C=90°,AB=AC,AD=AE.
(1)求证:BD=CE;
(2)求证:∠M=∠N.
23.(10分)小斌大学毕业后自主创业,用36000元购进甲乙两种商品,销售完后共获利6000元,其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)小斌购进甲乙两种商品各多少件;
(2)小斌第二次以原进价购进甲乙两种商品.购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8400元,乙种商品最低售价为每件多少元?
24.(12分)对a,b定义一种新运算T,规定:T(a,b)=(a+2b)(ax+by)(其中x,y均为非零实数).例如:T(1,1)=3x+3y.
(1)已知T(1,﹣1)=0,T(0,2)=8,求x,y的值;
(2)已知关于x,y的方程组,若a≥﹣2,求x+y的取值范围;
(3)在(2)的条件下,已知平面直角坐标系上的点A(x,y)落在坐标轴上,将线段OA沿x轴向右平移2个单位,得线段O′A′,坐标轴上有一点B满足三角形BOA′的面积为9,请直接写出点B的坐标.
25.(14分)在平面直角坐标系中,点C的坐标为(3,3).
(1)如图1,AC交x轴于点D,若在等腰直角△ABC中,∠A=∠C=45°,∠DBC=80°,则∠ADB= ;
(2)如图2,若点B在x轴负半轴上,CE⊥x轴于点E,CF⊥y轴于点F,∠BFN=45°,NF交直线CE于点N,若点B(﹣1,0),BN=5,求点N坐标.
(3)如图3,若点B,F分别在x,y轴的正半轴上,CF=BF,连接CB,点P、Q是BC边上的两点,设∠PFQ=θ(0°<θ<45°),∠BFC=2∠PFQ,则以线段CP、PQ、QB长度为边长的三角形的形状为 (①钝角三角形;②直角三角形;③锐角三角形;④随线段的长度而定),请选择,并给出证明.
一、选择题:(本题共10小题,每小题4分,共40分)
1.(4分)下列选项中,显示部分在总体中所占百分比的统计图是( )
A.扇形图 B.条形图 C.折线图 D.直方图
2.(4分)下列说法正确的是( )
A.9的平方根是3 B.
C.0的立方根是0 D.1的立方根是±1
3.(4分)下列长度的三条线段能组成三角形的是( )
A.4,5,10 B.5,6,11 C.4,4,8 D.8,8,8
4.(4分)已知是二元一次方程ax+3y=0的解,则点(a,a﹣3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(4分)已知AB∥x轴,且点A的坐标为(m,2m﹣1),点B的坐标为(2,4),则点A的坐标为( )
A.(2,3) B. C.(﹣2,﹣4) D.
6.(4分)若x>y,则下列不等式中不一定成立的是( )
A.x+1>y+1 B.x2>y2 C. D.2x>2y
7.(4分)茶叶作为浙江省农业十大主导产业之一,是助力乡村振兴的民生产业.某村有土地60公顷,计划将其中10%的土地种植蔬菜,其余的土地开辟为茶园和种植粮食,已知茶园的面积比种粮食面积的2倍少3公顷,问茶园和种粮食的面积各多少公顷?设茶园的面积为x公顷,种粮食的面积为y公顷,可列方程组为( )
A. B.
C. D.
8.(4分)如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为( )
A.3 B.4 C.5 D.6
9.(4分)如图,AD是△ABC的角平分线,CE⊥AD,垂足为F.若∠CAB=32°,∠B=56°,则∠BDE的度数为( )
A.36° B.42° C.45° D.50°
10.(4分)如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.下列结论:①∠AEF=∠AFE;②∠EBC=∠C;③AG⊥EF;④FG∥AC.其中正确的结论是( )
A.①②③④ B.①②③ C.①③④ D.①②
二、填空题:(本题共6小题,每小题4分,共24分)
11.(4分)将方程x+2y=6变形为用含y的式子表示x是 .
12.(4分)若一个多边形的每个外角均为40°,则这个多边形的边数为 .
13.(4分)已知数据总数是30,在样本频数分布直方图(如图)中,各小长方形的高之比为AE:BF:CG:DH=2:4:3:1,第二小组的频数为 .
14.(4分)如图,在△ABC中,点D是∠ABC和∠ACB的平分线的交点,如果∠A=50°,那么∠BDC= °.
15.(4分)若关于x的不等式组的解集是2<x≤5,则a的值为 .
16.(4分)如图,AO⊥OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为 .
三、解答题:(本大题共9小题,共86分)
17.(8分)(1)计算:.
(2)求式中x的值:4x2﹣3=6.
18.(8分)解方程组:
(1);
(2).
19.(8分)(1)解不等式,并把它的解集在数轴上表示出来.
(2)解不等式组.
20.(8分)已知,如图,△ABC.
(1)用尺规作△ABC的一条角平分线BD(保留作图痕迹,不写作法,写出结论);
(2)若∠A=80°,∠C=30°,则∠ADB= .
21.(8分)某校积极开展中学生社会实践活动,决定成立文明宣传、环境保护、交通监督三个志愿者队伍,每名学生最多选择一个队伍.为了了解学生的选择意向,随机抽取A,B,C,D四个班,共200名学生进行调查.将调查得到的数据进行整理,绘制成如下统计图.
(1)求扇形统计图中交通监督所在扇形的圆心角度数;
(2)求D班选择环境保护的学生人数,并补全折线统计图;
(3)若该校共有学生2500人,试估计该校选择文明宣传的学生人数.
22.(10分)已知△ABN和△ACM位置如图所示,∠B=∠C=90°,AB=AC,AD=AE.
(1)求证:BD=CE;
(2)求证:∠M=∠N.
23.(10分)小斌大学毕业后自主创业,用36000元购进甲乙两种商品,销售完后共获利6000元,其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)小斌购进甲乙两种商品各多少件;
(2)小斌第二次以原进价购进甲乙两种商品.购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8400元,乙种商品最低售价为每件多少元?
24.(12分)对a,b定义一种新运算T,规定:T(a,b)=(a+2b)(ax+by)(其中x,y均为非零实数).例如:T(1,1)=3x+3y.
(1)已知T(1,﹣1)=0,T(0,2)=8,求x,y的值;
(2)已知关于x,y的方程组,若a≥﹣2,求x+y的取值范围;
(3)在(2)的条件下,已知平面直角坐标系上的点A(x,y)落在坐标轴上,将线段OA沿x轴向右平移2个单位,得线段O′A′,坐标轴上有一点B满足三角形BOA′的面积为9,请直接写出点B的坐标.
25.(14分)在平面直角坐标系中,点C的坐标为(3,3).
(1)如图1,AC交x轴于点D,若在等腰直角△ABC中,∠A=∠C=45°,∠DBC=80°,则∠ADB= ;
(2)如图2,若点B在x轴负半轴上,CE⊥x轴于点E,CF⊥y轴于点F,∠BFN=45°,NF交直线CE于点N,若点B(﹣1,0),BN=5,求点N坐标.
(3)如图3,若点B,F分别在x,y轴的正半轴上,CF=BF,连接CB,点P、Q是BC边上的两点,设∠PFQ=θ(0°<θ<45°),∠BFC=2∠PFQ,则以线段CP、PQ、QB长度为边长的三角形的形状为 (①钝角三角形;②直角三角形;③锐角三角形;④随线段的长度而定),请选择,并给出证明.
同课章节目录
