2023-2024学年甘肃省兰州市城关区树人中学八年级(下)期末数学试卷(无答案)
文档属性
| 名称 | 2023-2024学年甘肃省兰州市城关区树人中学八年级(下)期末数学试卷(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 322.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-19 00:00:00 | ||
图片预览

文档简介
2023-2024学年甘肃省兰州市城关区树人中学八年级(下)期末数学试卷
一、选择题(每小题3分,共36分)
1.(3分)人工智能与5G时代已悄然来临,科技逐渐融入人类生活.下列设计的人工智能图标中,是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.(3分)若a<b<0,则下列结论正确的是( )
A.﹣a<﹣b B.a+1>b+1 C.﹣a+1>﹣b+1 D.2a>a+b
3.(3分)下列式子从左到右的变形是因式分解的是( )
A.(a﹣3)(a+2)=a2﹣a﹣6
B.x2﹣1+y2=(x+1)(x﹣1)+y2
C.2x2y=2x xy
D.a2+2a=a(a+2)
4.(3分)下列各式从左到右变形一定正确的是( )
A.= B.=﹣1
C.= D.=
5.(3分)如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
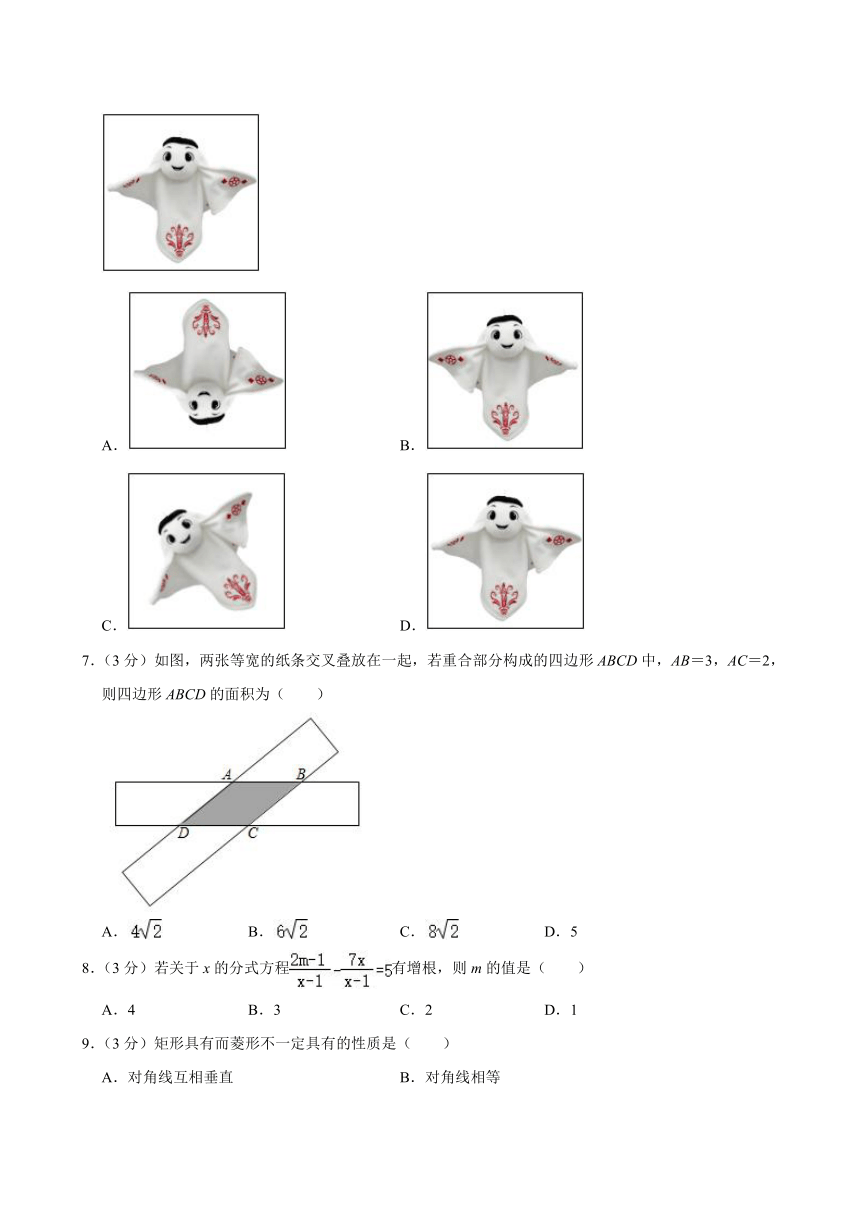
6.(3分)“会飞的饺子皮”刷爆朋友圈,卡塔尔世界杯吉祥物“拉伊卜”刷爆网络!下面是“拉伊卜”的形象图片,在下面的四个图形中,能由左图经过平移得到的图形是( )
A. B.
C. D.
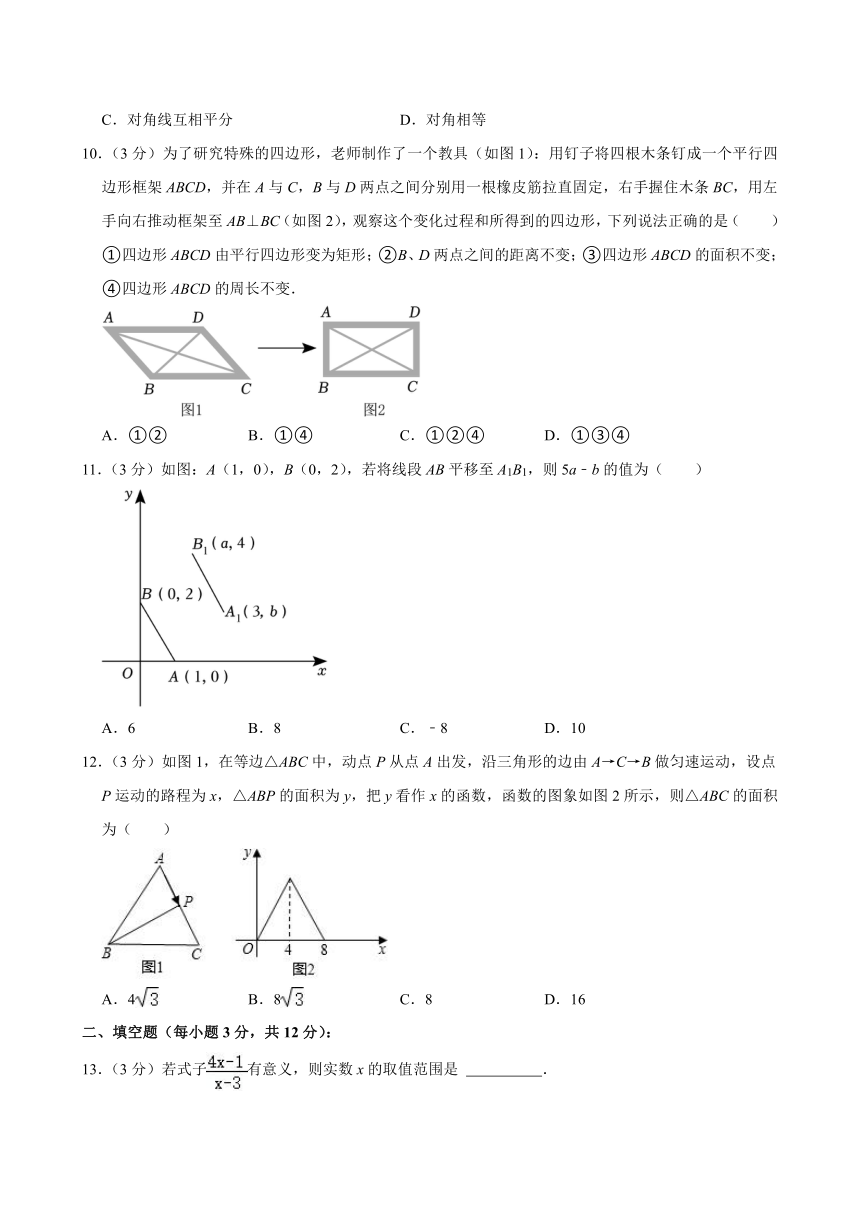
7.(3分)如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则四边形ABCD的面积为( )
A. B. C. D.5
8.(3分)若关于x的分式方程有增根,则m的值是( )
A.4 B.3 C.2 D.1
9.(3分)矩形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角线互相平分 D.对角相等
10.(3分)为了研究特殊的四边形,老师制作了一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD,并在A与C,B与D两点之间分别用一根橡皮筋拉直固定,右手握住木条BC,用左手向右推动框架至AB⊥BC(如图2),观察这个变化过程和所得到的四边形,下列说法正确的是( )
①四边形ABCD由平行四边形变为矩形;②B、D两点之间的距离不变;③四边形ABCD的面积不变;④四边形ABCD的周长不变.
A.①② B.①④ C.①②④ D.①③④
11.(3分)如图:A(1,0),B(0,2),若将线段AB平移至A1B1,则5a﹣b的值为( )
A.6 B.8 C.﹣8 D.10
12.(3分)如图1,在等边△ABC中,动点P从点A出发,沿三角形的边由A→C→B做匀速运动,设点P运动的路程为x,△ABP的面积为y,把y看作x的函数,函数的图象如图2所示,则△ABC的面积为( )
A.4 B.8 C.8 D.16
二、填空题(每小题3分,共12分):
13.(3分)若式子有意义,则实数x的取值范围是 .
14.(3分)如图,在△ABC中,点D、E分别是边AC、AB的中点,点F在线段DE上,AB=10,BF=8,AF=6,BC=14,线段DF的长度是 .
15.(3分)关于x的不等式组有且只有3个整数解,则常数k的取值范围是 .
16.(3分)如图,在边长为2的正方形ABCD中,E,F分别是边DC,CB上的动点,且始终满足DE=CF,AE,DF交于点P,则∠APD的度数为 ;连接CP,线段CP的最小值为 .
三、解答题(共72分)
17.(4分)分解因式:
(1)a3﹣6a2+9a;
(2)x2(x﹣3)+4(3﹣x).
18.(4分)已知x2﹣x﹣1=0,求的值.
19.(4分)解方程:.
20.(4分)解一元一次不等式组,并在数轴上表示其解集.
.
21.(6分)为了筹备第十八届春季越野比赛,学校计划购买甲、乙两种纪念品.已知购买7件甲种纪念品和2件乙种纪念品需用25元,购买5件甲种纪念品和4件乙种纪念品需用23元.
(1)求每件甲种纪念品和每件乙种纪念品各多少元;
(2)若学校购买甲、乙两种纪念品共1000件,总费用不超过2800元,那么最多可以购买甲种纪念品多少件?
22.(6分)列方程解应用题.
某工程队承担了750米长的道路改造任务,工程队在施工完210米道路后,引进了新设备,每天改造道路的长度比原来增加了20%,结果共用22天完成了任务.求引进新设备前工程队每天改造道路多少米?
23.(6分)下面是小东设计的“作△ABC中BC边上的高线”的尺规作图过程.
已知:△ABC.
求作:△ABC中BC边上的高线AD.
作法:如图,
①以点B为圆心,BA的长为半径作弧,以点C为圆心,CA的长为半径作弧,两弧在BC下方交于点E;
②连接AE交BC于点D.
所以线段AD是△ABC中BC边上的高线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ =BA, =CA,
∴点B,C分别在线段AE的垂直平分线上( )(填推理的依据).
∴BC垂直平分线段AE.
∴线段AD是△ABC中BC边上的高线.
24.(6分)森林火灾是一种常见的自然灾害,危害很大,随着中国科技、经济的不断发展,开始应用飞机洒水的方式扑灭火源.如图,有一台救火飞机沿东西方向AB,由点A飞向点B,已知点C为其中一个着火点,已知AB=1000m,AC=600m,BC=800m,飞机中心周围500m以内可以受到洒水影响.
(1)请通过计算说明着火点C是否受洒水影响?
(2)若该飞机的速度为14m/s,要想扑灭着火点C估计需要15秒,请你通过计算判断着火点C能否被扑灭?
25.(6分)今年5月20日是第35届中国学生营养日,某初中食堂当日营养午餐如表所示.
菜品名称 红烧排骨 三色肉丁 冬瓜鸡蛋 青椒包菜 米饭 水果
食物种类 猪小排 猪肉(瘦)、胡萝卜、玉米粒、青豆 冬瓜、鸡蛋 青椒、包菜 梗米(标一) 苹果
(1)午餐的营养素主要来自猪小排、猪肉(瘦)所含的蛋白质和脂肪,每克猪小排、猪肉(瘦)中的蛋白质和脂肪含量如表所示,按配餐要求推算该日午餐猪小排与猪肉(瘦)提供的蛋白质、脂肪质量应分别为31克、27.2克,求该日午餐所需要的猪小排与猪肉(瘦)的质量分别是多少克;
营养率食物类别 猪小排 猪肉(瘦)
蛋白质(克) 0.17 0.2
脂肪(克) 0.23 0.06
(2)按配餐要求菜品“青椒包菜”中青椒和包菜共150g,已知每克青椒与包菜分别含有0.022g、0.01g的膳食纤维,出于口感考虑,该菜品中青椒质量不超过包菜质量的一半,青椒与包菜的质量分别为多少时,该菜品膳食纤维的含量最高?
26.(8分)综合与实践
问题情境;如图①,D,E分别是△ABC中AB,AC上的两点,且AB=AC,AD=AE.
猜想证明:
(1)当∠A=60°时,将△ADE绕点A逆时针方向旋转一定角度,使点E落在BC上,如图②所示,连接BD,则BD与CE的数量关系是 ,∠DBC的度数是 .
(2)当∠A=90°时,将△ADE绕点A逆时针方向旋转一定角度,使点E落在BC上,如图③所示,连接BD,请写出BD与CE的数量关系与位置关系,并说明理由.
问题解决:
(3)当∠A=90°时,将△ABC绕点A逆时针旋转一定角度,使得点C落在ED的延长线上,如图④所示,直接写出AC,CD,CE之间的数量关系.
27.(9分)根据前面已经学过的“距离”我们知道:点到直线的“距离”是直线外一点和直线上各点连接的所有线段中最短的线段(即垂线段)的长度.类似的我们给出两个图形G1=G2的“距离”定义:如果点P为图形G1上的任意一点,点Q为图形G2上的任意一点,且P、Q两点的“距离”有最小值,那么称这个最小值为图形G1,G2的“距离”,记为d(G1,G2),特别地,当图形G1,G2有公共点时,图形G1,G2的“距离”d(G1,G2)=0.
(1)如图1,在平面直角坐标系中,△OAB是等边三角形,点B在第一象限,若A(5,0),D(﹣3,0),E(0,4),则d(D,△OAB)= ,d(E,△OAB)= ;
(2)如图2,已知△ABC的三个顶点的坐标分别为A(0,2),B(﹣2,0),C(2,0),将一次函数y=kx+6的图象记为L.
①若d(L,△ABC)=0,求k的取值范围;
②若k>0,且d(L,△ABC)=2,则k的值为 ;
(3)在平面直角坐标系中,点O为坐标原点,点P(4n,6﹣3n)为平面内一上点,其中n为任意实数,求d(0,P).
一、选择题(每小题3分,共36分)
1.(3分)人工智能与5G时代已悄然来临,科技逐渐融入人类生活.下列设计的人工智能图标中,是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.(3分)若a<b<0,则下列结论正确的是( )
A.﹣a<﹣b B.a+1>b+1 C.﹣a+1>﹣b+1 D.2a>a+b
3.(3分)下列式子从左到右的变形是因式分解的是( )
A.(a﹣3)(a+2)=a2﹣a﹣6
B.x2﹣1+y2=(x+1)(x﹣1)+y2
C.2x2y=2x xy
D.a2+2a=a(a+2)
4.(3分)下列各式从左到右变形一定正确的是( )
A.= B.=﹣1
C.= D.=
5.(3分)如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
6.(3分)“会飞的饺子皮”刷爆朋友圈,卡塔尔世界杯吉祥物“拉伊卜”刷爆网络!下面是“拉伊卜”的形象图片,在下面的四个图形中,能由左图经过平移得到的图形是( )
A. B.
C. D.
7.(3分)如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则四边形ABCD的面积为( )
A. B. C. D.5
8.(3分)若关于x的分式方程有增根,则m的值是( )
A.4 B.3 C.2 D.1
9.(3分)矩形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角线互相平分 D.对角相等
10.(3分)为了研究特殊的四边形,老师制作了一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD,并在A与C,B与D两点之间分别用一根橡皮筋拉直固定,右手握住木条BC,用左手向右推动框架至AB⊥BC(如图2),观察这个变化过程和所得到的四边形,下列说法正确的是( )
①四边形ABCD由平行四边形变为矩形;②B、D两点之间的距离不变;③四边形ABCD的面积不变;④四边形ABCD的周长不变.
A.①② B.①④ C.①②④ D.①③④
11.(3分)如图:A(1,0),B(0,2),若将线段AB平移至A1B1,则5a﹣b的值为( )
A.6 B.8 C.﹣8 D.10
12.(3分)如图1,在等边△ABC中,动点P从点A出发,沿三角形的边由A→C→B做匀速运动,设点P运动的路程为x,△ABP的面积为y,把y看作x的函数,函数的图象如图2所示,则△ABC的面积为( )
A.4 B.8 C.8 D.16
二、填空题(每小题3分,共12分):
13.(3分)若式子有意义,则实数x的取值范围是 .
14.(3分)如图,在△ABC中,点D、E分别是边AC、AB的中点,点F在线段DE上,AB=10,BF=8,AF=6,BC=14,线段DF的长度是 .
15.(3分)关于x的不等式组有且只有3个整数解,则常数k的取值范围是 .
16.(3分)如图,在边长为2的正方形ABCD中,E,F分别是边DC,CB上的动点,且始终满足DE=CF,AE,DF交于点P,则∠APD的度数为 ;连接CP,线段CP的最小值为 .
三、解答题(共72分)
17.(4分)分解因式:
(1)a3﹣6a2+9a;
(2)x2(x﹣3)+4(3﹣x).
18.(4分)已知x2﹣x﹣1=0,求的值.
19.(4分)解方程:.
20.(4分)解一元一次不等式组,并在数轴上表示其解集.
.
21.(6分)为了筹备第十八届春季越野比赛,学校计划购买甲、乙两种纪念品.已知购买7件甲种纪念品和2件乙种纪念品需用25元,购买5件甲种纪念品和4件乙种纪念品需用23元.
(1)求每件甲种纪念品和每件乙种纪念品各多少元;
(2)若学校购买甲、乙两种纪念品共1000件,总费用不超过2800元,那么最多可以购买甲种纪念品多少件?
22.(6分)列方程解应用题.
某工程队承担了750米长的道路改造任务,工程队在施工完210米道路后,引进了新设备,每天改造道路的长度比原来增加了20%,结果共用22天完成了任务.求引进新设备前工程队每天改造道路多少米?
23.(6分)下面是小东设计的“作△ABC中BC边上的高线”的尺规作图过程.
已知:△ABC.
求作:△ABC中BC边上的高线AD.
作法:如图,
①以点B为圆心,BA的长为半径作弧,以点C为圆心,CA的长为半径作弧,两弧在BC下方交于点E;
②连接AE交BC于点D.
所以线段AD是△ABC中BC边上的高线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ =BA, =CA,
∴点B,C分别在线段AE的垂直平分线上( )(填推理的依据).
∴BC垂直平分线段AE.
∴线段AD是△ABC中BC边上的高线.
24.(6分)森林火灾是一种常见的自然灾害,危害很大,随着中国科技、经济的不断发展,开始应用飞机洒水的方式扑灭火源.如图,有一台救火飞机沿东西方向AB,由点A飞向点B,已知点C为其中一个着火点,已知AB=1000m,AC=600m,BC=800m,飞机中心周围500m以内可以受到洒水影响.
(1)请通过计算说明着火点C是否受洒水影响?
(2)若该飞机的速度为14m/s,要想扑灭着火点C估计需要15秒,请你通过计算判断着火点C能否被扑灭?
25.(6分)今年5月20日是第35届中国学生营养日,某初中食堂当日营养午餐如表所示.
菜品名称 红烧排骨 三色肉丁 冬瓜鸡蛋 青椒包菜 米饭 水果
食物种类 猪小排 猪肉(瘦)、胡萝卜、玉米粒、青豆 冬瓜、鸡蛋 青椒、包菜 梗米(标一) 苹果
(1)午餐的营养素主要来自猪小排、猪肉(瘦)所含的蛋白质和脂肪,每克猪小排、猪肉(瘦)中的蛋白质和脂肪含量如表所示,按配餐要求推算该日午餐猪小排与猪肉(瘦)提供的蛋白质、脂肪质量应分别为31克、27.2克,求该日午餐所需要的猪小排与猪肉(瘦)的质量分别是多少克;
营养率食物类别 猪小排 猪肉(瘦)
蛋白质(克) 0.17 0.2
脂肪(克) 0.23 0.06
(2)按配餐要求菜品“青椒包菜”中青椒和包菜共150g,已知每克青椒与包菜分别含有0.022g、0.01g的膳食纤维,出于口感考虑,该菜品中青椒质量不超过包菜质量的一半,青椒与包菜的质量分别为多少时,该菜品膳食纤维的含量最高?
26.(8分)综合与实践
问题情境;如图①,D,E分别是△ABC中AB,AC上的两点,且AB=AC,AD=AE.
猜想证明:
(1)当∠A=60°时,将△ADE绕点A逆时针方向旋转一定角度,使点E落在BC上,如图②所示,连接BD,则BD与CE的数量关系是 ,∠DBC的度数是 .
(2)当∠A=90°时,将△ADE绕点A逆时针方向旋转一定角度,使点E落在BC上,如图③所示,连接BD,请写出BD与CE的数量关系与位置关系,并说明理由.
问题解决:
(3)当∠A=90°时,将△ABC绕点A逆时针旋转一定角度,使得点C落在ED的延长线上,如图④所示,直接写出AC,CD,CE之间的数量关系.
27.(9分)根据前面已经学过的“距离”我们知道:点到直线的“距离”是直线外一点和直线上各点连接的所有线段中最短的线段(即垂线段)的长度.类似的我们给出两个图形G1=G2的“距离”定义:如果点P为图形G1上的任意一点,点Q为图形G2上的任意一点,且P、Q两点的“距离”有最小值,那么称这个最小值为图形G1,G2的“距离”,记为d(G1,G2),特别地,当图形G1,G2有公共点时,图形G1,G2的“距离”d(G1,G2)=0.
(1)如图1,在平面直角坐标系中,△OAB是等边三角形,点B在第一象限,若A(5,0),D(﹣3,0),E(0,4),则d(D,△OAB)= ,d(E,△OAB)= ;
(2)如图2,已知△ABC的三个顶点的坐标分别为A(0,2),B(﹣2,0),C(2,0),将一次函数y=kx+6的图象记为L.
①若d(L,△ABC)=0,求k的取值范围;
②若k>0,且d(L,△ABC)=2,则k的值为 ;
(3)在平面直角坐标系中,点O为坐标原点,点P(4n,6﹣3n)为平面内一上点,其中n为任意实数,求d(0,P).
同课章节目录
