27.1 图形的相似(第2课时)
文档属性
| 名称 | 27.1 图形的相似(第2课时) |  | |
| 格式 | rar | ||
| 文件大小 | 991.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-18 19:28:00 | ||
图片预览




文档简介
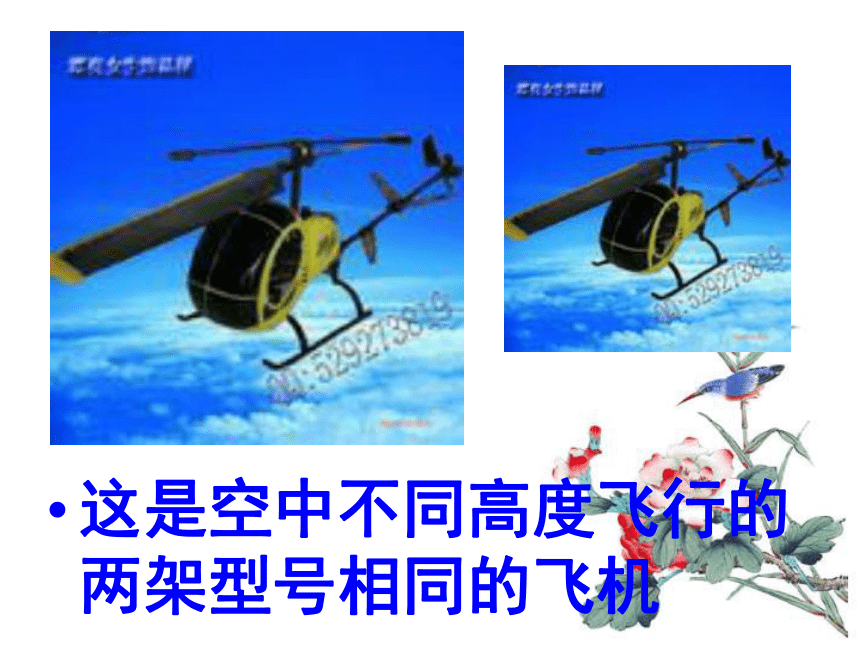
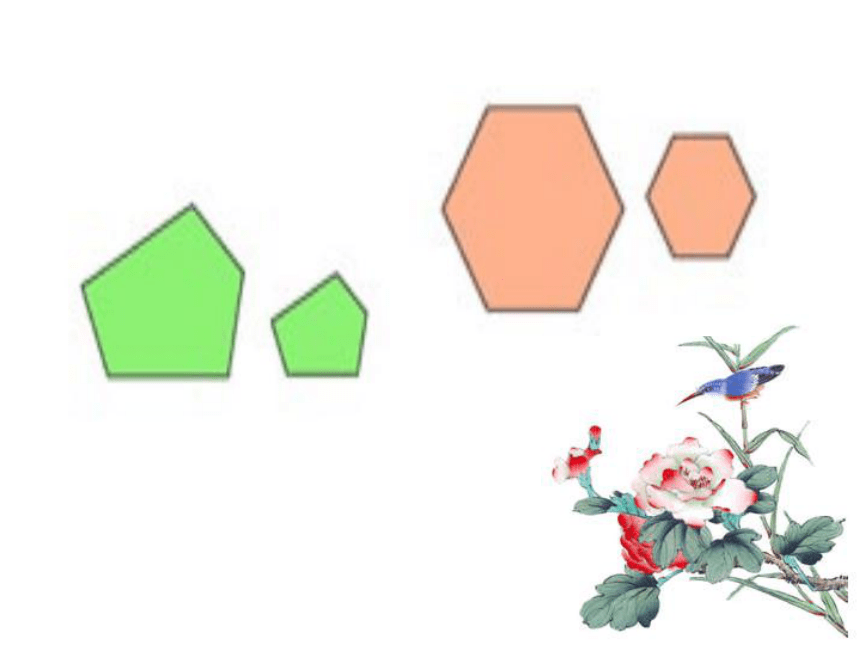
课件21张PPT。27.1 图形的相似(第2课时)义务教育课程标准实验教科书人民教育出版社这是空中不同高度飞行的两架型号相同的飞机大小不同的两个足球同一底片洗出的不同尺寸的照片 研究相似多边形的主要特征.
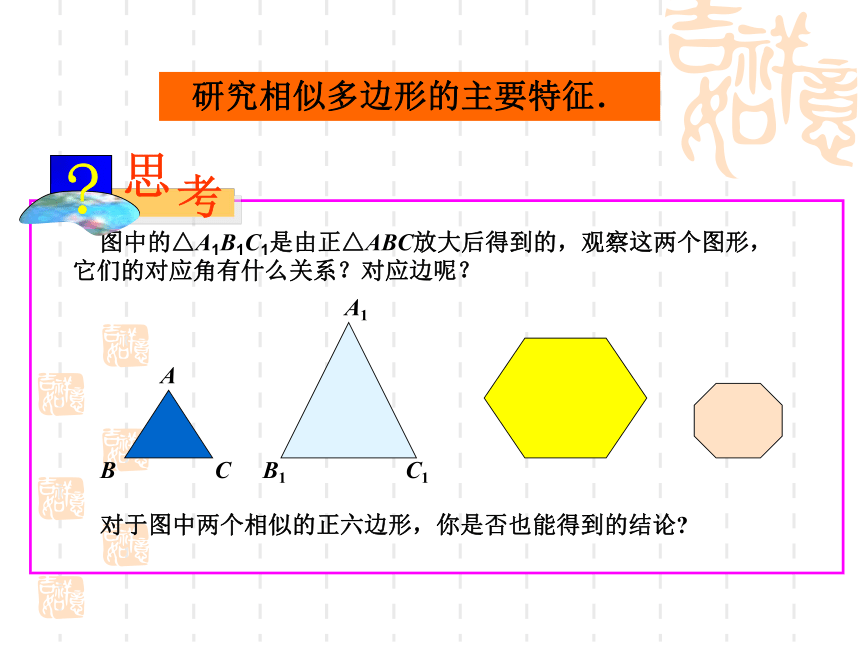
图中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?对于图中两个相似的正六边形,你是否也能得到的结论?
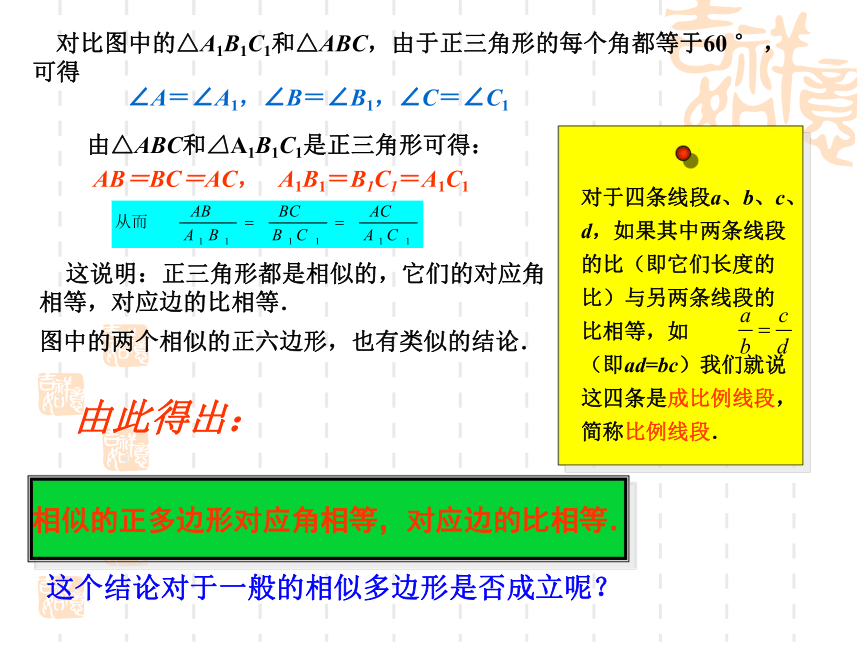
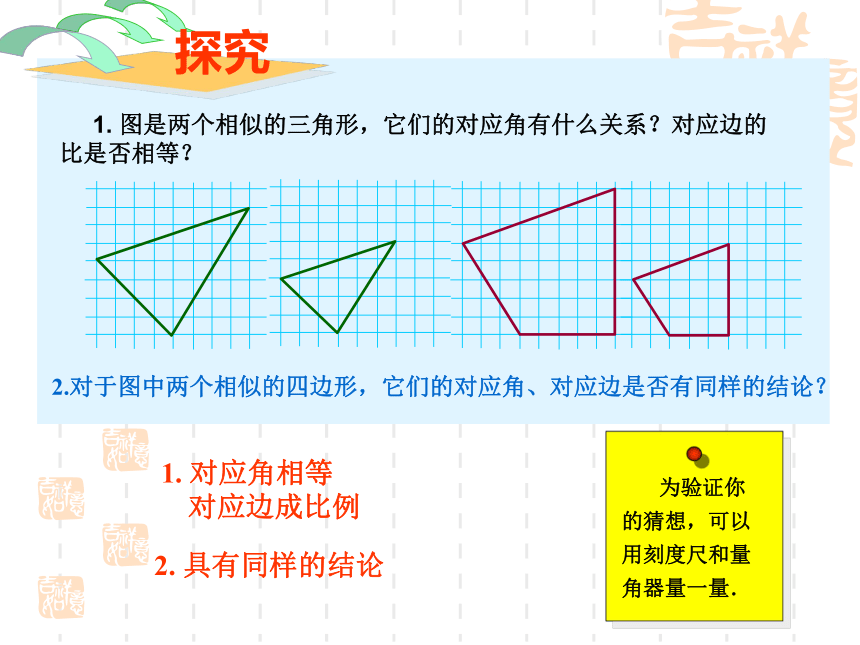
CABC1A1B1 对比图中的△A1B1C1和△ABC,由于正三角形的每个角都等于60 ° ,可得∠A=∠A1,∠B=∠B1,∠C=∠C1由△ABC和△A1B1C1是正三角形可得:AB=BC=AC, A1B1=B1C1=A1C1 这说明:正三角形都是相似的,它们的对应角相等,对应边的比相等.这个结论对于一般的相似多边形是否成立呢?图中的两个相似的正六边形,也有类似的结论.由此得出: 1. 图是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?2.对于图中两个相似的四边形,它们的对应角、对应边是否有同样的结论?1. 对应角相等对应边成比例2. 具有同样的结论多边形相似特征:相似比: 我们把相似多边形对应边的比称为相似比.多边形相似的定义:相似比为1时,相似的两个图形有什么关系?两图形全等例1 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得 四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得解得 x=28(cm)∠α=∠C=83°,∠A=∠E=118°在四边形ABCD中,∠β=360°-(78°+83°+118°)=81°.典型举例如图,△ABC与△DEF相似,求未知
边x,y的长度。举一反三例2、 在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离 实际运用设两地的实际距离为xcmx = 300000000(cm)x = 3000千米答: 甲,乙两地的实际距离为3000千米解:两地的实际距离是2000m,在地图上量得这两地的距离为2cm,这个地图的比例尺为多少?巩固练习 如图所示的两个三角形相似吗?为什么? 不 相 似灵活运用 如图矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所成的矩形是否相似?反馈1、若多边形ABCDEF与多边形A1B1C1D1E1F1相似,且∠A=780, ∠B=830,又∠A与∠A1是对应角,则∠A1=____2、下列说法正确的是 ( )
A、任意两个等腰三角形都相似
B、任意两个菱形都相似
C、任意两个矩形都相似
D、任意两个正方形都相似780D智力大比拼4、若五边形ABCDE与五边形FHGMN相似,且五边形ABCDE与五边形FHGMN的相似比为6,则五边形FHGMN与五边形ABCDE的相似比为( )A、6 B、5 C、1 D、 D3、若线段a=3cm,b=6cm,c=5cm,且a,b,c,d是成比例线段,则d=_______10cm振华机械厂接了一批焊制矩形钢板的业务,已知这种矩形钢板在图纸上(比例尺为1:400)的长和宽分别为3cm和2cm,该厂所用原料是边长为4m的正方形钢板,那么焊制一块这样的钢板要用几块边长为4m的正方形钢板运用拓展
1、对于四条线段a、b、c、d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 (即ad=bc)我们就说这四条是成比例线段,简称比例线段.
2、相似多边形的性质:相似多边形对应角相等,对应边的比相等及其应用。
3、相似多边形的定义:对应角相等,对应边的比相等的两个多边形相似及其应用。收获园地你收获了什么?
P34 T5、6、7作业再见
图中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?对于图中两个相似的正六边形,你是否也能得到的结论?
CABC1A1B1 对比图中的△A1B1C1和△ABC,由于正三角形的每个角都等于60 ° ,可得∠A=∠A1,∠B=∠B1,∠C=∠C1由△ABC和△A1B1C1是正三角形可得:AB=BC=AC, A1B1=B1C1=A1C1 这说明:正三角形都是相似的,它们的对应角相等,对应边的比相等.这个结论对于一般的相似多边形是否成立呢?图中的两个相似的正六边形,也有类似的结论.由此得出: 1. 图是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?2.对于图中两个相似的四边形,它们的对应角、对应边是否有同样的结论?1. 对应角相等对应边成比例2. 具有同样的结论多边形相似特征:相似比: 我们把相似多边形对应边的比称为相似比.多边形相似的定义:相似比为1时,相似的两个图形有什么关系?两图形全等例1 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得 四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得解得 x=28(cm)∠α=∠C=83°,∠A=∠E=118°在四边形ABCD中,∠β=360°-(78°+83°+118°)=81°.典型举例如图,△ABC与△DEF相似,求未知
边x,y的长度。举一反三例2、 在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离 实际运用设两地的实际距离为xcmx = 300000000(cm)x = 3000千米答: 甲,乙两地的实际距离为3000千米解:两地的实际距离是2000m,在地图上量得这两地的距离为2cm,这个地图的比例尺为多少?巩固练习 如图所示的两个三角形相似吗?为什么? 不 相 似灵活运用 如图矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所成的矩形是否相似?反馈1、若多边形ABCDEF与多边形A1B1C1D1E1F1相似,且∠A=780, ∠B=830,又∠A与∠A1是对应角,则∠A1=____2、下列说法正确的是 ( )
A、任意两个等腰三角形都相似
B、任意两个菱形都相似
C、任意两个矩形都相似
D、任意两个正方形都相似780D智力大比拼4、若五边形ABCDE与五边形FHGMN相似,且五边形ABCDE与五边形FHGMN的相似比为6,则五边形FHGMN与五边形ABCDE的相似比为( )A、6 B、5 C、1 D、 D3、若线段a=3cm,b=6cm,c=5cm,且a,b,c,d是成比例线段,则d=_______10cm振华机械厂接了一批焊制矩形钢板的业务,已知这种矩形钢板在图纸上(比例尺为1:400)的长和宽分别为3cm和2cm,该厂所用原料是边长为4m的正方形钢板,那么焊制一块这样的钢板要用几块边长为4m的正方形钢板运用拓展
1、对于四条线段a、b、c、d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 (即ad=bc)我们就说这四条是成比例线段,简称比例线段.
2、相似多边形的性质:相似多边形对应角相等,对应边的比相等及其应用。
3、相似多边形的定义:对应角相等,对应边的比相等的两个多边形相似及其应用。收获园地你收获了什么?
P34 T5、6、7作业再见
