3.1.1 椭圆及其标准方程 课件(共27张PPT)
文档属性
| 名称 | 3.1.1 椭圆及其标准方程 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 15.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-19 17:26:14 | ||
图片预览








文档简介
(共27张PPT)
双曲线
抛物线
椭圆
圆
圆锥曲线
学校: 授课教师:
3.1.1
椭圆及其标准方程
——仙女座星系
星系中的椭圆
德国天文学家开普勒(1571-1630)在最初研究他的导师家第谷(1546-1601)所记录的数据时,但是所得结果却与第谷的观测数据至少有8分的角度误差,这不容忽视的8分也许是因为人们认为行星绕太阳做匀速圆周运动所造成的。
至此,人们长期以来视为真理的观念——天体做匀速圆周运动,第一次受到了怀疑。
00 前情提要
椭圆曲线——RSA密码体系
Baignoire腕表
椭圆哲学
我们先把有疫情的区域,看成是一个椭圆图像,其两焦点到动点之距是一个常数(即总人口的定量值),其中心点是“人”,其两个焦点是“无感染人”和“已感染人”的两个群体。
00 前情提要
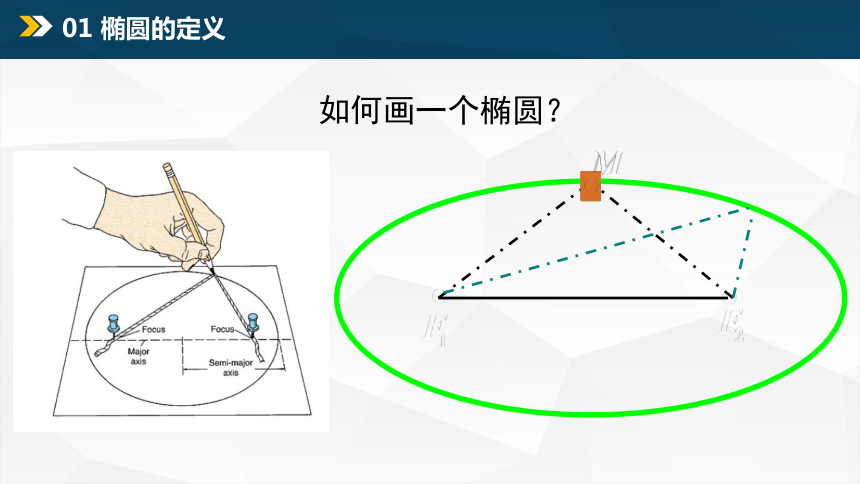
01 椭圆的定义
如何画一个椭圆?
【定义】平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
这两个定点叫做椭圆的焦点(F1、F2 ),
两焦点的距离叫做椭圆的焦距|F1F2|.
注:1. M是椭圆上任意一点,且|MF1| + |MF2| = 常数;
2. 将常数记为2a,焦距记为2c,且2a>2c;
2a>2c
2a=2c
2a<2c
F1
F2
不存在
01 椭圆的定义
【概念辨析】
1.思维辨析(对的打“√”,错的打“×”)
(1)已知F1(-4,0),F2(4,0),平面内到F1,F2两点的距离之和等于8的点的轨迹是椭圆. ( )
(2)已知F1(-4,0),F2(4,0),平面内到F1,F2两点的距离之和等于6的点的轨迹是椭圆. ( )
(3)平面内到点F1(-4,0),F2(4,0)两点的距离之和等于点M(5,3)到F1,F2的距离之和的点的轨迹是椭圆. ( )
×
×
√
|MF1|+|MF2|=2a
如图所示: F1、F2为两定点,且|F1F2|=2c,求平面内到两定点F1、F2距离之和为定值2a(2a>2c)的动点M的轨迹方程。
移项
两边平方
02 椭圆的标准方程
(-c,0)
(c,0)
(-c,0)
(c,0)
令a2-c2=b2
b2x2+a2y2=a2b2
两边同时除以a2b2:
(a>b>0)
两边平方
a
c
b
02 椭圆的标准方程
表示焦点在x轴上的椭圆标准方程
定义 图形
方程
焦点
a、b、c之间 的关系 |MF1|+|MF2|=2a (2a>|F1F2|)
(c,0)、( c,0)
(0,c)、(0, c)
a2=b2+c2
分母哪个大,焦点就在哪一根坐标轴上
02 椭圆的标准方程
【例1】已知椭圆的两个焦点坐标分别是(-2,0), (2,0),且经过点 ,求它的标准方程.
02 椭圆的标准方程
【例1】已知椭圆的两个焦点坐标分别是(-2,0), (2,0),且经过点 ,求它的标准方程.
02 椭圆的标准方程
练习
1.若方程4x2+ky2=1表示的曲线是焦点在y轴上的椭圆,则k的取值范围为________。
2.若方程 表示焦点在y轴上的椭圆,则实数m的取值范围是________.
3.椭圆的标准方程为 ,且焦距为6,则实数m=_____.
4. 椭圆 的一个焦点为(0,2),那么k=_________.
关于焦点与焦距的问题
F为圆心,F'为圆内一点,A为圆上的一点,线段AF '的垂直平分线交AF于点P,求P点轨迹的形状?
与椭圆相关的轨迹问题
(几何法)
【典例】已知定点A(0,-2),点B在圆C:x2+y2-4y-32=0上运动,C为圆心,线段AB的垂直平分线交BC于点P,则动点P的轨迹E的方程为 .
与椭圆相关的轨迹问题
(几何法)
与椭圆相关的轨迹问题
(几何法)
与椭圆相关的轨迹问题
(定义法)
例2 在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?
与椭圆相关的轨迹问题
(相关点法)
典例3 设A,B坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积为 ,求点M的轨迹方程.
A(-5,0)
B(5,0)
x
y
O
M
与椭圆相关的轨迹问题
(相关点法)
练习 若△ABC的三边长a,b,c成等差数列,且b=6,求顶点B的轨迹方程.
与椭圆相关的轨迹问题
椭圆的焦点三角形问题
【练习】1.椭圆 =1的焦点为F1,F2,点P在椭圆上.若|PF1|=4,则|PF2|= ,∠F1PF2的大小为 .
2.在椭圆 +y2=1中,有一沿直线运动的粒子从一个焦点F2出发经椭圆反射后经过另一个焦点F1,再次被椭圆反射后又回到F2,则该粒子在整个运动过程中经过的路程为 .
椭圆的焦点三角形问题
F为椭圆 的左焦点,P是椭圆上的动点,A(1,1)是一个定点,则|PA|+|PF1|的最大值和最小值是多少?
A(1,1)
x
O
F1(-1.0)
椭圆中距离最值问题
双曲线
抛物线
椭圆
圆
圆锥曲线
学校: 授课教师:
3.1.1
椭圆及其标准方程
——仙女座星系
星系中的椭圆
德国天文学家开普勒(1571-1630)在最初研究他的导师家第谷(1546-1601)所记录的数据时,但是所得结果却与第谷的观测数据至少有8分的角度误差,这不容忽视的8分也许是因为人们认为行星绕太阳做匀速圆周运动所造成的。
至此,人们长期以来视为真理的观念——天体做匀速圆周运动,第一次受到了怀疑。
00 前情提要
椭圆曲线——RSA密码体系
Baignoire腕表
椭圆哲学
我们先把有疫情的区域,看成是一个椭圆图像,其两焦点到动点之距是一个常数(即总人口的定量值),其中心点是“人”,其两个焦点是“无感染人”和“已感染人”的两个群体。
00 前情提要
01 椭圆的定义
如何画一个椭圆?
【定义】平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
这两个定点叫做椭圆的焦点(F1、F2 ),
两焦点的距离叫做椭圆的焦距|F1F2|.
注:1. M是椭圆上任意一点,且|MF1| + |MF2| = 常数;
2. 将常数记为2a,焦距记为2c,且2a>2c;
2a>2c
2a=2c
2a<2c
F1
F2
不存在
01 椭圆的定义
【概念辨析】
1.思维辨析(对的打“√”,错的打“×”)
(1)已知F1(-4,0),F2(4,0),平面内到F1,F2两点的距离之和等于8的点的轨迹是椭圆. ( )
(2)已知F1(-4,0),F2(4,0),平面内到F1,F2两点的距离之和等于6的点的轨迹是椭圆. ( )
(3)平面内到点F1(-4,0),F2(4,0)两点的距离之和等于点M(5,3)到F1,F2的距离之和的点的轨迹是椭圆. ( )
×
×
√
|MF1|+|MF2|=2a
如图所示: F1、F2为两定点,且|F1F2|=2c,求平面内到两定点F1、F2距离之和为定值2a(2a>2c)的动点M的轨迹方程。
移项
两边平方
02 椭圆的标准方程
(-c,0)
(c,0)
(-c,0)
(c,0)
令a2-c2=b2
b2x2+a2y2=a2b2
两边同时除以a2b2:
(a>b>0)
两边平方
a
c
b
02 椭圆的标准方程
表示焦点在x轴上的椭圆标准方程
定义 图形
方程
焦点
a、b、c之间 的关系 |MF1|+|MF2|=2a (2a>|F1F2|)
(c,0)、( c,0)
(0,c)、(0, c)
a2=b2+c2
分母哪个大,焦点就在哪一根坐标轴上
02 椭圆的标准方程
【例1】已知椭圆的两个焦点坐标分别是(-2,0), (2,0),且经过点 ,求它的标准方程.
02 椭圆的标准方程
【例1】已知椭圆的两个焦点坐标分别是(-2,0), (2,0),且经过点 ,求它的标准方程.
02 椭圆的标准方程
练习
1.若方程4x2+ky2=1表示的曲线是焦点在y轴上的椭圆,则k的取值范围为________。
2.若方程 表示焦点在y轴上的椭圆,则实数m的取值范围是________.
3.椭圆的标准方程为 ,且焦距为6,则实数m=_____.
4. 椭圆 的一个焦点为(0,2),那么k=_________.
关于焦点与焦距的问题
F为圆心,F'为圆内一点,A为圆上的一点,线段AF '的垂直平分线交AF于点P,求P点轨迹的形状?
与椭圆相关的轨迹问题
(几何法)
【典例】已知定点A(0,-2),点B在圆C:x2+y2-4y-32=0上运动,C为圆心,线段AB的垂直平分线交BC于点P,则动点P的轨迹E的方程为 .
与椭圆相关的轨迹问题
(几何法)
与椭圆相关的轨迹问题
(几何法)
与椭圆相关的轨迹问题
(定义法)
例2 在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?
与椭圆相关的轨迹问题
(相关点法)
典例3 设A,B坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积为 ,求点M的轨迹方程.
A(-5,0)
B(5,0)
x
y
O
M
与椭圆相关的轨迹问题
(相关点法)
练习 若△ABC的三边长a,b,c成等差数列,且b=6,求顶点B的轨迹方程.
与椭圆相关的轨迹问题
椭圆的焦点三角形问题
【练习】1.椭圆 =1的焦点为F1,F2,点P在椭圆上.若|PF1|=4,则|PF2|= ,∠F1PF2的大小为 .
2.在椭圆 +y2=1中,有一沿直线运动的粒子从一个焦点F2出发经椭圆反射后经过另一个焦点F1,再次被椭圆反射后又回到F2,则该粒子在整个运动过程中经过的路程为 .
椭圆的焦点三角形问题
F为椭圆 的左焦点,P是椭圆上的动点,A(1,1)是一个定点,则|PA|+|PF1|的最大值和最小值是多少?
A(1,1)
x
O
F1(-1.0)
椭圆中距离最值问题
