3.1.2 椭圆的简单几何性质 课件(共27张PPT)
文档属性
| 名称 | 3.1.2 椭圆的简单几何性质 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 990.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-19 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
学校:.... .....
日期:2024.09
3.1.2(1)
椭圆的简单几何性质(1)
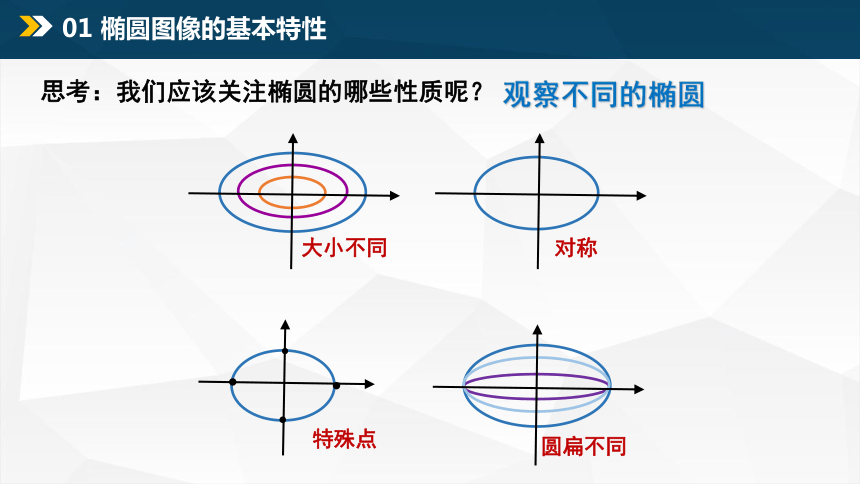
观察不同的椭圆
大小不同
圆扁不同
对称
特殊点
思考:我们应该关注椭圆的哪些性质呢?
01 椭圆图像的基本特性
01 椭圆图像的基本特性
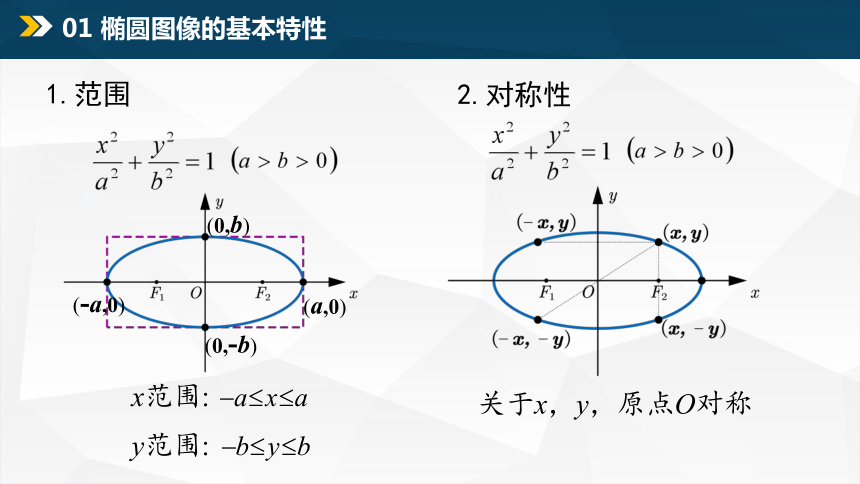
1.范围
(-a,0)
(a,0)
(0,-b)
(0,b)
x范围:
y范围:
2.对称性
关于x,y,原点O对称
01 椭圆图像的基本特性
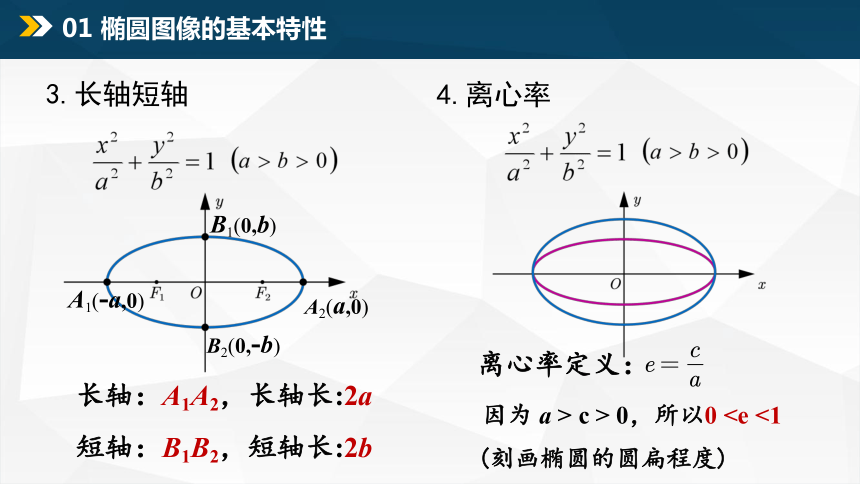
3.长轴短轴
A1(-a,0)
A2(a,0)
B2(0,-b)
B1(0,b)
长轴:A1A2,长轴长:2a
短轴:B1B2,短轴长:2b
4.离心率
离心率定义:
(刻画椭圆的圆扁程度)
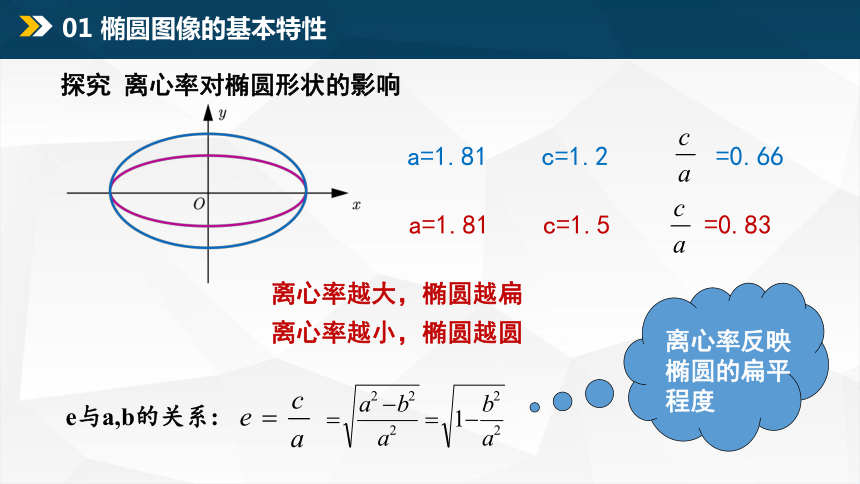
因为 a > c > 0,所以0离心率越大,椭圆越扁
离心率越小,椭圆越圆
离心率反映椭圆的扁平程度
探究 离心率对椭圆形状的影响
e与a,b的关系:
a=1.81 c=1.2 =0.66
a=1.81 c=1.5 =0.83
01 椭圆图像的基本特性
焦点的位置 焦点在x轴上 焦点在y轴上
图形
标准 方程
范围
对称性 对称轴是___________,对称中心是_____________ 顶点坐标
轴长 长轴长=______,短轴长=______ 焦点坐标
焦距 x的范围:__________
y的范围:__________
x的范围:__________
y的范围:__________
坐标原点
x轴,y轴
2c
2b
2a
-b≤ x≤ b
-a≤ y≤ a
(±b ,0), (0,±a)
(0,±c)
1
2
y
o
F
F
M
x
例已知椭圆方程为16x2+25y2=400.长轴长:.短轴长:.焦距:.离心率:.焦点坐标:.顶点坐标:186a=5b=4 c=3由椭圆的方程读取基本信息由椭圆的方程读取基本信息由椭圆的方程读取基本信息【变式】求椭圆m2x2+4m2y2=1(m>0)的长轴长、短轴长、焦点坐标、顶点坐标和离心率.【变式1】椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的2倍,则m的值为___.xyoF1F2例椭圆 上的点到焦点距离的最大值为_________,最小值为___________.椭圆中的距离问题椭圆中的距离问题椭圆中的离心率问题椭圆中的离心率问题
求椭圆的标准方程学校:.... .....
日期:2024.09
3.1.2(2)
椭圆的简单几何性质(2)
P在椭圆外 P在椭圆上 P在椭圆内
__1 =1 __1
设P(x0,y0),椭圆 =1(a>b>0),则点P与椭圆的位置关系如表所示:
>
<
O
x
y
O
x
y
O
x
y
类比
1.点与椭圆的位置关系
判断直线和椭圆位置关系的方法
直线l:y=kx+m与椭圆 =1(a>b>0)的位置关系的判断方法:联立
消去y,得关于x的一元二次方程.
当Δ>0时,方程有两个不同解,直线与椭圆_____;
当Δ=0时,方程有两个相同解,直线与椭圆_____;
当Δ<0时,方程无解,直线与椭圆_____.
相交
相切
相离
3.弦长公式
设直线l与椭圆的两个交点分别为A(x1,y1),B(x2,y2).
弦长公式①:|AB|= __________________________ .
弦长公式②:|AB|= ___________________________ .
O
x
y
A(x1,y1)
B(x2,y2)
2.直线与椭圆的位置关系
直线与椭圆的位置关系
例7. 已知直线l:4x-5y+m=0和椭圆 .m为何值时,直线l与椭圆C:(1)有两个公共点?(2)有且仅有一个公共点?(3)没有公共点?
直线与椭圆的位置关系
练习 1.直线y=kx-k+1(k≠0)与椭圆 =1的位置关系是( )
A.相交 B.相切 C.相离 D.不确定
弦长问题
弦长问题(三角形面积问题)
例 已知斜率为2的直线经过椭圆 =1的右焦点F1,与椭圆相交于A,B两点,左焦点为F,求△ABF的面积.
弦长问题
中点弦问题
中点弦问题
点差法:利用端点在曲线上,坐标满足方程,作差构造出中点坐标和斜率.
2.已知椭圆 =1(a> )的左、右焦点分别为F1,F2.过左焦点F1作斜率为-2的直线与椭圆交于A,B两点,P是AB的中点,O为坐标原点,若直线OP的斜率为 ,则a的值是 .
中点弦问题
【典例】已知椭圆E: =1(a>b>0)的左右焦点分别为F1,F2,上顶点为M,且△MF1F2为面积是1的等腰直角三角形.
(1)求椭圆E的方程;
(2)若直线l:y=-x+m与椭圆E交于A,B两点,以AB为直径的圆与y轴相切,求m的值.
综合问题
2.已知F是椭圆E: =1的左焦点,P为椭圆E上的动点,A(1, )为一个定点,则|PA|+|PF|的最大值为 .
学校:.... .....
日期:2024.09
3.1.2(1)
椭圆的简单几何性质(1)
观察不同的椭圆
大小不同
圆扁不同
对称
特殊点
思考:我们应该关注椭圆的哪些性质呢?
01 椭圆图像的基本特性
01 椭圆图像的基本特性
1.范围
(-a,0)
(a,0)
(0,-b)
(0,b)
x范围:
y范围:
2.对称性
关于x,y,原点O对称
01 椭圆图像的基本特性
3.长轴短轴
A1(-a,0)
A2(a,0)
B2(0,-b)
B1(0,b)
长轴:A1A2,长轴长:2a
短轴:B1B2,短轴长:2b
4.离心率
离心率定义:
(刻画椭圆的圆扁程度)
因为 a > c > 0,所以0
离心率越小,椭圆越圆
离心率反映椭圆的扁平程度
探究 离心率对椭圆形状的影响
e与a,b的关系:
a=1.81 c=1.2 =0.66
a=1.81 c=1.5 =0.83
01 椭圆图像的基本特性
焦点的位置 焦点在x轴上 焦点在y轴上
图形
标准 方程
范围
对称性 对称轴是___________,对称中心是_____________ 顶点坐标
轴长 长轴长=______,短轴长=______ 焦点坐标
焦距 x的范围:__________
y的范围:__________
x的范围:__________
y的范围:__________
坐标原点
x轴,y轴
2c
2b
2a
-b≤ x≤ b
-a≤ y≤ a
(±b ,0), (0,±a)
(0,±c)
1
2
y
o
F
F
M
x
例已知椭圆方程为16x2+25y2=400.长轴长:.短轴长:.焦距:.离心率:.焦点坐标:.顶点坐标:186a=5b=4 c=3由椭圆的方程读取基本信息由椭圆的方程读取基本信息由椭圆的方程读取基本信息【变式】求椭圆m2x2+4m2y2=1(m>0)的长轴长、短轴长、焦点坐标、顶点坐标和离心率.【变式1】椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的2倍,则m的值为___.xyoF1F2例椭圆 上的点到焦点距离的最大值为_________,最小值为___________.椭圆中的距离问题椭圆中的距离问题椭圆中的离心率问题椭圆中的离心率问题
求椭圆的标准方程学校:.... .....
日期:2024.09
3.1.2(2)
椭圆的简单几何性质(2)
P在椭圆外 P在椭圆上 P在椭圆内
__1 =1 __1
设P(x0,y0),椭圆 =1(a>b>0),则点P与椭圆的位置关系如表所示:
>
<
O
x
y
O
x
y
O
x
y
类比
1.点与椭圆的位置关系
判断直线和椭圆位置关系的方法
直线l:y=kx+m与椭圆 =1(a>b>0)的位置关系的判断方法:联立
消去y,得关于x的一元二次方程.
当Δ>0时,方程有两个不同解,直线与椭圆_____;
当Δ=0时,方程有两个相同解,直线与椭圆_____;
当Δ<0时,方程无解,直线与椭圆_____.
相交
相切
相离
3.弦长公式
设直线l与椭圆的两个交点分别为A(x1,y1),B(x2,y2).
弦长公式①:|AB|= __________________________ .
弦长公式②:|AB|= ___________________________ .
O
x
y
A(x1,y1)
B(x2,y2)
2.直线与椭圆的位置关系
直线与椭圆的位置关系
例7. 已知直线l:4x-5y+m=0和椭圆 .m为何值时,直线l与椭圆C:(1)有两个公共点?(2)有且仅有一个公共点?(3)没有公共点?
直线与椭圆的位置关系
练习 1.直线y=kx-k+1(k≠0)与椭圆 =1的位置关系是( )
A.相交 B.相切 C.相离 D.不确定
弦长问题
弦长问题(三角形面积问题)
例 已知斜率为2的直线经过椭圆 =1的右焦点F1,与椭圆相交于A,B两点,左焦点为F,求△ABF的面积.
弦长问题
中点弦问题
中点弦问题
点差法:利用端点在曲线上,坐标满足方程,作差构造出中点坐标和斜率.
2.已知椭圆 =1(a> )的左、右焦点分别为F1,F2.过左焦点F1作斜率为-2的直线与椭圆交于A,B两点,P是AB的中点,O为坐标原点,若直线OP的斜率为 ,则a的值是 .
中点弦问题
【典例】已知椭圆E: =1(a>b>0)的左右焦点分别为F1,F2,上顶点为M,且△MF1F2为面积是1的等腰直角三角形.
(1)求椭圆E的方程;
(2)若直线l:y=-x+m与椭圆E交于A,B两点,以AB为直径的圆与y轴相切,求m的值.
综合问题
2.已知F是椭圆E: =1的左焦点,P为椭圆E上的动点,A(1, )为一个定点,则|PA|+|PF|的最大值为 .
