海南省海口市2023-2024学年七年级下学期期末数学试卷(含详细解答)
文档属性
| 名称 | 海南省海口市2023-2024学年七年级下学期期末数学试卷(含详细解答) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 00:03:11 | ||
图片预览




文档简介
海南省海口市2023-2024学年七年级下学期期末数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若,则x等于( )
A. B.2 C. D.1
2.若,则下列不等式成立的是( )
A. B. C. D.
3.已知,当时,x的取值范围是( )
A. B. C. D.
4.已知是方程的一个解,则k的值为( )
A.-2 B.3 C. D.
5.下列四个图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
6.一副三角板按图所示方式叠放,点A,D分别在、上,若,则等于( )
A. B. C. D.
7.如图1是一根细铁丝围成的正方形,其边长为2,现将该细铁丝围成一个三角形(如图2所示),则的长可能为( )
A.3.5 B.4 C.4.5 D.5
8.一个多边形每个内角都是150°,则这个多边形的边数为( )
A.12 B.10 C.8 D.6
9.如图,在的正方形网格中,等于( )
A. B. C. D.
10.如图,在中,于点D,E是上一点,若,,,则的周长为( )
A.22 B.23 C.24 D.26
11.如图,将正方形纸片对折,得到折痕,把纸片展平,再沿折叠使点A落在折痕上的处,则等于( )
A. B. C. D.
12.中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有x个,甜果有y个,则可列方程组为( )
A. B.
C. D.
二、填空题
13.若关于x的方程的解是负数,则m的取值范围是______.
14.已知a、b满足,,则的值为______.
15.如图,O是内一点,.若,则______度.
16.如图,是等边三角形,D是边上任意一点(与点B,C不重合),经顺时针旋转后与重合.连接,则_____度;设,则的度数为______度(用含有x的代数式表示).
三、解答题
17.(1)解方程:;
(2)解方程组:;
(3)求不等式组的所有整数解.
18.甲、乙两名同学解方程组由于甲同学看错了系数a,得到方程组的解是,由于乙同学看错了系数b,得到方程组的解是求原方程组中的a、b的值.
19.某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆,由于熟练工不够,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装,生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车:2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)求每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,求所抽调的熟练工的人数.
20.如图,直线是的对称轴.
(1)画出中边上的高,与交于点O;
(2)试说明;
(3)若,求和的度数.
21.在如图的正方形网格中,每个小正方形的边长都是单位1,和的顶点均在格点上,且
(1)画出关于直线x对称的
(2)画出,使和关于点O成中心对称;
(3)与是否对称?若对称,请在图中画出对称轴或对称中心;
(4)写出一种由经过轴对称、平移和旋转变换得到的过程.
22.直线于点O,点A、B分别在射线、上(不与点O重合).
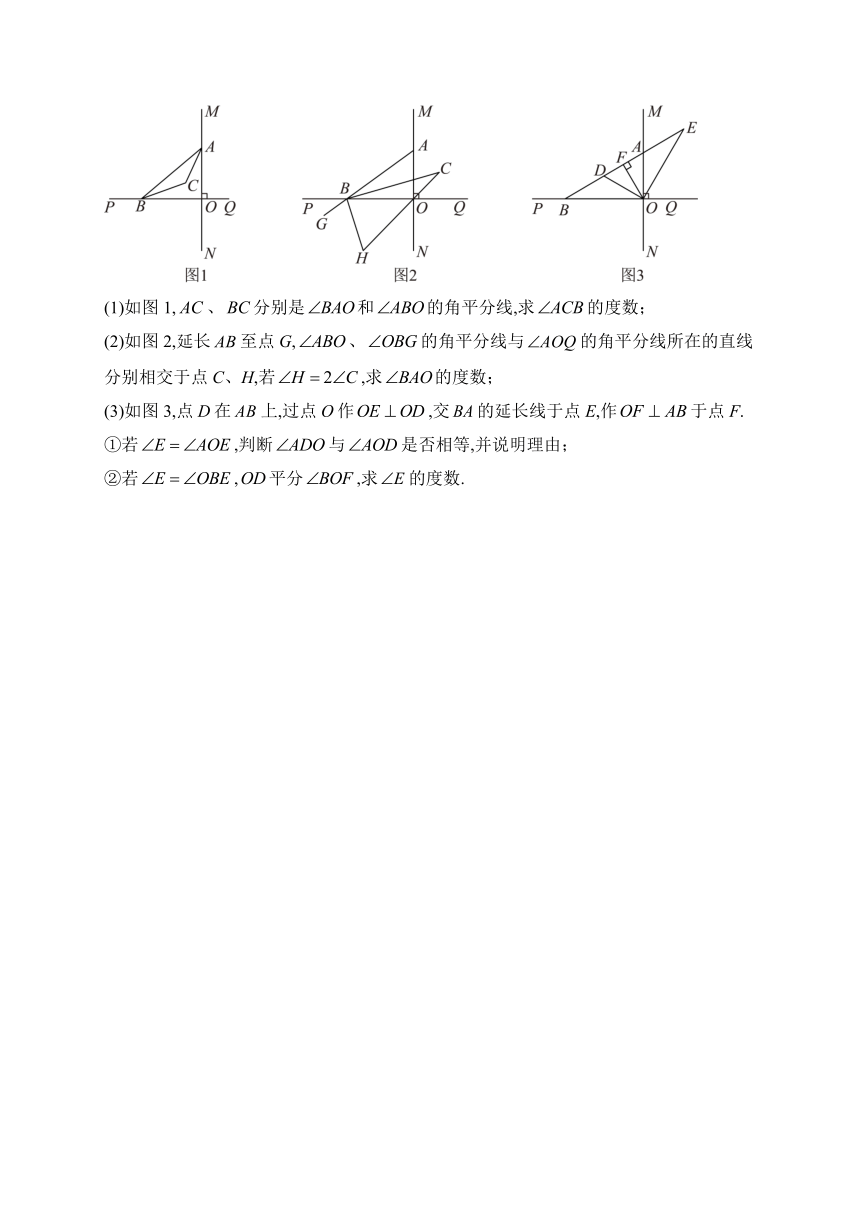
(1)如图1,、分别是和的角平分线,求的度数;
(2)如图2,延长至点G,、的角平分线与的角平分线所在的直线分别相交于点C、H,若,求的度数;
(3)如图3,点D在上,过点O作,交的延长线于点E,作于点F.
①若,判断与是否相等,并说明理由;
②若,平分,求的度数.
参考答案
1.答案:C
解析:,
移项得:,
合并同类项:,
系数化为1得:,
故选:C.
2.答案:D
解析:A、由得,不等式两边同时乘以,不等号改变方向,得,原式计算错误,故该选项不符合题意;
B、由得,不等式两边同时加,不等号方向不变,得,原式计算错误,故该选项不符合题意;
C、由得,不等式两边同时乘以2,不等号方向不变,得即,原式计算错误,故该选项不符合题意;
D、由得,不等式两边同时除以5,不等号方向不变,得即,原式计算正确,故该选项符合题意.
故选:D.
3.答案:B
解析:∵,
∴当时,,
解得,
故选:B.
4.答案:A
解析:把代入方程得
解得
故选A.
5.答案:D
解析:A、不是轴对称图形,是中心对称图形,不符合题意;
B、不是轴对称图形,是中心对称图形,不符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、是轴对称图形,也是中心对称图形,符合题意;
故选:D.
6.答案:B
解析:根据三角形的性质可得,,,
∵,
∴,
∵是外角,
∴,
故选:B.
7.答案:A
解析:铁丝的总长度为,
根据三角形的三边关系知,两边之和大于第三边,即,当时,,
∴边长度小于4,
故选:A.
8.答案:A
解析:,
.
故选A.
9.答案:C
解析:,,
故选:C.
10.答案:C
解析:∵,
∴,,
∵的周长为,
;
故选:C.
11.答案:D
解析:四边形是正方形,
,
将正方形纸片对折,得到折痕,
,,
沿折叠使点A落在折痕上的处,
,,
,
连接,
在和中
,
,
,
是等边三角形,
,
故选:D.
12.答案:A
解析:设苦果有x个,甜果有y个,由题意可得,
故选:A.
13.答案:
解析:由,得
.
∵关于x的方程的解是负数,
∴,
解得.
故答案是:.
14.答案:2
解析:根据题意得
,得,
,
故答案为:2.
15.答案:63
解析:∵,
,,是等腰三角形,
,,,
,
故答案为:63.
16.答案:60;
解析:∵是等边三角形,
∴,,
∵旋转与重合,
∴,,
∴是等边三角形,
∴;
∵旋转后与重合,
∴,
∵是等边三角形,
∴,
在中,是外角,
∴,
∴,
故答案为:60,.
17.答案:(1)
(2)
(3),,,0,1
解析:(1)
去分母,得,
去括号,得,
合并同类项,得,
系数化为1,得;
(2),
,得,即.
将代入①,得,
,
;
(3),
解不等式①,得.
解不等式②,得.
∴该不等式组的解集是:.
∴所有整数解为:,,,0,1.
18.答案:,
解析:∵甲同学看错了系数a,得到的方程组的解是,
是方程的解,
∴,
∴;
∵乙同学看错了系数b,得到的方程组的解是,
是方程的解,
∴,
∴.
19.答案:(1)每名熟练工和新工人每月分别可以安装4辆,2辆电动汽车
(2)所抽调的熟练工的人数为人
解析:(1)每名熟练工和新工人每月分别可以安装x、y辆电动汽车,
根据题意可列方程,,
解得.
答:每名熟练工和新工人每月分别可以安装4、2辆电动汽车;
(2)设需熟练工m名,
依题意有:,
整理得:.
所抽调的熟练工的人数为人.
20.答案:(1)图见解析
(2)见解析
(3),
解析:(1)如图,在中,线段是边上的高
(2)∵直线是的对称轴,
∴,,
∴,
∴,
∵,
∴,
∴,
∴.
∴;
(3)在中,
∴.
在中,
,
∴.
21.答案:(1)图见解析
(2)图见解析
(3)对称,对称轴为直线y,图见解析
(4)图见解析
解析:(1)如图,即为所求;
(2)如图,即为所求;
(3)如图与成轴对称,对称轴为直线y;
(4)答案不唯一.
①先将向右平移3个单位,然后绕点顺时针旋转,再关于直线x对称.
②先将向右平移3个单位,再向下平移2个单位,接着绕点逆时针旋转,然后再关于直线对称.
22.答案:(1)
(2)
(3)①,理由见解析
②
解析:(1)如图
∵、分别是和的角平分线,
,.
∵,
∴,
,
在中,
,
.
(2)如图:
,
∵、分别是和的角平分线,
,,
∴,
∵,
∴,
∵是的角平分线,,
,
,
∴.
(3)如图
①,理由如下:
∵,
∴.
∴,,
∵,
∴;
②在中,
∵,
∴.
∵.
∴.
∵平分,
∴.
∵,
∴.
在中,,
∴.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若,则x等于( )
A. B.2 C. D.1
2.若,则下列不等式成立的是( )
A. B. C. D.
3.已知,当时,x的取值范围是( )
A. B. C. D.
4.已知是方程的一个解,则k的值为( )
A.-2 B.3 C. D.
5.下列四个图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
6.一副三角板按图所示方式叠放,点A,D分别在、上,若,则等于( )
A. B. C. D.
7.如图1是一根细铁丝围成的正方形,其边长为2,现将该细铁丝围成一个三角形(如图2所示),则的长可能为( )
A.3.5 B.4 C.4.5 D.5
8.一个多边形每个内角都是150°,则这个多边形的边数为( )
A.12 B.10 C.8 D.6
9.如图,在的正方形网格中,等于( )
A. B. C. D.
10.如图,在中,于点D,E是上一点,若,,,则的周长为( )
A.22 B.23 C.24 D.26
11.如图,将正方形纸片对折,得到折痕,把纸片展平,再沿折叠使点A落在折痕上的处,则等于( )
A. B. C. D.
12.中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有x个,甜果有y个,则可列方程组为( )
A. B.
C. D.
二、填空题
13.若关于x的方程的解是负数,则m的取值范围是______.
14.已知a、b满足,,则的值为______.
15.如图,O是内一点,.若,则______度.
16.如图,是等边三角形,D是边上任意一点(与点B,C不重合),经顺时针旋转后与重合.连接,则_____度;设,则的度数为______度(用含有x的代数式表示).
三、解答题
17.(1)解方程:;
(2)解方程组:;
(3)求不等式组的所有整数解.
18.甲、乙两名同学解方程组由于甲同学看错了系数a,得到方程组的解是,由于乙同学看错了系数b,得到方程组的解是求原方程组中的a、b的值.
19.某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆,由于熟练工不够,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装,生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车:2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)求每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,求所抽调的熟练工的人数.
20.如图,直线是的对称轴.
(1)画出中边上的高,与交于点O;
(2)试说明;
(3)若,求和的度数.
21.在如图的正方形网格中,每个小正方形的边长都是单位1,和的顶点均在格点上,且
(1)画出关于直线x对称的
(2)画出,使和关于点O成中心对称;
(3)与是否对称?若对称,请在图中画出对称轴或对称中心;
(4)写出一种由经过轴对称、平移和旋转变换得到的过程.
22.直线于点O,点A、B分别在射线、上(不与点O重合).
(1)如图1,、分别是和的角平分线,求的度数;
(2)如图2,延长至点G,、的角平分线与的角平分线所在的直线分别相交于点C、H,若,求的度数;
(3)如图3,点D在上,过点O作,交的延长线于点E,作于点F.
①若,判断与是否相等,并说明理由;
②若,平分,求的度数.
参考答案
1.答案:C
解析:,
移项得:,
合并同类项:,
系数化为1得:,
故选:C.
2.答案:D
解析:A、由得,不等式两边同时乘以,不等号改变方向,得,原式计算错误,故该选项不符合题意;
B、由得,不等式两边同时加,不等号方向不变,得,原式计算错误,故该选项不符合题意;
C、由得,不等式两边同时乘以2,不等号方向不变,得即,原式计算错误,故该选项不符合题意;
D、由得,不等式两边同时除以5,不等号方向不变,得即,原式计算正确,故该选项符合题意.
故选:D.
3.答案:B
解析:∵,
∴当时,,
解得,
故选:B.
4.答案:A
解析:把代入方程得
解得
故选A.
5.答案:D
解析:A、不是轴对称图形,是中心对称图形,不符合题意;
B、不是轴对称图形,是中心对称图形,不符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、是轴对称图形,也是中心对称图形,符合题意;
故选:D.
6.答案:B
解析:根据三角形的性质可得,,,
∵,
∴,
∵是外角,
∴,
故选:B.
7.答案:A
解析:铁丝的总长度为,
根据三角形的三边关系知,两边之和大于第三边,即,当时,,
∴边长度小于4,
故选:A.
8.答案:A
解析:,
.
故选A.
9.答案:C
解析:,,
故选:C.
10.答案:C
解析:∵,
∴,,
∵的周长为,
;
故选:C.
11.答案:D
解析:四边形是正方形,
,
将正方形纸片对折,得到折痕,
,,
沿折叠使点A落在折痕上的处,
,,
,
连接,
在和中
,
,
,
是等边三角形,
,
故选:D.
12.答案:A
解析:设苦果有x个,甜果有y个,由题意可得,
故选:A.
13.答案:
解析:由,得
.
∵关于x的方程的解是负数,
∴,
解得.
故答案是:.
14.答案:2
解析:根据题意得
,得,
,
故答案为:2.
15.答案:63
解析:∵,
,,是等腰三角形,
,,,
,
故答案为:63.
16.答案:60;
解析:∵是等边三角形,
∴,,
∵旋转与重合,
∴,,
∴是等边三角形,
∴;
∵旋转后与重合,
∴,
∵是等边三角形,
∴,
在中,是外角,
∴,
∴,
故答案为:60,.
17.答案:(1)
(2)
(3),,,0,1
解析:(1)
去分母,得,
去括号,得,
合并同类项,得,
系数化为1,得;
(2),
,得,即.
将代入①,得,
,
;
(3),
解不等式①,得.
解不等式②,得.
∴该不等式组的解集是:.
∴所有整数解为:,,,0,1.
18.答案:,
解析:∵甲同学看错了系数a,得到的方程组的解是,
是方程的解,
∴,
∴;
∵乙同学看错了系数b,得到的方程组的解是,
是方程的解,
∴,
∴.
19.答案:(1)每名熟练工和新工人每月分别可以安装4辆,2辆电动汽车
(2)所抽调的熟练工的人数为人
解析:(1)每名熟练工和新工人每月分别可以安装x、y辆电动汽车,
根据题意可列方程,,
解得.
答:每名熟练工和新工人每月分别可以安装4、2辆电动汽车;
(2)设需熟练工m名,
依题意有:,
整理得:.
所抽调的熟练工的人数为人.
20.答案:(1)图见解析
(2)见解析
(3),
解析:(1)如图,在中,线段是边上的高
(2)∵直线是的对称轴,
∴,,
∴,
∴,
∵,
∴,
∴,
∴.
∴;
(3)在中,
∴.
在中,
,
∴.
21.答案:(1)图见解析
(2)图见解析
(3)对称,对称轴为直线y,图见解析
(4)图见解析
解析:(1)如图,即为所求;
(2)如图,即为所求;
(3)如图与成轴对称,对称轴为直线y;
(4)答案不唯一.
①先将向右平移3个单位,然后绕点顺时针旋转,再关于直线x对称.
②先将向右平移3个单位,再向下平移2个单位,接着绕点逆时针旋转,然后再关于直线对称.
22.答案:(1)
(2)
(3)①,理由见解析
②
解析:(1)如图
∵、分别是和的角平分线,
,.
∵,
∴,
,
在中,
,
.
(2)如图:
,
∵、分别是和的角平分线,
,,
∴,
∵,
∴,
∵是的角平分线,,
,
,
∴.
(3)如图
①,理由如下:
∵,
∴.
∴,,
∵,
∴;
②在中,
∵,
∴.
∵.
∴.
∵平分,
∴.
∵,
∴.
在中,,
∴.
同课章节目录
