2023-2024学年河南省漯河市郾城区冀教版八年级(下)期末数学试卷(含答案版)
文档属性
| 名称 | 2023-2024学年河南省漯河市郾城区冀教版八年级(下)期末数学试卷(含答案版) |  | |
| 格式 | doc | ||
| 文件大小 | 983.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 10:35:05 | ||
图片预览


文档简介
2023-2024学年河南省漯河市郾城区八年级(下)期末数学试卷
一、选择题(每小题3分,共30分)下列各题有四个选项,其中只有一个选项是正确的。
1.(3分)下列式子为最简二次根式的是( )
A. B. C. D.
2.(3分)下列四个算式正确的是( )
A. B.
C.=× D.
3.(3分)以下列长度的三条线段为边,能组成直角三角形的是( )
A.2,2,2 B.2,3,4 C.3,5,6 D.1,,2
4.(3分)下列关于直线y=x+2的说法中,正确的是( )
A.经过第一、三、四象限
B.与x轴交于(2,0)
C.与y轴交于(0,2)
D.将其图象向下平移2个单位得到y=2x的图象
5.(3分)如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
6.(3分)如图,将一张平行四边形纸片ABCD以DE为折痕进行折叠,点C的对应点为C′,若∠1=20°,∠2=60°,则∠C的度数为( )
A.40° B.50° C.60° D.70°
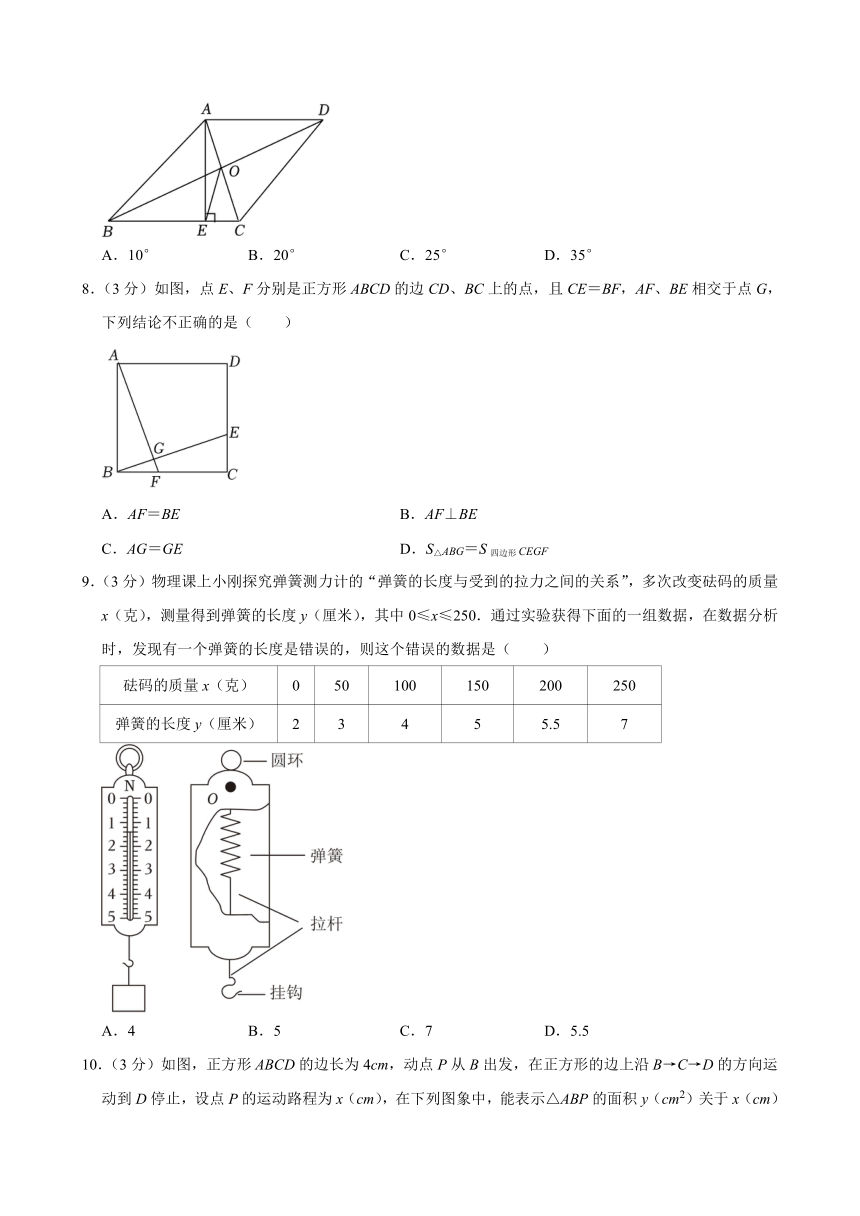
7.(3分)在菱形ABCD中,对角线AC和BD相交于点O,AE⊥BC于点E,连接OE,若∠ABD=20°,则∠AEO的度数为( )
A.10° B.20° C.25° D.35°
8.(3分)如图,点E、F分别是正方形ABCD的边CD、BC上的点,且CE=BF,AF、BE相交于点G,下列结论不正确的是( )
A.AF=BE B.AF⊥BE
C.AG=GE D.S△ABG=S四边形CEGF
9.(3分)物理课上小刚探究弹簧测力计的“弹簧的长度与受到的拉力之间的关系”,多次改变砝码的质量x(克),测量得到弹簧的长度y(厘米),其中0≤x≤250.通过实验获得下面的一组数据,在数据分析时,发现有一个弹簧的长度是错误的,则这个错误的数据是( )
砝码的质量x(克) 0 50 100 150 200 250
弹簧的长度y(厘米) 2 3 4 5 5.5 7
A.4 B.5 C.7 D.5.5
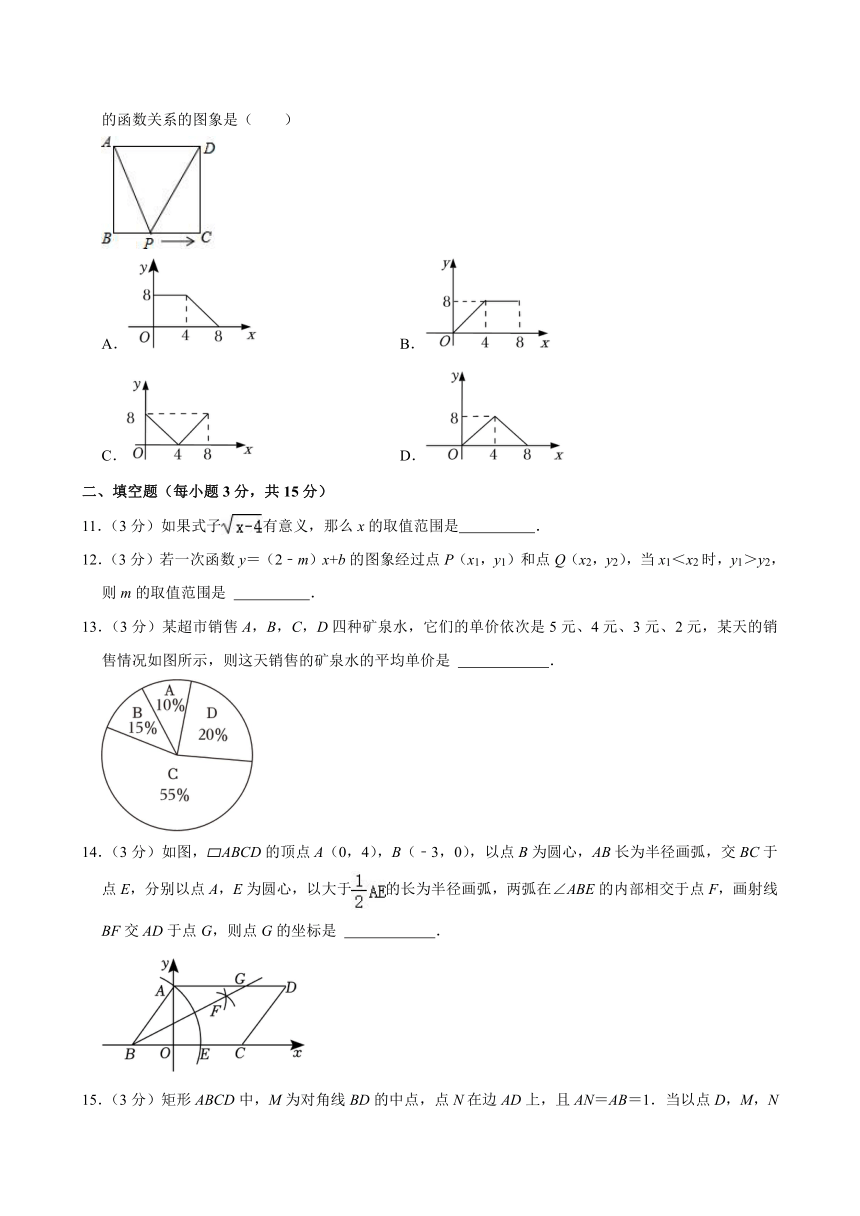
10.(3分)如图,正方形ABCD的边长为4cm,动点P从B出发,在正方形的边上沿B→C→D的方向运动到D停止,设点P的运动路程为x(cm),在下列图象中,能表示△ABP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B.
C. D.
二、填空题(每小题3分,共15分)
11.(3分)如果式子有意义,那么x的取值范围是 .
12.(3分)若一次函数y=(2﹣m)x+b的图象经过点P(x1,y1)和点Q(x2,y2),当x1<x2时,y1>y2,则m的取值范围是 .
13.(3分)某超市销售A,B,C,D四种矿泉水,它们的单价依次是5元、4元、3元、2元,某天的销售情况如图所示,则这天销售的矿泉水的平均单价是 .
14.(3分)如图, ABCD的顶点A(0,4),B(﹣3,0),以点B为圆心,AB长为半径画弧,交BC于点E,分别以点A,E为圆心,以大于的长为半径画弧,两弧在∠ABE的内部相交于点F,画射线BF交AD于点G,则点G的坐标是 .
15.(3分)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN=AB=1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为 .
三、解答题(本大题共8小题,共75分)
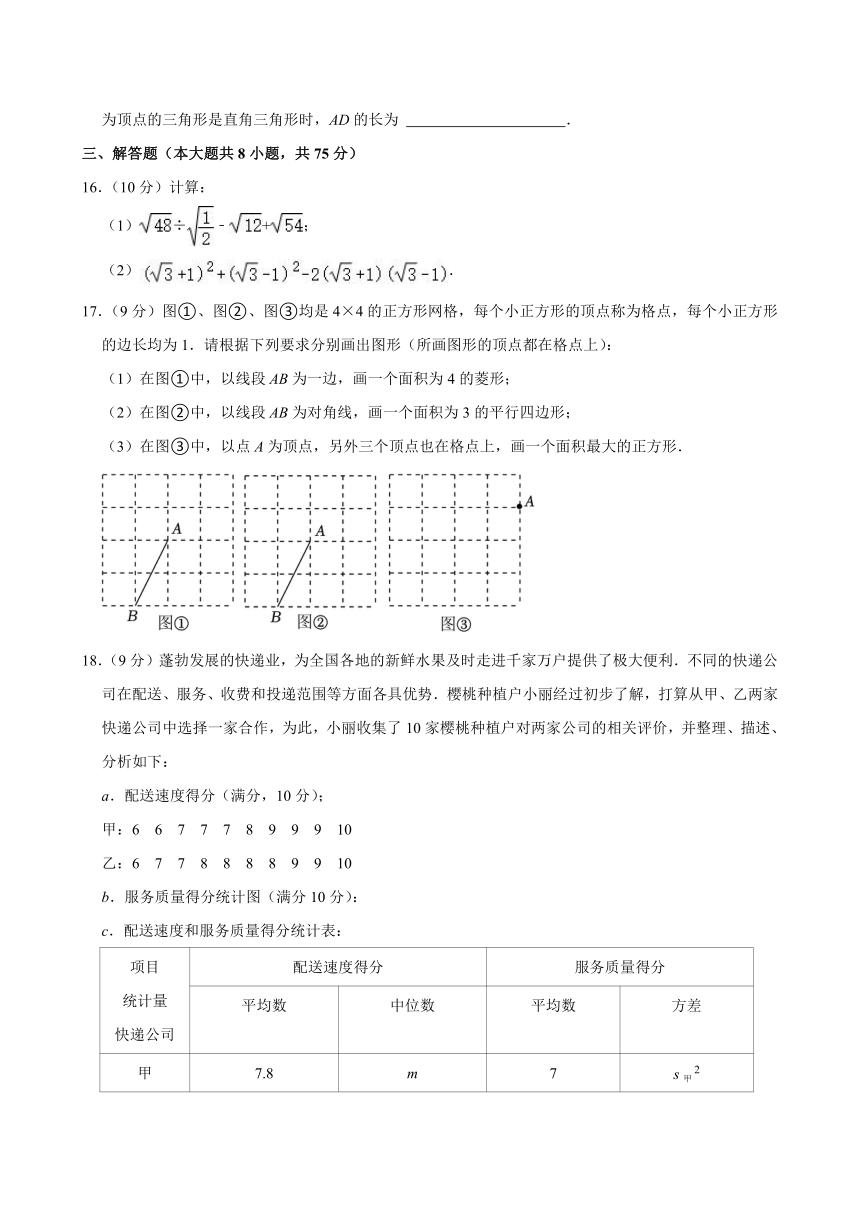
16.(10分)计算:
(1)÷﹣+;
(2).
17.(9分)图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.请根据下列要求分别画出图形(所画图形的顶点都在格点上):
(1)在图①中,以线段AB为一边,画一个面积为4的菱形;
(2)在图②中,以线段AB为对角线,画一个面积为3的平行四边形;
(3)在图③中,以点A为顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
18.(9分)蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分,10分);
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分统计图(满分10分):
c.配送速度和服务质量得分统计表:
项目统计量快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲 7.8 m 7 s甲2
乙 8 8 7 s乙2
根据以上信息,回答下列问题:
(1)表格中的m= ;s甲2 s乙2(填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?
19.(9分)如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=80°,∠DCE=30°,求∠CBE的度数.
20.(9分)如图,在 ABCD中,点M为AC的中点,过点D作DF⊥BC,延长CB到点E使BE=CF,连接AE,EM.
(1)求证:四边形AEFD是矩形;
(2)若AD=6,BF=3,∠ADC=120°,求EM的长.
21.(9分)暑假临近,某读书俱乐部推出了甲、乙两种消费卡,其中,甲卡按照次数收费,乙卡收取办卡费用后每次打折收费.设消费的次数为x次,所需费用为y元,且y与x的函数关系如图所示.根据图中信息,解答下列问题.
(1)分别求出选择这两种卡时,y与x的函数表达式;
(2)求消费多少次时,两者费用相差20元?
22.(10分)如图,已知直线AB:y1=﹣2x+4交x轴于点A,交y轴于点B,在直线AB上方以AB为腰作等腰Rt△ABC,直线AC:y2=kx+b交y轴于点D;
(1)求直线AC的解析式;
(2)填空:①当y1≥y2时,则x的取值范围为: ;
②点E是坐标平面上的一点,以A,B,D,E四点为顶点的四边形是平行四边形,则点E的坐标为 .
23.(10分)综合与实践
综合与实践课上,老师让同学们以“三角板的平移”为主题开展数学活动.
(1)操作判断
操作一:将一副等腰直角三角板两斜边重合,按图1放置;
操作二:将三角板ACD沿CA方向平移(两三角板始终接触)至图2位置.
根据以上操作,填空:
图2中AA'与CC'的数量关系是 ;四边形ABC′D′的形状是 ;
(2)迁移探究
小航将一副等腰直角三角板换成一副含30°角的直角三角板,继续探究,已知三角板AB边长为6cm,过程如下:
将三角板ACD按(1)中的方式操作,如图3,在平移过程中,四边形ABC'D'的形状能否是菱形,若不能,请说明理由,若能,请求出CC'的长;
(3)拓展应用
在(2)的探究过程中,当△BCC′为等腰三角形时,CC'的长是 cm.
2023-2024学年河南省漯河市郾城区八年级(下)期末数学试卷
参考答案
一、选择题(每小题3分,共30分)下列各题有四个选项,其中只有一个选项是正确的。
1.(3分)下列式子为最简二次根式的是( )
A. B. C. D.
选:C.
2.(3分)下列四个算式正确的是( )
A. B.
C.=× D.
选:B.
3.(3分)以下列长度的三条线段为边,能组成直角三角形的是( )
A.2,2,2 B.2,3,4 C.3,5,6 D.1,,2
选:D.
4.(3分)下列关于直线y=x+2的说法中,正确的是( )
A.经过第一、三、四象限
B.与x轴交于(2,0)
C.与y轴交于(0,2)
D.将其图象向下平移2个单位得到y=2x的图象
选:C.
5.(3分)如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
选:C.
6.(3分)如图,将一张平行四边形纸片ABCD以DE为折痕进行折叠,点C的对应点为C′,若∠1=20°,∠2=60°,则∠C的度数为( )
A.40° B.50° C.60° D.70°
选:A.
7.(3分)在菱形ABCD中,对角线AC和BD相交于点O,AE⊥BC于点E,连接OE,若∠ABD=20°,则∠AEO的度数为( )
A.10° B.20° C.25° D.35°
选:B.
8.(3分)如图,点E、F分别是正方形ABCD的边CD、BC上的点,且CE=BF,AF、BE相交于点G,下列结论不正确的是( )
A.AF=BE B.AF⊥BE
C.AG=GE D.S△ABG=S四边形CEGF
选:C.
9.(3分)物理课上小刚探究弹簧测力计的“弹簧的长度与受到的拉力之间的关系”,多次改变砝码的质量x(克),测量得到弹簧的长度y(厘米),其中0≤x≤250.通过实验获得下面的一组数据,在数据分析时,发现有一个弹簧的长度是错误的,则这个错误的数据是( )
砝码的质量x(克) 0 50 100 150 200 250
弹簧的长度y(厘米) 2 3 4 5 5.5 7
A.4 B.5 C.7 D.5.5
选:D.
10.(3分)如图,正方形ABCD的边长为4cm,动点P从B出发,在正方形的边上沿B→C→D的方向运动到D停止,设点P的运动路程为x(cm),在下列图象中,能表示△ABP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B.
C. D.
选:B.
二、填空题(每小题3分,共15分)
11.(3分)如果式子有意义,那么x的取值范围是 x≥4 .
12.(3分)若一次函数y=(2﹣m)x+b的图象经过点P(x1,y1)和点Q(x2,y2),当x1<x2时,y1>y2,则m的取值范围是 m>2 .
13.(3分)某超市销售A,B,C,D四种矿泉水,它们的单价依次是5元、4元、3元、2元,某天的销售情况如图所示,则这天销售的矿泉水的平均单价是 3.15元 .
14.(3分)如图, ABCD的顶点A(0,4),B(﹣3,0),以点B为圆心,AB长为半径画弧,交BC于点E,分别以点A,E为圆心,以大于的长为半径画弧,两弧在∠ABE的内部相交于点F,画射线BF交AD于点G,则点G的坐标是 (5,4) .
15.(3分)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN=AB=1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为 2或1+ .
三、解答题(本大题共8小题,共75分)
16.(10分)计算:
(1)÷﹣+;
(2).
【解答】解:(1)原式=﹣2+3
=4﹣2+3
=7﹣2;
(2)原式=3+2+1+3﹣2+1﹣2(3﹣1)
=4.
17.(9分)图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.请根据下列要求分别画出图形(所画图形的顶点都在格点上):
(1)在图①中,以线段AB为一边,画一个面积为4的菱形;
(2)在图②中,以线段AB为对角线,画一个面积为3的平行四边形;
(3)在图③中,以点A为顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
【解答】解:(1)如图1,
∵菱形的面积=对角线乘积的一半,
∴面积为4的菱形的对角线为4和2,
∴S菱形ABCD=×4×2=4,
∴菱形ABCD即为所求;
(2)如图,
∵CD=3,AB的纵高为2,
∴S四边形ACBD=×3×2=3,
∴四边形ACBD即为满足条件的图形;
(3)如图,
当正方形的边长为三个方格的斜边时,
即=的正方形ABCD的面积最大.
18.(9分)蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分,10分);
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分统计图(满分10分):
c.配送速度和服务质量得分统计表:
项目统计量快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲 7.8 m 7 s甲2
乙 8 8 7 s乙2
根据以上信息,回答下列问题:
(1)表格中的m= 7.5 ;s甲2 < s乙2(填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?
【解答】解:(1)甲公司配送速度得分从小到大排列为:6 6 7 7 7 8 9 9 9 10,
一共10个数据,其中第5个与第6个数据分别为7、8,
所以中位数m==7.5.
=×[3×(7﹣7)2+4×(8﹣7)2+2×(6﹣7)2+(5﹣7)2]=1,
=×[(4﹣7)2+(8﹣7)2+2×(10﹣7)2+2×(6﹣7)2+(9﹣7)2+2×(5﹣7)2+(7﹣7)2]=4.2,
∴<,
故答案为:7.5,<;
(2)小丽应选择甲公司(答案不唯一),理由如下:
∵配送速度得分甲和乙的得分相差不大,服务质量得分甲和乙的平均数相同,但是甲的方差明显小于乙的方差,
∴甲更稳定,
∴小丽应选择甲公司;
(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)
19.(9分)如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=80°,∠DCE=30°,求∠CBE的度数.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠BAE=∠BCD,
∵BF=BE,CG=CE,
∴BC是△EFG的中位线,
∴BC∥FG,BC=FG,
∵H为FG的中点,
∴FH=FG,
∴BC∥FH,BC=FH,
∴AD∥FH,AD=FH,
∴四边形AFHD是平行四边形;
(2)解:∵∠BAE=80°,
∴∠BCD=80°,
∵∠DCE=30°,
∴∠BCE=80°﹣30°=50°,
∵CB=CE,
∴∠CBE=∠CEB=(180°﹣50°)=65°.
20.(9分)如图,在 ABCD中,点M为AC的中点,过点D作DF⊥BC,延长CB到点E使BE=CF,连接AE,EM.
(1)求证:四边形AEFD是矩形;
(2)若AD=6,BF=3,∠ADC=120°,求EM的长.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴AD∥EF,
∵BE=CF,
∴BE+BF=CF+BF,即EF=BC,
∴AD=EF,
∴四边形AEFD是平行四边形,
又∵DF⊥BC,
∴∠DFE=90°,
∴四边形AEFD是矩形.
(2)解:由(1)可知,∠DFE=∠DFC=90°,AD=EF=BC,
∵AD=6,BF=3,
∴EB=CF=3,EC=9,
∵四边形ABCD是平行四边形,∠ADC=120°,
∴∠DCF=60°,∠CDF=30°,
∴DC=2CF=6,
在Rt△DFC中,由勾股定理得:DF2+CF2=DC2,
∴,
∵四边形AEFD是矩形,
∴,∠AEC=90°,
在Rt△ACE中,由勾股定理得:AE2+EC2=AC2,
∴,
∵M是AC的中点,∠AEC=90°,
∴.
21.(9分)暑假临近,某读书俱乐部推出了甲、乙两种消费卡,其中,甲卡按照次数收费,乙卡收取办卡费用后每次打折收费.设消费的次数为x次,所需费用为y元,且y与x的函数关系如图所示.根据图中信息,解答下列问题.
(1)分别求出选择这两种卡时,y与x的函数表达式;
(2)求消费多少次时,两者费用相差20元?
【解答】解:(1)设y甲=k1x,
把(4,80)代入解析式得4k1=80,
解得k1=20,
∴y甲=20x;
设y乙=k2x+80,
把(12,200)代入解析式得12k2+80=200,
解得k2=10,
∴y乙=10x+80;
(2)根据题意得:|20x﹣(10x+80)|=20,
解得x﹣6或x=10,
答:当消费6次或10次时,两者费用相差20元.
22.(10分)如图,已知直线AB:y1=﹣2x+4交x轴于点A,交y轴于点B,在直线AB上方以AB为腰作等腰Rt△ABC,直线AC:y2=kx+b交y轴于点D;
(1)求直线AC的解析式;
(2)填空:①当y1≥y2时,则x的取值范围为: x≤2 ;
②点E是坐标平面上的一点,以A,B,D,E四点为顶点的四边形是平行四边形,则点E的坐标为 (2,5)或(2,﹣5)或(﹣2,3) .
【解答】解:(1)当y=0时,x=2,
∴A(2,0),
当x=0时,y=4,
∴B(0,4),
过点C作CM⊥x轴交于M点,
∵∠BAC=90°,
∴∠BAO+∠ABO=90°,∠BAO+∠CAM=90°,
∴∠CAM=∠ABO,
∵AB=AC,
∴△ABO≌△CAM(AAS),
∴AM=BO=4,CM=AO=2,
∴C(6,2),
将点A、C代入直线y=kx+b中,
∴,
解得,
∴直线AC的解析式为y=x﹣1;
(2)①当x≤2时,y1≥y2,
故答案为:x≤2;
②当x=0时,y=﹣1,
∴D(0,﹣1),
设E(x,y),
当AB为平行四边形的对角线时,2=x,y﹣1=4,
∴E(2,5);
当AD为平行四边形的对角线时,2=x,y+4=﹣1,
∴E(2,﹣5);
当AE为平行四边形的对角线时,x+2=0,y=4﹣1,
∴E(﹣2,3);
综上所述:E点坐标为(2,5)或(2,﹣5)或(﹣2,3),
故答案为:(2,5)或(2,﹣5)或(﹣2,3).
23.(10分)综合与实践
综合与实践课上,老师让同学们以“三角板的平移”为主题开展数学活动.
(1)操作判断
操作一:将一副等腰直角三角板两斜边重合,按图1放置;
操作二:将三角板ACD沿CA方向平移(两三角板始终接触)至图2位置.
根据以上操作,填空:
图2中AA'与CC'的数量关系是 AA′=CC′ ;四边形ABC′D′的形状是 平行四边形 ;
(2)迁移探究
小航将一副等腰直角三角板换成一副含30°角的直角三角板,继续探究,已知三角板AB边长为6cm,过程如下:
将三角板ACD按(1)中的方式操作,如图3,在平移过程中,四边形ABC'D'的形状能否是菱形,若不能,请说明理由,若能,请求出CC'的长;
(3)拓展应用
在(2)的探究过程中,当△BCC′为等腰三角形时,CC'的长是 6或6 cm.
【解答】解:(1)∵△ABC,△ADC都是等腰直角三角形,
∴∠ABC=∠BCD=∠CDA=∠DAB=90°,AB=BC=CD=AD,
∴四边形ABCD是正方形;
根据平移的性质可得,AA′=CC′,
如图所示,连接AD′,BC′,
∵△ABC,△ADC都是等腰直角三角形,
∴AB=C′D′,
∵将三角板ACD沿CA方向平移(两个三角板始终接触),
∴AA′=CC′,A′D′=BC,且∠A′=∠BCC′=45°,
在△A′AD和△CC′B中,
,
∴△A′AD≌△CC′B(SAS),
∴AD′=C′B,且AB=C′D′,
∴四边形ABC′D′是平行四边形,
故答案为:AA′=CC′,平行四边形.
(2)可以是菱形,理由如下:
如图所示,连接AD′,BC′,
∵AB=6cm,∠ACB=30°,∠ABC=90°,
∴AC=12cm,∠BAC=60°,
∵将三角板ACD沿CA方向平移,
∴CD=C′D′=AB,CD∥C′D′∥AB,
∴四边形ABC′D′是平行四边形,
∴当BC′=AB=6cm时,四边形ABC′D′是菱形.
∵BC′=AB=6cm,∠BAC=60°,
∴△ABC′是等边三角形,
∴AB=AC′=BC′=6cm,
∴CC′=AC﹣AC′=12﹣6=6cm.
(3)∵含30°角的直角三角板,即∠ACB=30°,AB边长为6cm,
∴AC=2AB=2×6=12,
①当BC′=CC′时,△BCC′为等腰三角形,如图所示,
∵∠ACB=30°,BC′=CC′,
∴∠CBC′=∠BCC′=30°,
∴∠ABC′=∠ABC﹣∠CBC′=90°﹣30°=60°,且∠BAC′=60°,
∴BC′=AC′,
∴点C′是AC的中点,
∴;
②当BC=C′C时,△BCC′为等腰三角形,如图所示,
∵∠ACB=30°,AB=6,∠ABC=90°,
在Rt△ABC中,,
∵△BCC′为等腰三角形,BC=C′C,
∴;
③当BC=BC′时,△BCC′为等腰三角形,如图所示,
与“将三角板ACD沿CA方向平移(两个三角板始终接触)”矛盾,
∴不存在;
综上所示,当△BCC′为等腰三角形时,CC′的长为6cm或.
故答案为:6或6.
一、选择题(每小题3分,共30分)下列各题有四个选项,其中只有一个选项是正确的。
1.(3分)下列式子为最简二次根式的是( )
A. B. C. D.
2.(3分)下列四个算式正确的是( )
A. B.
C.=× D.
3.(3分)以下列长度的三条线段为边,能组成直角三角形的是( )
A.2,2,2 B.2,3,4 C.3,5,6 D.1,,2
4.(3分)下列关于直线y=x+2的说法中,正确的是( )
A.经过第一、三、四象限
B.与x轴交于(2,0)
C.与y轴交于(0,2)
D.将其图象向下平移2个单位得到y=2x的图象
5.(3分)如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
6.(3分)如图,将一张平行四边形纸片ABCD以DE为折痕进行折叠,点C的对应点为C′,若∠1=20°,∠2=60°,则∠C的度数为( )
A.40° B.50° C.60° D.70°
7.(3分)在菱形ABCD中,对角线AC和BD相交于点O,AE⊥BC于点E,连接OE,若∠ABD=20°,则∠AEO的度数为( )
A.10° B.20° C.25° D.35°
8.(3分)如图,点E、F分别是正方形ABCD的边CD、BC上的点,且CE=BF,AF、BE相交于点G,下列结论不正确的是( )
A.AF=BE B.AF⊥BE
C.AG=GE D.S△ABG=S四边形CEGF
9.(3分)物理课上小刚探究弹簧测力计的“弹簧的长度与受到的拉力之间的关系”,多次改变砝码的质量x(克),测量得到弹簧的长度y(厘米),其中0≤x≤250.通过实验获得下面的一组数据,在数据分析时,发现有一个弹簧的长度是错误的,则这个错误的数据是( )
砝码的质量x(克) 0 50 100 150 200 250
弹簧的长度y(厘米) 2 3 4 5 5.5 7
A.4 B.5 C.7 D.5.5
10.(3分)如图,正方形ABCD的边长为4cm,动点P从B出发,在正方形的边上沿B→C→D的方向运动到D停止,设点P的运动路程为x(cm),在下列图象中,能表示△ABP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B.
C. D.
二、填空题(每小题3分,共15分)
11.(3分)如果式子有意义,那么x的取值范围是 .
12.(3分)若一次函数y=(2﹣m)x+b的图象经过点P(x1,y1)和点Q(x2,y2),当x1<x2时,y1>y2,则m的取值范围是 .
13.(3分)某超市销售A,B,C,D四种矿泉水,它们的单价依次是5元、4元、3元、2元,某天的销售情况如图所示,则这天销售的矿泉水的平均单价是 .
14.(3分)如图, ABCD的顶点A(0,4),B(﹣3,0),以点B为圆心,AB长为半径画弧,交BC于点E,分别以点A,E为圆心,以大于的长为半径画弧,两弧在∠ABE的内部相交于点F,画射线BF交AD于点G,则点G的坐标是 .
15.(3分)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN=AB=1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为 .
三、解答题(本大题共8小题,共75分)
16.(10分)计算:
(1)÷﹣+;
(2).
17.(9分)图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.请根据下列要求分别画出图形(所画图形的顶点都在格点上):
(1)在图①中,以线段AB为一边,画一个面积为4的菱形;
(2)在图②中,以线段AB为对角线,画一个面积为3的平行四边形;
(3)在图③中,以点A为顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
18.(9分)蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分,10分);
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分统计图(满分10分):
c.配送速度和服务质量得分统计表:
项目统计量快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲 7.8 m 7 s甲2
乙 8 8 7 s乙2
根据以上信息,回答下列问题:
(1)表格中的m= ;s甲2 s乙2(填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?
19.(9分)如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=80°,∠DCE=30°,求∠CBE的度数.
20.(9分)如图,在 ABCD中,点M为AC的中点,过点D作DF⊥BC,延长CB到点E使BE=CF,连接AE,EM.
(1)求证:四边形AEFD是矩形;
(2)若AD=6,BF=3,∠ADC=120°,求EM的长.
21.(9分)暑假临近,某读书俱乐部推出了甲、乙两种消费卡,其中,甲卡按照次数收费,乙卡收取办卡费用后每次打折收费.设消费的次数为x次,所需费用为y元,且y与x的函数关系如图所示.根据图中信息,解答下列问题.
(1)分别求出选择这两种卡时,y与x的函数表达式;
(2)求消费多少次时,两者费用相差20元?
22.(10分)如图,已知直线AB:y1=﹣2x+4交x轴于点A,交y轴于点B,在直线AB上方以AB为腰作等腰Rt△ABC,直线AC:y2=kx+b交y轴于点D;
(1)求直线AC的解析式;
(2)填空:①当y1≥y2时,则x的取值范围为: ;
②点E是坐标平面上的一点,以A,B,D,E四点为顶点的四边形是平行四边形,则点E的坐标为 .
23.(10分)综合与实践
综合与实践课上,老师让同学们以“三角板的平移”为主题开展数学活动.
(1)操作判断
操作一:将一副等腰直角三角板两斜边重合,按图1放置;
操作二:将三角板ACD沿CA方向平移(两三角板始终接触)至图2位置.
根据以上操作,填空:
图2中AA'与CC'的数量关系是 ;四边形ABC′D′的形状是 ;
(2)迁移探究
小航将一副等腰直角三角板换成一副含30°角的直角三角板,继续探究,已知三角板AB边长为6cm,过程如下:
将三角板ACD按(1)中的方式操作,如图3,在平移过程中,四边形ABC'D'的形状能否是菱形,若不能,请说明理由,若能,请求出CC'的长;
(3)拓展应用
在(2)的探究过程中,当△BCC′为等腰三角形时,CC'的长是 cm.
2023-2024学年河南省漯河市郾城区八年级(下)期末数学试卷
参考答案
一、选择题(每小题3分,共30分)下列各题有四个选项,其中只有一个选项是正确的。
1.(3分)下列式子为最简二次根式的是( )
A. B. C. D.
选:C.
2.(3分)下列四个算式正确的是( )
A. B.
C.=× D.
选:B.
3.(3分)以下列长度的三条线段为边,能组成直角三角形的是( )
A.2,2,2 B.2,3,4 C.3,5,6 D.1,,2
选:D.
4.(3分)下列关于直线y=x+2的说法中,正确的是( )
A.经过第一、三、四象限
B.与x轴交于(2,0)
C.与y轴交于(0,2)
D.将其图象向下平移2个单位得到y=2x的图象
选:C.
5.(3分)如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
选:C.
6.(3分)如图,将一张平行四边形纸片ABCD以DE为折痕进行折叠,点C的对应点为C′,若∠1=20°,∠2=60°,则∠C的度数为( )
A.40° B.50° C.60° D.70°
选:A.
7.(3分)在菱形ABCD中,对角线AC和BD相交于点O,AE⊥BC于点E,连接OE,若∠ABD=20°,则∠AEO的度数为( )
A.10° B.20° C.25° D.35°
选:B.
8.(3分)如图,点E、F分别是正方形ABCD的边CD、BC上的点,且CE=BF,AF、BE相交于点G,下列结论不正确的是( )
A.AF=BE B.AF⊥BE
C.AG=GE D.S△ABG=S四边形CEGF
选:C.
9.(3分)物理课上小刚探究弹簧测力计的“弹簧的长度与受到的拉力之间的关系”,多次改变砝码的质量x(克),测量得到弹簧的长度y(厘米),其中0≤x≤250.通过实验获得下面的一组数据,在数据分析时,发现有一个弹簧的长度是错误的,则这个错误的数据是( )
砝码的质量x(克) 0 50 100 150 200 250
弹簧的长度y(厘米) 2 3 4 5 5.5 7
A.4 B.5 C.7 D.5.5
选:D.
10.(3分)如图,正方形ABCD的边长为4cm,动点P从B出发,在正方形的边上沿B→C→D的方向运动到D停止,设点P的运动路程为x(cm),在下列图象中,能表示△ABP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B.
C. D.
选:B.
二、填空题(每小题3分,共15分)
11.(3分)如果式子有意义,那么x的取值范围是 x≥4 .
12.(3分)若一次函数y=(2﹣m)x+b的图象经过点P(x1,y1)和点Q(x2,y2),当x1<x2时,y1>y2,则m的取值范围是 m>2 .
13.(3分)某超市销售A,B,C,D四种矿泉水,它们的单价依次是5元、4元、3元、2元,某天的销售情况如图所示,则这天销售的矿泉水的平均单价是 3.15元 .
14.(3分)如图, ABCD的顶点A(0,4),B(﹣3,0),以点B为圆心,AB长为半径画弧,交BC于点E,分别以点A,E为圆心,以大于的长为半径画弧,两弧在∠ABE的内部相交于点F,画射线BF交AD于点G,则点G的坐标是 (5,4) .
15.(3分)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN=AB=1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为 2或1+ .
三、解答题(本大题共8小题,共75分)
16.(10分)计算:
(1)÷﹣+;
(2).
【解答】解:(1)原式=﹣2+3
=4﹣2+3
=7﹣2;
(2)原式=3+2+1+3﹣2+1﹣2(3﹣1)
=4.
17.(9分)图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.请根据下列要求分别画出图形(所画图形的顶点都在格点上):
(1)在图①中,以线段AB为一边,画一个面积为4的菱形;
(2)在图②中,以线段AB为对角线,画一个面积为3的平行四边形;
(3)在图③中,以点A为顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
【解答】解:(1)如图1,
∵菱形的面积=对角线乘积的一半,
∴面积为4的菱形的对角线为4和2,
∴S菱形ABCD=×4×2=4,
∴菱形ABCD即为所求;
(2)如图,
∵CD=3,AB的纵高为2,
∴S四边形ACBD=×3×2=3,
∴四边形ACBD即为满足条件的图形;
(3)如图,
当正方形的边长为三个方格的斜边时,
即=的正方形ABCD的面积最大.
18.(9分)蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分,10分);
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分统计图(满分10分):
c.配送速度和服务质量得分统计表:
项目统计量快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲 7.8 m 7 s甲2
乙 8 8 7 s乙2
根据以上信息,回答下列问题:
(1)表格中的m= 7.5 ;s甲2 < s乙2(填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?
【解答】解:(1)甲公司配送速度得分从小到大排列为:6 6 7 7 7 8 9 9 9 10,
一共10个数据,其中第5个与第6个数据分别为7、8,
所以中位数m==7.5.
=×[3×(7﹣7)2+4×(8﹣7)2+2×(6﹣7)2+(5﹣7)2]=1,
=×[(4﹣7)2+(8﹣7)2+2×(10﹣7)2+2×(6﹣7)2+(9﹣7)2+2×(5﹣7)2+(7﹣7)2]=4.2,
∴<,
故答案为:7.5,<;
(2)小丽应选择甲公司(答案不唯一),理由如下:
∵配送速度得分甲和乙的得分相差不大,服务质量得分甲和乙的平均数相同,但是甲的方差明显小于乙的方差,
∴甲更稳定,
∴小丽应选择甲公司;
(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)
19.(9分)如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=80°,∠DCE=30°,求∠CBE的度数.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠BAE=∠BCD,
∵BF=BE,CG=CE,
∴BC是△EFG的中位线,
∴BC∥FG,BC=FG,
∵H为FG的中点,
∴FH=FG,
∴BC∥FH,BC=FH,
∴AD∥FH,AD=FH,
∴四边形AFHD是平行四边形;
(2)解:∵∠BAE=80°,
∴∠BCD=80°,
∵∠DCE=30°,
∴∠BCE=80°﹣30°=50°,
∵CB=CE,
∴∠CBE=∠CEB=(180°﹣50°)=65°.
20.(9分)如图,在 ABCD中,点M为AC的中点,过点D作DF⊥BC,延长CB到点E使BE=CF,连接AE,EM.
(1)求证:四边形AEFD是矩形;
(2)若AD=6,BF=3,∠ADC=120°,求EM的长.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴AD∥EF,
∵BE=CF,
∴BE+BF=CF+BF,即EF=BC,
∴AD=EF,
∴四边形AEFD是平行四边形,
又∵DF⊥BC,
∴∠DFE=90°,
∴四边形AEFD是矩形.
(2)解:由(1)可知,∠DFE=∠DFC=90°,AD=EF=BC,
∵AD=6,BF=3,
∴EB=CF=3,EC=9,
∵四边形ABCD是平行四边形,∠ADC=120°,
∴∠DCF=60°,∠CDF=30°,
∴DC=2CF=6,
在Rt△DFC中,由勾股定理得:DF2+CF2=DC2,
∴,
∵四边形AEFD是矩形,
∴,∠AEC=90°,
在Rt△ACE中,由勾股定理得:AE2+EC2=AC2,
∴,
∵M是AC的中点,∠AEC=90°,
∴.
21.(9分)暑假临近,某读书俱乐部推出了甲、乙两种消费卡,其中,甲卡按照次数收费,乙卡收取办卡费用后每次打折收费.设消费的次数为x次,所需费用为y元,且y与x的函数关系如图所示.根据图中信息,解答下列问题.
(1)分别求出选择这两种卡时,y与x的函数表达式;
(2)求消费多少次时,两者费用相差20元?
【解答】解:(1)设y甲=k1x,
把(4,80)代入解析式得4k1=80,
解得k1=20,
∴y甲=20x;
设y乙=k2x+80,
把(12,200)代入解析式得12k2+80=200,
解得k2=10,
∴y乙=10x+80;
(2)根据题意得:|20x﹣(10x+80)|=20,
解得x﹣6或x=10,
答:当消费6次或10次时,两者费用相差20元.
22.(10分)如图,已知直线AB:y1=﹣2x+4交x轴于点A,交y轴于点B,在直线AB上方以AB为腰作等腰Rt△ABC,直线AC:y2=kx+b交y轴于点D;
(1)求直线AC的解析式;
(2)填空:①当y1≥y2时,则x的取值范围为: x≤2 ;
②点E是坐标平面上的一点,以A,B,D,E四点为顶点的四边形是平行四边形,则点E的坐标为 (2,5)或(2,﹣5)或(﹣2,3) .
【解答】解:(1)当y=0时,x=2,
∴A(2,0),
当x=0时,y=4,
∴B(0,4),
过点C作CM⊥x轴交于M点,
∵∠BAC=90°,
∴∠BAO+∠ABO=90°,∠BAO+∠CAM=90°,
∴∠CAM=∠ABO,
∵AB=AC,
∴△ABO≌△CAM(AAS),
∴AM=BO=4,CM=AO=2,
∴C(6,2),
将点A、C代入直线y=kx+b中,
∴,
解得,
∴直线AC的解析式为y=x﹣1;
(2)①当x≤2时,y1≥y2,
故答案为:x≤2;
②当x=0时,y=﹣1,
∴D(0,﹣1),
设E(x,y),
当AB为平行四边形的对角线时,2=x,y﹣1=4,
∴E(2,5);
当AD为平行四边形的对角线时,2=x,y+4=﹣1,
∴E(2,﹣5);
当AE为平行四边形的对角线时,x+2=0,y=4﹣1,
∴E(﹣2,3);
综上所述:E点坐标为(2,5)或(2,﹣5)或(﹣2,3),
故答案为:(2,5)或(2,﹣5)或(﹣2,3).
23.(10分)综合与实践
综合与实践课上,老师让同学们以“三角板的平移”为主题开展数学活动.
(1)操作判断
操作一:将一副等腰直角三角板两斜边重合,按图1放置;
操作二:将三角板ACD沿CA方向平移(两三角板始终接触)至图2位置.
根据以上操作,填空:
图2中AA'与CC'的数量关系是 AA′=CC′ ;四边形ABC′D′的形状是 平行四边形 ;
(2)迁移探究
小航将一副等腰直角三角板换成一副含30°角的直角三角板,继续探究,已知三角板AB边长为6cm,过程如下:
将三角板ACD按(1)中的方式操作,如图3,在平移过程中,四边形ABC'D'的形状能否是菱形,若不能,请说明理由,若能,请求出CC'的长;
(3)拓展应用
在(2)的探究过程中,当△BCC′为等腰三角形时,CC'的长是 6或6 cm.
【解答】解:(1)∵△ABC,△ADC都是等腰直角三角形,
∴∠ABC=∠BCD=∠CDA=∠DAB=90°,AB=BC=CD=AD,
∴四边形ABCD是正方形;
根据平移的性质可得,AA′=CC′,
如图所示,连接AD′,BC′,
∵△ABC,△ADC都是等腰直角三角形,
∴AB=C′D′,
∵将三角板ACD沿CA方向平移(两个三角板始终接触),
∴AA′=CC′,A′D′=BC,且∠A′=∠BCC′=45°,
在△A′AD和△CC′B中,
,
∴△A′AD≌△CC′B(SAS),
∴AD′=C′B,且AB=C′D′,
∴四边形ABC′D′是平行四边形,
故答案为:AA′=CC′,平行四边形.
(2)可以是菱形,理由如下:
如图所示,连接AD′,BC′,
∵AB=6cm,∠ACB=30°,∠ABC=90°,
∴AC=12cm,∠BAC=60°,
∵将三角板ACD沿CA方向平移,
∴CD=C′D′=AB,CD∥C′D′∥AB,
∴四边形ABC′D′是平行四边形,
∴当BC′=AB=6cm时,四边形ABC′D′是菱形.
∵BC′=AB=6cm,∠BAC=60°,
∴△ABC′是等边三角形,
∴AB=AC′=BC′=6cm,
∴CC′=AC﹣AC′=12﹣6=6cm.
(3)∵含30°角的直角三角板,即∠ACB=30°,AB边长为6cm,
∴AC=2AB=2×6=12,
①当BC′=CC′时,△BCC′为等腰三角形,如图所示,
∵∠ACB=30°,BC′=CC′,
∴∠CBC′=∠BCC′=30°,
∴∠ABC′=∠ABC﹣∠CBC′=90°﹣30°=60°,且∠BAC′=60°,
∴BC′=AC′,
∴点C′是AC的中点,
∴;
②当BC=C′C时,△BCC′为等腰三角形,如图所示,
∵∠ACB=30°,AB=6,∠ABC=90°,
在Rt△ABC中,,
∵△BCC′为等腰三角形,BC=C′C,
∴;
③当BC=BC′时,△BCC′为等腰三角形,如图所示,
与“将三角板ACD沿CA方向平移(两个三角板始终接触)”矛盾,
∴不存在;
综上所示,当△BCC′为等腰三角形时,CC′的长为6cm或.
故答案为:6或6.
同课章节目录
