2024年湖北省襄阳市保康县中考数学适应性试卷(含答案)
文档属性
| 名称 | 2024年湖北省襄阳市保康县中考数学适应性试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 11:20:38 | ||
图片预览




文档简介
2024年湖北省襄阳市保康县中考数学适应性试卷
一、选择题(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号在答题卡上涂黑作答.
1.(3分)横冲国际滑雪场某一天的最高气温为1℃,最低气温为﹣9℃,则这天的最高气温比最低气温高( )
A.﹣10℃ B.﹣8℃ C.8℃ D.10℃
2.(3分)我国航天事业取得了跨越式发展,下列航天图标属于中心对称图形的是( )
A. B.
C. D.
3.(3分)关于x的一元一次不等式x﹣1≤m的解集在数轴上的表示如图所示,则m的值为( )
A.3 B.2 C.1 D.0
4.(3分)下列运算正确的是( )
A.4a2﹣2a2=2 B.a7÷a3=a4
C.5a2 a4=5a8 D.(a2b3)2=a4b5
5.(3分)下列说法正确的是( )
A.检测“神舟十六号”载人飞船零件的质量,应采用抽样调查
B.任意画一个三角形,其外角和是180°是不可能事件
C.某奖券的中奖率为,买100张奖券,一定会中奖1次
D.“任意两个等腰三角形是相似三角形”是必然事件
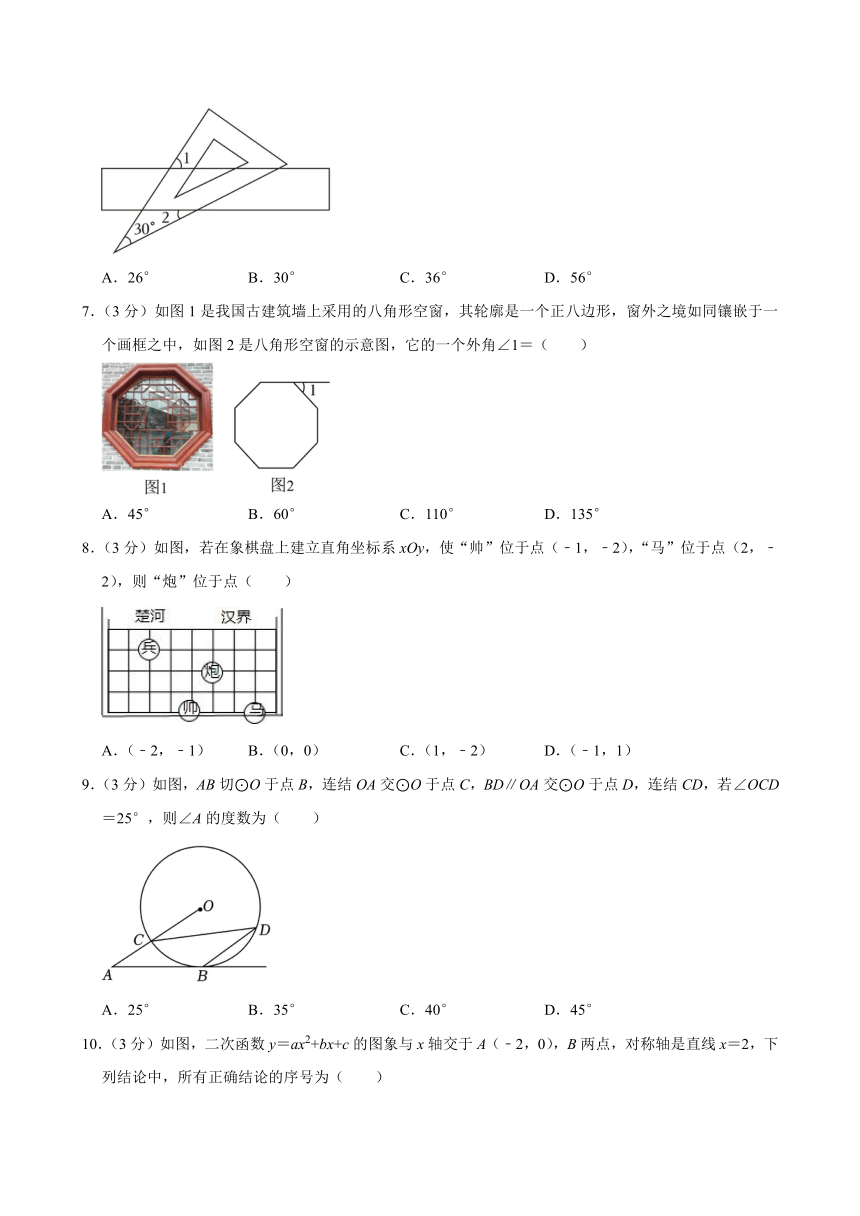
6.(3分)将直角三角板和直尺按照如图位置摆放,若∠1=56°,则∠2的度数是( )
A.26° B.30° C.36° D.56°
7.(3分)如图1是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中,如图2是八角形空窗的示意图,它的一个外角∠1=( )
A.45° B.60° C.110° D.135°
8.(3分)如图,若在象棋盘上建立直角坐标系xOy,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“炮”位于点( )
A.(﹣2,﹣1) B.(0,0) C.(1,﹣2) D.(﹣1,1)
9.(3分)如图,AB切⊙O于点B,连结OA交⊙O于点C,BD∥OA交⊙O于点D,连结CD,若∠OCD=25°,则∠A的度数为( )
A.25° B.35° C.40° D.45°
10.(3分)如图,二次函数y=ax2+bx+c的图象与x轴交于A(﹣2,0),B两点,对称轴是直线x=2,下列结论中,所有正确结论的序号为( )
①a>0;
②点B的坐标为(6,0);
③c=3b;
④对于任意实数m,都有4a+2b≥am2+bm.
A.①② B.②③ C.②③④ D.③④
二、填空题(本大题共5个小题,每小题3分,共15分)把答案填在答题卡的相应位置上.
11.(3分)计算:= .
12.(3分)一个函数过点(1,3),且y随x增大而增大,请写出一个符合上述条件的函数解析式 .
13.(3分)如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是 .
14.(3分)我国古代数学著作《张丘建算经》中著名的“百鸡问题”叙述如下:“鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁、母、雏各几何?”意思是公鸡五钱一只,母鸡三钱一只,小鸡一钱三只,要用一百钱买一百只鸡,问公鸡、母鸡、小鸡各多少只?若现已知母鸡买18只,则公鸡买 只,小鸡买 只.
15.(3分)如图,在△ABC中,∠ACB=90°,将△ABC绕点B顺时针旋转90°得到△DBE,连接AD,CE,延长EC交AD于点F,若CF=1,CE=2,则AF的长 .
三、解答题(本大题共9个小题,共75分)解答应写出文字说明,证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.
16.(6分).
17.(6分)如图,在四边形ABCD中,AB∥CD,AB=CD.过点D分别作DF⊥AB于点F,DE⊥BC于点E,且DE=DF.求证:四边形ABCD是菱形.
18.(6分)某综合实践研究小组为了测量广场上空气球A离地面的高度,已知水平面MN,该小组利用自制简易测角仪在水平面上点B,C处分别测得气球A的仰角∠ABN为37°,∠ACN为45°,已知BC=20m,求气球A离地面的高度.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
19.(8分)“惜餐为荣,敛物为耻.”为了解落实“光盘行动”的情况,某校调研了七、八年级部分班级某一天的厨余垃圾质量,并作出如下统计分析.
【收集数据】七、八年级各随机抽取10个班厨余垃圾质量的数据(单位:kg).
【整理数据】进行整理和分析(厨余垃圾质量用x表示,共分为四个等级:A.x<1;B.1≤x<1.5;C.1.5≤x<2;D.x≥2).
【描述数据】下面给出了部分信息,绘制如下统计图:
七年级10个班厨余垃圾质量:0.6,0.7,0.7,0.7,1.3,1.3,1.6,1.7,2,2.4.
八年级10个班厨余垃圾质量中B等级包含的所有数据为:1.1,1.1,1.1,1.3.
【分析数据】七、八年级抽取的班级厨余垃圾质量统计表如下:
年级 平均数 中位数 众数 方差 A等级所占百分比
七年级 1.3 1.3 a 0.352 40%
八年级 1.3 b 1.1 0.24 m%
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,m= ;
(2)该校八年级共有30个班,估计八年级这一天厨余垃圾质量符合A等级的班级数;
(3)根据以上信息,请你任选一个统计量,分析在此次“光盘行动”中,该校七、八年级的哪个年级落实得更好?并说明理由.
20.(8分)如图,在平面直角坐标系xOy中,直线AB:y=kx﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
(1)求直线AB的表达式;
(2)将直线AB沿y轴方向向上平移n个单位后与反比例函数图象在第一象限内交于点C,若S△ABC≤18,请求出n的取值范围.
21.(8分)如图,在△OAE中,OA=OE,B是AE中点,以O为圆心,OB为半径作⊙O,分别交AO及其延长线、OE于C,D,F点,连接BD交OE于点G.
(1)求证:AE是⊙O的切线;
(2)若C是OA的中点,,求阴影部分的面积.
22.(10分)如图1所示的某种发石车是古代一种远程攻击的武器.将发石车置于山坡底部O处,以点O为原点,水平方向为x轴方向,建立如图2所示的平面直角坐标系,将发射出去的石块当作一个点看,其飞行路线可以近似看作抛物线y=a(x﹣20)2+k的一部分,山坡OA上有一堵防御墙,其竖直截面为ABCD,墙宽BC=2米,BC与x轴平行,点B与点O的水平距离为28米、垂直距离为6米.
(1)若发射石块在空中飞行的最大高度为10米,
①求抛物线的解析式;
②试通过计算说明石块能否飞越防御墙;
(2)若要使石块恰好落在防御墙顶部BC上(包括端点B、C),求a的取值范围.
23.(11分)某数学兴趣小组开展矩形的折叠实验探究,折叠矩形ABCD的一边AD,使点D落在点F处,折痕为AE.
(1)如图1,当点F恰好在BC边上时,证明:△ABF∽△FCE.
(2)将矩形的边AB折叠,使点B落在AF边上的点M处,折痕为AN.
①如图2,当点F恰好在BC边上时,若AB=1,,连接EN,试判断△AEN的形状,并说明理由.
②如图3,当点F在矩形内部时,若AB=8,BC=12.点E是CD的中点,求FN的长.
24.(12分)在平面直角坐标系中,已知抛物线y=ax2﹣2ax﹣3a(a>0).
(1)抛物线的对称轴为直线 ;
(2)当﹣2≤x≤2时,函数值y的取值范围是﹣4≤y≤b,求a和b的值;
(3)当a=1时,解决下列问题.
①抛物线上一点P到x轴的距离为6,求点P的坐标;
②将该抛物线在0≤x≤4间的部分记为G,将G在直线y=t下方的部分沿y=t翻折,其余部分保持不变,得到的新图象记为Q.设Q的最高点、最低点的纵坐标分别为y1,y2,若y1﹣y2<6,直接写出t的取值范围.
2024年湖北省襄阳市保康县中考数学适应性试卷
参考答案
一、选择题(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号在答题卡上涂黑作答.
1.(3分)横冲国际滑雪场某一天的最高气温为1℃,最低气温为﹣9℃,则这天的最高气温比最低气温高( )
A.﹣10℃ B.﹣8℃ C.8℃ D.10℃
选:D.
2.(3分)我国航天事业取得了跨越式发展,下列航天图标属于中心对称图形的是( )
A. B.
C. D.
选:D.
3.(3分)关于x的一元一次不等式x﹣1≤m的解集在数轴上的表示如图所示,则m的值为( )
A.3 B.2 C.1 D.0
选:B.
4.(3分)下列运算正确的是( )
A.4a2﹣2a2=2 B.a7÷a3=a4
C.5a2 a4=5a8 D.(a2b3)2=a4b5
选:B.
5.(3分)下列说法正确的是( )
A.检测“神舟十六号”载人飞船零件的质量,应采用抽样调查
B.任意画一个三角形,其外角和是180°是不可能事件
C.某奖券的中奖率为,买100张奖券,一定会中奖1次
D.“任意两个等腰三角形是相似三角形”是必然事件
选:B.
6.(3分)将直角三角板和直尺按照如图位置摆放,若∠1=56°,则∠2的度数是( )
A.26° B.30° C.36° D.56°
选:A.
7.(3分)如图1是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中,如图2是八角形空窗的示意图,它的一个外角∠1=( )
A.45° B.60° C.110° D.135°
选:A.
8.(3分)如图,若在象棋盘上建立直角坐标系xOy,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“炮”位于点( )
A.(﹣2,﹣1) B.(0,0) C.(1,﹣2) D.(﹣1,1)
选:B.
9.(3分)如图,AB切⊙O于点B,连结OA交⊙O于点C,BD∥OA交⊙O于点D,连结CD,若∠OCD=25°,则∠A的度数为( )
A.25° B.35° C.40° D.45°
选:C.
10.(3分)如图,二次函数y=ax2+bx+c的图象与x轴交于A(﹣2,0),B两点,对称轴是直线x=2,下列结论中,所有正确结论的序号为( )
①a>0;
②点B的坐标为(6,0);
③c=3b;
④对于任意实数m,都有4a+2b≥am2+bm.
A.①② B.②③ C.②③④ D.③④
选:C.
二、填空题(本大题共5个小题,每小题3分,共15分)把答案填在答题卡的相应位置上.
11.(3分)计算:= a﹣b .
【解答】解:
=
=
=a﹣b,
故答案为:a﹣b.
12.(3分)一个函数过点(1,3),且y随x增大而增大,请写出一个符合上述条件的函数解析式 y=x+2
13.(3分)如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是 .
14.(3分)我国古代数学著作《张丘建算经》中著名的“百鸡问题”叙述如下:“鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁、母、雏各几何?”意思是公鸡五钱一只,母鸡三钱一只,小鸡一钱三只,要用一百钱买一百只鸡,问公鸡、母鸡、小鸡各多少只?若现已知母鸡买18只,则公鸡买 4 只,小鸡买 78 只.
15.(3分)如图,在△ABC中,∠ACB=90°,将△ABC绕点B顺时针旋转90°得到△DBE,连接AD,CE,延长EC交AD于点F,若CF=1,CE=2,则AF的长 .
三、解答题(本大题共9个小题,共75分)解答应写出文字说明,证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.
16.(6分).
【解答】解:
=3﹣2﹣(2﹣)+2×
=3﹣2﹣2++
=2﹣1.
17.(6分)如图,在四边形ABCD中,AB∥CD,AB=CD.过点D分别作DF⊥AB于点F,DE⊥BC于点E,且DE=DF.求证:四边形ABCD是菱形.
【解答】证明:连接BD,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵DF⊥AB于点F,DE⊥BC于点E,
∴∠BED=∠BFD=90°,
在Rt△BED和Rt△BFD中,
,
∴Rt△BED≌Rt△BFD(HL),
∴∠EBD=∠FBD,
∵∠FBD=∠CDB,
∴∠EBD=∠CDB,
∴CB=CD,
∴四边形ABCD是菱形.
18.(6分)某综合实践研究小组为了测量广场上空气球A离地面的高度,已知水平面MN,该小组利用自制简易测角仪在水平面上点B,C处分别测得气球A的仰角∠ABN为37°,∠ACN为45°,已知BC=20m,求气球A离地面的高度.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
【解答】解:过A作AD⊥MN于D,
设CD=x m,
∵BC=20m,
∴BD=BC+CD=(x+20)m,
在Rt△ACD中,∠ACD=45°,
∴AD=CD tan45°=x(m),
在Rt△ABD中,∠ABD=37°,
∴AD=BD tan37°≈0.75(x+20)m,
∴x=0.75(x+20),
解得:x=60,
∴AD=60m,
∴气球A离地面的高度AD约为60m.
19.(8分)“惜餐为荣,敛物为耻.”为了解落实“光盘行动”的情况,某校调研了七、八年级部分班级某一天的厨余垃圾质量,并作出如下统计分析.
【收集数据】七、八年级各随机抽取10个班厨余垃圾质量的数据(单位:kg).
【整理数据】进行整理和分析(厨余垃圾质量用x表示,共分为四个等级:A.x<1;B.1≤x<1.5;C.1.5≤x<2;D.x≥2).
【描述数据】下面给出了部分信息,绘制如下统计图:
七年级10个班厨余垃圾质量:0.6,0.7,0.7,0.7,1.3,1.3,1.6,1.7,2,2.4.
八年级10个班厨余垃圾质量中B等级包含的所有数据为:1.1,1.1,1.1,1.3.
【分析数据】七、八年级抽取的班级厨余垃圾质量统计表如下:
年级 平均数 中位数 众数 方差 A等级所占百分比
七年级 1.3 1.3 a 0.352 40%
八年级 1.3 b 1.1 0.24 m%
根据以上信息,解答下列问题:
(1)填空:a= 0.7 ,b= 1.1 ,m= 30 ;
(2)该校八年级共有30个班,估计八年级这一天厨余垃圾质量符合A等级的班级数;
(3)根据以上信息,请你任选一个统计量,分析在此次“光盘行动”中,该校七、八年级的哪个年级落实得更好?并说明理由.
【解答】解:(1)七年级10个数据中0.7最多,所以众数a=0.7,
八年级B等级有4个,C、D等级为10×20%=2个,10×10%=1个,
所以A等级有10﹣4﹣2﹣1=3个,
所以m%=×100%=30%,
所以中位数为b==1.1;
故答案为:0.7,1.1,30;
(2)30×30%=9(个),
答:估计八年级这一天厨余垃圾质量符合A等级的班级数为9个;
(3)八年级落实更好,
理由:①八年级各班餐厨垃圾质量的中位数1.1低于七年级各班餐厨垃圾质量的中位数1.2.②八年级各班餐厨垃圾质量的方差0.24低于七年级各班餐厨垃圾质量的方差0.352,更稳定,(答案不唯一).
20.(8分)如图,在平面直角坐标系xOy中,直线AB:y=kx﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
(1)求直线AB的表达式;
(2)将直线AB沿y轴方向向上平移n个单位后与反比例函数图象在第一象限内交于点C,若S△ABC≤18,请求出n的取值范围.
【解答】解:(1)∵点B(m,2)在反比例函数的图象上,
∴2m=8,
∴m=4.
∴点B(4,2).
把点B(4,2)代入y=kx﹣2,
得:4k﹣2=2,
∴k=1.
∴直线AB的表达式为:y=x﹣2.
(2)记平移后的直线与y轴的交点为D,则AD=n,
联结BD.
∵CD∥AB.
∴S△ABD=S△ABC.
即:n×4≤18.
∴n≤9.
21.(8分)如图,在△OAE中,OA=OE,B是AE中点,以O为圆心,OB为半径作⊙O,分别交AO及其延长线、OE于C,D,F点,连接BD交OE于点G.
(1)求证:AE是⊙O的切线;
(2)若C是OA的中点,,求阴影部分的面积.
【解答】(1)证明:连接OB,
∵OA=OE,B是AE中点,
∴AE⊥OB,
∵OB是⊙O的半径,且AE⊥OB,
∴AE是⊙O的切线.
(2)解:∵C是OA的中点,
∴OB=OC=AC=OA,
∴cos∠AOB==,
∴∠AOB=∠EOB=60°,
∵OD=OB,BD=4,
∴∠OBD=∠D=∠AOB=30°,
∴∠OGB=180°﹣∠OBD﹣∠EOB=90°,
∴OG⊥BD,
∴BG=DG=BD=2,
∵=tan30°=,
∴GO=BG=×2=2,
∴OB=2GO=4,
∴S阴影=S扇形OBF﹣S△OBG=﹣×4×2=﹣4,
∴阴影部分的面积是﹣4.
22.(10分)如图1所示的某种发石车是古代一种远程攻击的武器.将发石车置于山坡底部O处,以点O为原点,水平方向为x轴方向,建立如图2所示的平面直角坐标系,将发射出去的石块当作一个点看,其飞行路线可以近似看作抛物线y=a(x﹣20)2+k的一部分,山坡OA上有一堵防御墙,其竖直截面为ABCD,墙宽BC=2米,BC与x轴平行,点B与点O的水平距离为28米、垂直距离为6米.
(1)若发射石块在空中飞行的最大高度为10米,
①求抛物线的解析式;
②试通过计算说明石块能否飞越防御墙;
(2)若要使石块恰好落在防御墙顶部BC上(包括端点B、C),求a的取值范围.
【解答】解:(1)①设石块运行的函数关系式为y=a(x﹣20)2+10,
把(0,0)代入解析式得:400a+10=0,
解得:a=﹣,
∴解析式为:y=﹣(x﹣20)2+10,即y=﹣x2+x(0≤x≤40);
②石块能飞越防御墙AB,理由如下:
把x=30代入y=﹣x2+x得:
y=﹣×900+30=7.5,
∵7.5>6,
∴石块能飞越防御墙AB;
(3)由题可知B(28,6),抛物线y=a(x﹣20)2+k,
∴把(0,0),(28,6)代入得:,
解得a=﹣;
把C(30,6),(0,0)代入解析式,
解得a=﹣,
∴a的取值范围为﹣≤a≤﹣.
23.(11分)某数学兴趣小组开展矩形的折叠实验探究,折叠矩形ABCD的一边AD,使点D落在点F处,折痕为AE.
(1)如图1,当点F恰好在BC边上时,证明:△ABF∽△FCE.
(2)将矩形的边AB折叠,使点B落在AF边上的点M处,折痕为AN.
①如图2,当点F恰好在BC边上时,若AB=1,,连接EN,试判断△AEN的形状,并说明理由.
②如图3,当点F在矩形内部时,若AB=8,BC=12.点E是CD的中点,求FN的长.
【解答】(1)证明:由折叠可知,
△AFE≌△ADE,
∴∠AFE=∠D=90°,
∴∠AFB+∠CFE=90°,
∵∠AFB+∠BAF=90°,
∴∠BAF=∠CFE,
∵∠B=∠C=90°,
∴△ABF∽△FCE.
(2)解:①由折叠可知,
△AMN≌△ABN,
∴AM=AB=1,
∵AF=AD=BC=,
∵∠B=90°,
∴BF==1=AB,
∴△ABF为等腰直角三角形,
∵△ABF∽△FCE.
∴△FCE为等腰直角三角形,
∴CE=CF=﹣1,
∵∠AFE=90°,
∴∠MFN+∠CFE=90°,
∵∠CFE=45°,
∴∠MFN=45°,
∠FMN=∠AMN=90°,
△FMN为等腰直角三角形,
∴MN=FM=﹣1,
∴BN=﹣1=CE,
∴CN==1=AB,
∴△ABN≌△NCE(SAS),
∴AN=EN,
∵∠NAM+∠EAF=∠BAD=45°,
∴△AEN为等腰直角三角形,
②延长AF交BC于点H,连接EH,
∵AM=AB=DC=8,点E为DC中点,
∴CE=DE=4,EF=DE=4,AF=AD=BC=12,
∴FM=12﹣8=4,
∵∠EFH﹣∠AFE=∠D=90°,∠C=90°,
∴∠EFH=∠C,
在Rt△EFH和Rt△ECH中,
EH=EH,EF=EC,
∴Rt△EFH≌Rt△ECH(HL),
设FH=x,则CH=x,
∴BH=12﹣x,AH=12+x,
在Rt△ABH中,AB2=BH2+AH2,
即82+(12﹣x)2=(12+x)2,
解得x=,
∴MH=,
设MN=y,则BN=y,
∴MH=,
∵∠NMH=90°,
∴在Rt△NMH中,y2+()2=()2,
∴y=4,
∴FN==4.
故FN的长为4.
24.(12分)在平面直角坐标系中,已知抛物线y=ax2﹣2ax﹣3a(a>0).
(1)抛物线的对称轴为直线 x=1 ;
(2)当﹣2≤x≤2时,函数值y的取值范围是﹣4≤y≤b,求a和b的值;
(3)当a=1时,解决下列问题.
①抛物线上一点P到x轴的距离为6,求点P的坐标;
②将该抛物线在0≤x≤4间的部分记为G,将G在直线y=t下方的部分沿y=t翻折,其余部分保持不变,得到的新图象记为Q.设Q的最高点、最低点的纵坐标分别为y1,y2,若y1﹣y2<6,直接写出t的取值范围.
【解答】解:(1)函数的对称轴为:x=﹣=1,
∴x=1;
故答案为:x=1;
(2)函数对称轴为x=1,当﹣2≤x≤2时,函数值y的取值范围是﹣4≤y≤b.
故y=﹣4 是函数的最小值,即抛物线的顶点为(1,﹣4).
将函数顶点坐标代入函数表达式并解得:a=1.
故抛物线的表达式为:y=x2﹣2x﹣3,
则b=(﹣2)2﹣2(﹣2)﹣3=5;
(3)①∵抛物线上一点P到x轴的距离为6,而顶点坐标为(1,﹣4),
x2﹣2x﹣3=6,
解得
故点P的坐标为 ,6)或 ,6);
②﹣1<t≤2.
设图象折叠后顶点M的对应点为M,点H是x=4函数所处的位置,图象Q为C′M′NH区域,
点M(1,﹣4),点H(4,5),则点M′(1,2t+4)
当点M′在点H下方时,2t+4<5,t<,
函数Q的最高点为H,最低点为N.
则5﹣t<6.解得t>﹣1.
故﹣1<t<,
当点M′在点H上方时,同理可得:
故﹣1<t<2.
一、选择题(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号在答题卡上涂黑作答.
1.(3分)横冲国际滑雪场某一天的最高气温为1℃,最低气温为﹣9℃,则这天的最高气温比最低气温高( )
A.﹣10℃ B.﹣8℃ C.8℃ D.10℃
2.(3分)我国航天事业取得了跨越式发展,下列航天图标属于中心对称图形的是( )
A. B.
C. D.
3.(3分)关于x的一元一次不等式x﹣1≤m的解集在数轴上的表示如图所示,则m的值为( )
A.3 B.2 C.1 D.0
4.(3分)下列运算正确的是( )
A.4a2﹣2a2=2 B.a7÷a3=a4
C.5a2 a4=5a8 D.(a2b3)2=a4b5
5.(3分)下列说法正确的是( )
A.检测“神舟十六号”载人飞船零件的质量,应采用抽样调查
B.任意画一个三角形,其外角和是180°是不可能事件
C.某奖券的中奖率为,买100张奖券,一定会中奖1次
D.“任意两个等腰三角形是相似三角形”是必然事件
6.(3分)将直角三角板和直尺按照如图位置摆放,若∠1=56°,则∠2的度数是( )
A.26° B.30° C.36° D.56°
7.(3分)如图1是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中,如图2是八角形空窗的示意图,它的一个外角∠1=( )
A.45° B.60° C.110° D.135°
8.(3分)如图,若在象棋盘上建立直角坐标系xOy,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“炮”位于点( )
A.(﹣2,﹣1) B.(0,0) C.(1,﹣2) D.(﹣1,1)
9.(3分)如图,AB切⊙O于点B,连结OA交⊙O于点C,BD∥OA交⊙O于点D,连结CD,若∠OCD=25°,则∠A的度数为( )
A.25° B.35° C.40° D.45°
10.(3分)如图,二次函数y=ax2+bx+c的图象与x轴交于A(﹣2,0),B两点,对称轴是直线x=2,下列结论中,所有正确结论的序号为( )
①a>0;
②点B的坐标为(6,0);
③c=3b;
④对于任意实数m,都有4a+2b≥am2+bm.
A.①② B.②③ C.②③④ D.③④
二、填空题(本大题共5个小题,每小题3分,共15分)把答案填在答题卡的相应位置上.
11.(3分)计算:= .
12.(3分)一个函数过点(1,3),且y随x增大而增大,请写出一个符合上述条件的函数解析式 .
13.(3分)如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是 .
14.(3分)我国古代数学著作《张丘建算经》中著名的“百鸡问题”叙述如下:“鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁、母、雏各几何?”意思是公鸡五钱一只,母鸡三钱一只,小鸡一钱三只,要用一百钱买一百只鸡,问公鸡、母鸡、小鸡各多少只?若现已知母鸡买18只,则公鸡买 只,小鸡买 只.
15.(3分)如图,在△ABC中,∠ACB=90°,将△ABC绕点B顺时针旋转90°得到△DBE,连接AD,CE,延长EC交AD于点F,若CF=1,CE=2,则AF的长 .
三、解答题(本大题共9个小题,共75分)解答应写出文字说明,证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.
16.(6分).
17.(6分)如图,在四边形ABCD中,AB∥CD,AB=CD.过点D分别作DF⊥AB于点F,DE⊥BC于点E,且DE=DF.求证:四边形ABCD是菱形.
18.(6分)某综合实践研究小组为了测量广场上空气球A离地面的高度,已知水平面MN,该小组利用自制简易测角仪在水平面上点B,C处分别测得气球A的仰角∠ABN为37°,∠ACN为45°,已知BC=20m,求气球A离地面的高度.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
19.(8分)“惜餐为荣,敛物为耻.”为了解落实“光盘行动”的情况,某校调研了七、八年级部分班级某一天的厨余垃圾质量,并作出如下统计分析.
【收集数据】七、八年级各随机抽取10个班厨余垃圾质量的数据(单位:kg).
【整理数据】进行整理和分析(厨余垃圾质量用x表示,共分为四个等级:A.x<1;B.1≤x<1.5;C.1.5≤x<2;D.x≥2).
【描述数据】下面给出了部分信息,绘制如下统计图:
七年级10个班厨余垃圾质量:0.6,0.7,0.7,0.7,1.3,1.3,1.6,1.7,2,2.4.
八年级10个班厨余垃圾质量中B等级包含的所有数据为:1.1,1.1,1.1,1.3.
【分析数据】七、八年级抽取的班级厨余垃圾质量统计表如下:
年级 平均数 中位数 众数 方差 A等级所占百分比
七年级 1.3 1.3 a 0.352 40%
八年级 1.3 b 1.1 0.24 m%
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,m= ;
(2)该校八年级共有30个班,估计八年级这一天厨余垃圾质量符合A等级的班级数;
(3)根据以上信息,请你任选一个统计量,分析在此次“光盘行动”中,该校七、八年级的哪个年级落实得更好?并说明理由.
20.(8分)如图,在平面直角坐标系xOy中,直线AB:y=kx﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
(1)求直线AB的表达式;
(2)将直线AB沿y轴方向向上平移n个单位后与反比例函数图象在第一象限内交于点C,若S△ABC≤18,请求出n的取值范围.
21.(8分)如图,在△OAE中,OA=OE,B是AE中点,以O为圆心,OB为半径作⊙O,分别交AO及其延长线、OE于C,D,F点,连接BD交OE于点G.
(1)求证:AE是⊙O的切线;
(2)若C是OA的中点,,求阴影部分的面积.
22.(10分)如图1所示的某种发石车是古代一种远程攻击的武器.将发石车置于山坡底部O处,以点O为原点,水平方向为x轴方向,建立如图2所示的平面直角坐标系,将发射出去的石块当作一个点看,其飞行路线可以近似看作抛物线y=a(x﹣20)2+k的一部分,山坡OA上有一堵防御墙,其竖直截面为ABCD,墙宽BC=2米,BC与x轴平行,点B与点O的水平距离为28米、垂直距离为6米.
(1)若发射石块在空中飞行的最大高度为10米,
①求抛物线的解析式;
②试通过计算说明石块能否飞越防御墙;
(2)若要使石块恰好落在防御墙顶部BC上(包括端点B、C),求a的取值范围.
23.(11分)某数学兴趣小组开展矩形的折叠实验探究,折叠矩形ABCD的一边AD,使点D落在点F处,折痕为AE.
(1)如图1,当点F恰好在BC边上时,证明:△ABF∽△FCE.
(2)将矩形的边AB折叠,使点B落在AF边上的点M处,折痕为AN.
①如图2,当点F恰好在BC边上时,若AB=1,,连接EN,试判断△AEN的形状,并说明理由.
②如图3,当点F在矩形内部时,若AB=8,BC=12.点E是CD的中点,求FN的长.
24.(12分)在平面直角坐标系中,已知抛物线y=ax2﹣2ax﹣3a(a>0).
(1)抛物线的对称轴为直线 ;
(2)当﹣2≤x≤2时,函数值y的取值范围是﹣4≤y≤b,求a和b的值;
(3)当a=1时,解决下列问题.
①抛物线上一点P到x轴的距离为6,求点P的坐标;
②将该抛物线在0≤x≤4间的部分记为G,将G在直线y=t下方的部分沿y=t翻折,其余部分保持不变,得到的新图象记为Q.设Q的最高点、最低点的纵坐标分别为y1,y2,若y1﹣y2<6,直接写出t的取值范围.
2024年湖北省襄阳市保康县中考数学适应性试卷
参考答案
一、选择题(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号在答题卡上涂黑作答.
1.(3分)横冲国际滑雪场某一天的最高气温为1℃,最低气温为﹣9℃,则这天的最高气温比最低气温高( )
A.﹣10℃ B.﹣8℃ C.8℃ D.10℃
选:D.
2.(3分)我国航天事业取得了跨越式发展,下列航天图标属于中心对称图形的是( )
A. B.
C. D.
选:D.
3.(3分)关于x的一元一次不等式x﹣1≤m的解集在数轴上的表示如图所示,则m的值为( )
A.3 B.2 C.1 D.0
选:B.
4.(3分)下列运算正确的是( )
A.4a2﹣2a2=2 B.a7÷a3=a4
C.5a2 a4=5a8 D.(a2b3)2=a4b5
选:B.
5.(3分)下列说法正确的是( )
A.检测“神舟十六号”载人飞船零件的质量,应采用抽样调查
B.任意画一个三角形,其外角和是180°是不可能事件
C.某奖券的中奖率为,买100张奖券,一定会中奖1次
D.“任意两个等腰三角形是相似三角形”是必然事件
选:B.
6.(3分)将直角三角板和直尺按照如图位置摆放,若∠1=56°,则∠2的度数是( )
A.26° B.30° C.36° D.56°
选:A.
7.(3分)如图1是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中,如图2是八角形空窗的示意图,它的一个外角∠1=( )
A.45° B.60° C.110° D.135°
选:A.
8.(3分)如图,若在象棋盘上建立直角坐标系xOy,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“炮”位于点( )
A.(﹣2,﹣1) B.(0,0) C.(1,﹣2) D.(﹣1,1)
选:B.
9.(3分)如图,AB切⊙O于点B,连结OA交⊙O于点C,BD∥OA交⊙O于点D,连结CD,若∠OCD=25°,则∠A的度数为( )
A.25° B.35° C.40° D.45°
选:C.
10.(3分)如图,二次函数y=ax2+bx+c的图象与x轴交于A(﹣2,0),B两点,对称轴是直线x=2,下列结论中,所有正确结论的序号为( )
①a>0;
②点B的坐标为(6,0);
③c=3b;
④对于任意实数m,都有4a+2b≥am2+bm.
A.①② B.②③ C.②③④ D.③④
选:C.
二、填空题(本大题共5个小题,每小题3分,共15分)把答案填在答题卡的相应位置上.
11.(3分)计算:= a﹣b .
【解答】解:
=
=
=a﹣b,
故答案为:a﹣b.
12.(3分)一个函数过点(1,3),且y随x增大而增大,请写出一个符合上述条件的函数解析式 y=x+2
13.(3分)如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是 .
14.(3分)我国古代数学著作《张丘建算经》中著名的“百鸡问题”叙述如下:“鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁、母、雏各几何?”意思是公鸡五钱一只,母鸡三钱一只,小鸡一钱三只,要用一百钱买一百只鸡,问公鸡、母鸡、小鸡各多少只?若现已知母鸡买18只,则公鸡买 4 只,小鸡买 78 只.
15.(3分)如图,在△ABC中,∠ACB=90°,将△ABC绕点B顺时针旋转90°得到△DBE,连接AD,CE,延长EC交AD于点F,若CF=1,CE=2,则AF的长 .
三、解答题(本大题共9个小题,共75分)解答应写出文字说明,证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.
16.(6分).
【解答】解:
=3﹣2﹣(2﹣)+2×
=3﹣2﹣2++
=2﹣1.
17.(6分)如图,在四边形ABCD中,AB∥CD,AB=CD.过点D分别作DF⊥AB于点F,DE⊥BC于点E,且DE=DF.求证:四边形ABCD是菱形.
【解答】证明:连接BD,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵DF⊥AB于点F,DE⊥BC于点E,
∴∠BED=∠BFD=90°,
在Rt△BED和Rt△BFD中,
,
∴Rt△BED≌Rt△BFD(HL),
∴∠EBD=∠FBD,
∵∠FBD=∠CDB,
∴∠EBD=∠CDB,
∴CB=CD,
∴四边形ABCD是菱形.
18.(6分)某综合实践研究小组为了测量广场上空气球A离地面的高度,已知水平面MN,该小组利用自制简易测角仪在水平面上点B,C处分别测得气球A的仰角∠ABN为37°,∠ACN为45°,已知BC=20m,求气球A离地面的高度.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
【解答】解:过A作AD⊥MN于D,
设CD=x m,
∵BC=20m,
∴BD=BC+CD=(x+20)m,
在Rt△ACD中,∠ACD=45°,
∴AD=CD tan45°=x(m),
在Rt△ABD中,∠ABD=37°,
∴AD=BD tan37°≈0.75(x+20)m,
∴x=0.75(x+20),
解得:x=60,
∴AD=60m,
∴气球A离地面的高度AD约为60m.
19.(8分)“惜餐为荣,敛物为耻.”为了解落实“光盘行动”的情况,某校调研了七、八年级部分班级某一天的厨余垃圾质量,并作出如下统计分析.
【收集数据】七、八年级各随机抽取10个班厨余垃圾质量的数据(单位:kg).
【整理数据】进行整理和分析(厨余垃圾质量用x表示,共分为四个等级:A.x<1;B.1≤x<1.5;C.1.5≤x<2;D.x≥2).
【描述数据】下面给出了部分信息,绘制如下统计图:
七年级10个班厨余垃圾质量:0.6,0.7,0.7,0.7,1.3,1.3,1.6,1.7,2,2.4.
八年级10个班厨余垃圾质量中B等级包含的所有数据为:1.1,1.1,1.1,1.3.
【分析数据】七、八年级抽取的班级厨余垃圾质量统计表如下:
年级 平均数 中位数 众数 方差 A等级所占百分比
七年级 1.3 1.3 a 0.352 40%
八年级 1.3 b 1.1 0.24 m%
根据以上信息,解答下列问题:
(1)填空:a= 0.7 ,b= 1.1 ,m= 30 ;
(2)该校八年级共有30个班,估计八年级这一天厨余垃圾质量符合A等级的班级数;
(3)根据以上信息,请你任选一个统计量,分析在此次“光盘行动”中,该校七、八年级的哪个年级落实得更好?并说明理由.
【解答】解:(1)七年级10个数据中0.7最多,所以众数a=0.7,
八年级B等级有4个,C、D等级为10×20%=2个,10×10%=1个,
所以A等级有10﹣4﹣2﹣1=3个,
所以m%=×100%=30%,
所以中位数为b==1.1;
故答案为:0.7,1.1,30;
(2)30×30%=9(个),
答:估计八年级这一天厨余垃圾质量符合A等级的班级数为9个;
(3)八年级落实更好,
理由:①八年级各班餐厨垃圾质量的中位数1.1低于七年级各班餐厨垃圾质量的中位数1.2.②八年级各班餐厨垃圾质量的方差0.24低于七年级各班餐厨垃圾质量的方差0.352,更稳定,(答案不唯一).
20.(8分)如图,在平面直角坐标系xOy中,直线AB:y=kx﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
(1)求直线AB的表达式;
(2)将直线AB沿y轴方向向上平移n个单位后与反比例函数图象在第一象限内交于点C,若S△ABC≤18,请求出n的取值范围.
【解答】解:(1)∵点B(m,2)在反比例函数的图象上,
∴2m=8,
∴m=4.
∴点B(4,2).
把点B(4,2)代入y=kx﹣2,
得:4k﹣2=2,
∴k=1.
∴直线AB的表达式为:y=x﹣2.
(2)记平移后的直线与y轴的交点为D,则AD=n,
联结BD.
∵CD∥AB.
∴S△ABD=S△ABC.
即:n×4≤18.
∴n≤9.
21.(8分)如图,在△OAE中,OA=OE,B是AE中点,以O为圆心,OB为半径作⊙O,分别交AO及其延长线、OE于C,D,F点,连接BD交OE于点G.
(1)求证:AE是⊙O的切线;
(2)若C是OA的中点,,求阴影部分的面积.
【解答】(1)证明:连接OB,
∵OA=OE,B是AE中点,
∴AE⊥OB,
∵OB是⊙O的半径,且AE⊥OB,
∴AE是⊙O的切线.
(2)解:∵C是OA的中点,
∴OB=OC=AC=OA,
∴cos∠AOB==,
∴∠AOB=∠EOB=60°,
∵OD=OB,BD=4,
∴∠OBD=∠D=∠AOB=30°,
∴∠OGB=180°﹣∠OBD﹣∠EOB=90°,
∴OG⊥BD,
∴BG=DG=BD=2,
∵=tan30°=,
∴GO=BG=×2=2,
∴OB=2GO=4,
∴S阴影=S扇形OBF﹣S△OBG=﹣×4×2=﹣4,
∴阴影部分的面积是﹣4.
22.(10分)如图1所示的某种发石车是古代一种远程攻击的武器.将发石车置于山坡底部O处,以点O为原点,水平方向为x轴方向,建立如图2所示的平面直角坐标系,将发射出去的石块当作一个点看,其飞行路线可以近似看作抛物线y=a(x﹣20)2+k的一部分,山坡OA上有一堵防御墙,其竖直截面为ABCD,墙宽BC=2米,BC与x轴平行,点B与点O的水平距离为28米、垂直距离为6米.
(1)若发射石块在空中飞行的最大高度为10米,
①求抛物线的解析式;
②试通过计算说明石块能否飞越防御墙;
(2)若要使石块恰好落在防御墙顶部BC上(包括端点B、C),求a的取值范围.
【解答】解:(1)①设石块运行的函数关系式为y=a(x﹣20)2+10,
把(0,0)代入解析式得:400a+10=0,
解得:a=﹣,
∴解析式为:y=﹣(x﹣20)2+10,即y=﹣x2+x(0≤x≤40);
②石块能飞越防御墙AB,理由如下:
把x=30代入y=﹣x2+x得:
y=﹣×900+30=7.5,
∵7.5>6,
∴石块能飞越防御墙AB;
(3)由题可知B(28,6),抛物线y=a(x﹣20)2+k,
∴把(0,0),(28,6)代入得:,
解得a=﹣;
把C(30,6),(0,0)代入解析式,
解得a=﹣,
∴a的取值范围为﹣≤a≤﹣.
23.(11分)某数学兴趣小组开展矩形的折叠实验探究,折叠矩形ABCD的一边AD,使点D落在点F处,折痕为AE.
(1)如图1,当点F恰好在BC边上时,证明:△ABF∽△FCE.
(2)将矩形的边AB折叠,使点B落在AF边上的点M处,折痕为AN.
①如图2,当点F恰好在BC边上时,若AB=1,,连接EN,试判断△AEN的形状,并说明理由.
②如图3,当点F在矩形内部时,若AB=8,BC=12.点E是CD的中点,求FN的长.
【解答】(1)证明:由折叠可知,
△AFE≌△ADE,
∴∠AFE=∠D=90°,
∴∠AFB+∠CFE=90°,
∵∠AFB+∠BAF=90°,
∴∠BAF=∠CFE,
∵∠B=∠C=90°,
∴△ABF∽△FCE.
(2)解:①由折叠可知,
△AMN≌△ABN,
∴AM=AB=1,
∵AF=AD=BC=,
∵∠B=90°,
∴BF==1=AB,
∴△ABF为等腰直角三角形,
∵△ABF∽△FCE.
∴△FCE为等腰直角三角形,
∴CE=CF=﹣1,
∵∠AFE=90°,
∴∠MFN+∠CFE=90°,
∵∠CFE=45°,
∴∠MFN=45°,
∠FMN=∠AMN=90°,
△FMN为等腰直角三角形,
∴MN=FM=﹣1,
∴BN=﹣1=CE,
∴CN==1=AB,
∴△ABN≌△NCE(SAS),
∴AN=EN,
∵∠NAM+∠EAF=∠BAD=45°,
∴△AEN为等腰直角三角形,
②延长AF交BC于点H,连接EH,
∵AM=AB=DC=8,点E为DC中点,
∴CE=DE=4,EF=DE=4,AF=AD=BC=12,
∴FM=12﹣8=4,
∵∠EFH﹣∠AFE=∠D=90°,∠C=90°,
∴∠EFH=∠C,
在Rt△EFH和Rt△ECH中,
EH=EH,EF=EC,
∴Rt△EFH≌Rt△ECH(HL),
设FH=x,则CH=x,
∴BH=12﹣x,AH=12+x,
在Rt△ABH中,AB2=BH2+AH2,
即82+(12﹣x)2=(12+x)2,
解得x=,
∴MH=,
设MN=y,则BN=y,
∴MH=,
∵∠NMH=90°,
∴在Rt△NMH中,y2+()2=()2,
∴y=4,
∴FN==4.
故FN的长为4.
24.(12分)在平面直角坐标系中,已知抛物线y=ax2﹣2ax﹣3a(a>0).
(1)抛物线的对称轴为直线 x=1 ;
(2)当﹣2≤x≤2时,函数值y的取值范围是﹣4≤y≤b,求a和b的值;
(3)当a=1时,解决下列问题.
①抛物线上一点P到x轴的距离为6,求点P的坐标;
②将该抛物线在0≤x≤4间的部分记为G,将G在直线y=t下方的部分沿y=t翻折,其余部分保持不变,得到的新图象记为Q.设Q的最高点、最低点的纵坐标分别为y1,y2,若y1﹣y2<6,直接写出t的取值范围.
【解答】解:(1)函数的对称轴为:x=﹣=1,
∴x=1;
故答案为:x=1;
(2)函数对称轴为x=1,当﹣2≤x≤2时,函数值y的取值范围是﹣4≤y≤b.
故y=﹣4 是函数的最小值,即抛物线的顶点为(1,﹣4).
将函数顶点坐标代入函数表达式并解得:a=1.
故抛物线的表达式为:y=x2﹣2x﹣3,
则b=(﹣2)2﹣2(﹣2)﹣3=5;
(3)①∵抛物线上一点P到x轴的距离为6,而顶点坐标为(1,﹣4),
x2﹣2x﹣3=6,
解得
故点P的坐标为 ,6)或 ,6);
②﹣1<t≤2.
设图象折叠后顶点M的对应点为M,点H是x=4函数所处的位置,图象Q为C′M′NH区域,
点M(1,﹣4),点H(4,5),则点M′(1,2t+4)
当点M′在点H下方时,2t+4<5,t<,
函数Q的最高点为H,最低点为N.
则5﹣t<6.解得t>﹣1.
故﹣1<t<,
当点M′在点H上方时,同理可得:
故﹣1<t<2.
同课章节目录
