北师大版六年级下册数学圆柱的体积(课件)(共31张PPT)
文档属性
| 名称 | 北师大版六年级下册数学圆柱的体积(课件)(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 10:52:39 | ||
图片预览









文档简介
(共31张PPT)
圆柱的体积习题
北师大版六年级数学下册第一单元《圆柱和圆锥》
一、学习目标
1.理解并掌握圆柱的体积计算公式;
2.能运用公式计算圆柱的体积;
3.掌握几种典型的变型题:旋转、截圆柱、削圆柱、酒瓶问题;
4.利用所学知识分析、解决复杂综合题型。
1、说一说圆柱体积的计算公式。
圆柱体积=底面积×高
V=Sh=
160平方厘米=( )平方分米 3.7平方分米=( )平方毫米
40.06吨=( )千克 1.4立方米=( )立方分米
360平方米=( )公顷 7.05米=( )米( )厘米
2、填一填
复习准备
2、(1)两个圆柱的高相等,底面周长的比是2:5,则体积之比是( : )
(2)两个圆柱的高相等,底面半径的比是2:3,则体积之比是( : )
二、探索新知
谁的体积大?你是如何判断的?
h = h
高相等时底面积越大的体积越大。
当底面积相等时,高越长的体积越大。
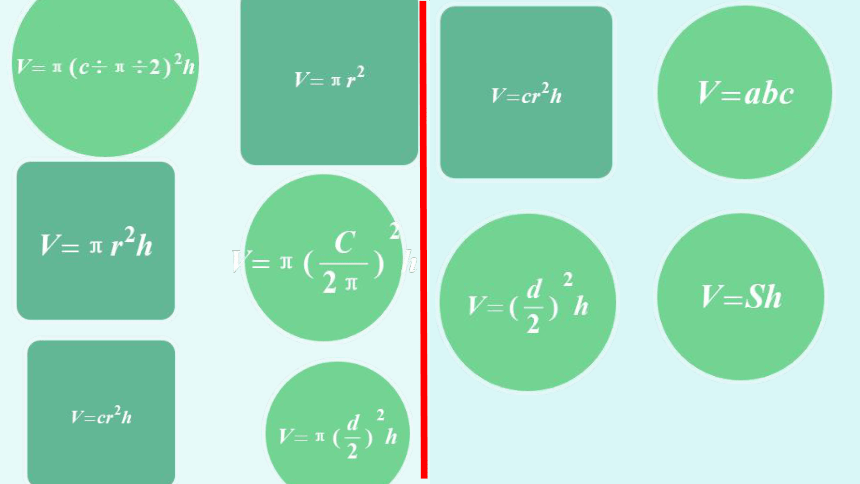
V=Sh
V=πr2h
V=π(d÷2)2h
V=π(c÷π÷2)2h
圆柱体积公式
综合应用
1
一个用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个半径为2米的半圆形。
搭建这个大棚大约要用多少平方米的塑料薄膜?
大棚内的空间大约有多大?
求圆柱表面积的一半
求圆柱容积的一半
答:……
一个圆柱形油桶,从里面量,底面直径是40厘米, 高是50厘米。
(1)做这样一个油桶,至少需要铁皮多少平方分米?(得数保留 一位小数)
(2)它的容积是多少升?
(3)如果1升柴油重0.85千克,这个油桶可装柴油多少千克?
2
综合应用
(1) 3.14×(4÷2) ×2+3.14×4×5
=87.92≈87.9(平方分米)
求表面积=底面积×2+侧面积
求体积=底面积×高
(3) 0.85×62.8=53.38(千克)
(2) 3.14×(4÷2) ×5=62.8(立方分米)=62.8(升)
解:40厘米=4分米 50厘米=5分米
答:……
专题解析
把一张长5厘米、宽4厘米的长方形纸分别绕它的长和宽旋转一周(如下图),形成两个圆柱。
1
4cm
5cm
4cm
5cm
旋转问题
专题解析
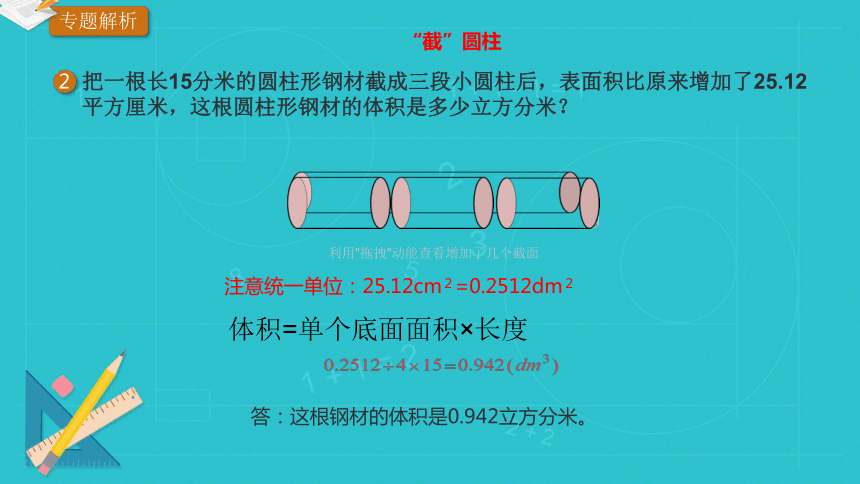
“截”圆柱
2
把一根长15分米的圆柱形钢材截成三段小圆柱后,表面积比原来增加了25.12平方厘米,这根圆柱形钢材的体积是多少立方分米?
利用"拖拽"动能查看增加了几个截面
注意统一单位:25.12cm2=0.2512dm2
答:这根钢材的体积是0.942立方分米。
体积=单个底面面积×长度
专题解析
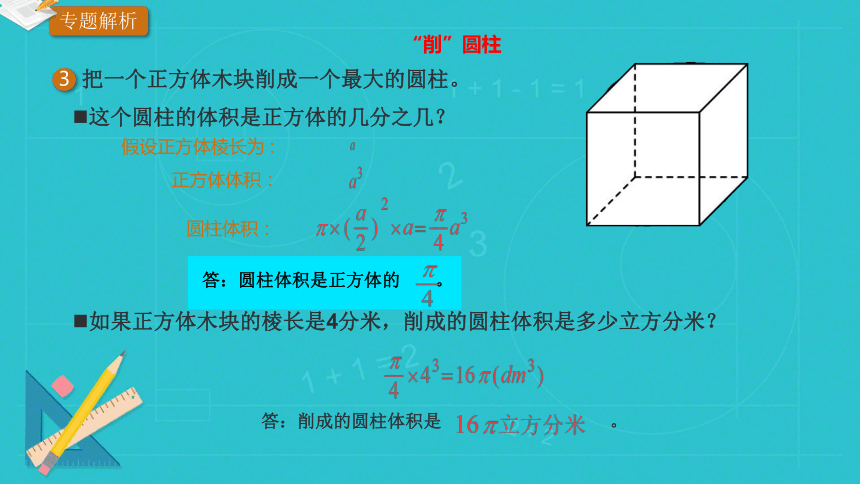
“削”圆柱
3
把一个正方体木块削成一个最大的圆柱。
如果正方体木块的棱长是4分米,削成的圆柱体积是多少立方分米?
这个圆柱的体积是正方体的几分之几?
假设正方体棱长为 :
正方体体积:
圆柱体积:
答:削成的圆柱体积是 。
答:圆柱体积是正方体的 。
专题解析
"酒瓶"问题
4
郭老师买了一瓶深30厘米,底面直径是10厘米的酒,瓶里的酒深15厘米。把酒瓶塞紧后,使瓶口向下倒立,这时酒深25厘米,这个酒瓶的容积是多少毫升?
25
cm
30
cm
10cm
15
cm
上部空白部分可以移动
5cm
5
有一种饮料瓶的容积是480ml。现在饮料瓶中装有一些饮料,饮料瓶正放时饮料的高度是20cm,倒放时空余部分的高度为4cm(如图)。饮料瓶中现有饮料多少毫升?
20cm
4cm
上部空白部分可以移动
分析:饮料的体积=底面积×饮料高度
瓶子的容积=底面积×(饮料高度+空气高度)
举一反三
1、一个瓶子的瓶身呈圆柱形(不包括瓶颈),它的底面直径是10cm,高是30cm,瓶子里装有15cm高的水,把瓶盖拧紧后倒放,水深25cm,(如下图),这个瓶子的容积是多少?(瓶子的厚度忽略不计)
举一反三
2、一个瓶子如下图,它的瓶身呈圆柱形(不包括瓶颈)。瓶内装有340mL饮料,瓶子正放时瓶内饮料高17cm,倒放时瓶内空余部分高5cm,这个瓶子的容积是多少?
1.(易错题)判断。
课堂练习
(1)圆柱的底面积越大,体积越大。 ( )
(2)把正方体木块削成一个最大的圆柱,则此圆柱的直径与高相等 ( )
(3)圆柱体的高不变,底面积扩大2倍,体积扩大4倍.( )
(4)一个圆柱体的高扩大2倍,底面积缩小2倍,它的体积不变。( )
(5) 一个圆柱和一个正方体的底面积和高都相等,它们的体积一定相等。( )
(6)两圆柱的侧面积相等,它们的体积也一定相等。( )
(7)圆柱体的体积公式是由长方体的体积计算公式推导而来的。( )
(8)把一个圆柱切成两半,表面积和体积都增加了。 ( )
2.一根圆柱形钢材长4米,将它沿着横截面锯成2段后,表面积增加了3.14平方厘米。这根钢材的体积是多少立方厘米
课堂练习
底面积:3.14÷2=1.57cm
高:4米=400厘米
体积:1.57×400=628cm
3.把一根9dm长的圆柱形木材沿着直径向下切成两半后,表面积增加了36平方分米。这根钢材的体积是多少立方分米
课堂练习
9dm
r=36÷2÷9÷2=1(分米)
V=3.14×1×1×9=28.26dm
4.一个圆柱的侧面展开恰好是一个边长为18.84厘米的正方形,求这个圆柱体的体积(得数保留整数)。
课堂练习
高:18.84厘米
半径:18.84÷3.14÷2=3(厘米)
体积:3.14×3×3×18.84≈532(cm )
5.(创新题)一个圆柱,如果把它的高截短3厘米,它的表面积减少94.2平方厘米,那么它的体积减小多少立方厘米
随堂练习
侧面积94.2cm 高 3cm
半径:94.2÷3÷3.14÷2=5cm
体积减少:3.14×5×5×3=235.5cm
6. 学校要在教学区和操场之间修一道围墙,原计划用土石 35 m3。后来多开了一个厚度为25cm的月亮门,减少了土石的用量。现在用了多少立方米土石
25cm=0.25m
35-3.14×(2÷2)2×0.25
= 35-0.785
= 34.215 (m3)
答: 现在用了 34.215立方米土石。
7.明明家里来了两位小客人,妈妈冲了1L果汁。如果用右图中的玻璃杯喝果汁,够明明和客人每人一杯吗?
3.14×(6÷2)2×11×3
= 9×3.14×11×3
= 932.58(cm3)= 932.58(mL)
1L=1000mL>932.58 mL
答:所以够明明和客人每人一杯。
8.一种电热水炉的水龙头的内直径是1.2cm,打开水龙头后水的流速是20厘米/秒。一个容积为1L的保温壶,50秒能装满水吗?
3.14×(1.2÷2)2×20×50
=3.14×0.36×20×50
=1130.4 (cm3)
1L=1000 cm3
,1130.4>1000
答:所以50秒能装满水。
9.下图某各规格的卷筒纸,求纸所占的体积。(单位:cm)
6
16
12
你发现了什么?
上下匀称的物体,都可以用底面积乘高计算出体积。
你还能用不同的方法计算吗?
2411.52-339.12=
2072.4
2072.4
拓展提升
1
在长40cm、宽20cm、高20cm的长方体中挖去一个底面半径为6cm的圆柱的一半后得到如图的一个几何体。这个几何体的体积是多少?
20cm
20cm
40cm
长方体体积:
半个圆柱体积:
几何体体积:
方法二:
底面积:20×20-3.14×6 ÷2=343.48(cm )
体积:343.48×40=
13739.2cm
答:……
拓展提升
木棒的体积是多少?
2
6cm
7cm
5cm
7cm
6cm
两根这样的木棒可以拼成一个圆柱
拓展提升
哪一组圆能和长方形纸搭配围成圆柱?
3
围成的圆柱体积最大是多少?
3cm
3cm
2cm
2cm
4cm
4cm
12.56cm
6.28cm
A
B
C
答:A组和B组。
答:围成圆柱体积最大是25.12πcm3。
思考题
下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?(单位:dm)
18
2
12
3
9
4
6
6
用下面的长方形围成圆柱,哪组圆能做圆柱的底?用哪组圆做圆柱的底围成的圆柱的体积大?
挑战奥数
4厘米
9厘米
拉出8厘米
4厘米高水柱的体积=8厘米高钢材的体积
钢材的体积=9厘米高水柱体积
水桶的底面积:
钢材的体积:
答:……
下面是一根钢管,求制作这根钢管所用钢材的体积。(单位:厘米)
圆柱的体积习题
北师大版六年级数学下册第一单元《圆柱和圆锥》
一、学习目标
1.理解并掌握圆柱的体积计算公式;
2.能运用公式计算圆柱的体积;
3.掌握几种典型的变型题:旋转、截圆柱、削圆柱、酒瓶问题;
4.利用所学知识分析、解决复杂综合题型。
1、说一说圆柱体积的计算公式。
圆柱体积=底面积×高
V=Sh=
160平方厘米=( )平方分米 3.7平方分米=( )平方毫米
40.06吨=( )千克 1.4立方米=( )立方分米
360平方米=( )公顷 7.05米=( )米( )厘米
2、填一填
复习准备
2、(1)两个圆柱的高相等,底面周长的比是2:5,则体积之比是( : )
(2)两个圆柱的高相等,底面半径的比是2:3,则体积之比是( : )
二、探索新知
谁的体积大?你是如何判断的?
h = h
高相等时底面积越大的体积越大。
当底面积相等时,高越长的体积越大。
V=Sh
V=πr2h
V=π(d÷2)2h
V=π(c÷π÷2)2h
圆柱体积公式
综合应用
1
一个用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个半径为2米的半圆形。
搭建这个大棚大约要用多少平方米的塑料薄膜?
大棚内的空间大约有多大?
求圆柱表面积的一半
求圆柱容积的一半
答:……
一个圆柱形油桶,从里面量,底面直径是40厘米, 高是50厘米。
(1)做这样一个油桶,至少需要铁皮多少平方分米?(得数保留 一位小数)
(2)它的容积是多少升?
(3)如果1升柴油重0.85千克,这个油桶可装柴油多少千克?
2
综合应用
(1) 3.14×(4÷2) ×2+3.14×4×5
=87.92≈87.9(平方分米)
求表面积=底面积×2+侧面积
求体积=底面积×高
(3) 0.85×62.8=53.38(千克)
(2) 3.14×(4÷2) ×5=62.8(立方分米)=62.8(升)
解:40厘米=4分米 50厘米=5分米
答:……
专题解析
把一张长5厘米、宽4厘米的长方形纸分别绕它的长和宽旋转一周(如下图),形成两个圆柱。
1
4cm
5cm
4cm
5cm
旋转问题
专题解析
“截”圆柱
2
把一根长15分米的圆柱形钢材截成三段小圆柱后,表面积比原来增加了25.12平方厘米,这根圆柱形钢材的体积是多少立方分米?
利用"拖拽"动能查看增加了几个截面
注意统一单位:25.12cm2=0.2512dm2
答:这根钢材的体积是0.942立方分米。
体积=单个底面面积×长度
专题解析
“削”圆柱
3
把一个正方体木块削成一个最大的圆柱。
如果正方体木块的棱长是4分米,削成的圆柱体积是多少立方分米?
这个圆柱的体积是正方体的几分之几?
假设正方体棱长为 :
正方体体积:
圆柱体积:
答:削成的圆柱体积是 。
答:圆柱体积是正方体的 。
专题解析
"酒瓶"问题
4
郭老师买了一瓶深30厘米,底面直径是10厘米的酒,瓶里的酒深15厘米。把酒瓶塞紧后,使瓶口向下倒立,这时酒深25厘米,这个酒瓶的容积是多少毫升?
25
cm
30
cm
10cm
15
cm
上部空白部分可以移动
5cm
5
有一种饮料瓶的容积是480ml。现在饮料瓶中装有一些饮料,饮料瓶正放时饮料的高度是20cm,倒放时空余部分的高度为4cm(如图)。饮料瓶中现有饮料多少毫升?
20cm
4cm
上部空白部分可以移动
分析:饮料的体积=底面积×饮料高度
瓶子的容积=底面积×(饮料高度+空气高度)
举一反三
1、一个瓶子的瓶身呈圆柱形(不包括瓶颈),它的底面直径是10cm,高是30cm,瓶子里装有15cm高的水,把瓶盖拧紧后倒放,水深25cm,(如下图),这个瓶子的容积是多少?(瓶子的厚度忽略不计)
举一反三
2、一个瓶子如下图,它的瓶身呈圆柱形(不包括瓶颈)。瓶内装有340mL饮料,瓶子正放时瓶内饮料高17cm,倒放时瓶内空余部分高5cm,这个瓶子的容积是多少?
1.(易错题)判断。
课堂练习
(1)圆柱的底面积越大,体积越大。 ( )
(2)把正方体木块削成一个最大的圆柱,则此圆柱的直径与高相等 ( )
(3)圆柱体的高不变,底面积扩大2倍,体积扩大4倍.( )
(4)一个圆柱体的高扩大2倍,底面积缩小2倍,它的体积不变。( )
(5) 一个圆柱和一个正方体的底面积和高都相等,它们的体积一定相等。( )
(6)两圆柱的侧面积相等,它们的体积也一定相等。( )
(7)圆柱体的体积公式是由长方体的体积计算公式推导而来的。( )
(8)把一个圆柱切成两半,表面积和体积都增加了。 ( )
2.一根圆柱形钢材长4米,将它沿着横截面锯成2段后,表面积增加了3.14平方厘米。这根钢材的体积是多少立方厘米
课堂练习
底面积:3.14÷2=1.57cm
高:4米=400厘米
体积:1.57×400=628cm
3.把一根9dm长的圆柱形木材沿着直径向下切成两半后,表面积增加了36平方分米。这根钢材的体积是多少立方分米
课堂练习
9dm
r=36÷2÷9÷2=1(分米)
V=3.14×1×1×9=28.26dm
4.一个圆柱的侧面展开恰好是一个边长为18.84厘米的正方形,求这个圆柱体的体积(得数保留整数)。
课堂练习
高:18.84厘米
半径:18.84÷3.14÷2=3(厘米)
体积:3.14×3×3×18.84≈532(cm )
5.(创新题)一个圆柱,如果把它的高截短3厘米,它的表面积减少94.2平方厘米,那么它的体积减小多少立方厘米
随堂练习
侧面积94.2cm 高 3cm
半径:94.2÷3÷3.14÷2=5cm
体积减少:3.14×5×5×3=235.5cm
6. 学校要在教学区和操场之间修一道围墙,原计划用土石 35 m3。后来多开了一个厚度为25cm的月亮门,减少了土石的用量。现在用了多少立方米土石
25cm=0.25m
35-3.14×(2÷2)2×0.25
= 35-0.785
= 34.215 (m3)
答: 现在用了 34.215立方米土石。
7.明明家里来了两位小客人,妈妈冲了1L果汁。如果用右图中的玻璃杯喝果汁,够明明和客人每人一杯吗?
3.14×(6÷2)2×11×3
= 9×3.14×11×3
= 932.58(cm3)= 932.58(mL)
1L=1000mL>932.58 mL
答:所以够明明和客人每人一杯。
8.一种电热水炉的水龙头的内直径是1.2cm,打开水龙头后水的流速是20厘米/秒。一个容积为1L的保温壶,50秒能装满水吗?
3.14×(1.2÷2)2×20×50
=3.14×0.36×20×50
=1130.4 (cm3)
1L=1000 cm3
,1130.4>1000
答:所以50秒能装满水。
9.下图某各规格的卷筒纸,求纸所占的体积。(单位:cm)
6
16
12
你发现了什么?
上下匀称的物体,都可以用底面积乘高计算出体积。
你还能用不同的方法计算吗?
2411.52-339.12=
2072.4
2072.4
拓展提升
1
在长40cm、宽20cm、高20cm的长方体中挖去一个底面半径为6cm的圆柱的一半后得到如图的一个几何体。这个几何体的体积是多少?
20cm
20cm
40cm
长方体体积:
半个圆柱体积:
几何体体积:
方法二:
底面积:20×20-3.14×6 ÷2=343.48(cm )
体积:343.48×40=
13739.2cm
答:……
拓展提升
木棒的体积是多少?
2
6cm
7cm
5cm
7cm
6cm
两根这样的木棒可以拼成一个圆柱
拓展提升
哪一组圆能和长方形纸搭配围成圆柱?
3
围成的圆柱体积最大是多少?
3cm
3cm
2cm
2cm
4cm
4cm
12.56cm
6.28cm
A
B
C
答:A组和B组。
答:围成圆柱体积最大是25.12πcm3。
思考题
下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?(单位:dm)
18
2
12
3
9
4
6
6
用下面的长方形围成圆柱,哪组圆能做圆柱的底?用哪组圆做圆柱的底围成的圆柱的体积大?
挑战奥数
4厘米
9厘米
拉出8厘米
4厘米高水柱的体积=8厘米高钢材的体积
钢材的体积=9厘米高水柱体积
水桶的底面积:
钢材的体积:
答:……
下面是一根钢管,求制作这根钢管所用钢材的体积。(单位:厘米)
