3.2.1 双曲线及其标准方程 课件(共23张PPT)
文档属性
| 名称 | 3.2.1 双曲线及其标准方程 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 31.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 14:42:53 | ||
图片预览


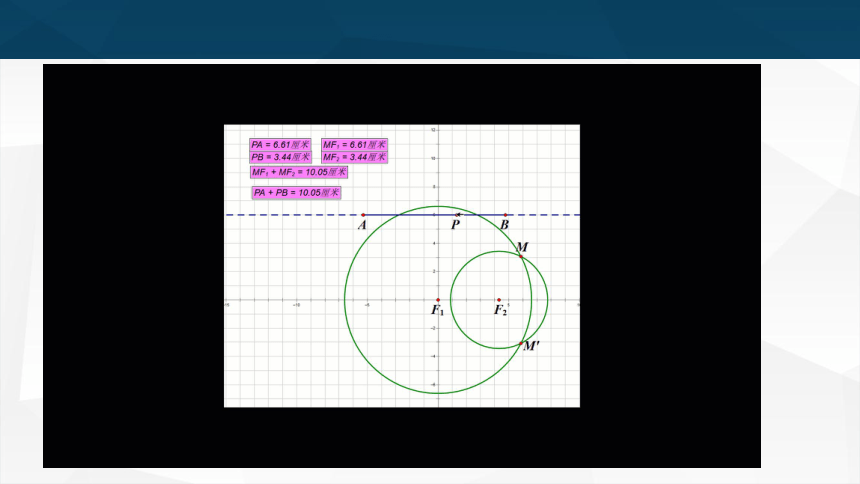






文档简介
(共23张PPT)
授课教师:.... .....
授课时间:2024.11
3.2.1
双曲线及其标准方程
定义 图形
方程
焦点
a、b、c之间的关系
F1
F2
M
y
x
O
y
x
O
M
F1
F2
|MF1|+|MF2|=2a (2a>|F1F2|)
(c,0)、( c,0)
(0,c)、(0, c)
a2=b2+c2
分母哪个大,焦点就在哪一根坐标轴上
00 复习:椭圆的标准方程
平面内到两个定点F1、F2的距离的差的绝对值等于常数2a的动点的轨迹是怎样的图形?
双曲线
01 探究:轨迹方程
如何理解绝对值?若去掉绝对值则图像有何变化?
02 双曲线的定义
F2F1MxOy2.设点:设M(x,y),双曲线的焦距为2c(c>0),F1(-c,0),F2(c,0)常数=2a1.建系:如图建立直角坐标系xOy,使x轴经过点F1,F2,并且点O与线段F1F2中点重合.即3.列式:03双曲线的标准方程4.化简.
03 双曲线的标准方程
问题:如何判断双曲线的焦点在哪个轴上?
(二次项系数为正,焦点在相应的轴上)
F ( ±c, 0)
F(0, ± c)
O
x
y
03 双曲线的标准方程
双曲线定义 双曲线图象
标准方程
焦点
a.b.c 的关系 | |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
F ( ±c, 0) F(0, ± c)
谁正谁对应a
03 双曲线的标准方程
定义 图形
方程
焦点
a、b、c之间的关系
F1
F2
M
y
x
O
y
x
O
M
F1
F2
|MF1|+|MF2|=2a (2a>|F1F2|)
(c,0)、( c,0)
(0,c)、(0, c)
a2=b2+c2
分母哪个大,焦点就在哪一根坐标轴上
双曲线的定义
双曲线的定义
双曲线的定义
双曲线的标准方程
双曲线的标准方程
含参问题
类比:一个动圆与圆Q1:(x+3)2+y2=1外切,与圆Q2:(x-3)2+y2=81内切,求这个动圆圆心的轨迹方程。
利用定义求轨迹方程
P127 习题3.2 第5题
如图,圆O的半径为定长 ,A是圆O外一定点,P是圆上任意一点,线段AP的垂直平分线l和直线OP相交于点Q,当点P在圆O上运动时,点Q的轨迹是什么 为什么
P
O
A
Q
P115 习题3.1 第6题
如图,圆O的半径为定长 ,A是圆O内一定点,P是圆上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆O上运动时,点Q的轨迹是什么 为什么
P
O
A
Q
利用定义求轨迹方程
P
O
A
Q
P
O
A
Q
|QO|+|QA|=|QO|+|QP|=|OP|=r
||QA|-|QO||=||QP|-|QO||=|OP|=r
双曲线中的周长/距离最值问题
授课教师:.... .....
授课时间:2024.11
3.2.1
双曲线及其标准方程
定义 图形
方程
焦点
a、b、c之间的关系
F1
F2
M
y
x
O
y
x
O
M
F1
F2
|MF1|+|MF2|=2a (2a>|F1F2|)
(c,0)、( c,0)
(0,c)、(0, c)
a2=b2+c2
分母哪个大,焦点就在哪一根坐标轴上
00 复习:椭圆的标准方程
平面内到两个定点F1、F2的距离的差的绝对值等于常数2a的动点的轨迹是怎样的图形?
双曲线
01 探究:轨迹方程
如何理解绝对值?若去掉绝对值则图像有何变化?
02 双曲线的定义
F2F1MxOy2.设点:设M(x,y),双曲线的焦距为2c(c>0),F1(-c,0),F2(c,0)常数=2a1.建系:如图建立直角坐标系xOy,使x轴经过点F1,F2,并且点O与线段F1F2中点重合.即3.列式:03双曲线的标准方程4.化简.
03 双曲线的标准方程
问题:如何判断双曲线的焦点在哪个轴上?
(二次项系数为正,焦点在相应的轴上)
F ( ±c, 0)
F(0, ± c)
O
x
y
03 双曲线的标准方程
双曲线定义 双曲线图象
标准方程
焦点
a.b.c 的关系 | |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
F ( ±c, 0) F(0, ± c)
谁正谁对应a
03 双曲线的标准方程
定义 图形
方程
焦点
a、b、c之间的关系
F1
F2
M
y
x
O
y
x
O
M
F1
F2
|MF1|+|MF2|=2a (2a>|F1F2|)
(c,0)、( c,0)
(0,c)、(0, c)
a2=b2+c2
分母哪个大,焦点就在哪一根坐标轴上
双曲线的定义
双曲线的定义
双曲线的定义
双曲线的标准方程
双曲线的标准方程
含参问题
类比:一个动圆与圆Q1:(x+3)2+y2=1外切,与圆Q2:(x-3)2+y2=81内切,求这个动圆圆心的轨迹方程。
利用定义求轨迹方程
P127 习题3.2 第5题
如图,圆O的半径为定长 ,A是圆O外一定点,P是圆上任意一点,线段AP的垂直平分线l和直线OP相交于点Q,当点P在圆O上运动时,点Q的轨迹是什么 为什么
P
O
A
Q
P115 习题3.1 第6题
如图,圆O的半径为定长 ,A是圆O内一定点,P是圆上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆O上运动时,点Q的轨迹是什么 为什么
P
O
A
Q
利用定义求轨迹方程
P
O
A
Q
P
O
A
Q
|QO|+|QA|=|QO|+|QP|=|OP|=r
||QA|-|QO||=||QP|-|QO||=|OP|=r
双曲线中的周长/距离最值问题
