初中数学北师大版(2024)八年级下册5.4 分式方程课件(第2课时)(18张PPT)
文档属性
| 名称 | 初中数学北师大版(2024)八年级下册5.4 分式方程课件(第2课时)(18张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 12:03:36 | ||
图片预览






文档简介
(共18张PPT)
北师大版八年级下册第五章
分式与分式方程
分式方程
第二课时
回顾与复习
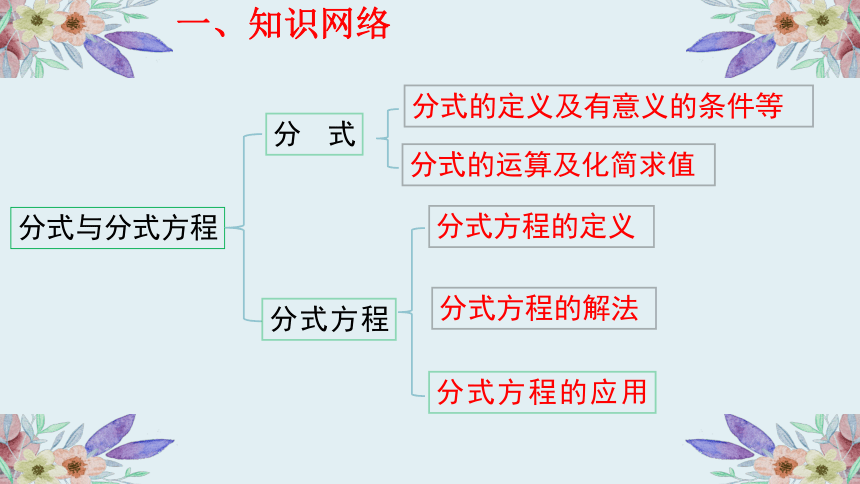
分式与分式方程
分式
分式的定义及有意义的条件等
分式方程
分式方程的应用
分式的运算及化简求值
分式方程的定义
分式方程的解法
一、知识网络
学习目标:
1.进一步掌握分式方程的定义、解法、增根及应用。
2.熟练利用分式方程分析问题、解决问题。
指出下列关于x的方程中,那些是分式方程( )(只填序号).
二、分式方程的定义
分母中含有未知数的方程叫做分式方程.
①
②
③
④
⑤
②
③
1.化:
三、解分式方程
解分式方程的步骤:
2.解:
方法2:把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程
的解,否则原分式方程无解(增根)。
3.检验:
方法1:代入原分式方程,看等号的左右两边是否 相等。
在方程的两边都乘以最简公分母,约去分母,
化成整式方程.
解这个整式方程.
作业本纠错
例: 解方程:
解 :方程两边都乘最简公分母(x - 2), 得 1= - 1+x -3(x - 2)
解这个一元一次方程,得 x = 2.
检验:把 x=2 代入最简公分母(x - 2),值为零
因此 x = 2 不是原方程的解.从而原方程无解.
典例精析
x - 2
跟踪练习:
解下列分式方程
用框图的方式总结为:
分式方程
整式方程
去分母
解整式方程
x =a
检验
x =a是分式
方程的解
x =a不是分式
方程的解
x =a
最简公分母是
否为零?
否
是
增根
增根:
产生增根的原因是:
一般地,解分式方程时,去分母后所得整式方程的解有可能使原分式方程的分母或最简公分母为0,我们把这个根叫做分式方程的增根。
我们在方程的两边同乘了一个可能使分母为零的整式.
因此解分式方程可能产生增根,所以解分式方程必须检验.
四、直击难点:分式方程增根的复习及灵活运用
例题:若关于x的分式方程:
会产生增根,试求k的值。
跟踪训练:
若关于x的分式方程: 有增根,试求n的值。
拓展延伸:
已知关于x的分式方程:
的根是非负数,求m的取值范围。
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有三次检验.
6.答:注意单位和语言完整.
五、分式方程的应用:
从广州到某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
六、分式方程的应用:
520
x
400
2.5x
-
=3
解:设普通列车的平均速度为x(千米/时),则高铁的平均速度2.5x(千米/时),根据题意列方程得:
解得 x=120
2.5x=2.5x120=300
经检验, x=120是所列方程的根,且符合题意.
答:高铁的平均速度300千米/时.
总结:本节课的收获
北师大版八年级下册第五章
分式与分式方程
分式方程
第二课时
回顾与复习
分式与分式方程
分式
分式的定义及有意义的条件等
分式方程
分式方程的应用
分式的运算及化简求值
分式方程的定义
分式方程的解法
一、知识网络
学习目标:
1.进一步掌握分式方程的定义、解法、增根及应用。
2.熟练利用分式方程分析问题、解决问题。
指出下列关于x的方程中,那些是分式方程( )(只填序号).
二、分式方程的定义
分母中含有未知数的方程叫做分式方程.
①
②
③
④
⑤
②
③
1.化:
三、解分式方程
解分式方程的步骤:
2.解:
方法2:把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程
的解,否则原分式方程无解(增根)。
3.检验:
方法1:代入原分式方程,看等号的左右两边是否 相等。
在方程的两边都乘以最简公分母,约去分母,
化成整式方程.
解这个整式方程.
作业本纠错
例: 解方程:
解 :方程两边都乘最简公分母(x - 2), 得 1= - 1+x -3(x - 2)
解这个一元一次方程,得 x = 2.
检验:把 x=2 代入最简公分母(x - 2),值为零
因此 x = 2 不是原方程的解.从而原方程无解.
典例精析
x - 2
跟踪练习:
解下列分式方程
用框图的方式总结为:
分式方程
整式方程
去分母
解整式方程
x =a
检验
x =a是分式
方程的解
x =a不是分式
方程的解
x =a
最简公分母是
否为零?
否
是
增根
增根:
产生增根的原因是:
一般地,解分式方程时,去分母后所得整式方程的解有可能使原分式方程的分母或最简公分母为0,我们把这个根叫做分式方程的增根。
我们在方程的两边同乘了一个可能使分母为零的整式.
因此解分式方程可能产生增根,所以解分式方程必须检验.
四、直击难点:分式方程增根的复习及灵活运用
例题:若关于x的分式方程:
会产生增根,试求k的值。
跟踪训练:
若关于x的分式方程: 有增根,试求n的值。
拓展延伸:
已知关于x的分式方程:
的根是非负数,求m的取值范围。
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有三次检验.
6.答:注意单位和语言完整.
五、分式方程的应用:
从广州到某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
六、分式方程的应用:
520
x
400
2.5x
-
=3
解:设普通列车的平均速度为x(千米/时),则高铁的平均速度2.5x(千米/时),根据题意列方程得:
解得 x=120
2.5x=2.5x120=300
经检验, x=120是所列方程的根,且符合题意.
答:高铁的平均速度300千米/时.
总结:本节课的收获
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
