【人教版数学八年级上册同步练习】 第12章全等三角形综合检测题(含答案)
文档属性
| 名称 | 【人教版数学八年级上册同步练习】 第12章全等三角形综合检测题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 14:25:46 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【人教版数学八年级上册同步练习】
第12章全等三角形综合检测题
一、单选题
1.如图,下列条件中,不能证明 的是( )
A. , B. ,
C. , D. ,
2.小明同学有一块玻璃的三角板,不小心掉到地上碎成了三块,现要去文具店买一块同样的三角板,最省事的是( )
A.带②去 B.带①去 C.带③去 D.三块都带去
3.如图,是的平分线,若是直角,,则的度数是( )
A. B. C. D.
4.如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )
A.AM=CN B.AB=CD C.AM∥CN D.∠M=∠N
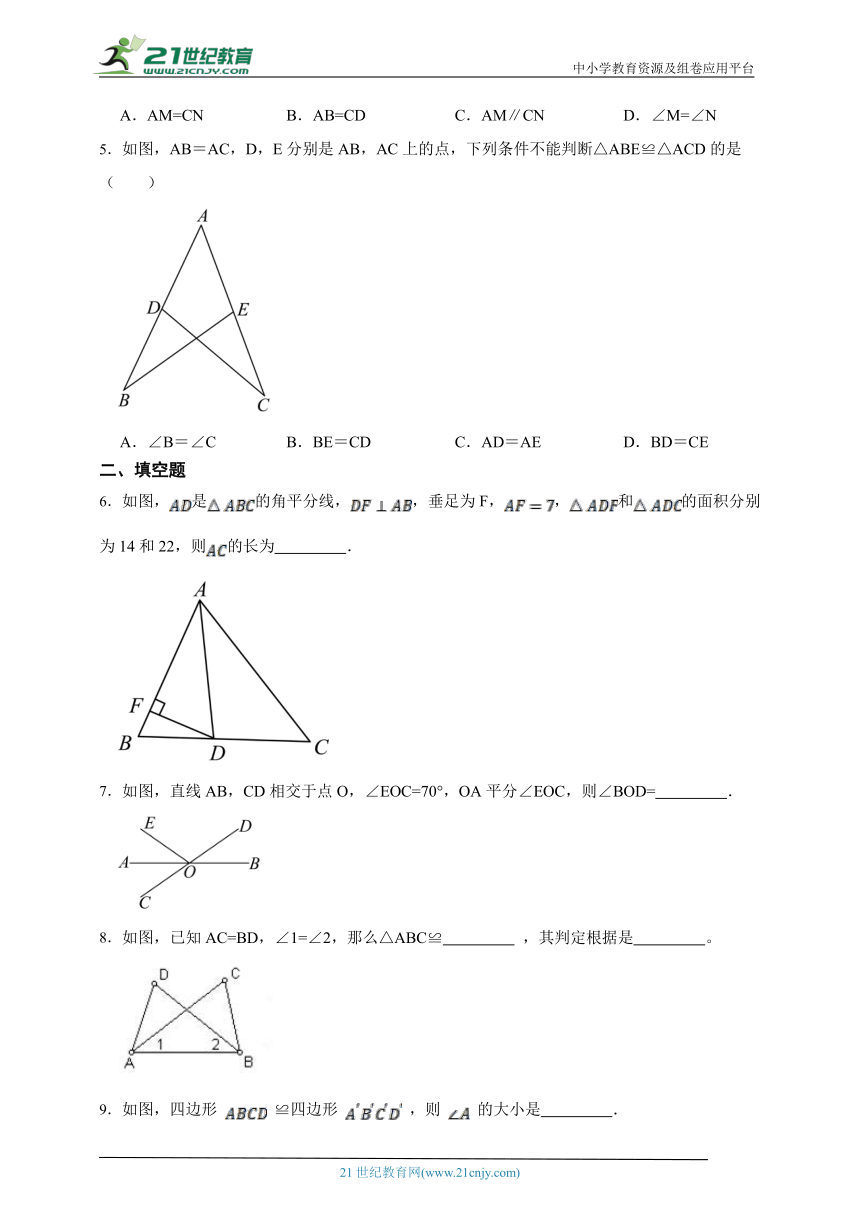
5.如图,AB=AC,D,E分别是AB,AC上的点,下列条件不能判断△ABE≌△ACD的是( )
A.∠B=∠C B.BE=CD C.AD=AE D.BD=CE
二、填空题
6.如图,是的角平分线,,垂足为F,,和的面积分别为14和22,则的长为 .
7.如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC,则∠BOD= .
8.如图,已知AC=BD,∠1=∠2,那么△ABC≌ ,其判定根据是 。
9.如图,四边形 ≌四边形 ,则 的大小是 .
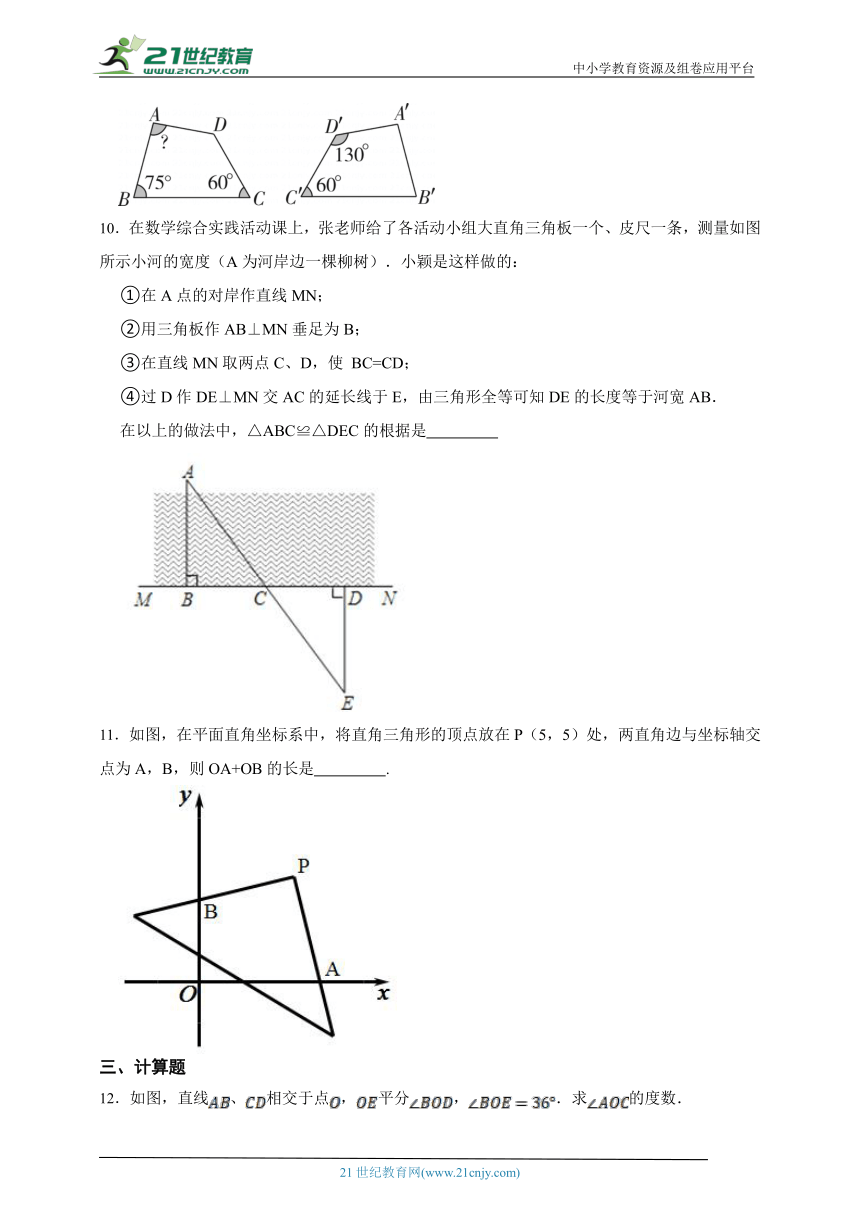
10.在数学综合实践活动课上,张老师给了各活动小组大直角三角板一个、皮尺一条,测量如图所示小河的宽度(A为河岸边一棵柳树).小颖是这样做的:
①在A点的对岸作直线MN;
②用三角板作AB⊥MN垂足为B;
③在直线MN取两点C、D,使 BC=CD;
④过D作DE⊥MN交AC的延长线于E,由三角形全等可知DE的长度等于河宽AB.
在以上的做法中,△ABC≌△DEC的根据是
11.如图,在平面直角坐标系中,将直角三角形的顶点放在P(5,5)处,两直角边与坐标轴交点为A,B,则OA+OB的长是 .
三、计算题
12.如图,直线、相交于点,平分,.求的度数.
13.如图,中,于点,平分,若,.
(1)求的度数;
(2)若点为线段上的任意一点,当为直角三角形时,求的度数.
四、解答题
14.如图,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.写出图中全等的三角形并证明。
15.如图,点B、E、C、F在同一直线上,BE=CF,AB=DE,AC=DF.
求证:AB∥DE.
16.如图所示,在中,于D,于E,与交于点F,且.
(1)求证:;
(2)已知,求的长.
五、综合题
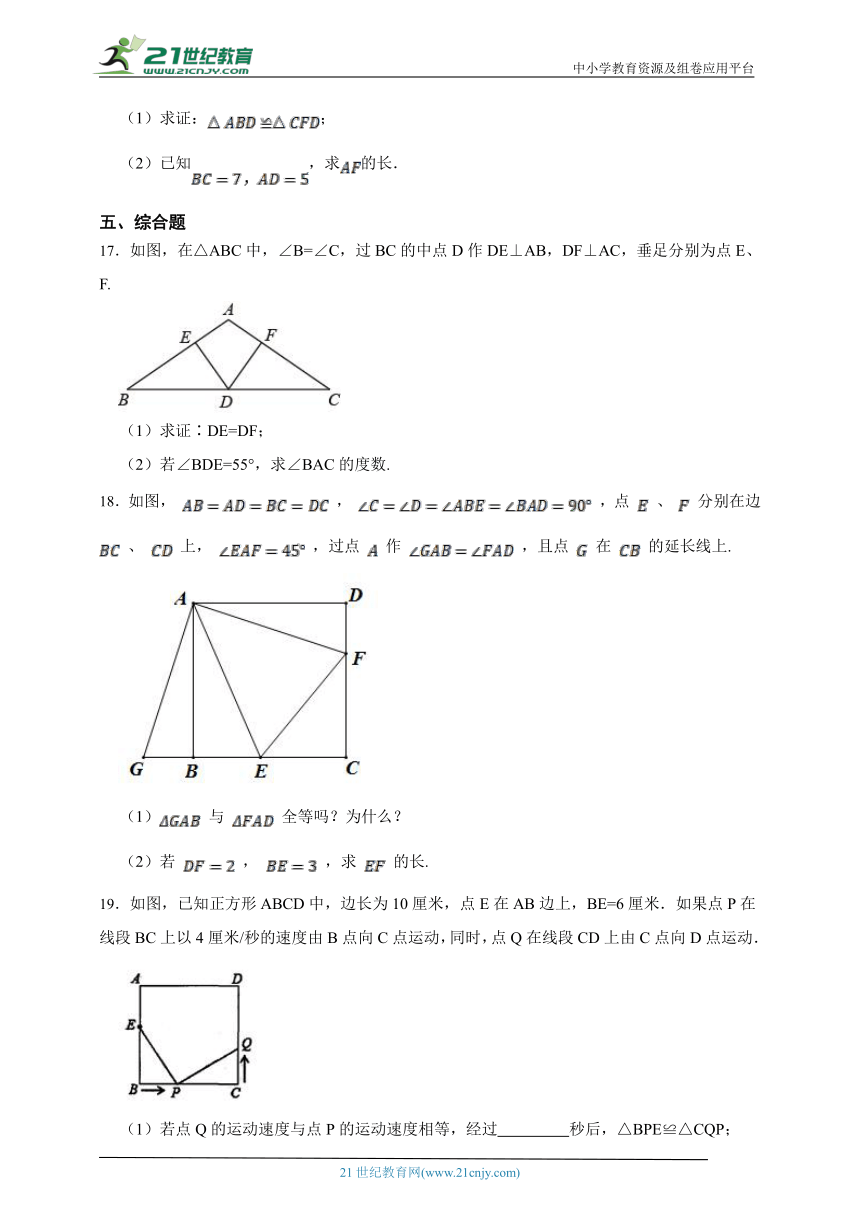
17.如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证∶DE=DF;
(2)若∠BDE=55°,求∠BAC的度数.
18.如图, , ,点 、 分别在边 、 上, ,过点 作 ,且点 在 的延长线上.
(1) 与 全等吗?为什么?
(2)若 , ,求 的长.
19.如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过 秒后,△BPE≌△CQP;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
六、实践探究题
20.如图
(1)【探索发现】在一次数学学习活动中,刘华遇到了下面的这个问题:
如图①,在△ABC中,BP平分∠ABC,CP平分∠ACB,请你判断∠A和∠P间的数量关系并说明理由.
刘华对这个问题进行了判断并给出了证明过程,下面是部分证明过程,请你补全余下的证明过程.
解:结论:∠P=_ .
理由:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB.
∴∠P=180°-∠PBC-∠PCB.
=180°-(∠ABC+∠ACB)
=180°-(180°-∠A)
=_
(2)【模型发展】如图②,点P是△ABC的外角平分线BP与CP的交点,请你判断∠A和∠P间的数量关系并说明理由.
(3)【解决问题】如图③,在△ABC中,BP平分∠ABC,CP平分∠ACB,点Q是△PBC的外角平分线BQ与CQ的交点.若∠A=68°,则∠Q=_ 度.
答案解析部分
1.【答案】D
【知识点】三角形全等的判定
2.【答案】C
【知识点】三角形全等的判定-ASA
3.【答案】C
【知识点】角的运算;角平分线的性质
4.【答案】A
【知识点】三角形全等的判定
5.【答案】B
【知识点】三角形全等及其性质
6.【答案】11
【知识点】三角形的角平分线、中线和高;角平分线的性质
7.【答案】35°
【知识点】角平分线的性质;对顶角及其性质
8.【答案】△BAD;SAS
【知识点】三角形全等的判定
9.【答案】
【知识点】全等图形的概念
10.【答案】ASA
【知识点】全等三角形的应用
11.【答案】10
【知识点】三角形全等及其性质;三角形全等的判定
12.【答案】
【知识点】角平分线的性质;对顶角及其性质
13.【答案】(1)
(2)的度数为或
【知识点】角的运算;三角形内角和定理;三角形的外角性质;角平分线的性质
14.【答案】证明:结论:△BAC≌△DAE.
理由:∵∠1=∠2,
∴∠1+∠DAC=∠DAC+∠2,
即∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(ASA)
【知识点】三角形全等的判定
15.【答案】证明:∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠B=∠DEF,
∴AB∥DE.
【知识点】全等三角形的判定与性质
16.【答案】(1)证明:∵,,
∴,
∴,
∴,
在和中
∴,
(2)解:∵,
∴,
∵,
∴,
∴;
【知识点】三角形全等及其性质;三角形全等的判定-AAS
17.【答案】(1)证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵D是BC的中点,
∴BD=CD,
在△BED与△CFD中
∴ ,
∴DE=DF
(2)解:∵
∴∠C=∠B= ,
∴∠BAC=
【知识点】三角形内角和定理;三角形全等的判定-AAS
18.【答案】(1)解:∵ ,点 在 的延长线上,
∴∠ABG=∠D=90°,
在△GAB和△FAD中,
∵ ,AB=AD,∠ABG=∠D,
∴△GAB≌△FAD(ASA);
(2)解:∵△GAB≌△FAD,
∴AG=AF,GB=DF,
∵ , ,
∴∠BAE+∠DAF=45°,
∴∠BAE+∠GAB=45°,即∠GAE=45°,
∴∠GAE=∠EAF,
在△GAE和△FAE中,
∵AG=AF,∠GAE=∠EAF,AE=AE,
∴△GAE≌△FAE(SAS),
∴GE=EF,
∵GE=GB+BE=DF+BE=2+3=5,
∴EF=5.
【知识点】三角形全等的判定-SAS;三角形全等的判定-ASA
19.【答案】(1)1
(2)解:∵点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△OQP全等,只要BP=PC=5厘米,CQ=BE=6厘米即可,
∴点P,Q运动的时间t= 秒,
∴点Q的运动速度为: 厘米/秒,
即当点Q的运动速度为 厘米/秒时,能够使△BPE与△CQP全等.
【知识点】三角形全等及其性质;三角形全等的判定;一元一次方程的实际应用-行程问题
20.【答案】(1)90°+∠A;90°+∠A;
(2)解:∠P=90°-∠A
(3)28
【知识点】三角形内角和定理;角平分线的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【人教版数学八年级上册同步练习】
第12章全等三角形综合检测题
一、单选题
1.如图,下列条件中,不能证明 的是( )
A. , B. ,
C. , D. ,
2.小明同学有一块玻璃的三角板,不小心掉到地上碎成了三块,现要去文具店买一块同样的三角板,最省事的是( )
A.带②去 B.带①去 C.带③去 D.三块都带去
3.如图,是的平分线,若是直角,,则的度数是( )
A. B. C. D.
4.如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )
A.AM=CN B.AB=CD C.AM∥CN D.∠M=∠N
5.如图,AB=AC,D,E分别是AB,AC上的点,下列条件不能判断△ABE≌△ACD的是( )
A.∠B=∠C B.BE=CD C.AD=AE D.BD=CE
二、填空题
6.如图,是的角平分线,,垂足为F,,和的面积分别为14和22,则的长为 .
7.如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC,则∠BOD= .
8.如图,已知AC=BD,∠1=∠2,那么△ABC≌ ,其判定根据是 。
9.如图,四边形 ≌四边形 ,则 的大小是 .
10.在数学综合实践活动课上,张老师给了各活动小组大直角三角板一个、皮尺一条,测量如图所示小河的宽度(A为河岸边一棵柳树).小颖是这样做的:
①在A点的对岸作直线MN;
②用三角板作AB⊥MN垂足为B;
③在直线MN取两点C、D,使 BC=CD;
④过D作DE⊥MN交AC的延长线于E,由三角形全等可知DE的长度等于河宽AB.
在以上的做法中,△ABC≌△DEC的根据是
11.如图,在平面直角坐标系中,将直角三角形的顶点放在P(5,5)处,两直角边与坐标轴交点为A,B,则OA+OB的长是 .
三、计算题
12.如图,直线、相交于点,平分,.求的度数.
13.如图,中,于点,平分,若,.
(1)求的度数;
(2)若点为线段上的任意一点,当为直角三角形时,求的度数.
四、解答题
14.如图,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.写出图中全等的三角形并证明。
15.如图,点B、E、C、F在同一直线上,BE=CF,AB=DE,AC=DF.
求证:AB∥DE.
16.如图所示,在中,于D,于E,与交于点F,且.
(1)求证:;
(2)已知,求的长.
五、综合题
17.如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证∶DE=DF;
(2)若∠BDE=55°,求∠BAC的度数.
18.如图, , ,点 、 分别在边 、 上, ,过点 作 ,且点 在 的延长线上.
(1) 与 全等吗?为什么?
(2)若 , ,求 的长.
19.如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过 秒后,△BPE≌△CQP;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
六、实践探究题
20.如图
(1)【探索发现】在一次数学学习活动中,刘华遇到了下面的这个问题:
如图①,在△ABC中,BP平分∠ABC,CP平分∠ACB,请你判断∠A和∠P间的数量关系并说明理由.
刘华对这个问题进行了判断并给出了证明过程,下面是部分证明过程,请你补全余下的证明过程.
解:结论:∠P=_ .
理由:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB.
∴∠P=180°-∠PBC-∠PCB.
=180°-(∠ABC+∠ACB)
=180°-(180°-∠A)
=_
(2)【模型发展】如图②,点P是△ABC的外角平分线BP与CP的交点,请你判断∠A和∠P间的数量关系并说明理由.
(3)【解决问题】如图③,在△ABC中,BP平分∠ABC,CP平分∠ACB,点Q是△PBC的外角平分线BQ与CQ的交点.若∠A=68°,则∠Q=_ 度.
答案解析部分
1.【答案】D
【知识点】三角形全等的判定
2.【答案】C
【知识点】三角形全等的判定-ASA
3.【答案】C
【知识点】角的运算;角平分线的性质
4.【答案】A
【知识点】三角形全等的判定
5.【答案】B
【知识点】三角形全等及其性质
6.【答案】11
【知识点】三角形的角平分线、中线和高;角平分线的性质
7.【答案】35°
【知识点】角平分线的性质;对顶角及其性质
8.【答案】△BAD;SAS
【知识点】三角形全等的判定
9.【答案】
【知识点】全等图形的概念
10.【答案】ASA
【知识点】全等三角形的应用
11.【答案】10
【知识点】三角形全等及其性质;三角形全等的判定
12.【答案】
【知识点】角平分线的性质;对顶角及其性质
13.【答案】(1)
(2)的度数为或
【知识点】角的运算;三角形内角和定理;三角形的外角性质;角平分线的性质
14.【答案】证明:结论:△BAC≌△DAE.
理由:∵∠1=∠2,
∴∠1+∠DAC=∠DAC+∠2,
即∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(ASA)
【知识点】三角形全等的判定
15.【答案】证明:∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠B=∠DEF,
∴AB∥DE.
【知识点】全等三角形的判定与性质
16.【答案】(1)证明:∵,,
∴,
∴,
∴,
在和中
∴,
(2)解:∵,
∴,
∵,
∴,
∴;
【知识点】三角形全等及其性质;三角形全等的判定-AAS
17.【答案】(1)证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵D是BC的中点,
∴BD=CD,
在△BED与△CFD中
∴ ,
∴DE=DF
(2)解:∵
∴∠C=∠B= ,
∴∠BAC=
【知识点】三角形内角和定理;三角形全等的判定-AAS
18.【答案】(1)解:∵ ,点 在 的延长线上,
∴∠ABG=∠D=90°,
在△GAB和△FAD中,
∵ ,AB=AD,∠ABG=∠D,
∴△GAB≌△FAD(ASA);
(2)解:∵△GAB≌△FAD,
∴AG=AF,GB=DF,
∵ , ,
∴∠BAE+∠DAF=45°,
∴∠BAE+∠GAB=45°,即∠GAE=45°,
∴∠GAE=∠EAF,
在△GAE和△FAE中,
∵AG=AF,∠GAE=∠EAF,AE=AE,
∴△GAE≌△FAE(SAS),
∴GE=EF,
∵GE=GB+BE=DF+BE=2+3=5,
∴EF=5.
【知识点】三角形全等的判定-SAS;三角形全等的判定-ASA
19.【答案】(1)1
(2)解:∵点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△OQP全等,只要BP=PC=5厘米,CQ=BE=6厘米即可,
∴点P,Q运动的时间t= 秒,
∴点Q的运动速度为: 厘米/秒,
即当点Q的运动速度为 厘米/秒时,能够使△BPE与△CQP全等.
【知识点】三角形全等及其性质;三角形全等的判定;一元一次方程的实际应用-行程问题
20.【答案】(1)90°+∠A;90°+∠A;
(2)解:∠P=90°-∠A
(3)28
【知识点】三角形内角和定理;角平分线的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
