【人教版数学八年级上册同步练习】 第13章轴对称综合检测题(含解析)
文档属性
| 名称 | 【人教版数学八年级上册同步练习】 第13章轴对称综合检测题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 14:07:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【人教版数学八年级上册同步练习】
第13章轴对称综合检测题
一、单选题
1.如图,在△ABC中,AB=AC,AD∥BC,若∠BAD=110°,则∠BCA的大小为( )
A.30° B.40° C.50° D.70°
2.点 关于y轴对称的点的坐标为( )
A. B. C. D.
3.下列图形中,是中心对称图形但不是轴对称图形的是( )
A. B.
C. D.
4.如图,△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD,连接DE.下面给出的四个结论,其中正确的个数是( )
① BD⊥AC; ②BD平分∠ABC; ③BD=DE; ④∠BDE=120°
A.1个 B.2个 C.3个 D.4个
5.如图,在矩形中,,对角线与相交于点O,,垂足为E,,则的长为( ).
A. B. C. D.
二、判断题
6.长方形、正方形、平行四边形和圆都是轴对称图形。( )
7.梯形、长方形和圆都是轴对称图形.
8.长方形、正方形、平行四边形和圆都是轴对称图形.
9.判断题,填写“正确”或“错误”:角的平分线是角的对称轴.
三、填空题
10.如图,用圆规以直角顶点O为圆心,以适当半径画一条弧交两直角边于A,B两点,若再以A点为圆心,以OA为半径画弧,与弧AB交于点C,则∠BOC等于 .
11.已知点O为△ABC三边垂直平分线的交点,点O到顶点A的距离为6cm,则OA+OB+OC= .
12.如图,中,,将逆时针旋转得到,交于F.当时,点D恰好落在上,此时等于 .
13.如图,四边形ABCD,∠B=∠C=90°,边BC上一点E,连结AE、DE得等边△ADE,若=,则=
14.关于y轴对称的点的坐标是 .
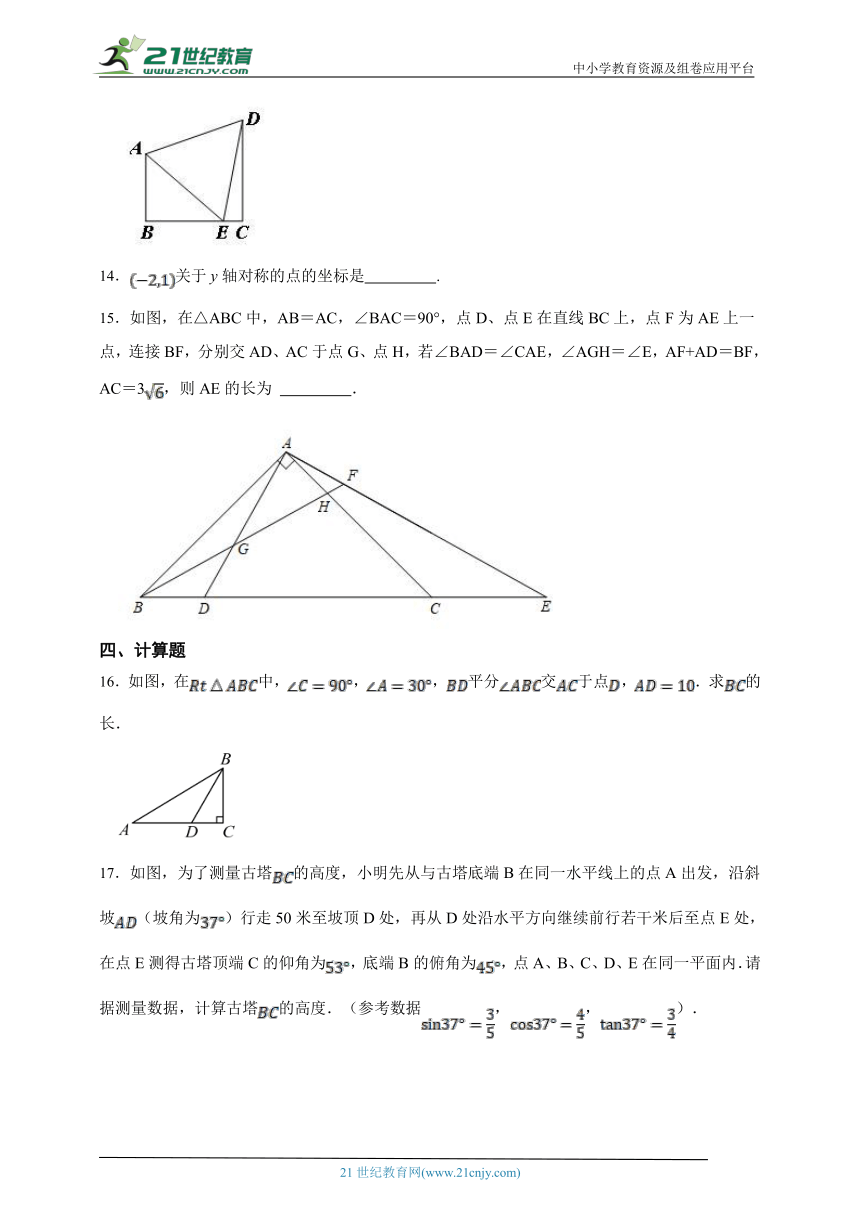
15.如图,在△ABC中,AB=AC,∠BAC=90°,点D、点E在直线BC上,点F为AE上一点,连接BF,分别交AD、AC于点G、点H,若∠BAD=∠CAE,∠AGH=∠E,AF+AD=BF,AC=3,则AE的长为 .
四、计算题
16.如图,在中,,,平分交于点,.求的长.
17.如图,为了测量古塔的高度,小明先从与古塔底端B在同一水平线上的点A出发,沿斜坡(坡角为)行走50米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在点E测得古塔顶端C的仰角为,底端B的俯角为,点A、B、C、D、E在同一平面内.请据测量数据,计算古塔的高度.(参考数据,,).
18.如图1,在平面直角坐标系中,抛物线过点,和,作直线,点为抛物线上一动点,过点P作轴交直线于点M,交x轴于点N.
(1)直接写出抛物线和直线的解析式;
(2)如图2,连接,当为等腰三角形时,求m的值;
(3)当点在运动的过程中,在轴上是否存在点,使得以点,,为顶点的三角形与以点,,为顶点的三角形相似(其中点与点相对应),若存在,直接写出点的坐标;若不存在,请说明理由.
五、解答题
19.如图,一艘船在海岛望灯塔在北偏西方向上,上午8时此船从海岛出发,以30海里/时的速度向正北航行,上午10时到达海岛,此时望灯塔在北偏西方向上.
(1)求从海岛到灯塔的距离;
(2)如果船到达海岛后,不停留,继续沿正北方向航行,请问船什么时候距离灯塔最近?
20.如图,的半径为5,是外一点,,,求的长.
21.如图,抛物线与x轴交于点和点B,与y轴交于点,顶点为D,连接,P是第一象限内抛物线上的动点,连接,设点P的横坐标为t.
(1)求抛物线的解析式;
(2)当t为何值时,的面积最大?并求出最大面积;
(3)M为直线上一点,求的最小值;
(4)过P点作轴,交于E点.是否存在点P,使得为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
六、综合题
22.如图,PA、PB是⊙O的切线,A、B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
(1)求证:∠APO=∠CPO;
(2)若⊙O的半径为3,OP=6,∠C=30°,求PC的长.
23.定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到这边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连接AD,若AD2=BD CD,则称点D是△ABC中BC边上的“好点”.
(1)如图2,的顶点是网格图的格点,请仅用直尺画出、(或在图中直接描出)AB边上的所有“好点”点D;
(2)中,,,,点D是BC边上的“好点”,求线段BD的长;
(3)如图3,是⊙O的内接三角形,点H在AB上,连结CH并延长交⊙O于点D.若点H是中CD边上的“好点”.
①求证:;
②若,⊙O的半径为r,且,求的值.
24.如图,在平面直角坐标系xOy中,已知点A(0,4),点B是x轴正半轴上一点,连接AB,过点A作AC⊥AB,交x轴于点C, 点D是点C关于点A的对称点,连接BD,以AD为直径作⊙Q交BD于点E,连接并延长AE交x轴于点F,连接DF。
(1) 求线段AE的长;
(2)若AB-BO=2,求tan∠AFC的值;
(3)若△DEF与△AEB相似,求EF的值。
七、实践探究题
25.爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(1)【特例探究】
如图1,当tan∠PAB=1,c=4 时,a= ,b= ;
如图2,当∠PAB=30°,c=2时,a= ,b= ;
(2)【归纳证明】
请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)【拓展证明】
如图4, ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ,AB=3,求AF的长.
答案解析部分
1.【答案】D
【知识点】等腰三角形的性质
2.【答案】A
【知识点】关于坐标轴对称的点的坐标特征
3.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】D
【知识点】三角形的外角性质;等腰三角形的性质;等边三角形的性质
5.【答案】A
【知识点】线段垂直平分线的性质;勾股定理;矩形的性质
6.【答案】错误
【知识点】轴对称图形
7.【答案】错误
【知识点】轴对称图形
8.【答案】
【知识点】轴对称图形
9.【答案】错误
【知识点】轴对称图形;角平分线的概念
10.【答案】30°
【知识点】等边三角形的判定与性质
11.【答案】18cm
【知识点】线段垂直平分线的性质
12.【答案】
【知识点】三角形内角和定理;三角形的外角性质;等腰三角形的性质;旋转的性质
13.【答案】
【知识点】等边三角形的性质;相似三角形的判定与性质;三角形全等的判定-AAS
14.【答案】
【知识点】关于坐标轴对称的点的坐标特征
15.【答案】
【知识点】三角形全等的判定;等腰三角形的性质;含30°角的直角三角形;勾股定理;等腰直角三角形
16.【答案】
【知识点】等腰三角形的判定与性质;含30°角的直角三角形;勾股定理
17.【答案】70米
【知识点】等腰三角形的判定与性质;矩形的判定与性质;解直角三角形的实际应用﹣仰角俯角问题
18.【答案】(1)
(2)或或
(3),或,
或,或,
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式;等腰三角形的判定与性质;相似三角形的判定与性质
19.【答案】(1)60海里
(2)11时
【知识点】含30°角的直角三角形;方位角
20.【答案】解:过点O作OE⊥PC,垂足为E,
∴CE=DE,
∵∠P=30°,PO=8,半径为5,
∴OE=4,OA=OD=5,PA=3,
∴PE==,DE==3,
∴CD=2DE=6,PD=PE-DE=.
【知识点】含30°角的直角三角形;勾股定理
21.【答案】(1)解:由题意得:,解得:,
∴抛物线的解析式为:;
(2)当时,得或,
∴,
设直线的解析式为,
则,
解得
∴直线的解析式为.
如图,过点P作轴,交x轴于点F,交于点G.
设点,.
∴.
∴,
∴当时,的面积最大,最大面积为32;
(3)作O关于直线的对称点为,连接,如图,
∵,,
∴四边形为正方形,则,
则,
当A、M、三点共线时,最小,即为线段的长,
∴最小值为.
(4)∵,
∴,
∵,
∴,
∵
∴,
∴,
,
,
当时,,解得或,
∴;
当时,则,
∴,
解得(舍去)或,
∴;
当时,则,
∴,
解得或(舍去),
∴,
综上,P点的坐标为,,.
【知识点】等腰三角形的判定与性质;轴对称的应用-最短距离问题;二次函数-动态几何问题
22.【答案】(1)证明:∵PA、PB是⊙O的切线,
∴∠APO=∠CPO;
(2)解:∵PA是⊙O的切线,
∴∠PAC=90°,
∴AP= ,
在Rt△CAP中,∠C=30°,
∴PC=2AP=6 .
【知识点】含30°角的直角三角形;勾股定理;切线的性质;切线长定理
23.【答案】(1)解:如图,当CD⊥AB或点D是AB的中点时,CD2=AD BD;
(2)解:如图:
过A作AH⊥BC于H,
∵tanB=,tanC=1,
∴,,
设AH=3k,则BH=4k,CH=3k,
∵BC=7,
∴3k+4k=7,解得k=1,
∴BH=4,AH=CH=3,
设BD=x,则CD=7-x,DH=4-x,
Rt△ADH中,AD2=AH2+DH2=32+(4-x)2,
而点D是BC边上的“好点”,有AD2=BD CD=x (7-x),
∴32+(4-x)2=x (7-x),
解得x=5或x=,
∴BD=5或BD=;
(3)解:①∵∠CAH=∠HDB,∠AHC=∠BHD,
∴△ACH∽△DBH,
∴,
∴AH BH=CH DH,
∵点H是△BCD中CD边上的“好点”,
∴BH2=CH DH,
∴AH=BH,
∴OH⊥AB;
②如图:连接AD,
∵OH⊥AB,OH∥BD,
∴AB⊥BD,
∴AD是直径,
∵r=3OH,
设OH=m,则OA=3m,BD=2m,
Rt△AOH中,AH=,
∴BH=2m,
Rt△BHD中,HD=,
∵点H是△BCD中CD边上的“好点”,
∴BH2=CH DH,
∴CH=,
∴.
【知识点】等腰三角形的性质;相似三角形的判定与性质;锐角三角函数的定义;定义新运算;直角三角形斜边上的中线
24.【答案】(1)解:∵AD是⊙Q的直径,
∴∠AEB=∠AED=90°,
∴∠AEB=∠AOB=90°,
∵BA垂直平分CD,
∴BC=BD
∴∠ABO=∠ABE
∵BA=BA,
∴△ABE≌△ABO(A AS)
∴AE=AO=4;
(2)解:设BO=x,则AB=x+2,
在Rt△ABO中,由AO2+OB =AB 得4 +x =(x+2) ,解得:x=3,
∴OB=BE=3,AB=5,
∵∠EAB+∠ABE=90°,∠ACB+∠ABC=90°
∴∠EAB=∠ACB
∵∠BFA=∠AFC
∴△BFA∽△AFC
∴BF:AF=BE:AO=3:4,
设EF=x,则AF=4+x,BF= (4+x)
∵在Rt△BEF中,BE +EF =BF2
∴32+x =[ (4+x)]2
解得,x= ,即EF=
tan∠AFC=
(3)解:①如图1,
当△DEF∽△AEB时,有
∠BAE=∠FDE
∴∠ADE=∠FDE
∴BD垂直平分AF
∴EF=AE=4-
②如图2,
设⊙Q交y轴于点G,连接DG,作FH⊥DG于H,
当△DEF∽△BEA时,有∠ABE=∠FDE
∴∠DAE=∠DAG=∠FDE=∠FDH
∴AG=AE=4,EF=FH=OG=8
综上所述,EF=4或8
【知识点】全等三角形的判定与性质;线段垂直平分线的性质;勾股定理;圆周角定理;相似三角形的判定与性质
25.【答案】(1)4 ;4 ;;
(2)解:结论a2+b2=5c2.
证明:如图3中,连接MN.
∵AM、BN是中线,
∴MN∥AB,MN= AB,
∴△MPN∽△APB,
∴ = = ,
设MP=x,NP=y,则AP=2x,BP=2y,
∴a2=BC2=4BM2=4(MP2+BP2)=4x2+16y2,
b2=AC2=4AN2=4(PN2+AP2)=4y2+16x2,
c2=AB2=AP2+BP2=4x2+4y2,
∴a2+b2=20x2+20y2=5(4x2+4y2)=5c2
(3)解:解:如图4中,在△AGE和△FGB中,
,
∴△AGE≌△FGB,
∴BG=FG,取AB中点H,连接FH并且延长交DA的延长线于P点,
同理可证△APH≌△BFH,
∴AP=BF,PE=CF=2BF,
即PE∥CF,PE=CF,
∴四边形CEPF是平行四边形,
∴FP∥CE,
∵BE⊥CE,
∴FP⊥BE,即FH⊥BG,
∴△ABF是中垂三角形,
由(2)可知AB2+AF2=5BF2,
∵AB=3,BF= AD= ,
∴9+AF2=5×( )2,
∴AF=4.
【知识点】等腰三角形的判定与性质;平行四边形的判定与性质;相似三角形的判定与性质;求特殊角的三角函数值;三角形的中位线定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【人教版数学八年级上册同步练习】
第13章轴对称综合检测题
一、单选题
1.如图,在△ABC中,AB=AC,AD∥BC,若∠BAD=110°,则∠BCA的大小为( )
A.30° B.40° C.50° D.70°
2.点 关于y轴对称的点的坐标为( )
A. B. C. D.
3.下列图形中,是中心对称图形但不是轴对称图形的是( )
A. B.
C. D.
4.如图,△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD,连接DE.下面给出的四个结论,其中正确的个数是( )
① BD⊥AC; ②BD平分∠ABC; ③BD=DE; ④∠BDE=120°
A.1个 B.2个 C.3个 D.4个
5.如图,在矩形中,,对角线与相交于点O,,垂足为E,,则的长为( ).
A. B. C. D.
二、判断题
6.长方形、正方形、平行四边形和圆都是轴对称图形。( )
7.梯形、长方形和圆都是轴对称图形.
8.长方形、正方形、平行四边形和圆都是轴对称图形.
9.判断题,填写“正确”或“错误”:角的平分线是角的对称轴.
三、填空题
10.如图,用圆规以直角顶点O为圆心,以适当半径画一条弧交两直角边于A,B两点,若再以A点为圆心,以OA为半径画弧,与弧AB交于点C,则∠BOC等于 .
11.已知点O为△ABC三边垂直平分线的交点,点O到顶点A的距离为6cm,则OA+OB+OC= .
12.如图,中,,将逆时针旋转得到,交于F.当时,点D恰好落在上,此时等于 .
13.如图,四边形ABCD,∠B=∠C=90°,边BC上一点E,连结AE、DE得等边△ADE,若=,则=
14.关于y轴对称的点的坐标是 .
15.如图,在△ABC中,AB=AC,∠BAC=90°,点D、点E在直线BC上,点F为AE上一点,连接BF,分别交AD、AC于点G、点H,若∠BAD=∠CAE,∠AGH=∠E,AF+AD=BF,AC=3,则AE的长为 .
四、计算题
16.如图,在中,,,平分交于点,.求的长.
17.如图,为了测量古塔的高度,小明先从与古塔底端B在同一水平线上的点A出发,沿斜坡(坡角为)行走50米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在点E测得古塔顶端C的仰角为,底端B的俯角为,点A、B、C、D、E在同一平面内.请据测量数据,计算古塔的高度.(参考数据,,).
18.如图1,在平面直角坐标系中,抛物线过点,和,作直线,点为抛物线上一动点,过点P作轴交直线于点M,交x轴于点N.
(1)直接写出抛物线和直线的解析式;
(2)如图2,连接,当为等腰三角形时,求m的值;
(3)当点在运动的过程中,在轴上是否存在点,使得以点,,为顶点的三角形与以点,,为顶点的三角形相似(其中点与点相对应),若存在,直接写出点的坐标;若不存在,请说明理由.
五、解答题
19.如图,一艘船在海岛望灯塔在北偏西方向上,上午8时此船从海岛出发,以30海里/时的速度向正北航行,上午10时到达海岛,此时望灯塔在北偏西方向上.
(1)求从海岛到灯塔的距离;
(2)如果船到达海岛后,不停留,继续沿正北方向航行,请问船什么时候距离灯塔最近?
20.如图,的半径为5,是外一点,,,求的长.
21.如图,抛物线与x轴交于点和点B,与y轴交于点,顶点为D,连接,P是第一象限内抛物线上的动点,连接,设点P的横坐标为t.
(1)求抛物线的解析式;
(2)当t为何值时,的面积最大?并求出最大面积;
(3)M为直线上一点,求的最小值;
(4)过P点作轴,交于E点.是否存在点P,使得为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
六、综合题
22.如图,PA、PB是⊙O的切线,A、B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
(1)求证:∠APO=∠CPO;
(2)若⊙O的半径为3,OP=6,∠C=30°,求PC的长.
23.定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到这边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连接AD,若AD2=BD CD,则称点D是△ABC中BC边上的“好点”.
(1)如图2,的顶点是网格图的格点,请仅用直尺画出、(或在图中直接描出)AB边上的所有“好点”点D;
(2)中,,,,点D是BC边上的“好点”,求线段BD的长;
(3)如图3,是⊙O的内接三角形,点H在AB上,连结CH并延长交⊙O于点D.若点H是中CD边上的“好点”.
①求证:;
②若,⊙O的半径为r,且,求的值.
24.如图,在平面直角坐标系xOy中,已知点A(0,4),点B是x轴正半轴上一点,连接AB,过点A作AC⊥AB,交x轴于点C, 点D是点C关于点A的对称点,连接BD,以AD为直径作⊙Q交BD于点E,连接并延长AE交x轴于点F,连接DF。
(1) 求线段AE的长;
(2)若AB-BO=2,求tan∠AFC的值;
(3)若△DEF与△AEB相似,求EF的值。
七、实践探究题
25.爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(1)【特例探究】
如图1,当tan∠PAB=1,c=4 时,a= ,b= ;
如图2,当∠PAB=30°,c=2时,a= ,b= ;
(2)【归纳证明】
请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)【拓展证明】
如图4, ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ,AB=3,求AF的长.
答案解析部分
1.【答案】D
【知识点】等腰三角形的性质
2.【答案】A
【知识点】关于坐标轴对称的点的坐标特征
3.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】D
【知识点】三角形的外角性质;等腰三角形的性质;等边三角形的性质
5.【答案】A
【知识点】线段垂直平分线的性质;勾股定理;矩形的性质
6.【答案】错误
【知识点】轴对称图形
7.【答案】错误
【知识点】轴对称图形
8.【答案】
【知识点】轴对称图形
9.【答案】错误
【知识点】轴对称图形;角平分线的概念
10.【答案】30°
【知识点】等边三角形的判定与性质
11.【答案】18cm
【知识点】线段垂直平分线的性质
12.【答案】
【知识点】三角形内角和定理;三角形的外角性质;等腰三角形的性质;旋转的性质
13.【答案】
【知识点】等边三角形的性质;相似三角形的判定与性质;三角形全等的判定-AAS
14.【答案】
【知识点】关于坐标轴对称的点的坐标特征
15.【答案】
【知识点】三角形全等的判定;等腰三角形的性质;含30°角的直角三角形;勾股定理;等腰直角三角形
16.【答案】
【知识点】等腰三角形的判定与性质;含30°角的直角三角形;勾股定理
17.【答案】70米
【知识点】等腰三角形的判定与性质;矩形的判定与性质;解直角三角形的实际应用﹣仰角俯角问题
18.【答案】(1)
(2)或或
(3),或,
或,或,
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式;等腰三角形的判定与性质;相似三角形的判定与性质
19.【答案】(1)60海里
(2)11时
【知识点】含30°角的直角三角形;方位角
20.【答案】解:过点O作OE⊥PC,垂足为E,
∴CE=DE,
∵∠P=30°,PO=8,半径为5,
∴OE=4,OA=OD=5,PA=3,
∴PE==,DE==3,
∴CD=2DE=6,PD=PE-DE=.
【知识点】含30°角的直角三角形;勾股定理
21.【答案】(1)解:由题意得:,解得:,
∴抛物线的解析式为:;
(2)当时,得或,
∴,
设直线的解析式为,
则,
解得
∴直线的解析式为.
如图,过点P作轴,交x轴于点F,交于点G.
设点,.
∴.
∴,
∴当时,的面积最大,最大面积为32;
(3)作O关于直线的对称点为,连接,如图,
∵,,
∴四边形为正方形,则,
则,
当A、M、三点共线时,最小,即为线段的长,
∴最小值为.
(4)∵,
∴,
∵,
∴,
∵
∴,
∴,
,
,
当时,,解得或,
∴;
当时,则,
∴,
解得(舍去)或,
∴;
当时,则,
∴,
解得或(舍去),
∴,
综上,P点的坐标为,,.
【知识点】等腰三角形的判定与性质;轴对称的应用-最短距离问题;二次函数-动态几何问题
22.【答案】(1)证明:∵PA、PB是⊙O的切线,
∴∠APO=∠CPO;
(2)解:∵PA是⊙O的切线,
∴∠PAC=90°,
∴AP= ,
在Rt△CAP中,∠C=30°,
∴PC=2AP=6 .
【知识点】含30°角的直角三角形;勾股定理;切线的性质;切线长定理
23.【答案】(1)解:如图,当CD⊥AB或点D是AB的中点时,CD2=AD BD;
(2)解:如图:
过A作AH⊥BC于H,
∵tanB=,tanC=1,
∴,,
设AH=3k,则BH=4k,CH=3k,
∵BC=7,
∴3k+4k=7,解得k=1,
∴BH=4,AH=CH=3,
设BD=x,则CD=7-x,DH=4-x,
Rt△ADH中,AD2=AH2+DH2=32+(4-x)2,
而点D是BC边上的“好点”,有AD2=BD CD=x (7-x),
∴32+(4-x)2=x (7-x),
解得x=5或x=,
∴BD=5或BD=;
(3)解:①∵∠CAH=∠HDB,∠AHC=∠BHD,
∴△ACH∽△DBH,
∴,
∴AH BH=CH DH,
∵点H是△BCD中CD边上的“好点”,
∴BH2=CH DH,
∴AH=BH,
∴OH⊥AB;
②如图:连接AD,
∵OH⊥AB,OH∥BD,
∴AB⊥BD,
∴AD是直径,
∵r=3OH,
设OH=m,则OA=3m,BD=2m,
Rt△AOH中,AH=,
∴BH=2m,
Rt△BHD中,HD=,
∵点H是△BCD中CD边上的“好点”,
∴BH2=CH DH,
∴CH=,
∴.
【知识点】等腰三角形的性质;相似三角形的判定与性质;锐角三角函数的定义;定义新运算;直角三角形斜边上的中线
24.【答案】(1)解:∵AD是⊙Q的直径,
∴∠AEB=∠AED=90°,
∴∠AEB=∠AOB=90°,
∵BA垂直平分CD,
∴BC=BD
∴∠ABO=∠ABE
∵BA=BA,
∴△ABE≌△ABO(A AS)
∴AE=AO=4;
(2)解:设BO=x,则AB=x+2,
在Rt△ABO中,由AO2+OB =AB 得4 +x =(x+2) ,解得:x=3,
∴OB=BE=3,AB=5,
∵∠EAB+∠ABE=90°,∠ACB+∠ABC=90°
∴∠EAB=∠ACB
∵∠BFA=∠AFC
∴△BFA∽△AFC
∴BF:AF=BE:AO=3:4,
设EF=x,则AF=4+x,BF= (4+x)
∵在Rt△BEF中,BE +EF =BF2
∴32+x =[ (4+x)]2
解得,x= ,即EF=
tan∠AFC=
(3)解:①如图1,
当△DEF∽△AEB时,有
∠BAE=∠FDE
∴∠ADE=∠FDE
∴BD垂直平分AF
∴EF=AE=4-
②如图2,
设⊙Q交y轴于点G,连接DG,作FH⊥DG于H,
当△DEF∽△BEA时,有∠ABE=∠FDE
∴∠DAE=∠DAG=∠FDE=∠FDH
∴AG=AE=4,EF=FH=OG=8
综上所述,EF=4或8
【知识点】全等三角形的判定与性质;线段垂直平分线的性质;勾股定理;圆周角定理;相似三角形的判定与性质
25.【答案】(1)4 ;4 ;;
(2)解:结论a2+b2=5c2.
证明:如图3中,连接MN.
∵AM、BN是中线,
∴MN∥AB,MN= AB,
∴△MPN∽△APB,
∴ = = ,
设MP=x,NP=y,则AP=2x,BP=2y,
∴a2=BC2=4BM2=4(MP2+BP2)=4x2+16y2,
b2=AC2=4AN2=4(PN2+AP2)=4y2+16x2,
c2=AB2=AP2+BP2=4x2+4y2,
∴a2+b2=20x2+20y2=5(4x2+4y2)=5c2
(3)解:解:如图4中,在△AGE和△FGB中,
,
∴△AGE≌△FGB,
∴BG=FG,取AB中点H,连接FH并且延长交DA的延长线于P点,
同理可证△APH≌△BFH,
∴AP=BF,PE=CF=2BF,
即PE∥CF,PE=CF,
∴四边形CEPF是平行四边形,
∴FP∥CE,
∵BE⊥CE,
∴FP⊥BE,即FH⊥BG,
∴△ABF是中垂三角形,
由(2)可知AB2+AF2=5BF2,
∵AB=3,BF= AD= ,
∴9+AF2=5×( )2,
∴AF=4.
【知识点】等腰三角形的判定与性质;平行四边形的判定与性质;相似三角形的判定与性质;求特殊角的三角函数值;三角形的中位线定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
