2024年黑龙江省大庆市中考数学试卷(含答案)
文档属性
| 名称 | 2024年黑龙江省大庆市中考数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 16:54:21 | ||
图片预览


文档简介
2024年黑龙江省大庆市中考数学试卷
一、选择题:本题10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项符合要求。
1.(3分)下列各组数中,互为相反数的是( )
A.|﹣2024|和﹣2024 B.2024和
C.|﹣2024|和2024 D.﹣2024和
2.(3分)人体内一种细胞的直径约为1.56微米,相当于0.00000156米,数字0.00000156用科学记数法表示为( )
A.1.56×10﹣5 B.0.156×10﹣5
C.1.56×10﹣6 D.15.6×10﹣7
3.(3分)垃圾分类功在当代,利在千秋.下列垃圾分类指引标志中,文字上方的图形既是轴对称图形又是中心对称图形的是( )
A.厨余垃圾 B.有害垃圾 C.其他垃圾 D.可回收物
4.(3分)下列常见的几何体中,主视图和左视图不同的是( )
A. B. C. D.
5.(3分)“铁人王进喜纪念馆”“龙凤湿地公园”“滨水绿道”和“数字大庆中心”是大庆市四个有代表性的旅游景点.若小娜从这四个景点中随机选择两个景点游览,则这两个景点中有“铁人王进喜纪念馆”的概率是( )
A. B. C. D.
6.(3分)下列说法正确的是( )
A.若>2,则b>2a
B.一件衣服降价20%后又提价20%,这件衣服的价格不变
C.一个锐角和一条边分别相等的两个直角三角形全等
D.若一个多边形的内角和是外角和的2倍,则这个多边形是六边形
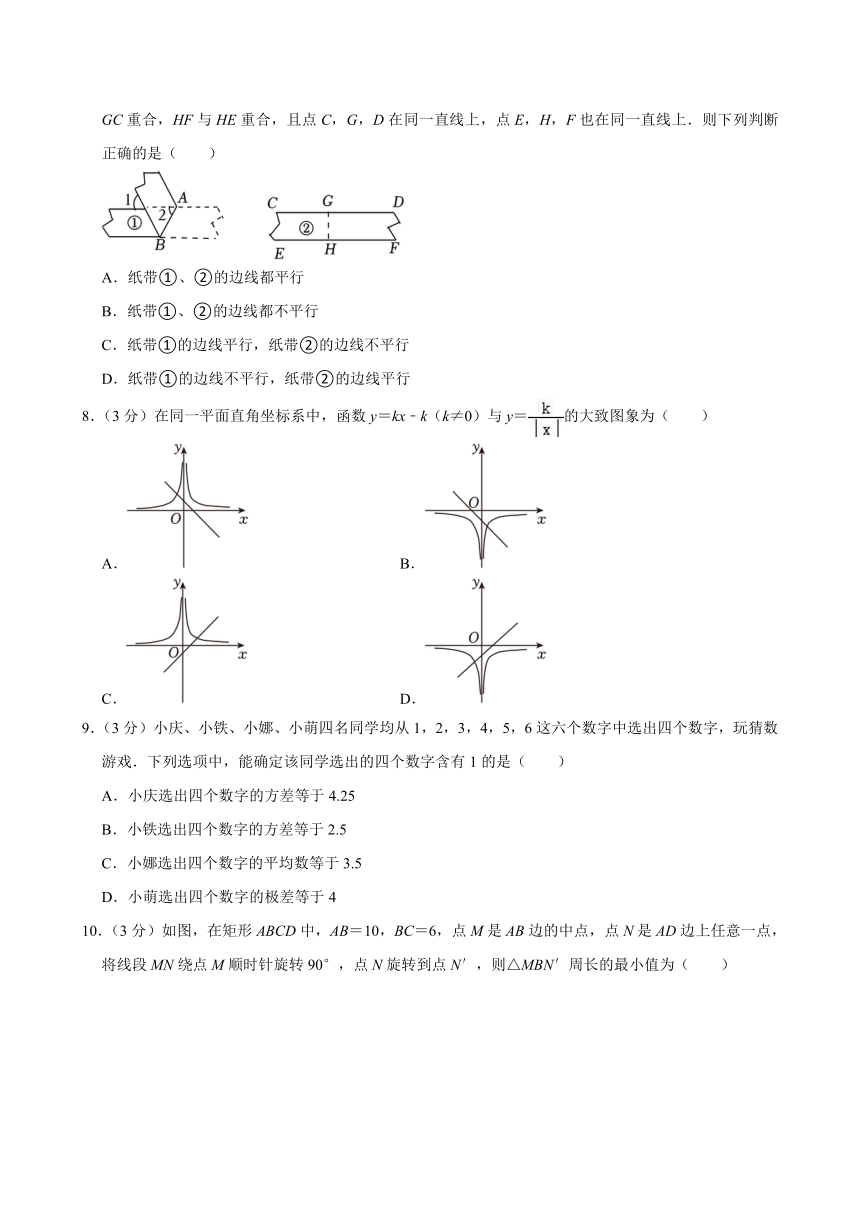
7.(3分)如图,在一次综合实践课上,为检验纸带①、②的边线是否平行,小庆和小铁采用了两种不同的方法:小庆把纸带①沿AB折叠,量得∠1=∠2=59°;小铁把纸带②沿GH折叠,发现GD与GC重合,HF与HE重合,且点C,G,D在同一直线上,点E,H,F也在同一直线上.则下列判断正确的是( )
A.纸带①、②的边线都平行
B.纸带①、②的边线都不平行
C.纸带①的边线平行,纸带②的边线不平行
D.纸带①的边线不平行,纸带②的边线平行
8.(3分)在同一平面直角坐标系中,函数y=kx﹣k(k≠0)与y=的大致图象为( )
A. B.
C. D.
9.(3分)小庆、小铁、小娜、小萌四名同学均从1,2,3,4,5,6这六个数字中选出四个数字,玩猜数游戏.下列选项中,能确定该同学选出的四个数字含有1的是( )
A.小庆选出四个数字的方差等于4.25
B.小铁选出四个数字的方差等于2.5
C.小娜选出四个数字的平均数等于3.5
D.小萌选出四个数字的极差等于4
10.(3分)如图,在矩形ABCD中,AB=10,BC=6,点M是AB边的中点,点N是AD边上任意一点,将线段MN绕点M顺时针旋转90°,点N旋转到点N′,则△MBN′周长的最小值为( )
A.15 B.5+5 C.10+5 D.18
二、填空题:本题8小题,每小题3分,共24分。不需写出解答过程,请把答案直接填写在答题卡相应位置上。
11.(3分)= .
12.(3分)若a+=,则a2+= .
13.(3分)如图所示,一个球恰好放在一个圆柱形盘子里,记球的体枳为V1,图柱形盒子的容积为V2,则= (球体体积公式:V=.其中r为球体半径).
14.(3分)写出一个过点(1,1)且y的值随着x值增大而减小的函数表达式 .
15.(3分)不等式组的整数解有 个.
16.(3分)如图所示的曲边三角形也称作“莱洛三角形”,它可以按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作,,.三段弧所围成的图形就是一个曲边三角形.若该“莱洛三角形”的周长为3π,则它的面积是 .
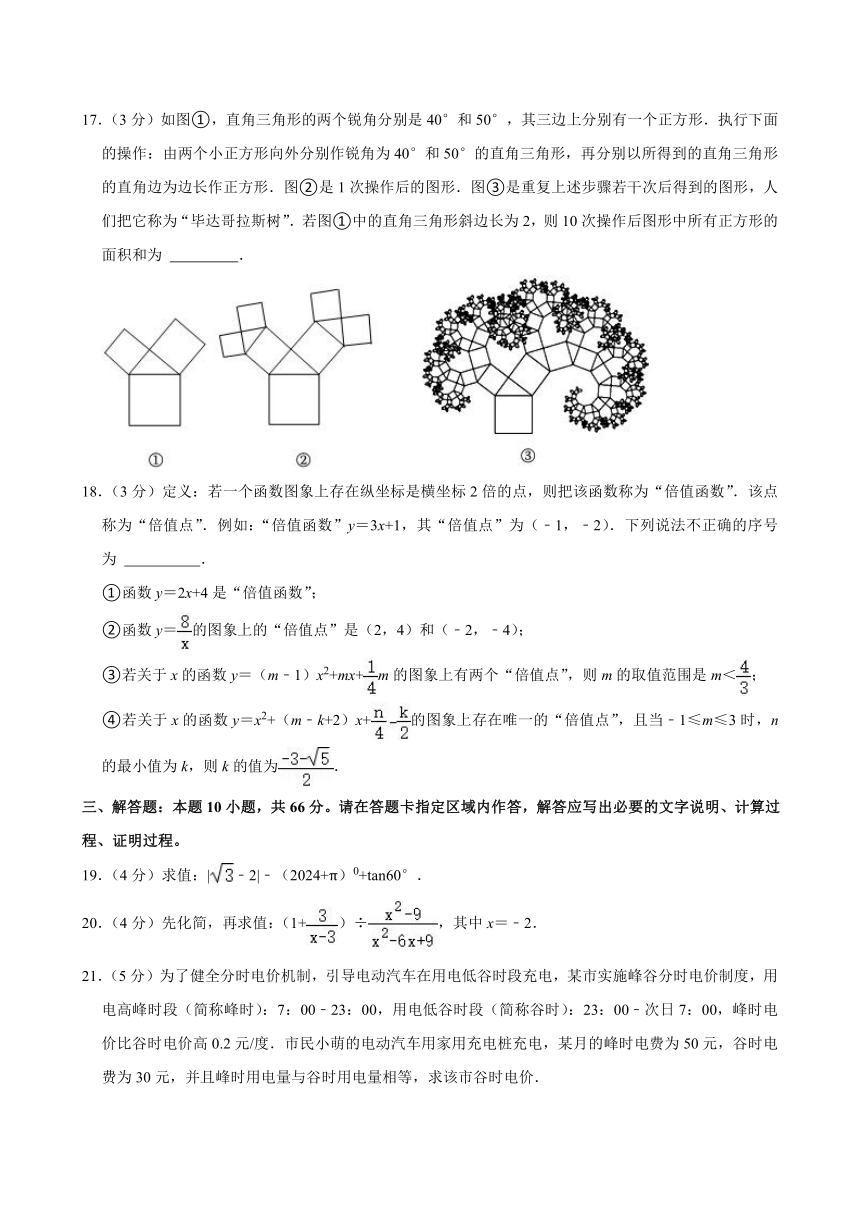
17.(3分)如图①,直角三角形的两个锐角分别是40°和50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为40°和50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图②是1次操作后的图形.图③是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图①中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为 .
18.(3分)定义:若一个函数图象上存在纵坐标是横坐标2倍的点,则把该函数称为“倍值函数”.该点称为“倍值点”.例如:“倍值函数”y=3x+1,其“倍值点”为(﹣1,﹣2).下列说法不正确的序号为 .
①函数y=2x+4是“倍值函数”;
②函数y=的图象上的“倍值点”是(2,4)和(﹣2,﹣4);
③若关于x的函数y=(m﹣1)x2+mx+m的图象上有两个“倍值点”,则m的取值范围是m<;
④若关于x的函数y=x2+(m﹣k+2)x+的图象上存在唯一的“倍值点”,且当﹣1≤m≤3时,n的最小值为k,则k的值为.
三、解答题:本题10小题,共66分。请在答题卡指定区域内作答,解答应写出必要的文字说明、计算过程、证明过程。
19.(4分)求值:|﹣2|﹣(2024+π)0+tan60°.
20.(4分)先化简,再求值:(1+)÷,其中x=﹣2.
21.(5分)为了健全分时电价机制,引导电动汽车在用电低谷时段充电,某市实施峰谷分时电价制度,用电高峰时段(简称峰时):7:00﹣23:00,用电低谷时段(简称谷时):23:00﹣次日7:00,峰时电价比谷时电价高0.2元/度.市民小萌的电动汽车用家用充电桩充电,某月的峰时电费为50元,谷时电费为30元,并且峰时用电量与谷时用电量相等,求该市谷时电价.
22.(6分)如图,CD是一座南北走向的大桥,一辆汽车在笔直的公路l上由北向南行驶,在A处测得桥头C在南偏东30°方向上,继续行驶1500米后到达B处,测得桥头C在南偏东60°方向上,桥头D在南偏东45°方向上,求大桥CD的长度.(结果精确到1米,参考数据:≈1.73)
23.(7分)根据教育部制定的《国防教育进中小学课程教材指南》.某中学开展了形式多样的国防教育培训活动.为了解培训效果,该校组织学生参加了国防知识竞赛,将学生的百分制成绩(x分)用5级记分法呈现:“x<60”记为1分,“60≤x<70”记为2分,“70≤x<80”记为3分,“80≤x<90”记为4分,“90≤x≤100”记为5分.现随机将全校学生以20人为一组进行分组,并从中随机抽取了3个小组的学生成绩进行整理,绘制统计图表,部分信息如下:
平均数 中位数 众数
第1小组 3.9 4 a
第2小组 b 3.5 5
第3小组 3.25 c 3
请根据以上信息,完成下列问题:
(1)①第2小组得分扇形统计图中,“得分为1分”这一项所对应的圆心角为 度;
②请补全第1小组得分条形统计图;
(2)a= ,b= ,c= ;
(3)已知该校共有4200名学生,以这3个小组的学生成绩作为样本,请你估计该校有多少名学生竞赛成绩不低于90分?
24.(7分)如图,在平行四边形ABCD中,AE,CF分别是∠BAD、∠BCD的平分线,且点E,F分别在边BC,AD上.
(1)求证:四边形AECF是平行四边形;
(2)若∠ADC=60°,DF=2AF=2,求△GDF的面积.
25.(7分)“尔滨”火了,带动了黑龙江省的经济发展,农副产品也随之畅销全国.某村民在网上直播推销某种农副产品,在试销售的30天中,第x天(1≤x≤30且x为整数)的售价为y(元/千克),当1≤x≤20时,y=kx+b;当20<x≤30时,y=15.销量z(千克)与x的函数关系式为z=x+10,已知该产品第10天的售价为20元/千克,第15天的售价为15元/千克,设第x天的销售额为M(元).
(1)k= ,b= ;
(2)写出第x天的销售额M与x之间的函数关系式;
(3)求在试销售的30天中,共有多少天销售额超过500元?
26.(8分)如图1,在平面直角坐标系中,O为坐标原点,点A在x轴的正半轴上.点B,C在第一象限,四边形OABC是平行四边形,点C在反比例函数y=的图象上,点C的横坐标为2.点B的纵坐标为3.
提示:在平面直角坐标系中,若两点分别为P1(x1,y1),P2(x2,y2),则P1P2中点坐标为(,).
(1)求反比例函数的表达式;
(2)如图2,点D是AB边的中点,且在反比例函数y=图象上,求平行四边形OABC的面积;
(3)如图3,将直线l1:y=﹣x向上平移6个单位得到直线l2,直线l2与函数y=(x>0)图象交于M1,M2两点,点P为M1M2的中点,过点M1作M1N⊥l1于点N.请直接写出P点坐标和的值.
27.(9分)如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,将△ABC沿直线AB翻折到△ABD,点D在⊙O上.连接CD,交AB于点E,延长BD,CA,两线相交于点P,过点A作⊙O的切线交BP于点G.
(1)求证:AG∥CD;
(2)求证:PA2=PG PB;
(3)若sin∠APD=,PG=6.求tan∠AGB的值.
28.(9分)如图,已知二次函数y=ax2+2x+c的图象与x轴交于A,B两点,A点坐标为(﹣1,0),与y轴交于点C(0,3),点M为抛物线顶点,点E为AB中点.
(1)求二次函数的表达式;
(2)在直线BC上方的抛物线上存在点Q.使得∠QCB=2∠ABC,求点Q的坐标;
(3)已知D,F为抛物线上不与A,B重合的相异两点.
①若点F与点C重合,D(m,﹣12),且m>1,求证:D,E,F三点共线;
②若直线AD,BF交于点P,则无论D,F在抛物线上如何运动,只要D,E,F三点共线,△AMP,△MEP,△ABP中必存在面积为定值的三角形,请直接写出其中面积为定值的三角形及其面积,不必说明理由.
2024年黑龙江省大庆市中考数学试卷
参考答案
一、选择题:本题10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项符合要求。
1.(3分)下列各组数中,互为相反数的是( )
A.|﹣2024|和﹣2024 B.2024和
C.|﹣2024|和2024 D.﹣2024和
选:A.
2.(3分)人体内一种细胞的直径约为1.56微米,相当于0.00000156米,数字0.00000156用科学记数法表示为( )
A.1.56×10﹣5 B.0.156×10﹣5
C.1.56×10﹣6 D.15.6×10﹣7
选:C.
3.(3分)垃圾分类功在当代,利在千秋.下列垃圾分类指引标志中,文字上方的图形既是轴对称图形又是中心对称图形的是( )
A.厨余垃圾 B.有害垃圾 C.其他垃圾 D.可回收物
选:B.
4.(3分)下列常见的几何体中,主视图和左视图不同的是( )
A. B. C. D.
选:B.
5.(3分)“铁人王进喜纪念馆”“龙凤湿地公园”“滨水绿道”和“数字大庆中心”是大庆市四个有代表性的旅游景点.若小娜从这四个景点中随机选择两个景点游览,则这两个景点中有“铁人王进喜纪念馆”的概率是( )
A. B. C. D.
选:D.
6.(3分)下列说法正确的是( )
A.若>2,则b>2a
B.一件衣服降价20%后又提价20%,这件衣服的价格不变
C.一个锐角和一条边分别相等的两个直角三角形全等
D.若一个多边形的内角和是外角和的2倍,则这个多边形是六边形
选:D.
7.(3分)如图,在一次综合实践课上,为检验纸带①、②的边线是否平行,小庆和小铁采用了两种不同的方法:小庆把纸带①沿AB折叠,量得∠1=∠2=59°;小铁把纸带②沿GH折叠,发现GD与GC重合,HF与HE重合,且点C,G,D在同一直线上,点E,H,F也在同一直线上.则下列判断正确的是( )
A.纸带①、②的边线都平行
B.纸带①、②的边线都不平行
C.纸带①的边线平行,纸带②的边线不平行
D.纸带①的边线不平行,纸带②的边线平行
选:D.
8.(3分)在同一平面直角坐标系中,函数y=kx﹣k(k≠0)与y=的大致图象为( )
A. B.
C. D.
选:C.
9.(3分)小庆、小铁、小娜、小萌四名同学均从1,2,3,4,5,6这六个数字中选出四个数字,玩猜数游戏.下列选项中,能确定该同学选出的四个数字含有1的是( )
A.小庆选出四个数字的方差等于4.25
B.小铁选出四个数字的方差等于2.5
C.小娜选出四个数字的平均数等于3.5
D.小萌选出四个数字的极差等于4
选:A.
10.(3分)如图,在矩形ABCD中,AB=10,BC=6,点M是AB边的中点,点N是AD边上任意一点,将线段MN绕点M顺时针旋转90°,点N旋转到点N′,则△MBN′周长的最小值为( )
A.15 B.5+5 C.10+5 D.18
选:B.
二、填空题:本题8小题,每小题3分,共24分。不需写出解答过程,请把答案直接填写在答题卡相应位置上。
11.(3分)= ﹣2 .
12.(3分)若a+=,则a2+= 3 .
13.(3分)如图所示,一个球恰好放在一个圆柱形盘子里,记球的体枳为V1,图柱形盒子的容积为V2,则= (球体体积公式:V=.其中r为球体半径).
14.(3分)写出一个过点(1,1)且y的值随着x值增大而减小的函数表达式 y=﹣x+2
15.(3分)不等式组的整数解有 4 个.
16.(3分)如图所示的曲边三角形也称作“莱洛三角形”,它可以按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作,,.三段弧所围成的图形就是一个曲边三角形.若该“莱洛三角形”的周长为3π,则它的面积是 ( ﹣ )
17.(3分)如图①,直角三角形的两个锐角分别是40°和50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为40°和50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图②是1次操作后的图形.图③是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图①中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为 48 .
18.(3分)定义:若一个函数图象上存在纵坐标是横坐标2倍的点,则把该函数称为“倍值函数”.该点称为“倍值点”.例如:“倍值函数”y=3x+1,其“倍值点”为(﹣1,﹣2).下列说法不正确的序号为 ①③④ .
①函数y=2x+4是“倍值函数”;
②函数y=的图象上的“倍值点”是(2,4)和(﹣2,﹣4);
③若关于x的函数y=(m﹣1)x2+mx+m的图象上有两个“倍值点”,则m的取值范围是m<;
④若关于x的函数y=x2+(m﹣k+2)x+的图象上存在唯一的“倍值点”,且当﹣1≤m≤3时,n的最小值为k,则k的值为.
三、解答题:本题10小题,共66分。请在答题卡指定区域内作答,解答应写出必要的文字说明、计算过程、证明过程。
19.(4分)求值:|﹣2|﹣(2024+π)0+tan60°.
【解答】解:原式=2﹣﹣1+
=1.
20.(4分)先化简,再求值:(1+)÷,其中x=﹣2.
【解答】解:原式=÷
=×
=,
当x=﹣2时,
原式==﹣2.
21.(5分)为了健全分时电价机制,引导电动汽车在用电低谷时段充电,某市实施峰谷分时电价制度,用电高峰时段(简称峰时):7:00﹣23:00,用电低谷时段(简称谷时):23:00﹣次日7:00,峰时电价比谷时电价高0.2元/度.市民小萌的电动汽车用家用充电桩充电,某月的峰时电费为50元,谷时电费为30元,并且峰时用电量与谷时用电量相等,求该市谷时电价.
【解答】解:设该市谷时电价为x元/度,则该市峰时电价为(x+0.2)元/度,
根据题意得:=,
解得:x=0.3,
经检验,x=0.3是所列方程的解,且符合题意.
答:该市谷时电价为0.3元/度.
22.(6分)如图,CD是一座南北走向的大桥,一辆汽车在笔直的公路l上由北向南行驶,在A处测得桥头C在南偏东30°方向上,继续行驶1500米后到达B处,测得桥头C在南偏东60°方向上,桥头D在南偏东45°方向上,求大桥CD的长度.(结果精确到1米,参考数据:≈1.73)
【解答】解:分别过点C和点D作AB的垂线,垂足分别为M,N,
在Rt△CBM中,
tan∠CBM=,
所以CM=,
在Rt△ACM中,
tanA=,
所以,
则BM=750,
所以CM=(米),
所以DN=CM=(米).
在Rt△DBN中,
tan∠DBN=,
所以BN=DN=,
所以MN=BN﹣BM=米,
则CD=MN=≈548(米),
故大桥CD的长为548米.
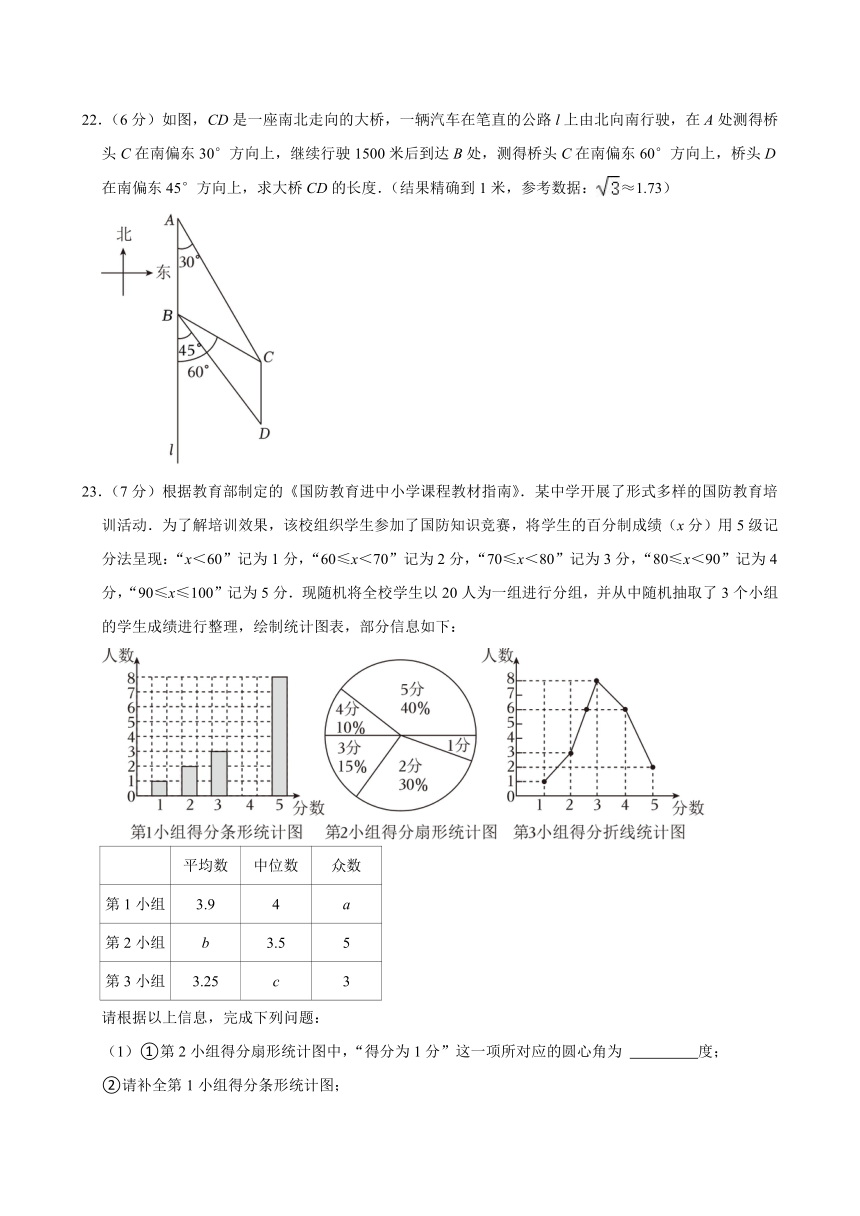
23.(7分)根据教育部制定的《国防教育进中小学课程教材指南》.某中学开展了形式多样的国防教育培训活动.为了解培训效果,该校组织学生参加了国防知识竞赛,将学生的百分制成绩(x分)用5级记分法呈现:“x<60”记为1分,“60≤x<70”记为2分,“70≤x<80”记为3分,“80≤x<90”记为4分,“90≤x≤100”记为5分.现随机将全校学生以20人为一组进行分组,并从中随机抽取了3个小组的学生成绩进行整理,绘制统计图表,部分信息如下:
平均数 中位数 众数
第1小组 3.9 4 a
第2小组 b 3.5 5
第3小组 3.25 c 3
请根据以上信息,完成下列问题:
(1)①第2小组得分扇形统计图中,“得分为1分”这一项所对应的圆心角为 18 度;
②请补全第1小组得分条形统计图;
(2)a= 5 ,b= 3.5 ,c= 3 ;
(3)已知该校共有4200名学生,以这3个小组的学生成绩作为样本,请你估计该校有多少名学生竞赛成绩不低于90分?
【解答】解:(1)①360°×(1﹣30%﹣15%﹣10%﹣40%)
=360°×5%
=18°,
故答案为:18;
②第一小组中,得分为4分的人数为20﹣1﹣2﹣3﹣8=6(人),补全条形统计图如下:
(2)第一小组学生得分出现次数最多的是5分,共出现8次,因此第一小组学生成绩的众数是5分,即a=5,
第二小组20名学生成绩的平均数为=3.5(分),即b=3.5,
将第三小组20名学生成绩从小到大排列,处在中间位置的两个数的平均数为=3(分),所以中位数是3分,即c=3,
故答案为:5,3.5,3;
(3)4200×=1260(名),
答:该校4200名学生中大约有1260名学生竞赛成绩不低于90分.
24.(7分)如图,在平行四边形ABCD中,AE,CF分别是∠BAD、∠BCD的平分线,且点E,F分别在边BC,AD上.
(1)求证:四边形AECF是平行四边形;
(2)若∠ADC=60°,DF=2AF=2,求△GDF的面积.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠BAD=∠BCD,
∴∠AEB=∠DAE,
∵AE,CF分别是∠BAD、∠BCD的平分线,
∴∠AEB=∠DAE=∠BAD,∠BCF=∠BCD,
∴∠AEB=∠BCF,
∴AE∥CF,
又∵AF∥CE,
∴四边形AECF是平行四边形;
(2)解:如图,过点C作CH⊥AD于点H,
则∠CHD=90°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠BCD=180°﹣∠ADC=180°﹣60°=120°,
∵CF是∠BCD的平分线,
∴∠DCF=∠BCD=×120°=60°,
∴∠ADC=∠DCF=60°,
∴△CDF是等边三角形,
∴CD=DF=2,DH=DF=1,
在Rt△CHD中,由勾股定理得:CH===,
∴S△CDF=DF CH=×2×=,
由(1)得:四边形AECF是平行四边形,
∴CE=AF=DF=×2=1,
∵AD∥BC,
∴△DGF∽△EGC,
∴==,
∴FG=CF,
∴S△GDF=S△CDF=.
25.(7分)“尔滨”火了,带动了黑龙江省的经济发展,农副产品也随之畅销全国.某村民在网上直播推销某种农副产品,在试销售的30天中,第x天(1≤x≤30且x为整数)的售价为y(元/千克),当1≤x≤20时,y=kx+b;当20<x≤30时,y=15.销量z(千克)与x的函数关系式为z=x+10,已知该产品第10天的售价为20元/千克,第15天的售价为15元/千克,设第x天的销售额为M(元).
(1)k= ﹣1 ,b= 30 ;
(2)写出第x天的销售额M与x之间的函数关系式;
(3)求在试销售的30天中,共有多少天销售额超过500元?
【解答】解:(1)由题意得,,
∴.
故答案为:﹣1;30.
(2)由题意,当1≤x≤20时,由(1)得y=﹣x+30,
∴M=(x+10)(﹣x+30)=﹣x2+20x+300.
当20≤x≤30时,M=15(x+10)=15x+150.
∴M=.
(3)由题意,当1≤x≤20时,M=﹣x2+20x+300=﹣(x﹣10)2+400.
∵﹣1<0,
∴当x=10时,M取最大值为400.
∴此时销售额不超过500元.
当20<x≤30时,令M=15x+150>500,
∴x>23.
∴共有7天销售额超过500元.
26.(8分)如图1,在平面直角坐标系中,O为坐标原点,点A在x轴的正半轴上.点B,C在第一象限,四边形OABC是平行四边形,点C在反比例函数y=的图象上,点C的横坐标为2.点B的纵坐标为3.
提示:在平面直角坐标系中,若两点分别为P1(x1,y1),P2(x2,y2),则P1P2中点坐标为(,).
(1)求反比例函数的表达式;
(2)如图2,点D是AB边的中点,且在反比例函数y=图象上,求平行四边形OABC的面积;
(3)如图3,将直线l1:y=﹣x向上平移6个单位得到直线l2,直线l2与函数y=(x>0)图象交于M1,M2两点,点P为M1M2的中点,过点M1作M1N⊥l1于点N.请直接写出P点坐标和的值.
【解答】解:(1)∵四边形OABC是平行四边形,点C在反比例函数y=的图象上,点C的横坐标为2.点B的纵坐标为3.
∴C(2,3),
∵点C(2,3)在反比例函数y=图象上,
∴k=6,
∴反比例函数解析式为y=;
(2)设点A坐标为(m,0),
∵C(2,3),
∴OC==,
∵OABC是平行四边形,
∴AB=OC=,
∵点D是AB边的中点,点A的纵坐标为3,
∴点D的纵坐标为,
∵点D在反比例函数y=图象上,
∴D(4,),
由中点坐标公式可得点B坐标为(8﹣m,3)
∴AB2=(8﹣m﹣m)2+32=13,
解得m=3或m=5(舍去),
∴S OABC=3×3=9.
(3)∵将直线l1:y=﹣x向上平移6个单位得到直线l2,
∴l2解析式为y=﹣+6,
设直线l2与y轴交于点E,则E(0,6),
如图3,作OF⊥l1交l2于点F,
∵M1N⊥l1,
∴M1N=OF,
在函数y=﹣+6中,当y=0时,x=8,
∴G(8,0),
∴OE=6,OG=8,
在Rt△EOG中,由勾股定理得EG===10,
由三角形面积公式可得:OE OG=OF EG,
∴OF===,
∴M1N=OF=,
列函数联立方程组得,解得,,
∴M1(4﹣2,),M2(4+2,),
∵点P为M1M2的中点,
∴P(4,3),
∴OP==5,
∴==.
27.(9分)如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,将△ABC沿直线AB翻折到△ABD,点D在⊙O上.连接CD,交AB于点E,延长BD,CA,两线相交于点P,过点A作⊙O的切线交BP于点G.
(1)求证:AG∥CD;
(2)求证:PA2=PG PB;
(3)若sin∠APD=,PG=6.求tan∠AGB的值.
【解答】(1)证明:∵将△ABC沿直线AB翻折到△ABD,
∴AB⊥CD,
∵AB为⊙O的直径,AG是切线,
∴AG⊥AB,
∴AG∥CD;
(2)证明:∵AG是切线,
∴AG⊥AB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠ABD=90°﹣∠DAB=∠GAD,
∵由折叠可得∠ABD=∠ABC,
∴∠CBD=2∠ABD,
∵四边形ADBC是⊙O的内接四边形,
∴∠PAD=180°﹣∠CAD=∠DBC=2∠ABD,
∴∠PAG=∠PAD﹣∠GAD=2∠ABD﹣∠ABD=∠ABD,
又∵∠APG=∠BPA,
∴△APG∽△BPA,
∵,即PA2=PG PB;
(3)解:∵sin∠,
设AD=a,则AP=3a,
∴,
∴,
∵由折叠可得AC=AD=a,
∴PC=PA+AC=3a+a=4a,
∵在Rt△PCB中,,
∴,
∵AD⊥BD,GA⊥AB,
∴∠AGB=90°﹣∠GAD=∠DAB,
∴.
28.(9分)如图,已知二次函数y=ax2+2x+c的图象与x轴交于A,B两点,A点坐标为(﹣1,0),与y轴交于点C(0,3),点M为抛物线顶点,点E为AB中点.
(1)求二次函数的表达式;
(2)在直线BC上方的抛物线上存在点Q.使得∠QCB=2∠ABC,求点Q的坐标;
(3)已知D,F为抛物线上不与A,B重合的相异两点.
①若点F与点C重合,D(m,﹣12),且m>1,求证:D,E,F三点共线;
②若直线AD,BF交于点P,则无论D,F在抛物线上如何运动,只要D,E,F三点共线,△AMP,△MEP,△ABP中必存在面积为定值的三角形,请直接写出其中面积为定值的三角形及其面积,不必说明理由.
【解答】(1)解:将A(﹣1,0),C(0,3)代入y=ax2+2x+c,
得:,
解得:,
∴抛物线解析式为y=﹣x2+2x+3;
(2)解:对于y=﹣x2+2x+3,令y=0,
﹣x2+2x+3=0,
解得:x1=﹣1,x2=3,
∴B(3,0),
∴OB=OC=3,
∴△OBC是等腰直角三角形,
∴∠ABC=45°,
∵∠QCB=2∠ABC,
∴∠QCB=90°,
如图所示,过点C作CQ⊥BC交抛物线于点Q,过点Q作QG⊥y轴于点G,
∴∠GCQ=90°﹣∠ABC=45°,
∴△GCQ是等腰直角三角形,
∵CQ=QG,
设Q(q,﹣q2+2q+3),则G(0,﹣q2+2q+3),
∴CG=﹣q2+2q,GQ=q,
∴﹣q2+2q=q,
解得:q=0(舍去)或q=1,
∴Q(1,4);
(3)①证明:点F与点C重合,则F(0,3),
∵点E为AB中点,A(﹣1,0),B(3,0),
∴E(1,0),
设直线EF的解析式为y=kx+b(k≠0),代入E(1,0),F(0,3),
∴,
解得:,
∴y=﹣3x+3,
联立,
解得:或,
∴D(5,﹣12),在直线EF上,即D,E,F三点共线;
②解:设D(x1,y1),F(x2,y2),
∵D,E,F三点共线,E(1,0)
∴设DF的解析式y=k(x﹣1),
联立,
消去y得,﹣x2+(2﹣k)x+(3+k)=0,
∴x1+x2=2﹣k,x1x3=﹣3﹣k,
∵A(﹣1,0),B(3,0),
设直线AD解析式为y=k1(x+1),直线BF的解析式为y=k2(x﹣3),
联立,
解得:,
∴,
∵,,
∴,,
∴====8,
而===不为定值,
∴P在直线y=8上运动,
∴P到x轴的距离为定值8,
∵直线AD,BF交于点P,则无论D,F在抛物线上如何运动,只要D,E,F三点共线,△AMP,△MEP,△ABP中必存在面积为定值的三角形,P到AM,EM的距离是变化的,
∴△ABP的面积为是定值.
一、选择题:本题10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项符合要求。
1.(3分)下列各组数中,互为相反数的是( )
A.|﹣2024|和﹣2024 B.2024和
C.|﹣2024|和2024 D.﹣2024和
2.(3分)人体内一种细胞的直径约为1.56微米,相当于0.00000156米,数字0.00000156用科学记数法表示为( )
A.1.56×10﹣5 B.0.156×10﹣5
C.1.56×10﹣6 D.15.6×10﹣7
3.(3分)垃圾分类功在当代,利在千秋.下列垃圾分类指引标志中,文字上方的图形既是轴对称图形又是中心对称图形的是( )
A.厨余垃圾 B.有害垃圾 C.其他垃圾 D.可回收物
4.(3分)下列常见的几何体中,主视图和左视图不同的是( )
A. B. C. D.
5.(3分)“铁人王进喜纪念馆”“龙凤湿地公园”“滨水绿道”和“数字大庆中心”是大庆市四个有代表性的旅游景点.若小娜从这四个景点中随机选择两个景点游览,则这两个景点中有“铁人王进喜纪念馆”的概率是( )
A. B. C. D.
6.(3分)下列说法正确的是( )
A.若>2,则b>2a
B.一件衣服降价20%后又提价20%,这件衣服的价格不变
C.一个锐角和一条边分别相等的两个直角三角形全等
D.若一个多边形的内角和是外角和的2倍,则这个多边形是六边形
7.(3分)如图,在一次综合实践课上,为检验纸带①、②的边线是否平行,小庆和小铁采用了两种不同的方法:小庆把纸带①沿AB折叠,量得∠1=∠2=59°;小铁把纸带②沿GH折叠,发现GD与GC重合,HF与HE重合,且点C,G,D在同一直线上,点E,H,F也在同一直线上.则下列判断正确的是( )
A.纸带①、②的边线都平行
B.纸带①、②的边线都不平行
C.纸带①的边线平行,纸带②的边线不平行
D.纸带①的边线不平行,纸带②的边线平行
8.(3分)在同一平面直角坐标系中,函数y=kx﹣k(k≠0)与y=的大致图象为( )
A. B.
C. D.
9.(3分)小庆、小铁、小娜、小萌四名同学均从1,2,3,4,5,6这六个数字中选出四个数字,玩猜数游戏.下列选项中,能确定该同学选出的四个数字含有1的是( )
A.小庆选出四个数字的方差等于4.25
B.小铁选出四个数字的方差等于2.5
C.小娜选出四个数字的平均数等于3.5
D.小萌选出四个数字的极差等于4
10.(3分)如图,在矩形ABCD中,AB=10,BC=6,点M是AB边的中点,点N是AD边上任意一点,将线段MN绕点M顺时针旋转90°,点N旋转到点N′,则△MBN′周长的最小值为( )
A.15 B.5+5 C.10+5 D.18
二、填空题:本题8小题,每小题3分,共24分。不需写出解答过程,请把答案直接填写在答题卡相应位置上。
11.(3分)= .
12.(3分)若a+=,则a2+= .
13.(3分)如图所示,一个球恰好放在一个圆柱形盘子里,记球的体枳为V1,图柱形盒子的容积为V2,则= (球体体积公式:V=.其中r为球体半径).
14.(3分)写出一个过点(1,1)且y的值随着x值增大而减小的函数表达式 .
15.(3分)不等式组的整数解有 个.
16.(3分)如图所示的曲边三角形也称作“莱洛三角形”,它可以按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作,,.三段弧所围成的图形就是一个曲边三角形.若该“莱洛三角形”的周长为3π,则它的面积是 .
17.(3分)如图①,直角三角形的两个锐角分别是40°和50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为40°和50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图②是1次操作后的图形.图③是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图①中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为 .
18.(3分)定义:若一个函数图象上存在纵坐标是横坐标2倍的点,则把该函数称为“倍值函数”.该点称为“倍值点”.例如:“倍值函数”y=3x+1,其“倍值点”为(﹣1,﹣2).下列说法不正确的序号为 .
①函数y=2x+4是“倍值函数”;
②函数y=的图象上的“倍值点”是(2,4)和(﹣2,﹣4);
③若关于x的函数y=(m﹣1)x2+mx+m的图象上有两个“倍值点”,则m的取值范围是m<;
④若关于x的函数y=x2+(m﹣k+2)x+的图象上存在唯一的“倍值点”,且当﹣1≤m≤3时,n的最小值为k,则k的值为.
三、解答题:本题10小题,共66分。请在答题卡指定区域内作答,解答应写出必要的文字说明、计算过程、证明过程。
19.(4分)求值:|﹣2|﹣(2024+π)0+tan60°.
20.(4分)先化简,再求值:(1+)÷,其中x=﹣2.
21.(5分)为了健全分时电价机制,引导电动汽车在用电低谷时段充电,某市实施峰谷分时电价制度,用电高峰时段(简称峰时):7:00﹣23:00,用电低谷时段(简称谷时):23:00﹣次日7:00,峰时电价比谷时电价高0.2元/度.市民小萌的电动汽车用家用充电桩充电,某月的峰时电费为50元,谷时电费为30元,并且峰时用电量与谷时用电量相等,求该市谷时电价.
22.(6分)如图,CD是一座南北走向的大桥,一辆汽车在笔直的公路l上由北向南行驶,在A处测得桥头C在南偏东30°方向上,继续行驶1500米后到达B处,测得桥头C在南偏东60°方向上,桥头D在南偏东45°方向上,求大桥CD的长度.(结果精确到1米,参考数据:≈1.73)
23.(7分)根据教育部制定的《国防教育进中小学课程教材指南》.某中学开展了形式多样的国防教育培训活动.为了解培训效果,该校组织学生参加了国防知识竞赛,将学生的百分制成绩(x分)用5级记分法呈现:“x<60”记为1分,“60≤x<70”记为2分,“70≤x<80”记为3分,“80≤x<90”记为4分,“90≤x≤100”记为5分.现随机将全校学生以20人为一组进行分组,并从中随机抽取了3个小组的学生成绩进行整理,绘制统计图表,部分信息如下:
平均数 中位数 众数
第1小组 3.9 4 a
第2小组 b 3.5 5
第3小组 3.25 c 3
请根据以上信息,完成下列问题:
(1)①第2小组得分扇形统计图中,“得分为1分”这一项所对应的圆心角为 度;
②请补全第1小组得分条形统计图;
(2)a= ,b= ,c= ;
(3)已知该校共有4200名学生,以这3个小组的学生成绩作为样本,请你估计该校有多少名学生竞赛成绩不低于90分?
24.(7分)如图,在平行四边形ABCD中,AE,CF分别是∠BAD、∠BCD的平分线,且点E,F分别在边BC,AD上.
(1)求证:四边形AECF是平行四边形;
(2)若∠ADC=60°,DF=2AF=2,求△GDF的面积.
25.(7分)“尔滨”火了,带动了黑龙江省的经济发展,农副产品也随之畅销全国.某村民在网上直播推销某种农副产品,在试销售的30天中,第x天(1≤x≤30且x为整数)的售价为y(元/千克),当1≤x≤20时,y=kx+b;当20<x≤30时,y=15.销量z(千克)与x的函数关系式为z=x+10,已知该产品第10天的售价为20元/千克,第15天的售价为15元/千克,设第x天的销售额为M(元).
(1)k= ,b= ;
(2)写出第x天的销售额M与x之间的函数关系式;
(3)求在试销售的30天中,共有多少天销售额超过500元?
26.(8分)如图1,在平面直角坐标系中,O为坐标原点,点A在x轴的正半轴上.点B,C在第一象限,四边形OABC是平行四边形,点C在反比例函数y=的图象上,点C的横坐标为2.点B的纵坐标为3.
提示:在平面直角坐标系中,若两点分别为P1(x1,y1),P2(x2,y2),则P1P2中点坐标为(,).
(1)求反比例函数的表达式;
(2)如图2,点D是AB边的中点,且在反比例函数y=图象上,求平行四边形OABC的面积;
(3)如图3,将直线l1:y=﹣x向上平移6个单位得到直线l2,直线l2与函数y=(x>0)图象交于M1,M2两点,点P为M1M2的中点,过点M1作M1N⊥l1于点N.请直接写出P点坐标和的值.
27.(9分)如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,将△ABC沿直线AB翻折到△ABD,点D在⊙O上.连接CD,交AB于点E,延长BD,CA,两线相交于点P,过点A作⊙O的切线交BP于点G.
(1)求证:AG∥CD;
(2)求证:PA2=PG PB;
(3)若sin∠APD=,PG=6.求tan∠AGB的值.
28.(9分)如图,已知二次函数y=ax2+2x+c的图象与x轴交于A,B两点,A点坐标为(﹣1,0),与y轴交于点C(0,3),点M为抛物线顶点,点E为AB中点.
(1)求二次函数的表达式;
(2)在直线BC上方的抛物线上存在点Q.使得∠QCB=2∠ABC,求点Q的坐标;
(3)已知D,F为抛物线上不与A,B重合的相异两点.
①若点F与点C重合,D(m,﹣12),且m>1,求证:D,E,F三点共线;
②若直线AD,BF交于点P,则无论D,F在抛物线上如何运动,只要D,E,F三点共线,△AMP,△MEP,△ABP中必存在面积为定值的三角形,请直接写出其中面积为定值的三角形及其面积,不必说明理由.
2024年黑龙江省大庆市中考数学试卷
参考答案
一、选择题:本题10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项符合要求。
1.(3分)下列各组数中,互为相反数的是( )
A.|﹣2024|和﹣2024 B.2024和
C.|﹣2024|和2024 D.﹣2024和
选:A.
2.(3分)人体内一种细胞的直径约为1.56微米,相当于0.00000156米,数字0.00000156用科学记数法表示为( )
A.1.56×10﹣5 B.0.156×10﹣5
C.1.56×10﹣6 D.15.6×10﹣7
选:C.
3.(3分)垃圾分类功在当代,利在千秋.下列垃圾分类指引标志中,文字上方的图形既是轴对称图形又是中心对称图形的是( )
A.厨余垃圾 B.有害垃圾 C.其他垃圾 D.可回收物
选:B.
4.(3分)下列常见的几何体中,主视图和左视图不同的是( )
A. B. C. D.
选:B.
5.(3分)“铁人王进喜纪念馆”“龙凤湿地公园”“滨水绿道”和“数字大庆中心”是大庆市四个有代表性的旅游景点.若小娜从这四个景点中随机选择两个景点游览,则这两个景点中有“铁人王进喜纪念馆”的概率是( )
A. B. C. D.
选:D.
6.(3分)下列说法正确的是( )
A.若>2,则b>2a
B.一件衣服降价20%后又提价20%,这件衣服的价格不变
C.一个锐角和一条边分别相等的两个直角三角形全等
D.若一个多边形的内角和是外角和的2倍,则这个多边形是六边形
选:D.
7.(3分)如图,在一次综合实践课上,为检验纸带①、②的边线是否平行,小庆和小铁采用了两种不同的方法:小庆把纸带①沿AB折叠,量得∠1=∠2=59°;小铁把纸带②沿GH折叠,发现GD与GC重合,HF与HE重合,且点C,G,D在同一直线上,点E,H,F也在同一直线上.则下列判断正确的是( )
A.纸带①、②的边线都平行
B.纸带①、②的边线都不平行
C.纸带①的边线平行,纸带②的边线不平行
D.纸带①的边线不平行,纸带②的边线平行
选:D.
8.(3分)在同一平面直角坐标系中,函数y=kx﹣k(k≠0)与y=的大致图象为( )
A. B.
C. D.
选:C.
9.(3分)小庆、小铁、小娜、小萌四名同学均从1,2,3,4,5,6这六个数字中选出四个数字,玩猜数游戏.下列选项中,能确定该同学选出的四个数字含有1的是( )
A.小庆选出四个数字的方差等于4.25
B.小铁选出四个数字的方差等于2.5
C.小娜选出四个数字的平均数等于3.5
D.小萌选出四个数字的极差等于4
选:A.
10.(3分)如图,在矩形ABCD中,AB=10,BC=6,点M是AB边的中点,点N是AD边上任意一点,将线段MN绕点M顺时针旋转90°,点N旋转到点N′,则△MBN′周长的最小值为( )
A.15 B.5+5 C.10+5 D.18
选:B.
二、填空题:本题8小题,每小题3分,共24分。不需写出解答过程,请把答案直接填写在答题卡相应位置上。
11.(3分)= ﹣2 .
12.(3分)若a+=,则a2+= 3 .
13.(3分)如图所示,一个球恰好放在一个圆柱形盘子里,记球的体枳为V1,图柱形盒子的容积为V2,则= (球体体积公式:V=.其中r为球体半径).
14.(3分)写出一个过点(1,1)且y的值随着x值增大而减小的函数表达式 y=﹣x+2
15.(3分)不等式组的整数解有 4 个.
16.(3分)如图所示的曲边三角形也称作“莱洛三角形”,它可以按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作,,.三段弧所围成的图形就是一个曲边三角形.若该“莱洛三角形”的周长为3π,则它的面积是 ( ﹣ )
17.(3分)如图①,直角三角形的两个锐角分别是40°和50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为40°和50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图②是1次操作后的图形.图③是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图①中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为 48 .
18.(3分)定义:若一个函数图象上存在纵坐标是横坐标2倍的点,则把该函数称为“倍值函数”.该点称为“倍值点”.例如:“倍值函数”y=3x+1,其“倍值点”为(﹣1,﹣2).下列说法不正确的序号为 ①③④ .
①函数y=2x+4是“倍值函数”;
②函数y=的图象上的“倍值点”是(2,4)和(﹣2,﹣4);
③若关于x的函数y=(m﹣1)x2+mx+m的图象上有两个“倍值点”,则m的取值范围是m<;
④若关于x的函数y=x2+(m﹣k+2)x+的图象上存在唯一的“倍值点”,且当﹣1≤m≤3时,n的最小值为k,则k的值为.
三、解答题:本题10小题,共66分。请在答题卡指定区域内作答,解答应写出必要的文字说明、计算过程、证明过程。
19.(4分)求值:|﹣2|﹣(2024+π)0+tan60°.
【解答】解:原式=2﹣﹣1+
=1.
20.(4分)先化简,再求值:(1+)÷,其中x=﹣2.
【解答】解:原式=÷
=×
=,
当x=﹣2时,
原式==﹣2.
21.(5分)为了健全分时电价机制,引导电动汽车在用电低谷时段充电,某市实施峰谷分时电价制度,用电高峰时段(简称峰时):7:00﹣23:00,用电低谷时段(简称谷时):23:00﹣次日7:00,峰时电价比谷时电价高0.2元/度.市民小萌的电动汽车用家用充电桩充电,某月的峰时电费为50元,谷时电费为30元,并且峰时用电量与谷时用电量相等,求该市谷时电价.
【解答】解:设该市谷时电价为x元/度,则该市峰时电价为(x+0.2)元/度,
根据题意得:=,
解得:x=0.3,
经检验,x=0.3是所列方程的解,且符合题意.
答:该市谷时电价为0.3元/度.
22.(6分)如图,CD是一座南北走向的大桥,一辆汽车在笔直的公路l上由北向南行驶,在A处测得桥头C在南偏东30°方向上,继续行驶1500米后到达B处,测得桥头C在南偏东60°方向上,桥头D在南偏东45°方向上,求大桥CD的长度.(结果精确到1米,参考数据:≈1.73)
【解答】解:分别过点C和点D作AB的垂线,垂足分别为M,N,
在Rt△CBM中,
tan∠CBM=,
所以CM=,
在Rt△ACM中,
tanA=,
所以,
则BM=750,
所以CM=(米),
所以DN=CM=(米).
在Rt△DBN中,
tan∠DBN=,
所以BN=DN=,
所以MN=BN﹣BM=米,
则CD=MN=≈548(米),
故大桥CD的长为548米.
23.(7分)根据教育部制定的《国防教育进中小学课程教材指南》.某中学开展了形式多样的国防教育培训活动.为了解培训效果,该校组织学生参加了国防知识竞赛,将学生的百分制成绩(x分)用5级记分法呈现:“x<60”记为1分,“60≤x<70”记为2分,“70≤x<80”记为3分,“80≤x<90”记为4分,“90≤x≤100”记为5分.现随机将全校学生以20人为一组进行分组,并从中随机抽取了3个小组的学生成绩进行整理,绘制统计图表,部分信息如下:
平均数 中位数 众数
第1小组 3.9 4 a
第2小组 b 3.5 5
第3小组 3.25 c 3
请根据以上信息,完成下列问题:
(1)①第2小组得分扇形统计图中,“得分为1分”这一项所对应的圆心角为 18 度;
②请补全第1小组得分条形统计图;
(2)a= 5 ,b= 3.5 ,c= 3 ;
(3)已知该校共有4200名学生,以这3个小组的学生成绩作为样本,请你估计该校有多少名学生竞赛成绩不低于90分?
【解答】解:(1)①360°×(1﹣30%﹣15%﹣10%﹣40%)
=360°×5%
=18°,
故答案为:18;
②第一小组中,得分为4分的人数为20﹣1﹣2﹣3﹣8=6(人),补全条形统计图如下:
(2)第一小组学生得分出现次数最多的是5分,共出现8次,因此第一小组学生成绩的众数是5分,即a=5,
第二小组20名学生成绩的平均数为=3.5(分),即b=3.5,
将第三小组20名学生成绩从小到大排列,处在中间位置的两个数的平均数为=3(分),所以中位数是3分,即c=3,
故答案为:5,3.5,3;
(3)4200×=1260(名),
答:该校4200名学生中大约有1260名学生竞赛成绩不低于90分.
24.(7分)如图,在平行四边形ABCD中,AE,CF分别是∠BAD、∠BCD的平分线,且点E,F分别在边BC,AD上.
(1)求证:四边形AECF是平行四边形;
(2)若∠ADC=60°,DF=2AF=2,求△GDF的面积.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠BAD=∠BCD,
∴∠AEB=∠DAE,
∵AE,CF分别是∠BAD、∠BCD的平分线,
∴∠AEB=∠DAE=∠BAD,∠BCF=∠BCD,
∴∠AEB=∠BCF,
∴AE∥CF,
又∵AF∥CE,
∴四边形AECF是平行四边形;
(2)解:如图,过点C作CH⊥AD于点H,
则∠CHD=90°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠BCD=180°﹣∠ADC=180°﹣60°=120°,
∵CF是∠BCD的平分线,
∴∠DCF=∠BCD=×120°=60°,
∴∠ADC=∠DCF=60°,
∴△CDF是等边三角形,
∴CD=DF=2,DH=DF=1,
在Rt△CHD中,由勾股定理得:CH===,
∴S△CDF=DF CH=×2×=,
由(1)得:四边形AECF是平行四边形,
∴CE=AF=DF=×2=1,
∵AD∥BC,
∴△DGF∽△EGC,
∴==,
∴FG=CF,
∴S△GDF=S△CDF=.
25.(7分)“尔滨”火了,带动了黑龙江省的经济发展,农副产品也随之畅销全国.某村民在网上直播推销某种农副产品,在试销售的30天中,第x天(1≤x≤30且x为整数)的售价为y(元/千克),当1≤x≤20时,y=kx+b;当20<x≤30时,y=15.销量z(千克)与x的函数关系式为z=x+10,已知该产品第10天的售价为20元/千克,第15天的售价为15元/千克,设第x天的销售额为M(元).
(1)k= ﹣1 ,b= 30 ;
(2)写出第x天的销售额M与x之间的函数关系式;
(3)求在试销售的30天中,共有多少天销售额超过500元?
【解答】解:(1)由题意得,,
∴.
故答案为:﹣1;30.
(2)由题意,当1≤x≤20时,由(1)得y=﹣x+30,
∴M=(x+10)(﹣x+30)=﹣x2+20x+300.
当20≤x≤30时,M=15(x+10)=15x+150.
∴M=.
(3)由题意,当1≤x≤20时,M=﹣x2+20x+300=﹣(x﹣10)2+400.
∵﹣1<0,
∴当x=10时,M取最大值为400.
∴此时销售额不超过500元.
当20<x≤30时,令M=15x+150>500,
∴x>23.
∴共有7天销售额超过500元.
26.(8分)如图1,在平面直角坐标系中,O为坐标原点,点A在x轴的正半轴上.点B,C在第一象限,四边形OABC是平行四边形,点C在反比例函数y=的图象上,点C的横坐标为2.点B的纵坐标为3.
提示:在平面直角坐标系中,若两点分别为P1(x1,y1),P2(x2,y2),则P1P2中点坐标为(,).
(1)求反比例函数的表达式;
(2)如图2,点D是AB边的中点,且在反比例函数y=图象上,求平行四边形OABC的面积;
(3)如图3,将直线l1:y=﹣x向上平移6个单位得到直线l2,直线l2与函数y=(x>0)图象交于M1,M2两点,点P为M1M2的中点,过点M1作M1N⊥l1于点N.请直接写出P点坐标和的值.
【解答】解:(1)∵四边形OABC是平行四边形,点C在反比例函数y=的图象上,点C的横坐标为2.点B的纵坐标为3.
∴C(2,3),
∵点C(2,3)在反比例函数y=图象上,
∴k=6,
∴反比例函数解析式为y=;
(2)设点A坐标为(m,0),
∵C(2,3),
∴OC==,
∵OABC是平行四边形,
∴AB=OC=,
∵点D是AB边的中点,点A的纵坐标为3,
∴点D的纵坐标为,
∵点D在反比例函数y=图象上,
∴D(4,),
由中点坐标公式可得点B坐标为(8﹣m,3)
∴AB2=(8﹣m﹣m)2+32=13,
解得m=3或m=5(舍去),
∴S OABC=3×3=9.
(3)∵将直线l1:y=﹣x向上平移6个单位得到直线l2,
∴l2解析式为y=﹣+6,
设直线l2与y轴交于点E,则E(0,6),
如图3,作OF⊥l1交l2于点F,
∵M1N⊥l1,
∴M1N=OF,
在函数y=﹣+6中,当y=0时,x=8,
∴G(8,0),
∴OE=6,OG=8,
在Rt△EOG中,由勾股定理得EG===10,
由三角形面积公式可得:OE OG=OF EG,
∴OF===,
∴M1N=OF=,
列函数联立方程组得,解得,,
∴M1(4﹣2,),M2(4+2,),
∵点P为M1M2的中点,
∴P(4,3),
∴OP==5,
∴==.
27.(9分)如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,将△ABC沿直线AB翻折到△ABD,点D在⊙O上.连接CD,交AB于点E,延长BD,CA,两线相交于点P,过点A作⊙O的切线交BP于点G.
(1)求证:AG∥CD;
(2)求证:PA2=PG PB;
(3)若sin∠APD=,PG=6.求tan∠AGB的值.
【解答】(1)证明:∵将△ABC沿直线AB翻折到△ABD,
∴AB⊥CD,
∵AB为⊙O的直径,AG是切线,
∴AG⊥AB,
∴AG∥CD;
(2)证明:∵AG是切线,
∴AG⊥AB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠ABD=90°﹣∠DAB=∠GAD,
∵由折叠可得∠ABD=∠ABC,
∴∠CBD=2∠ABD,
∵四边形ADBC是⊙O的内接四边形,
∴∠PAD=180°﹣∠CAD=∠DBC=2∠ABD,
∴∠PAG=∠PAD﹣∠GAD=2∠ABD﹣∠ABD=∠ABD,
又∵∠APG=∠BPA,
∴△APG∽△BPA,
∵,即PA2=PG PB;
(3)解:∵sin∠,
设AD=a,则AP=3a,
∴,
∴,
∵由折叠可得AC=AD=a,
∴PC=PA+AC=3a+a=4a,
∵在Rt△PCB中,,
∴,
∵AD⊥BD,GA⊥AB,
∴∠AGB=90°﹣∠GAD=∠DAB,
∴.
28.(9分)如图,已知二次函数y=ax2+2x+c的图象与x轴交于A,B两点,A点坐标为(﹣1,0),与y轴交于点C(0,3),点M为抛物线顶点,点E为AB中点.
(1)求二次函数的表达式;
(2)在直线BC上方的抛物线上存在点Q.使得∠QCB=2∠ABC,求点Q的坐标;
(3)已知D,F为抛物线上不与A,B重合的相异两点.
①若点F与点C重合,D(m,﹣12),且m>1,求证:D,E,F三点共线;
②若直线AD,BF交于点P,则无论D,F在抛物线上如何运动,只要D,E,F三点共线,△AMP,△MEP,△ABP中必存在面积为定值的三角形,请直接写出其中面积为定值的三角形及其面积,不必说明理由.
【解答】(1)解:将A(﹣1,0),C(0,3)代入y=ax2+2x+c,
得:,
解得:,
∴抛物线解析式为y=﹣x2+2x+3;
(2)解:对于y=﹣x2+2x+3,令y=0,
﹣x2+2x+3=0,
解得:x1=﹣1,x2=3,
∴B(3,0),
∴OB=OC=3,
∴△OBC是等腰直角三角形,
∴∠ABC=45°,
∵∠QCB=2∠ABC,
∴∠QCB=90°,
如图所示,过点C作CQ⊥BC交抛物线于点Q,过点Q作QG⊥y轴于点G,
∴∠GCQ=90°﹣∠ABC=45°,
∴△GCQ是等腰直角三角形,
∵CQ=QG,
设Q(q,﹣q2+2q+3),则G(0,﹣q2+2q+3),
∴CG=﹣q2+2q,GQ=q,
∴﹣q2+2q=q,
解得:q=0(舍去)或q=1,
∴Q(1,4);
(3)①证明:点F与点C重合,则F(0,3),
∵点E为AB中点,A(﹣1,0),B(3,0),
∴E(1,0),
设直线EF的解析式为y=kx+b(k≠0),代入E(1,0),F(0,3),
∴,
解得:,
∴y=﹣3x+3,
联立,
解得:或,
∴D(5,﹣12),在直线EF上,即D,E,F三点共线;
②解:设D(x1,y1),F(x2,y2),
∵D,E,F三点共线,E(1,0)
∴设DF的解析式y=k(x﹣1),
联立,
消去y得,﹣x2+(2﹣k)x+(3+k)=0,
∴x1+x2=2﹣k,x1x3=﹣3﹣k,
∵A(﹣1,0),B(3,0),
设直线AD解析式为y=k1(x+1),直线BF的解析式为y=k2(x﹣3),
联立,
解得:,
∴,
∵,,
∴,,
∴====8,
而===不为定值,
∴P在直线y=8上运动,
∴P到x轴的距离为定值8,
∵直线AD,BF交于点P,则无论D,F在抛物线上如何运动,只要D,E,F三点共线,△AMP,△MEP,△ABP中必存在面积为定值的三角形,P到AM,EM的距离是变化的,
∴△ABP的面积为是定值.
同课章节目录
