八年级上册沪科版数学 13.2 命题与证明专项练习八 (含答案)
文档属性
| 名称 | 八年级上册沪科版数学 13.2 命题与证明专项练习八 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 250.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 19:26:00 | ||
图片预览

文档简介
专项练习八 命题与证明
(时间:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
1.下列语句中,不是命题的是( )
A.同旁内角相等
B.对顶角不相等
C.同角的余角相等
D.作∠ABC的平分线
2.判断命题“如果n<1,那么 是假命题,只需举出一个反例.反例中的n可以为( )
A.-2
C.0 D.
3.在 Rt△ABC 中,∠C=90°,∠A-∠B=70°,则∠A的度数为( )
A.80° B.70° C.60° D.50°
4.如图,两条直线a,b被直线 c 所截,下列命题错误的是( )
A.若∠1=∠3,则∠2+∠5=180°
B.若∠1≠∠4,则∠2≠∠5
C.若∠2+∠5=180°,则∠1,∠4 不可能相等
D.若∠1≠∠5,则∠2+∠3≠180°
5.如图,∠x的两条边被一直线所截,用含α和β 的 式 子 表 示 ∠x为( )
A.α-β
B.β-α
6.如图,CD∥AB,∠A=35°,∠DCB=55°,则 △ABC 的 形 状为( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.等边三角形
二、填空题(每小题4分,共16分)
7.命题“如果a+b=0,那么a,b互为相反数”的逆命题为
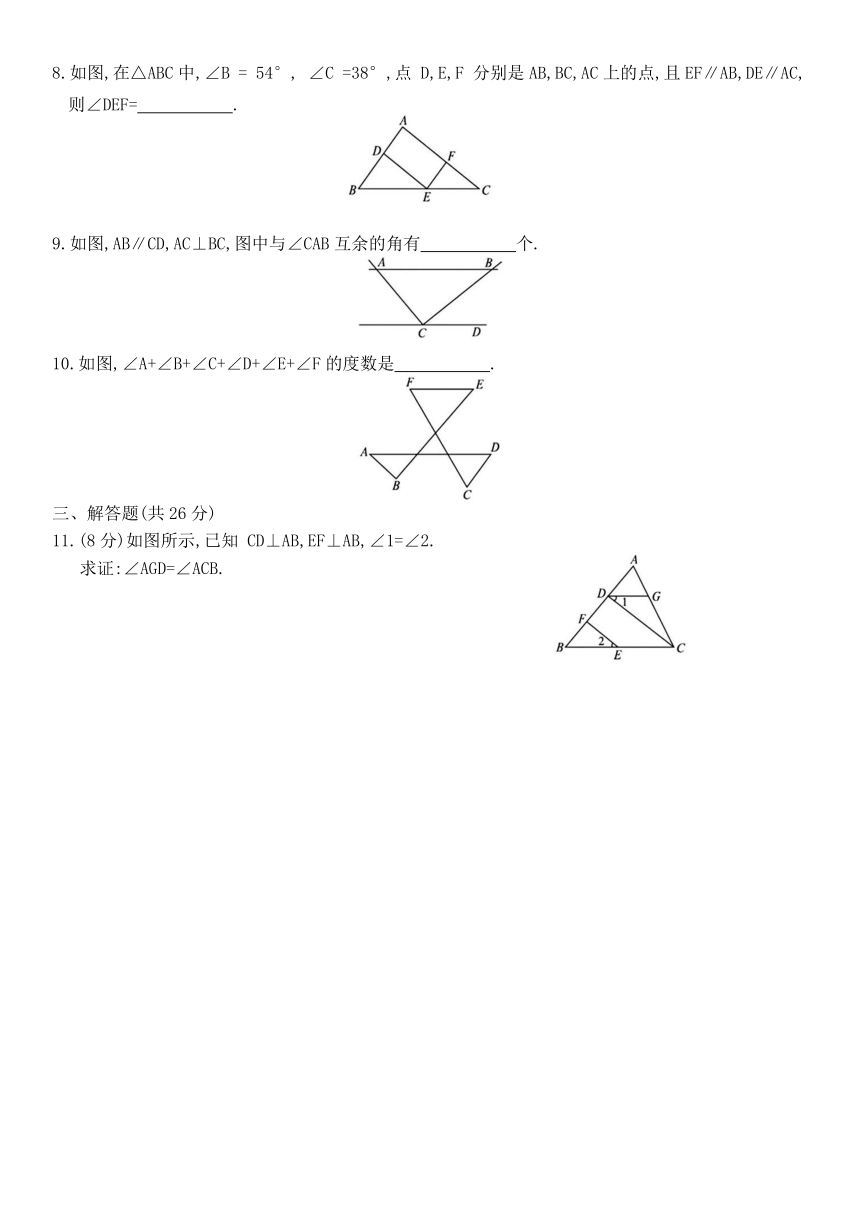
8.如图,在△ABC中,∠B = 54°, ∠C =38°,点 D,E,F 分别是AB,BC,AC上的点,且EF∥AB,DE∥AC,则∠DEF= .
9.如图,AB∥CD,AC⊥BC,图中与∠CAB互余的角有 个.
10.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
三、解答题(共26分)
11.(8分)如图所示,已知 CD⊥AB,EF⊥AB,∠1=∠2.
求证:∠AGD=∠ACB.
12.(9 分) 如图,在△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=70°, ,求∠DAE的度数;
(2)在(1)中,如果把条件“∠B=70°,∠C=30°”改为条件“∠B-∠C=40°”,那么能否求出∠DAE 的度数 若能,写出求解过程;若不能,请说明理由.
13. (9 分) 如图, 在△ABC中,三条内角平分线AD,BE,CF 相交于点 O,OG⊥BC于点G.
(1) 若 ∠ABC = 40°, ∠BAC = 60°, 求∠BOD 和∠COG的度数;
(2)若∠ABC=α,∠BAC=β,则∠BOD和∠COG相等吗 请说明理由.
专项练习八 命题与证明
1. D 2. A 3. A 4. C 5. B 6. C
7.如果a,b互为相反数,那么a+b=0
8.88° 9.3 10.360°
11.证明∵CD⊥AB,EF⊥AB(已知),
∴∠EFB=∠CDB=90°(垂直的定义). (同位角相等,两直线平行).∴∠2=∠DCB(两直线平行,同位角相等).又∵∠1=∠2(已知),∴∠1=∠DCB(等量代换).∴DG∥BC(内错角相等,两直线平行).
∴∠AGD=∠ACB(两直线平行,同位角相等).
12.解(1)∵∠B=70°,∠C=30°,
∵AE平分
∵AD⊥BC,∴∠DAC=90°-30°=60°.
∴∠DAE=∠DAC--∠EAC=60°-40°=20°.
(2)能.理由:设∠C=x°,则
∵AE平分
∵AD⊥BC,∴∠DAC=90°-x°.
∴∠DAE=∠DAC--∠EAC
13.解(1)∵三条内角平分线AD,BE,CF相交于点O,
(2)∠BOD和∠COG相等.理由如下:
(时间:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
1.下列语句中,不是命题的是( )
A.同旁内角相等
B.对顶角不相等
C.同角的余角相等
D.作∠ABC的平分线
2.判断命题“如果n<1,那么 是假命题,只需举出一个反例.反例中的n可以为( )
A.-2
C.0 D.
3.在 Rt△ABC 中,∠C=90°,∠A-∠B=70°,则∠A的度数为( )
A.80° B.70° C.60° D.50°
4.如图,两条直线a,b被直线 c 所截,下列命题错误的是( )
A.若∠1=∠3,则∠2+∠5=180°
B.若∠1≠∠4,则∠2≠∠5
C.若∠2+∠5=180°,则∠1,∠4 不可能相等
D.若∠1≠∠5,则∠2+∠3≠180°
5.如图,∠x的两条边被一直线所截,用含α和β 的 式 子 表 示 ∠x为( )
A.α-β
B.β-α
6.如图,CD∥AB,∠A=35°,∠DCB=55°,则 △ABC 的 形 状为( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.等边三角形
二、填空题(每小题4分,共16分)
7.命题“如果a+b=0,那么a,b互为相反数”的逆命题为
8.如图,在△ABC中,∠B = 54°, ∠C =38°,点 D,E,F 分别是AB,BC,AC上的点,且EF∥AB,DE∥AC,则∠DEF= .
9.如图,AB∥CD,AC⊥BC,图中与∠CAB互余的角有 个.
10.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
三、解答题(共26分)
11.(8分)如图所示,已知 CD⊥AB,EF⊥AB,∠1=∠2.
求证:∠AGD=∠ACB.
12.(9 分) 如图,在△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=70°, ,求∠DAE的度数;
(2)在(1)中,如果把条件“∠B=70°,∠C=30°”改为条件“∠B-∠C=40°”,那么能否求出∠DAE 的度数 若能,写出求解过程;若不能,请说明理由.
13. (9 分) 如图, 在△ABC中,三条内角平分线AD,BE,CF 相交于点 O,OG⊥BC于点G.
(1) 若 ∠ABC = 40°, ∠BAC = 60°, 求∠BOD 和∠COG的度数;
(2)若∠ABC=α,∠BAC=β,则∠BOD和∠COG相等吗 请说明理由.
专项练习八 命题与证明
1. D 2. A 3. A 4. C 5. B 6. C
7.如果a,b互为相反数,那么a+b=0
8.88° 9.3 10.360°
11.证明∵CD⊥AB,EF⊥AB(已知),
∴∠EFB=∠CDB=90°(垂直的定义). (同位角相等,两直线平行).∴∠2=∠DCB(两直线平行,同位角相等).又∵∠1=∠2(已知),∴∠1=∠DCB(等量代换).∴DG∥BC(内错角相等,两直线平行).
∴∠AGD=∠ACB(两直线平行,同位角相等).
12.解(1)∵∠B=70°,∠C=30°,
∵AE平分
∵AD⊥BC,∴∠DAC=90°-30°=60°.
∴∠DAE=∠DAC--∠EAC=60°-40°=20°.
(2)能.理由:设∠C=x°,则
∵AE平分
∵AD⊥BC,∴∠DAC=90°-x°.
∴∠DAE=∠DAC--∠EAC
13.解(1)∵三条内角平分线AD,BE,CF相交于点O,
(2)∠BOD和∠COG相等.理由如下:
