八年级上册沪科版数学 14.1 全等三角形 专项练习九 (含答案)
文档属性
| 名称 | 八年级上册沪科版数学 14.1 全等三角形 专项练习九 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 476.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 00:00:00 | ||
图片预览

文档简介
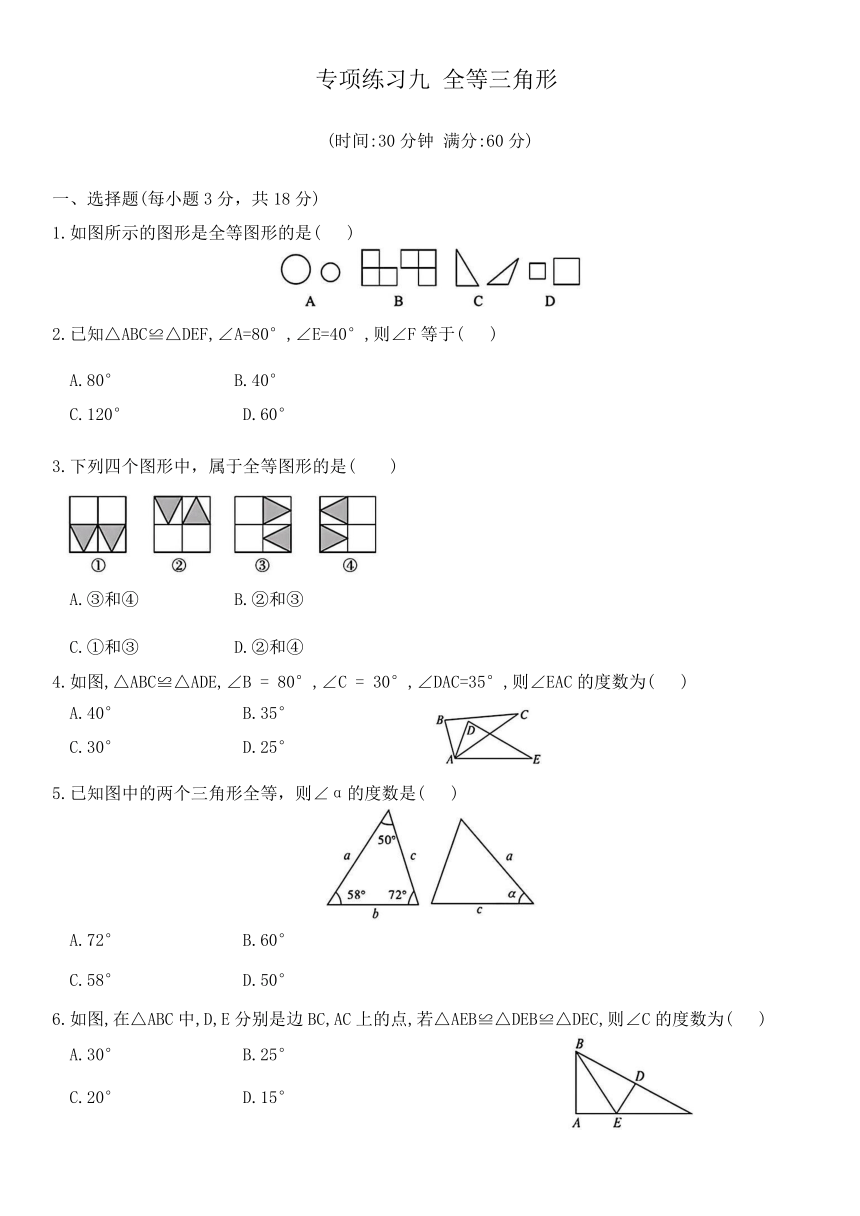
专项练习九 全等三角形
(时间:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
1.如图所示的图形是全等图形的是( )
2.已知△ABC≌△DEF,∠A=80°,∠E=40°,则∠F等于( )
A.80° B.40°
C.120° D.60°
3.下列四个图形中,属于全等图形的是( )
A.③和④ B.②和③
C.①和③ D.②和④
4.如图,△ABC≌△ADE,∠B = 80°,∠C = 30°,∠DAC=35°,则∠EAC的度数为( )
A.40° B.35°
C.30° D.25°
5.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60°
C.58° D.50°
6.如图,在△ABC中,D,E分别是边BC,AC上的点,若△AEB≌△DEB≌△DEC,则∠C的度数为( )
A.30° B.25°
C.20° D.15°
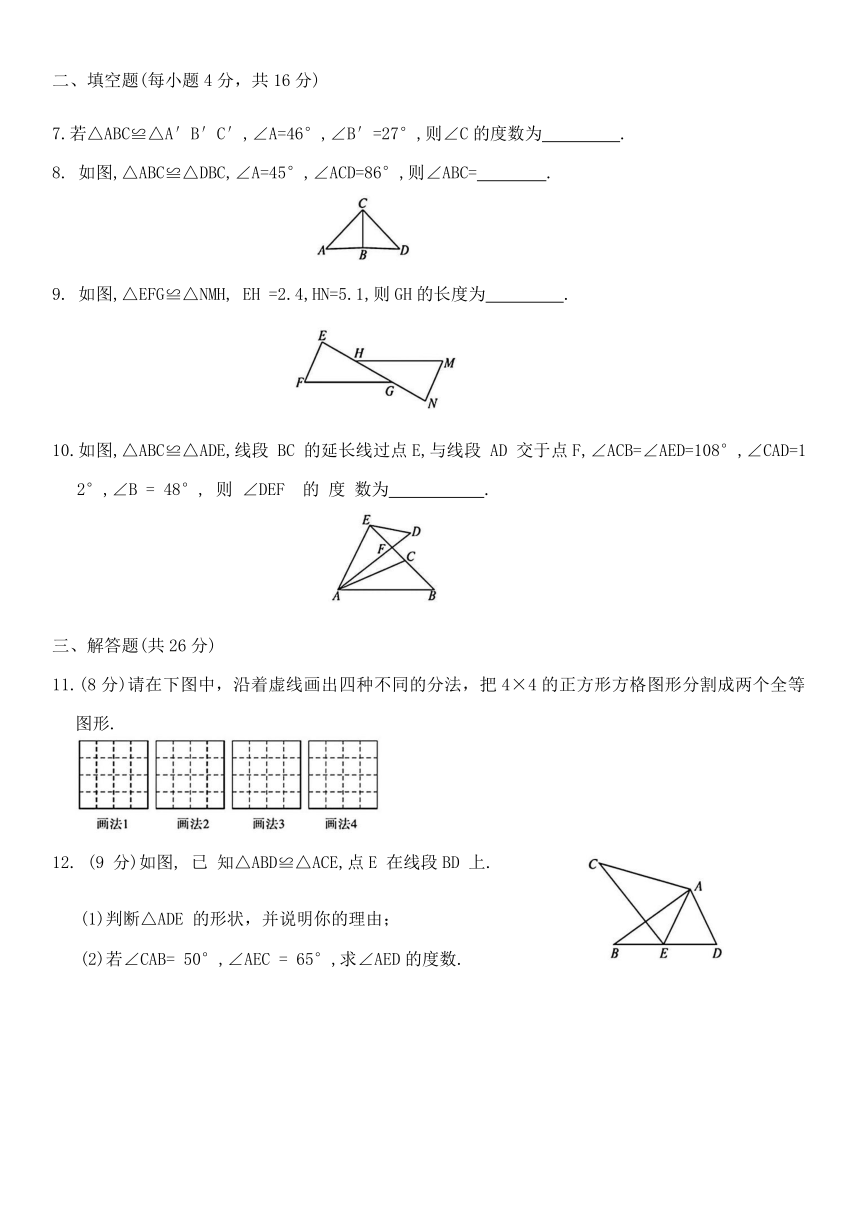
二、填空题(每小题4分,共16分)
7.若△ABC≌△A′B′C′,∠A=46°,∠B′=27°,则∠C的度数为 .
8. 如图,△ABC≌△DBC,∠A=45°,∠ACD=86°,则∠ABC= .
9. 如图,△EFG≌△NMH, EH =2.4,HN=5.1,则GH的长度为 .
10.如图,△ABC≌△ADE,线段 BC 的延长线过点E,与线段 AD 交于点F,∠ACB=∠AED=108°,∠CAD=12°,∠B = 48°, 则 ∠DEF 的 度 数为 .
三、解答题(共26分)
11.(8分)请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形.
12. (9 分)如图, 已 知△ABD≌△ACE,点E 在线段BD 上.
(1)判断△ADE 的形状,并说明你的理由;
(2)若∠CAB= 50°,∠AEC = 65°,求∠AED的度数.
13.(9 分)如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8cm ,D为AB的中点,点P 在线段上以 3 cm/s的速度由点 B 向点 C 运动,同时,点 Q 在线段CA 上以相同速度由点 C 向点 A 运动,一个点到达终点后另一个点也停止运动.当△BPD 与△CQP 全等时,求点 P 运动的时间.
专项练习九 全等三角形
1. B 2. D 3. D 4. B 5. D 6. A 7.107° 8.92° 9.2.7
11.解 答案不唯一,如图所示.
12.解 是等腰三角形.理由: 是等腰三角形.
(2)∵△ABD≌△ACE,∴∠CAE=∠BAD,∠D= 于是
13.解 因为D为AB 的中点, 所以.
设点 P,Q的运动时间为t,则BP=CQ=3t cm,PC=(8—3t) cm.
若BD与CQ 是对应边,则BD=CQ,所以5=3t,解得t= ,此时 CP,不合题意,舍去;
若BD与CP 是对应边,则BD=CP,所以5=8—3t,解得t=1,符合题意.
综上可知,点 P运动的时间为1 s.
(时间:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
1.如图所示的图形是全等图形的是( )
2.已知△ABC≌△DEF,∠A=80°,∠E=40°,则∠F等于( )
A.80° B.40°
C.120° D.60°
3.下列四个图形中,属于全等图形的是( )
A.③和④ B.②和③
C.①和③ D.②和④
4.如图,△ABC≌△ADE,∠B = 80°,∠C = 30°,∠DAC=35°,则∠EAC的度数为( )
A.40° B.35°
C.30° D.25°
5.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60°
C.58° D.50°
6.如图,在△ABC中,D,E分别是边BC,AC上的点,若△AEB≌△DEB≌△DEC,则∠C的度数为( )
A.30° B.25°
C.20° D.15°
二、填空题(每小题4分,共16分)
7.若△ABC≌△A′B′C′,∠A=46°,∠B′=27°,则∠C的度数为 .
8. 如图,△ABC≌△DBC,∠A=45°,∠ACD=86°,则∠ABC= .
9. 如图,△EFG≌△NMH, EH =2.4,HN=5.1,则GH的长度为 .
10.如图,△ABC≌△ADE,线段 BC 的延长线过点E,与线段 AD 交于点F,∠ACB=∠AED=108°,∠CAD=12°,∠B = 48°, 则 ∠DEF 的 度 数为 .
三、解答题(共26分)
11.(8分)请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形.
12. (9 分)如图, 已 知△ABD≌△ACE,点E 在线段BD 上.
(1)判断△ADE 的形状,并说明你的理由;
(2)若∠CAB= 50°,∠AEC = 65°,求∠AED的度数.
13.(9 分)如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8cm ,D为AB的中点,点P 在线段上以 3 cm/s的速度由点 B 向点 C 运动,同时,点 Q 在线段CA 上以相同速度由点 C 向点 A 运动,一个点到达终点后另一个点也停止运动.当△BPD 与△CQP 全等时,求点 P 运动的时间.
专项练习九 全等三角形
1. B 2. D 3. D 4. B 5. D 6. A 7.107° 8.92° 9.2.7
11.解 答案不唯一,如图所示.
12.解 是等腰三角形.理由: 是等腰三角形.
(2)∵△ABD≌△ACE,∴∠CAE=∠BAD,∠D= 于是
13.解 因为D为AB 的中点, 所以.
设点 P,Q的运动时间为t,则BP=CQ=3t cm,PC=(8—3t) cm.
若BD与CQ 是对应边,则BD=CQ,所以5=3t,解得t= ,此时 CP,不合题意,舍去;
若BD与CP 是对应边,则BD=CP,所以5=8—3t,解得t=1,符合题意.
综上可知,点 P运动的时间为1 s.
