八年级上册沪科版数学 14.2 三角形全等的判定 专项练习十 (含答案)
文档属性
| 名称 | 八年级上册沪科版数学 14.2 三角形全等的判定 专项练习十 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 487.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 00:00:00 | ||
图片预览

文档简介
专项练习十 三角形全等的判定
(时间:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
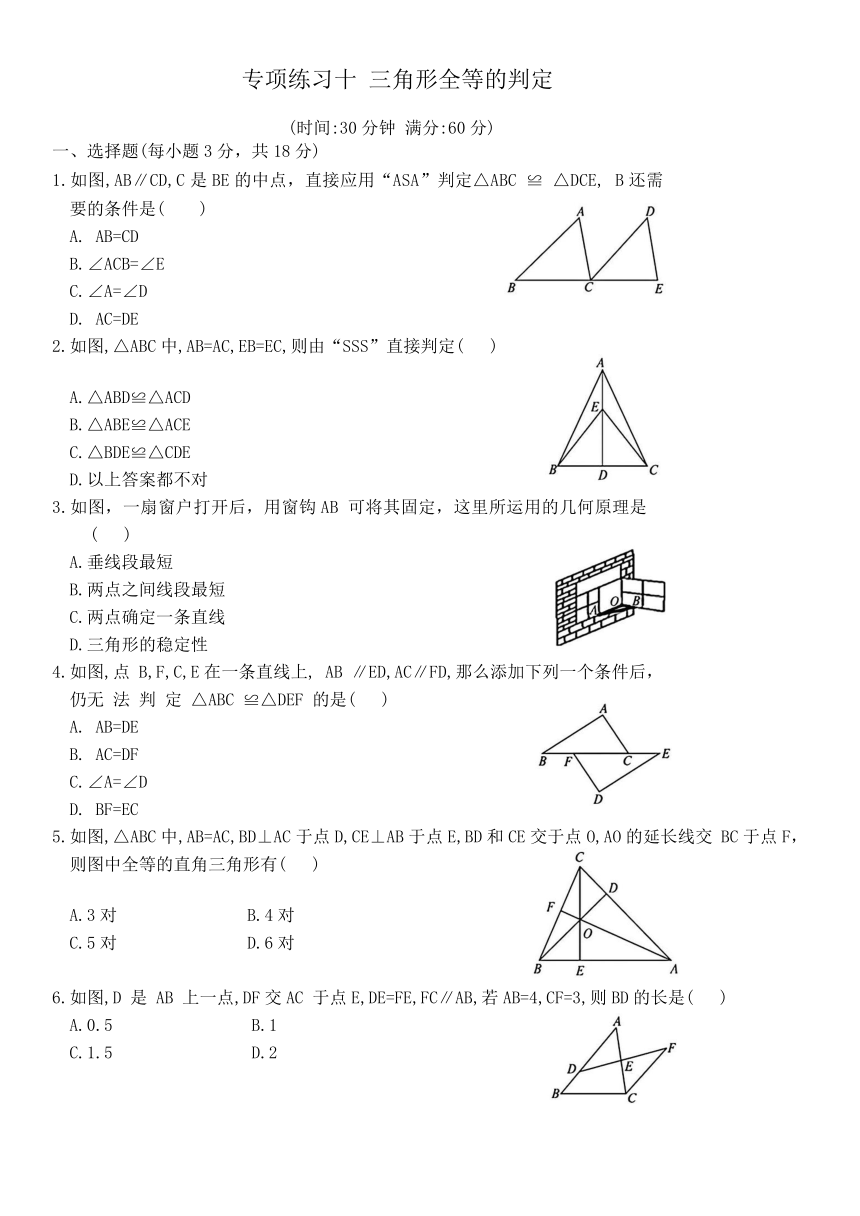
1.如图,AB∥CD,C是BE的中点,直接应用“ASA”判定△ABC ≌ △DCE, B还需要的条件是( )
A. AB=CD
B.∠ACB=∠E
C.∠A=∠D
D. AC=DE
2.如图,△ABC中,AB=AC,EB=EC,则由“SSS”直接判定( )
A.△ABD≌△ACD
B.△ABE≌△ACE
C.△BDE≌△CDE
D.以上答案都不对
3.如图,一扇窗户打开后,用窗钩AB 可将其固定,这里所运用的几何原理是 ( )
A.垂线段最短
B.两点之间线段最短
C.两点确定一条直线
D.三角形的稳定性
4.如图,点 B,F,C,E在一条直线上, AB ∥ED,AC∥FD,那么添加下列一个条件后,仍无 法 判 定 △ABC ≌△DEF 的是( )
A. AB=DE
B. AC=DF
C.∠A=∠D
D. BF=EC
5.如图,△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD和CE交于点O,AO的延长线交 BC于点F,则图中全等的直角三角形有( )
A.3对 B.4对
C.5对 D.6对
6.如图,D 是 AB 上一点,DF交AC 于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1
C.1.5 D.2
二、填空题(每小题4分,共16分)
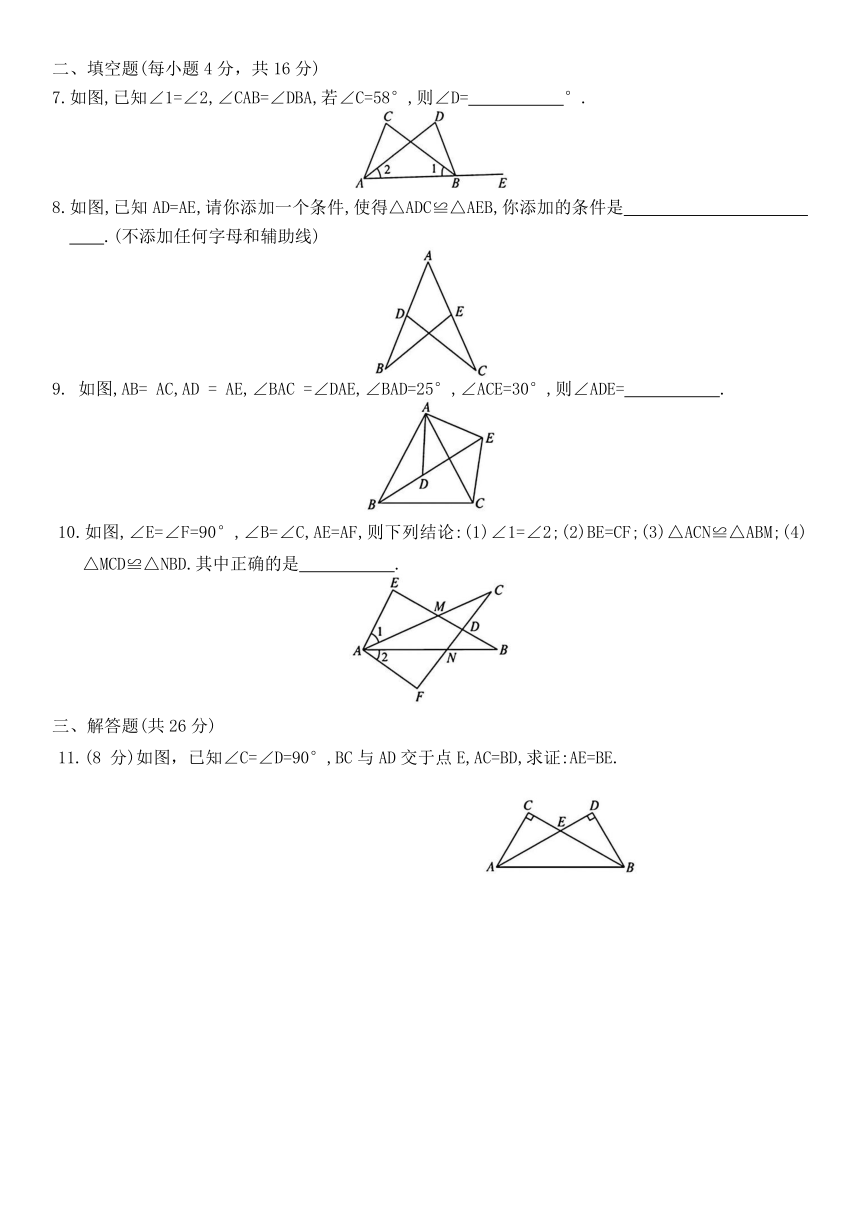
7.如图,已知∠1=∠2,∠CAB=∠DBA,若∠C=58°,则∠D= °.
8.如图,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是 .(不添加任何字母和辅助线)
9. 如图,AB= AC,AD = AE,∠BAC =∠DAE,∠BAD=25°,∠ACE=30°,则∠ADE= .
10.如图,∠E=∠F=90°,∠B=∠C,AE=AF,则下列结论:(1)∠1=∠2;(2)BE=CF;(3)△ACN≌△ABM;(4)△MCD≌△NBD.其中正确的是 .
三、解答题(共26分)
11.(8 分)如图,已知∠C=∠D=90°,BC与AD交于点E,AC=BD,求证:AE=BE.
12.(9分)已知△ABN 和△ACM 位置如图所示,AB = AC, AD =AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.
13.(9 分)已知,如图,△ABC 中, AC = AB,AD平分∠BAC,AD=BD.求证:CD⊥AC.
专项练习十 三角形全等的判定
1. B 2. B 3. D 4. C 5. D 6. B 7.58
8. AB=AC或∠ADC=∠AEB或∠ABE=∠ACD
9.55° 10.(1)(2)(3)(4)
11.证明 由∠C=∠D=90°,可知△ACB和△BDA是直角三角形.
在Rt△ACB和Rt△BDA中,
∴Rt△ACB≌Rt△BDA(HL),
∴∠ABC=∠BAD,∴AE=BE.
12.证明(1)在△ABD和△ACE中,因为AB=AC,∠1=∠2,AD=∠AE,所以△ABD≌△ACE(SAS).所以BD=CE.
(2)方法 1:因为∠1=∠2,所以∠1+∠DAE=∠2+∠DAE,即∠BAN=∠CAM.
由(1)得△ABD≌△ACE,所以∠B=∠C.
在△ACM和△ABN中,
因为∠C=∠B,AC=AB,∠CAM=∠BAN,
所以△ACM≌△ABN(ASA).所以∠M=∠N.
方法2:由(1)得△ABD≌△ACE,
所以∠BDA=∠CEA,所以∠MDO=∠NEO.
又因为∠MOD=∠NOE,所以∠M=∠N.
13.证明如图,在AB上截取AE=AC,连接DE.
因为 所以AE=
AB.所以AE=BE.
又因为AD=BD,DE=DE,所以△ADE≌△BDE(SSS).
所以∠AED=∠BED=90°.
因为AC=AE,∠DAC=∠DAE,AD=AD,
所以△ACD≌△AED(SAS).
所以∠ACD=∠AED=90°.所以CD⊥AC.
(时间:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
1.如图,AB∥CD,C是BE的中点,直接应用“ASA”判定△ABC ≌ △DCE, B还需要的条件是( )
A. AB=CD
B.∠ACB=∠E
C.∠A=∠D
D. AC=DE
2.如图,△ABC中,AB=AC,EB=EC,则由“SSS”直接判定( )
A.△ABD≌△ACD
B.△ABE≌△ACE
C.△BDE≌△CDE
D.以上答案都不对
3.如图,一扇窗户打开后,用窗钩AB 可将其固定,这里所运用的几何原理是 ( )
A.垂线段最短
B.两点之间线段最短
C.两点确定一条直线
D.三角形的稳定性
4.如图,点 B,F,C,E在一条直线上, AB ∥ED,AC∥FD,那么添加下列一个条件后,仍无 法 判 定 △ABC ≌△DEF 的是( )
A. AB=DE
B. AC=DF
C.∠A=∠D
D. BF=EC
5.如图,△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD和CE交于点O,AO的延长线交 BC于点F,则图中全等的直角三角形有( )
A.3对 B.4对
C.5对 D.6对
6.如图,D 是 AB 上一点,DF交AC 于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1
C.1.5 D.2
二、填空题(每小题4分,共16分)
7.如图,已知∠1=∠2,∠CAB=∠DBA,若∠C=58°,则∠D= °.
8.如图,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是 .(不添加任何字母和辅助线)
9. 如图,AB= AC,AD = AE,∠BAC =∠DAE,∠BAD=25°,∠ACE=30°,则∠ADE= .
10.如图,∠E=∠F=90°,∠B=∠C,AE=AF,则下列结论:(1)∠1=∠2;(2)BE=CF;(3)△ACN≌△ABM;(4)△MCD≌△NBD.其中正确的是 .
三、解答题(共26分)
11.(8 分)如图,已知∠C=∠D=90°,BC与AD交于点E,AC=BD,求证:AE=BE.
12.(9分)已知△ABN 和△ACM 位置如图所示,AB = AC, AD =AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.
13.(9 分)已知,如图,△ABC 中, AC = AB,AD平分∠BAC,AD=BD.求证:CD⊥AC.
专项练习十 三角形全等的判定
1. B 2. B 3. D 4. C 5. D 6. B 7.58
8. AB=AC或∠ADC=∠AEB或∠ABE=∠ACD
9.55° 10.(1)(2)(3)(4)
11.证明 由∠C=∠D=90°,可知△ACB和△BDA是直角三角形.
在Rt△ACB和Rt△BDA中,
∴Rt△ACB≌Rt△BDA(HL),
∴∠ABC=∠BAD,∴AE=BE.
12.证明(1)在△ABD和△ACE中,因为AB=AC,∠1=∠2,AD=∠AE,所以△ABD≌△ACE(SAS).所以BD=CE.
(2)方法 1:因为∠1=∠2,所以∠1+∠DAE=∠2+∠DAE,即∠BAN=∠CAM.
由(1)得△ABD≌△ACE,所以∠B=∠C.
在△ACM和△ABN中,
因为∠C=∠B,AC=AB,∠CAM=∠BAN,
所以△ACM≌△ABN(ASA).所以∠M=∠N.
方法2:由(1)得△ABD≌△ACE,
所以∠BDA=∠CEA,所以∠MDO=∠NEO.
又因为∠MOD=∠NOE,所以∠M=∠N.
13.证明如图,在AB上截取AE=AC,连接DE.
因为 所以AE=
AB.所以AE=BE.
又因为AD=BD,DE=DE,所以△ADE≌△BDE(SSS).
所以∠AED=∠BED=90°.
因为AC=AE,∠DAC=∠DAE,AD=AD,
所以△ACD≌△AED(SAS).
所以∠ACD=∠AED=90°.所以CD⊥AC.
