八年级上册沪科版数学14.2 三角形全等的性质与判定的应用 专项练习十一 (含答案)
文档属性
| 名称 | 八年级上册沪科版数学14.2 三角形全等的性质与判定的应用 专项练习十一 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 583.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 00:00:00 | ||
图片预览

文档简介
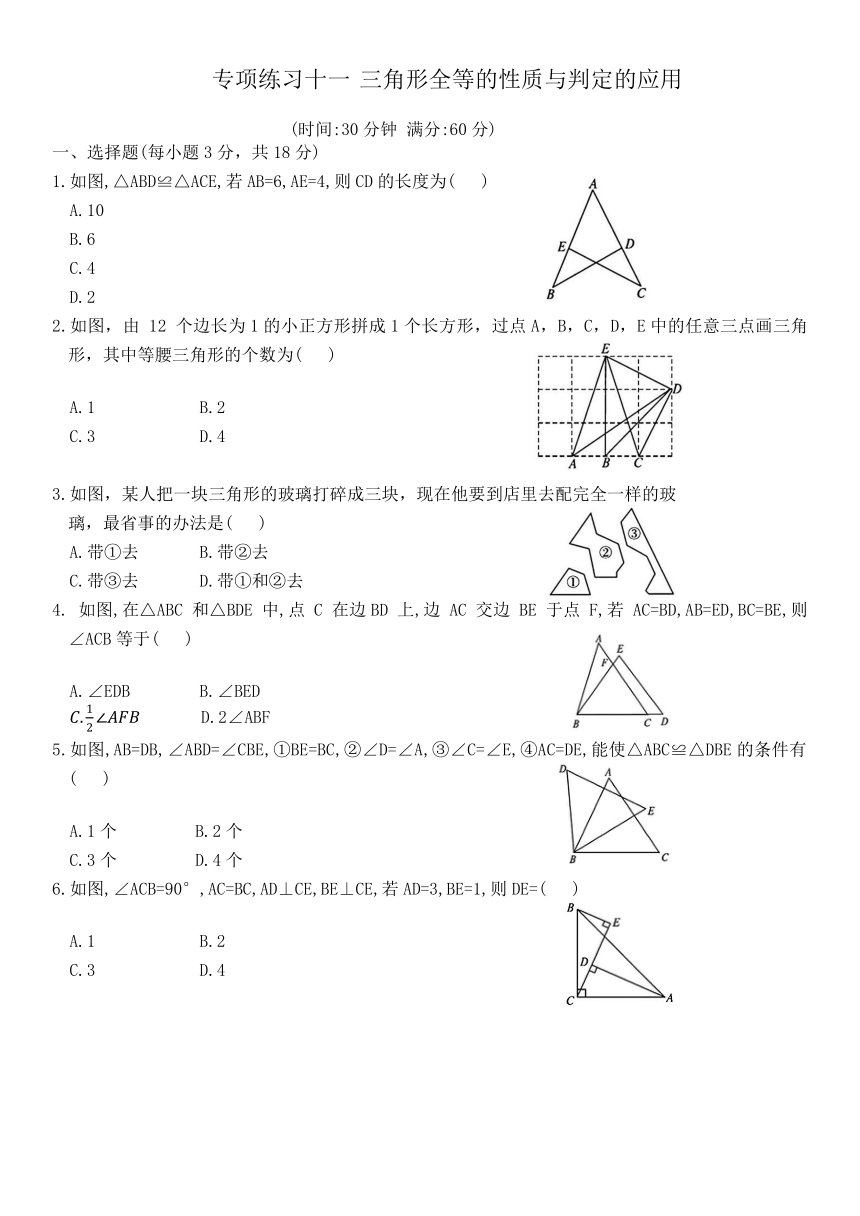
专项练习十一 三角形全等的性质与判定的应用
(时间:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
1.如图,△ABD≌△ACE,若AB=6,AE=4,则CD的长度为( )
A.10
B.6
C.4
D.2
2.如图,由 12 个边长为1的小正方形拼成1个长方形,过点A,B,C,D,E中的任意三点画三角形,其中等腰三角形的个数为( )
A.1 B.2
C.3 D.4
3.如图,某人把一块三角形的玻璃打碎成三块,现在他要到店里去配完全一样的玻璃,最省事的办法是( )
A.带①去 B.带②去
C.带③去 D.带①和②去
4. 如图,在△ABC 和△BDE 中,点 C 在边BD 上,边 AC 交边 BE 于点 F,若 AC=BD,AB=ED,BC=BE,则∠ACB等于( )
A.∠EDB B.∠BED
D.2∠ABF
5.如图,AB=DB,∠ABD=∠CBE,①BE=BC,②∠D=∠A,③∠C=∠E,④AC=DE,能使△ABC≌△DBE的条件有( )
A.1个 B.2个
C.3个 D.4个
6.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,若AD=3,BE=1,则DE=( )
A.1 B.2
C.3 D.4
二、填空题(每小题4分,共16分)
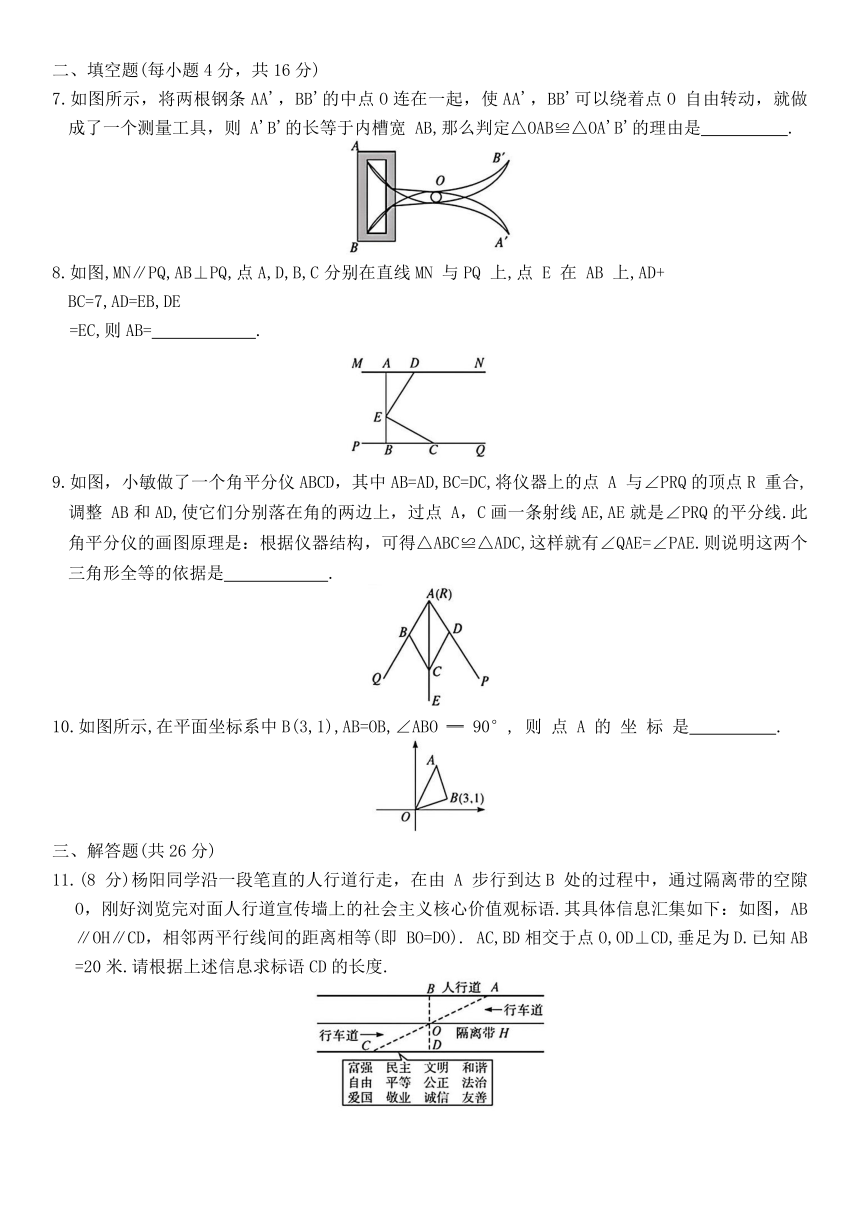
7.如图所示,将两根钢条AA',BB'的中点O连在一起,使AA',BB'可以绕着点O 自由转动,就做成了一个测量工具,则 A'B'的长等于内槽宽 AB,那么判定△OAB≌△OA'B'的理由是 .
8.如图,MN∥PQ,AB⊥PQ,点A,D,B,C分别在直线MN 与PQ 上,点 E 在 AB 上,AD+BC=7,AD=EB,DE
=EC,则AB= .
9.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点 A 与∠PRQ的顶点R 重合,调整 AB和AD,使它们分别落在角的两边上,过点 A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是 .
10.如图所示,在平面坐标系中B(3,1),AB=OB,∠ABO ═ 90°, 则 点 A 的 坐 标 是 .
三、解答题(共26分)
11.(8 分)杨阳同学沿一段笔直的人行道行走,在由 A 步行到达B 处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下:如图,AB∥OH∥CD,相邻两平行线间的距离相等(即 BO=DO). AC,BD相交于点O,OD⊥CD,垂足为D.已知AB=20米.请根据上述信息求标语CD的长度.
12.(9分)如图,点 B,F,C,E 在一条直线上(点 F,C之间不能直接测量),点 A,D 在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)求证:△ABC≌△DEF;
(2)若 BE=14 m,BF=5 m,求 FC 的长度.
13.(9 分)如图 1 所示,已知在△ABC 中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B 点和C 点在AE 的异侧,BD⊥AE于D点,CE⊥AE于E点.
(1)求证:BD=DE+CE;
(2)若直线 AE 绕点 A 旋转到图 2 所示的位置时(BD(3)若直线AE 绕点 A 旋转到图 3 所示的位置时(BD>CE),其余条件不变,问BD 与DE,CE的关系如何 直接写出结果,不需证明.
专项练习十一 三角形全等的性质与判定的应用
1. D 2. B 3. C 4. C 5. C 6. B 7. SAS 8.7 9. SSS10.(2,4)
11.解 ∵AB∥DC,DO⊥CD,∴∠ABO=∠CDO=90°.
又∵∠AOB=∠COD,BO=DO,∴△BOA≌△DOC.
∴CD=AB=20米.
12.解(1)证明 ∵AB∥DE,
∴∠ABC=∠DEF.
∵AC∥DF,
∴∠ACB=∠DFE.
在△ABC与△DEF中
∴△ABC≌△DEF(AAS).
(2)∵△ABC≌△DEF,∴BC=EF.
∴BF+FC=EC+FC.
∴BF=EC.
∵BE=14m,BF=5m,
∴FC=14-5-5=4(m).
13.解(1)证明∵BD⊥AE于D点,CE⊥AE 于E点,
∴∠ADB=∠AEC=90°.
∵∠BAC=90°,∠ADB=90°,
∵∠ABD+∠BAD=∠CAE+∠BAD=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∠ABD=∠CAE,∠ADB=∠CEA,AB=AC.
∴△ABD≌△CAE(AAS).
∴BD=AE,AD=CE.
∵AE=AD+DE,
∴BD=DE+CE.
(2)BD=DE-CE.
证明如下:
∵BD⊥AE于D点,CE⊥AE于E点,
∴∠DAB+∠DBA=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°.
∴∠DBA=∠CAE.
在△DBA和△EAC中,∠D=∠E=90°,∠DBA=∠CAE,AB=AC,
∴△DBA≌△EAC(AAS).
∴BD=AE,AD=CE.
∴BD=AE=DE-AD=DE--CE.
(3)DE=BD+CE.
(时间:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
1.如图,△ABD≌△ACE,若AB=6,AE=4,则CD的长度为( )
A.10
B.6
C.4
D.2
2.如图,由 12 个边长为1的小正方形拼成1个长方形,过点A,B,C,D,E中的任意三点画三角形,其中等腰三角形的个数为( )
A.1 B.2
C.3 D.4
3.如图,某人把一块三角形的玻璃打碎成三块,现在他要到店里去配完全一样的玻璃,最省事的办法是( )
A.带①去 B.带②去
C.带③去 D.带①和②去
4. 如图,在△ABC 和△BDE 中,点 C 在边BD 上,边 AC 交边 BE 于点 F,若 AC=BD,AB=ED,BC=BE,则∠ACB等于( )
A.∠EDB B.∠BED
D.2∠ABF
5.如图,AB=DB,∠ABD=∠CBE,①BE=BC,②∠D=∠A,③∠C=∠E,④AC=DE,能使△ABC≌△DBE的条件有( )
A.1个 B.2个
C.3个 D.4个
6.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,若AD=3,BE=1,则DE=( )
A.1 B.2
C.3 D.4
二、填空题(每小题4分,共16分)
7.如图所示,将两根钢条AA',BB'的中点O连在一起,使AA',BB'可以绕着点O 自由转动,就做成了一个测量工具,则 A'B'的长等于内槽宽 AB,那么判定△OAB≌△OA'B'的理由是 .
8.如图,MN∥PQ,AB⊥PQ,点A,D,B,C分别在直线MN 与PQ 上,点 E 在 AB 上,AD+BC=7,AD=EB,DE
=EC,则AB= .
9.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点 A 与∠PRQ的顶点R 重合,调整 AB和AD,使它们分别落在角的两边上,过点 A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是 .
10.如图所示,在平面坐标系中B(3,1),AB=OB,∠ABO ═ 90°, 则 点 A 的 坐 标 是 .
三、解答题(共26分)
11.(8 分)杨阳同学沿一段笔直的人行道行走,在由 A 步行到达B 处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下:如图,AB∥OH∥CD,相邻两平行线间的距离相等(即 BO=DO). AC,BD相交于点O,OD⊥CD,垂足为D.已知AB=20米.请根据上述信息求标语CD的长度.
12.(9分)如图,点 B,F,C,E 在一条直线上(点 F,C之间不能直接测量),点 A,D 在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)求证:△ABC≌△DEF;
(2)若 BE=14 m,BF=5 m,求 FC 的长度.
13.(9 分)如图 1 所示,已知在△ABC 中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B 点和C 点在AE 的异侧,BD⊥AE于D点,CE⊥AE于E点.
(1)求证:BD=DE+CE;
(2)若直线 AE 绕点 A 旋转到图 2 所示的位置时(BD
专项练习十一 三角形全等的性质与判定的应用
1. D 2. B 3. C 4. C 5. C 6. B 7. SAS 8.7 9. SSS10.(2,4)
11.解 ∵AB∥DC,DO⊥CD,∴∠ABO=∠CDO=90°.
又∵∠AOB=∠COD,BO=DO,∴△BOA≌△DOC.
∴CD=AB=20米.
12.解(1)证明 ∵AB∥DE,
∴∠ABC=∠DEF.
∵AC∥DF,
∴∠ACB=∠DFE.
在△ABC与△DEF中
∴△ABC≌△DEF(AAS).
(2)∵△ABC≌△DEF,∴BC=EF.
∴BF+FC=EC+FC.
∴BF=EC.
∵BE=14m,BF=5m,
∴FC=14-5-5=4(m).
13.解(1)证明∵BD⊥AE于D点,CE⊥AE 于E点,
∴∠ADB=∠AEC=90°.
∵∠BAC=90°,∠ADB=90°,
∵∠ABD+∠BAD=∠CAE+∠BAD=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
∠ABD=∠CAE,∠ADB=∠CEA,AB=AC.
∴△ABD≌△CAE(AAS).
∴BD=AE,AD=CE.
∵AE=AD+DE,
∴BD=DE+CE.
(2)BD=DE-CE.
证明如下:
∵BD⊥AE于D点,CE⊥AE于E点,
∴∠DAB+∠DBA=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°.
∴∠DBA=∠CAE.
在△DBA和△EAC中,∠D=∠E=90°,∠DBA=∠CAE,AB=AC,
∴△DBA≌△EAC(AAS).
∴BD=AE,AD=CE.
∴BD=AE=DE-AD=DE--CE.
(3)DE=BD+CE.
