八年级上册沪科版数学 15.2 线段的垂直平分线 专项练习十三(含答案)
文档属性
| 名称 | 八年级上册沪科版数学 15.2 线段的垂直平分线 专项练习十三(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 527.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 19:35:35 | ||
图片预览

文档简介
专项练习十三 线段的垂直平分线
(时间:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
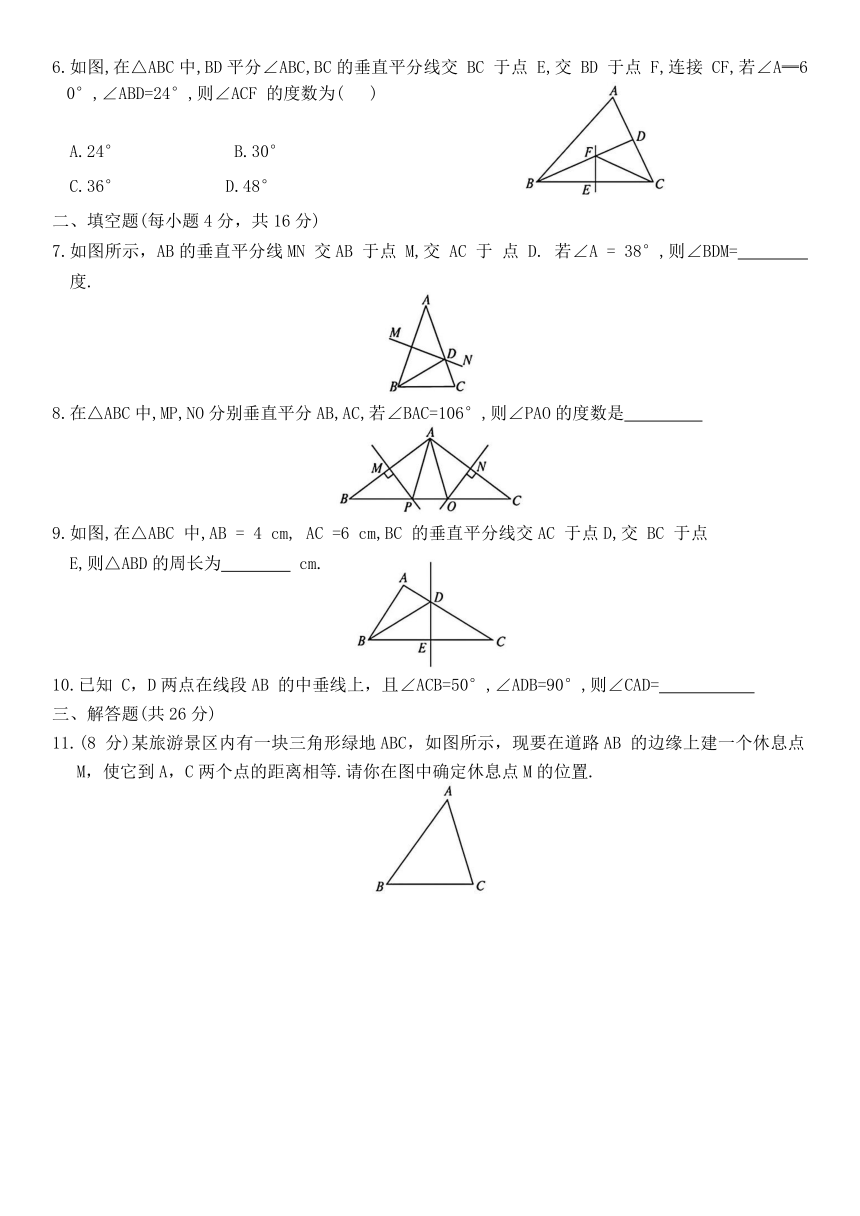
1.通过如下尺规作图,能确定点D是BC边中点的是( )
2.如图,在△ABC中,DE是AC 的垂直平分线,分别交 BC,AC于点 D,E,连接AD,若△ABD 的周长(C△ABD=16 cm,AB=5cm ,则线段 BC的长度等于( )
A.8 cm B.9 cm
C.10 cm D.11 cm
3.如图,P是△ABC内一点,若PB=PC,则( )
A.点 P 在∠ABC的平分线上
B.点 P 在∠ACB的平分线上
C.点 P 在边AB 的垂直平分线上
D.点 P 在边BC 的垂直平分线上
4.如图,已知 BD 是△ABC的角平分线,ED是BC的垂直平分线,CE=4,△ABD的周长为12,则△ABC的周长为( )
A.12 B.16
C.20 D.24
5.如图,分别以线段AC的两个端点A,C为圆心,大于 AC的长为半径画弧,两弧相交于 B,D两点,连接 BD,AB,BC,CD,DA.以下结论:①BD垂直平分AC,②AC平分∠BAD,③AC=BD,④四边形ABCD是轴对称图形.其中正确的有( )
A.①②③ B.①③④
C.①②④ D. ②③④
6.如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交 BC 于点 E,交 BD 于点 F,连接 CF,若∠A═60°,∠ABD=24°,则∠ACF 的度数为( )
A.24° B.30°
C.36° D.48°
二、填空题(每小题4分,共16分)
7.如图所示,AB的垂直平分线MN 交AB 于点 M,交 AC 于 点 D. 若∠A = 38°,则∠BDM= 度.
8.在△ABC中,MP,NO分别垂直平分AB,AC,若∠BAC=106°,则∠PAO的度数是
9.如图,在△ABC 中,AB = 4 cm, AC =6 cm,BC 的垂直平分线交AC 于点D,交 BC 于点 E,则△ABD的周长为 cm.
10.已知 C,D两点在线段AB 的中垂线上,且∠ACB=50°,∠ADB=90°,则∠CAD=
三、解答题(共26分)
11.(8 分)某旅游景区内有一块三角形绿地ABC,如图所示,现要在道路AB 的边缘上建一个休息点M,使它到A,C两个点的距离相等.请你在图中确定休息点M的位置.
12.(9分)如图,在△ABC中,∠C=60°,∠A=40°.
(1)用尺规作图作AB 的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
13.如图所示,∠ABD=∠CBD.
(1)如图①,DE⊥AB 于点E,DF⊥BC于点F.求证:BD 垂直平分EF;
(2)如图②,当有一点 G 从点 D 向点 B 运动时,GE⊥AB于点E,GF⊥BC于点F,此时(1)中的结论是否成立 请证明;
(3)如图③,当点 G 从点 D 在 BD 的延长线上运动时,GE⊥AB(或其延长线)于点E,GF⊥BC(或其延长线)于点 F,此时(1)中的结论是否成立 不需要证明.
专项练习十三 线段的垂直平分线
1. A 2. D 3. D 4. C 5. C 6. D 7.52 8.32° 9.10 或
11.解如图所示,作AC的垂直平分线交AB 于点M,则点 M为所求.
12.解(1)如图1所示:
(2)连接BD,如图2所示:
∵DE是AB的垂直平分线,
∴BD平分
13.解(1)证明: 于点E, 于点F,
在 和 中
∴点D,B在EF 的垂直平分线上.∴BD垂直平分EF.
(2)成立.证明如下:
同(1)可证
∴点G,B在EF 的垂直平分线上.∴BD垂直平分EF.
(3)成立.
(时间:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
1.通过如下尺规作图,能确定点D是BC边中点的是( )
2.如图,在△ABC中,DE是AC 的垂直平分线,分别交 BC,AC于点 D,E,连接AD,若△ABD 的周长(C△ABD=16 cm,AB=5cm ,则线段 BC的长度等于( )
A.8 cm B.9 cm
C.10 cm D.11 cm
3.如图,P是△ABC内一点,若PB=PC,则( )
A.点 P 在∠ABC的平分线上
B.点 P 在∠ACB的平分线上
C.点 P 在边AB 的垂直平分线上
D.点 P 在边BC 的垂直平分线上
4.如图,已知 BD 是△ABC的角平分线,ED是BC的垂直平分线,CE=4,△ABD的周长为12,则△ABC的周长为( )
A.12 B.16
C.20 D.24
5.如图,分别以线段AC的两个端点A,C为圆心,大于 AC的长为半径画弧,两弧相交于 B,D两点,连接 BD,AB,BC,CD,DA.以下结论:①BD垂直平分AC,②AC平分∠BAD,③AC=BD,④四边形ABCD是轴对称图形.其中正确的有( )
A.①②③ B.①③④
C.①②④ D. ②③④
6.如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交 BC 于点 E,交 BD 于点 F,连接 CF,若∠A═60°,∠ABD=24°,则∠ACF 的度数为( )
A.24° B.30°
C.36° D.48°
二、填空题(每小题4分,共16分)
7.如图所示,AB的垂直平分线MN 交AB 于点 M,交 AC 于 点 D. 若∠A = 38°,则∠BDM= 度.
8.在△ABC中,MP,NO分别垂直平分AB,AC,若∠BAC=106°,则∠PAO的度数是
9.如图,在△ABC 中,AB = 4 cm, AC =6 cm,BC 的垂直平分线交AC 于点D,交 BC 于点 E,则△ABD的周长为 cm.
10.已知 C,D两点在线段AB 的中垂线上,且∠ACB=50°,∠ADB=90°,则∠CAD=
三、解答题(共26分)
11.(8 分)某旅游景区内有一块三角形绿地ABC,如图所示,现要在道路AB 的边缘上建一个休息点M,使它到A,C两个点的距离相等.请你在图中确定休息点M的位置.
12.(9分)如图,在△ABC中,∠C=60°,∠A=40°.
(1)用尺规作图作AB 的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
13.如图所示,∠ABD=∠CBD.
(1)如图①,DE⊥AB 于点E,DF⊥BC于点F.求证:BD 垂直平分EF;
(2)如图②,当有一点 G 从点 D 向点 B 运动时,GE⊥AB于点E,GF⊥BC于点F,此时(1)中的结论是否成立 请证明;
(3)如图③,当点 G 从点 D 在 BD 的延长线上运动时,GE⊥AB(或其延长线)于点E,GF⊥BC(或其延长线)于点 F,此时(1)中的结论是否成立 不需要证明.
专项练习十三 线段的垂直平分线
1. A 2. D 3. D 4. C 5. C 6. D 7.52 8.32° 9.10 或
11.解如图所示,作AC的垂直平分线交AB 于点M,则点 M为所求.
12.解(1)如图1所示:
(2)连接BD,如图2所示:
∵DE是AB的垂直平分线,
∴BD平分
13.解(1)证明: 于点E, 于点F,
在 和 中
∴点D,B在EF 的垂直平分线上.∴BD垂直平分EF.
(2)成立.证明如下:
同(1)可证
∴点G,B在EF 的垂直平分线上.∴BD垂直平分EF.
(3)成立.
