八年级上册沪科版数学 15.4角的平分线 专项练习十五(含答案)
文档属性
| 名称 | 八年级上册沪科版数学 15.4角的平分线 专项练习十五(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 277.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 00:00:00 | ||
图片预览

文档简介
专项练习十五 角的平分线
(时间:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
1.如图,OP平分∠MON,PA⊥OA 于点A,点Q是射线OM 上的一个动点,若PA=2,则 PQ的值为( )
A.1 B.2
C.大于2 D.不小于2
2.如图,有两把完全相同的直尺,一把直尺压住射线OB,另一把直尺压住射线OA 并且与第一把直尺交于点 P,小明说:“射线OP就是∠BOA 的平分线.”他这样说的依据是( )
A.角的内部到角的两边的距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
3.如图,以C为圆心,以大于点C到AB距离为半径作弧交 AB 于点 D,E,再以D,E为圆心,以大于 DE 为半径作弧,两弧交于点 F,作射线CF,则( )
A. CF平分∠ACB B. CF⊥AB
C. CF平分AB D. CF 垂直平分AB
4.如图,△ABC的三边AB,BC,CA 的长分别是60,70,80,其三条角平分线将△ABC
分为三个三角形,则S△ABO : S△BCO :S△CAO等于( )
A.1:1:1 B.1:2:3
C.3:7:4 D.6:7: 8
5.已知∠AOB=60°,以O为圆心,以任意长为半径作弧,交OA,OB于点M,N,分别以点 M,N为圆心,以大于 MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )
A.15° B.45°
C.15°或 30° D.15°或45°
6.如图,∠B=∠C=90°,M是BC 的中点,DM 平分∠ADC,且∠ADC = 110°, 则∠MAB=( )
A.30° B.35°
C.45° D.60°
二、填空题(每小题4分,共16分)
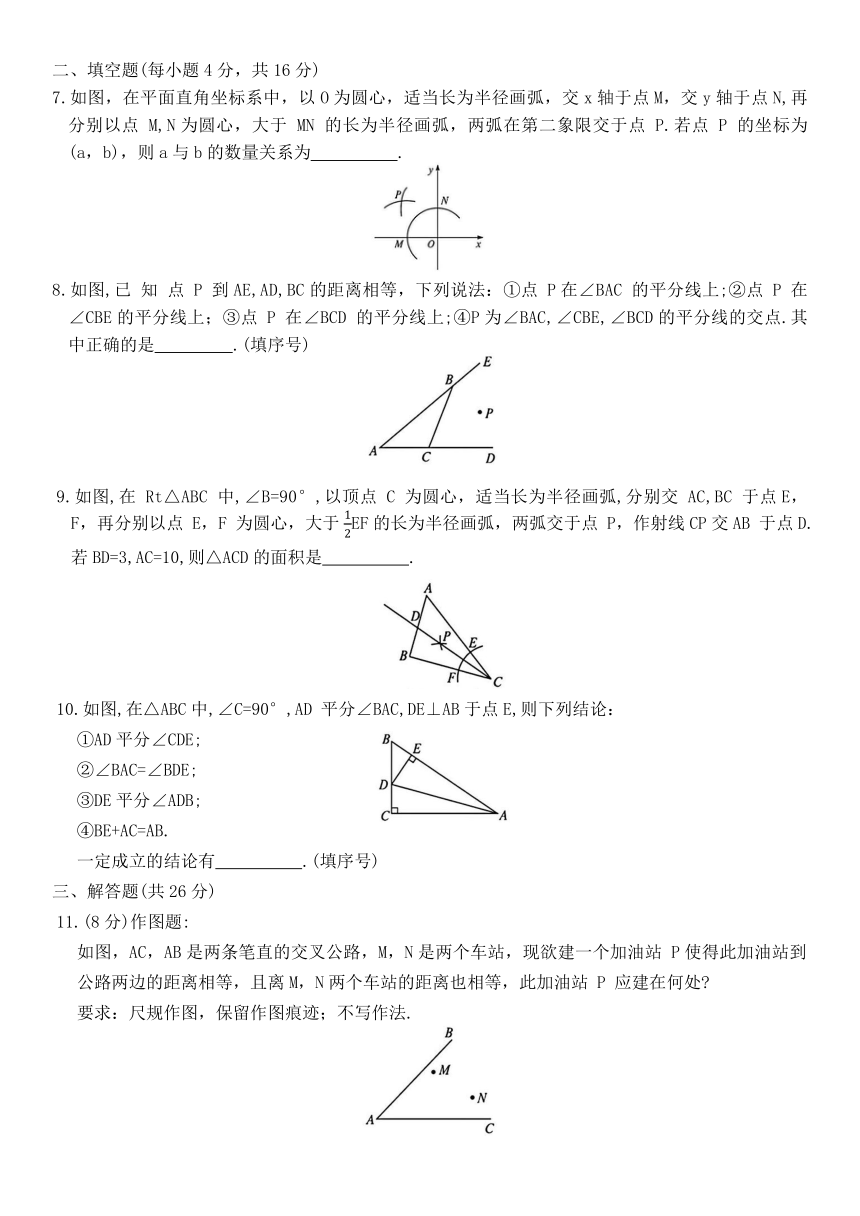
7.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点 M,N为圆心,大于 MN 的长为半径画弧,两弧在第二象限交于点 P.若点 P 的坐标为(a,b),则a与b的数量关系为 .
8.如图,已 知 点 P 到AE,AD,BC的距离相等,下列说法:①点 P在∠BAC 的平分线上;②点 P 在∠CBE的平分线上;③点 P 在∠BCD 的平分线上;④P为∠BAC,∠CBE,∠BCD的平分线的交点.其中正确的是 .(填序号)
9.如图,在 Rt△ABC 中,∠B=90°,以顶点 C 为圆心,适当长为半径画弧,分别交 AC,BC 于点E,F,再分别以点 E,F 为圆心,大于 EF的长为半径画弧,两弧交于点 P,作射线CP交AB 于点D.若BD=3,AC=10,则△ACD的面积是 .
10.如图,在△ABC中,∠C=90°,AD 平分∠BAC,DE⊥AB于点E,则下列结论:
①AD平分∠CDE;
②∠BAC=∠BDE;
③DE平分∠ADB;
④BE+AC=AB.
一定成立的结论有 .(填序号)
三、解答题(共26分)
11.(8分)作图题:
如图,AC,AB是两条笔直的交叉公路,M,N是两个车站,现欲建一个加油站 P使得此加油站到公路两边的距离相等,且离M,N两个车站的距离也相等,此加油站 P 应建在何处
要求:尺规作图,保留作图痕迹;不写作法.
12.(9分)如图,在△ABC中,AD 是∠BAC 的平分线,且BD=CD.
求证:∠B=∠C.
13. (9 分) 如 图, 在△ABC中,D 是BC边的中点,PD⊥BC交∠BAC的平分线于点 P,PE⊥AB交其延长线于点E,PF⊥AC于点F,则BE=CF,为什么
专项练习十五 角的平分线
1. D 2. A 3. B 4. D 5. D 6. B 7. a+b=08.①②③④ 9.15 10.①②④
11.解 如图所示,点P就是所求的点.
12.证明作DM⊥AB,DN⊥AC,垂足分别为M,N.
∵AD 是∠BAC的平分线,∴DM=DN.
又∵BD=CD,∴Rt△BDM≌Rt△CDN(HL).
∴∠B=∠C.
13.证明连接PB,PC,
∵PE⊥AB,PF⊥AC,AP 平分∠BAC,∴PE=PF.
∵PD垂直平分线段BC,
∴PB=PC.
在Rt△PEB和Rt△PFC中,
∴Rt△PEB≌Rt△PFC(HL).∴BE=CF.
(时间:30分钟 满分:60分)
一、选择题(每小题3分,共18分)
1.如图,OP平分∠MON,PA⊥OA 于点A,点Q是射线OM 上的一个动点,若PA=2,则 PQ的值为( )
A.1 B.2
C.大于2 D.不小于2
2.如图,有两把完全相同的直尺,一把直尺压住射线OB,另一把直尺压住射线OA 并且与第一把直尺交于点 P,小明说:“射线OP就是∠BOA 的平分线.”他这样说的依据是( )
A.角的内部到角的两边的距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
3.如图,以C为圆心,以大于点C到AB距离为半径作弧交 AB 于点 D,E,再以D,E为圆心,以大于 DE 为半径作弧,两弧交于点 F,作射线CF,则( )
A. CF平分∠ACB B. CF⊥AB
C. CF平分AB D. CF 垂直平分AB
4.如图,△ABC的三边AB,BC,CA 的长分别是60,70,80,其三条角平分线将△ABC
分为三个三角形,则S△ABO : S△BCO :S△CAO等于( )
A.1:1:1 B.1:2:3
C.3:7:4 D.6:7: 8
5.已知∠AOB=60°,以O为圆心,以任意长为半径作弧,交OA,OB于点M,N,分别以点 M,N为圆心,以大于 MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )
A.15° B.45°
C.15°或 30° D.15°或45°
6.如图,∠B=∠C=90°,M是BC 的中点,DM 平分∠ADC,且∠ADC = 110°, 则∠MAB=( )
A.30° B.35°
C.45° D.60°
二、填空题(每小题4分,共16分)
7.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点 M,N为圆心,大于 MN 的长为半径画弧,两弧在第二象限交于点 P.若点 P 的坐标为(a,b),则a与b的数量关系为 .
8.如图,已 知 点 P 到AE,AD,BC的距离相等,下列说法:①点 P在∠BAC 的平分线上;②点 P 在∠CBE的平分线上;③点 P 在∠BCD 的平分线上;④P为∠BAC,∠CBE,∠BCD的平分线的交点.其中正确的是 .(填序号)
9.如图,在 Rt△ABC 中,∠B=90°,以顶点 C 为圆心,适当长为半径画弧,分别交 AC,BC 于点E,F,再分别以点 E,F 为圆心,大于 EF的长为半径画弧,两弧交于点 P,作射线CP交AB 于点D.若BD=3,AC=10,则△ACD的面积是 .
10.如图,在△ABC中,∠C=90°,AD 平分∠BAC,DE⊥AB于点E,则下列结论:
①AD平分∠CDE;
②∠BAC=∠BDE;
③DE平分∠ADB;
④BE+AC=AB.
一定成立的结论有 .(填序号)
三、解答题(共26分)
11.(8分)作图题:
如图,AC,AB是两条笔直的交叉公路,M,N是两个车站,现欲建一个加油站 P使得此加油站到公路两边的距离相等,且离M,N两个车站的距离也相等,此加油站 P 应建在何处
要求:尺规作图,保留作图痕迹;不写作法.
12.(9分)如图,在△ABC中,AD 是∠BAC 的平分线,且BD=CD.
求证:∠B=∠C.
13. (9 分) 如 图, 在△ABC中,D 是BC边的中点,PD⊥BC交∠BAC的平分线于点 P,PE⊥AB交其延长线于点E,PF⊥AC于点F,则BE=CF,为什么
专项练习十五 角的平分线
1. D 2. A 3. B 4. D 5. D 6. B 7. a+b=08.①②③④ 9.15 10.①②④
11.解 如图所示,点P就是所求的点.
12.证明作DM⊥AB,DN⊥AC,垂足分别为M,N.
∵AD 是∠BAC的平分线,∴DM=DN.
又∵BD=CD,∴Rt△BDM≌Rt△CDN(HL).
∴∠B=∠C.
13.证明连接PB,PC,
∵PE⊥AB,PF⊥AC,AP 平分∠BAC,∴PE=PF.
∵PD垂直平分线段BC,
∴PB=PC.
在Rt△PEB和Rt△PFC中,
∴Rt△PEB≌Rt△PFC(HL).∴BE=CF.
