2023-2024学年重庆市主城四区高二下学期期末高中学生学业质量调研测试数学试题(含解析)
文档属性
| 名称 | 2023-2024学年重庆市主城四区高二下学期期末高中学生学业质量调研测试数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 498.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 17:20:05 | ||
图片预览




文档简介
2023-2024学年重庆市主城四区高二下学期期末
数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.若的展开式中二项式系数之和为,则展开式中含项的系数为( )
A. B. C. D.
3.若命题“,”为假命题,则实数的取值范围是( )
A. B. C. D.
4.某次高二质量抽测中,学生的数学成绩X服从正态分布N(96,144).已知参加本次考试的学生约有10000人,如果小明在这次考试中数学成绩为120分,则小明的数学成绩在本次抽测的名次大约是( ) 附:若X~N(,),则P(-< X<+)=0.6827,P(-2< X<+2)=0.9545
A. 第228名 B. 第455名 C. 第1587名 D. 第3173名
5.若,则“”是“”的( )
A. 充要条件 B. 充分不必要条件
C. 必要不充分条件 D. 既不充分也不必要条件
6.阿基米德有句名言:“给我一个支点,我就能撬起整个地球”这句话说的使是杠杆原理,即“动力动力臂阻力阻力臂”现有一商店使用两臂不等长的天平称黄金,一位顾客到店里预购买黄金,售货员先将的砝码放在天平左盘中,取出黄金放在天平右盘中使天平平衡再将的砝码放在天平右盘中,取黄金放在天平左盘中使天平平衡,最后将称得的和黄金交给顾客,则顾客购得的黄金重量( )
A. 大于 B. 等于 C. 小于 D. 无法确定
7.春节期间,第二十条、热辣滚烫和飞驰人生三部电影引爆了电影市场某班有四名同学都要观看电影并且每人只能选择这三部中的一部电影观看,如果他们中有同学选择观看第二十条,则这四名同学不同的观影情况种数为( )
A. B. C. D.
8.若方程恰有三个不相等的实根,则的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.若,,则下列结论正确的是( )
A.
B.
C.
D.
10.下列说法正确的有( )
A. 若,两组成对数据的样本相关系数分别为,,则组数据比组数据的相关性更强
B. 若关于的经验回归方程为,则样本点的残差为
C. 已知随机变量服从二项分布,若,则
D. 已知随机变量~N(2,81),若=3+1,则D()=9
11.已知,且,则下列结论正确的是( )
A. B. C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.已知,则 .
13.某同学参加学校组织的数学知识竞赛,在道四选一的单选题中,有道有思路,有道完全没有思路,有思路的题每道做对的概率均为,没有思路的题只好任意猜一个答案若从这道题中任选题作答,则该同学道题都做对的概率为 .
14.哈希算法是一种特殊的函数,也是一种加密技术已知是最简单的哈希算法之一,它把一个较大数字的每一位改成它除以素数所得到的余数例如:对于数字进行得到的哈希值为,那么对于数字进行得到的哈希值为 现对一个正整数进行后得到哈希值为,则这样的正整数共有 个用数字作答
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知函数,,若在处与直线相切.
求,的值
求的最大值.
16.本小题分
喝酒不开车,开车不喝酒根据中华人民共和国道路交通安全法规定:血液酒精浓度在含以上认定为醉酒驾车某地统计近年来查处的醉酒驾车共人,这人血液酒精浓度检测结果按,,,分组,得到如图所示的频率分布直方图.
求这人血液酒精浓度的平均值同一组数据用该区间中点值作为代表
求这人中血液酒精浓度在的人数
按比例分配分层随机抽样的方法,在酒精浓度为和人员中随机抽取人集中学习现从这人中抽取人检查学习效果,求抽到的人员恰有人酒精浓度为的概率.
17.本小题分
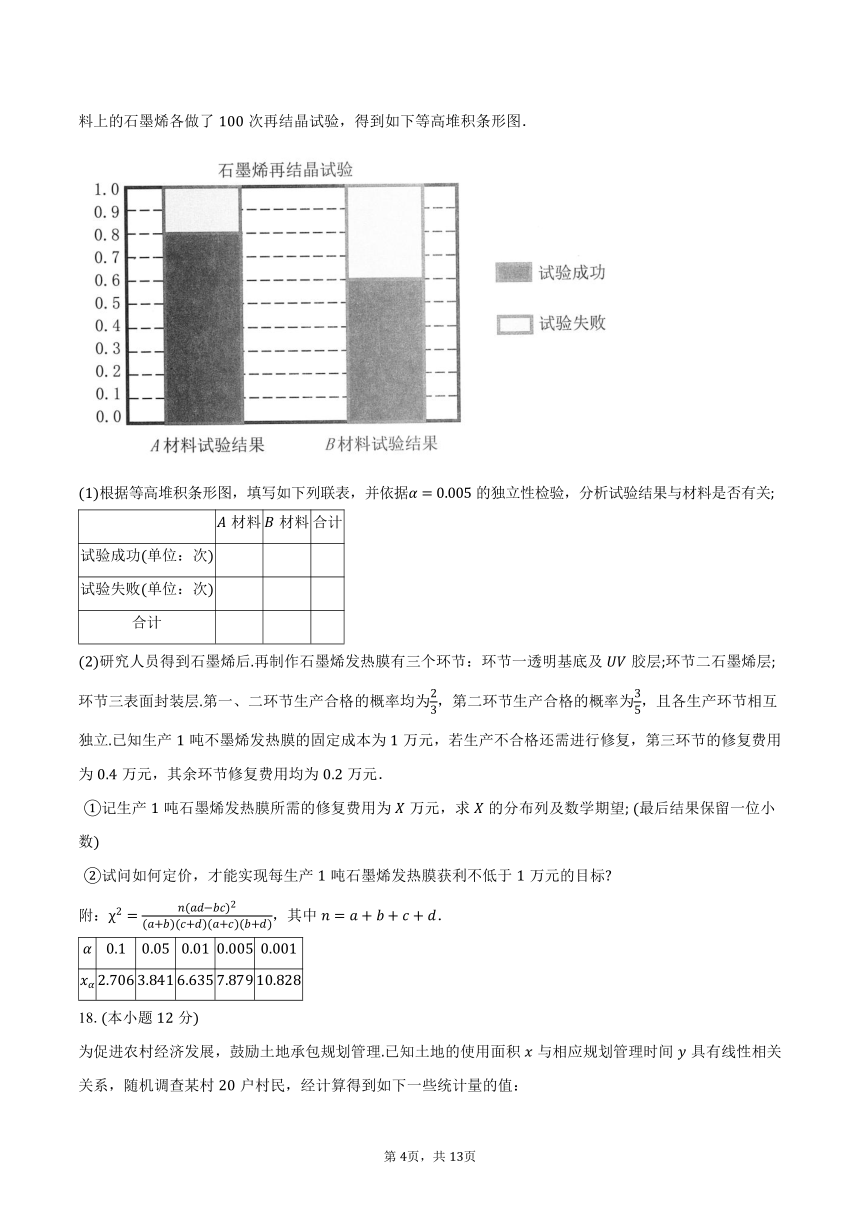
从石墨中通过化学气相沉积法分离出石墨烯,升华后附着在材料上再结晶制成石墨烯发热膜。石墨烯发热膜轻薄、保暖,广泛应用于冬装衣服。现在有材料、材料可供选择,研究人员对附着在材料、材料上的石墨烯各做了次再结晶试验,得到如下等高堆积条形图.
根据等高堆积条形图,填写如下列联表,并依据的独立性检验,分析试验结果与材料是否有关
材料 材料 合计
试验成功单位:次
试验失败单位:次
合计
研究人员得到石墨烯后再制作石墨烯发热膜有三个环节:环节一透明基底及胶层环节二石墨烯层环节三表面封装层第一、二环节生产合格的概率均为,第二环节生产合格的概率为,且各生产环节相互独立已知生产吨不墨烯发热膜的固定成本为万元,若生产不合格还需进行修复,第三环节的修复费用为万元,其余环节修复费用均为万元.
记生产吨石墨烯发热膜所需的修复费用为万元,求的分布列及数学期望最后结果保留一位小数
试问如何定价,才能实现每生产吨石墨烯发热膜获利不低于万元的目标
附:,其中.
18.本小题分
为促进农村经济发展,鼓励土地承包规划管理已知土地的使用面积与相应规划管理时间具有线性相关关系,随机调查某村户村民,经计算得到如下一些统计量的值:
,,,.
求关于的经验回归方程
调查发现,家庭中女士不同意参与规划管理的概率为,男士不同意参与规划管理的概率为,男女是否同意参与规划管理相互独立只要有一方不同意参与规划管理,则该家庭就决定不参与规划管理若在抽查中发现家不同意参与规划管理,求其中至少家有女士不同意参与规划管理的概率.
参考公式:对于一组数据,,,,其经验回归方程的斜率和截距的最小二乘法估计公式分别为,.
19.本小题分
已知函数.
若函数在上单调递增,求实数的取值范围
若函数恰有两个极值点,,且的最大值为,求证:.
答案解析
1.
【解析】解:因为,
所以,
又,
所以
故选C.
2.
【解析】解:因为二项式的所有二项式系数之和等于,
所以,解得,
二项展开式的通项公式为,
令,得,
所以展开式中含项的系数是.
故选B.
3.
【解析】解:命题“,”为假命题,
命题“,”为真命题,
,解得,
所以实数的取值范围是
故选D.
4.A
【解析】解:由X~N(96,144),+2=96+24=120,-2=96-24=72,
则P(72< X<120)=0.9545,
故P(X120)==0.02275,100000.02275=227.5228,
故小明的数学成绩在本次抽测的名次大约是第228名.
故选:A.
5.
【解析】解:当时,,满足充分性;
当时,即,
即,则有或,不满足必要性;
故“”是“”的充分不必要条件.
故选B.
6.
【解析】解:由于天平的两臂不等长,故可设天平的左臂长为,右臂长为 , .
由杠杆原理得 , ,解得 , ,
则 ,当且仅当 取等号.
又 ,故 ,
故选A.
7.
【解析】解:四人去看三部电影,每人只看一部电影,则不同的选择共有种.
四人只看其中两部电影热辣滚烫和飞驰人生,
每人只看一部电影,则不同的选择共有种.
则这四名同学不同的观影情况种数为,
故选:.
8.
【解析】解:由可得,
令,
则,
当或时,,当时,,
故在,上单调递减,在上单调递增,
故在取得极小值,,在处取得极大值,,
而时,恒有成立,方程恰有三个不相等的实根,
即曲线与直线恰有三个不相等的交点,与直线图象如下,
由图知,当时,曲线与直线恰有三个不相等的实根
故选:
9.
【解析】解:对于,令,则,故A正确
对于,令,则,
所以,故B错误
对于,二项式展开式的通项公式为,
令,得,
所以,故C错误
对于,令,则,
所以
,故D正确.
10.
【解析】解:对由,故B组数据比组数据的相关性更强,故A正确
对当时,,有,
故样本点的残差为,故B错误
对由,则,故,故C正确
对由,,则有,故D,故D正确.
故选:.
11.
【解析】解:由于,,若,则,不可能满足,故,则,
对于,,当且仅当,即取等号,
由于不满足,故等号取不到,即,A错误;
对于,由于由于不满足,故等号取不到,
因此,B正确;
对于,由,可得,
故,因此,由于,故等号取不到,即,C正确;
对于,由,可得,故由于不可能成立,故等号取不到,
因此,故,由选项B可知,则, D正确.
故选:
12.
【解析】解:,
则.
故答案为:.
13.
【解析】解:设事件表示“两道题全做对”,
若两个题目都有思路,则
若两个题目中一个有思路一个没有思路,则
故.
14.
【解析】解:由除以的余数为,除以的余数为,除以的余数为,
除以的余数为,除以的余数为,除以的余数为,
可知数字进行得到的哈希值为
除以的余数为的正整数可能为、、、,
除以的余数为的正整数可能为、、,
除以的余数为的正整数可能为、、,
则对一个正整数进行后得到哈希值为,
则这样的正整数共有个.
故答案为:.
15.解:由函数,
可得,且,
因为曲线在处与直线相切,
可得,解得,;
解:由知,
可得其定义域为且,
当时,当时,,
所以函数在上单调递增,在单调递减,
当时,函数取得极大值,也是最大值.
【解析】由题意得,且,联立得出的值;
先利用导数研究单调性,可得的最大值.
16.解:由题,解得,
平均值:;
人;
按比例分层抽样,酒精浓度为和人员抽样比例为,
则共抽人中,酒精浓度为的有人,酒精浓度为的有人,
则所求概率为:.
【解析】由题解得,即可求解平均值;
根据求解即可;
按比例分层抽样,酒精浓度为和人员抽样比例为,则共抽人中,酒精浓度为的有人,酒精浓度为的有人,即可求解.
17.解:得列联表如下:
材料 材料 合计
试验成功单位:次
试验失败单位:次
合计
零假设为试验结果与材料无关计算可得,
依据的独立性检验,推断不成立,即认为试验结果与材料有关.
生产吨石墨烯发热膜所需的修复费用为万元.
易知的可能取值为,,,,,,
,
,
,
,则的分布列为
修复费用的期望.石墨烯发热膜的定价至少为万元吨,才能实现预期的利润目标.
【解析】先得出列联表,由公式得出,对照临界值表可得结论;
易知的可能取值为,,,,,得出对应概率,可得的分布列及数学期望;
得出石墨烯发热膜的定价,可得结论.
18.解:
,
所以.
家庭中女士不同意参与规划管理的概率为,男士不同意参与规划管理的概率为,男女是否同意参与规划管理相互独立,
设不同意参与规划管理为事件,设有女士不同意参与规划管理为事件,
,
若在抽查中发现家不同意参与规划管理,设其中至少家有女士不同意参与规划管理为事件.
【解析】先求出样本中心点,再结合公式计算得出回归方程即可
先应用条件概率求出概率,再应用次独立重复实验求出概率即得.
19.解:函数的定义域为,,
在上单调递增,在上恒成立,在上恒成立,
设,,
由解得,故在单调递减,在单调递增,
实数的取值范围是.
依题意,,则,两式相除得,,设,则,,,,,
,
设,则,设,则在单调递增,则
,则在单调递增,
,,所以
【解析】由题意知在上恒成立,利用导数研究函数的最小值即可求出的取值范围;
存在两个极值点,,所以,构造函数,利用导数研究它的单调性即可解答.
第1页,共1页
数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.若的展开式中二项式系数之和为,则展开式中含项的系数为( )
A. B. C. D.
3.若命题“,”为假命题,则实数的取值范围是( )
A. B. C. D.
4.某次高二质量抽测中,学生的数学成绩X服从正态分布N(96,144).已知参加本次考试的学生约有10000人,如果小明在这次考试中数学成绩为120分,则小明的数学成绩在本次抽测的名次大约是( ) 附:若X~N(,),则P(-< X<+)=0.6827,P(-2< X<+2)=0.9545
A. 第228名 B. 第455名 C. 第1587名 D. 第3173名
5.若,则“”是“”的( )
A. 充要条件 B. 充分不必要条件
C. 必要不充分条件 D. 既不充分也不必要条件
6.阿基米德有句名言:“给我一个支点,我就能撬起整个地球”这句话说的使是杠杆原理,即“动力动力臂阻力阻力臂”现有一商店使用两臂不等长的天平称黄金,一位顾客到店里预购买黄金,售货员先将的砝码放在天平左盘中,取出黄金放在天平右盘中使天平平衡再将的砝码放在天平右盘中,取黄金放在天平左盘中使天平平衡,最后将称得的和黄金交给顾客,则顾客购得的黄金重量( )
A. 大于 B. 等于 C. 小于 D. 无法确定
7.春节期间,第二十条、热辣滚烫和飞驰人生三部电影引爆了电影市场某班有四名同学都要观看电影并且每人只能选择这三部中的一部电影观看,如果他们中有同学选择观看第二十条,则这四名同学不同的观影情况种数为( )
A. B. C. D.
8.若方程恰有三个不相等的实根,则的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.若,,则下列结论正确的是( )
A.
B.
C.
D.
10.下列说法正确的有( )
A. 若,两组成对数据的样本相关系数分别为,,则组数据比组数据的相关性更强
B. 若关于的经验回归方程为,则样本点的残差为
C. 已知随机变量服从二项分布,若,则
D. 已知随机变量~N(2,81),若=3+1,则D()=9
11.已知,且,则下列结论正确的是( )
A. B. C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.已知,则 .
13.某同学参加学校组织的数学知识竞赛,在道四选一的单选题中,有道有思路,有道完全没有思路,有思路的题每道做对的概率均为,没有思路的题只好任意猜一个答案若从这道题中任选题作答,则该同学道题都做对的概率为 .
14.哈希算法是一种特殊的函数,也是一种加密技术已知是最简单的哈希算法之一,它把一个较大数字的每一位改成它除以素数所得到的余数例如:对于数字进行得到的哈希值为,那么对于数字进行得到的哈希值为 现对一个正整数进行后得到哈希值为,则这样的正整数共有 个用数字作答
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知函数,,若在处与直线相切.
求,的值
求的最大值.
16.本小题分
喝酒不开车,开车不喝酒根据中华人民共和国道路交通安全法规定:血液酒精浓度在含以上认定为醉酒驾车某地统计近年来查处的醉酒驾车共人,这人血液酒精浓度检测结果按,,,分组,得到如图所示的频率分布直方图.
求这人血液酒精浓度的平均值同一组数据用该区间中点值作为代表
求这人中血液酒精浓度在的人数
按比例分配分层随机抽样的方法,在酒精浓度为和人员中随机抽取人集中学习现从这人中抽取人检查学习效果,求抽到的人员恰有人酒精浓度为的概率.
17.本小题分
从石墨中通过化学气相沉积法分离出石墨烯,升华后附着在材料上再结晶制成石墨烯发热膜。石墨烯发热膜轻薄、保暖,广泛应用于冬装衣服。现在有材料、材料可供选择,研究人员对附着在材料、材料上的石墨烯各做了次再结晶试验,得到如下等高堆积条形图.
根据等高堆积条形图,填写如下列联表,并依据的独立性检验,分析试验结果与材料是否有关
材料 材料 合计
试验成功单位:次
试验失败单位:次
合计
研究人员得到石墨烯后再制作石墨烯发热膜有三个环节:环节一透明基底及胶层环节二石墨烯层环节三表面封装层第一、二环节生产合格的概率均为,第二环节生产合格的概率为,且各生产环节相互独立已知生产吨不墨烯发热膜的固定成本为万元,若生产不合格还需进行修复,第三环节的修复费用为万元,其余环节修复费用均为万元.
记生产吨石墨烯发热膜所需的修复费用为万元,求的分布列及数学期望最后结果保留一位小数
试问如何定价,才能实现每生产吨石墨烯发热膜获利不低于万元的目标
附:,其中.
18.本小题分
为促进农村经济发展,鼓励土地承包规划管理已知土地的使用面积与相应规划管理时间具有线性相关关系,随机调查某村户村民,经计算得到如下一些统计量的值:
,,,.
求关于的经验回归方程
调查发现,家庭中女士不同意参与规划管理的概率为,男士不同意参与规划管理的概率为,男女是否同意参与规划管理相互独立只要有一方不同意参与规划管理,则该家庭就决定不参与规划管理若在抽查中发现家不同意参与规划管理,求其中至少家有女士不同意参与规划管理的概率.
参考公式:对于一组数据,,,,其经验回归方程的斜率和截距的最小二乘法估计公式分别为,.
19.本小题分
已知函数.
若函数在上单调递增,求实数的取值范围
若函数恰有两个极值点,,且的最大值为,求证:.
答案解析
1.
【解析】解:因为,
所以,
又,
所以
故选C.
2.
【解析】解:因为二项式的所有二项式系数之和等于,
所以,解得,
二项展开式的通项公式为,
令,得,
所以展开式中含项的系数是.
故选B.
3.
【解析】解:命题“,”为假命题,
命题“,”为真命题,
,解得,
所以实数的取值范围是
故选D.
4.A
【解析】解:由X~N(96,144),+2=96+24=120,-2=96-24=72,
则P(72< X<120)=0.9545,
故P(X120)==0.02275,100000.02275=227.5228,
故小明的数学成绩在本次抽测的名次大约是第228名.
故选:A.
5.
【解析】解:当时,,满足充分性;
当时,即,
即,则有或,不满足必要性;
故“”是“”的充分不必要条件.
故选B.
6.
【解析】解:由于天平的两臂不等长,故可设天平的左臂长为,右臂长为 , .
由杠杆原理得 , ,解得 , ,
则 ,当且仅当 取等号.
又 ,故 ,
故选A.
7.
【解析】解:四人去看三部电影,每人只看一部电影,则不同的选择共有种.
四人只看其中两部电影热辣滚烫和飞驰人生,
每人只看一部电影,则不同的选择共有种.
则这四名同学不同的观影情况种数为,
故选:.
8.
【解析】解:由可得,
令,
则,
当或时,,当时,,
故在,上单调递减,在上单调递增,
故在取得极小值,,在处取得极大值,,
而时,恒有成立,方程恰有三个不相等的实根,
即曲线与直线恰有三个不相等的交点,与直线图象如下,
由图知,当时,曲线与直线恰有三个不相等的实根
故选:
9.
【解析】解:对于,令,则,故A正确
对于,令,则,
所以,故B错误
对于,二项式展开式的通项公式为,
令,得,
所以,故C错误
对于,令,则,
所以
,故D正确.
10.
【解析】解:对由,故B组数据比组数据的相关性更强,故A正确
对当时,,有,
故样本点的残差为,故B错误
对由,则,故,故C正确
对由,,则有,故D,故D正确.
故选:.
11.
【解析】解:由于,,若,则,不可能满足,故,则,
对于,,当且仅当,即取等号,
由于不满足,故等号取不到,即,A错误;
对于,由于由于不满足,故等号取不到,
因此,B正确;
对于,由,可得,
故,因此,由于,故等号取不到,即,C正确;
对于,由,可得,故由于不可能成立,故等号取不到,
因此,故,由选项B可知,则, D正确.
故选:
12.
【解析】解:,
则.
故答案为:.
13.
【解析】解:设事件表示“两道题全做对”,
若两个题目都有思路,则
若两个题目中一个有思路一个没有思路,则
故.
14.
【解析】解:由除以的余数为,除以的余数为,除以的余数为,
除以的余数为,除以的余数为,除以的余数为,
可知数字进行得到的哈希值为
除以的余数为的正整数可能为、、、,
除以的余数为的正整数可能为、、,
除以的余数为的正整数可能为、、,
则对一个正整数进行后得到哈希值为,
则这样的正整数共有个.
故答案为:.
15.解:由函数,
可得,且,
因为曲线在处与直线相切,
可得,解得,;
解:由知,
可得其定义域为且,
当时,当时,,
所以函数在上单调递增,在单调递减,
当时,函数取得极大值,也是最大值.
【解析】由题意得,且,联立得出的值;
先利用导数研究单调性,可得的最大值.
16.解:由题,解得,
平均值:;
人;
按比例分层抽样,酒精浓度为和人员抽样比例为,
则共抽人中,酒精浓度为的有人,酒精浓度为的有人,
则所求概率为:.
【解析】由题解得,即可求解平均值;
根据求解即可;
按比例分层抽样,酒精浓度为和人员抽样比例为,则共抽人中,酒精浓度为的有人,酒精浓度为的有人,即可求解.
17.解:得列联表如下:
材料 材料 合计
试验成功单位:次
试验失败单位:次
合计
零假设为试验结果与材料无关计算可得,
依据的独立性检验,推断不成立,即认为试验结果与材料有关.
生产吨石墨烯发热膜所需的修复费用为万元.
易知的可能取值为,,,,,,
,
,
,
,则的分布列为
修复费用的期望.石墨烯发热膜的定价至少为万元吨,才能实现预期的利润目标.
【解析】先得出列联表,由公式得出,对照临界值表可得结论;
易知的可能取值为,,,,,得出对应概率,可得的分布列及数学期望;
得出石墨烯发热膜的定价,可得结论.
18.解:
,
所以.
家庭中女士不同意参与规划管理的概率为,男士不同意参与规划管理的概率为,男女是否同意参与规划管理相互独立,
设不同意参与规划管理为事件,设有女士不同意参与规划管理为事件,
,
若在抽查中发现家不同意参与规划管理,设其中至少家有女士不同意参与规划管理为事件.
【解析】先求出样本中心点,再结合公式计算得出回归方程即可
先应用条件概率求出概率,再应用次独立重复实验求出概率即得.
19.解:函数的定义域为,,
在上单调递增,在上恒成立,在上恒成立,
设,,
由解得,故在单调递减,在单调递增,
实数的取值范围是.
依题意,,则,两式相除得,,设,则,,,,,
,
设,则,设,则在单调递增,则
,则在单调递增,
,,所以
【解析】由题意知在上恒成立,利用导数研究函数的最小值即可求出的取值范围;
存在两个极值点,,所以,构造函数,利用导数研究它的单调性即可解答.
第1页,共1页
同课章节目录
