2023-2024学年宁夏银川市第二中学高一下学期期末考试数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年宁夏银川市第二中学高一下学期期末考试数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 436.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 17:21:14 | ||
图片预览




文档简介
2023-2024学年宁夏银川市第二中学高一下学期期末考试数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,则 .
A. B. C. D.
2.已知向量,,则( )
A. B. C. D.
3.若为两条不同的直线,为一个平面,则下列结论中正确的是( )
A. 若,,则 B. 若,则
C. 若,则 D. 若,则与相交
4.某农业研究部门在面积相等的块稻田上种植一种新型水稻,得到各块稻田的亩产量单位:并整理下表:
据表中数据,结论中正确的是( )
亩产量
频数
A. 块稻田亩产量中位数小于
B. 块稻田中的亩产量低于的稻田所占比例超过
C. 块稻田亩产量的极差介于至之间
D. 块稻田亩产量的平均值介于至之间
5.如图,矩形是水平放置的一个平面图形由斜二测画法得到的直观图,其中,则原图形的面积为( )
A. B. C. D.
6.某学校举办作文比赛,共个主题,每位参赛同学从中随机抽取一个主题准备作文,则甲、乙两位参赛同学抽到不同主题概率为( )
A. B. C. D.
7.在中,,则( )
A. B. C. D.
8.连掷两次骰子得到的点数分别为和,记向量与向量的夹角为,则的概率是( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
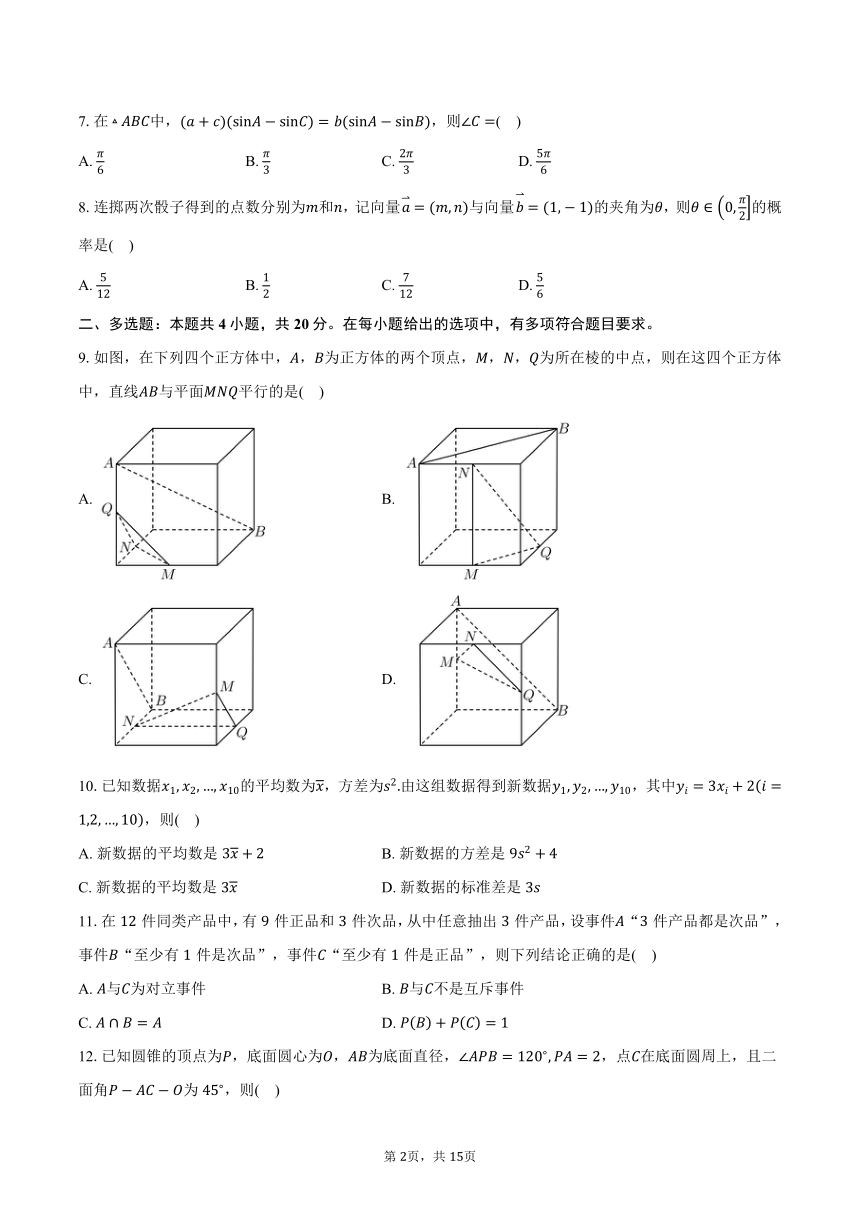
9.如图,在下列四个正方体中,,为正方体的两个顶点,,,为所在棱的中点,则在这四个正方体中,直线与平面平行的是( )
A. B.
C. D.
10.已知数据的平均数为,方差为由这组数据得到新数据,其中,则( )
A. 新数据的平均数是 B. 新数据的方差是
C. 新数据的平均数是 D. 新数据的标准差是
11.在件同类产品中,有件正品和件次品,从中任意抽出件产品,设事件“件产品都是次品”,事件“至少有件是次品”,事件“至少有件是正品”,则下列结论正确的是( )
A. 与为对立事件 B. 与不是互斥事件
C. D.
12.已知圆锥的顶点为,底面圆心为,为底面直径,,点在底面圆周上,且二面角为,则( )
A. 该圆锥的体积为 B. 该圆锥的侧面积为
C. D. 的面积为
三、填空题:本题共4小题,每小题5分,共20分。
13.已知某学校共有高中生名,为了解学生的视力情况,按男生女生比例用分层随机抽样的方法从该校高中生中抽取一个容量为的样本,其中男生有人,根据样本可以估计该校高中生中女生的人数为 .
14.甲和乙两个箱子中各装有个球,其中甲箱子中有个红球、个白球,乙箱子中有个红球、个白球,现随机选择一个箱子,然后从该箱子中随机取出一个球,则取出的球是白球的概率为 .
15.在正四棱台中,,,,则该棱台的体积为
16.设,为单位向量,满足,,,设,的夹角为,则的最小值为 .
四、解答题:本题共6小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
为探究某药物对小鼠的生长抑制作用,将只小鼠均分为两组:对照组不加药物和实验组加药物测得只小鼠体重单位:如下:
对照组:
实验组:
对照组和实验组的小鼠体重的样本平均数分别记为和,样本方差分别记为和.
求,,,;
判断该药物对小鼠的生长是否有显著的抑制作用若,则认为该药物对小鼠的生长有显著的抑制作用,否则不认为有显著的抑制作用.
18.本小题分
已知的内角,,所对的边分别为,,,向量,,且.
求角;
若,,求的面积.
19.本小题分
如图为正四棱锥为底面的中心.
若,求绕旋转一周形成的几何体的体积;
若为的中点,求直线与平面所成角的大小.
20.本小题分
年中国全名健身走跑大赛四川射洪站城市联动接力赛在射洪市举行,志愿者的服务工作是城市联动接力赛成功举办的重要保障,射洪市新时代文明实践中心承办了志愿者选拔的面试工作现随机抽取了名候选者的面试成绩,并分成五组:第一组,第二组,第三组,第四组,第五组,绘制成如图所示的频率分布直方图已知第一、二组的频率之和为,第一组和第五组的频率相同.
求,的值;
估计这名候选者面试成绩的平均数和第百分位数;
现从以上各组中用分层随机抽样的方法选取人,担任本市的宣传者若本市宣传者中第二组面试者的面试成绩的平均数和方差分别为和,第四组面试者的面试成绩的平均数和方差分别为和,据此估计这次第二组和第四组所有面试者的面试成绩的方差.
21.本小题分
如图,四棱锥中,底面,,,.
若,证明:平面
若,且二面角的正弦值为,求.
22.本小题分
甲、乙、丙三人进行台球比赛,比赛规则如下:先由两人上场比赛,第三人旁观,一局结束后,败者下场作为旁观者,原旁观者上场与胜者比赛,按此规则循环下去若比赛中有人累计获胜局,则该人获得最终胜利,比赛结束,三人经过抽签决定由甲、乙先上场比赛,丙作为旁观者根据以往经验,每局比赛中,甲、乙比赛甲胜概率为,乙、丙比赛乙胜概率为,丙、甲比赛丙胜概率为,每局比赛相互独立且每局比赛没有平局.
比赛完局时,求甲、乙、丙各旁观局的概率;
已知比赛进行局后结束,求甲获得最终胜利的概率.
答案解析
1.
【解析】解: .
2.
【解析】解:,,.
.
3.
【解析】解:对于,若,,则平行或异面,故 A错误.
对于,若,则平行或异面或相交,故 B错误.
对于,,过作平面,使得,
因为,故,而,故,故,故 C正确.
对于,若,则与相交或异面,故 D错误.
故选:.
4.
【解析】解:对于:
,,
所以中位数位于区间内,中位数不小于,A错误;
对于:块稻田中的亩产量低于的稻田所占比例为,B错误;
对于:设块稻田亩产量的极差为,则,即,C正确;
对于:设块稻田亩产量的极差为,则
,D错误.
5.
【解析】依题意,矩形的面积为,
而水平放置的平面图形的直观图面积是原图形面积的,
所以原图形面积为.
故选:
6.
【解析】解:设六个主题作文分别编号为,,,,,,
甲乙两位同学抽主题的情况有
,,,,,,
,,
,,,,,
共有种,
而甲乙主题不同的共有种,
所以所求概率.
故选
7.
【解析】解:因为,
所以由正弦定理得,即,
则,故,
又,所以.
故选:.
8.
【解析】,即,
事件“”所包含的基本事件有:、、、、、、、、、、、、、、、、、、、、,共个,
所有的基本事件数为,因此,事件“”的概率为.
故选:.
9.
【解析】解:对于,如图,
为底面对角线的交点,可得,
又平面,所以直线与平面不平行,错误;
对于,由于,平面,平面,所以平面,正确;
对于,由于,平面,平面,所以平面,正确;
对于,由于,平面,平面,所以平面,正确;
故答案为:.
10.
【解析】由题意得,
由平均数与方差公式得的平均数是,
方差是,标准差是,故 AD正确,BC错误
故选:
11.
【解析】从中任意抽出件产品,共有种情况:件产品都是次品,件次品件正品,件次品件正品,件产品都是正品.
事件的可能情况有:件产品都是次品,件次品件正品,件次品件正品,
事件的可能情况有:件次品件正品,件次品件正品,件产品都是正品.
与为对立事件,故 A正确;
件次品件正品,件次品件正品,则与不是互斥事件,故 B正确;
,,故 C正确;
由上知,故 D错误.
故选:
12.
【解析】解:对于:在中,,则,,
故圆锥的体积,故 A正确;
对于:圆锥的侧面展开图为扇形,扇形的半径为,弧长为,
故圆锥的侧面积为,故 B错误;
对于:取中点,连接,则,
则为二面角的平面角,即,
在中,,故,
在中,,故,故 C正确;
对于:,故 D错误
故选AC.
13.
【解析】根据题意,样本中女生有人,
所以,解得,
故估计该校高中生中女生的人数为.
故答案为:
14.或
【解析】依题意,取出的球是白球的事件是取甲箱并取白球的事件与取乙箱并取白球的事件的和,
显然事件与互斥,,,
所以.
故答案为:
15.
【解析】解:如图,
将正四棱台补成正四棱锥,则,
,,故,
.
16.
【解析】解:,为单位向量,则,即,
,得,
令,
,
,
,
,
,
由,则,即,得,
,即.
故答案为:.
17.解:
,
,
,
.
,
,
所以,所以没有显著的抑制作用.
【解析】根据平均数和方差等知识求得正确答案.
由“”,结合的结论进行判断.
18.解:因为,所以.
由正弦定理,得,
因为,所以.
又为的内角,
所以.
由余弦定理,得,即,
解得或舍去,
所以的面积.
【解析】根据平行向量的运用法则建立关系,利用正弦定理即可求角的大小.
由余弦定理,得,故由面积公式可得的面积.
19.解:由题意可知平面,由平面,则,
又正四棱锥底面是正方形,由可得,,
故,
根据圆锥的定义,可知绕旋转一周形成的几何体是以为轴,为底面半径的圆锥,
即圆锥的高为,底面半径为,
根据圆锥的体积公式可知圆锥的体积为.
连接,如图所示,
由,并结合正四棱锥的性质可知,正四棱锥的每个侧面都是等边三角形,
由是中点,则,,又,平面,
故平面,即平面,
又平面,于是直线与平面所成角的大小即为,
不妨设,则,,所以,
又直线与平面夹角的范围是,故,
所以直线与平面所成角的大小为.
【解析】由题意可知平面,则,可知绕旋转一周形成的几何体是以为轴,为底面半径的圆锥,先算出和的大小,再根据圆锥的体积公式即可得到答案;
连接,可先证平面,于是直线与平面所成角的大小即为,然后结合即可得到答案.
20.解:
,解得
可知每组的频率依次为:,,,,,
所以平均数为,
因为,
设第百分位数为,则,则,
解得,故第百分位数为.
设第二组、第四组面试者的面试成绩的平均数与方差分别为,且两组频率之比为,
则第二组和第四组所有面试者的面试成绩的平均数,
第二组和第四组所有面试者的面试成绩的方差
.
故估计第二组和第四组所有面试者的面试成绩的方差是.
【解析】根据频率分布直方图分别表示出各组的频率,由第一、二组的频率之和为及总的频率之和为列方程组解出,的值;
分别写出每一组的频率,由平均数计算公式得到平均数,根据频率和得到第百分位数所在的组,由概率和为解出第百分位数的值;
由第二组、第四组的频率之比得到分层抽样后两组人数所占比例,再结合两组各自的平均数和方差,由公式、分别求出两组所有面试者的方差.
21.证明:因为平面,平面,所以,
又因为,,平面,所以平面,
又平面,所以,
因为,,,,所以,
于是,又平面,平面.
所以平面.
因为,以为原点,分别以,,为,轴,过点作的平行线为轴,建立空间直角坐标系,
设,则,,,,,
设平面的一个法向量,因为,,
所以由,即,
可取;
又,,
设平面的一个法向量,所以由
取,
因为二面角的正弦值为,所以余弦值的绝对值为.
所以由,得,,
因此,.
【解析】首先证明平面,可得,进而证明,再根据线面平行的判定定理即可完成证明
在已知条件下,可以为原点,分别以,,为,轴,过点作的平行线为轴,建立空间直角坐标系,利用空间向量解决问题.
22.解:
由题可知,甲、乙、丙各旁观局只需讨论前两局的胜负情况,可分为:
甲胜乙、丙胜甲;乙胜甲,丙胜乙.
设甲、乙比赛甲胜,乙、丙比赛乙胜,丙、甲比赛丙胜分别为事件,,,则,,相互独立,
设比赛完局时,甲、乙、丙各旁观局为事件,则,
则,
所以甲、乙、丙各旁观局的概率为.
设甲、乙、丙第局比赛获胜分别为事件,,,,
设比赛完局甲获得最终胜利为事件,则
,
,
,
,
,
,
所以.
所以,已知比赛进行局后结束,甲获得最终胜利的概率为.
【解析】根据独立事件的概率公式进行求解即可;
分析比赛情况,根据和事件的概率公式进行求解即可.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,则 .
A. B. C. D.
2.已知向量,,则( )
A. B. C. D.
3.若为两条不同的直线,为一个平面,则下列结论中正确的是( )
A. 若,,则 B. 若,则
C. 若,则 D. 若,则与相交
4.某农业研究部门在面积相等的块稻田上种植一种新型水稻,得到各块稻田的亩产量单位:并整理下表:
据表中数据,结论中正确的是( )
亩产量
频数
A. 块稻田亩产量中位数小于
B. 块稻田中的亩产量低于的稻田所占比例超过
C. 块稻田亩产量的极差介于至之间
D. 块稻田亩产量的平均值介于至之间
5.如图,矩形是水平放置的一个平面图形由斜二测画法得到的直观图,其中,则原图形的面积为( )
A. B. C. D.
6.某学校举办作文比赛,共个主题,每位参赛同学从中随机抽取一个主题准备作文,则甲、乙两位参赛同学抽到不同主题概率为( )
A. B. C. D.
7.在中,,则( )
A. B. C. D.
8.连掷两次骰子得到的点数分别为和,记向量与向量的夹角为,则的概率是( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.如图,在下列四个正方体中,,为正方体的两个顶点,,,为所在棱的中点,则在这四个正方体中,直线与平面平行的是( )
A. B.
C. D.
10.已知数据的平均数为,方差为由这组数据得到新数据,其中,则( )
A. 新数据的平均数是 B. 新数据的方差是
C. 新数据的平均数是 D. 新数据的标准差是
11.在件同类产品中,有件正品和件次品,从中任意抽出件产品,设事件“件产品都是次品”,事件“至少有件是次品”,事件“至少有件是正品”,则下列结论正确的是( )
A. 与为对立事件 B. 与不是互斥事件
C. D.
12.已知圆锥的顶点为,底面圆心为,为底面直径,,点在底面圆周上,且二面角为,则( )
A. 该圆锥的体积为 B. 该圆锥的侧面积为
C. D. 的面积为
三、填空题:本题共4小题,每小题5分,共20分。
13.已知某学校共有高中生名,为了解学生的视力情况,按男生女生比例用分层随机抽样的方法从该校高中生中抽取一个容量为的样本,其中男生有人,根据样本可以估计该校高中生中女生的人数为 .
14.甲和乙两个箱子中各装有个球,其中甲箱子中有个红球、个白球,乙箱子中有个红球、个白球,现随机选择一个箱子,然后从该箱子中随机取出一个球,则取出的球是白球的概率为 .
15.在正四棱台中,,,,则该棱台的体积为
16.设,为单位向量,满足,,,设,的夹角为,则的最小值为 .
四、解答题:本题共6小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
为探究某药物对小鼠的生长抑制作用,将只小鼠均分为两组:对照组不加药物和实验组加药物测得只小鼠体重单位:如下:
对照组:
实验组:
对照组和实验组的小鼠体重的样本平均数分别记为和,样本方差分别记为和.
求,,,;
判断该药物对小鼠的生长是否有显著的抑制作用若,则认为该药物对小鼠的生长有显著的抑制作用,否则不认为有显著的抑制作用.
18.本小题分
已知的内角,,所对的边分别为,,,向量,,且.
求角;
若,,求的面积.
19.本小题分
如图为正四棱锥为底面的中心.
若,求绕旋转一周形成的几何体的体积;
若为的中点,求直线与平面所成角的大小.
20.本小题分
年中国全名健身走跑大赛四川射洪站城市联动接力赛在射洪市举行,志愿者的服务工作是城市联动接力赛成功举办的重要保障,射洪市新时代文明实践中心承办了志愿者选拔的面试工作现随机抽取了名候选者的面试成绩,并分成五组:第一组,第二组,第三组,第四组,第五组,绘制成如图所示的频率分布直方图已知第一、二组的频率之和为,第一组和第五组的频率相同.
求,的值;
估计这名候选者面试成绩的平均数和第百分位数;
现从以上各组中用分层随机抽样的方法选取人,担任本市的宣传者若本市宣传者中第二组面试者的面试成绩的平均数和方差分别为和,第四组面试者的面试成绩的平均数和方差分别为和,据此估计这次第二组和第四组所有面试者的面试成绩的方差.
21.本小题分
如图,四棱锥中,底面,,,.
若,证明:平面
若,且二面角的正弦值为,求.
22.本小题分
甲、乙、丙三人进行台球比赛,比赛规则如下:先由两人上场比赛,第三人旁观,一局结束后,败者下场作为旁观者,原旁观者上场与胜者比赛,按此规则循环下去若比赛中有人累计获胜局,则该人获得最终胜利,比赛结束,三人经过抽签决定由甲、乙先上场比赛,丙作为旁观者根据以往经验,每局比赛中,甲、乙比赛甲胜概率为,乙、丙比赛乙胜概率为,丙、甲比赛丙胜概率为,每局比赛相互独立且每局比赛没有平局.
比赛完局时,求甲、乙、丙各旁观局的概率;
已知比赛进行局后结束,求甲获得最终胜利的概率.
答案解析
1.
【解析】解: .
2.
【解析】解:,,.
.
3.
【解析】解:对于,若,,则平行或异面,故 A错误.
对于,若,则平行或异面或相交,故 B错误.
对于,,过作平面,使得,
因为,故,而,故,故,故 C正确.
对于,若,则与相交或异面,故 D错误.
故选:.
4.
【解析】解:对于:
,,
所以中位数位于区间内,中位数不小于,A错误;
对于:块稻田中的亩产量低于的稻田所占比例为,B错误;
对于:设块稻田亩产量的极差为,则,即,C正确;
对于:设块稻田亩产量的极差为,则
,D错误.
5.
【解析】依题意,矩形的面积为,
而水平放置的平面图形的直观图面积是原图形面积的,
所以原图形面积为.
故选:
6.
【解析】解:设六个主题作文分别编号为,,,,,,
甲乙两位同学抽主题的情况有
,,,,,,
,,
,,,,,
共有种,
而甲乙主题不同的共有种,
所以所求概率.
故选
7.
【解析】解:因为,
所以由正弦定理得,即,
则,故,
又,所以.
故选:.
8.
【解析】,即,
事件“”所包含的基本事件有:、、、、、、、、、、、、、、、、、、、、,共个,
所有的基本事件数为,因此,事件“”的概率为.
故选:.
9.
【解析】解:对于,如图,
为底面对角线的交点,可得,
又平面,所以直线与平面不平行,错误;
对于,由于,平面,平面,所以平面,正确;
对于,由于,平面,平面,所以平面,正确;
对于,由于,平面,平面,所以平面,正确;
故答案为:.
10.
【解析】由题意得,
由平均数与方差公式得的平均数是,
方差是,标准差是,故 AD正确,BC错误
故选:
11.
【解析】从中任意抽出件产品,共有种情况:件产品都是次品,件次品件正品,件次品件正品,件产品都是正品.
事件的可能情况有:件产品都是次品,件次品件正品,件次品件正品,
事件的可能情况有:件次品件正品,件次品件正品,件产品都是正品.
与为对立事件,故 A正确;
件次品件正品,件次品件正品,则与不是互斥事件,故 B正确;
,,故 C正确;
由上知,故 D错误.
故选:
12.
【解析】解:对于:在中,,则,,
故圆锥的体积,故 A正确;
对于:圆锥的侧面展开图为扇形,扇形的半径为,弧长为,
故圆锥的侧面积为,故 B错误;
对于:取中点,连接,则,
则为二面角的平面角,即,
在中,,故,
在中,,故,故 C正确;
对于:,故 D错误
故选AC.
13.
【解析】根据题意,样本中女生有人,
所以,解得,
故估计该校高中生中女生的人数为.
故答案为:
14.或
【解析】依题意,取出的球是白球的事件是取甲箱并取白球的事件与取乙箱并取白球的事件的和,
显然事件与互斥,,,
所以.
故答案为:
15.
【解析】解:如图,
将正四棱台补成正四棱锥,则,
,,故,
.
16.
【解析】解:,为单位向量,则,即,
,得,
令,
,
,
,
,
,
由,则,即,得,
,即.
故答案为:.
17.解:
,
,
,
.
,
,
所以,所以没有显著的抑制作用.
【解析】根据平均数和方差等知识求得正确答案.
由“”,结合的结论进行判断.
18.解:因为,所以.
由正弦定理,得,
因为,所以.
又为的内角,
所以.
由余弦定理,得,即,
解得或舍去,
所以的面积.
【解析】根据平行向量的运用法则建立关系,利用正弦定理即可求角的大小.
由余弦定理,得,故由面积公式可得的面积.
19.解:由题意可知平面,由平面,则,
又正四棱锥底面是正方形,由可得,,
故,
根据圆锥的定义,可知绕旋转一周形成的几何体是以为轴,为底面半径的圆锥,
即圆锥的高为,底面半径为,
根据圆锥的体积公式可知圆锥的体积为.
连接,如图所示,
由,并结合正四棱锥的性质可知,正四棱锥的每个侧面都是等边三角形,
由是中点,则,,又,平面,
故平面,即平面,
又平面,于是直线与平面所成角的大小即为,
不妨设,则,,所以,
又直线与平面夹角的范围是,故,
所以直线与平面所成角的大小为.
【解析】由题意可知平面,则,可知绕旋转一周形成的几何体是以为轴,为底面半径的圆锥,先算出和的大小,再根据圆锥的体积公式即可得到答案;
连接,可先证平面,于是直线与平面所成角的大小即为,然后结合即可得到答案.
20.解:
,解得
可知每组的频率依次为:,,,,,
所以平均数为,
因为,
设第百分位数为,则,则,
解得,故第百分位数为.
设第二组、第四组面试者的面试成绩的平均数与方差分别为,且两组频率之比为,
则第二组和第四组所有面试者的面试成绩的平均数,
第二组和第四组所有面试者的面试成绩的方差
.
故估计第二组和第四组所有面试者的面试成绩的方差是.
【解析】根据频率分布直方图分别表示出各组的频率,由第一、二组的频率之和为及总的频率之和为列方程组解出,的值;
分别写出每一组的频率,由平均数计算公式得到平均数,根据频率和得到第百分位数所在的组,由概率和为解出第百分位数的值;
由第二组、第四组的频率之比得到分层抽样后两组人数所占比例,再结合两组各自的平均数和方差,由公式、分别求出两组所有面试者的方差.
21.证明:因为平面,平面,所以,
又因为,,平面,所以平面,
又平面,所以,
因为,,,,所以,
于是,又平面,平面.
所以平面.
因为,以为原点,分别以,,为,轴,过点作的平行线为轴,建立空间直角坐标系,
设,则,,,,,
设平面的一个法向量,因为,,
所以由,即,
可取;
又,,
设平面的一个法向量,所以由
取,
因为二面角的正弦值为,所以余弦值的绝对值为.
所以由,得,,
因此,.
【解析】首先证明平面,可得,进而证明,再根据线面平行的判定定理即可完成证明
在已知条件下,可以为原点,分别以,,为,轴,过点作的平行线为轴,建立空间直角坐标系,利用空间向量解决问题.
22.解:
由题可知,甲、乙、丙各旁观局只需讨论前两局的胜负情况,可分为:
甲胜乙、丙胜甲;乙胜甲,丙胜乙.
设甲、乙比赛甲胜,乙、丙比赛乙胜,丙、甲比赛丙胜分别为事件,,,则,,相互独立,
设比赛完局时,甲、乙、丙各旁观局为事件,则,
则,
所以甲、乙、丙各旁观局的概率为.
设甲、乙、丙第局比赛获胜分别为事件,,,,
设比赛完局甲获得最终胜利为事件,则
,
,
,
,
,
,
所以.
所以,已知比赛进行局后结束,甲获得最终胜利的概率为.
【解析】根据独立事件的概率公式进行求解即可;
分析比赛情况,根据和事件的概率公式进行求解即可.
第1页,共1页
同课章节目录
