2023-2024学年湖北省孝感市云梦县八年级(下)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年湖北省孝感市云梦县八年级(下)期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 127.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 21:37:52 | ||
图片预览



文档简介
2023-2024学年湖北省孝感市云梦县八年级(下)期末数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若在实数范围有意义,则的值可能是( )
A. B. C. D.
2.如果一个三角形的两条直角边为和,那么斜边长为( )
A. B. C. D. 或
3.某校举行“预防溺水,从我做起”演讲比赛,位评委给选手甲的评分如下:,,,,,,,则这组数据的众数和中位数分别是( )
A. , B. , C. , D. ,
4.如果一次函数的图象经过点,则的值为( )
A. B. C. D.
5.下列运算正确的是( )
A. B.
C. D.
6.如图,为平行四边形外一点,且,,若,则的度数为( )
A.
B.
C.
D.
7.关于正比例函数,下列结论正确的是( )
A. 图象必经过点 B. 图象经过第二、四象限
C. 随的增大而增大 D. 不论取何值,总有
8.如图,为正方形的对角线上一点,四边形为矩形,若正方形的边长为,则的长为( )
A.
B.
C.
D.
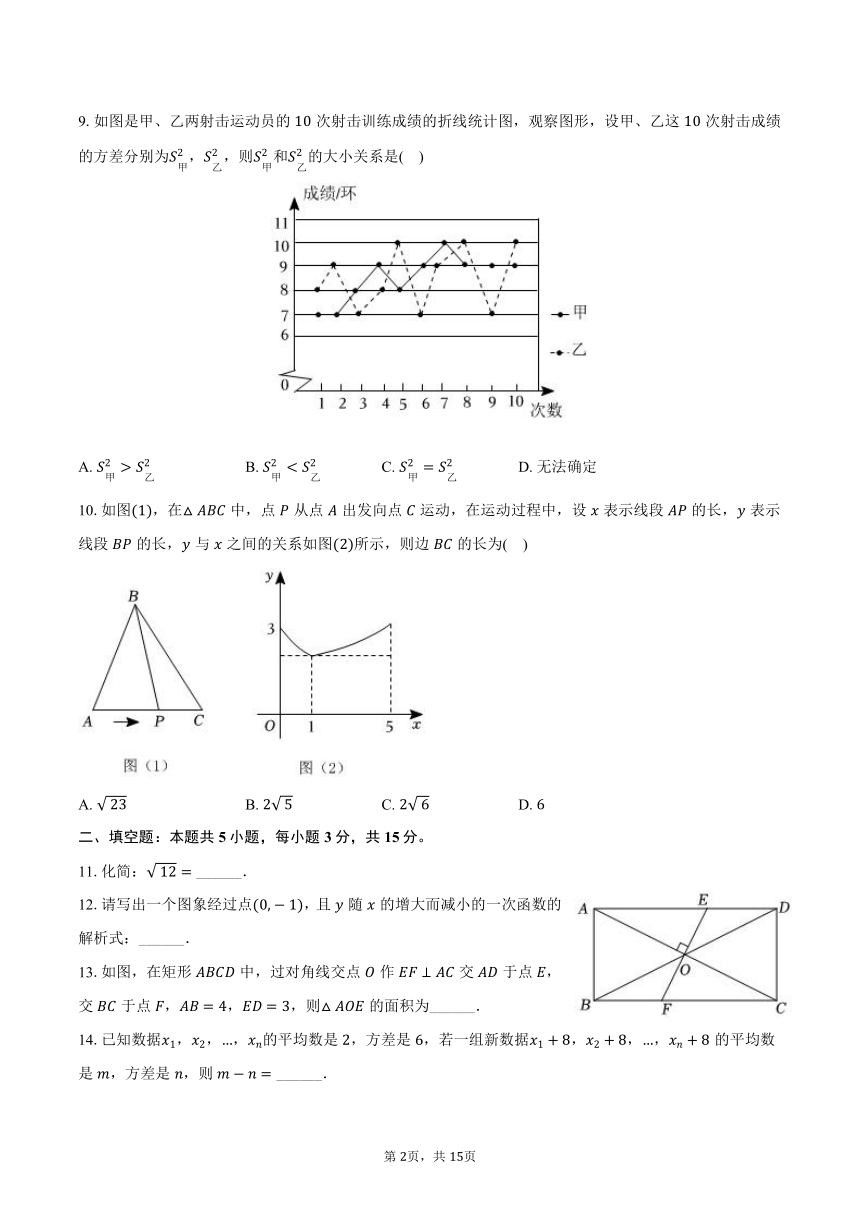
9.如图是甲、乙两射击运动员的次射击训练成绩的折线统计图,观察图形,设甲、乙这次射击成绩的方差分别为,,则和的大小关系是( )
A. B. C. D. 无法确定
10.如图,在中,点从点出发向点运动,在运动过程中,设表示线段的长,表示线段的长,与之间的关系如图所示,则边的长为( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
11.化简: ______.
12.请写出一个图象经过点,且随的增大而减小的一次函数的
解析式:______.
13.如图,在矩形中,过对角线交点作交于点,交于点,,,则的面积为______.
14.已知数据,,,的平均数是,方差是,若一组新数据,,,的平均数是,方差是,则 ______.
15.如图,在边长为的菱形中,,点是边的中点,连接,将菱形翻折,使点落在线段上的点处,折痕交于点,则线段的长为____________.
三、解答题:本题共9小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:
;
.
17.本小题分
如图:在平行四边形中,的平分线交于,若,,求的长.
18.本小题分
已知一次函数的图象过点与.
求出这个一次函数的解析式;
将此一次函数的图象向上平移个单位得到直线,若直线与轴交于点,求点的坐标.
19.本小题分
如图,已知四边形是平行四边形,对角线、交于点,是等边三角形.
求证:四边形是矩形;
若,求的长.
20.本小题分
如图,在四边形中,,是的中点,,,于点.
求证:四边形是菱形;
若,,求的长.
21.本小题分
为提高全校师生消防安全意识,崇文中学在校开展了“消防安全知识学习周”活动,并举行了全体学生消防安全知识竞赛学校从七,八两个年级中各随机抽取了名同学的竞赛成绩,对他们的竞赛成绩进行收集、整理、分析,过程如下:用表示成绩分数,满分分,共分为四个等级:等:,等:,等:,等:,其中等级为优秀,所有学生成绩都不低于分
收集数据:
七年级抽取的成绩中等学生人数是等学生人数的倍;
八年级抽取的成绩中等成绩为:,,,,,,,,
数据分析:
抽取的七,八年级学生竞赛成绩的平均数、中位数、众数、优秀人数如表所示:
七年级 八年级
平均数
中位数
众数
优秀人数
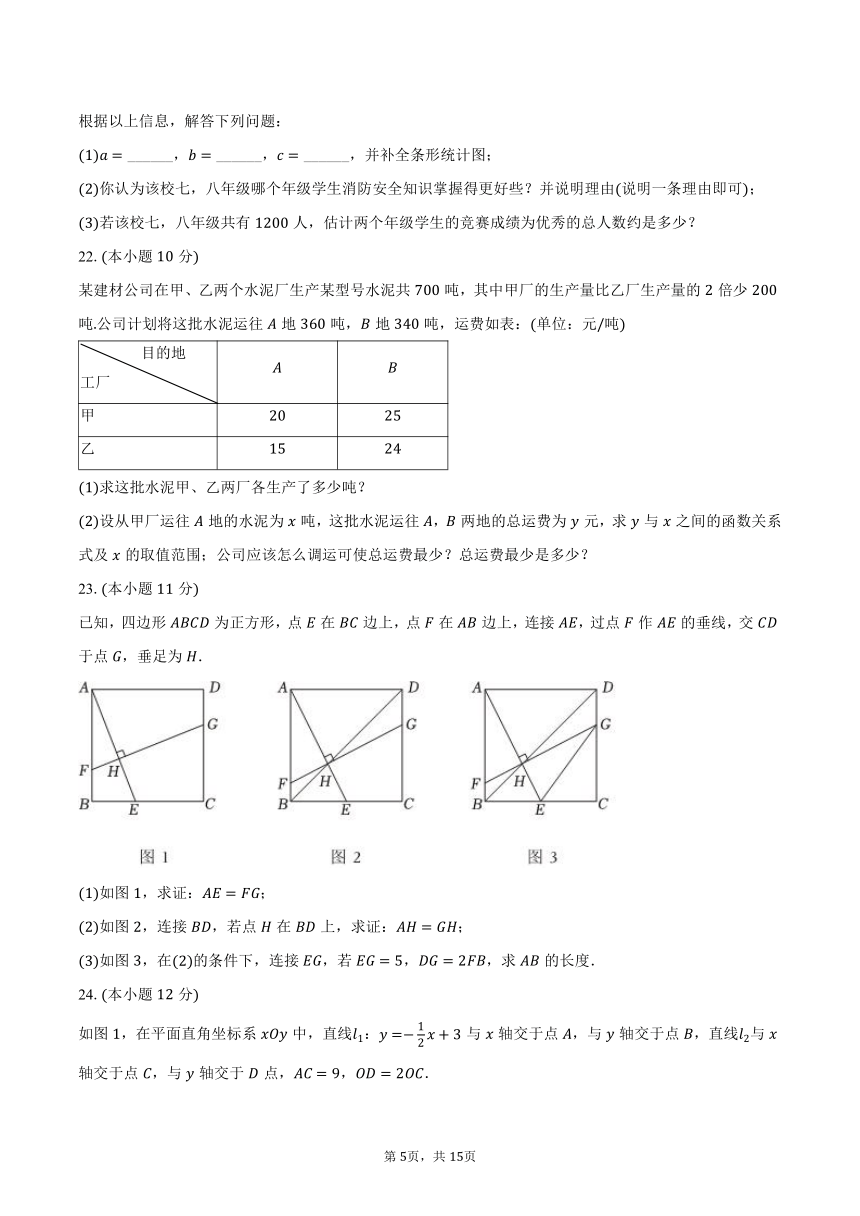
根据以上信息,解答下列问题:
______, ______, ______,并补全条形统计图;
你认为该校七,八年级哪个年级学生消防安全知识掌握得更好些?并说明理由说明一条理由即可;
若该校七,八年级共有人,估计两个年级学生的竞赛成绩为优秀的总人数约是多少?
22.本小题分
某建材公司在甲、乙两个水泥厂生产某型号水泥共吨,其中甲厂的生产量比乙厂生产量的倍少吨公司计划将这批水泥运往地吨,地吨,运费如表:单位:元吨
目的地
工厂
甲
乙
求这批水泥甲、乙两厂各生产了多少吨?
设从甲厂运往地的水泥为吨,这批水泥运往,两地的总运费为元,求与之间的函数关系式及的取值范围;公司应该怎么调运可使总运费最少?总运费最少是多少?
23.本小题分
已知,四边形为正方形,点在边上,点在边上,连接,过点作的垂线,交于点,垂足为.
如图,求证:;
如图,连接,若点在上,求证:;
如图,在的条件下,连接,若,,求的长度.
24.本小题分
如图,在平面直角坐标系中,直线:与轴交于点,与轴交于点,直线与轴交于点,与轴交于点,,.
求直线的解析式;
连接,点为直线上一动点,若有,求点的坐标;
点为直线上一点,点为轴上一点,若,,三点构成以为直角边的等腰直角三角形,求点的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.解:
;
.
17.解:四边形是平行四边形,,,
,,,
,
平分,
,
,
,
,
的长为.
18.解:设这个一次函数的解析式为,
图象过点与,
.
解得.
这个一次函数的解析式为.
将一次函数的图象向上平移个单位得到直线,
直线的表达式为,
由解得,
点的坐标为.
19.证明:四边形是平行四边形,
,.
是等边三角形,
,
,
四边形是矩形.
解:四边形是矩形,
.
是等边三角形,
,则,
.
20.证明:,,
四边形是平行四边形,
,是的中点,
,
四边形是菱形;
解:过作于点,如图所示
,,,
,
的面积,
,
点是的中点,四边形是菱形,
,
,
.
21.;;.
补全条形统计图如图所示.
我认为七年级学生知识竞赛成绩更好.
理由:七年级学生知识竞赛成绩的中位数为,大于八年级学生知识竞赛成绩的中位数,
所以七年级学生知识竞赛成绩更好.
人,
估计两个年级学生的竞赛成绩被评为优秀的总人数约人.
22.解:设这批水泥甲厂生产了吨,乙厂生产了吨,
由题意可得:,
解得:,
这批水泥甲厂生产了吨,乙厂生产了吨;
甲厂运往地的水泥为吨,
甲厂运往地的水泥为吨,乙厂运往地的水泥为吨,乙厂运往地的水泥为吨,
,
且,
解得,
,
随的增大而增大,
当时总运费最小为元,
此时,,,
公司从甲厂运往地水泥吨,运往地吨;乙厂生产的水泥吨全部运往地时,总运费最小,最小费用为元.
23.证明:如图,过点作于,则,
四边形为正方形,
,,
四边形为矩形,
,,
,
,
,
,
在和中,
,
≌,
;
证明:如图,作于,延长交于,则,
四边形为正方形,
,,
,
为等腰直角三角形,
四边形为矩形,,
,
,即,
,
,
,
,
,
在和中,
,
≌,
;
解:如图,
由可知≌,
,
又由可知,,
,
,
≌ ,
,
设,则,,,
,
,,
在中,由勾股定理得,
,
解得或不符合题意,舍去,
.
24.解:当时,,
.
当时,,
.
,
,
.
,
,
.
设直线的解析式为,
,
直线的解析式为;
解:设,
,
,
点在延长线上时,
则,
,在轴上方,
,
,
,
;
点在延长线上时,
则,
,在轴下方,
,
,
,
,
综上所述,点的坐标为或.
设点,
当时,如图,作于点,作于点.
.
,,
,
又
≌,
.
,
解得或,
或.
当时,如图过点作,作于点,作于点.
同理可证:≌,
,.
设
,
解得:或或舍
或.
综上所述,点的坐标为或或或.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若在实数范围有意义,则的值可能是( )
A. B. C. D.
2.如果一个三角形的两条直角边为和,那么斜边长为( )
A. B. C. D. 或
3.某校举行“预防溺水,从我做起”演讲比赛,位评委给选手甲的评分如下:,,,,,,,则这组数据的众数和中位数分别是( )
A. , B. , C. , D. ,
4.如果一次函数的图象经过点,则的值为( )
A. B. C. D.
5.下列运算正确的是( )
A. B.
C. D.
6.如图,为平行四边形外一点,且,,若,则的度数为( )
A.
B.
C.
D.
7.关于正比例函数,下列结论正确的是( )
A. 图象必经过点 B. 图象经过第二、四象限
C. 随的增大而增大 D. 不论取何值,总有
8.如图,为正方形的对角线上一点,四边形为矩形,若正方形的边长为,则的长为( )
A.
B.
C.
D.
9.如图是甲、乙两射击运动员的次射击训练成绩的折线统计图,观察图形,设甲、乙这次射击成绩的方差分别为,,则和的大小关系是( )
A. B. C. D. 无法确定
10.如图,在中,点从点出发向点运动,在运动过程中,设表示线段的长,表示线段的长,与之间的关系如图所示,则边的长为( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
11.化简: ______.
12.请写出一个图象经过点,且随的增大而减小的一次函数的
解析式:______.
13.如图,在矩形中,过对角线交点作交于点,交于点,,,则的面积为______.
14.已知数据,,,的平均数是,方差是,若一组新数据,,,的平均数是,方差是,则 ______.
15.如图,在边长为的菱形中,,点是边的中点,连接,将菱形翻折,使点落在线段上的点处,折痕交于点,则线段的长为____________.
三、解答题:本题共9小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:
;
.
17.本小题分
如图:在平行四边形中,的平分线交于,若,,求的长.
18.本小题分
已知一次函数的图象过点与.
求出这个一次函数的解析式;
将此一次函数的图象向上平移个单位得到直线,若直线与轴交于点,求点的坐标.
19.本小题分
如图,已知四边形是平行四边形,对角线、交于点,是等边三角形.
求证:四边形是矩形;
若,求的长.
20.本小题分
如图,在四边形中,,是的中点,,,于点.
求证:四边形是菱形;
若,,求的长.
21.本小题分
为提高全校师生消防安全意识,崇文中学在校开展了“消防安全知识学习周”活动,并举行了全体学生消防安全知识竞赛学校从七,八两个年级中各随机抽取了名同学的竞赛成绩,对他们的竞赛成绩进行收集、整理、分析,过程如下:用表示成绩分数,满分分,共分为四个等级:等:,等:,等:,等:,其中等级为优秀,所有学生成绩都不低于分
收集数据:
七年级抽取的成绩中等学生人数是等学生人数的倍;
八年级抽取的成绩中等成绩为:,,,,,,,,
数据分析:
抽取的七,八年级学生竞赛成绩的平均数、中位数、众数、优秀人数如表所示:
七年级 八年级
平均数
中位数
众数
优秀人数
根据以上信息,解答下列问题:
______, ______, ______,并补全条形统计图;
你认为该校七,八年级哪个年级学生消防安全知识掌握得更好些?并说明理由说明一条理由即可;
若该校七,八年级共有人,估计两个年级学生的竞赛成绩为优秀的总人数约是多少?
22.本小题分
某建材公司在甲、乙两个水泥厂生产某型号水泥共吨,其中甲厂的生产量比乙厂生产量的倍少吨公司计划将这批水泥运往地吨,地吨,运费如表:单位:元吨
目的地
工厂
甲
乙
求这批水泥甲、乙两厂各生产了多少吨?
设从甲厂运往地的水泥为吨,这批水泥运往,两地的总运费为元,求与之间的函数关系式及的取值范围;公司应该怎么调运可使总运费最少?总运费最少是多少?
23.本小题分
已知,四边形为正方形,点在边上,点在边上,连接,过点作的垂线,交于点,垂足为.
如图,求证:;
如图,连接,若点在上,求证:;
如图,在的条件下,连接,若,,求的长度.
24.本小题分
如图,在平面直角坐标系中,直线:与轴交于点,与轴交于点,直线与轴交于点,与轴交于点,,.
求直线的解析式;
连接,点为直线上一动点,若有,求点的坐标;
点为直线上一点,点为轴上一点,若,,三点构成以为直角边的等腰直角三角形,求点的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.解:
;
.
17.解:四边形是平行四边形,,,
,,,
,
平分,
,
,
,
,
的长为.
18.解:设这个一次函数的解析式为,
图象过点与,
.
解得.
这个一次函数的解析式为.
将一次函数的图象向上平移个单位得到直线,
直线的表达式为,
由解得,
点的坐标为.
19.证明:四边形是平行四边形,
,.
是等边三角形,
,
,
四边形是矩形.
解:四边形是矩形,
.
是等边三角形,
,则,
.
20.证明:,,
四边形是平行四边形,
,是的中点,
,
四边形是菱形;
解:过作于点,如图所示
,,,
,
的面积,
,
点是的中点,四边形是菱形,
,
,
.
21.;;.
补全条形统计图如图所示.
我认为七年级学生知识竞赛成绩更好.
理由:七年级学生知识竞赛成绩的中位数为,大于八年级学生知识竞赛成绩的中位数,
所以七年级学生知识竞赛成绩更好.
人,
估计两个年级学生的竞赛成绩被评为优秀的总人数约人.
22.解:设这批水泥甲厂生产了吨,乙厂生产了吨,
由题意可得:,
解得:,
这批水泥甲厂生产了吨,乙厂生产了吨;
甲厂运往地的水泥为吨,
甲厂运往地的水泥为吨,乙厂运往地的水泥为吨,乙厂运往地的水泥为吨,
,
且,
解得,
,
随的增大而增大,
当时总运费最小为元,
此时,,,
公司从甲厂运往地水泥吨,运往地吨;乙厂生产的水泥吨全部运往地时,总运费最小,最小费用为元.
23.证明:如图,过点作于,则,
四边形为正方形,
,,
四边形为矩形,
,,
,
,
,
,
在和中,
,
≌,
;
证明:如图,作于,延长交于,则,
四边形为正方形,
,,
,
为等腰直角三角形,
四边形为矩形,,
,
,即,
,
,
,
,
,
在和中,
,
≌,
;
解:如图,
由可知≌,
,
又由可知,,
,
,
≌ ,
,
设,则,,,
,
,,
在中,由勾股定理得,
,
解得或不符合题意,舍去,
.
24.解:当时,,
.
当时,,
.
,
,
.
,
,
.
设直线的解析式为,
,
直线的解析式为;
解:设,
,
,
点在延长线上时,
则,
,在轴上方,
,
,
,
;
点在延长线上时,
则,
,在轴下方,
,
,
,
,
综上所述,点的坐标为或.
设点,
当时,如图,作于点,作于点.
.
,,
,
又
≌,
.
,
解得或,
或.
当时,如图过点作,作于点,作于点.
同理可证:≌,
,.
设
,
解得:或或舍
或.
综上所述,点的坐标为或或或.
第1页,共1页
同课章节目录
